Optimization of Water Distribution Networks Using Genetic Algorithm Based SOP–WDN Program
Abstract
:1. Introduction
Background and Related Work
2. Materials and Methods
2.1. Problem Formulation
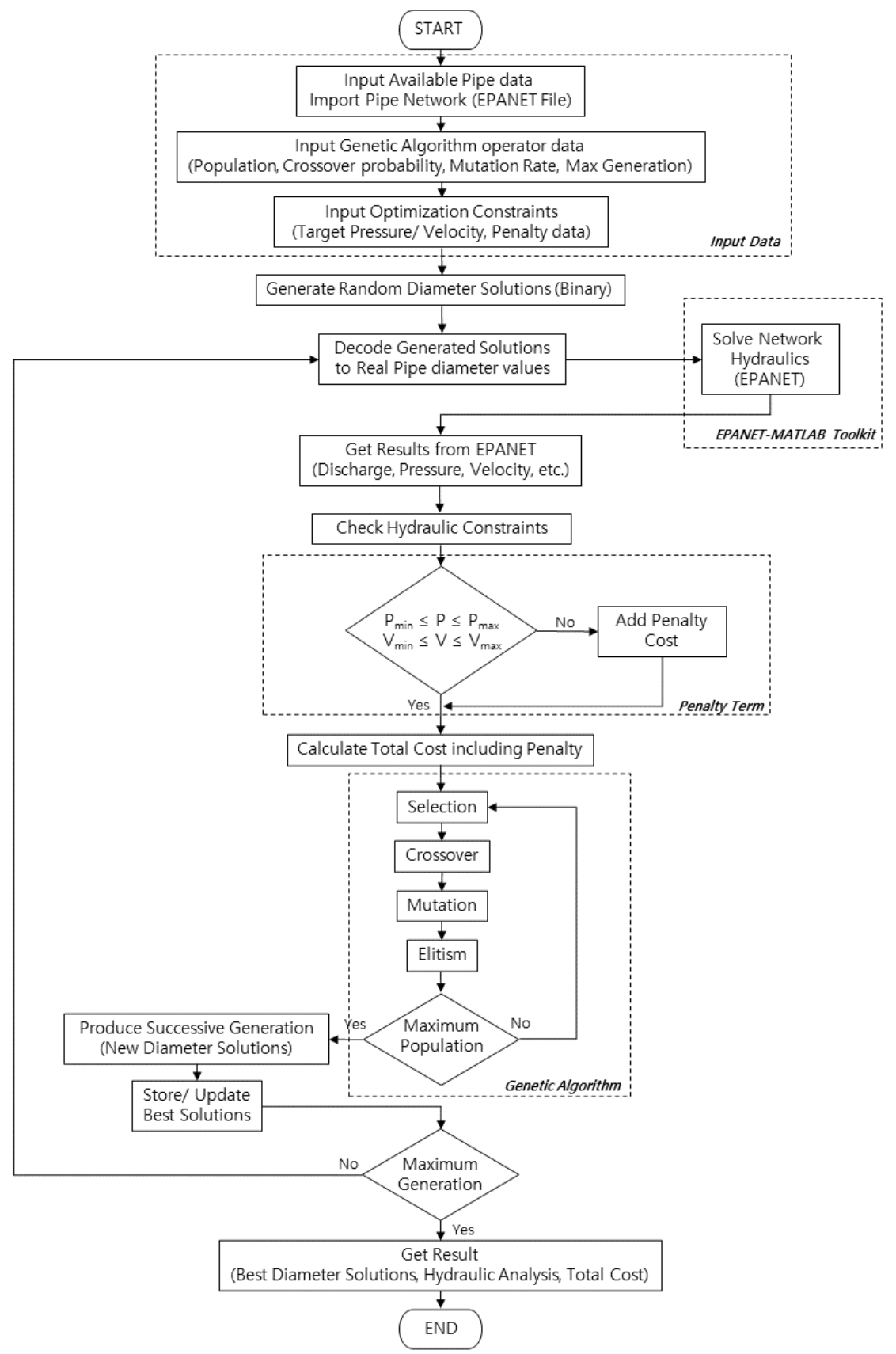
2.2. Genetic Algorithm
- 1.
- Generation of initial population
- 2.
- Computation of network cost
- 3
- Hydraulic analysis of each network
- 4.
- Computation of penalty cost
- 5.
- Computation of total network cost
- 6.
- Computation of the fitness
- 7.
- Generation of a new population using the selection operator
- 8.
- The crossover operator
- 9.
- The mutation operator
- 10.
- Production of successive generations
2.3. EPANET
2.4. SOP–WDN
2.4.1. Encoding Scheme, Interpretation and Redundancy
2.4.2. Genetic Algorithm Operators
- 1.
- Selection
- 2.
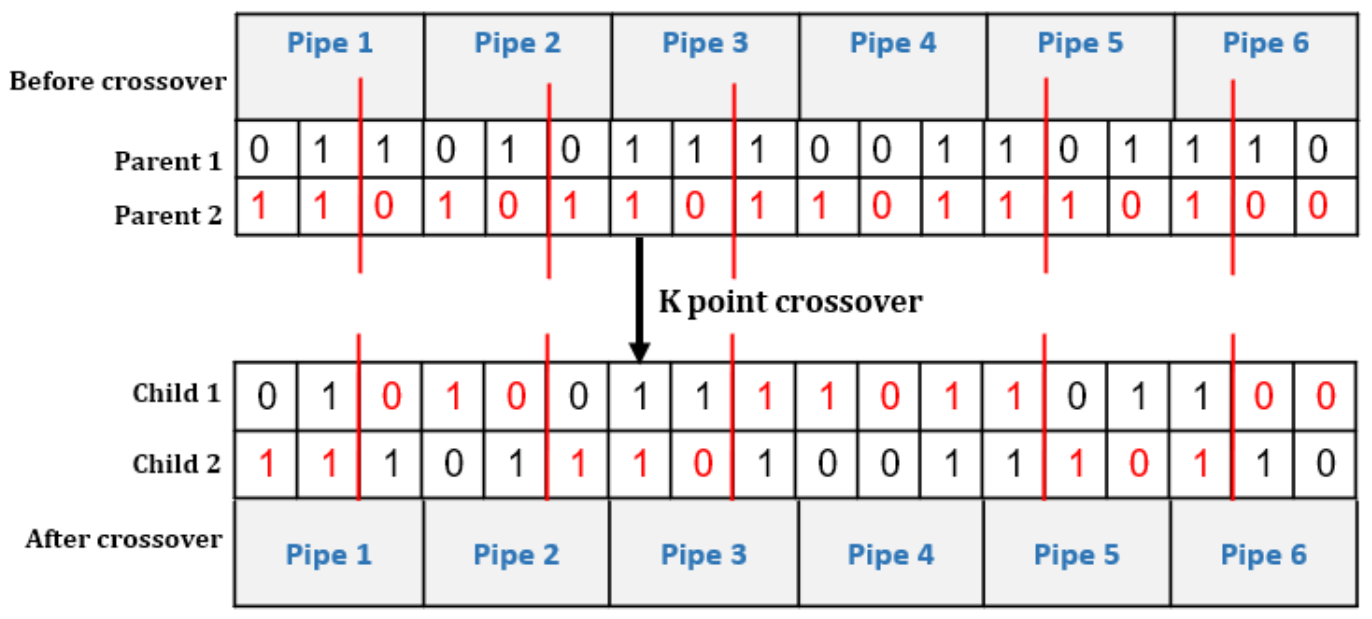
- Crossover
- 3.
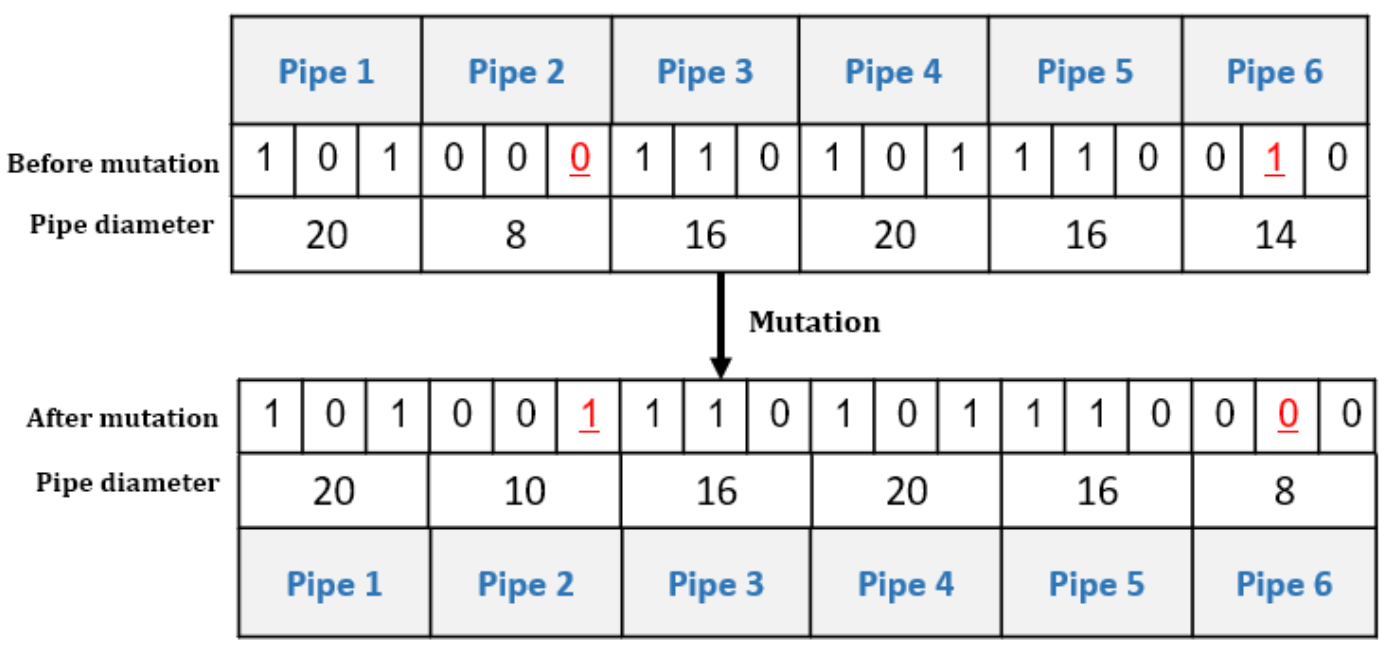
- Mutation
- 4.
- Elitism
2.4.3. Penalty Functions
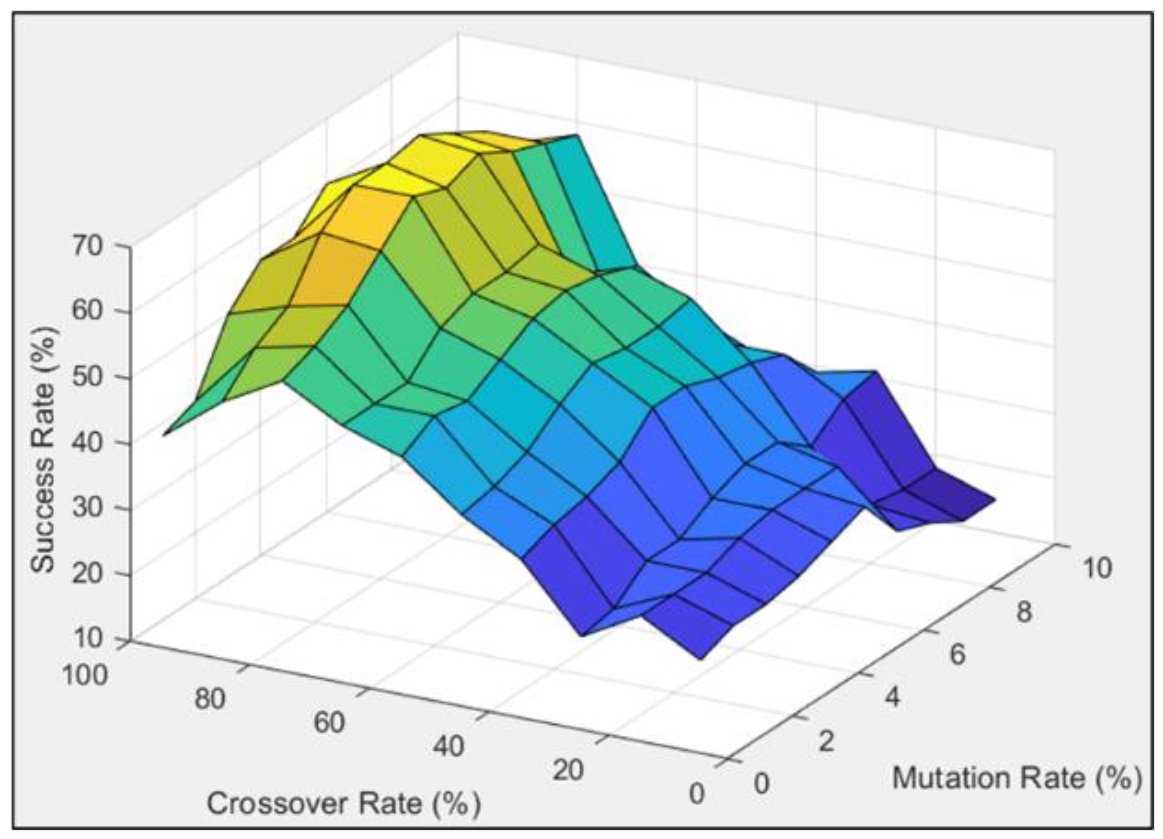
2.4.4. Sensitivity Analysis
- Population Size
- Crossover Probability
- Mutation Rate
- Velocity Penalty 1
- Velocity Penalty 2
- Pressure Penalty 1
- Pressure Penalty 2
3. Results and Discussion
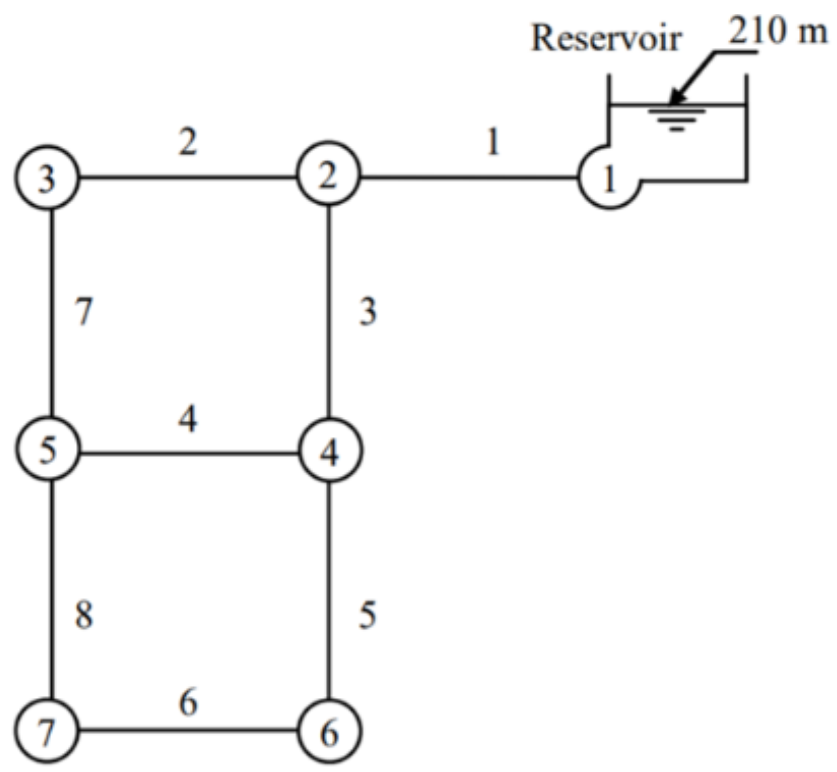
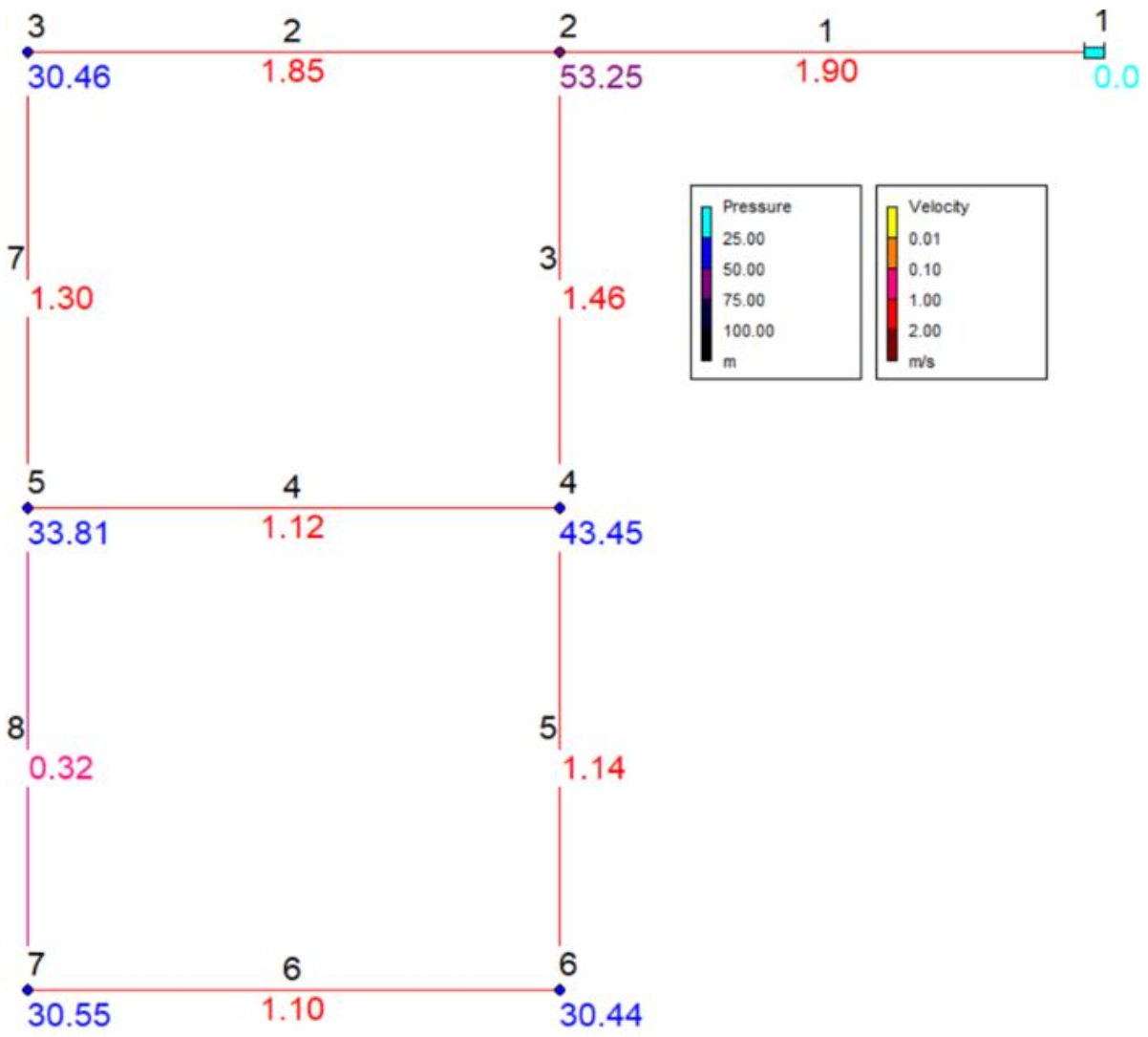
3.1. Example 1: Two-Loop Network
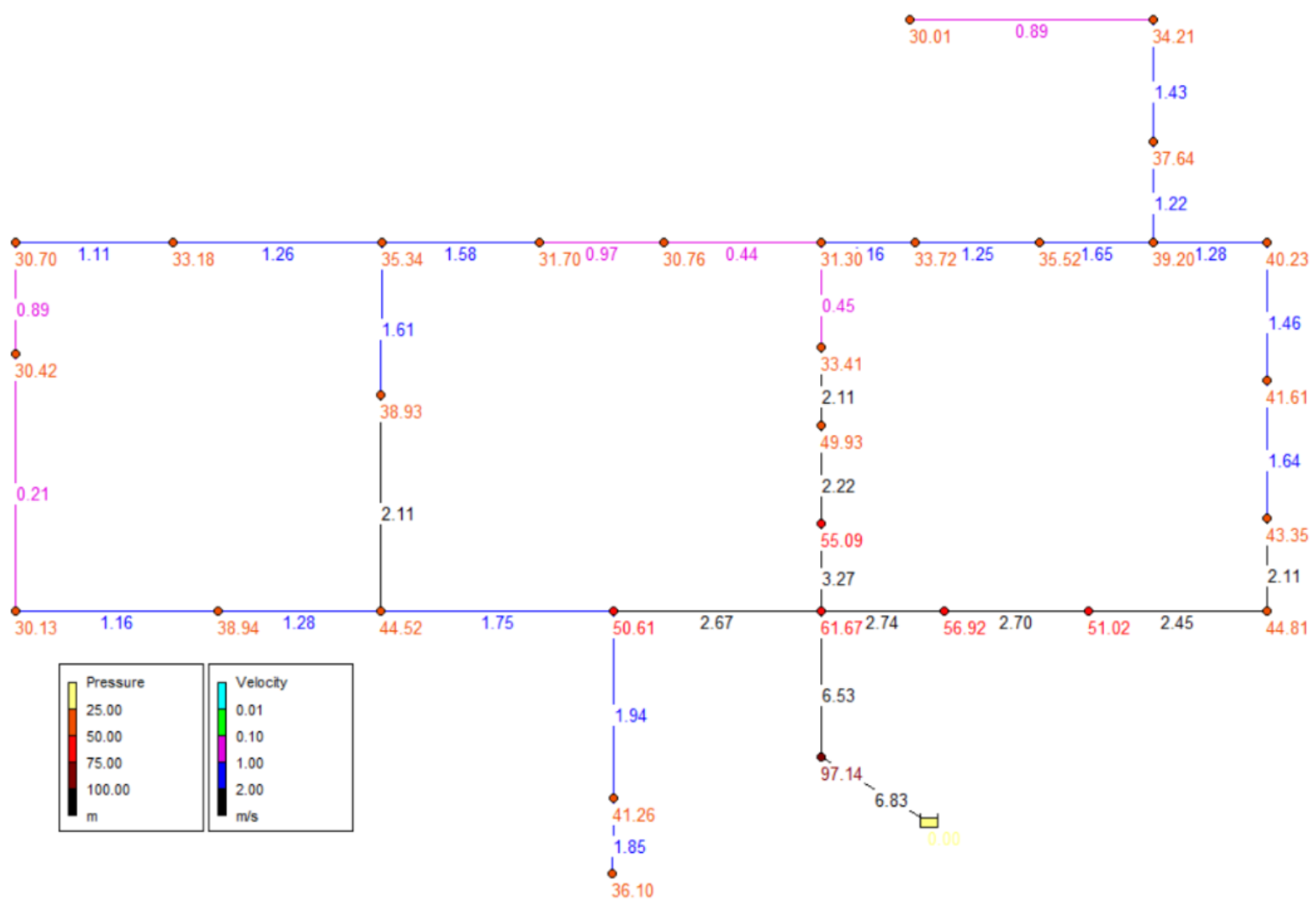
3.2. Example 2: Hanoi Network
3.3. Example 3: GoYang Network
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| Node No. | Elevation (m) | Demand (m3/h) |
|---|---|---|
| 1 | 210 | Reservoir |
| 2 | 150 | 100 |
| 3 | 160 | 100 |
| 4 | 155 | 120 |
| 5 | 150 | 270 |
| 6 | 165 | 330 |
| 7 | 160 | 200 |
| Pipe No. | Begin Node | End Node | Length (m) |
|---|---|---|---|
| 1 | 1 | 2 | 1000 |
| 2 | 2 | 3 | 1000 |
| 3 | 2 | 4 | 1000 |
| 4 | 4 | 5 | 1000 |
| 5 | 4 | 6 | 1000 |
| 6 | 6 | 7 | 1000 |
| 7 | 3 | 5 | 1000 |
| 8 | 5 | 7 | 1000 |
| Node No. | Demand (m3/h) |
|---|---|
| 1 | Reservoir |
| 2 | 890 |
| 3 | 850 |
| 4 | 130 |
| 5 | 725 |
| 6 | 1005 |
| 7 | 1350 |
| 8 | 550 |
| 9 | 525 |
| 10 | 525 |
| 11 | 500 |
| 12 | 560 |
| 13 | 940 |
| 14 | 615 |
| 15 | 280 |
| 16 | 310 |
| 17 | 865 |
| 18 | 1345 |
| 19 | 60 |
| 20 | 1275 |
| 21 | 930 |
| 22 | 485 |
| 23 | 1045 |
| 24 | 820 |
| 25 | 170 |
| 26 | 900 |
| 27 | 370 |
| 28 | 290 |
| 29 | 360 |
| 30 | 360 |
| 31 | 105 |
| 32 | 805 |
| Pipe No. | Begin Node | End Node | Length (m) |
|---|---|---|---|
| 1 | 1 | 2 | 100 |
| 2 | 2 | 3 | 1350 |
| 3 | 3 | 4 | 900 |
| 4 | 4 | 5 | 1150 |
| 5 | 5 | 6 | 1450 |
| 6 | 6 | 7 | 450 |
| 7 | 7 | 8 | 850 |
| 8 | 8 | 9 | 850 |
| 9 | 9 | 10 | 800 |
| 10 | 10 | 11 | 950 |
| 11 | 11 | 12 | 1200 |
| 12 | 12 | 13 | 3500 |
| 13 | 10 | 14 | 800 |
| 14 | 14 | 15 | 500 |
| 15 | 15 | 16 | 550 |
| 16 | 17 | 16 | 2730 |
| 17 | 18 | 17 | 1750 |
| 18 | 19 | 18 | 800 |
| 19 | 3 | 19 | 400 |
| 20 | 3 | 20 | 2200 |
| 21 | 20 | 21 | 1500 |
| 22 | 21 | 22 | 500 |
| 23 | 20 | 23 | 2650 |
| 24 | 23 | 24 | 1230 |
| 25 | 24 | 25 | 1300 |
| 26 | 26 | 25 | 850 |
| 27 | 27 | 26 | 300 |
| 28 | 16 | 27 | 750 |
| 29 | 23 | 28 | 1500 |
| 30 | 28 | 29 | 2000 |
| 31 | 29 | 30 | 1600 |
| 32 | 30 | 31 | 150 |
| 33 | 32 | 31 | 860 |
| 34 | 25 | 32 | 950 |
| Node No. | Elevation (m) | Demand (m3/d) |
|---|---|---|
| 1 | 71.0 | Reservoir |
| 2 | 56.4 | 153.0 |
| 3 | 53.8 | 70.5 |
| 4 | 54.9 | 58.5 |
| 5 | 56.0 | 75.0 |
| 6 | 57.0 | 67.5 |
| 7 | 53.9 | 63.0 |
| 8 | 54.5 | 48.0 |
| 9 | 57.9 | 42.0 |
| 10 | 62.1 | 30.0 |
| 11 | 62.8 | 42.0 |
| 12 | 58.6 | 37.5 |
| 13 | 59.3 | 37.5 |
| 14 | 59.8 | 63.0 |
| 15 | 59.2 | 445.5 |
| 16 | 53.6 | 108.0 |
| 17 | 54.8 | 79.5 |
| 18 | 55.1 | 55.5 |
| 19 | 54.2 | 118.5 |
| 20 | 54.5 | 124.5 |
| 21 | 62.9 | 31.5 |
| Pipe No. | Begin Node | End Node | Length (m) |
|---|---|---|---|
| 1 | 1 | 2 | 165 |
| 2 | 2 | 3 | 124 |
| 3 | 3 | 4 | 118 |
| 4 | 4 | 5 | 81 |
| 5 | 5 | 6 | 134 |
| 6 | 6 | 12 | 135 |
| 7 | 12 | 15 | 202 |
| 8 | 2 | 22 | 135 |
| 9 | 2 | 21 | 170 |
| 10 | 21 | 22 | 113 |
| 11 | 22 | 20 | 335 |
| 12 | 20 | 19 | 115 |
| 13 | 2 | 19 | 345 |
| 14 | 19 | 17 | 114 |
| 15 | 3 | 16 | 103 |
| 16 | 16 | 17 | 261 |
| 17 | 17 | 18 | 72 |
| 18 | 7 | 18 | 373 |
| 19 | 3 | 7 | 98 |
| 20 | 7 | 8 | 110 |
| 21 | 4 | 8 | 98 |
| 22 | 8 | 9 | 246 |
| 23 | 5 | 11 | 174 |
| 24 | 10 | 11 | 102 |
| 25 | 6 | 10 | 92 |
| 26 | 6 | 9 | 100 |
| 27 | 10 | 13 | 130 |
| 28 | 12 | 13 | 90 |
| 29 | 13 | 14 | 185 |
| 30 | 15 | 14 | 90 |
References
- Swamee, P.K.; Sharma, A.K. Design of Water Supply Pipe Networks; John Wiley & Sons: Hoboken, NJ, USA, 2008. [Google Scholar]
- Cross, H. Analysis of Flow in Networks of Conduits or Conductors; University of Illinois at Urbana Champaign, College of Engineering, Engineering Experiment Station: Urbana, IL, USA, 1936. [Google Scholar]
- Alperovits, E.; Shamir, U. Design of optimal water distribution systems. Water Resour. Res. 1977, 13, 885–900. [Google Scholar] [CrossRef]
- Goulter, I.C.; Lussier, B.M.; Morgan, D.R. Implications of head loss path choice in the optimization of water distribution networks. Water Resour. Res. 1986, 22, 819–822. [Google Scholar] [CrossRef]
- Quindry, G.E.; Liebman, J.C.; Brill, E.D. Optimization of looped water distribution systems. J. Environ. Eng. Div. 1981, 107, 665–679. [Google Scholar] [CrossRef]
- Bifulco, I.; Cirillo, S. Discovery Multiple Data Structures in Big Data through Global Optimization and Clustering Methods. In Proceedings of the 2018 22nd International Conference Information Visualisation (IV), Fisciano, Italy, 10–13 July 2018; pp. 117–121. [Google Scholar]
- Goldberg, D.E.; Kuo, C.H. Genetic algorithms in pipeline optimization. J. Comput. Civ. Eng. 1987, 1, 128–141. [Google Scholar] [CrossRef]
- Simpson, A.; Murphy, L.; Dandy, G. Pipe Network Optimisation Using Genetic Algorithms; American Society of Civil Engineers: Seattle, WA, USA, 1993. [Google Scholar]
- Simpson, A.R.; Dandy, G.C.; Murphy, L.J. Genetic algorithms compared to other techniques for pipe optimization. J. Water Resour. Plan. Manag. 1994, 120, 423–443. [Google Scholar] [CrossRef]
- Dandy, G.C.; Simpson, A.R.; Murphy, L.J. An improved genetic algorithm for pipe network optimization. Water Resour. Res. 1996, 32, 449–458. [Google Scholar] [CrossRef]
- Savic, D.A.; Walters, G.A. Genetic algorithms for least-cost design of water distribution networks. J. Water Resour. Plan. Manag. 1997, 123, 67–77. [Google Scholar] [CrossRef]
- Deb, K.; Agrawal, S. A niched-penalty approach for constraint handling in genetic algorithms. In Artificial Neural Nets and Genetic Algorithms; Springer: Vienna, Austria, 1996; pp. 235–243. [Google Scholar]
- Wu, Z.Y.; Simpson, A.R. A self-adaptive boundary search genetic algorithm and its application to water distribution systems. J. Hydraul. Res. 2002, 40, 191–203. [Google Scholar] [CrossRef]
- Liong, S.Y.; Atiquzzaman, M. Optimal design of water distribution network using shuffled complex evolution. J. Inst. Eng. Singap. 2004, 44, 93–107. [Google Scholar]
- Eusuff, M.; Lansey, K.; Pasha, F. Shuffled frog-leaping algorithm: A memetic meta-heuristic for discrete optimization. Eng. Optim. 2006, 38, 129–154. [Google Scholar] [CrossRef]
- Geem, Z.W. Optimal cost design of water distribution networks using harmony search. Eng. Optim. 2006, 38, 259–277. [Google Scholar] [CrossRef]
- Di Pierro, F.; Khu, S.T.; Savić, D.; Berardi, L. Efficient multi-objective optimal design of water distribution networks on a budget of simulations using hybrid algorithms. Environ. Model. Softw. 2009, 24, 202–213. [Google Scholar] [CrossRef]
- Chandramouli, S.; Malleswararao, P. Reliability based optimal design of a water distribution network for municipal water supply. Int. J. Eng. Technol. 2011, 3, 13–19. [Google Scholar]
- Jin, X.; Zhang, J.; Gao, J.L.; Wu, W.Y. Multi-objective optimization of water supply network rehabilitation with non-dominated sorting genetic algorithm-II. J. Zhejiang Univ. Sci. A 2008, 9, 391–400. [Google Scholar] [CrossRef]
- Prasad, T.D.; Park, N.S. Multiobjective genetic algorithms for design of water distribution networks. J. Water Resour. Plan. Manag. 2004, 130, 73–82. [Google Scholar] [CrossRef]
- Kang, D.; Lansey, K. Revisiting optimal water-distribution system design: Issues and a heuristic hierarchical approach. J. Water Resour. Plan. Manag. 2012, 138, 208–217. [Google Scholar] [CrossRef]
- Cisty, M.; Bajtek, Z.; Celar, L. A two-stage evolutionary optimization approach for an irrigation system design. J. Hydroinform. 2017, 19, 115–122. [Google Scholar] [CrossRef]
- Martínez-Bahena, B.; Cruz-Chávez, M.A.; Ávila-Melgar, E.Y.; Cruz-Rosales, M.H.; Rivera-Lopez, R. Using a genetic algorithm with a mathematical programming solver to optimize a real water distribution system. Water 2018, 10, 1318. [Google Scholar] [CrossRef]
- Bi, W.; Dandy, G. Optimization of water distribution systems using online retrained metamodels. J. Water Resour. Plan. Manag. 2014, 140, 04014032. [Google Scholar] [CrossRef]
- Khalifeh, S.; Akbarifard, S.; Khalifeh, V.; Zallaghi, E. Optimization of water distribution of network systems using the Harris Hawks optimization algorithm (Case study: Homashahr city). MethodsX 2020, 7, 100948. [Google Scholar] [CrossRef]
- Bilal; Pant, M. Parameter Optimization of Water Distribution Network—A Hybrid Metaheuristic Approach. Mater. Manuf. Process. 2020, 35, 737–749. [Google Scholar] [CrossRef]
- Praneeth, P.; Vasan, A.; Srinivasa Raju, K. Pipe size design optimization of water distribution networks using water cycle algorithm. In Harmony Search and Nature Inspired Optimization Algorithm; Springer: Singapore, 2019; pp. 1057–1067. [Google Scholar]
- Pankaj, B.S.; Naidu, M.N.; Vasan, A.; Varma, M.R. Self-adaptive cuckoo search algorithm for optimal design of water distribution systems. Water Resour. Manag. 2020, 34, 3129–3146. [Google Scholar] [CrossRef]
- Surco, D.F.; Vecchi, T.P.; Ravagnani, M.A. Optimization of water distribution networks using a modified particle swarm optimization algorithm. Water Sci. Technol. Water Supply 2018, 18, 660–678. [Google Scholar] [CrossRef]
- Cassiolato, G.; Carvalho, E.P.; Caballero, J.A.; Ravagnani, M.A. Optimization of water distribution networks using a deterministic approach. Eng. Optim. 2021, 53, 107–124. [Google Scholar] [CrossRef]
- Pant, M.; Snasel, V. Design optimization of water distribution networks through a novel differential evolution. IEEE Access 2021, 9, 16133–16151. [Google Scholar]
- Bi, W.; Xu, Y.; Wang, H. Comparison of searching behaviour of three evolutionary algorithms applied to water distribution system design optimization. Water 2020, 12, 695. [Google Scholar] [CrossRef]
- Zhao, R.H.; He, W.Q.; Lou, Z.K.; Nie, W.B.; Ma, X.Y. Synchronization optimization of pipeline layout and pipe diameter selection in a self-pressurized drip irrigation network system based on the genetic algorithm. Water 2019, 11, 489. [Google Scholar] [CrossRef]
- Shao, Y.; Yao, H.; Zhang, T.; Chu, S.; Liu, X. An improved genetic algorithm for optimal layout of flow meters and valves in water network partitioning. Water 2019, 11, 1087. [Google Scholar] [CrossRef]
- Mala-Jetmarova, H.; Sultanova, N.; Savic, D. Lost in optimisation of water distribution systems? A literature review of system operation. Environ. Model. Softw. 2017, 93, 209–254. [Google Scholar] [CrossRef]
- Bene, J.G.; Selek, I.; Hős, C. Comparison of deterministic and heuristic optimization solvers for water network scheduling problems. Water Sci. Technol. Water Supply 2013, 13, 1367–1376. [Google Scholar] [CrossRef]
- Pasha, M.F.K.; Lansey, K. Optimal pump scheduling by linear programming. In World Environmental and Water Resources Congress 2009: Great Rivers; American Society of Civil Engineers (ASCE): Kansas City, MO, USA, 2009; pp. 1–10. [Google Scholar]
- Martin-Candilejo, A.; Santillan, D.; Iglesias, A.; Garrote, L. Optimization of the design of water distribution systems for variable pumping flow rates. Water 2020, 12, 359. [Google Scholar] [CrossRef]
- Cimorelli, L.; Covelli, C.; Molino, B.; Pianese, D. Optimal regulation of pumping station in water distribution networks using constant and variable speed pumps: A technical and economical comparison. Energies 2020, 13, 2530. [Google Scholar] [CrossRef]
- Broad, D.R.; Maier, H.R.; Dandy, G.C. Optimal operation of complex water distribution systems using metamodels. J. Water Resour. Plan. Manag. 2010, 136, 433–443. [Google Scholar] [CrossRef]
- Brentan, B.M.; Luvizotto, E., Jr.; Montalvo, I.; Izquierdo, J.; Pérez-García, R. Near real time pump optimization and pressure management. Procedia Eng. 2017, 186, 666–675. [Google Scholar] [CrossRef]
- Jung, D.; Kang, D.; Kang, M.; Kim, B. Real-time pump scheduling for water transmission systems: Case study. KSCE J. Civ. Eng. 2015, 19, 1987–1993. [Google Scholar] [CrossRef]
- Tu, M.Y.; Tsai, F.T.C.; Yeh, W.W.G. Optimization of water distribution and water quality by hybrid genetic algorithm. J. Water Resour. Plan. Manag. 2005, 131, 431–440. [Google Scholar] [CrossRef]
- Mackle, G.; Savic, G.A.; Walters, G.A. Application of genetic algorithms to pump scheduling for water supply. In Proceedings of the First International Conference on Genetic Algorithms in Engineering Systems: Innovations and Applications IET, Sheffield, UK, 12–14 September 1995; pp. 400–405. [Google Scholar]
- Van Zyl, J.E.; Savic, D.A.; Walters, G.A. Operational optimization of water distribution systems using a hybrid genetic algorithm. J. Water Resour. Plan. Manag. 2004, 130, 160–170. [Google Scholar] [CrossRef]
- de Oliveira Turci, L.; Sun, H.; Bai, M.; Wang, J.; Hu, P. Water pump station scheduling optimization using an improved genetic algorithm approach. In Proceedings of the Congress on Evolutionary Computation (CEC), Wellington, New Zealand, 10–13 June 2019; pp. 944–951. [Google Scholar]
- Mala-Jetmarova, H.; Sultanova, N.; Savic, D. Lost in optimisation of water distribution systems? A literature review of system design. Water 2018, 10, 307. [Google Scholar] [CrossRef]
- Khan, S.; Grudniewski, P.; Muhammad, Y.S.; Sobey, A.J. The benefits of co-evolutionary Genetic Algorithms in voyage optimisation. Ocean. Eng. 2022, 245, 110261. [Google Scholar] [CrossRef]
- Caruccio, L.; Deufemia, V.; Polese, G. A genetic algorithm to discover relaxed functional dependencies from data. In Proceedings of the 25th Italian Symposium on Advanced Database Systems; University of Salerno: Fisciano, Italy, 2017; Volume 2037, pp. 1–12. [Google Scholar]
- Mayer, M.J.; Szilágyi, A.; Gróf, G. Environmental and economic multi-objective optimization of a household level hybrid renewable energy system by genetic algorithm. Appl. Energy 2020, 269, 115058. [Google Scholar] [CrossRef]
- Katoch, S.; Chauhan, S.S.; Kumar, V. A review on genetic algorithm: Past, present, and future. Multimed. Tools Appl. 2021, 80, 8091–8126. [Google Scholar] [CrossRef]
- Van Dijk, M.; van Vuuren, S.J.; Van Zyl, J.E. Optimising water distribution systems using a weighted penalty in a genetic algorithm. Water SA 2008, 34, 537–548. [Google Scholar] [CrossRef]
- Lansey, K.E.; Mays, L.W. Optimization models for design of water distribution systems. In Reliability Analysis of Water Distribution Systems; Mays, L.R., Ed.; ASCE: New York, NY, USA, 1989; pp. 37–84. [Google Scholar]
- Keedwell, E.; Khu, S.T. A hybrid genetic algorithm for the design of water distribution networks. Eng. Appl. Artif. Intell. 2005, 18, 461–472. [Google Scholar] [CrossRef]
- Lamont, P.A. Common pipe flow formulas compared with the theory of roughness. J. Am. Water Work. Assoc. 1981, 73, 274–280. [Google Scholar] [CrossRef]
- Goldberg, D.E. A Gentle Introduction to Genetic Algorithms; Addison-Wesley Publishing Company: Boston, MA, USA, 1989. [Google Scholar]
- Abuiziah, I.; Nidal, S. A Review of Genetic Algorithm Optimization: Operations and Applications to Water Pipeline Systems. Int. J. Math. Comput. Phys. Electr. Comput. Eng. 2013, 7, 341–347. [Google Scholar]
- Rossman, L.A. EPANET 2: User’s Manual; United States Environmental Protection Agency: Washington, DC, USA, 2000. [Google Scholar]
- Eliades, D.G.; Kyriakou, M.; Vrachimis, S.; Polycarpou, M.M. EPANET-MATLAB toolkit: An open-source software for interfacing EPANET with MATLAB. In Proceedings of the 14th International Conference on Computing and Control for the Water Industry, Amsterdam, The Netherlands, 7–9 November 2016. [Google Scholar]
- Czajkowska, A.M. Maximum Entropy Based Evolutionary Optimization of Water Distribution Networks under Multiple Operating Conditions and Self-Adaptive Search Space Reduction Method. Ph.D. Thesis, University of Strathclyde, Glasgow, UK, 2016. [Google Scholar]
- Saleh, S.H.; Tanyimboh, T.T. Optimal design of water distribution systems based on entropy and topology. Water Resour. Manag. 2014, 28, 3555–3575. [Google Scholar] [CrossRef]
- Tanyimboh, T.T. Redundant binary codes in genetic algorithms: Multi-objective design optimization of water distribution networks. Water Supply 2021, 21, 444–457. [Google Scholar] [CrossRef]
- Güç, G. Optimization of Water Distribution Networks Using Genetic Algorithm. Master’s Thesis, Middle East Technical University, Ankara, Turkey, 2006. [Google Scholar]
- Mora-Melia, D.; Iglesias-Rey, P.L.; Martinez-Solano, F.J.; Fuertes-Miquel, V.S. Design of water distribution networks using a pseudo-genetic algorithm and sensitivity of genetic operators. Water Resour. Manag. 2013, 27, 4149–4162. [Google Scholar] [CrossRef]
- Eiben, A.E.; Michalewicz, Z.; Schoenauer, M.; Smith, J.E. Parameter control in evolutionary algorithms. In Parameter Setting in Evolutionary Algorithms; Springer: Berlin/Heidelberg, Germany, 2007; pp. 19–46. [Google Scholar]
- Fujiwara, O.; Kang, D.B. A two-phase decomposition method for optimal design of looped water distribution networks. Water Resour. Res. 1990, 26, 539–549. [Google Scholar] [CrossRef]
- Kim, J.H.; Kim, T.G.; Kim, J.H.; Yoon, Y.N. A study on the pipe network system design using non-linear programming. J. Korean Water Resour. Assoc. 1994, 27, 59–67. [Google Scholar]
- Menon, K.K.; Narulkar, S.M. Application of heuristic based algorithm in water distribution network design. J. Water Resour. Pollut. Stud. 2016, 1, 1–14. [Google Scholar]







| S.N. | Available Pipe Sizes (mm) | Unit Cost (per m) | 3-Bit (Binary) Representation | 3-Bit (Grey) Representation |
|---|---|---|---|---|
| 1 | 8 | 100 | 000 | 000 |
| 2 | 10 | 120 | 001 | 001 |
| 3 | 12 | 150 | 010 | 011 |
| 4 | 14 | 180 | 011 | 010 |
| 5 | 16 | 200 | 100 | 110 |
| 6 | 18 | 250 | 101 | 111 |
| 7 | 20 | 300 | 110 | 101 |
| 8 | 24 | 350 | 111 | 100 |
| Randomly Generated Binary String | 101110011001000111 | |||||
|---|---|---|---|---|---|---|
| 6 Individual Pipes | 101, 110, 011, 001, 000, 111 | |||||
| Pipe Position in WDN | Pipe No.1 | Pipe No.2 | Pipe No.3 | Pipe No.4 | Pipe No.5 | Pipe No.6 |
| Chromosome (Binary) | 101 | 110 | 011 | 001 | 000 | 111 |
| Pipe Diameter (mm) | 20 | 16 | 12 | 10 | 8 | 18 |
| Unit Cost (per m) | 300 | 200 | 150 | 120 | 100 | 250 |
| Length (m) | 100 | 100 | 100 | 100 | 100 | 100 |
| Cost of individual pipe | 30,000 | 20,000 | 15,000 | 12,000 | 10,000 | 25,000 |
| Total Cost of Network | 112,000 | |||||
| S.N. | GA Parameters | Values |
|---|---|---|
| 1 | Population Size | 80–100 |
| 2 | Crossover Probability (%) | 85–90 |
| 3 | Mutation Rate (%) | 4–6 |
| 4 | Velocity Penalty 1 | 0.3 |
| 5 | Velocity Penalty 2 | 0.06 |
| 6 | Pressure Penalty 1 | 0.02 |
| 7 | Pressure Penalty 2 | 1.9 |
| Diameter (in) | Diameter (mm) | Unit Cost (USD/m) |
|---|---|---|
| 1 | 25.4 | 2 |
| 2 | 50.8 | 5 |
| 4 | 101.6 | 11 |
| 6 | 152.4 | 16 |
| 10 | 254.0 | 32 |
| 14 | 355.6 | 60 |
| 16 | 406.4 | 90 |
| 18 | 457.2 | 130 |
| Pipe No. | Pipe Diameter (mm) | Pipe Length (m) | Cost (USD) | Node No. | Nodal Pressure (m) |
|---|---|---|---|---|---|
| 1 | 457.2 | 1000 | 130,000 | 1 | Reservoir |
| 2 | 254.0 | 1000 | 32,000 | 2 | 53.25 |
| 3 | 406.4 | 1000 | 90,000 | 3 | 30.46 |
| 4 | 101.6 | 1000 | 11,000 | 4 | 43.45 |
| 5 | 406.4 | 1000 | 90,000 | 5 | 33.81 |
| 6 | 254.0 | 1000 | 32,000 | 6 | 30.44 |
| 7 | 254.0 | 1000 | 32,000 | 7 | 30.55 |
| 8 | 25.4 | 1000 | 2000 | - | - |
| Total Cost: | 419,000 | Check | OK | ||
| Studies | Alperovitz and Shamir | Savic and Walters | Geem | Van Dijk et al. | SOP–WDN |
|---|---|---|---|---|---|
| Least cost obtained (USD) | 479,525 | 420,000 | 419,000 | 419,000 | 419,000 |
| Diameter (in) | Diameter (mm) | Unit Cost (USD/m) |
|---|---|---|
| 12 | 304.8 | 45.73 |
| 16 | 406.4 | 70.40 |
| 20 | 508 | 98.38 |
| 24 | 609.6 | 129.33 |
| 30 | 762 | 180.75 |
| 40 | 1016 | 278.28 |
| Pipe No. | Pipe Diameter (mm) | Pipe Length (m) | Cost (USD) | Node No. | Nodal Pressure (m) |
|---|---|---|---|---|---|
| 1 | 1016 | 100 | 27,828 | 1 | 100 (Reservoir) |
| 2 | 1016 | 1350 | 375,678 | 2 | 97.14 |
| 3 | 1016 | 900 | 250,452 | 3 | 61.67 |
| 4 | 1016 | 1150 | 320,022 | 4 | 56.92 |
| 5 | 1016 | 1450 | 403,506 | 5 | 51.02 |
| 6 | 1016 | 450 | 125,226 | 6 | 44.81 |
| 7 | 1016 | 850 | 236,538 | 7 | 43.35 |
| 8 | 1016 | 850 | 236,538 | 8 | 41.61 |
| 9 | 1016 | 800 | 222,624 | 9 | 40.23 |
| 10 | 762 | 950 | 171,712.5 | 10 | 39.20 |
| 11 | 609.6 | 1200 | 155,196 | 11 | 37.64 |
| 12 | 609.6 | 3500 | 452,655 | 12 | 34.21 |
| 13 | 508 | 800 | 78,704 | 13 | 30.01 |
| 14 | 406.4 | 500 | 35,200 | 14 | 35.52 |
| 15 | 304.8 | 550 | 25,151.5 | 15 | 33.72 |
| 16 | 304.8 | 2730 | 124,842.9 | 16 | 31.30 |
| 17 | 406.4 | 1750 | 123,200 | 17 | 33.41 |
| 18 | 609.6 | 800 | 103,464 | 18 | 49.93 |
| 19 | 508 | 400 | 39,352 | 19 | 55.09 |
| 20 | 1016 | 2200 | 612,216 | 20 | 50.61 |
| 21 | 508 | 1500 | 147,570 | 21 | 41.26 |
| 22 | 304.8 | 500 | 22,865 | 22 | 36.10 |
| 23 | 1016 | 2650 | 737,442 | 23 | 44.52 |
| 24 | 762 | 1230 | 222,322.5 | 24 | 38.93 |
| 25 | 762 | 1300 | 234,975 | 25 | 35.34 |
| 26 | 508 | 850 | 83,623 | 26 | 31.70 |
| 27 | 304.8 | 300 | 13,719 | 27 | 30.76 |
| 28 | 304.8 | 750 | 34,297.5 | 28 | 38.94 |
| 29 | 406.4 | 1500 | 105,600 | 29 | 30.13 |
| 30 | 304.8 | 2000 | 91,460 | 30 | 30.42 |
| 31 | 304.8 | 1600 | 73,168 | 31 | 30.70 |
| 32 | 406.4 | 150 | 10,560 | 32 | 33.18 |
| 33 | 406.4 | 860 | 60,544 | - | - |
| 34 | 609.6 | 950 | 122,863.5 | - | - |
| Total Cost: | 6,081,115.4 | Check | OK | ||
| Studies | Savic and Walters | Liong and Atiquzzaman | Geem | Van Dijk et al. | SOP–WDN |
|---|---|---|---|---|---|
| Least cost obtained (Million USD) | 6.187 | 6.220 | 6.056 | 6.110 | 6.081 |
| Diameter (mm) | Unit Cost (Won/m) |
|---|---|
| 80 | 37,890 |
| 100 | 38,933 |
| 125 | 40,563 |
| 150 | 42,554 |
| 200 | 47,624 |
| 250 | 54,125 |
| 300 | 62,109 |
| 350 | 71,524 |
| Pipe No. | Pipe Diameter (mm) | Pipe Length (m) | Cost (Won) | Node No. | Nodal Pressure (m) |
|---|---|---|---|---|---|
| 1 | 200 | 165.0 | 7,857,960 | 1 | 15.62 |
| 2 | 125 | 124.0 | 5,029,812 | 2 | 29.33 |
| 3 | 125 | 118.0 | 4,786,434 | 3 | 28.73 |
| 4 | 100 | 81.0 | 3,153,573 | 4 | 26.58 |
| 5 | 80 | 134.0 | 5,077,260 | 5 | 24.20 |
| 6 | 80 | 135.0 | 5,115,150 | 6 | 21.51 |
| 7 | 80 | 202.0 | 7,653,780 | 7 | 27.72 |
| 8 | 80 | 135.0 | 5,115,150 | 8 | 26.70 |
| 9 | 80 | 170.0 | 6,441,300 | 9 | 21.20 |
| 10 | 80 | 113.0 | 4,281,570 | 10 | 16.17 |
| 11 | 80 | 335.0 | 12,693,150 | 11 | 16.03 |
| 12 | 80 | 115.0 | 4,357,350 | 12 | 18.16 |
| 13 | 80 | 345.0 | 13,072,050 | 13 | 17.46 |
| 14 | 80 | 114.0 | 4,319,460 | 14 | 15.33 |
| 15 | 80 | 103.0 | 3,902,670 | 15 | 15.48 |
| 16 | 80 | 261.0 | 9,889,290 | 16 | 28.31 |
| 17 | 80 | 72.0 | 2,728,080 | 17 | 26.75 |
| 18 | 80 | 373.0 | 14,132,970 | 18 | 26.44 |
| 19 | 80 | 98.0 | 3,713,220 | 19 | 27.36 |
| 20 | 80 | 110.0 | 4,167,900 | 20 | 26.68 |
| 21 | 80 | 98.0 | 3,713,220 | 21 | 19.74 |
| 22 | 80 | 246.0 | 9,320,940 | 22 | 19.36 |
| 23 | 80 | 174.0 | 6,592,860 | - | - |
| 24 | 80 | 102.0 | 3,864,780 | - | - |
| 25 | 80 | 92.0 | 3,485,880 | - | - |
| 26 | 80 | 100.0 | 3,789,000 | - | - |
| 27 | 80 | 130.0 | 4,925,700 | - | - |
| 28 | 80 | 90.0 | 3,410,100 | - | - |
| 29 | 80 | 185.0 | 7,009,650 | - | - |
| 30 | 80 | 90.0 | 3,410,100 | - | - |
| Total Cost: | 177,010,359 | Check | OK | ||
| Studies | Original Network | Kim et al. | Geem | Menon et al. [68] | SOP–WDN |
|---|---|---|---|---|---|
| Least cost obtained (Million Won) | 179.428 | 179.142 | 177.135 | 177.417 | 177.010 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sangroula, U.; Han, K.-H.; Koo, K.-M.; Gnawali, K.; Yum, K.-T. Optimization of Water Distribution Networks Using Genetic Algorithm Based SOP–WDN Program. Water 2022, 14, 851. https://doi.org/10.3390/w14060851
Sangroula U, Han K-H, Koo K-M, Gnawali K, Yum K-T. Optimization of Water Distribution Networks Using Genetic Algorithm Based SOP–WDN Program. Water. 2022; 14(6):851. https://doi.org/10.3390/w14060851
Chicago/Turabian StyleSangroula, Uchit, Kuk-Heon Han, Kang-Min Koo, Kapil Gnawali, and Kyung-Taek Yum. 2022. "Optimization of Water Distribution Networks Using Genetic Algorithm Based SOP–WDN Program" Water 14, no. 6: 851. https://doi.org/10.3390/w14060851






