Drag Coefficient of Submerged Flexible Vegetation Patches in Gravel Bed Rivers
Abstract
:1. Introduction
2. Theory
2.1. Saint-Venant Equation
2.2. Flexible Vegetated Drag Coefficient under Submerged Conditions
2.3. Cauchy Number
3. Material and Methods
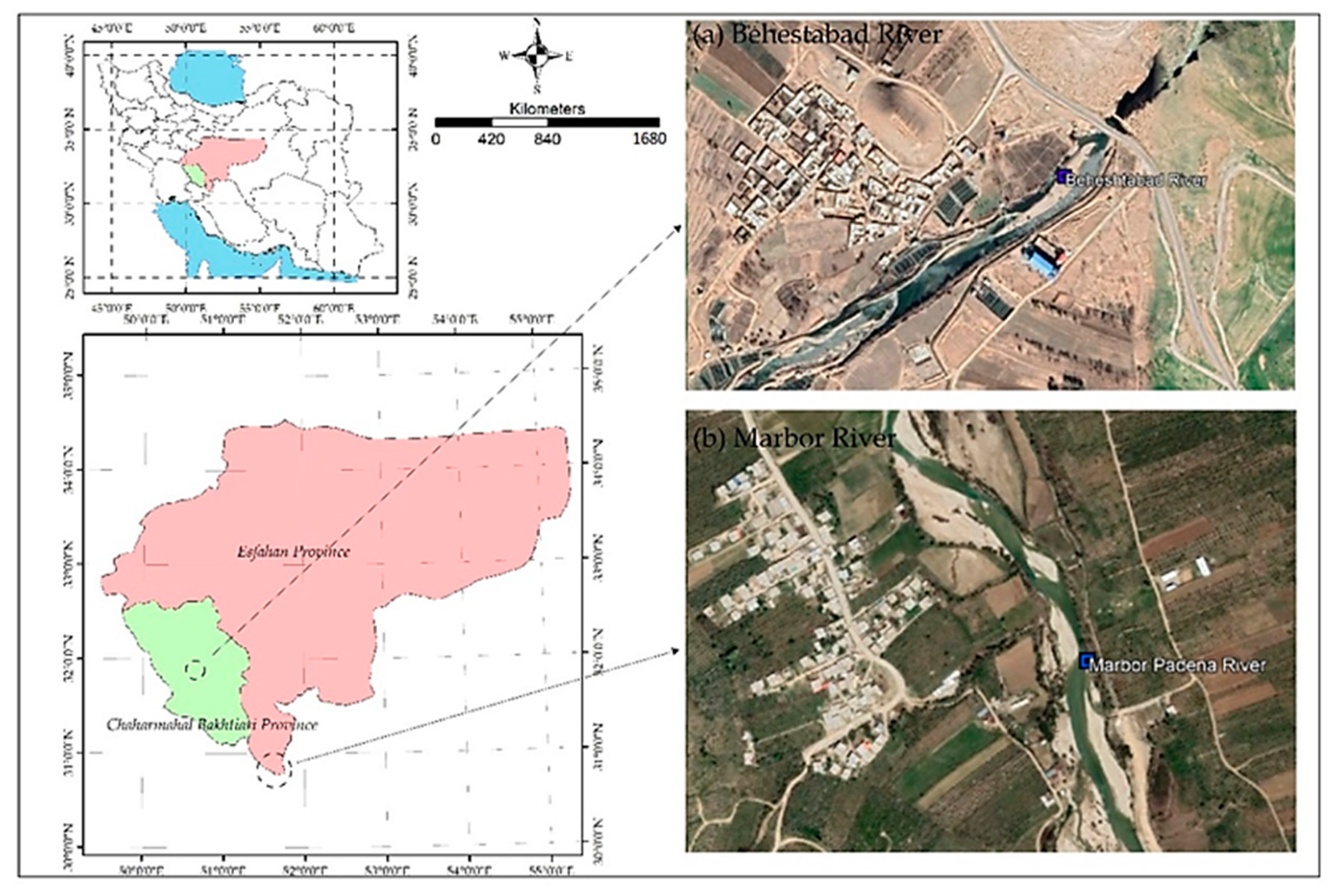
3.1. Study Site
3.2. Characteristics of Vegetated Patches
3.3. Experimental Setup and Duration of the Data Acquisition
4. Results
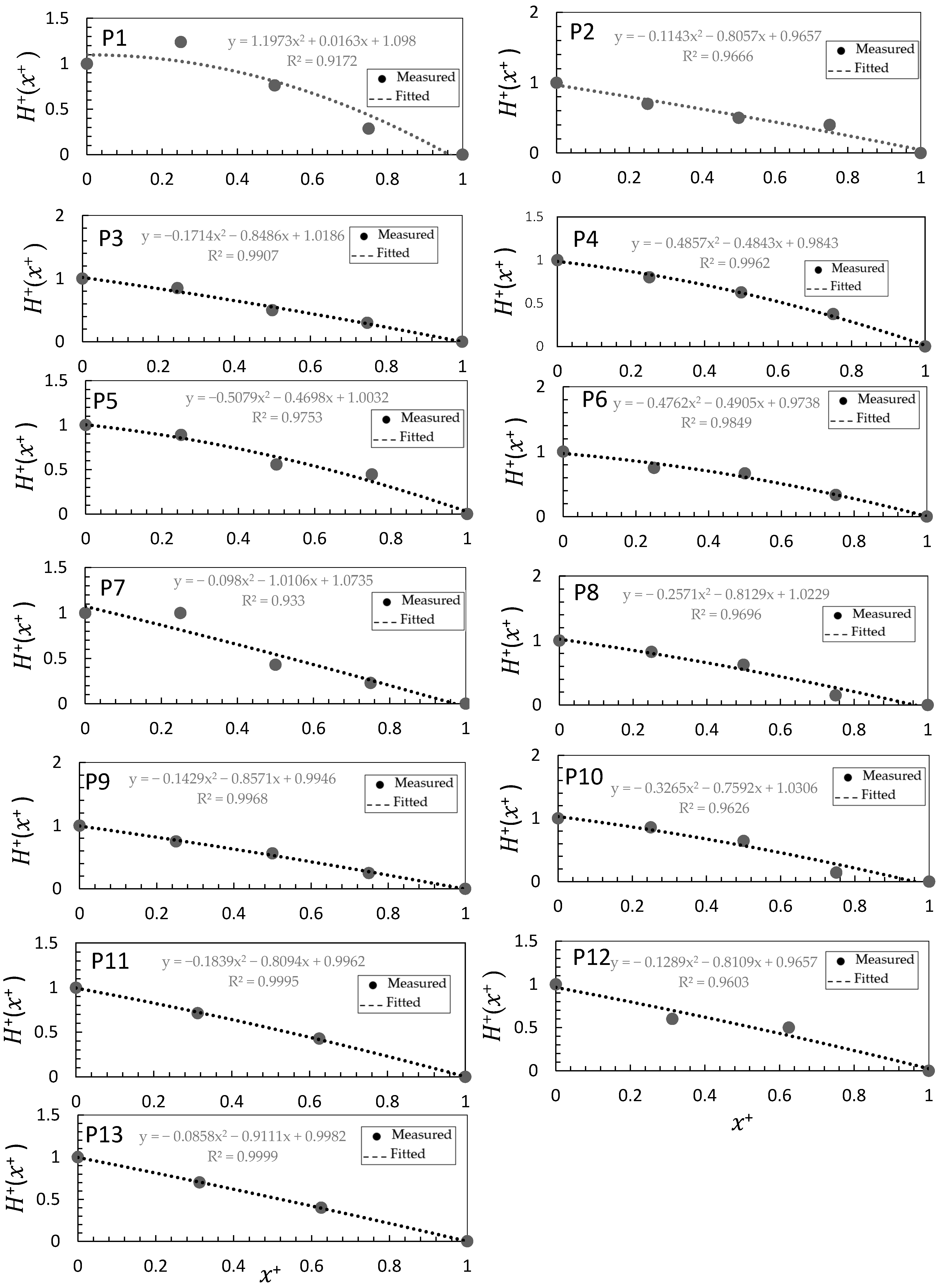
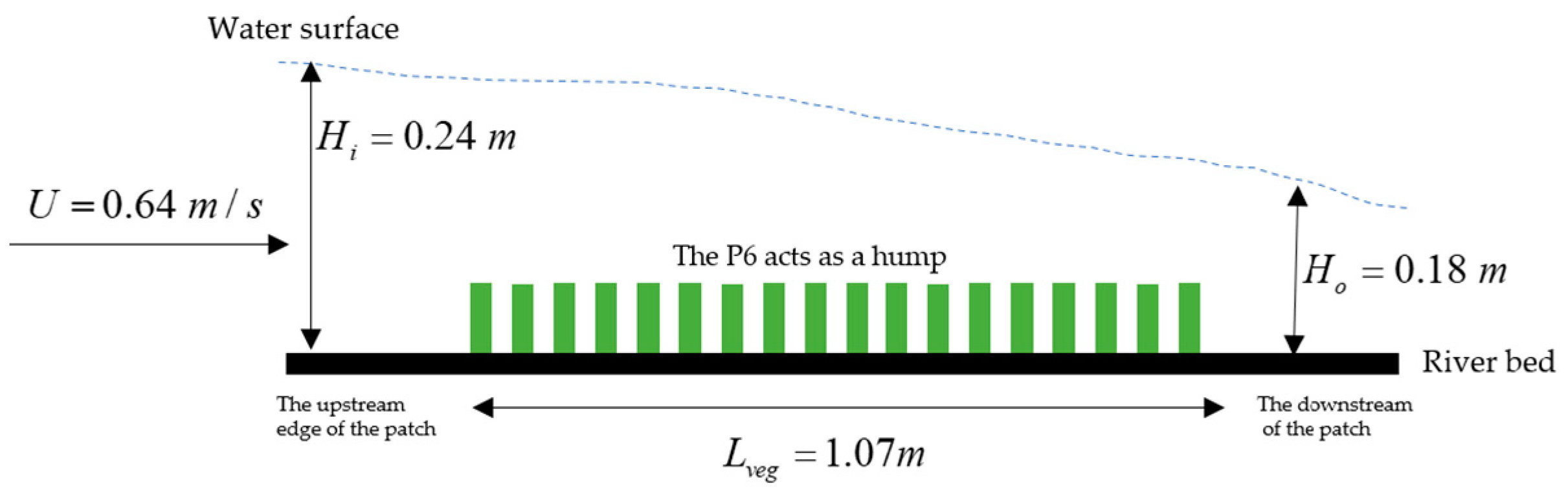
4.1. Water Surface Profile
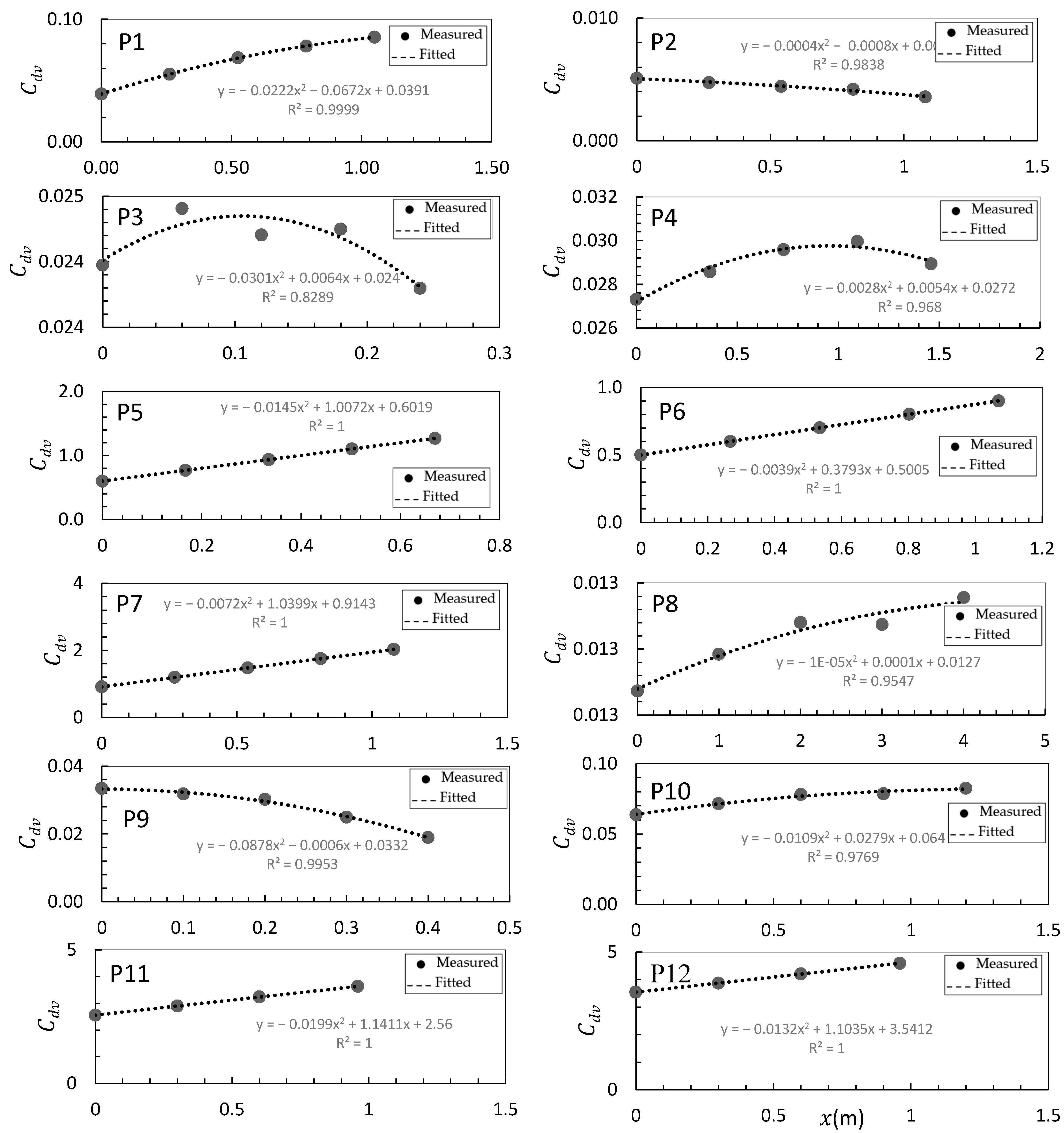
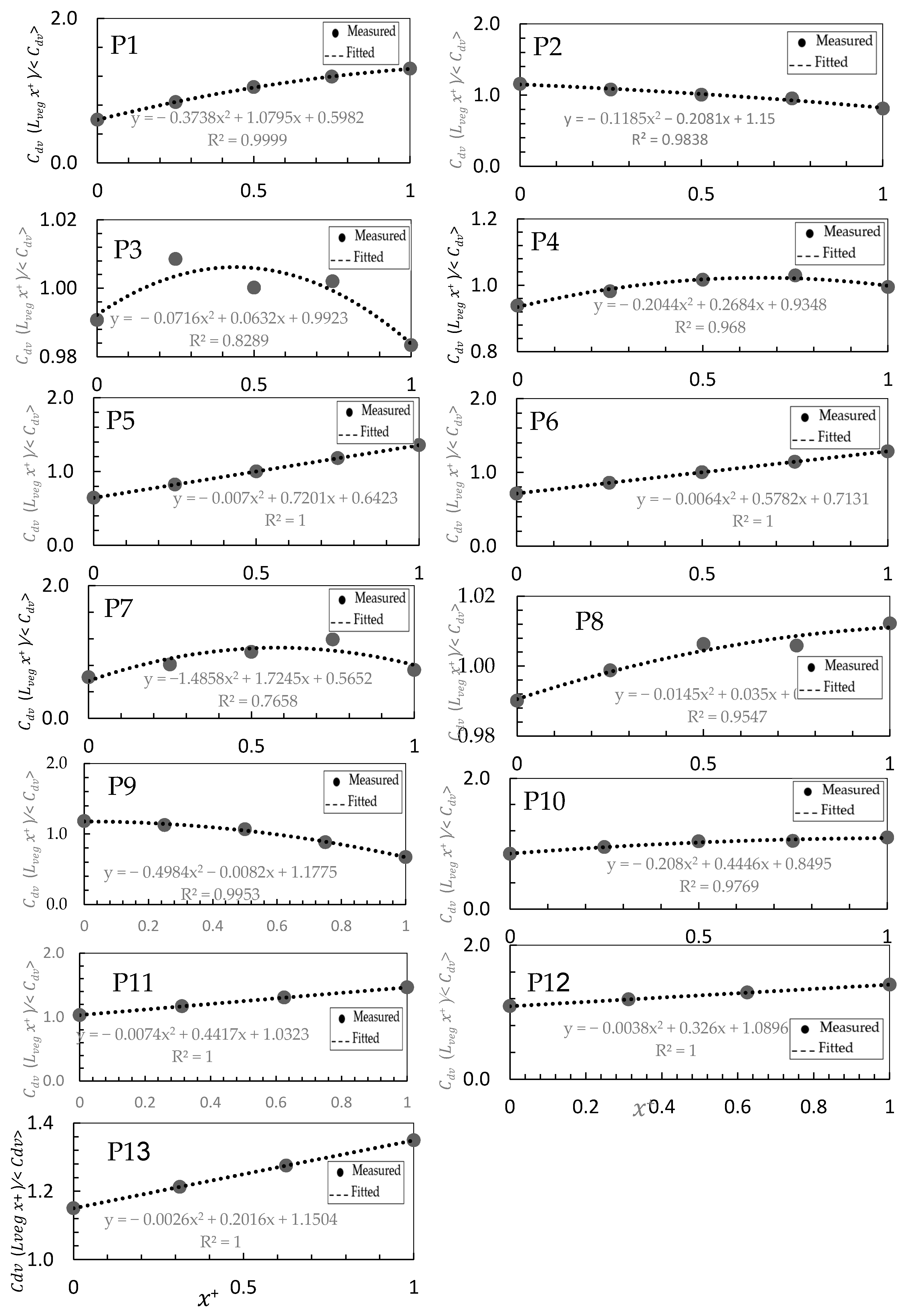
4.2. Streamwise Distribuation of
4.3. Drag Coefficient Factor
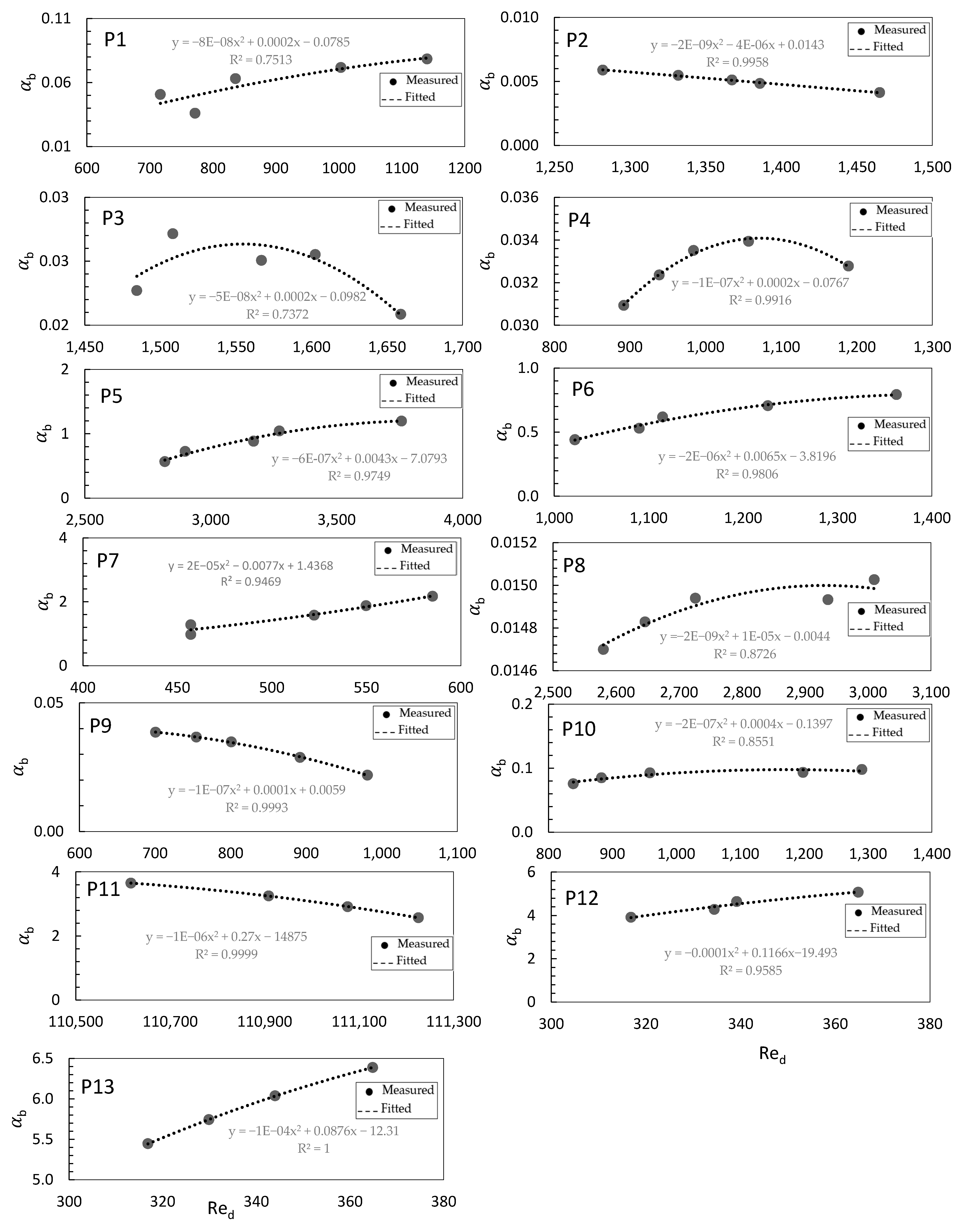
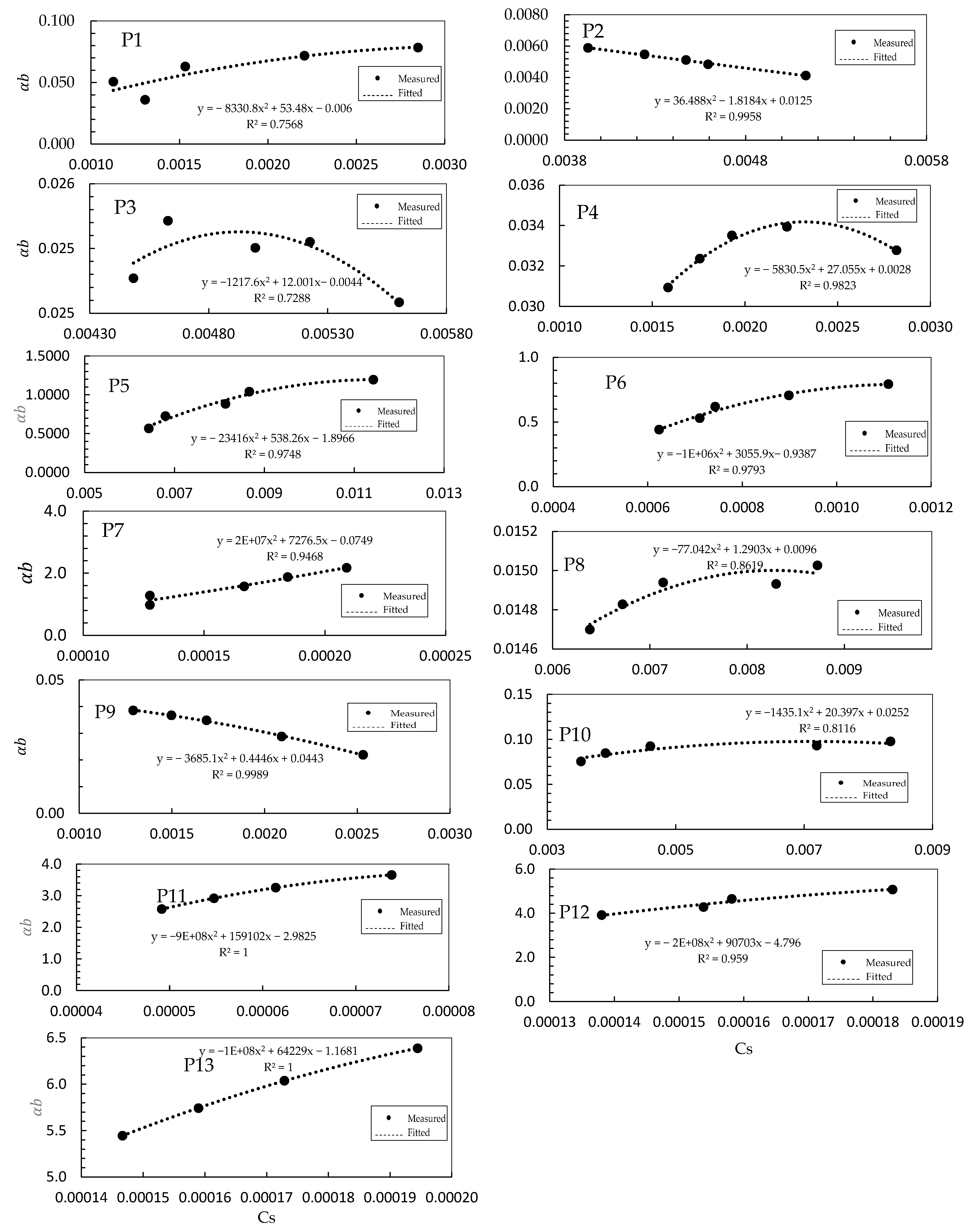
4.4. Analysis of Using the Cauchy Number
5. Discussion
6. Conclusions
- The nonmonotonic change in is due to the effect of flow nonuniformity in the rivers. In addition, the nonuniformity of the grain size distribution around each vegetated patch influences this nonmonotonic variation in .
- The maximum value of the drag coefficient is observed near the trailing edge of the vegetation patch in gravel-bed streams.
- The drag coefficient for vegetation patches, e.g., P1 to P4, P6, and P8 to P10, is lower than the drag coefficient of isolated vegetation , implying a sheltering effect. On the other hand, for some vegetation patches, e.g., P11 to P13, the drag coefficient is larger than, indicating a blockage effect.
- The blockage effect appears as , and the sheltering effect is observed for . Both the blockage effect and sheltering effect appear in the range of , especially for vegetation patches P5 and P7. Meanwhile, the bending deformation results in a significant reduction in the spacing distance between the bodies, causing an intensified sheltering effect and a lower form drag force.
- The drag coefficient factor changes with the Cauchy number in the streamwise flow direction. The variation in this factor is not stable from the leading to the trailing edge, showing a very complex flow pattern along a vegetation patch in rivers.
- Equation (18) can be used to predict the drag coefficient factor for submerged flexible vegetation patches in gravel bed rivers by using the velocity and Young’s modulus However, more data considering the boundary layer concept are needed along submerged flexible vegetation patches in rivers to predict a better drag coefficient.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Patch | a | b | c | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| P1 | 0.0341 | 0.44 | 0.13 | 0.14 | 0.12 | - | - | 0.1 | 0.088 | −0.0456 | 0.0007 | 0.1341 | 0.9172 | 3.63 | 0.67 | 0.32 | 0.0402 |
| P2 | 0.0186 | 0.65 | 0.16 | 0.154 | 0.15 | - | - | 0.148 | 0.14 | −0.002 | −0.0149 | 0.1593 | 0.9666 | 3.63 | 1.44 | 0.84 | 0.0309 |
| P3 | 0.0303 | 0.54 | 0.19 | 0.187 | 0.18 | - | - | 0.176 | 0.17 | −0.0595 | −0.0707 | 0.1904 | 0.9907 | 3.63 | 1.167 | 0.80 | 0.042 |
| P4 | 0.0201 | 0.60 | 0.16 | 0.152 | 0.145 | - | 0.135 | 0.12 | −0.0091 | −0.0133 | 0.1594 | 0.9962 | 3.63 | 0.982 | 0.57 | 0.04 | |
| P5 | 0.0655 | 0.29 | 0.18 | 0.175 | 0.16 | - | - | 0.155 | 0.135 | −0.0509 | −0.0316 | 0.1801 | 0.9753 | 3.85 | 1.01 | 1.25 | 0.029 |
| P6 | 0.0469 | 0.34 | 0.24 | 0.225 | 0.22 | - | - | 0.2 | 0.18 | −0.025 | −0.0275 | 0.2384 | 0.9849 | 4.8 | 0.64 | 0.93 | 0.038 |
| P7 | 0.0203 | 0.61 | 0.32 | 0.32 | 0.28 | - | - | 0.266 | 0.25 | −0.0059 | −0.0655 | 0.3251 | 0.933 | 4.5 | 0.6 | 0.7 | 0.037 |
| P8 | 0.0254 | 0.53 | 0.28 | 0.273 | 0.265 | - | - | 0.246 | 0.24 | −0.0006 | −0.0081 | 0.2809 | 0.8452 | 4.42 | 1.091 | 3.09 | 0.021 |
| P9 | 0.0186 | 0.65 | 0.28 | 0.26 | 0.245 | - | - | 0.22 | 0.2 | −0.0714 | −0.1714 | 0.2796 | 0.9968 | 3.88 | 1.365 | 0.847 | 0.041 |
| P10 | 0.0142 | 0.75 | 0.4 | 0.38 | 0.35 | - | - | 0.28 | 0.26 | −0.0317 | −0.0886 | 0.4043 | 0.9626 | 5.09 | 1.07 | 2.179 | 0.04 |
| P11 | 0.0321 | 0.42 | 0.38 | 0.35 | 0.34 | 0.36 | 0.35 | 0.34 | 0.31 | −0.1839 | −0.8094 | 0.9962 | 0.995 | 8.16 | 0.36 | 0.99 | 0.008 |
| P12 | 0.0233 | 0.58 | 0.38 | 0.35 | 0.36 | 0.34 | 0.33 | 0.33 | 0.33 | −0.1289 | −0.8109 | 0.9657 | 0.9603 | 8.16 | 0.36 | 0.99 | 0.008 |
| P13 | 0.0191 | 0.71 | 0.38 | 0.34 | 0.35 | 0.365 | 0.33 | 0.33 | 0.33 | −0.0858 | −0.9111 | 0.9982 | 0.9999 | 8.16 | 0.36 | 0.99 | 0.008 |
References
- Shi, H.; Liang, X.; Huai, W.; Wang, Y. Predicting the bulk average velocity of open-channel flow with submerged rigid vegetation. J. Hydrol. 2019, 572, 213–225. [Google Scholar] [CrossRef]
- Nepf, H.M. Drag, turbulence, and diffusion in flow through emergent vegetation. Water Resour. Res. 1999, 35, 479–489. [Google Scholar] [CrossRef]
- Afzalimehr, H.; Subhasish, D. Influence of bank vegetation and gravel bed on velocity and Reynolds stress distributions. Int. J. Sediment Res. 2009, 24, 236–246. [Google Scholar] [CrossRef]
- Afzalimehr, H.; Moghbel, R.; Gallichand, J.; Jueyi, S.U. Investigation of turbulence characteristics in channel with dense vegetation. Int. J. Sediment Res. 2011, 26, 269–282. [Google Scholar] [CrossRef]
- Stephan, U.; Gutknecht, D. Hydraulic resistance of submerged flexible vegetation. J. Hydrol. 2002, 269, 27–43. [Google Scholar] [CrossRef]
- Shahmohammadi, R.; Afzalimehr, H.; Sui, J. Impacts of turbulent flow over a channel bed with a vegetation patch on the incipient motion of sediment. Can. J. Civ. Eng. 2018, 45, 803–816. [Google Scholar] [CrossRef]
- Duan, J.G.; Barkdoll, B.; French, R. Lodging velocity for an emergent aquatic plant in open channels. J. Hydraul. Eng. 2006, 132, 1015–1020. [Google Scholar] [CrossRef]
- Afzalimehr, H.; Nosrati, K.; Kazem, M. Resistance to Flow in a Cobble-Gravel Bed River with Irregular Vegetation Patches and Pool-Riffle Bedforms (Case study: Padena Marbor River). Ferdowsi Civ. Eng. (JFCEI) 2021, 2, 35–50. [Google Scholar]
- Wilson, C.; Hoyt, J.; Schnauder, I. Impact of foliage on the drag force of vegetation in aquatic flows. J. Hydraul. Eng. 2008, 134, 885–891. [Google Scholar] [CrossRef] [Green Version]
- Kazem, M.; Afzalimehr, H.; Sui, J. Characteristics of Turbulence in the Downstream Region of a Vegetation Patch. Water 2021, 13, 3468. [Google Scholar] [CrossRef]
- Cheng, N.S. Representative roughness height of submerged vegetation. Water Resour. Res. 2011, 47, 1–18. [Google Scholar] [CrossRef]
- Wilson, C. Flow resistance models for flexible submerged vegetation. J. Hydrol. 2007, 342, 213–222. [Google Scholar] [CrossRef]
- Schoneboom, T.; Aberle, J.; Dittrich, A. Hydraulic resistance of vegetated flows: Contribution of bed shear stress and vegetative drag to total hydraulic resistance. River Flow 2010, 2010, 269–276. [Google Scholar]
- Tang, H.; Tian, Z.; Yan, J.; Yuan, S. Determining drag coefficients and their application in modelling of turbulent flow with submerged vegetation. Adv. Water Resour. 2014, 69, 134–145. [Google Scholar] [CrossRef]
- Etminan, V.; Lowe, R.J.; Ghisalberti, M. A new model for predicting the drag exerted by vegetation canopies. Water Resour. Res. 2017, 53, 3179–3196. [Google Scholar] [CrossRef]
- Tanino, Y.; Nepf, H.M. Laboratory investigation of mean drag in a random array of rigid, emergent cylinders. J. Hydraul. Eng. 2008, 134, 34–41. [Google Scholar] [CrossRef]
- Kazem, M.; Afzalimehr, H.; Sui, J. Formation of Coherent Flow Structures beyond Vegetation Patches in Channel. Water 2021, 13, 2812. [Google Scholar] [CrossRef]
- Cheng, N.-S. Calculation of drag coefficient for arrays of emergent circular cylinders with pseudofluid model. J. Hydraul. Eng. 2013, 139, 602–611. [Google Scholar] [CrossRef]
- Gosselin, F.P.; De Langre, E. Drag reduction by reconfiguration of a poroelastic system. J. Fluids Struct. 2011, 27, 1111–1123. [Google Scholar] [CrossRef]
- Kubrak, E.; Kubrak, J.; Rowiński, P.M. Influence of a method of evaluation of the curvature of flexible vegetation elements on vertical distributions of flow velocities. Acta Geophys. 2012, 60, 1098–1119. [Google Scholar] [CrossRef]
- Blackman, K.; Perret, L.; Savory, E. Effects of the upstream-flow regime and canyon aspect ratio on non-linear interactions between a street-canyon flow and the overlying boundary layer. Bound.-Layer Meteorol. 2018, 169, 537–558. [Google Scholar] [CrossRef]
- Aberle, J.; Järvelä, J. Flow resistance of emergent rigid and flexible floodplain vegetation. J. Hydraul. Res. 2013, 51, 33–45. [Google Scholar] [CrossRef]
- Kubrak, E.; Kubrak, J.; Rowiński, P.M. Vertical velocity distributions through and above submerged, flexible vegetation. Hydrol. Sci. J. 2008, 53, 905–920. [Google Scholar] [CrossRef]
- Vogel, S. Drag and reconfiguration of broad leaves in high winds. J. Exp. Bot. 1989, 40, 941–948. [Google Scholar] [CrossRef]
- Vettori, D.; Nikora, P.M. Morphological and mechanical properties of blades of Saccharina latissima. Estuarine. Coast. Shelf Sci. 2017, 196, 1–9. [Google Scholar] [CrossRef] [Green Version]
- Łoboda, A.M.; Przyborowski, Ł.; Karpiński, M.; Bialik, R.J.; Nikora, V.I. Biomechanical properties of aquatic plants: The effect of test conditions. Limnol. Oceanogr. Methods 2018, 16, 222–236. [Google Scholar] [CrossRef]
- Luhar, M.; Nepf, H.M. Flow-induced reconfiguration of buoyant and flexible aquatic vegetation. Limnol. Oceanogr. 2011, 56, 2003–2017. [Google Scholar] [CrossRef] [Green Version]
- Whittaker, P.; Wilson, C.A.; Aberle, J. An improved Cauchy number approach for predicting the drag and reconfiguration of flexible vegetation. Adv. Water Resour. 2015, 83, 28–35. [Google Scholar] [CrossRef]
- Rietkerk, M.; Boerlijst, M.C.; van Langevelde, F.; HilleRisLambers, R.; de Koppel, J.V.; Kumar, L.; Prins, H.H.; de Roos, A.M. Self-organization of vegetation in arid ecosystems. Am. Nat. 2002, 160, 524–530. [Google Scholar] [CrossRef]
- Nabaei, S.F.; Afzalimehr, H.; Sui, J.; Kumar, B.; Nabaei, S.H. Investigation of the Effect of Vegetation on Flow Structures and Turbulence Anisotropy around Semi-Elliptical Abutment. Water 2021, 13, 3108. [Google Scholar] [CrossRef]
- Wang, W.J.; Huai, W.X.; Thompson, S.; Katul, G.G. Steady nonuniform shallow flow within emergent vegetation. Water Resour. Res. 2015, 51, 10047–10064. [Google Scholar] [CrossRef]
- Dijkstra, J.; Uittenbogaard, R. Modeling the interaction between flow and highly flexible aquatic vegetation. Water Resour. Res. 2010, 46, 1–14. [Google Scholar] [CrossRef] [Green Version]
- Houser, C.; Trimble, S.; Morales, B. Influence of blade flexibility on the drag coefficient of aquatic vegetation. Estuaries Coasts 2015, 38, 569–577. [Google Scholar] [CrossRef]
- Luhar, M.; Infantes, E.; Nepf, H. Seagrass blade motion under waves and its impact on wave decay. J. Geophys. Res. Ocean. 2017, 122, 3736–3752. [Google Scholar] [CrossRef] [Green Version]
- Cavallaro, L.; Viviano, A.; Paratore, G.; Foti, E. Experiments on surface waves interacting with flexible aquatic vegetation. Ocean. Sci. J. 2018, 53, 461–474. [Google Scholar] [CrossRef] [Green Version]
- Wang, W.J.; Huai, W.X.; Thompson, S.; Peng, W.Q.; Katul, G.G. Drag coefficient estimation using flume experiments in shallow non-uniform water flow within emergent vegetation during rainfall. Ecol. Indic. 2018, 92, 367–378. [Google Scholar] [CrossRef]
- Liu, X.; Zeng, Y. Drag coefficient for rigid vegetation in subcritical open-channel flow. Environ. Fluid Mech. 2017, 17, 1035–1050. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, P.; Cheng, J.; Wang, W.J.; Zeng, L.; Wang, B. Drag coefficient of emergent flexible vegetation in steady nonuniform flow. Water Resour. Res. 2020, 56, e2020WR027613. [Google Scholar] [CrossRef]
- Niklas, K.J. Plant Biomechanics: An Engineering Approach to Plant form and Function; University of Chicago Press: Chicago, IL, USA, 1992. [Google Scholar]
- Jahadi, M.; Afzalimehr, H.; Rowinski, P.M. Flow structure within a vegetation patch in a gravel-bed river. J. Hydrol. Hydromech. 2019, 67, 154–162. [Google Scholar] [CrossRef] [Green Version]
- Wolman, M.G. A method of sampling coarse river-bed material. EOS Trans. Am. Geophys. Union 1954, 35, 951–956. [Google Scholar] [CrossRef]
- Chow, V.T. Open-Channel Hydraulics; McGraw-Hill Civil Engineering Series; McGraw-Hill: New York, NY, USA, 1959. [Google Scholar]
- Ghisalberti, M.; Nepf, H. The structure of the shear layer in flows over rigid and flexible canopies. Environ. Fluid Mech. 2006, 6, 277–301. [Google Scholar] [CrossRef]
- Melis, M.; Poggi, D.; Fasanella, G.O.; Cordero, S.; Katul, G.G. Resistance to flow on a sloping channel covered by dense vegetation following a dam break. Water Resour. Res. 2019, 55, 1040–1058. [Google Scholar] [CrossRef]
- Chapman, J.A.; Wilson, B.N.; Gulliver, J.S. Drag force parameters of rigid and flexible vegetal elements. Water Resour. Res. 2015, 51, 3292–3302. [Google Scholar] [CrossRef]
- Freeman, G.E.; Rahmeyer, W.; Derrick, D.L.; Copeland, R.R. Manning’s n Values for Floodplains with Shrubs and Woody Vegetation. Ph.D. Thesis, Colorado State University, Fort Collins, CO, USA, December 1998. [Google Scholar]
- Schlichting, H.; Gersten, K. Boundary-Layer Theory; Springer: Berlin/Heidelberg, Germany, 2016. [Google Scholar]





| Patch | Δs (mm) | ||||
|---|---|---|---|---|---|
| P1 | 1.05 | 0.013 | 0.048 | 1 | 4.8 |
| P2 | 0.59 | 0.27 | 0.055 | 0.8 | 5.2 |
| P3 | 0.24 | 0.09 | 0.047 | 1.1 | 5.6 |
| P4 | 1.46 | 0.47 | 0.066 | 0.8 | 5 |
| P5 | 0.67 | 0.29 | 0.1 | 1.3 | 4.5 |
| P6 | 1.07 | 0.53 | 0.16 | 1.1 | 4.5 |
| P7 | 1.08 | 0.72 | 0.21 | 0.82 | 5.1 |
| P8 | 4 | 0.25 | 0.12 | 0.9 | 5 |
| P9 | 0.4 | 0.15 | 0.05 | 0.8 | 5.2 |
| P10 | 1.2 | 0.38 | 0.03 | 0.7 | 5.2 |
| P11 | 0.96 | 0.72 | 0.28 | 0.9 | 4.45 |
| P12 | 0.96 | 0.72 | 0.085 | 0.9 | 5.22 |
| P13 | 0.96 | 0.72 | 0.08 | 0.9 | 5.77 |
| River | |||||||
|---|---|---|---|---|---|---|---|
| Beheshtabad | 3.5 | 0.16 | 0.3 | 7 | 0.99 | 0.2 | 116 |
| Padena Marbor | 14.25 | 0.15–0.21 | 0.8–1.0 | 3.37–5.2 | 0.54–0.87 | 0.59–0.85 | 150–182 |
| 10 | 0.26–0.64 | 1.0–1.1 | 1.8–14.6 | 1.8–3.09 | 0.44–0.5 | 424–698 | |
| 8.5 | 0.16–0.4 | 0.9–1.3 | 2.03–9.7 | 0.85–2.18 | 0.62–1.09 | 218–428 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nosrati, K.; Afzalimehr, H.; Sui, J. Drag Coefficient of Submerged Flexible Vegetation Patches in Gravel Bed Rivers. Water 2022, 14, 743. https://doi.org/10.3390/w14050743
Nosrati K, Afzalimehr H, Sui J. Drag Coefficient of Submerged Flexible Vegetation Patches in Gravel Bed Rivers. Water. 2022; 14(5):743. https://doi.org/10.3390/w14050743
Chicago/Turabian StyleNosrati, Kourosh, Hossein Afzalimehr, and Jueyi Sui. 2022. "Drag Coefficient of Submerged Flexible Vegetation Patches in Gravel Bed Rivers" Water 14, no. 5: 743. https://doi.org/10.3390/w14050743
APA StyleNosrati, K., Afzalimehr, H., & Sui, J. (2022). Drag Coefficient of Submerged Flexible Vegetation Patches in Gravel Bed Rivers. Water, 14(5), 743. https://doi.org/10.3390/w14050743





