Swine Wastewater Treatment in Constructed Wetland Systems: Hydraulic and Kinetic Modeling
Abstract
1. Introduction
2. Materials and Methods
2.1. Treatment System
2.2. Experimental Design
2.3. Hydrodynamic and Kinetic Studies
2.4. Statistical Analysis
3. Results and Discussion
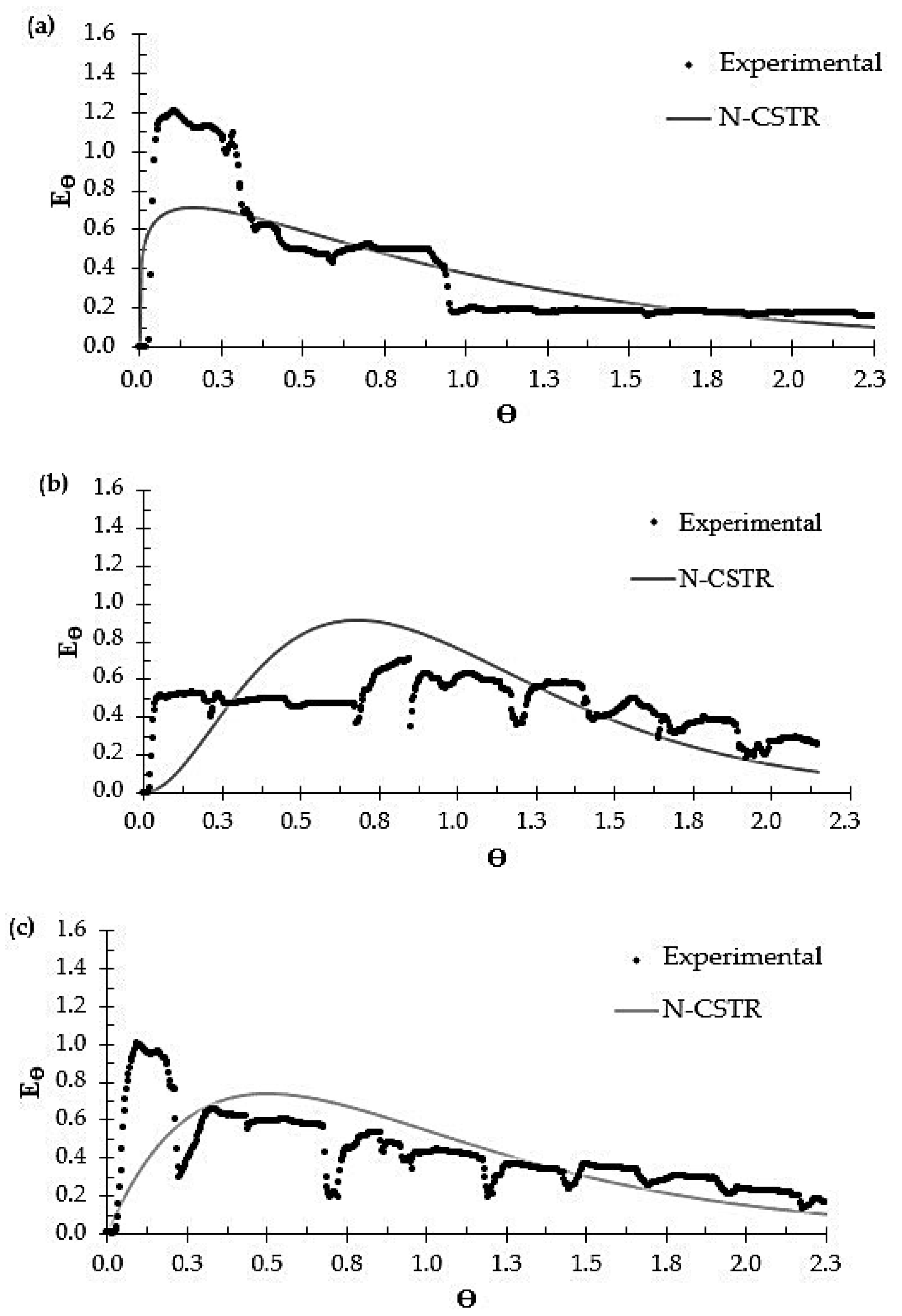
3.1. Hydrodynamic Study
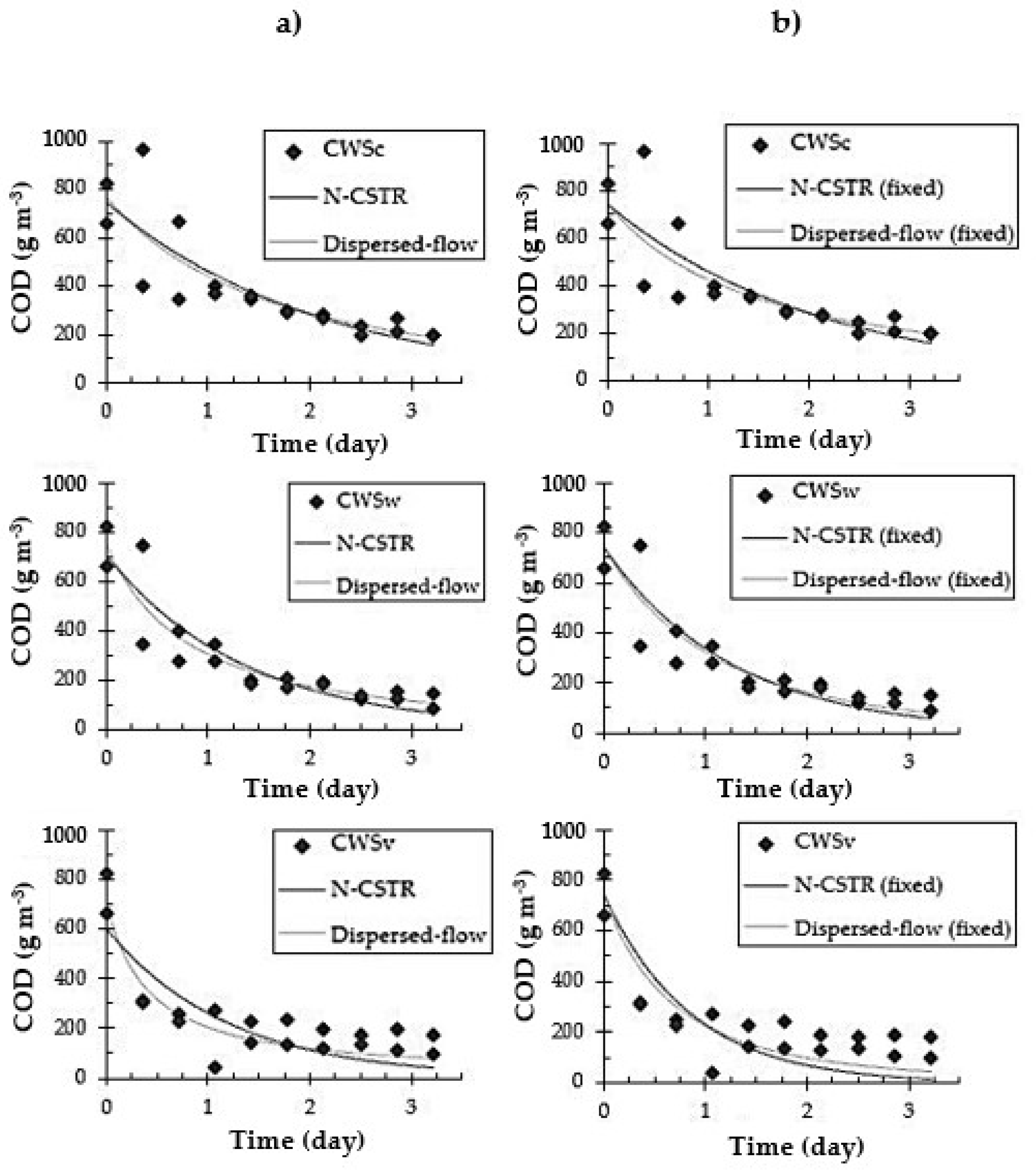
3.2. Fitting N-CSTR and Dispersed-Flow Models
3.3. Fitting Modified First-Order Models
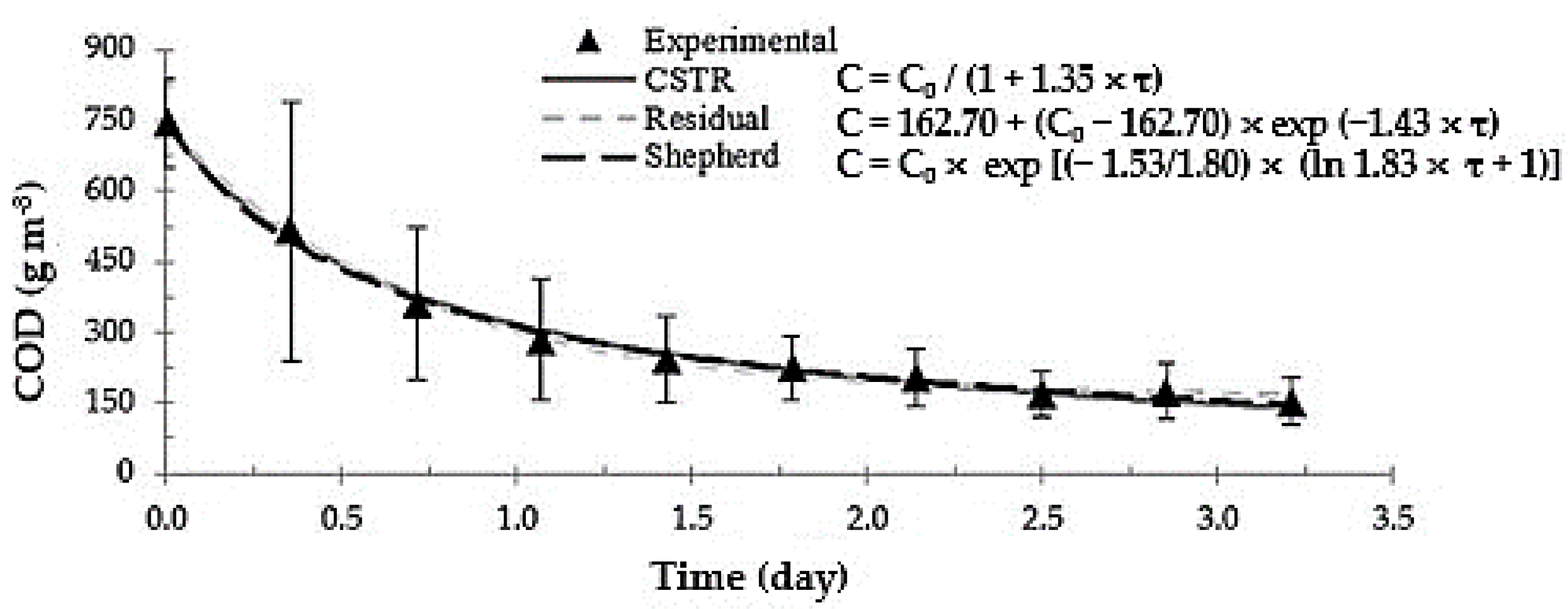
3.4. Fitting of Classic Models and Analysis of CW Systems Modeling
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Gómez-Limón, J.A.; Gutiérrez-Martín, C.; Montilla-López, N.M. Agricultural water allocation under cyclical scarcity: The role of priority water rights. Water 2020, 12, 1835. [Google Scholar] [CrossRef]
- Wang, D.; Hubacek, K.; Shan, Y.; Gerbens-Leenes, W.; Liu, J. A review of water stress and water footprint accounting. Water 2021, 13, 201. [Google Scholar] [CrossRef]
- Oliveira, G.A.; Colares, G.S.; Lutterbeck, C.A.; Dell’Osbel, N.; Machado, Ê.L.; Rodrigues, L.R. Floating treatment wetlands in domestic wastewater treatment as a decentralized sanitation alternative. Sci. Total Environ. 2021, 773, 145609. [Google Scholar] [CrossRef] [PubMed]
- Moreira, F.D.; Dias, E.H.O. Constructed wetlands applied in rural sanitation: A review. Environ. Res. 2020, 190, 110016. [Google Scholar] [CrossRef]
- Wang, Z.; Shi, Y.; Cheng, M.; He, C.; Zhuang, J.; Sheng, L. Purification of small-scale stagnant water in urban regions: Human-powered water lift and bank-based constructed wetland. Ecol. Eng. 2015, 83, 108–111. [Google Scholar] [CrossRef]
- Parde, D.; Patwa, A.; Shukla, A.; Vijay, R.; Killedar, D.J.; Kumar, R. A review of constructed wetland on type, treatment and technology of wastewater. Environ. Technol. Innov. 2021, 21, 101261. [Google Scholar] [CrossRef]
- Ji, Z.; Tang, W.; Pei, Y. Constructed wetland substrates: A review on development, function mechanisms, and application in contaminants removal. Chemosphere 2022, 286, 131564. [Google Scholar] [CrossRef] [PubMed]
- Vymazal, J. Constructed wetlands for wastewater treatment. Encycl. Ecol. 2018, 45, 14–21. [Google Scholar] [CrossRef]
- Zhang, D.Q.; Jinadasa, K.B.S.N.; Gersberg, R.M.; Liu, Y.; Ng, W.J.; Tan, S.K. Application of constructed wetlands for wastewater treatment in developing countries—A review of recent developments (2000–2013). J. Environ. Manag. 2014, 141, 116–131. [Google Scholar] [CrossRef]
- Zhang, D.Q.; Jinadasa, K.B.S.N.; Gersberg, R.M.; Liu, Y.; Tan, S.K.; Ng, W.J. Application of constructed wetlands for wastewater treatment in tropical and subtropical regions (2000–2013). J. Environ. Sci. 2015, 30, 30–46. [Google Scholar] [CrossRef]
- Sezerino, P.H.; Bento, A.P.; Decezaro, S.T.; Magri, M.E.; Philippi, L.S. Experiências brasileiras com wetlands construídos aplicados ao tratamento de águas residuárias: Parámetros de projeto para sistemas horizontais. Eng. Sanit. Ambient. 2015, 20, 151–158. [Google Scholar] [CrossRef]
- Machado, A.I.; Beretta, M.; Fragoso, R.; Duarte, E. Overview of the state of the art of constructed wetlands for decentralized wastewater management in Brazil. J. Environ. Manag. 2017, 187, 560–570. [Google Scholar] [CrossRef]
- Guo, C.; Cui, Y.; Dong, B.; Liu, F. Tracer study of the hydraulic performance of constructed wetlands planted with three different aquatic plant species. Ecol. Eng. 2017, 102, 433–442. [Google Scholar] [CrossRef]
- Kataki, S.; Chatterjee, S.; Vairale, M.G.; Dwivedi, S.K.; Gupta, D.K. Constructed wetland, an eco-technology for wastewater treatment: A review on types of wastewater treated and components of the technology (macrophyte, biofilm and substrate). J. Environ. Manag. 2021, 283, 111986. [Google Scholar] [CrossRef] [PubMed]
- Rizzo, A.; Langergraber, G. Novel insights on the response of horizontal flow constructed wetlands to sudden changes of influent organic load: A modeling study. Ecol. Eng. 2016, 93, 242–249. [Google Scholar] [CrossRef]
- Wang, H.; Sheng, L.; Xu, J. Clogging mechanisms of constructed wetlands: A critical review. J. Clean. Prod. 2021, 295, 126455. [Google Scholar] [CrossRef]
- Vymazal, J.; Zhao, Y.; Mander, Ü. Recent research challenges in constructed wetlands for wastewater treatment: A review. Ecol. Eng. 2021, 169, 106318. [Google Scholar] [CrossRef]
- Jehawi, O.H.; Abdullah, S.R.S.; Kurniawan, S.B.; Ismail, N.I.; Idris, M.; Al Sbani, N.H.; Muhamad, M.H.; Abu Hasan, H. Performance of pilot Hybrid Reed Bed constructed wetland with aeration system on nutrient removal for domestic wastewater treatment. Environ. Technol. Innov. 2020, 19, 100891. [Google Scholar] [CrossRef]
- Bakhshoodeh, R.; Alavi, N.; Majlesi, M.; Paydary, P. Compost leachate treatment by a pilot-scale subsurface horizontal flow constructed wetland. Ecol. Eng. 2017, 105, 7–14. [Google Scholar] [CrossRef]
- Hussain, Z.; Arslan, M.; Malik, M.H.; Mohsin, M.; Iqbal, S.; Afzal, M. Treatment of the textile industry effluent in a pilot-scale vertical flow constructed wetland system augmented with bacterial endophytes. Sci. Total Environ. 2018, 645, 966–973. [Google Scholar] [CrossRef]
- Ji, G.D.; Sun, T.H.; Ni, J.R. Surface flow constructed wetland for heavy oil-produced water treatment. Bioresour. Technol. 2007, 98, 436–441. [Google Scholar] [CrossRef] [PubMed]
- Schierano, M.C.; Panigatti, M.C.; Maine, M.A.; Griffa, C.A.; Boglione, R. Horizontal subsurface flow constructed wetland for tertiary treatment of dairy wastewater: Removal efficiencies and plant uptake. J. Environ. Manag. 2020, 272, 111094. [Google Scholar] [CrossRef] [PubMed]
- Feng, L.; Wang, R.; Jia, L.; Wu, H. Can biochar application improve nitrogen removal in constructed wetlands for treating anaerobically-digested swine wastewater? Chem. Eng. J. 2020, 379, 122273. [Google Scholar] [CrossRef]
- Fioreze, M.; Mancuso, M.A. MODFLOW and MODPATH for hydrodynamic simulation of porous media in horizontal subsurface flow constructed wetlands: A tool for design criteria. Ecol. Eng. 2019, 130, 45–52. [Google Scholar] [CrossRef]
- von Sperling, M.; Paoli, A.C. First-order COD decay coefficients associated with different hydraulic models applied to planted and unplanted horizontal subsurface-flow constructed wetlands. Ecol. Eng. 2013, 57, 205–209. [Google Scholar] [CrossRef]
- Stephenson, R.; Sheridan, C. Review of experimental procedures and modelling techniques for flow behaviour and their relation to residence time in constructed wetlands. J. Water Process Eng. 2021, 41, 102044. [Google Scholar] [CrossRef]
- Jiang, L.; Chui, T.F.M. A review of the application of constructed wetlands (CWs) and their hydraulic, water quality and biological responses to changing hydrological conditions. Ecol. Eng. 2022, 174, 106459. [Google Scholar] [CrossRef]
- Levenspiel, O. Engenharia das Reações Químicas: Cálculo de Reatores; Editora Edgard Blucher: São Paulo, Brazil, 2000. [Google Scholar]
- Kadlec, R.H.; Wallace, S. Treatment Wetlands, 2nd ed.; Taylor & Francis Group: Boca Raton, FL, USA, 2009; ISBN 978-1-56670-526-4. [Google Scholar]
- Brasil, M.D.; Matos, A.T.; Silva, C.M.; Cecon, P.R.; Soares, A.A. Modeling of pollution removal in constructed wetlands with horizontal subsurface flow. Agrartech. Forsch.-Agric. Eng. Res. 2007, 13, 48–56. [Google Scholar]
- Shepherd, H.L.; Tchobanoglous, G.; Grismer, M.E. Time-Dependent Retardation Model for Chemical Oxygen Demand Removal in a Subsurface-Flow Constructed Wetland for Winery Wastewater Treatment. Water Environ. Res. 2001, 73, 597–606. [Google Scholar] [CrossRef] [PubMed]
- Ramos, N.F.S.; Borges, A.C.; Gonçalves, G.C.; Matos, A.T. Tratamento de águas residuárias de suinocultura em sistemas alagados construídos, com Chrysopogon zizanioides e Polygonum punctatum cultivadas em leito de argila expandida. Eng. Sanit. Ambient. 2017, 22, 123–132. [Google Scholar] [CrossRef]
- APHA; AWWA; WEF. Standard Method for Examination of Water and Wastewater; APHA; AWWA; WEF: Washington, DC, USA, 2017. [Google Scholar]
- Matos, M.P.; Sperling, M.V.; Matos, A.T.; Passos, R.G. Uso de traçador salino para avaliação da colmatação e das condições hidrodinâmicas em sistemas alagados construídos de escoamento horizontal subsuperficial. Eng. Agric. 2015, 35, 1137–1148. [Google Scholar] [CrossRef]
- Paoli, A.C. Avaliação das condições hidrodinâmicas de wetlands construídos de escoamento horizontal subsuperficial (unidades plantada e não plantada). Rev. Eletrônica Gestão E Tecnol. Ambient. 2013, 1, 213–222. [Google Scholar] [CrossRef][Green Version]
- Bonner, R.; Aylward, L.; Kappelmeyer, U.; Sheridan, C. A comparison of three different residence time distribution modelling methodologies for horizontal subsurface flow constructed wetlands. Ecol. Eng. 2017, 99, 99–113. [Google Scholar] [CrossRef]
- Headley, T.R.; Davison, L.; Huett, D.O.; Mueller, R. Evapotranspiration from subsurface horizontal flow wetlands planted with Phragmites australis in sub-tropical Australia. Water Res. 2012, 46, 345–354. [Google Scholar] [CrossRef] [PubMed]
- Runkel, R.L. On the use of rhodamine WT for the characterization of stream hydrodynamics and transient storage. Water Resour. Res. 2015, 51, 6125–6142. [Google Scholar] [CrossRef]
- Metcalf, W.; Eddy, P. Wastewater Engineering: Treatment and Reuse; McGraw-Hill Inc.: New York, NY, USA, 2016. [Google Scholar]
- Barca, C.; Roche, N.; Troesch, S.; Andrès, Y.; Chazarenc, F. Modelling hydrodynamics of horizontal flow steel slag filters designed to upgrade phosphorus removal in small wastewater treatment plants. J. Environ. Manag. 2018, 206, 349–356. [Google Scholar] [CrossRef] [PubMed]
- De Nardi, I.R.; Zaiat, M.; Foresti, E. Influence of the tracer characteristics on hydrodynamic models of packed-bed bioreactors. Bioprocess Eng. 1999, 21, 469–476. [Google Scholar] [CrossRef]
- Dierberg, F.E.; DeBusk, T.A. An evaluation of two tracers in surface-flow wetlands: Rhodamine-WT and lithium. Wetlands 2005, 25, 8–25. [Google Scholar] [CrossRef]
- Aylward, L.; Bonner, R.; Sheridan, C.; Kappelmeyer, U. Hydraulic study of a non-steady horizontal sub-surface flow constructed wetland during start-up. Sci. Total Environ. 2019, 646, 880–892. [Google Scholar] [CrossRef]
- Colares, A.P.F.; Borges, A.C.; Carvalho, K.Q.; Rosa, A.P. Lítio, dextrana e rodamina na avaliação da hidrodinâmica de sistemas alagados construídos. Eng. Sanit. Ambient. 2021, 26, 701–710. [Google Scholar] [CrossRef]
- Spiess, A.N.; Neumeyer, N. An evaluation of R2as an inadequate measure for nonlinear models in pharmacological and biochemical research: A Monte Carlo approach. BMC Pharmacol. 2010, 10, 6. [Google Scholar] [CrossRef] [PubMed]
- Matos, A.T.; Matos, M.P.; Costa, R.A.; von Sperling, M. Influence of the geometric configuration of unplanted horizontal subsurface flow constructed wetlands in the adjustment of parameters of organic matter decay models. J. Water Process Eng. 2018, 22, 123–130. [Google Scholar] [CrossRef]
- Matos, A.T.; Freitas, W.S.; Borges, A.C. Estudo cinético da remoção de matéria orgânica de águas residuárias da suinocultura em sistemas alagados construídos com diferentes espécies vegetais. Eng. Agric. 2011, 31, 1179–1188. [Google Scholar] [CrossRef]
- Kadlec, R.H. The inadequacy of first-order treatment wetland models. Ecol. Eng. 2000, 15, 105–119. [Google Scholar] [CrossRef]
- Fia, F.R.L. Models for Removal of Organic Matter and Nutrients from Swine Wastewater in Constructed Wetland. Ph.D. Thesis, Federal University of Viçosa, Viçosa-MG, Brasil, 2006. (In Portuguese). [Google Scholar]
- Freitas, W.S. Performance of Constructed Wetland Systems Cropped with Different Vegetal Species in the Treatment of Swine Feedlot Wastewater. Ph.D. Thesis, Federal University of Viçosa, Viçosa-MG, Brasil, 2006. (In Portuguese). [Google Scholar]
- Fogler, H.S. Elementos de Engenharia das Reações Químicas, 4th ed.; LTC: Rio de Janeiro, Brasil, 2009; ISBN 978-85-216-1716-7. [Google Scholar]


| Wastewater | CWS | Plant | 1 L/W | HRT (d) | Flow Rate (L d−1) | 2 OP | 3 Co (mg L−1) | Ref |
|---|---|---|---|---|---|---|---|---|
| Domestic | 4 Hybrid | Scirpus grossus | 2 | 3 | 120 d | 72.42 | [18] | |
| Landfill leachate | HSSF | Chrysopogonzizanioides | 3 | 5 | 24 | 140 d | 16,366 | [19] |
| Textile | VF | Brachiaria mutica | 0.8 | Batch | 1 yr | 493 | [20] | |
| Petroleum | FWS | Phragmites australis | 10 | 7–15 | 3 yr | 390 | [21] | |
| Dairy | HSSF | Typha domingensis | 2.63 | 7 | 60 | 6 m | 269.1 | [22] |
| Swine | VF | Iris pseudacorus | 3 | Batch | 6 m | Stage 1:170 Stage 2:230 Stage 2:270 | [23] |
| Treatment | Plant Species |
|---|---|
| CWSV | Chrysopogon zizanioides (“vetiver grass”) |
| CWSw | Polygonum punctatum (“water pepper” or “dotted smartweed”) |
| CWSC | Control unit (unplanted) |
| Model | Equation |
|---|---|
| Dispersed-model | |
| N-CSTR (tanks-in-series) | |
| Plug flow reactor (PFR) | |
| PFR with residual C* | |
| Continuous stirred tank reactor (CSTR) | |
| CSTR with residual C* | |
| Brasil et al. [30] | |
| Shepherd et al. [31] |
| Model | Parameter | CWSC | CWSw | CWSV |
|---|---|---|---|---|
| N-CSTR | k (d−1) | 1.11 | 1.7 | 2.05 |
| N | 1 | 1.61 | 1.71 | |
| R2 | 0.72 | 0.83 | 0.65 | |
| RMSE | 122.17 | 92.53 | 116.91 | |
| Dispersed-flow | k (d−1) | 0.67 | 1.31 | 2.51 |
| d | 0.63 | 1.64 | 1.18 × 1010 | |
| R2 | 0.73 | 0.86 | 0.84 | |
| RMSE | 120.21 | 84.67 | 79.54 |
| Model | Parameter | CWSC | CWSw | CWSV |
|---|---|---|---|---|
| N-CSTR | k (d−1) | 0.97 | 1.22 | 3.45 |
| R2 | 0.72 | 0.83 | 0.6 | |
| RMSE | 115.56 | 88.75 | 119.33 | |
| Dispersed-flow | k (d−1) | 0.7 | 0.95 | 1.59 |
| R2 | 0.72 | 0.85 | 0.72 | |
| RMSE | 114.76 | 82.99 | 98.68 |
| Model | Coefficient | CWSC | CWSw | CWSV |
|---|---|---|---|---|
| 1 | k (d−1) | 0.85 | 1.56 | 2.4 |
| C* (g m−3) | 0 | 6.28 × 10−8 | 1.07 × 10−16 | |
| R2 | 0.72 | 0.86 | 0.84 | |
| RMSE | 121.37 | 85.71 | 74.03 | |
| 2 | k (d−1) | 0.78 | 1.25 | 3.5 |
| C* (g m−3) | 148.6 | 115.57 | 160.09 | |
| R2 | 0.73 | 0.86 | 0.90 | |
| RMSE | 119.48 | 83.6 | 62.58 | |
| 3 | k (d−1) | 0.54 | 0.87 | 1.26 |
| n | 0.86 | 0.73 | 0.28 | |
| R2 | 0.72 | 0.86 | 0.90 | |
| RMSE | 121.2 | 86.22 | 62.21 | |
| 4 | k (d−1) | 0.66 | 0.87 | 10.91 |
| b (d−1) | 0.35 | 0.73 | 29.13 | |
| R2 | 0.73 | 0.86 | 0.90 | |
| RMSE | 120.09 | 86.22 | 62.45 |
| Model | Parameter | CWS |
|---|---|---|
| CSTR | k (d−1) | 1.35 |
| R2 | 0.71 | |
| RMSE | 115.72 | |
| PFR | k (d−1) | 0.62 |
| R2 | 0.66 | |
| RMSE | 125.47 |
| Model | RMSE |
|---|---|
| Dispersed-flow | 16.58 |
| Tanks-in-series (N-CSTR) | 59.37 |
| PRF with residual C* | 11.74 |
| CSTR with residual C* | 16.58 |
| Brasil | 23.25 |
| Shepherd | 14.62 |
| PFR | 55.54 |
| CSTR | 15.51 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ramos, N.d.F.S.; Borges, A.C.; Coimbra, E.C.L.; Gonçalves, G.C.; Colares, A.P.F.; de Matos, A.T. Swine Wastewater Treatment in Constructed Wetland Systems: Hydraulic and Kinetic Modeling. Water 2022, 14, 681. https://doi.org/10.3390/w14050681
Ramos NdFS, Borges AC, Coimbra ECL, Gonçalves GC, Colares APF, de Matos AT. Swine Wastewater Treatment in Constructed Wetland Systems: Hydraulic and Kinetic Modeling. Water. 2022; 14(5):681. https://doi.org/10.3390/w14050681
Chicago/Turabian StyleRamos, Nilton de Freitas Souza, Alisson Carraro Borges, Eder Carlos Lopes Coimbra, Gustavo Castro Gonçalves, Ana Paula Ferreira Colares, and Antonio Teixeira de Matos. 2022. "Swine Wastewater Treatment in Constructed Wetland Systems: Hydraulic and Kinetic Modeling" Water 14, no. 5: 681. https://doi.org/10.3390/w14050681
APA StyleRamos, N. d. F. S., Borges, A. C., Coimbra, E. C. L., Gonçalves, G. C., Colares, A. P. F., & de Matos, A. T. (2022). Swine Wastewater Treatment in Constructed Wetland Systems: Hydraulic and Kinetic Modeling. Water, 14(5), 681. https://doi.org/10.3390/w14050681






