Future Climate-Driven Runoff Change in the Large River Basins in Eastern Siberia and the Far East Using Process-Based Hydrological Models
Abstract
:1. Introduction
2. Materials and Methods
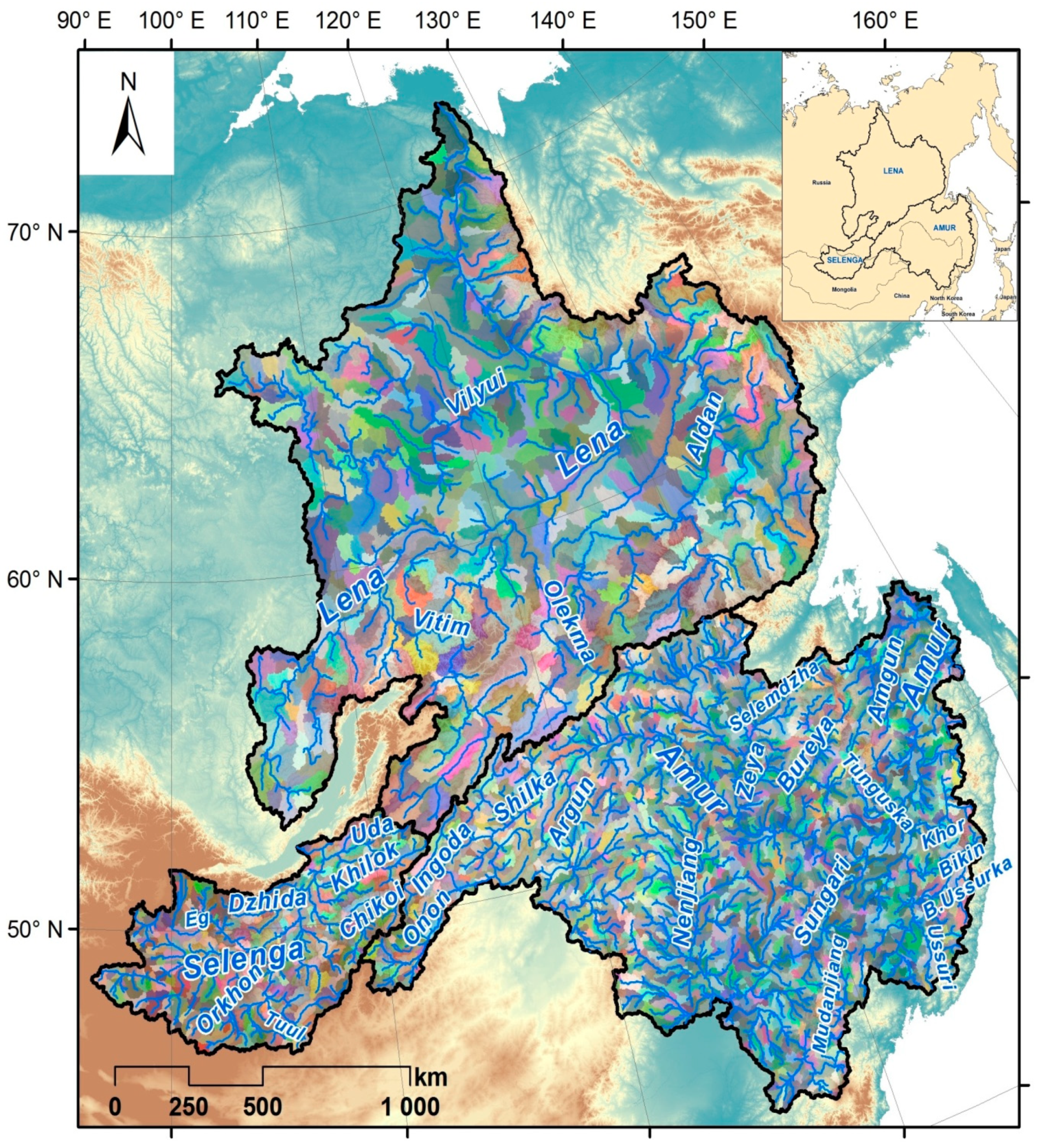
2.1. Study Area
2.2. Hydrological Models
2.3. Hydrological Modeling Using the GCM Output Data for the Historical Period
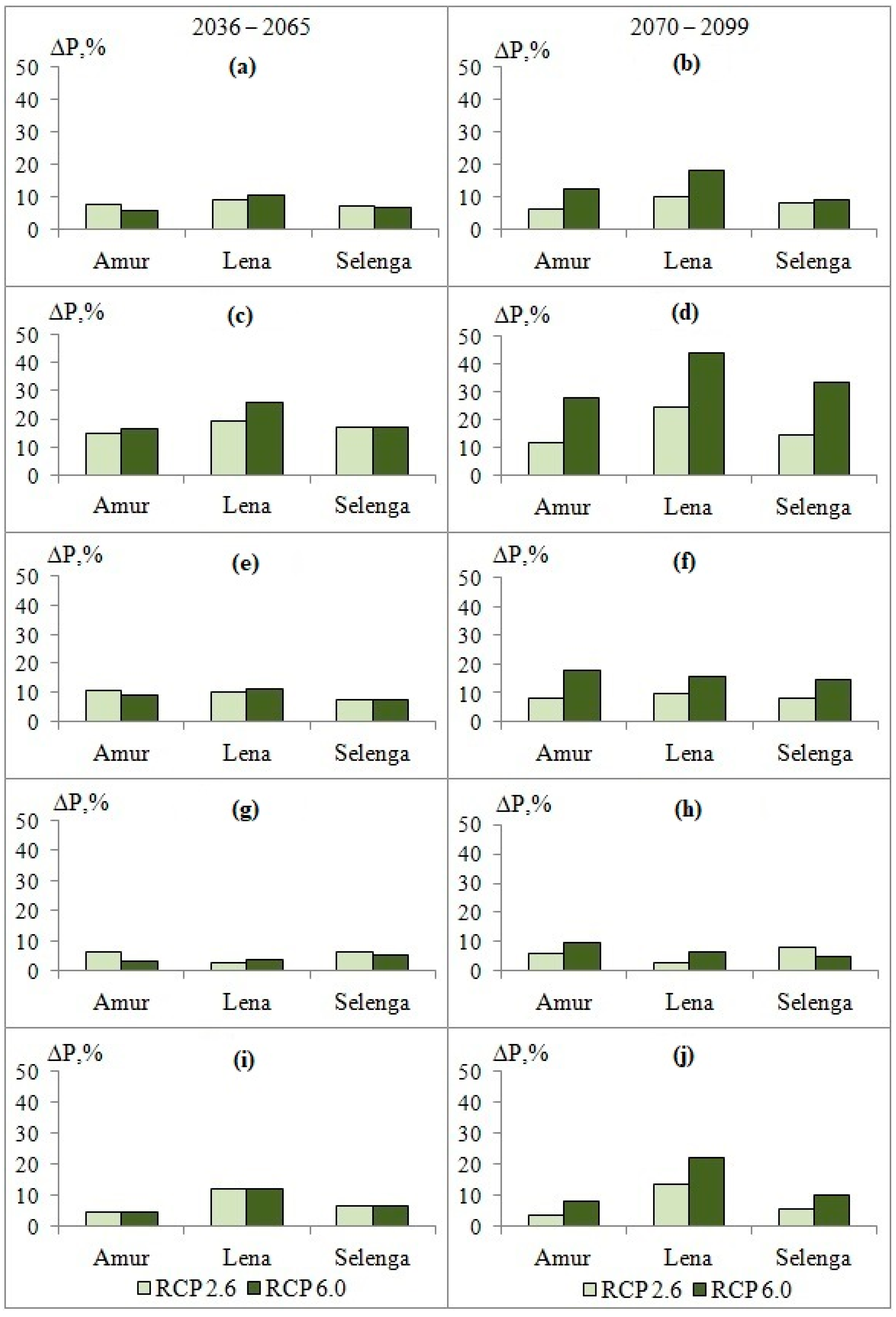
2.4. Changes in Air Temperature and Precipitation Using the GCM Output Data for the Future Period
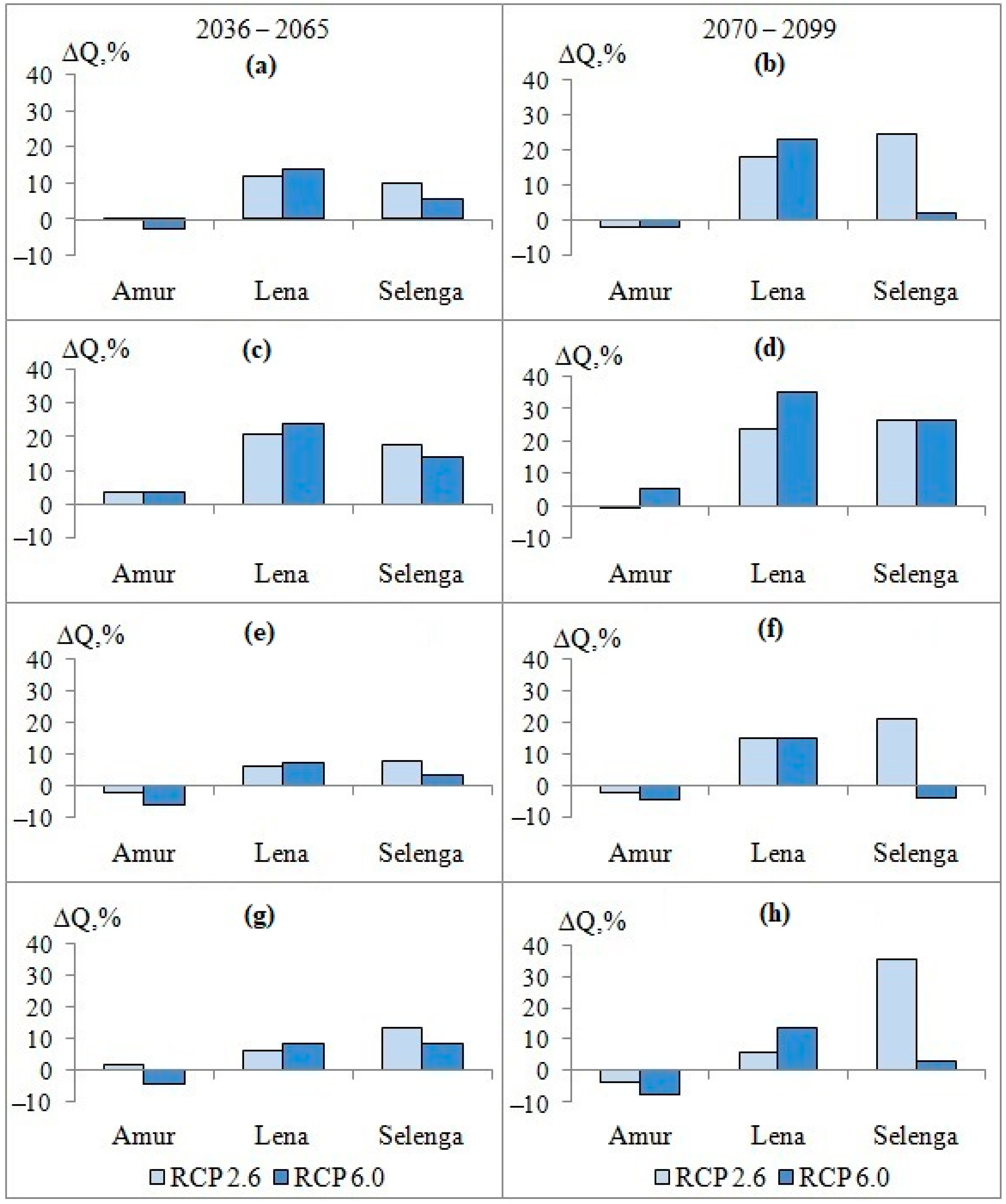
2.5. Hydrological Modeling Using the GCM Output Data for the Future Period
3. Results and Discussion
3.1. Hydrological Models
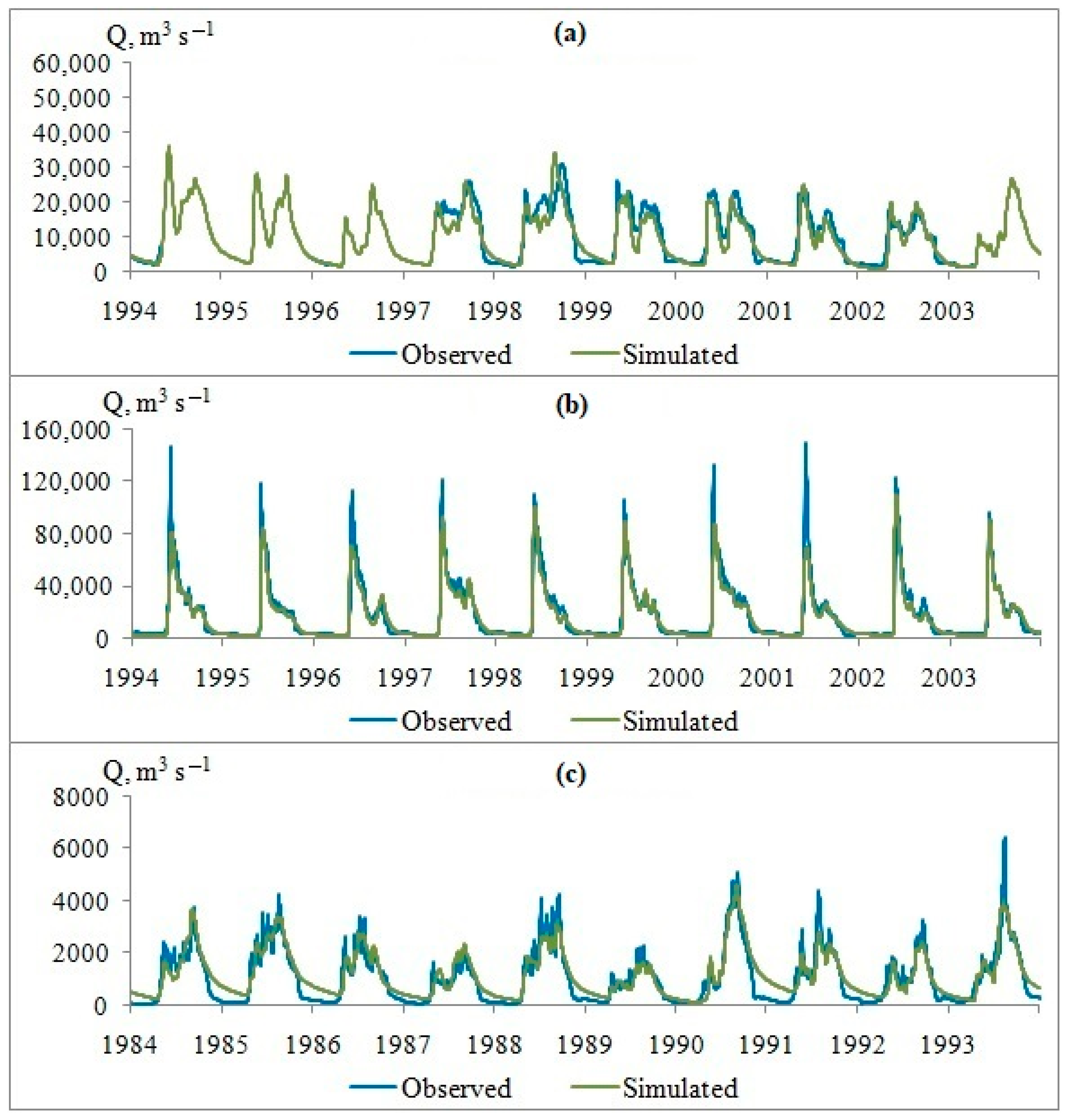
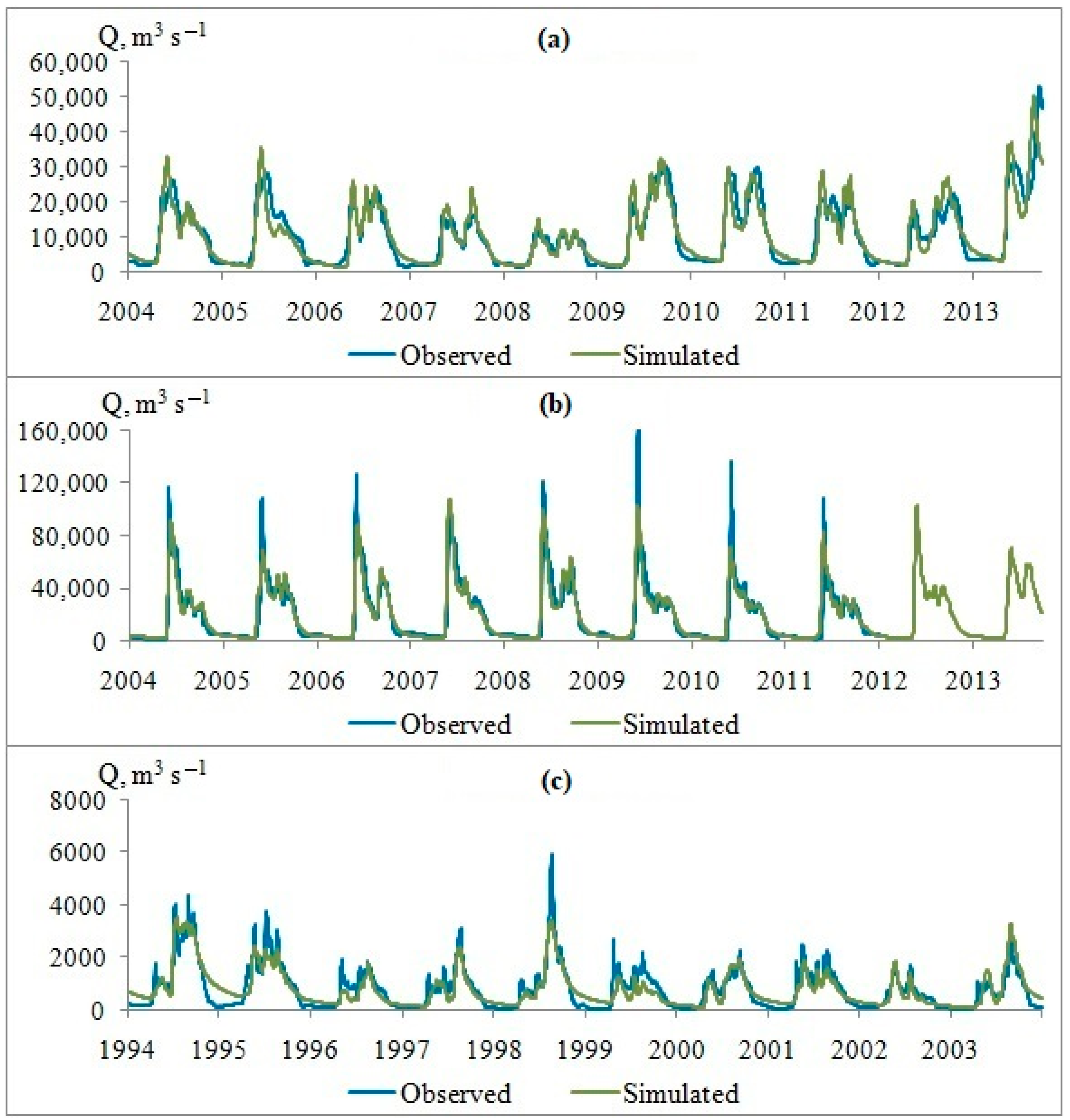
3.2. Hydrological Modeling Using the GCM Output Data for the Historical Period
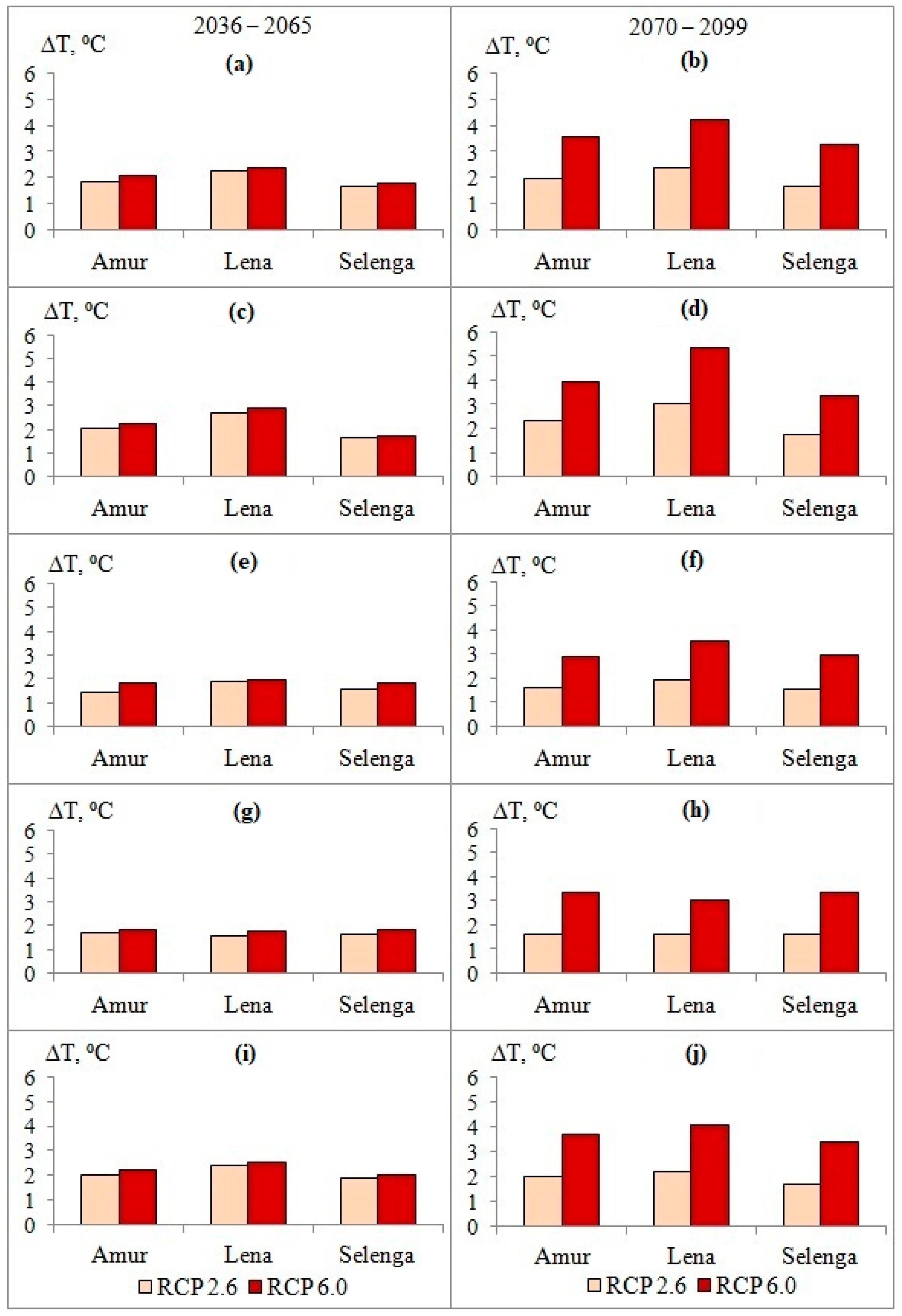
3.3. Changes in Air Temperature and Precipitation Using the GCM Output Data for the Future Period
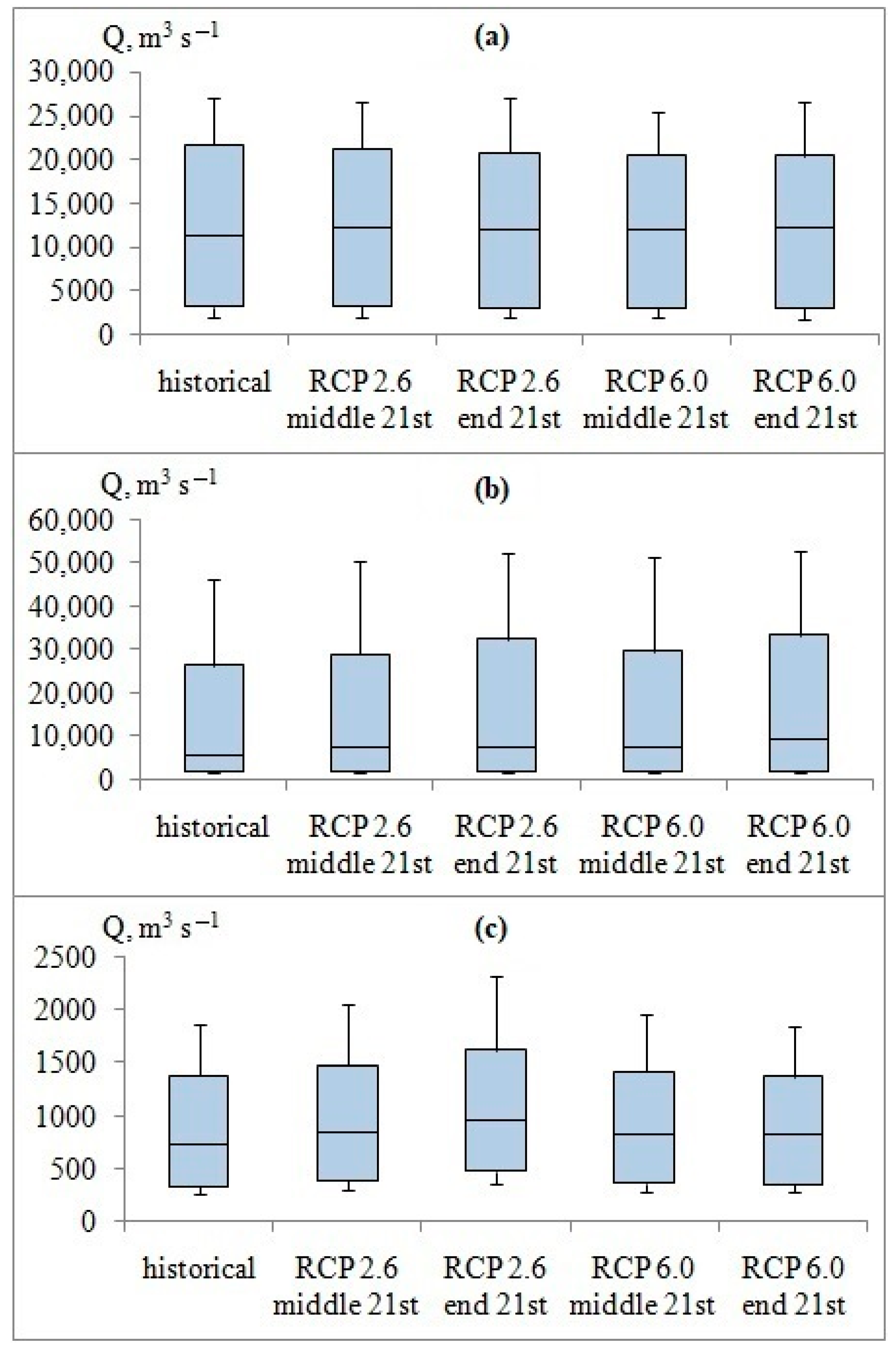
3.4. Hydrological Modeling Using the GCM Output Data for the Future Period
4. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Huang, S.; Kumar, R.; Florke, M.; Yang, T.; Hundecha, Y.; Kraft, P.; Gao, C.; Gelfan, A.; Liersch, S.; Lobanova, A.; et al. Evaluation of an ensemble of regional hydrological models in 12 large-scale river basins worldwide. Clim. Chang. 2017, 141, 381–397. [Google Scholar] [CrossRef]
- Krysanova, V.; Hattermann, F. Intercomparison of climate change impacts in 12 large river basins: Overview of methods and summary of results. Clim. Chang. 2017, 141, 363–379. [Google Scholar] [CrossRef]
- Krysanova, V.; Vetter, T.; Eisner, S.; Huang, S.; Pechlivanidis, I.; Strauch, M.; Gelfan, A.; Kumar, R.; Aich, V.; Arheimer, B.; et al. Intercomparison of regional-scale hydrological models and climate change impacts projected for 12 large river basins worldwide-a synthesis. Environ. Res. Lett. 2017, 12, 10. [Google Scholar] [CrossRef]
- Krysanova, V.; Donnelly, C.; Gelfan, A.; Gerten, D.; Arheimer, B.; Hattermann, F.; Kundzewicz, Z. How the performance of hydrological models relates to credibility of projections under climate change. Hydrol. Sci. J. 2018, 63, 696–720. [Google Scholar] [CrossRef]
- Gel’fan, A.; Kalugin, A.; Krylenko, I.; Nasonova, O.; Gusev, E.; Kovalev, E. Testing a hydrological model to evaluate climate change impact on river runoff. Russ. Meteorol. Hydrol. 2020, 45, 353–359. [Google Scholar] [CrossRef]
- Krysanova, V.; Hattermann, F.; Kundzewicz, Z. How evaluation of hydrological models influences results of climate impact assessment—An editorial. Clim. Chang. 2020, 163, 1121–1141. [Google Scholar] [CrossRef]
- Klemeš, V. Operational testing of hydrological simulation models. Hydrol. Sci. J. 1986, 31, 13–24. [Google Scholar] [CrossRef]
- Hattermann, F.; Krysanova, V.; Gosling, S.; Dankers, R.; Daggupati, P.; Donnelly, C.; Huang, S.; Motovilov, Y.; Buda, S.; Yang, T.; et al. Cross-scale intercomparison of climate change impacts simulated by regional and global hydrological models in eleven large river basins. Clim. Chang. 2017, 141, 561–576. [Google Scholar] [CrossRef]
- Gelfan, A.; Kalugin, A.; Krylenko, I.; Nasonova, O.; Gusev, Y.; Kovalev, E. Does a successful comprehensive evaluation increase confidence in a hydrological model intended for climate impact assessment? Clim. Chang. 2020, 163, 1165–1185. [Google Scholar] [CrossRef]
- Danilov-Danilyan, V.; Gelfan, A.; Motovilov, Y.; Kalugin, A. Disastrous flood of 2013 in the Amur basin: Genesis, recurrence assessment, simulation results. Water Resour. 2014, 41, 115–125. [Google Scholar] [CrossRef]
- Bugaets, A.; Gartsman, B.; Gelfan, A.; Motovilov, Y.; Sokolov, O.; Gonchukov, L.; Kalugin, A.; Moreido, V.; Suchilina, Z.; Fingert, E. The integrated system of hydrological forecasting in the Ussuri River basin based on the ECOMAG model. Geosciences 2018, 8, 5. [Google Scholar] [CrossRef] [Green Version]
- Magritsky, D.; Frolova, N.; Evstigneev, V.; Povalishnikova, E.; Kireeva, M.; Pakhomova, O. Long-term changes of river water inflow into the seas of the Russian Arctic sector. Polarforschung 2017, 87, 177–194. [Google Scholar] [CrossRef]
- Törnqvist, R.; Jarsjö, J.; Pietron, J.; Bring, A.; Rogberg, P.; Asokanb, S.; Destouni, G. Evolution of the hydro-climate system in the Lake Baikal basin. J. Hydrol. 2014, 519, 1953–1962. [Google Scholar] [CrossRef] [Green Version]
- Gelfan, A.; Kalugin, A.; Motovilov, Y. Assessing Amur water regime variations in the XXI century with two methods used to specify climate projections in river runoff formation model. Water Resour. 2018, 45, 307–317. [Google Scholar] [CrossRef]
- Moreido, V.; Kalugin, A. Assessing possible changes in Selenga River water regime in the XXI century based on a runoff formation model. Water Resour. 2017, 44, 390–398. [Google Scholar] [CrossRef]
- Eisner, S.; Florke, M.; Chamorro, A.; Daggupati, P.; Donnelly, C.; Huang, J.; Hundecha, Y.; Koch, H.; Kalugin, A.; Krylenko, I.; et al. An ensemble analysis of climate change impacts on streamflow seasonality across 11 large river basins. Clim. Chang. 2017, 141, 401–417. [Google Scholar] [CrossRef]
- Gusev, E.; Nasonova, O.; Kovalev, E.; Ayzel, G. Impact of possible climate change on extreme annual runoff from river basins located in different regions of the globe. Water Resour. 2019, 46, S126–S136. [Google Scholar] [CrossRef]
- Pechlivanidis, I.; Arheimer, B.; Donnelly, C.; Hundecha, Y.; Huang, S.; Aich, V.; Samaniego, L.; Eisner, S.; Shi, P. Analysis of hydrological extremes at different hydro-climatic regimes under present and future conditions. Clim. Chang. 2017, 141, 467–481. [Google Scholar] [CrossRef] [Green Version]
- Vetter, T.; Reinhardt, J.; Flörke, M.; van Griensven, A.; Hattermann, F.; Huang, S.; Koch, H.; Pechlivanidis, I.; Plötner, S.; Seidou, O.; et al. Evaluation of sources of uncertainty in projected hydrological changes under climate change in 12 large-scale river basins. Clim. Chang. 2017, 141, 419–433. [Google Scholar] [CrossRef]
- Gosling, S.; Zaherpour, J.; Mount, N.; Hattermann, F.; Dankers, R.; Arheimer, B.; Breuer, L.; Ding, J.; Haddeland, I.; Kumar, R.; et al. A comparison of changes in river runoff from multiple global and catchment-scale hydrological models under global warming scenarios of 1 °C, 2 °C and 3 °C. Clim. Chang. 2017, 141, 577–595. [Google Scholar] [CrossRef]
- Hudson, C.; Thompson, J. Hydrological modelling of climate change impacts on river flows in Siberia’s Lena River Basin and implications for the Atlantic Meridional Overturning Circulation. Hydrol. Res. 2019, 50, 1577–1595. [Google Scholar] [CrossRef] [Green Version]
- Gelfan, A.; Gustafsson, D.; Motovilov, Y.; Arheimer, B.; Kalugin, A.; Krylenko, I.; Lavrenov, A. Climate change impact on the water regime of two great Arctic rivers: Modeling and uncertainty issues. Clim. Chang. 2017, 141, 499–515. [Google Scholar] [CrossRef]
- Motovilov, Y.; Danilov-Danilyan, V.; Dod, E.; Kalugin, A. Assessing the flood control effect of the existing and projected reservoirs in the Middle Amur basin based on physical-mathematical hydrological models. Water Resour. 2015, 42, 580–593. [Google Scholar] [CrossRef]
- Motovilov, Y.; Gottschalk, L.; Engeland, K.; Rodhe, A. Validation of a distributed hydrological model against spatial observations. Agric. For. Meteorol. 1999, 98–99, 257–277. [Google Scholar] [CrossRef]
- Motovilov, Y. Hydrological simulation of river basins at different spatial scales: 1. Generalization and averaging algorithms. Water Resour. 2016, 43, 429–437. [Google Scholar] [CrossRef]
- Kalugin, A. Process-based modeling of the high flow of a semi-mountain river under current and future climatic conditions: A case study of the Iya River (Eastern Siberia). Water 2021, 13, 1042. [Google Scholar] [CrossRef]
- Motovilov, Y. Hydrological simulation of river basins at different spatial scales: 2. test results. Water Resour. 2016, 43, 743–753. [Google Scholar] [CrossRef]
- Kalugin, A. The impact of climate change on surface, subsurface and groundwater flow: A case study of the Oka River (European Russia). Water Resour. 2019, 46, S31–S39. [Google Scholar] [CrossRef]
- Frolova, N.; Grigorev, V.; Krylenko, I.; Zakharova, E. State-of-the-art potential of the GRACE satellite mission for solving modern hydrological problems. Vestn. St. Petersburg Univ. Earth Sci. 2021, 66, 107–122. [Google Scholar] [CrossRef]
- Gelfan, A.; Kalugin, A. Permafrost in the Caspian Basin as a possible trigger of the Late khvalynian transgression: Testing hypothesis using a hydrological model. Water Resour. 2021, 48, 831–843. [Google Scholar] [CrossRef]
- Kalugin, A. Modelling of future changes in the water regime of the Upper Kama River. In IOP Conference Series: Earth and Environmental Science; IOP Publishing: Bristol, UK, 2021; Volume 834, p. 012007. [Google Scholar] [CrossRef]
- Kalugin, A. Climate change attribution in the Lena and Selenga River runoff: An evaluation based on the Earth system and regional hydrological models. Water 2022, 14, 118. [Google Scholar] [CrossRef]
- Kalugin, A.; Lebedeva, L. Runoff generation at the small permafrost river basin in Eastern Siberia: Data analysis and hydrological modeling. In E3S Web of Conferences; EDP Sciences: Ulis, France, 2020; Volume 163, p. 01006. [Google Scholar] [CrossRef]
- Kornilova, E.D.; Krylenko, I.N.; Rets, E.P.; Motovilov, Y.G.; Bogachenko, E.M.; Krylenko, I.V.; Petrakov, D.A. Modeling of Extreme Hydrological Events in the Baksan River Basin, the Central Caucasus, Russia. Hydrology 2021, 8, 24. [Google Scholar] [CrossRef]
- Kalugin, A.; Motovilov, Y. Runoff formation model for the Amur River basin. Water Resour. 2018, 45, 149–159. [Google Scholar] [CrossRef]
- Gelfan, A.; Motovilov, Y.; Krylenko, I.; Moreido, V.; Zakharova, E. Testing the robustness of the physically-based ECOMAG model with respect to changing conditions. Hydrol. Sci. J. 2015, 60, 1266–1285. [Google Scholar] [CrossRef]
- Motovilov, Y.; Bugaets, A.; Gartsman, B.; Gonchukov, L.; Kalugin, A.; Moreido, V.; Suchilina, Z.; Fingert, E. Assessing the sensitivity of a model of runoff formation in the Ussuri River basin. Water Resour. 2018, 45, S128–S134. [Google Scholar] [CrossRef]
- Kalugin, A. Variations of the present-day annual and seasonal runoff in the Far East and Siberia with the use of regional hydrological and global climate models. Water Resour. 2018, 45, S102–S111. [Google Scholar] [CrossRef]
- Karthe, D.; Chalov, S.; Moreydo, V.; Efimov, V.; Romanchenko, A.; Batbayar, G.; Kalugin, A.; Westphal, K.; Malsy, M.; Flörke, M. Assessment of runoff, water and sediment quality in the Selenga river basin aided by a web-based geoservice. Water Resour. 2017, 44, 399–416. [Google Scholar] [CrossRef]
- Frieler, K.; Lange, S.; Piontek, F.; Reyer, C.; Schewe, J.; Warszawski, L.; Zhao, F.; Chini, L.; Denvil, S.; Emanuel, K.; et al. Assessing the impacts of 1.5 °C global warming—Simulation protocol of the Inter-Sectoral Impact Model Intercomparison Project (ISIMIP2b). Geosci. Model Dev. 2017, 10, 4321–4345. [Google Scholar] [CrossRef] [Green Version]
- Moriasi, D.; Arnold, J.; Van Liew, M.; Bingner, R.; Harmel, R.; Veith, T. Model evaluation guidelines for systematic quantification of accuracy in watershed simulations. Trans. Asabe 2007, 50, 885–900. [Google Scholar] [CrossRef]
- Hempel, S.; Frieler, K.; Warszawski, L.; Schewe, J.; Piontek, F. A trend-preserving bias correction—The ISI-MIP approach. Earth Syst. Dyn. 2013, 4, 219–236. [Google Scholar] [CrossRef] [Green Version]
- Lange, S. Trend-preserving bias adjustment and statistical downscaling with ISIMIP3BASD (v1.0). Geosci. Model Dev. 2019, 12, 3055–3070. [Google Scholar] [CrossRef] [Green Version]
- Mann, H.; Whitney, D. On a test of whether one of two random variables is stochastically larger than the other. Ann. Math. Stat. 1947, 18, 50–60. [Google Scholar] [CrossRef]
- Ren, Y.; Lü, Y.; Comber, A.; Fu, B.; Harris, P.; Wu, L. Spatially explicit simulation of land use/land cover changes: Current coverage and future prospects. Earth-Sci. Rev. 2019, 190, 398–415. [Google Scholar] [CrossRef]
- Sohl, T.; Wimberly, M.; Radeloff, V.; Theobald, D.; Sleeter, B. Divergent projections of future land use in the United States arising from different models and scenarios. Ecol. Model. 2016, 337, 281–297. [Google Scholar] [CrossRef] [Green Version]
| Parameter | Amur | Lena | Selenga |
|---|---|---|---|
| Catchment area, km2 | 1,855,000 | 2,490,000 | 447,000 |
| DEM | Hydro1k | ||
| Basin schematization, number of HRUs | 1947 | 664 | 469 |
| Soil | Harmonized World Soil Database | ||
| LULC | Global Land Cover Characterization | ||
| Meteorological data | 232 weather stations | 203 weather stations | EWEMBI reanalysis |
| Air temperature, °C | −0.3 | −8.9 | −2.3 |
| Precipitation, mm | 555 | 372 | 322 |
| Runoff depth, mm | 181 | 229 | 61 |
| River–Gauge | Catchment Area, km2 | Calibration | Validation | ||||
|---|---|---|---|---|---|---|---|
| NSE | KGE | PBIAS, % | NSE | KGE | PBIAS, % | ||
| Amur–Bogorodskoe | 1,790,000 | 0.83 | 0.89 | −5.7 | 0.83 | 0.91 | 0.7 |
| Lena–Kusur | 2,430,000 | 0.91 | 0.89 | −6.9 | 0.90 | 0.91 | −2.7 |
| Selenga–Mostovoi | 440,000 | 0.84 | 0.73 | 10.8 | 0.80 | 0.86 | −6.4 |
| River | Period | Annual | Spring Flood | Summer–Autumn Floods | Winter Low Flow | ||||
|---|---|---|---|---|---|---|---|---|---|
| RCP 2.6 | RCP 6.0 | RCP 2.6 | RCP 6.0 | RCP 2.6 | RCP 6.0 | RCP 2.6 | RCP 6.0 | ||
| Amur | 2036–2065 | − | − | − | − | − | − | − | + |
| 2070–2099 | − | − | − | − | − | − | − | − | |
| Lena | 2036–2065 | + | + | + | + | + | + | + | + |
| 2070–2099 | + | + | + | + | + | + | + | + | |
| Selenga | 2036–2065 | − | − | − | − | − | − | − | − |
| 2070–2099 | − | − | − | − | − | − | − | − | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kalugin, A. Future Climate-Driven Runoff Change in the Large River Basins in Eastern Siberia and the Far East Using Process-Based Hydrological Models. Water 2022, 14, 609. https://doi.org/10.3390/w14040609
Kalugin A. Future Climate-Driven Runoff Change in the Large River Basins in Eastern Siberia and the Far East Using Process-Based Hydrological Models. Water. 2022; 14(4):609. https://doi.org/10.3390/w14040609
Chicago/Turabian StyleKalugin, Andrey. 2022. "Future Climate-Driven Runoff Change in the Large River Basins in Eastern Siberia and the Far East Using Process-Based Hydrological Models" Water 14, no. 4: 609. https://doi.org/10.3390/w14040609
APA StyleKalugin, A. (2022). Future Climate-Driven Runoff Change in the Large River Basins in Eastern Siberia and the Far East Using Process-Based Hydrological Models. Water, 14(4), 609. https://doi.org/10.3390/w14040609






