Breaking Solitary Wave Impact on a Vertical Seawall
Abstract
:1. Introduction
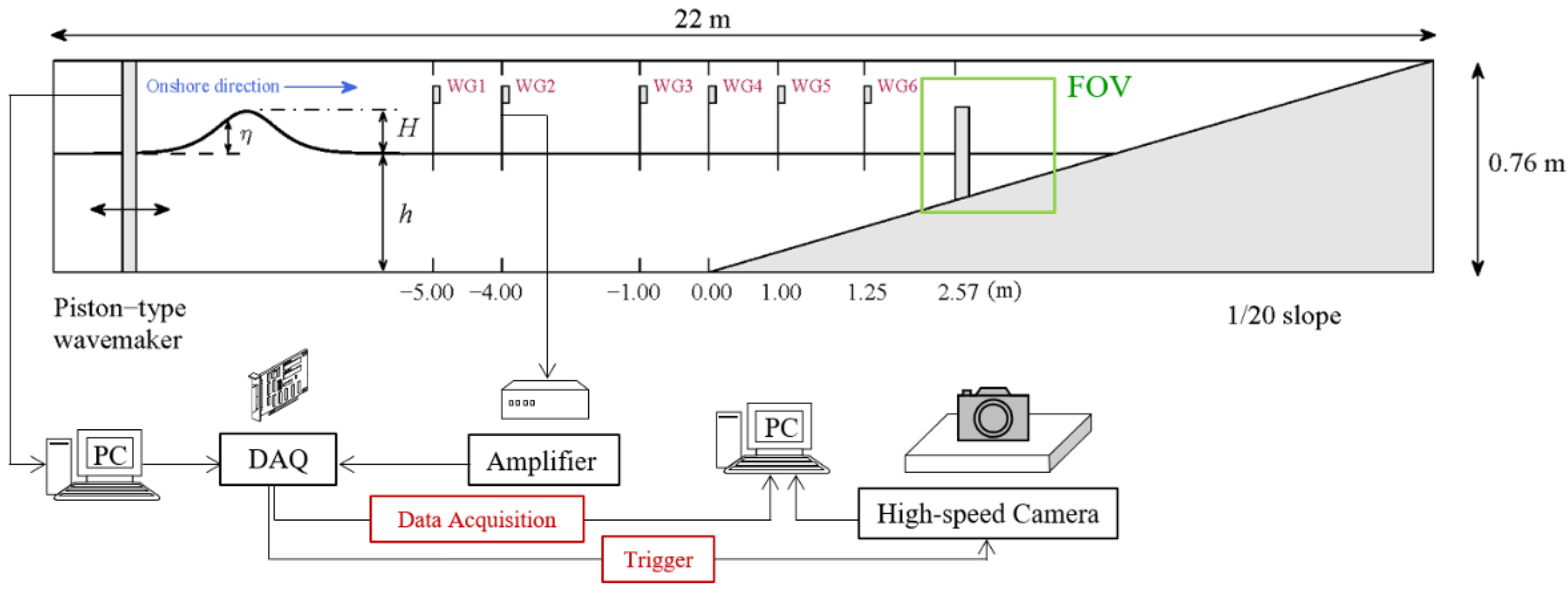
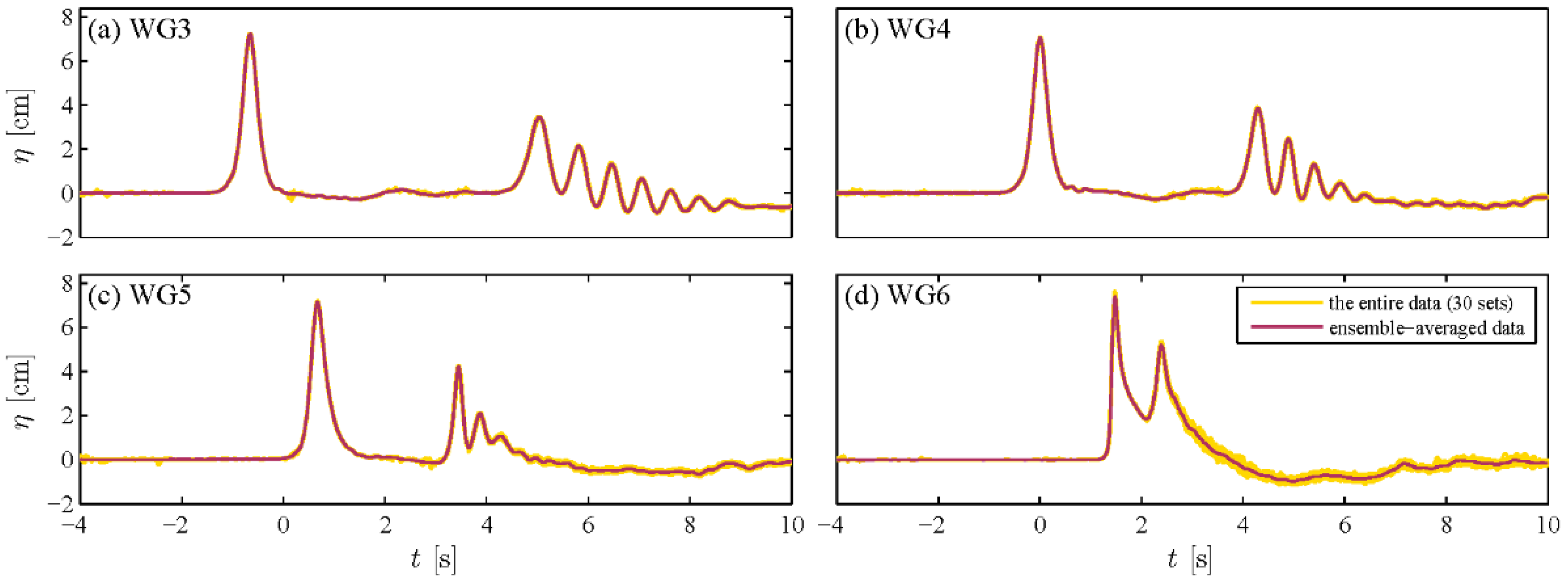
2. Experiment
3. Results and Discussion
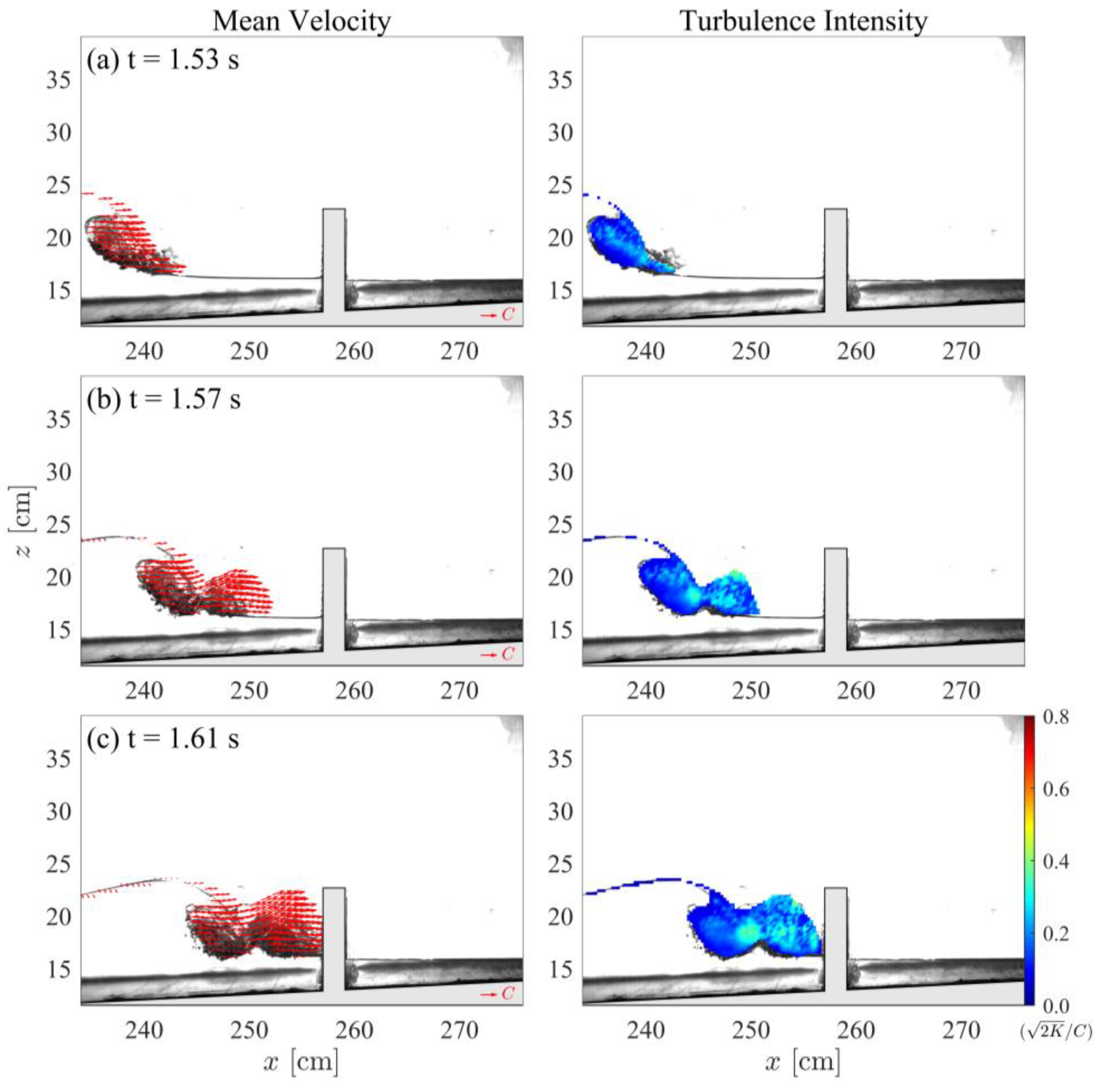
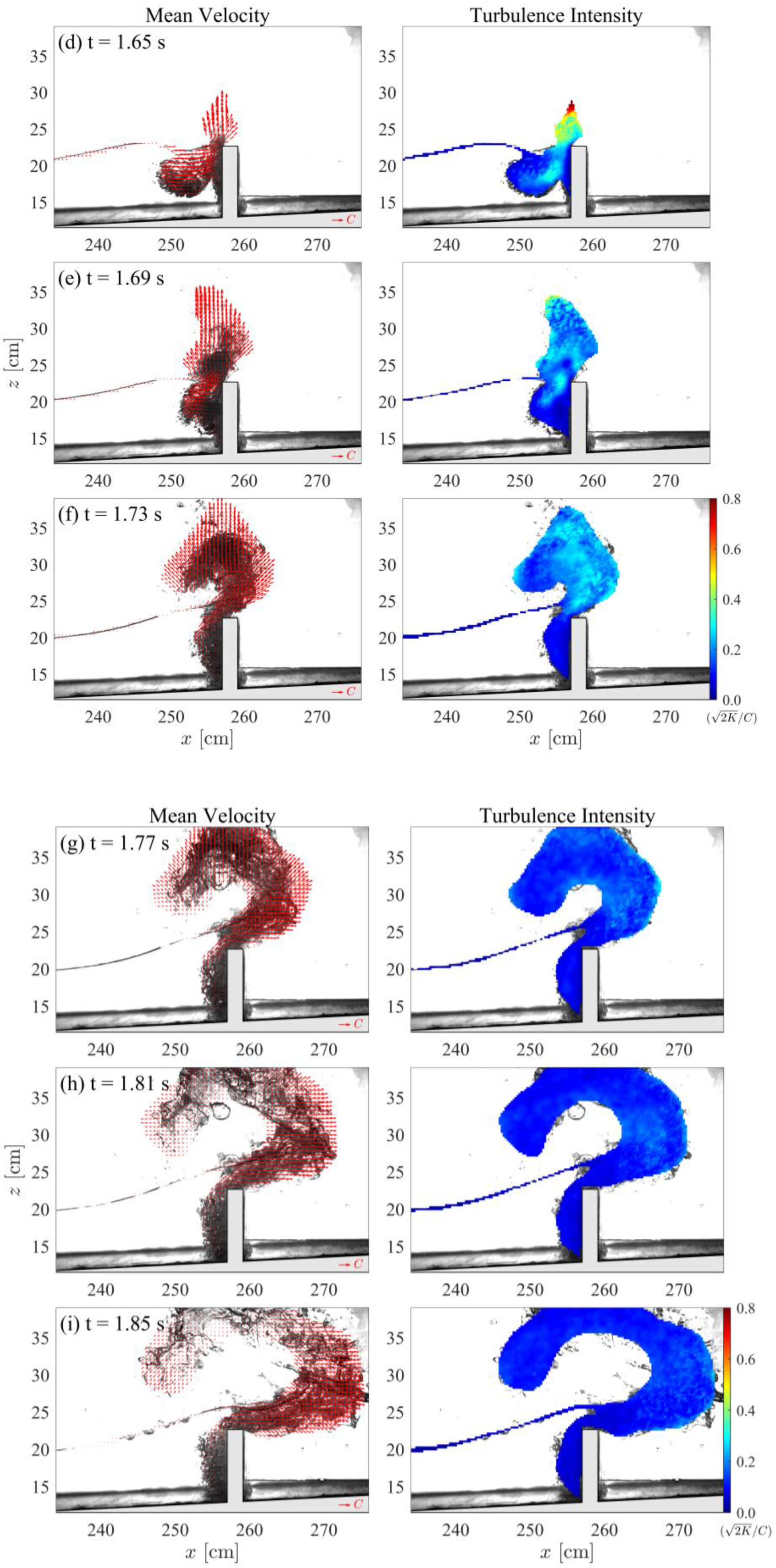
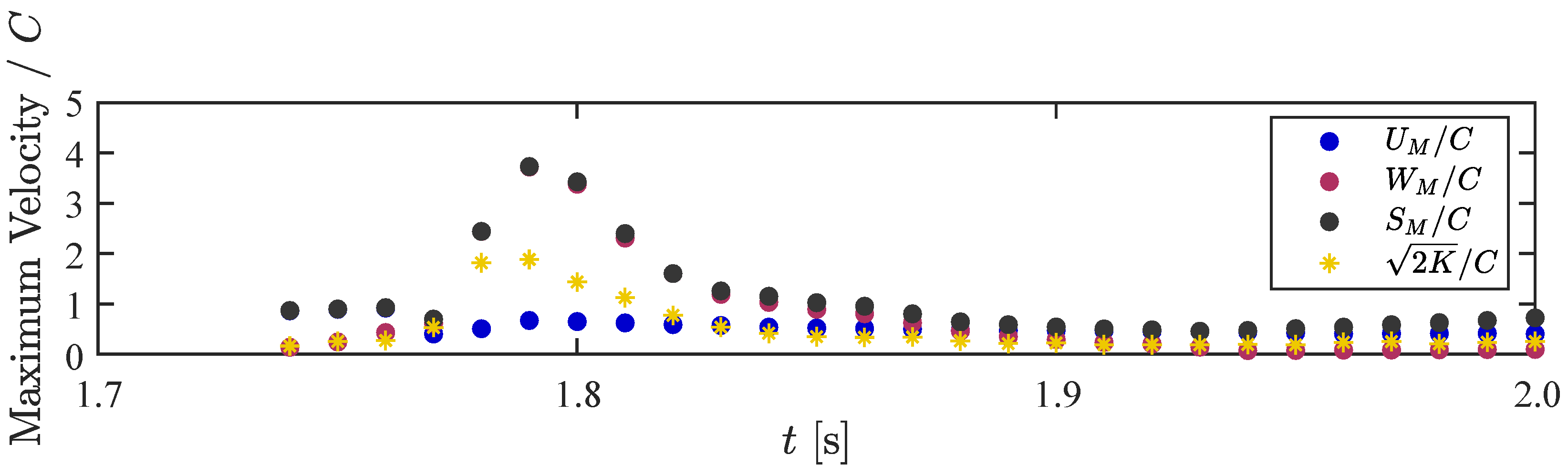
3.1. High-Aerated Case (H/h = 0.46)
3.2. Low-Aerated Case (H/h = 0.30)
4. Conclusions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Koosheh, A.; Etemad-Shahidi, A.; Cartwright, N.; Tomlinson, R.; van Gent, M.R.A. Individual wave overtopping at coastal structures: A critical review and the existing challenges. Appl. Ocean Res. 2021, 106, 102476. [Google Scholar] [CrossRef]
- Wang, D.; Li, S.; Arikawa, T.; Gen, H. ISPH simulation of scour behind seawall due to continuous tsunami overflow. Coast. Eng. J. 2016, 58, 1650014. [Google Scholar] [CrossRef]
- Mase, H.; Kimura, Y.; Yamakawa, Y.; Yasuda, T.; Mori, N.; Cox, D. Were coastal defensive structures completely broken by an unexpectedly large tsunami? A field survey. Earthq. Spectra 2013, 29, S145–S160. [Google Scholar] [CrossRef]
- Jayaratne, M.P.R.; Premaratne, B.; Adewale, A.; Mikami, T.; Matsuba, S.; Shibayama, T.; Esteban, M.; Nistor, I. Failure mechanisms and local scour at coastal structures induced by tsunami. Coast. Eng. J. 2016, 58, 1640017. [Google Scholar] [CrossRef] [Green Version]
- Xiao, H.; Huang, W.; Tao, J. Numerical modeling of wave overtopping a levee during Hurricane Katrina. Comput. Fluids 2009, 38, 991–996. [Google Scholar] [CrossRef]
- EurOtop. Manual on Wave Overtopping of Sea Defences and Related Structures: An Overtopping Manual Largely Based on European Research, but for Worldwide Application; 2018; Available online: http://www.overtopping-manual.com/assets/downloads/EurOtop_II_2018_Final_version.pdf (accessed on 11 January 2022).
- Chan, E.S.; Melville, W.K. Deep-water plunging wave pressures on a vertical plane wall. Proc. Roy. Soc. A-Math Phy. 1988, 417, 95–131. [Google Scholar]
- Kirkgöz, M.S. An experimental investigation of a vertical wall response to breaking wave impact. Ocean Eng. 1990, 17, 379–391. [Google Scholar] [CrossRef]
- Kirkgöz, M.S. Influence of water depth on the breaking wave impact on vertical and sloping walls. Coast. Eng. 1992, 18, 297–314. [Google Scholar] [CrossRef]
- Hattori, M.; Arami, A.; Yui, T. Wave impact pressure on vertical walls under breaking waves of various types. Coast. Eng. 1994, 22, 79–114. [Google Scholar] [CrossRef]
- Hull, P.; Müller, G. An investigation of breaker heights, shapes and pressures. Ocean Eng. 2002, 29, 59–79. [Google Scholar] [CrossRef]
- Bruce, T.; Pearson, J.; Allsop, W. Hazards at coast and harbour seawalls—velocities and trajectories of violent overtopping jets. In Proceedings of the 28th International Conference on Coastal Engineering, Cardiff, Wales, 7–12 July 2003; pp. 2216–2226. [Google Scholar]
- Jensen, A. Solitary wave impact on a vertical wall. Eur. J. Mech.—B/Fluids 2019, 73, 69–74. [Google Scholar] [CrossRef]
- Watanabe, Y.; Ingram, D.M. Transverse instabilities of ascending planar jets formed by wave impacts on vertical walls. Proc. R. Soc. A Math. Phys. Eng. Sci. 2015, 471, 20150397. [Google Scholar] [CrossRef] [Green Version]
- Watanabe, Y.; Ingram, D.M. Size distributions of sprays produced by violent wave impacts on vertical sea walls. Proc. R. Soc. A Math. Phys. Eng. Sci. 2016, 472, 20160423. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bullock, G.N.; Obhrai, C.; Peregrine, D.H.; Bredmose, H. Violent breaking wave impacts. Part 1: Results from large-scale regular wave tests on vertical and sloping walls. Coast. Eng. 2007, 54, 602–617. [Google Scholar] [CrossRef]
- Cuomo, G.; Allsop, W.; Bruce, T.; Pearson, J. Breaking wave loads at vertical seawalls and breakwaters. Coast. Eng. 2010, 57, 424–439. [Google Scholar] [CrossRef] [Green Version]
- Peregrine, D.H. Water-wave impact on walls. Annu. Rev. Fluid Mech. 2003, 35, 23–43. [Google Scholar] [CrossRef]
- Chuang, W.-L.; Chang, K.-A.; Mercier, R. Impact pressure and void fraction due to plunging breaking wave impact on a 2D TLP structure. Exp. Fluids 2017, 58, 68. [Google Scholar] [CrossRef]
- Chang, K.-A.; Liu, P.L.-F. Experimental investigation of turbulence generated by breaking waves in water of intermediate depth. Phys. Fluids 1999, 11, 3390–3400. [Google Scholar] [CrossRef]
- Ryu, Y.; Chang, K.-A.; Lim, H.-J. Use of bubble image velocimetry for measurement of plunging wave impinging on structure and associated greenwater. Meas. Sci. Technol. 2005, 16, 1945–1953. [Google Scholar] [CrossRef]
- Wu, Y.-T.; Liu, P.L.-F.; Hwang, K.-S.; Hwung, H.-H. Runup of laboratory-generated breaking solitary and periodic waves on a uniform slope. J. Waterw. Port Coast. Eng. 2018, 144, 04018023. [Google Scholar] [CrossRef]
- Lin, C.; Wong, W.-Y.; Kao, M.-J.; Tsai, C.-P.; Hwung, H.-H.; Wu, Y.-T.; Raikar, R. Evolution of velocity field and vortex structure during run-down of solitary wave over very steep beach. Water 2018, 10, 1713. [Google Scholar] [CrossRef] [Green Version]
- Tsaousis, T.D.; Chatjigeorgiou, I.K. An analytical approach for the two-dimensional plunging breaking wave impact on a vertical wall with air entrapment. Fluids 2020, 5, 58. [Google Scholar] [CrossRef]
- Wu, Y.-T.; Higuera, P.; Liu, P.L.-F. On the evolution and runup of a train of solitary waves on a uniform beach. Coast. Eng. 2021, 170, 104015. [Google Scholar] [CrossRef]
- Goring, D.G. Tsunamis-the Propagation of Long Waves onto a Shelf. Ph.D. Thesis, California Institute of Technology, Pasadena, CA, USA, 1978. [Google Scholar]
- Wu, Y.-T.; Hsiao, S.-C.; Huang, Z.-C.; Hwang, K.-S. Propagation of solitary waves over a bottom-mounted barrier. Coast. Eng. 2012, 62, 31–47. [Google Scholar] [CrossRef]
- Wu, Y.-T.; Hsiao, S.-C. Generation of stable and accurate solitary waves in a viscous numerical wave tank. Ocean Eng. 2018, 167, 102–113. [Google Scholar] [CrossRef]
- Grimshaw, R. The solitary wave in water of variable depth. Part 2. J. Fluid Mech. 1971, 46, 611–622. [Google Scholar] [CrossRef]
- Grilli, S.T.; Svendsen, I.A.; Subramanya, R. Breaking criterion and characteristics for solitary waves on slopes. J. Waterw. Port Coast. Eng. 1997, 123, 102–112. [Google Scholar] [CrossRef] [Green Version]
- Ryu, Y.; Chang, K.-A.; Mercier, R. Runup and green water velocities due to breaking wave impinging and overtopping. Exp. Fluids 2007, 43, 555–567. [Google Scholar] [CrossRef]
- Wu, Y.-T.; Hsiao, S.-C. Propagation of solitary waves over a submerged slotted barrier. J. Mar. Sci. Eng. 2020, 8, 419. [Google Scholar] [CrossRef]
- Mori, N.; Chang, K.-A. Introduction to MPIV. Available online: http://www.oceanwave.jp/softwares/mpiv/ (accessed on 11 January 2022).
- Chang, K.-A.; Ariyarathne, K.; Mercier, R. Three-dimensional green water velocity on a model structure. Exp. Fluids 2011, 51, 327–345. [Google Scholar] [CrossRef]
- Song, Y.K.; Chang, K.-A.; Ariyarathne, K.; Mercier, R. Surface velocity and impact pressure of green water flow on a fixed model structure in a large wave basin. Ocean Eng. 2015, 104, 40–51. [Google Scholar] [CrossRef]
- Song, Y.K.; Chang, K.-A.; Ryu, Y.; Kwon, S. Experimental study on flow kinematics and impact pressure in liquid sloshing. Exp. Fluids 2013, 54, 1592. [Google Scholar] [CrossRef]
- Lim, H.-J.; Chang, K.-A.; Huang, Z.-C.; Na, B. Experimental study on plunging breaking waves in deep water. J. Geophys. Res. Ocean. 2015, 120, 2007–2049. [Google Scholar] [CrossRef]
- Rivillas-Ospina, G.; Pedrozo-Acuña, A.; Silva, R.; Torres-Freyermuth, A.; Gutierrez, C. Estimation of the velocity field induced by plunging breakers in the surf and swash zones. Exp. Fluids 2012, 52, 53–68. [Google Scholar] [CrossRef]
- Wu, Y.-T.; Huang, K.-W.; Kobayashi, N. Runup of breaking solitary waves on rough uniform slopes. Ocean Eng. 2022, 245, 110551. [Google Scholar] [CrossRef]
- Lin, C.; Hsieh, S.-C.; Lin, I.-J.; Chang, K.-A.; Raikar, R.V. Flow property and self-similarity in steady hydraulic jumps. Exp. Fluids 2012, 53, 1591–1616. [Google Scholar] [CrossRef]
- Boussinesq, M.J. Théorie de l’intumescence liquide, appelée onde solitaire ou de translation, se propageant dans un canal rectangulaire. C. R. Acad. Sci. Paris 1871, 72, 755–759. [Google Scholar]
- Zhao, E.; Qu, K.; Mu, L. Numerical study of morphological response of the sandy bed after tsunami-like wave overtopping an impermeable seawall. Ocean Eng. 2019, 186, 106076. [Google Scholar] [CrossRef]
- Ahmad, N.; Bihs, H.; Myrhaug, D.; Kamath, A.; Arntsen, Ø.A. Numerical modeling of breaking wave induced seawall scour. Coast. Eng. 2019, 150, 108–120. [Google Scholar] [CrossRef]
- Chuang, W.-L.; Chang, K.-A.; Mercier, R. Green water velocity due to breaking wave impingement on a tension leg platform. Exp. Fluids 2015, 56, 139. [Google Scholar] [CrossRef]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, Y.-T. Breaking Solitary Wave Impact on a Vertical Seawall. Water 2022, 14, 583. https://doi.org/10.3390/w14040583
Wu Y-T. Breaking Solitary Wave Impact on a Vertical Seawall. Water. 2022; 14(4):583. https://doi.org/10.3390/w14040583
Chicago/Turabian StyleWu, Yun-Ta. 2022. "Breaking Solitary Wave Impact on a Vertical Seawall" Water 14, no. 4: 583. https://doi.org/10.3390/w14040583
APA StyleWu, Y.-T. (2022). Breaking Solitary Wave Impact on a Vertical Seawall. Water, 14(4), 583. https://doi.org/10.3390/w14040583





