Impacts of Precipitation Type Variations on Runoff Changes in the Source Regions of the Yangtze and Yellow River Basins in the Past 40 Years
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Identification of Precipitation Types
2.3. Modified Budyko Framework Considering Snowfall Factor
2.4. Statistical Analysis
2.5. Data
3. Results
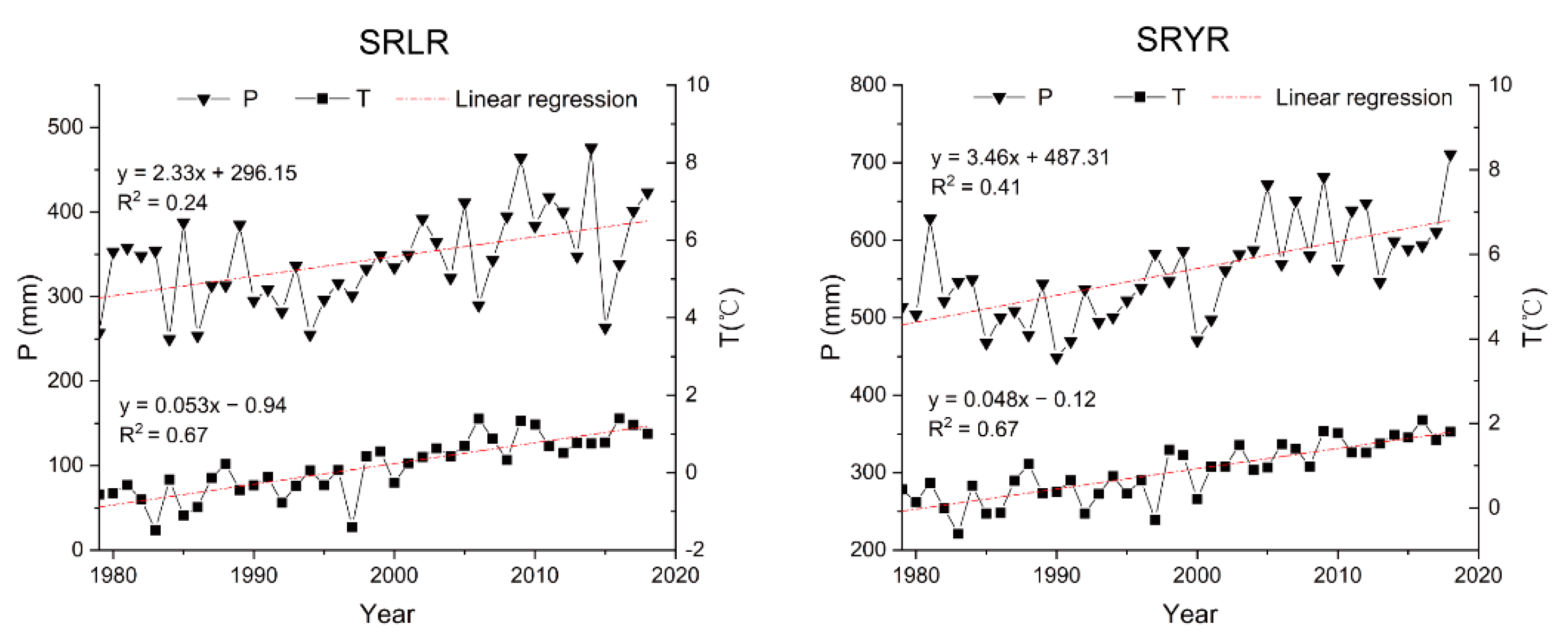
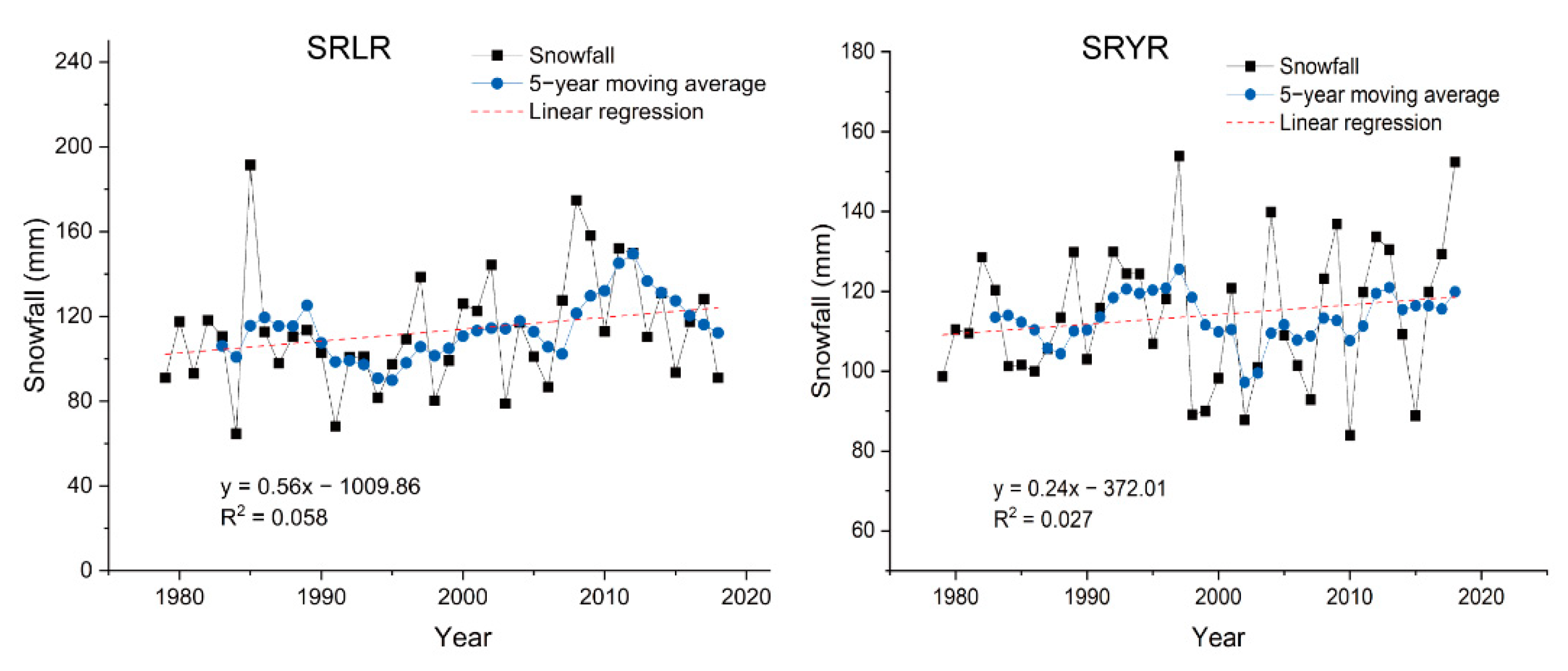
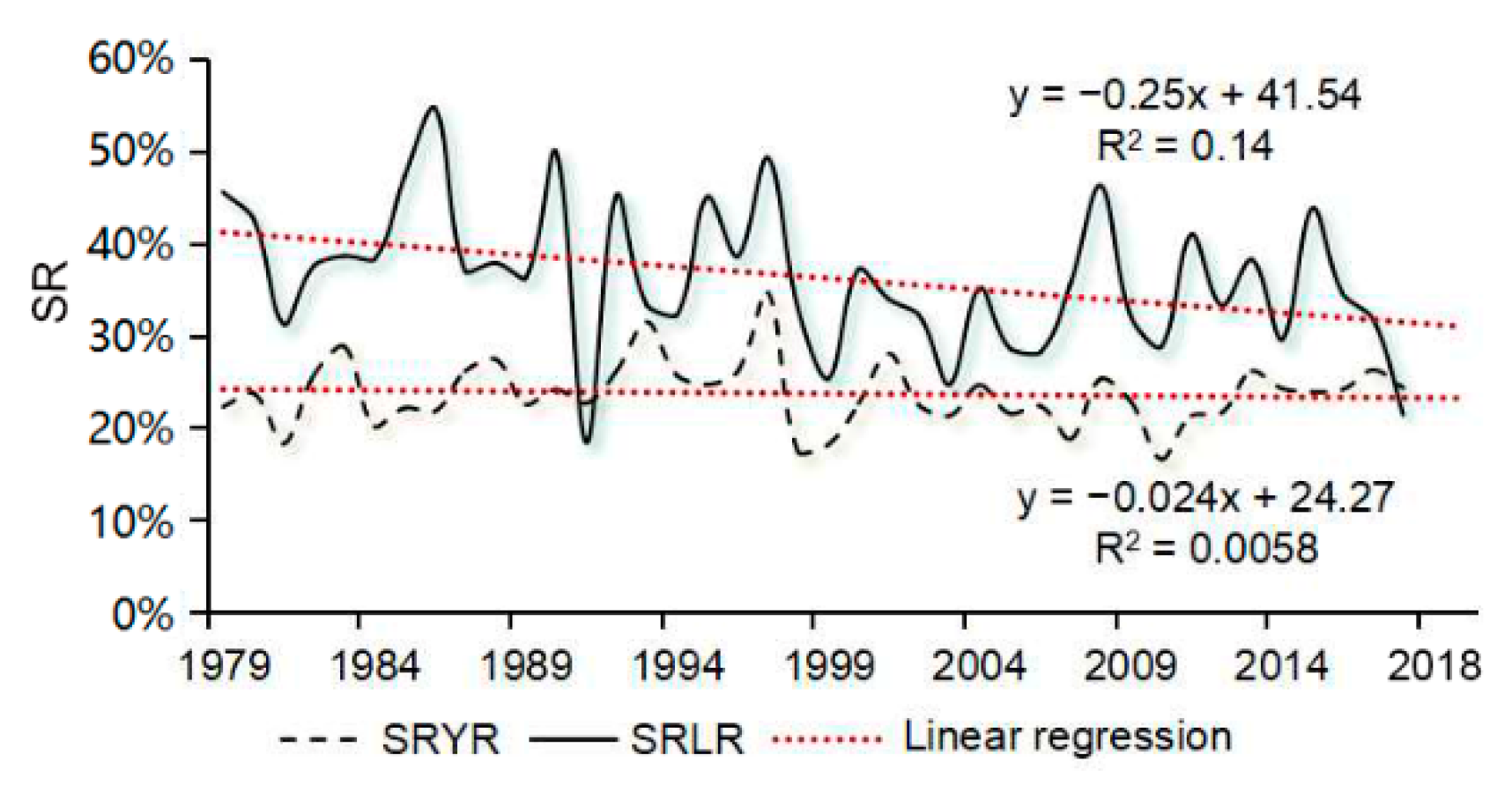
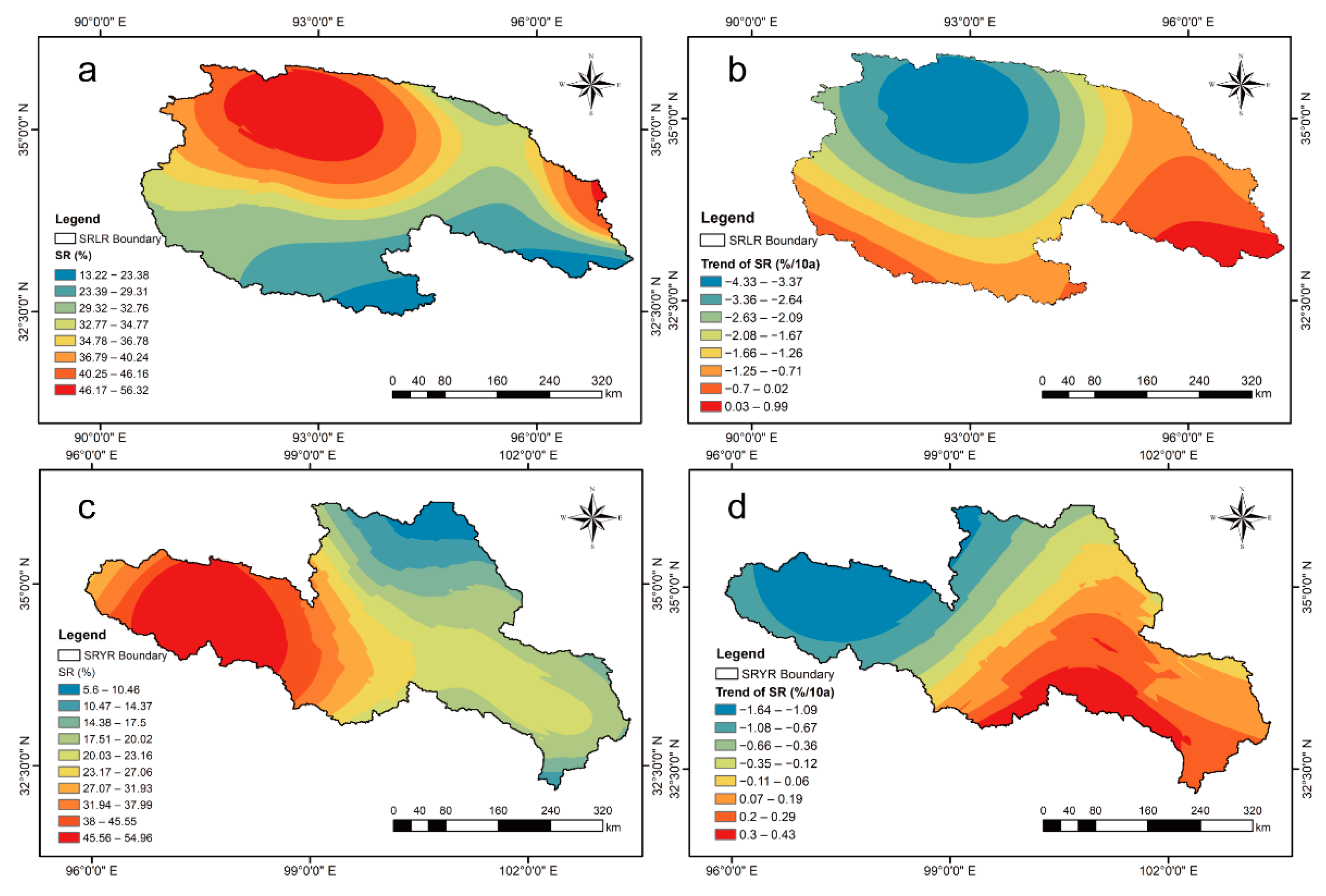
3.1. Variations of the Precipitation Type of the SRLR and SRYR
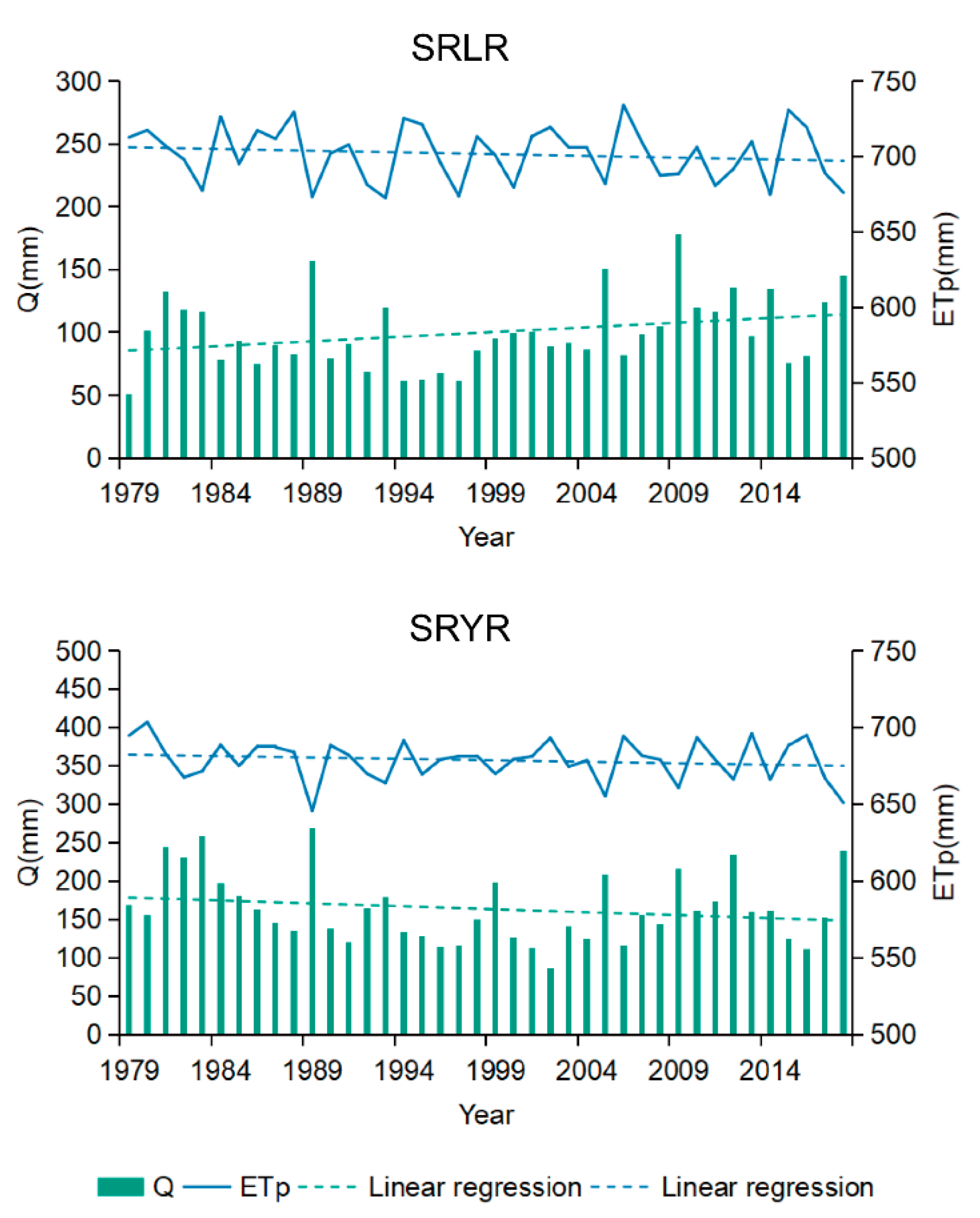
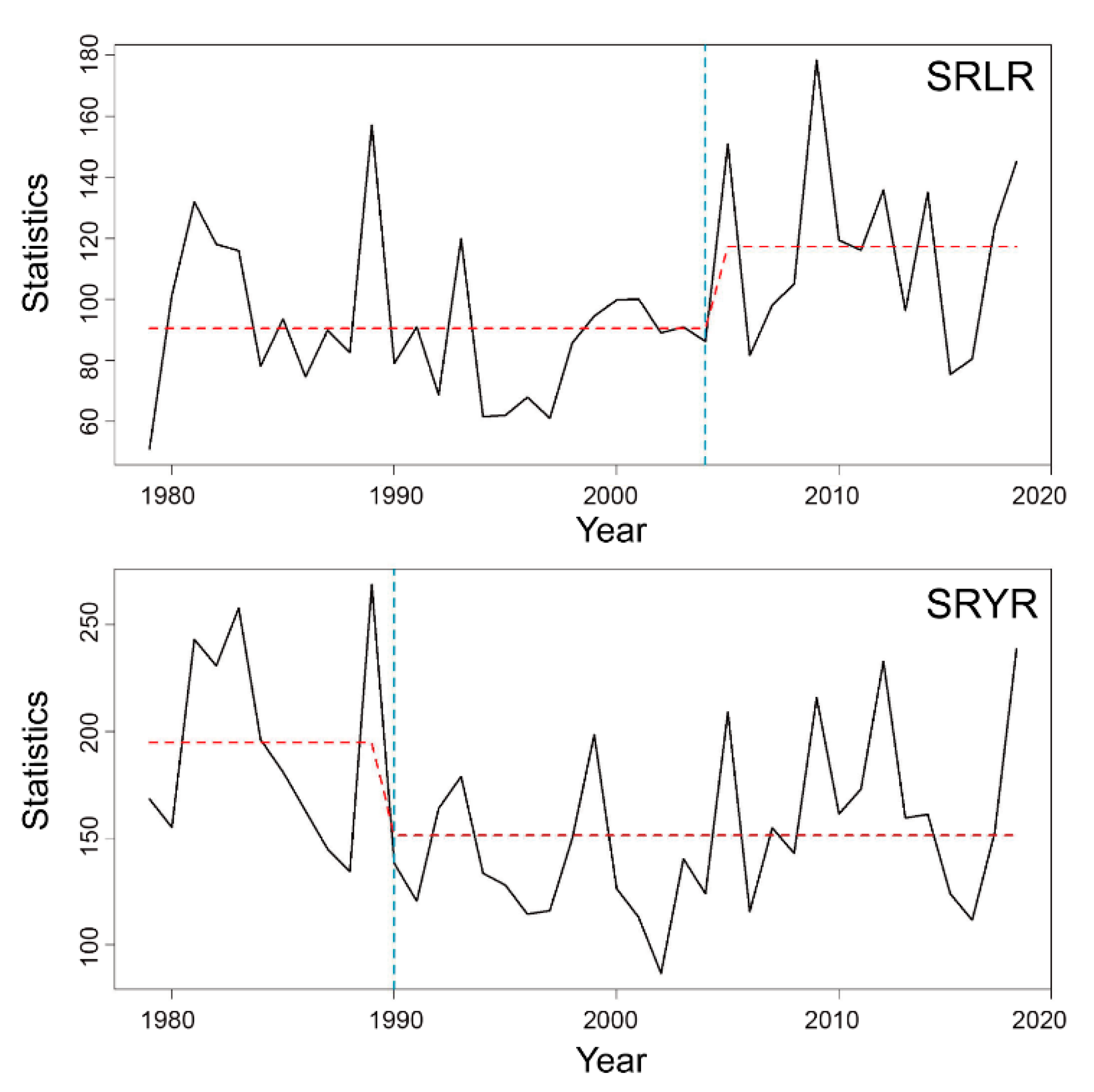
3.2. Variations and Attributions of Runoff Changes of the SRLR and SRYR
4. Discussion
4.1. Precipitation Type Identification in High-Altitude Regions
4.2. Impacts of Precipitation Type Variations on Runoff Changes at River Basin Scale
4.3. Impacts of Underlying Surface Conditions on Runoff Changes in High-Altitude Regions
5. Conclusions
- (1)
- The proportions of snowfall decreased at 2.50%/10a and 0.24%/10a for the source regions of the Yangtze and Yellow River basins, respectively, while the snowfall amount increased due to the increase of P amount.
- (2)
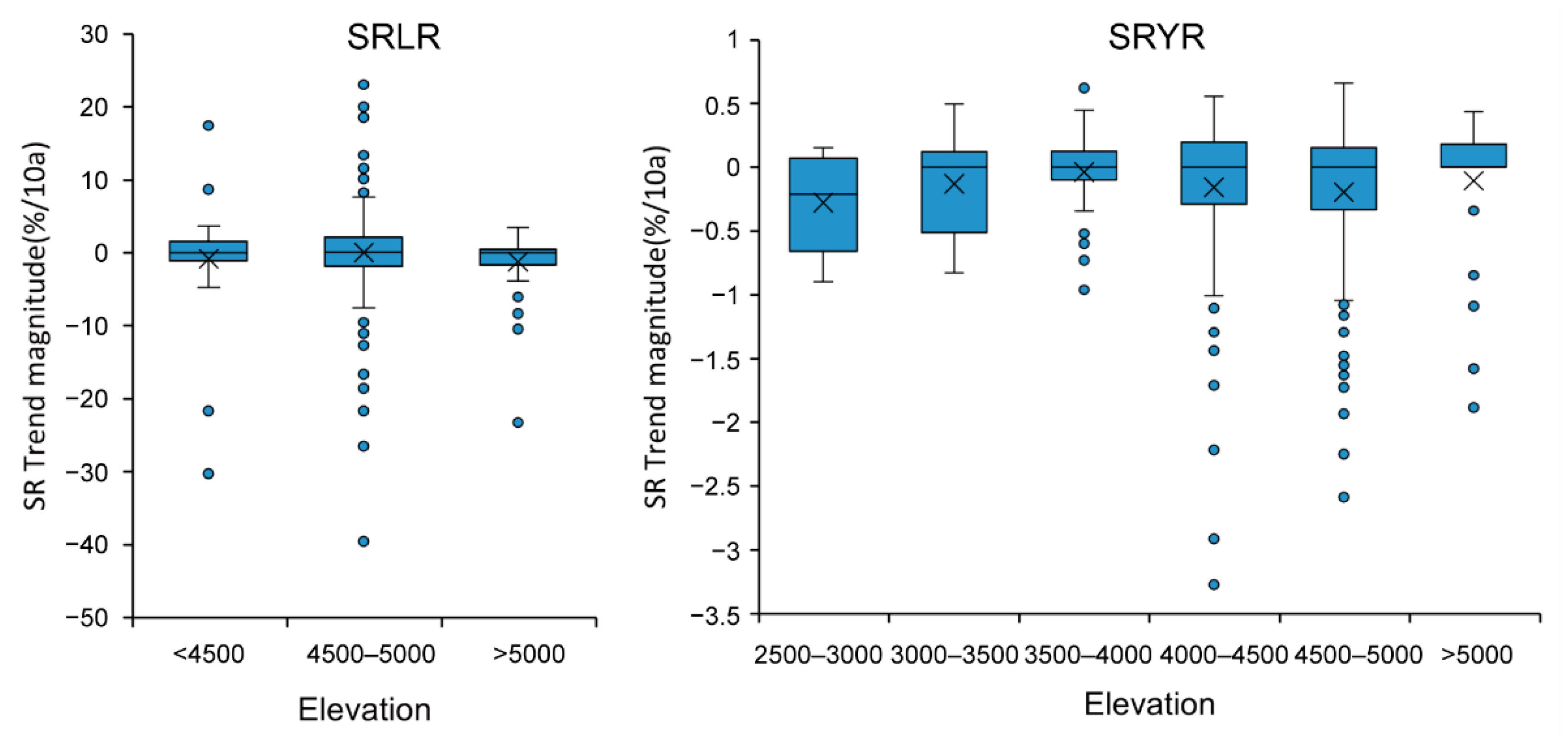
- Strong spatial heterogeneity of the SR variations has been found in the two regions. Particularly, SR trends for SRLR and SRYR are more stable below the 4500 m and 3500 m thresholds, respectively, and more volatile above the thresholds.
- (3)
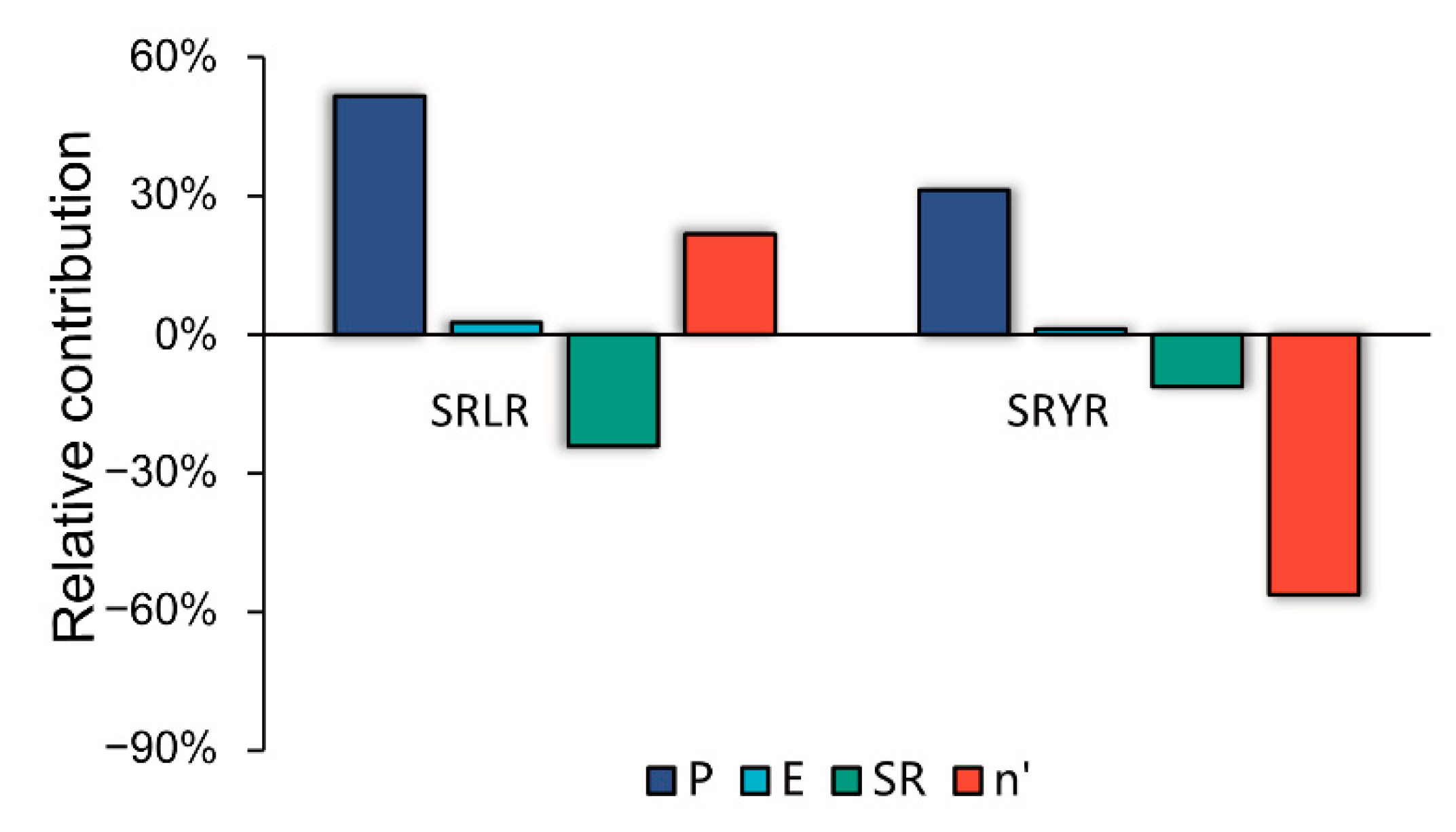
- The impacts of PT variations on runoff changes in the SRLR were relatively larger than that in the SRYR, with a relative contribution of −24.06% and −11.29%, respectively. Particularly, the impacts of underlying surfaces on annual runoff changes were not negligible in the SRYR, since a significant increasing trend was found in the vegetation recovery in this region. Apart from that, the variations of PT and cryospheric conditions will exert substantial impacts on the inter-annual and intra-annual runoff changes.
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Liu, Z.; Wang, T.; Han, J.; Yang, W.; Yang, H. Decreases in mean annual streamflow and interannual streamflow variability across snow−affected catchments under a warming climate. Geophys. Res. Lett. 2022, 49, e2021GL097442. [Google Scholar] [CrossRef]
- Dingman, S.L. Physical Hydrology, 3rd ed.; Waveland Press, Inc.: Long Grove, IL, USA, 2014; ISBN 978-1-4786-1118-9. [Google Scholar]
- Barnhart, T.B.; Molotch, N.P.; Livneh, B.; Harpold, A.A.; Knowles, J.F.; Schneider, D. Snowmelt rate dictates streamflow. Geophys. Res. Lett. 2016, 43, 8006–8016. [Google Scholar] [CrossRef]
- Dai, A. Temperature and pressure dependence of the rain-snow phase transition over land and ocean. Geophys. Res. Lett. 2008, 35, 62–77. [Google Scholar] [CrossRef]
- Foster, L.M.; Bearup, L.A.; Molotch, N.P.; Brooks, P.D.; Maxwell, R.M. Energy budget increases reduce mean streamflow more than snow–rain transitions: Using integrated modeling to isolate climate change impacts on rocky mountain hydrology. Environ. Res. Lett. 2016, 11, 044015. [Google Scholar] [CrossRef]
- Berghuijs, W.R.; Woods, R.A.; Hrachowitz, M. A precipitation shift from snow towards rain leads to a decrease in streamflow. Nat. Clim. Chang. 2014, 4, 583–586. [Google Scholar] [CrossRef] [Green Version]
- Wang, J.; Zhang, M.; Wang, S.; Ren, Z.; Che, Y.; Qiang, F.; Qu, D. Decrease in snowfall/rainfall ratio in the Tibetan Plateau from 1961 to 2013. J. Geogr. Sci. 2016, 26, 1277–1288. [Google Scholar] [CrossRef]
- Su, B.; Xiao, C.; Zhao, H.; Huang, Y.; Dou, T.; Wang, X.; Chen, D. Estimated changes in different forms of precipitation (snow, sleet, and rain) across China: 1961–2016. Atmos. Res. 2022, 270, 106078. [Google Scholar] [CrossRef]
- Zhu, X.; Wu, T.; Li, R.; Wang, S.; Hu, G.; Wang, W.; Qin, Y.; Yang, S. Characteristics of the ratios of snow, rain and sleet to precipitation on the Qinghai-Tibet Plateau during 1961–2014. Quat. Int. 2017, 444, 137–150. [Google Scholar] [CrossRef]
- Hasan, E.; Tarhule, A.; Kirstetter, P.-E.; Clark, R.; Hong, Y. Runoff sensitivity to climate change in the Nile River Basin. J. Hydrol. 2018, 561, 312–321. [Google Scholar] [CrossRef]
- Zhai, R.; Tao, F. Contributions of climate change and human activities to runoff change in seven typical catchments across China. Sci. Total Environ. 2017, 605–606, 219–229. [Google Scholar] [CrossRef]
- Zhang, Y.; Guan, D.; Jin, C.; Wang, A.; Wu, J.; Yuan, F. Analysis of impacts of climate variability and human activity on streamflow for a River Basin in Northeast China. J. Hydrol. 2011, 410, 239–247. [Google Scholar] [CrossRef]
- Zhang, A.; Zhang, C.; Fu, G.; Wang, B.; Bao, Z.; Zheng, H. Assessments of impacts of climate change and human activities on runoff with SWAT for the Huifa River Basin, Northeast China. Water Resour. Manag. 2012, 26, 2199–2217. [Google Scholar] [CrossRef]
- Bi, H.; Liu, B.; Wu, J.; Yun, L.; Chen, Z.; Cui, Z. Effects of precipitation and landuse on runoff during the past 50 years in a typical watershed in Loess Plateau, China. Int. J. Sediment Res. 2009, 24, 352–364. [Google Scholar] [CrossRef]
- Zeng, S.; Xia, J.; Du, H. Separating the effects of climate change and human activities on runoff over different time scales in the Zhang River Basin. Stoch. Environ. Res. Risk Assess. 2014, 28, 401–413. [Google Scholar] [CrossRef]
- Li, Z.; Liu, W.; Zhang, X.; Zheng, F. Impacts of land use change and climate variability on hydrology in an agricultural catchment on the Loess Plateau of China. J. Hydrol. 2009, 377, 35–42. [Google Scholar] [CrossRef]
- Ning, T.; Li, Z.; Liu, W. Separating the impacts of climate change and land surface alteration on runoff reduction in the Jing River Catchment of China. CATENA 2016, 147, 80–86. [Google Scholar] [CrossRef]
- Kirchner, J.W. Getting the right answers for the right reasons: Linking measurements, analyses, and models to advance the science of hydrology. Water Resour. Res. 2006, 42, 3. [Google Scholar] [CrossRef]
- Yuan, Z.; Yan, D.; Yang, Z.; Xu, J.; Huo, J.; Zhou, Y.; Zhang, C. Attribution assessment and projection of natural runoff change in the Yellow River Basin of China. Mitig. Adapt. Strateg. Glob. Chang. 2018, 23, 27–49. [Google Scholar] [CrossRef]
- Budyko, M.I. Evaporation under Natural Conditions; Office of Technical Services, U.S. Dept. of Commerce: Washington, DC, USA, 1963. [Google Scholar]
- Wang, C.; Wang, S.; Fu, B.; Zhang, L. Advances in hydrological modelling with the Budyko framework: A review. Prog. Phys. Geogr. Earth Environ. 2016, 40, 409–430. [Google Scholar] [CrossRef]
- Fu, B. On the calculation of the evaporation from land surface. Chin. J. Atmos. Sci. 1981, 5, 23–31. [Google Scholar]
- He, Y.; Song, J.; Hu, Y.; Tu, X.; Zhao, Y. Impacts of different weather conditions and landuse change on runoff variations in the Beiluo River Watershed, China. Sustain. Cities Soc. 2019, 50, 101674. [Google Scholar] [CrossRef]
- Liu, J.; Chen, J.; Xu, J.; Lin, Y.; Yuan, Z.; Zhou, M. Attribution of runoff variation in the headwaters of the Yangtze River Based on the Budyko hypothesis. Int. J. Environ. Res. Public Health 2019, 16, 2506. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jiang, C.; Li, D.; Gao, Y.; Liu, W.; Zhang, L. Impact of climate variability and anthropogenic activity on streamflow in the three rivers headwater region, Tibetan Plateau, China. Theor. Appl. Climatol. 2017, 129, 667–681. [Google Scholar] [CrossRef]
- Zhang, D.; Cong, Z.; Ni, G.; Yang, D.; Hu, S. Effects of snow ratio on annual runoff within the Budyko Framework. Hydrol. Earth Syst. Sci. 2015, 19, 1977–1992. [Google Scholar] [CrossRef] [Green Version]
- Zhang, W.; Zhou, T.; Zhang, L. Wetting and greening tibetan plateau in early summer in recent decades. J. Geophys. Res. Atmos. 2017, 122, 5808–5822. [Google Scholar] [CrossRef]
- Chen, H.; Zhu, Q.; Peng, C.; Wu, N.; Wang, Y.; Fang, X.; Gao, Y.; Zhu, D.; Yang, G.; Tian, J.; et al. The impacts of climate change and human activities on biogeochemical cycles on the Qinghai-Tibetan Plateau. Glob. Chang. Biol. 2013, 19, 2940–2955. [Google Scholar] [CrossRef]
- Ding, B.; Yang, K.; Qin, J.; Wang, L.; Chen, Y.; He, X. The dependence of precipitation types on surface elevation and meteorological conditions and its parameterization. J. Hydrol. 2014, 513, 154–163. [Google Scholar] [CrossRef]
- Hock, R.; Holmgren, B. A distributed surface energy-balance model for complex topography and its application to Storglaciären, Sweden. J. Glaciol. 2005, 51, 25–36. [Google Scholar] [CrossRef] [Green Version]
- Schuur, T.J.; Park, H.-S.; Ryzhkov, A.V.; Reeves, H.D. Classification of precipitation types during transitional winter weather using the RUC model and polarimetric radar retrievals. J. Appl. Meteorol. Climatol. 2012, 51, 763–779. [Google Scholar] [CrossRef]
- Chen, R.; Lu, S.; Kang, E.; Ji, X.; Zhang, Z.; Yang, Y.; Qing, W. A distributed water-heat coupled model for mountainous watershed of an Inland River Basin of Northwest China (I) model structure and equations. Environ. Geol. 2008, 53, 1299–1309. [Google Scholar] [CrossRef]
- Yang, H.; Yang, D.; Lei, Z.; Sun, F. New analytical derivation of the mean annual water-energy balance equation. Water Resour. Res. 2008, 44. [Google Scholar] [CrossRef]
- Allan, R.; Pereira, L.; Smith, M. Crop Evapotranspiration—Guidelines for Computing Crop Water Requirements; FAO Irrigation and Drainage Paper 56; FAO: Rome, Italy, 1998; Volume 56. [Google Scholar]
- Zhang, J. Physical Hydrology; The Yellow River Water Conservancy Press: Zhengzhou, China, 2007. [Google Scholar]
- Zhou, S.; Yu, B.; Zhang, L.; Huang, Y.; Pan, M.; Wang, G. A new method to partition climate and catchment effect on the mean annual runoff based on the Budyko complementary relationship. Water Resour. Res. 2016, 52, 7163–7177. [Google Scholar] [CrossRef] [Green Version]
- Zhang, L.; Potter, N.; Hickel, K.; Zhang, Y.; Shao, Q. Water balance modeling over variable time scales based on the Budyko framework—Model development and testing. J. Hydrol. 2008, 360, 117–131. [Google Scholar] [CrossRef]
- Ryberg, K.R.; Hodgkins, G.A.; Dudley, R.W. Change points in annual peak streamflows: Method comparisons and historical change points in the United States. J. Hydrol. 2020, 583, 124307. [Google Scholar] [CrossRef]
- Zuo, D.; Xu, Z.; Wu, W.; Zhao, J.; Zhao, F. Identification of streamflow response to climate change and human activities in the Wei River Basin, China. Water Resour. Manag. 2014, 28, 833–851. [Google Scholar] [CrossRef]
- Pettitt, A.N. A non-parametric approach to the change-point problem. J. R. Stat. Soc. Ser. C Appl. Stat. 1979, 28, 126–135. [Google Scholar] [CrossRef]
- Liu, X.; Cheng, Z.; Yan, L.; Yin, Z.-Y. Elevation dependency of recent and future minimum surface air temperature trends in the Tibetan Plateau and its surroundings. Glob. Planet. Chang. 2009, 68, 164–174. [Google Scholar] [CrossRef]
- Guo, D.; Sun, J.; Yang, K.; Pepin, N.; Xu, Y. Revisiting recent elevation-dependent warming on the Tibetan Plateau using satellite-based data sets. J. Geophys. Res. Atmos. 2019, 124, 8511–8521. [Google Scholar] [CrossRef] [Green Version]
- Wang, X.; Pang, G.; Yang, M. Precipitation over the Tibetan Plateau during recent decades: A review based on observations and simulations. Int. J. Climatol. 2018, 38, 1116–1131. [Google Scholar] [CrossRef]
- Yan, L.; Liu, X. Has climatic warming over the Tibetan Plateau paused or continued in recent years? J. Earth Ocean Atmos.Sci. 2014, 1, 13–28. [Google Scholar]
- Li, Z.; Chen, Y.; Li, Y.; Wang, Y. Declining snowfall fraction in the Alpine regions, Central Asia. Sci. Rep. 2020, 10, 3476. [Google Scholar] [CrossRef] [Green Version]
- Deng, H.; Pepin, N.C.; Chen, Y. Changes of snowfall under warming in the Tibetan Plateau. J. Geophys. Res. Atmos. 2017, 122, 7323–7341. [Google Scholar] [CrossRef]
- Feng, S.; Hu, Q. Changes in winter snowfall/precipitation ratio in the contiguous United States. J. Geophys. Res. Atmos. 2007, 112, D15. [Google Scholar] [CrossRef]
- Huntington, T.G.; Hodgkins, G.A.; Keim, B.D.; Dudley, R.W. Changes in the proportion of precipitation occurring as snow in New England (1949–2000). J. Clim. 2004, 17, 2626–2636. [Google Scholar] [CrossRef]
- Wang, G.; He, Y.; Huang, J.; Guan, X.; Wang, X.; Hu, H.; Wang, S.; Xie, Y. The influence of precipitation phase changes on the recharge process of terrestrial water storage in the cold season over the Tibetan Plateau. J. Geophys. Res. Atmos. 2022, 127, e2021JD035824. [Google Scholar] [CrossRef]
- Li, Q.; Yang, T.; Qi, Z.; Li, L. Spatiotemporal variation of snowfall to precipitation ratio and its implication on water resources by a regional climate model over Xinjiang, China. Water 2018, 10, 1463. [Google Scholar] [CrossRef] [Green Version]
- Guo, L.; Li, L. Variation of the proportion of precipitation occurring as snow in the Tian Shan mountains, China. Int. J. Climatol. 2015, 35, 1379–1393. [Google Scholar] [CrossRef]
- Huntington, T.G. Evidence for intensification of the global water cycle: Review and synthesis. J. Hydrol. 2006, 319, 8395. [Google Scholar] [CrossRef]
- Jia, J.; He, K.; Wang, D. A study on the change pattern of runoff and its influencing factors in the Yangtze River source area in the past 55 years. In Proceedings of the China Water Resources Society 2021 Annual Academic Conference, Beijing, China, 25 October 2021; The Yellow River Water Conservancy Press: Zhengzhou, China, 2021; pp. 44–53. [Google Scholar]
- Zhao, F.; Xu, Z.; Zhang, L.; Zuo, D. Streamflow response to climate variability and human activities in the upper catchment of the Yellow River Basin. Sci. China Ser. E Technol. Sci. 2009, 52, 3249. [Google Scholar] [CrossRef]
- Ellis, A.; Sauter, K. The significance of snow to surface water supply: An empirical case study from the southwestern United States. Phys. Geogr. 2017, 38, 211–230. [Google Scholar] [CrossRef]
- Bocchiola, D. Long term (1921–2011) hydrological regime of alpine catchments in Northern Italy. Adv. Water Resour. 2014, 70, 51–64. [Google Scholar] [CrossRef]
- Tang, Y.; Hooshyar, M.; Zhu, T.; Ringler, C.; Sun, A.Y.; Long, D.; Wang, D. Reconstructing annual groundwater storage changes in a large-scale irrigation region using GRACE data and Budyko model. J. Hydrol. 2017, 551, 397–406. [Google Scholar] [CrossRef]
- Tang, Y.; Wang, D. Evaluating the role of watershed properties in long-term water balance through a Budyko equation based on two-stage partitioning of precipitation. Water Resour. Res. 2017, 53, 4142–4157. [Google Scholar] [CrossRef]
- Ning, T.; Li, Z.; Liu, W. Vegetation dynamics and climate seasonality jointly control the interannual catchment water balance in the loess Plateau under the Budyko framework. Hydrol. Earth Syst. Sci. 2017, 21, 1515–1526. [Google Scholar] [CrossRef] [Green Version]
- Xing, W.; Wang, W.; Shao, Q.; Yong, B. Identification of dominant interactions between climatic seasonality, catchment characteristics and agricultural activities on Budyko-type equation parameter estimation. J. Hydrol. 2018, 556, 585–599. [Google Scholar] [CrossRef]
- Zheng, H.; Zhang, L.; Zhu, R.; Liu, C.; Sato, Y.; Fukushima, Y. Responses of streamflow to climate and land surface change in the headwaters of the Yellow River Basin. Water Resour Res. 2009, 45, 7. [Google Scholar] [CrossRef]
- Liu, L.; Cao, W.; Shao, Q.; Huang, L.; He, T. Characteristics of land use/cover and macroscopic ecological changes in the headwaters of the Yangtze River and of the Yellow River over the past 30 years. Sustainability 2016, 8, 237. [Google Scholar] [CrossRef] [Green Version]
- Yang, Y.; Shang, S.; Jiang, L. Remote sensing temporal and spatial patterns of evapotranspiration and the responses to water management in a large irrigation district of North China. Agric. For. Meteorol. 2012, 164, 112–122. [Google Scholar] [CrossRef]
- Han, P.; Long, D.; Han, Z.; Du, M.; Dai, L.; Hao, X. Improved understanding of snowmelt runoff from the headwaters of China’s Yangtze River using remotely sensed snow products and hydrological modeling. Remote Sens. Environ. 2019, 224, 44–59. [Google Scholar] [CrossRef]
- Yao, Z.; Liu, Z.; Huang, H.; Liu, G.; Wu, S. Statistical estimation of the impacts of glaciers and climate change on river runoff in the headwaters of the Yangtze River. Quat. Int. 2014, 336, 89–97. [Google Scholar] [CrossRef]
- Jin, X.; Jin, H.; Luo, D.; Sheng, Y.; Wu, Q.; Wu, J.; Wang, W.; Huang, S.; Li, X.; Liang, S.; et al. Impacts of permafrost degradation on hydrology and vegetation in the source area of the Yellow River on Northeastern Qinghai-Tibet Plateau, Southwest China. Front. Earth Sci. 2022, 10, 845824. [Google Scholar] [CrossRef]
- Shi, R.; Yang, H.; Yang, D. Spatiotemporal variations in frozen ground and their impacts on hydrological components in the source region of the Yangtze River. J. Hydrol. 2020, 590, 125237. [Google Scholar] [CrossRef]

| Elasticity Coefficient | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Watershed | Period | ETp/mm | Q/mm | P/mm | SR | n′ | βET | βp | βSR | βn′ |
| SRLR | 1979–2018 | 701.5 | 99.95 | 343.89 | 0.36 | 1.32 | −2.01 | 1.43 | 1.15 | −0.86 |
| 1979–2004 | 703.13 | 90.58 | 323.20 | 0.38 | 1.25 | −2.12 | 1.44 | 1.29 | −0.95 | |
| 2005–2018 | 698.48 | 117.35 | 383.32 | 0.34 | 1.15 | −2.23 | 1.53 | 1.14 | −1.07 | |
| SRYR | 1979–2018 | 678.54 | 163.40 | 558.27 | 0.24 | 1.00 | −1.49 | 1.93 | 0.47 | −1.61 |
| 1979–1990 | 681.30 | 190.31 | 517.31 | 0.27 | 0.99 | −2.31 | 1.62 | 0.85 | −1.13 | |
| 1991–2018 | 677.36 | 151.87 | 575.82 | 0.23 | 1.04 | −2.84 | 2.10 | 0.84 | −1.81 | |
| ETp | P | SR | n′ | Error | |||
|---|---|---|---|---|---|---|---|
| SRLR | 1.31 | 25.88 | −12.06 | 10.87 | 26.00 | 26.77 | 2.88% |
| SRYR | 1.35 | 33.57 | −12.14 | −60.44 | −37.66 | −38.45 | 2.05% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, Y.; Zhou, Y.; Wang, Y.; Lu, F.; Xiao, W.; Hou, B.; Yu, Y.; Liu, J.; Xue, W. Impacts of Precipitation Type Variations on Runoff Changes in the Source Regions of the Yangtze and Yellow River Basins in the Past 40 Years. Water 2022, 14, 4115. https://doi.org/10.3390/w14244115
Hu Y, Zhou Y, Wang Y, Lu F, Xiao W, Hou B, Yu Y, Liu J, Xue W. Impacts of Precipitation Type Variations on Runoff Changes in the Source Regions of the Yangtze and Yellow River Basins in the Past 40 Years. Water. 2022; 14(24):4115. https://doi.org/10.3390/w14244115
Chicago/Turabian StyleHu, Yingying, Yuyan Zhou, Yicheng Wang, Fan Lu, Weihua Xiao, Baodeng Hou, Yuanhui Yu, Jianwei Liu, and Wei Xue. 2022. "Impacts of Precipitation Type Variations on Runoff Changes in the Source Regions of the Yangtze and Yellow River Basins in the Past 40 Years" Water 14, no. 24: 4115. https://doi.org/10.3390/w14244115





