Experimental Investigation of Uniaxial Compressive Strength of Distilled Water Ice at Different Growth Temperatures
Abstract
:1. Introduction
2. Methods
2.1. Preparation of Distilled Water Ice and Test Ice Samples
2.2. Physical Properties Measurement
2.2.1. Ice Density Measurement and Porosity Calculation
2.2.2. Ice Crystal Structure Measurement
2.3. Uniaxial Compression Test
2.3.1. Test Devices
2.3.2. Test Principle and Procedure
3. Results
3.1. Results of Uniaxial Compressive Strength Test
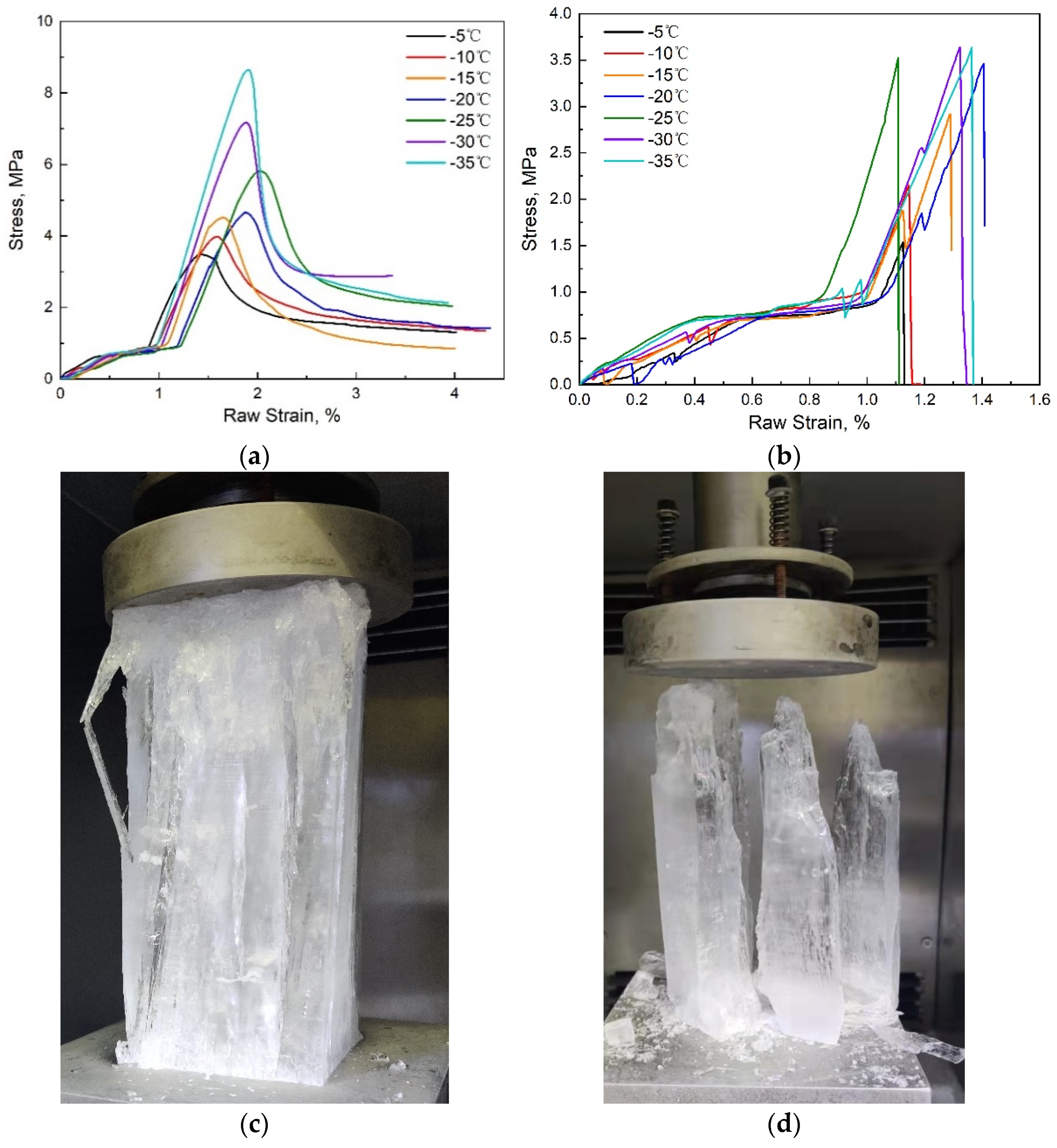
3.1.1. Deformation Types
3.1.2. Stress-Strain Curves Correction
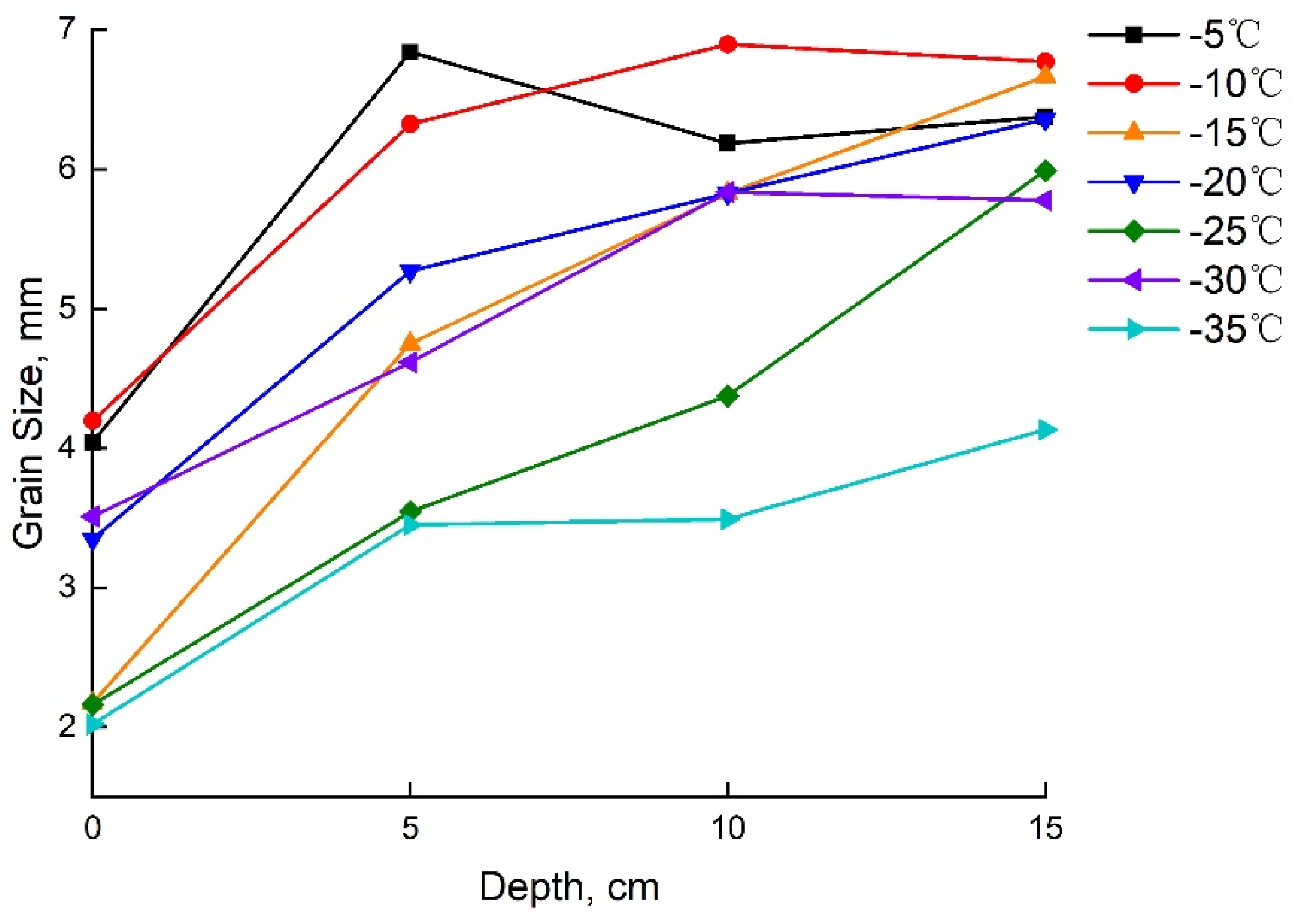
3.2. Physical Properties and Crystal Structure of Distill Water Ice
4. Discussion
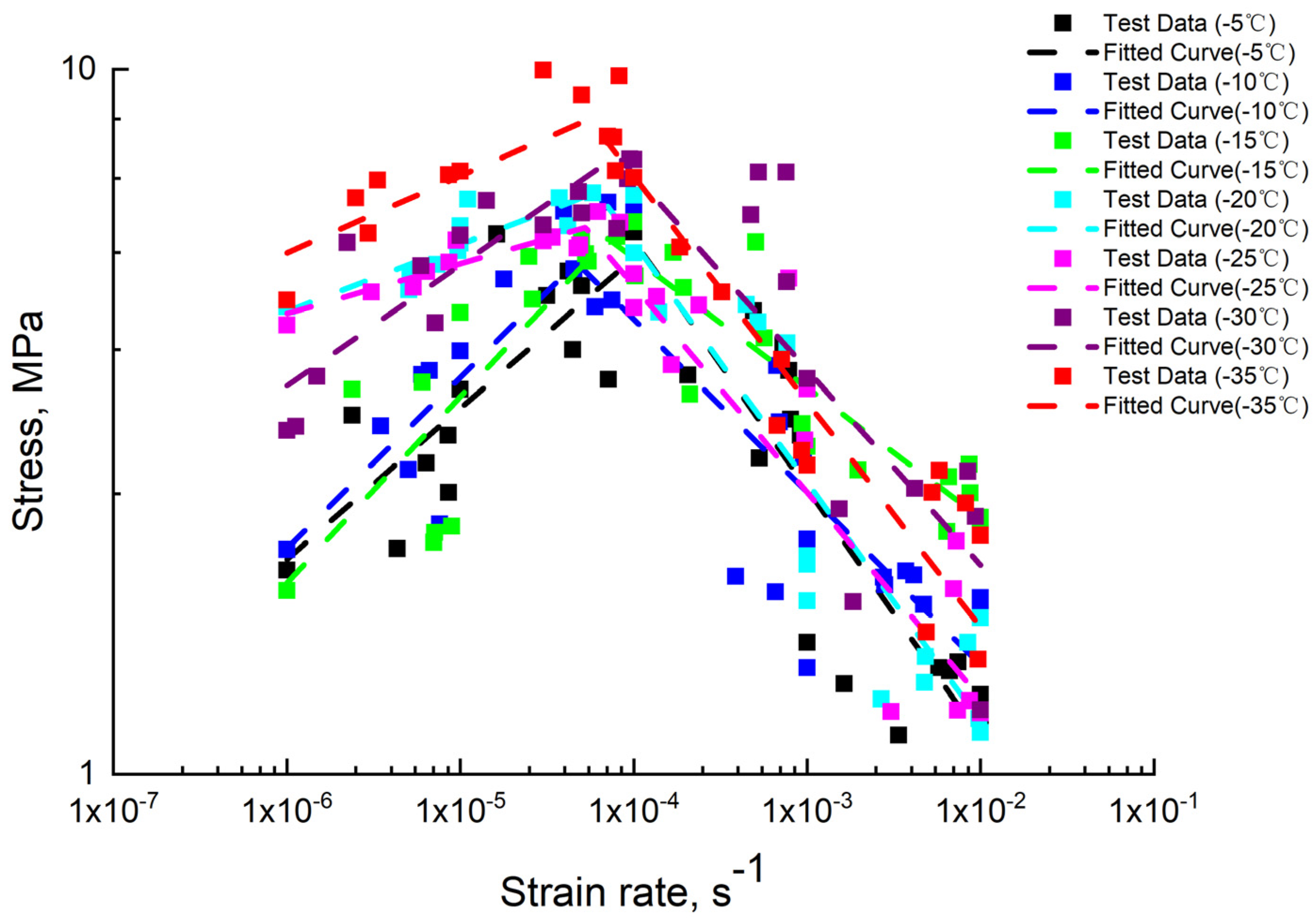
4.1. Stress vs. Strain Rate
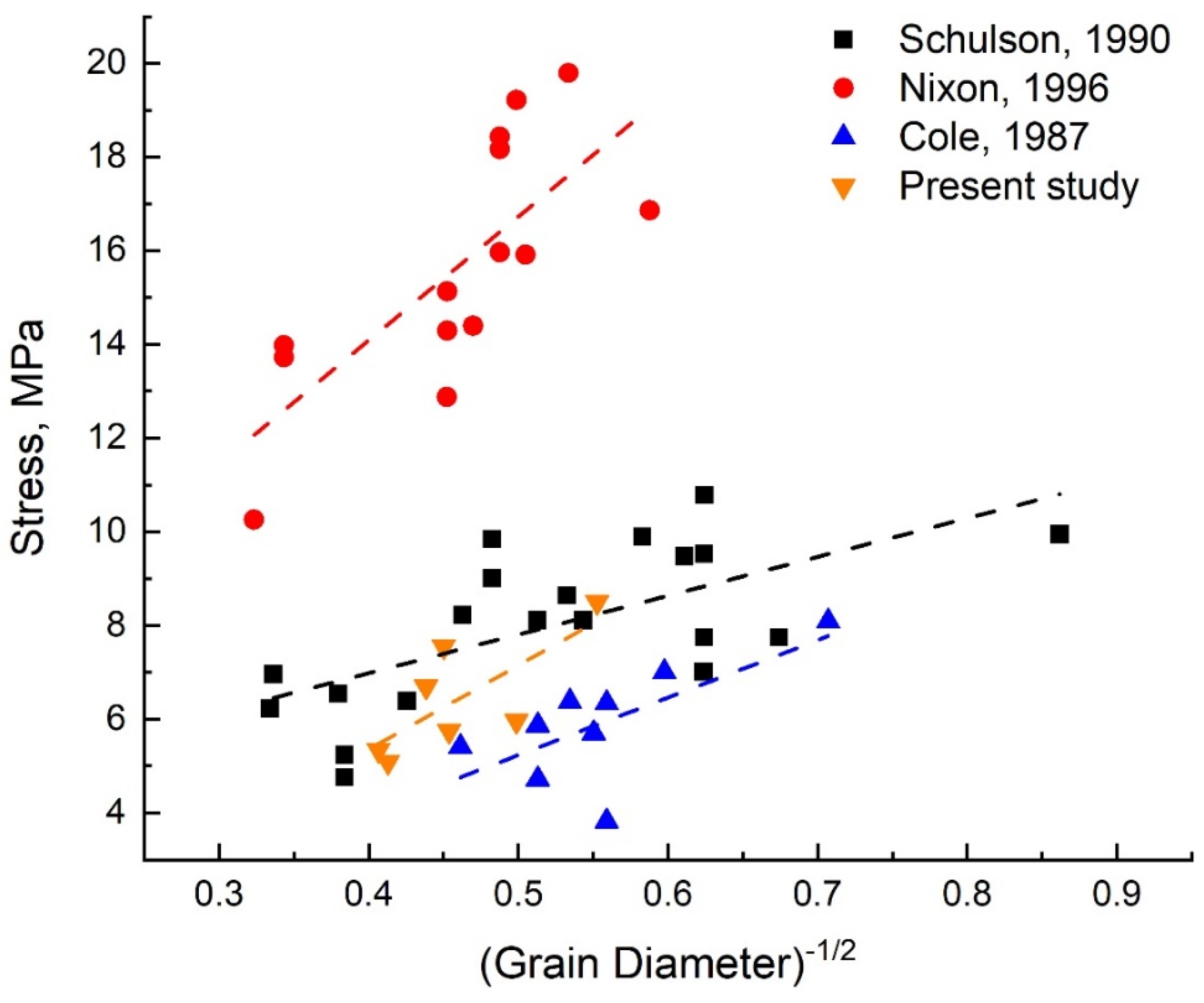
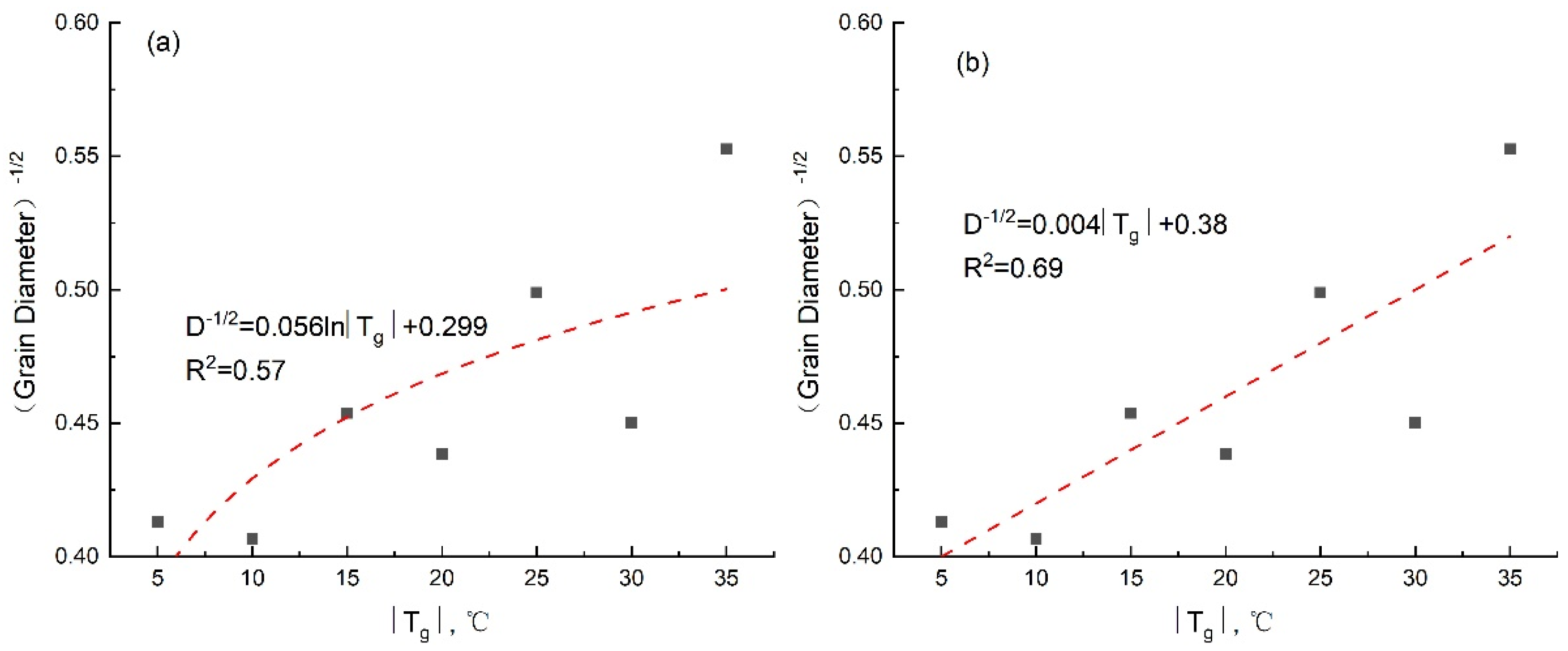
4.2. Stress vs. Grain Size
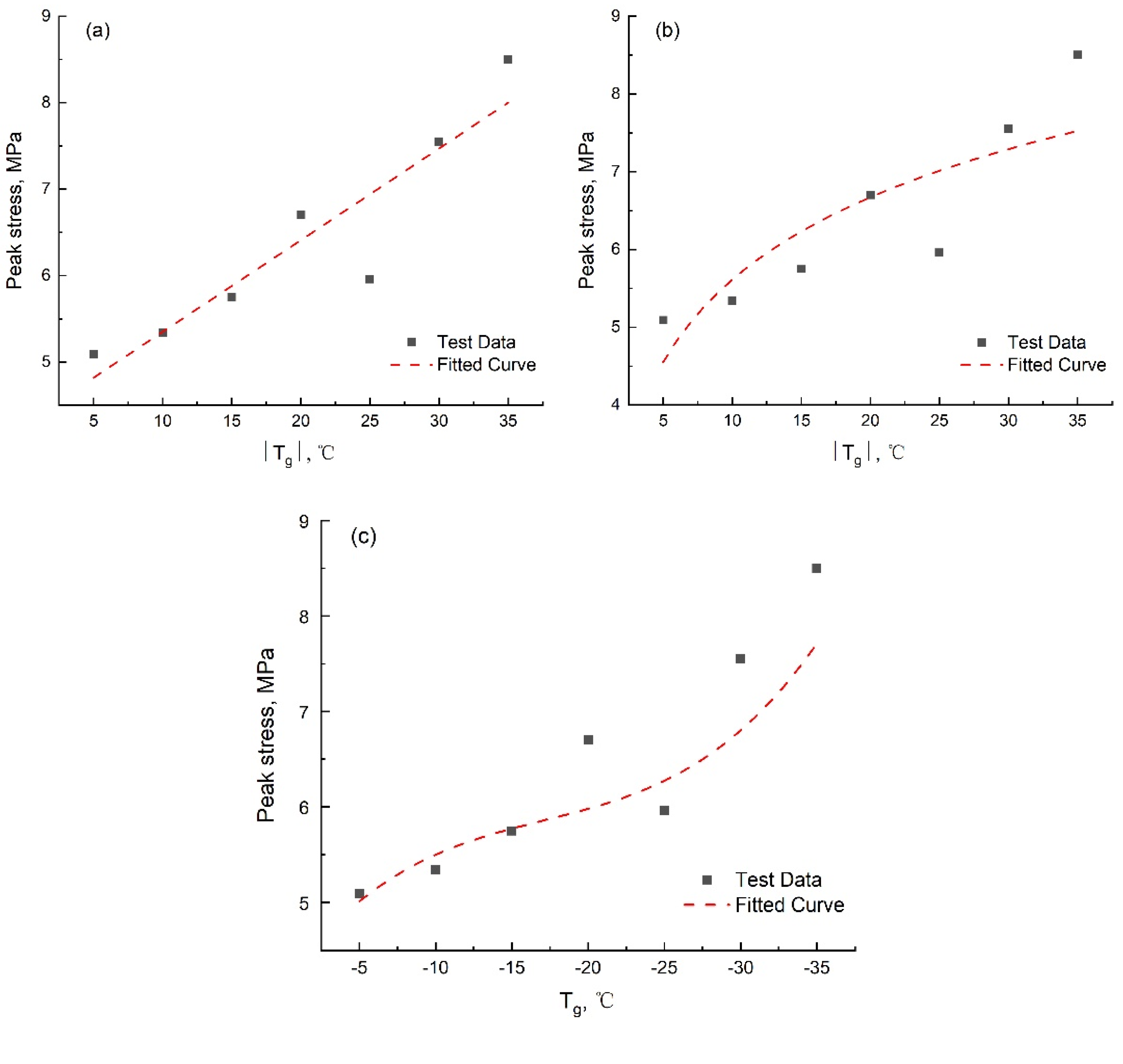
4.3. Stress vs. Growth Temperature
5. Conclusions
- The growth temperatures were set at −5 °C, −10 °C, −15 °C, −20 °C, −25 °C, −30 °C and −35 °C. The ice crystal structure in this study is columnar. Ice density ranges from 900 kg/m3 to 920 kg/m3 and increases with decreasing temperature. Grain size increases with the increases in ice depth, and the average grain size range is 2–7 mm, which roughly decreases with the decrease in temperature.
- The uniaxial compressive strength of ice at different strain rates is obtained, which first increases with the increase in strain rate, and then decreases with the increase in strain rate after reaching the peak value. The results show that ice is ductile at a low strain rate and brittle at a high strain rate. The relationship between uniaxial compressive strength and strain rate is a power function.
- Compared with previous studies, it is found that the peak compressive strength of ice gradually increases with the decrease in grain size. The results show that the relationship between the peak compressive strength and the—1/2 power of grain size is a linear function.
- Referring to the previous research, three functional forms of linear, logarithmic and polynomial have been proposed. The experimental results of this study are fitted in three functions to reveal the mathematical relationship. In addition, by summarizing the relationship between growth temperature and grain size, combined with mathematical requirements and physical facts, it is finally determined that the relationship between ice peak compressive strength and growth temperature conforms to the logarithmic function. This result explains that the growth temperature affects the compressive strength of ice by controlling the grain size.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Overland, J.E.; McNutt, S.L.; Salo, S.; Groves, J.; Li, S. Arctic sea ice as a granular plastic. J. Geophys. Res.-Oceans. 1998, 103, 21845–21867. [Google Scholar] [CrossRef]
- Schulson, E.M. Brittle failure of ice. Eng. Fract. Mech. 2001, 68, 1839–1887. [Google Scholar] [CrossRef]
- Snyder, S.A.; Schulson, E.M.; Renshaw, C.E. Effects of prestrain on the ductile-to-brittle transition of ice. Acta. Mater. 2016, 108, 110–127. [Google Scholar] [CrossRef] [Green Version]
- Kjerstad, Ø.K.; Metrikin, I.; Løset, S.; Skjetne, R. Experimental and phenomenological investigation of dynamic positioning in managed ice. Cold Reg. Sci. Technol. 2015, 111, 67–79. [Google Scholar] [CrossRef]
- Montewka, J.; Goerlandt, F.; Kujala, P.; Lensu, M. Towards probabilistic models for the prediction of a ship performance in dynamic ice. Cold Reg. Sci. Technol. 2015, 112, 14–28. [Google Scholar] [CrossRef]
- Sinha, N.K. Uniaxial compressive strength of first-year and multi-year sea ice. Can. J. Civ. Eng. 1984, 11, 82–91. [Google Scholar] [CrossRef]
- Saeki, H.; Ozaki, A.; Kubo, Y. Experimental study on flexural strength and elastic modulus of sea ice. In Proceedings of the 6th international Conference on Port and Ocean Engineering under Arctic Conditions, Quebec City, QC, Canada, 27–31 July 1981. [Google Scholar]
- Zhang, Y.; Zhang, Y.; Guo, R.; Cui, B. Method for Testing Shear and Tensile Strengths of Freshwater/Seawater Ice. Water 2022, 14, 1363. [Google Scholar] [CrossRef]
- Lainey, L.; Tinawi, R. The Mechanical Properties of Sea Ice—A compilation of available data. Can. J. Civ. Eng. 1984, 11, 884–923. [Google Scholar] [CrossRef]
- Richter, M.J.A. US Research in Ice Mechanics: 1987–1990. Cold Reg. Sci. Technol. 1992, 20, 231–246. [Google Scholar] [CrossRef]
- Moslet, P.O. Field Testing of Uniaxial Compression strength of columnar sea ice. Cold Reg. Sci. Technol. 2007, 48, 1–14. [Google Scholar] [CrossRef]
- Weertman, J. Creep deformation of ice. J. Annu. Rev. Earth Planet. Sci. 1983, 11, 215–240. [Google Scholar] [CrossRef] [Green Version]
- Timco, G.W.; Weeks, W.F. A review of the engineering properties of sea ice. Cold Reg. Sci. Technol. 2010, 60, 107–129. [Google Scholar] [CrossRef]
- Jones, S.J.; Glen, J.W. The mechanical properties of single crystals of pure ice. J. Glaciol. 1969, 54, 463–473. [Google Scholar] [CrossRef] [Green Version]
- Wu, X.; Prakash, V. Dynamic strength of distill water and lake water ice at high strain rates. Int. J. Impact. Eng. 2015, 76, 155–165. [Google Scholar] [CrossRef]
- Kim, H.; Keune, J.N. Compressive strength of ice at impact strain rates. J. Mater. Sci. 2007, 42, 2802–2806. [Google Scholar] [CrossRef]
- Timco, G.W.; Frederking, R.M.W. Comparative strengths of fresh water ice. Cold Reg. Sci. Technol. 1982, 6, 21–27. [Google Scholar] [CrossRef] [Green Version]
- Bonath, V.; Edeskär, T.; Lintzén, N.; Fransson, L.; Cwirzen, A. Properties of ice from first-year ridges in the Barents Sea and Fram Strait. Cold Reg. Sci. Technol. 2019, 168, 102890. [Google Scholar] [CrossRef]
- Sinha, N.K. Constant strain- and stress-rate compressive strength of columnar-grained ice. J. Mater. Sci. 1982, 17, 785–802. [Google Scholar] [CrossRef] [Green Version]
- Chen, A.C.T.; Lee, J. Large-Scale Ice Strength Tests at Slow Strain Rates. J. Offshore Mech. Arct. 1988, 110, 302–306. [Google Scholar] [CrossRef]
- Qi, S.; Schulson, E.M. The effect of temperature on the ductile-to-brittle transition in columnar ice. In Proceedings of the 14th International Symposium on ice, Potsdam, NY, USA, 27–31 July 1998. [Google Scholar]
- Deng, K.; Feng, X.; Tian, X.; Hu, Y. Experimental research on compressive mechanical properties of ice under low strain rates. Mater. Today Commun. 2020, 24, 101029. [Google Scholar] [CrossRef]
- Schulson, E.M.; Buck, S.E. The ductile-to-brittle transition and ductile failure envelopes of orthotropic ice under biaxial compression. Acta. Metall. Mater. 1995, 43, 3661–3668. [Google Scholar] [CrossRef]
- Baker, R.W. The influence of ice-crystal size on creep. J. Glaciol. 1978, 21, 485–500. [Google Scholar] [CrossRef] [Green Version]
- Jones, S.J.; Chew, H.A.M. Effect of sample and grain size on the compressive strength of ice. Ann. Glaciol. 1983, 4, 129–132. [Google Scholar] [CrossRef] [Green Version]
- Schulson, E.M. The brittle compressive fracture of ice. Acta Metall. Mater. 1990, 38, 1963–1976. [Google Scholar] [CrossRef]
- Iliescu, D.; Baker, I. The structure and mechanical properties of river and lake ice. Cold Reg. Sci. Technol. 2007, 48, 202–217. [Google Scholar] [CrossRef]
- Cole, D.M. Strain-rate and Grain-size Effects in Ice. J. Glaciol. 1987, 33, 274–280. [Google Scholar] [CrossRef] [Green Version]
- Potter, R.S.; Cammack, J.M.; Braithwaite, C.H.; Church, P.D.; Walley, S.M. A study of the compressive mechanical properties of defect-free, porous and sintered water-ice at low and high strain rates. Icarus 2020, 351, 113940. [Google Scholar] [CrossRef]
- Ouyang, Q.; Qi, C.; Lian, J.; Zhao, X. Dynamic Compressive Strength and Failure of Natural Lake Ice Under Moderate Strain Rates at Near Melting Point Temperature. Lat. Am. J. Solids. Stru. 2017, 14, 1669–1694. [Google Scholar] [CrossRef]
- Kovacs, A. Estimating the full-scale flexural and compressive strength of first-year sea ice. J. Geophys. Res-Oceans. 1997, 102, 8681–8689. [Google Scholar] [CrossRef]
- Han, H.; Li, Z.; Huang, W.; Lu, P.; Lei, R. The uniaxial compressive strength of the Arctic summer sea ice. Acta. Oceanol. Sin. 2015, 34, 129–136. [Google Scholar] [CrossRef]
- Timco, G.W.; Frederking, R.M.W. Compressive strength of sea ice sheets. Cold Reg. Sci. Technol. 1990, 17, 227–240. [Google Scholar] [CrossRef]
- Shazly, M.; Prakash, V.; Lerch, B.A. High strain-rate behavior of ice under uniaxial compression. Int. J. Solids Struct. 2009, 46, 1499–1515. [Google Scholar] [CrossRef] [Green Version]
- Farid, H.; Saeidi, A.; Farzaneh, M. Prediction of failure in atmospheric ice under triaxial compressive stress. Cold Reg. Sci. Technol. 2017, 138, 46–56. [Google Scholar] [CrossRef]
- Arakawa, M.; Maeno, N. Mechanical strength of polycrystalline ice under uniaxial compression. Cold Reg. Sci. Technol. 1997, 26, 215–229. [Google Scholar] [CrossRef]
- Wu, X.; Prakash, V. Dynamic compressive behavior of ice at cryogenic temperatures. Cold Reg. Sci. Technol. 2015, 118, 1–13. [Google Scholar] [CrossRef] [Green Version]
- Schwarz, J.; Frederking, R.; Gavrillo, V.; Petrov, I.G.; Hirayama, K.I.; Mellor, M.; Tryde, P.; Vaudrey, K.D. Standardized testing methods for measuring mechanical properties of ice. Cold Reg. Sci. Technol. 1981, 4, 245–253. [Google Scholar] [CrossRef]
- Cox, G.F.N.; Weeks, W.F. Equations for Determining the Gas and Brine Volumes in Sea-Ice Samples. J. Glaciol. 1983, 29, 306–316. [Google Scholar] [CrossRef] [Green Version]
- Sinha, N.K.; Frederking, R.M.W. Effect of test system stiffness on strength of ice. In Proceedings of the Fifth International Conference on Port and Ocean Engineering under Arctic Conditions, Trondheim, Norway, 13–18 August 1979. [Google Scholar]
- Timco, G.W.; Frederking, R.M.W. A procedure to account for machine stiffness in uni-axial compressive compression tests. In Proceedings of the International Symposium on Ice (IAHR), Hamburg, Germany, 27–31 August 1984. [Google Scholar]
- Jones, S.J. High strain-rate compression tests on ice. J. Phys. Chem. B. 1997, 101, 6099–6101. [Google Scholar] [CrossRef]
- Glen, J.W. The creep of polycrystalline ice. P. Roy. Soc. A-Math. Phy. 1955, 228, 519–538. [Google Scholar] [CrossRef]
- Nixon, W.A. Wing crack models of the brittle compressive failure of ice. Cold Reg. Sci. Technol. 1996, 24, 41–55. [Google Scholar] [CrossRef]
- Yu, T.; Wang, J.; Du, F.; Zhang, L. Experimental research on ice disaster in Huma River. J. Nat. Disaster. 2007, 16, 43–48. (In Chinese) [Google Scholar] [CrossRef]
- Li, Z.; Zhang, L.; Lu, P.; Leppäranta, M.; Li, G. Experimental study on the effect of porosity on the uniaxial compressive strength of sea ice in Bohai Sea. Sci. China Technol. Sci. 2011, 54, 2429–2436. [Google Scholar] [CrossRef]








| T (°C) | (s−1) | ||
|---|---|---|---|
| 1.95 | 0.51 | ||
| 3.52 | 0.64 | ||
| −5 | 5.88 | 0.71 | |
| 1.54 | 0.18 | ||
| 1.30 | 0.26 | ||
| 2.08 | 0.49 | ||
| 3.98 | 0.72 | ||
| −10 | 6.39 | 0.71 | |
| 2.11 | 0.22 | ||
| 1.75 | 0.27 | ||
| 1.82 | 0.40 | ||
| 4.51 | 0.67 | ||
| −15 | 6.08 | 0.54 | |
| 2.91 | 0.29 | ||
| 2.29 | 0.27 | ||
| 4.61 | 0.63 | ||
| 4.67 | 0.79 | ||
| −20 | 5.49 | 0.77 | |
| 3.46 | 0.36 | ||
| 1.75 | 0.48 | ||
| 4.34 | 0.73 | ||
| 5.81 | 0.87 | ||
| −25 | 5.13 | 0.52 | |
| 3.52 | 0.27 | ||
| 1.22 | 0.34 | ||
| 3.07 | 0.83 | ||
| 7.17 | 0.94 | ||
| −30 | 7.45 | 0.87 | |
| 3.64 | 0.38 | ||
| 1.23 | 0.31 | ||
| 4.70 | 1.09 | ||
| 8.65 | 0.99 | ||
| −35 | 7.02 | 0.74 | |
| 3.63 | 0.48 | ||
| 2.18 | 0.22 |
| Growth Temperature (°C) | Average Density (kg/m3) | Average Porosity (‰) |
|---|---|---|
| −5 | 906 | 12.75 |
| −10 | 907 | 12.42 |
| −15 | 915 | 4.47 |
| −20 | 916 | 4.14 |
| −25 | 918 | 2.72 |
| −30 | 919 | 2.40 |
| −35 | 919 | 3.16 |
(°C) | Ductile Regime | Brittle Regime | (MPa) | ||||
|---|---|---|---|---|---|---|---|
| B | n | R2 | B | n | R2 | ||
| −5 | 38.798 | 0.214 | 0.58 | 0.225 | −0.35 | 0.78 | 5.09 |
| −10 | 60.236 | 0.243 | 0.70 | 0.460 | −0.246 | 0.76 | 5.34 |
| −15 | 71.611 | 0.264 | 0.77 | 0.991 | −0.184 | 0.77 | 5.75 |
| −20 | 16.837 | 0.095 | 0.73 | 0.248 | −0.34 | 0.88 | 6.70 |
| −25 | 12.001 | 0.071 | 0.75 | 0.332 | −0.293 | 0.85 | 5.96 |
| −30 | 38.262 | 0.172 | 0.71 | 0.553 | −0.277 | 0.63 | 7.55 |
| −35 | 24.741 | 0.109 | 0.60 | 0.370 | −0.32 | 0.89 | 8.50 |
| (°C) | Average Grain Size (mm) | (MPa) |
|---|---|---|
| −5 | 5.86 | 5.09 |
| −10 | 6.05 | 5.34 |
| −15 | 4.85 | 5.75 |
| −20 | 5.20 | 6.70 |
| −25 | 4.02 | 5.96 |
| −30 | 4.93 | 7.55 |
| −35 | 2.37 | 8.50 |
| Items | Schulson, 1990 | Nixon, 1996 | Cole, 1987 | Present Study |
|---|---|---|---|---|
| 3.67 | 3.52 | −0.89 | −1.81 | |
| 8.27 | 26.4 | 12.25 | 17.91 | |
| R2 | 0.44 | 0.56 | 0.45 | 0.54 |
| Function Type | Fit Coefficients | R2 | |||
|---|---|---|---|---|---|
| A | B | C | D | ||
| Linear | 0.106 | 4.290 | / | / | 0.85 |
| Logarithmic | 1.527 | 2.096 | / | / | 0.71 |
| Polynomial | −0.0002 | −0.0103 | −0.217 | 4.16 | 0.91 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Qian, Z.; Lv, S.; Huang, W.; Ren, J.; Fang, Z.; Chen, X. Experimental Investigation of Uniaxial Compressive Strength of Distilled Water Ice at Different Growth Temperatures. Water 2022, 14, 4079. https://doi.org/10.3390/w14244079
Zhang Y, Qian Z, Lv S, Huang W, Ren J, Fang Z, Chen X. Experimental Investigation of Uniaxial Compressive Strength of Distilled Water Ice at Different Growth Temperatures. Water. 2022; 14(24):4079. https://doi.org/10.3390/w14244079
Chicago/Turabian StyleZhang, Yujia, Zuoqin Qian, Song Lv, Weilong Huang, Jie Ren, Ziwei Fang, and Xiaodong Chen. 2022. "Experimental Investigation of Uniaxial Compressive Strength of Distilled Water Ice at Different Growth Temperatures" Water 14, no. 24: 4079. https://doi.org/10.3390/w14244079
APA StyleZhang, Y., Qian, Z., Lv, S., Huang, W., Ren, J., Fang, Z., & Chen, X. (2022). Experimental Investigation of Uniaxial Compressive Strength of Distilled Water Ice at Different Growth Temperatures. Water, 14(24), 4079. https://doi.org/10.3390/w14244079










