Abstract
This study investigates the potential of Sentinel-1 data in assisting flood modeling procedures. Two different synthetic aperture radar (SAR) processing methodologies, one simplified based on single-flood image thresholding and one automatic based on SAR statistical temporal analysis, were exploited to delineate the flooding caused by a storm event that took place in Spercheios River, Central Greece. The storm event was simulated by coupling a HEC-HMS hydrologic model and an integrated 1D/2D HEC-RAS hydraulic model. Both SAR methodologies were compared to each other and also used as a reference to test the sensitivity of the hydraulic model in the variation of upstream discharge and roughness coefficient. Model sensitivity was investigated with respect to the change in the derived inundation extent and three additional metrics: the Critical Success Index (CSI), the Hit Rate (HR), and the False Alarm Ratio (FAR). The model response was found to be affected in the following order: by the upstream inflow, and by the variation of the roughness coefficient in the main channel and in the land use “cultivated crops”. The discrepancies observed between model- and SAR-derived inundation products are associated with the uncertainty accompanying the SAR processing and the utilized satellite data itself, the underlying topography, and the structural uncertainty inherent in the modeling procedure. Regarding the SAR methodologies tested, the second one (FLOMPY approach) proved to be more suitable, yielding a more coherent and realistic flooded area. According to the applied metrics and considering as reference the FLOMPY result, model performance ranged between 22–27.5% (CSI), 36.9–60.4% (HR), and 62.1–68.2% (FAR).
1. Introduction
Floods are the most frequent and disastrous natural hazards worldwide, with severe impacts on both the anthropogenic and the natural environment [1,2,3,4,5,6,7]. The foreseen increases in their frequency and magnitude due to climate change and economic growth are expected to put flood-prone areas at even higher risk [3,8,9]. In order to mitigate the subsequent flood damages, monitoring and prediction of flood events are of vital importance [10]. Flood forecasting systems commonly rely on hydrologic and/or hydraulic models, whose response typically requires a prior calibration against in situ data, i.e., water levels and velocities. However, the sparse distribution of gauging stations in most areas, along with their vulnerability to the extreme events, render in situ observations particularly rare and thus inadequate to support calibration and validation processes all by themselves [10,11].
To this end, exploiting Earth observation (EO) data to map the extent of flooded areas may provide key information to decision-makers and flood disaster managers [12]. In particular, satellite-derived flood maps have the potential to provide a near real-time and synoptic view of the overall area affected by a given flood, which in turn allows for timely disaster response, quantification of damages, and estimation of the respective compensations needed to be assigned from the insurance companies [10,13,14]. At the same time, flood forecasting can be significantly benefited by incorporating distributed information in the form of an inundation map, instead of or in complement with in situ data, as a reference to calibrate and validate flood simulation models [12,15].
The incorporation of remote sensing techniques in flood modeling has gained much attention over the last two decades (e.g., [16,17,18,19,20,21,22,23,24,25]), revealing the substantial benefit arising from the cooperation of the two scientific fields. Many studies have been carried out with the purpose of delineating the extent of flooded areas, exploiting satellite images from different kinds of sensors, or utilizing different processing techniques (e.g., [26,27,28,29,30,31,32,33,34]).
Detection and mapping of floods has been performed utilizing both optical and microwave space-borne sensors. The use of the former dataset presents advantages mostly related to its straightforward interpretability and is thus preferred in case of clear weather conditions. Nevertheless, in the case of cloud cover or heavy rain, optical sensors (visible, infrared, thermal bands) cannot successfully detect flooding. On the other hand, microwave sensors, and especially the synthetic aperture radar (SAR), are capable of extracting information about flood extent under almost all weather conditions thanks to their inherent ability to penetrate clouds, while they also provide their own source of illumination, thus allowing operation during day and night. In addition to the abovementioned features, radar sensors, under certain conditions, also permit flood detection beneath vegetation, which is not feasible when optical sensors are used, rendering SAR particularly popular in flood mapping applications [12,15,35,36,37,38,39].
The applicability of SAR sensors in flood mapping lies in their high sensitivity to open water. Smooth water surfaces behave as specular reflectors, hence reflecting only a very little part of the incident radar signal back to the sensor. This results in significantly low backscatter values recorded in the radar system for the areas covered with water. On the other hand, land areas, which are typically rougher, scatter the energy emitted by the radar in many different directions, thus deriving much higher values of the backscatter coefficient. The differentiation in terms of scattering mechanism between water and land surfaces produces an image of high contrast between these two classes, i.e., flooded areas (or permanent water bodies) are depicted in dark tones, whereas dry land (non-flooded areas) is represented with brighter ones [33,35]. This principle has been encompassed in various approaches, either manual or semi- and fully automatic, developed to detect and delineate flooding in SAR images. Radiometric thresholding, either manual [40,41] or automatic [39], is one of the most widely applied methodologies, mainly preferred because of its high computational efficiency, which renders it ideal for fast mapping [42]. Other approaches found in the literature include visual interpretation, change detection (CD) techniques based on intensity and/or coherence data, region growing algorithms (RGA), segmentation techniques, such as active contour models, multi-temporal analysis, or hybrid approaches, e.g., [33,43,44,45,46,47,48]. Moreover, several researchers have addressed the issue of uncertainty arising from map delineation due to several sources, such as: (a) partly submerged vegetation and water roughening due to wind, which may both lead to misclassification of the respective areas as dry land; (b) particularly dry or smooth terrain, which is likely to have similar backscatter signature with that of surface water; (c) increased soil moisture, which may erroneously be attributed to double-bounce effect; (d) random discrepancy in backscatter coefficient due to speckle, etc. In this direction, methodologies based on fuzzy theory or Bayesian statistics have been also established, which are capable of yielding flood maps incorporating classification results for different degrees of uncertainty [49,50,51,52,53]. Some of the satellites carrying SAR sensors and having been employed in flood delineation studies are the ERS-1/ERS-2, ENVISAT, Radarsat-1, COSMO-SkyMed, and the TerraSAR-X [13,32,43,44,45,54].
In the last few years, Sentinel-1 (S1) mission has increased the potential for flood monitoring from SAR sensors, through a constellation of two radar satellites, i.e., S1-A and S1-B, operating since 2014 and 2016, respectively. The S1 mission was developed by the European Space Agency (ESA) as part of the EU Copernicus Program and is capable of monitoring the entire Earth with a 6-day revisit time, thus enabling the access to a long and continuous time-series of archived SAR scenes [8]. Both S1-A and S1-B satellites carry a C-band SAR instrument and have as primary operational mode over land the Interferometric Wide (IW) swath mode, providing acquisitions in dual polarization, that is, vertical–vertical (VV) along with vertical–horizontal (VH) polarization (VV + VH). Sentinel-1 products are freely available through the Copernicus Open Access Hub data portal of the ESA. Some previous studies having exploited S1 SAR data to detect and map floods include those of Psomiadis [55], Twele et al. [50], Bioresita et al. [12], Cian et al. [8], Li et al. [3], Chini et al. [41], Udin et al. [56], Zotou et al. [10], Gebremichael et al. [57], and Karamvasis and Karathanassi [58].
The present study aims at investigating the potential of S1 radar data in supporting flood modeling application. In particular, two distinct flood mapping approaches have been employed in this work: (a) a simplified one which involves thresholding of a single flood image, after appropriate preprocessing and calculation of its statistics; and (b) an automatic approach, in the form of a free and open-source python toolbox, named Flood Mapping Python toolbox—FLOMPY [58]—based on SAR statistical temporal analysis. Both flood mapping methodologies were applied on a flood event that took place in early February 2015 in Spercheios River, Central Greece, in order to delineate inundation extent at a specific time point, namely on 3 February 2015, at 04:31 a.m. UTC. The purpose of incorporating the abovementioned techniques was twofold. On one hand, we anticipated them to assist the hydrological–hydraulic modeling process in aspects such as guiding the modeling procedure of a coupled 1D/2D hydrodynamic model, examining its sensitivity in changing model parameters, e.g., roughness coefficient values and upstream inflow boundary conditions, and evaluating its response with respect to inundation extent. On the other hand, by using two different flood delineation approaches, we intended, apart from making comparisons regarding the discrepancies between the derived results, to gain insights on their relative suitability for supporting flood modeling applications. Given the considerable increase in the volume of archived SAR data over the last years, exploiting multitemporal information presents great potential for surmounting classification errors that often arise when conventional thresholding approaches are used. In this context, investigating the benefits derived from such a methodology (FLOMPY algorithm) compared to a single image thresholding approach is of great importance. In addition, although several studies implementing 1D or 2D hydraulic modeling can be found in the literature, far fewer have investigated the capabilities of the integrated 1D/2D modeling approach. Furthermore, contrary to the 1D and 2D approaches, the relative sensitivity of the combined 1D/2D models to different sources of uncertainty has not been thoroughly investigated. Since a clear view on which modeling approach is more appropriate does not exist yet in the literature, the predictive capability of the 1D/2D approach needs to be further examined.
2. Materials and Methods
2.1. Study Area
The study area, namely Spercheios River Basin (GR07), is located in Central Greece and extends from 38°44′ to 39°05′ N, and from 21°50′ to 22°45′ E. Administratively, it belongs to the Regional Unit of Fthiotida, whereas it is also one of the main river basins comprising the Water District of East Sterea Ellada (GR17), covering a total area of 2318 km2.
Spercheios River springs mainly from Tymfristos Mountain situated in the western part of the river basin and from Oity and Vardousia Mountains, which occupy the southern and southwestern part of the basin. It flows in an eastern direction, crossing Spercheios Valley and traversing a total distance of 82 km before discharging in Maliakos Gulf. The river receives the flows from more than 20 major tributaries, with most of them joining the main river at an almost perpendicular direction and forming a drainage network of dendritic type [55]. The upstream part of the main course is characterized by mountainous topography with steep slopes, while, when moving downstream towards the river mouth, the terrain gradually becomes flatter and the river presents intense meanders. The entire basin has a mean and maximum altitude of 626 m and 2282 m, respectively. Agricultural areas and natural vegetation along with bare land are the dominant land uses within the examined area, occupying 32% and 66% of its total extent, respectively, whereas built-up areas cover hardly 2% of it. The largest part of Spercheios river basin is covered with impermeable formations (62.6%), whereas the rest of it is occupied by semipermeable, alluvial, and karst formations at respective percentages of 0.2%, 20.5%, and 16.7%. The mean annual precipitation in the area has been estimated at about 788 mm [59].
Figure 1 depicts the location and boundaries of the entire study area (Spercheios River Basin) along with its main drainage network. The three individual watersheds, namely the Upper Spercheios, Gorgopotamos, and Asopos watersheds, considered in the present hydrological simulation, as well as the four precipitation gages exploited as boundary conditions in the hydrological model, are also illustrated.
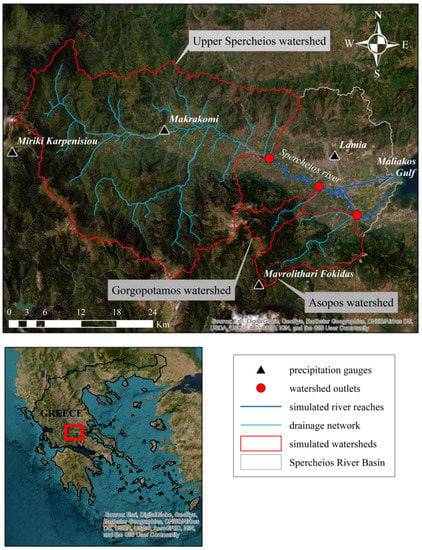
Figure 1.
Spercheios river basin along with its main drainage network, the three simulated watersheds, and the precipitation gages considered. The river reaches which were included in the hydrodynamic model are also shown.
2.2. Methodology
The methodology applied comprises four individual parts: (a) SAR image processing to extract an inundation map at a specific time point by employing both a simplified approach based on thresholding technique and an automatic flood mapping methodology (FLOMPY); (b) hydrologic modeling using HEC-HMS software in order to simulate the hydrological processes within the examined watersheds and generate the flow hydrographs at their respective outlets; (c) hydrodynamic modeling by means of a coupled 1D/2D HEC-RAS model, exploiting as upstream conditions the HEC-HMS-generated outflows, with the intention to derive the inundation extent at the same time with that of SAR image acquisitions; (d) comparison of the model against the SAR-derived inundation outputs, considering both remote sensing methodologies, with a view to investigate the 1D/2D model response, test its sensitivity to selected model parameters and identify eventual weaknesses of the applied SAR methodologies for use in flood modeling applications. The implementation of each individual part of the applied methodology is described below in detail. In addition, a flowchart describing the entire process is presented in Figure 2.
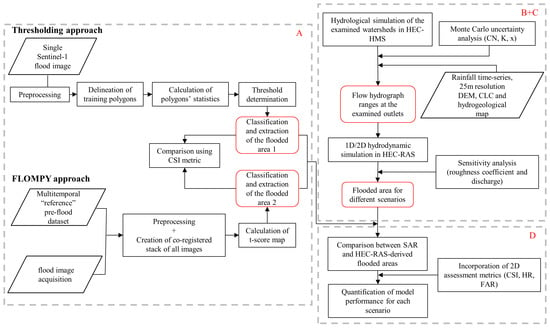
Figure 2.
Schematic flow diagram of the methodological framework; (A), (B + C), and (D) correspond to the four individual parts of the methodology, i.e., SAR image processing, hydrologic and hydraulic simulation, and comparison–evaluation, respectively.
2.2.1. Inundation Boundary Extraction through SAR Image Processing
The satellite data exploited to map the inundation area of the examined event was freely obtained through the Copernicus Open Access Hub of the European Space Agency [60]. All images utilized in both approaches were Level-1, Ground Range Detected (GRD), Interferometric Wide (IW) products of 10-m resolution. In the three following paragraphs, the first approach is described, whereas in the last paragraph of this subsection a brief description of the FLOMPY approach is provided.
For the first approach, a single Sentinel-1 image was acquired, depicting the area during flood, namely on 3 February 2015, at 04:31 am. (UTC). A single image was exploited, contrary to the common approach where two satellite scenes (one pre-flood and one post-flood) are typically considered in order to distinguish between flooded area and permanent water bodies.
The reason for this is that we meant to detect all pixels covered with water, including also the main channel, and thus derive a water extent result more suitable for comparison with the HEC-RAS output. The VV polarization was selected for the study needs, as it exhibited a better separability between flooded area and dry land, according to visual inspection. The satellite image processing was performed using SNAP software, which is freely available via the ESA’s website. In the two following paragraphs, the preprocessing and the thresholding workflows are described. The pre-processing steps implemented on the flood image included: (a) applying precise orbit file so as to correct the orbit state vectors, thus providing accurate information on satellite position and velocity; (b) subsetting the initial image at a specific spatial extent to include only the affected area; (c) converting image intensity values into the corresponding sigma nought values through radiometric correction (calibration); (d) applying Lee filter as a despeckling technique at a 3 × 3 window size; (e) converting the image from a linear to a logarithmic scale, called decibel (dB) scale, to improve image visualization and interpretation; and (f) applying Range–Doppler terrain correction in order to correct the image for inherent geometric distortions and project it into a map system.
Following the implementation of the pre-processing workflow, a threshold technique was applied on the flood image, so that flooded pixels could be distinguished from non-flooded ones. To do so, we delineated training polygons over representative areas exhibiting very low backscatter values (dark areas) incorporating both areas belonging to the main river and to the flooded overbank areas. Afterwards, the statistics of the digitized regions were calculated, and then, a threshold was determined based on the value corresponding to the 95th percentile. Subsequently, all pixels having a backscatter value lower than the defined threshold were classified as water, whereas those presenting higher sigma nought values were categorized as dry land. The classification was performed using appropriate expression within the band math tool of SNAP. The final output was exported in a GeoTIFF format for further processing in ArcGIS software (ver. 10.2.2).
The second methodology (FLOMPY) exploited in this study consists of an automatic approach, which is based on SAR statistical temporal analysis and has been validated using Emergency Management Service (EMS) products [58]. Multitemporal analysis, in general, allows for: (a) the identification of the backscatter temporal variability under pre-flood conditions, thus leading to a more reliable detection of changes due to flood; and (b) enhanced backscatter denoising by exploiting temporal information while maintaining the spatial accuracy of SAR images. Therefore, a more accurate classification result can be achieved without degrading spatial resolution. The inputs were the geographical boundaries of the region of interest and the time of interest. FLOMPY exploits the multi-temporal information of both polarizations (VV and VH) of Sentinel-1 products in order to construct two datasets. The first dataset was related to the pre-flood state using recent (3-month) “dry” (low precipitation) acquisitions. ERA-5 reanalysis model precipitation data were downloaded and used to characterize “dry” acquisitions. The second dataset was related to the flood state, i.e., it consisted of the same scene with that utilized in the first approach (3 February 2015, at 04:31 am. UTC). A t-score map related to the changes due to floodwater was calculated from the two aforementioned datasets. A classification pipeline based on spatially adaptive thresholding yielded the inundation output [58].
2.2.2. Hydrologic Simulation in HEC-HMS Software
This stage of the methodology consists of simulating the hydrological processes taking place within Spercheios river basin, in order to derive the flow hydrographs at the outlets of the three watersheds of interest (Figure 1). The aforementioned watersheds included: (a) the hydrological region draining the upper part of Spercheios River; (b) Gorgopotamos watershed; and (c) Asopos watershed, covering surface areas of approximately 1064 km2, 49 km2, and 137 km2, respectively. The flow hydrograph generated at each of these outlets was exploited as upper boundary condition to the respective branch of the main river encompassed in the hydrodynamic simulation (Figure 1).
In performing the hydrological simulation, the well-known Hydrologic Modeling System (HEC-HMS) software of the US Army Corps of Engineers Hydrologic Engineering Center [61] was used. Moreover, a GIS companion product, called Geospatial Hydrologic Modeling Extension (HEC-GeoHMS), was also employed to carry out the hydrologic analysis and prepare the required inputs for HEC-HMS. The following methods were selected in order to simulate the hydrologic procedures throughout the modeled area during the examined precipitation event: (a) the SCS Curve Number (CN) method for estimating the rainfall losses and the excess rainfall; (b) the SCS Unit Hydrograph for transforming excess rainfall into surface runoff; and (c) the Muskingum method for performing the hydrologic routing.
The utilized input data was precipitation time-series from four meteorological station recordings within the study area or at a near distance from its boundary (see Figure 1 for the exact locations), a Digital Elevation Model (DEM) of 25-m resolution acquired through Copernicus Land Monitoring Service [62], a CORINE Land Cover map available through the same source and, lastly, a hydrogeological map of the area obtained via the Federal Institute for Geosciences and Natural Resources of Germany [63]. The simulation time window was from the 23 January 2015 (starting date) to the 6 February 2015 (ending date), whereas a 10-min time interval was selected for the computations.
To determine the CN value for each individual subbasin element within the modeled area, the land use map along with the lithological map and a look-up table containing information on the appropriate CN value (according to the literature) for each given combination of land use and soil group (soil hydrological category A, B, C, or D) were combined. Regarding Muskingum parameters, K was estimated separately for each reach of the examined watershed through Equation (1), in accordance with the HEC-HMS User Manual. Parameter x is a dimensionless weighting parameter used in Muskingum routing method to represent flood wave attenuation, which ranges between 0 and 0.5. Practically, a value equal to 0.5 indicates that inflow and outflow have the same influence on storage, and subsequently, very low or no attenuation takes place, whereas a value equal to 0 indicates maximum attenuation, which means that inflow has little or no effect on storage. According to the literature, x ranges between 0.2 and 0.3 for the case of natural streams; therefore, an initial value of 0.2 was selected to be representative for this study [64].
where K is the travel time through a given reach (h), L is the actual reach length (m), and V is the wave celerity assumed to be equal to 1 m/s in this study.
Furthermore, the number of subreaches into which each individual reach element should be subdivided was specified in accordance with Qaiser and Yuan [65] through Equation (2):
where N is the number of subreaches, x is the attenuation parameter of the Muskingum method (dimensionless), L is the actual length of the reach (m), V (m/s) is the mean flow velocity (assumed to be equal to 1 m/s), and Δt (min) is the simulation time step (equal to 10 min in the present study).
The number of subreaches determined through the above equation was subsequently checked to assure that the condition described in Equation (3) is satisfied [65]:
where K (min) is the travel time through each given subreach, x is the attenuation parameter of the Muskingum method (assumed to be equal to 0.2 in all reaches), and Δt (min) is the simulation time step (10 min).
2Kx < Δt < K
In this study, apart from performing the simulation on the basis of user-specified values for the parameters of the hydrological model, a probabilistic approach was also encompassed by using the Monte Carlo method. Specifically, recognizing the total error introduced in the simulated watershed response, as a result of the uncertainty accompanying the determination of model parameter values, we decided to integrate an extended uncertainty analysis, performed within HEC-HMS software. The purpose was to investigate how a different estimation of model parameters affects the flow hydrographs generated at the outlets of the examined watersheds and, consequently, how this uncertainty is transferred to the results of the hydrodynamic simulation. In order for the uncertainty analysis to be implemented, we created several alternative models of the examined watershed, each integrating a different combination of values for the selected parameters. These combinations are typically produced through an automatic sampling procedure accomplished for each particular parameter according to a probability distribution specified by the user. In addition, an upper and lower value should also be determined separately for each parameter to confine sampling procedure within user-specified boundaries. In this study, the parameters considered in performing the Monte Carlo analysis were CN, K, and x for all subbasins and reach elements throughout the examined area. All of them were assumed to follow a uniform distribution and their value range for the sampling was set as ±20% of the initially specified values. To decide upon the number of samples needed to be generated for each parameter and, subsequently, upon the number of the required simulations to be performed to adequately reflect the total range of uncertainty, a convergence analysis was undertaken, considering as a statistical measure the standard deviation of the peak discharge, among all the hydrographs computed at the outlet. To achieve a convergence in the selected statistical measure, the latter should not change even when a greater number of samples is computed. In the present work, we performed the Monte Carlo analysis several times, specifying each time a different number of samples to be generated, i.e., 50, 100, 200, 500, 800, 1000, 2000, 3000, and 5000 and determining the standard deviation of the peak discharge. It should also be clarified that in order to perform the Monte Carlo analysis, due to the increased computational time, the total area being examined, i.e., Spercheios river basin, was subdivided in three separate models, encompassing only the three watersheds of interest and excluding all hydrological regions found downstream of their respective outlets, so as to accelerate the simulations. Figure 3 illustrates how both standard deviation and mean value of the peak discharge of the generated hydrographs change with the number of simulations performed for each of the three watersheds. Based on the above-described analysis, we decided to select a number of 1000 samples for performing the Monte Carlo analysis, since at this number the standard deviation of peak discharge begins to be stabilized and converges towards a value for all three watersheds. Figure 4a–c depict the range of flow hydrographs generated from the uncertainty analysis at the outlets of the examined watersheds.
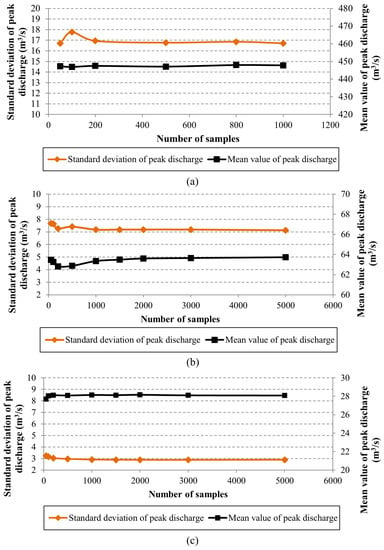
Figure 3.
Standard deviation and mean value of the peak discharge of the hydrographs computed at the outlet of each of the three watersheds of interest for different numbers of samples: (a) Upper Spercheios watershed; (b) Asopos watershed, and (c) Gorgopotamos watershed.
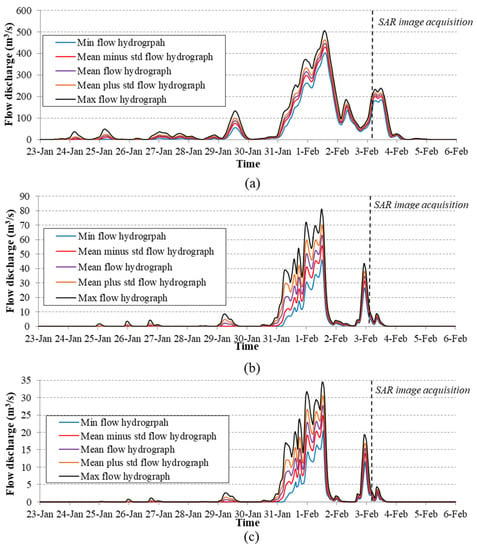
Figure 4.
Flow hydrographs generated through the Monte Carlo analysis at the outlets of the three simulated watersheds and time of SAR image acquisition: (a) Upper Spercheios watershed; (b) Asopos watershed; (c) Gorgopotamos watershed.
2.2.3. Hydrodynamic Simulation in HEC-RAS Software
Regarding the hydrodynamic simulation, a coupled 1D/2D model was built using the Hydrologic Engineering Center’s River Analysis System (HEC-RAS) software in order to propagate the runoff generated from the hydrologic simulation and reproduce the inundation extent induced by the examined rainfall. HEC-RAS software has been developed by the US Army Corps of Engineers and is capable of performing one-dimensional (1D), two-dimensional (2D), or coupled (1D/2D) flow simulation considering steady or unsteady flow conditions along both natural and constructed channels. Integrated 1D/2D models are most commonly implemented by assuming lateral structures, which couple the 1D cross-sections with the 2D domain. These connections may either be real structures, e.g., weirs, culverts, etc., or simply represent high ground separating flow in the main river from the floodplain. Flow overtopping the structure is computed through the weir equation or 2D flow equations [66]. In the present work, the 1D part of the model included the branches of the main channel whereas the 2D one was utilized to simulate the overbank flow in the floodplains.
For the 1D unsteady flow simulation, the continuity equation (conservation of mass) and the momentum equation (conservation of momentum) were used. HEC-RAS assumes a horizontal water surface at each cross section normal to the direction of flow, so that the exchange of momentum between the channel and the floodplain is negligible, and the discharge is distributed according to conveyance [67]. Given this assumption, the 1D equations of motion are the following Equations (4) and (5):
where t [T] is the time, Q [L3T-1] is the total flow, A [L2] is the flow area, Φ [dimensionless] is the ratio of channel conveyance over the total conveyance, z [L] is the elevation of water surface, Sf is the friction slope, and the subscripts c and f refer to the channel and floodplain, respectively. HEC-RAS uses an implicit finite difference scheme to approximate these equations and solves them numerically using the Newton–Raphson iteration methodology [67,68,69].
To perform the simulation in the 2D domain, HEC-RAS solves either the full Saint-Venant equations (i.e., the Shallow Water Equations—SWE) or the Diffusion Wave Equation, with the latter providing faster and more stable solutions [70].
The continuity (Equation (6)) and momentum (Equations (7) and (8)) equations comprising the full SWE in two dimensions are presented below [67]:
where H is the water surface elevation [L], u and v are the velocities in the Cartesian directions [LT−1], q is the source/sink flux term, g is the gravitational acceleration [LT−2], vxx and vyy are the horizontal eddy viscosity coefficients in the x and y directions [L2T−1], fc is the bottom friction coefficient [Τ−1], τs is the surface wind stress [ML−1T−2], h is the water depth [L], ρ is the water density [M/L3], and f is the Coriolis parameter [T−1]. The left-hand side of Equations (7) and (8) contains the acceleration terms (unsteady and advective accelerations) whereas their right-hand side represents the internal or external forces acting on the fluid. An implicit finite volume algorithm is exploited for the solution of the 2D unsteady flow equations, allowing for larger time intervals compared to the explicit method.
The Diffusion Wave approximation of the SWE (DSW), which has been selected to be applied in this study, constitutes a simplification of the momentum equation, where the unsteady and advective acceleration, turbulence, and Coriolis effect terms are disregarded. In order to use such an approximation, the flow should be principally driven by the barotropic pressure gradient balanced by bottom friction [67]. The simplified version of the momentum equation derived based on the aforementioned assumption is as follows (Equation (9)):
where V is the velocity vector [LT−1], R = R(H) is the hydraulic radius [L] as a function of the water surface elevation, ∇H is the water surface elevation gradient [L] and n is the Manning’s roughness coefficient [TL−1/3].
When the Diffusion Wave form of the momentum equation is used instead of the full momentum equation, the corresponding system of equations can actually be unified into a single equation model. This is achieved through direct substitution of the Diffusion Wave equation in the mass conservation equation, which yields the classical differential form of the Diffusion Wave Approximation of the Shallow Water (DSW) equation presented hereunder [67]:
where .
The 1D elements of the model, which practically constitute the geometric representation of the main river, included the stream centerline for each of the totally seven river branches encompassed, the corresponding bank lines, the flow path centerlines, and the cross-sections along the examined river network. The above set of layers were digitized in ArcGIS environment, using HEC-GeoRAS extension and exploiting as underlying terrain a 5-m resolution DEM. The geometric data was then imported in HEC-RAS, along with the utilized terrain, where the rest of model geometry was set up by gradually adding the 2D flow areas and the centerlines of the corresponding lateral connections to allow for the coupling between the 1D channel and the 2D domain. The lateral structures were located on both sides of the examined river branches, so as to cover their entire length. Due to a restriction of HEC-RAS software, which imposes that each lateral connection does not contain more than 500 station-elevation points, it was necessary to break the initial lateral connection centerlines in several pieces so as to overcome this limitation. Subsequently, thirty-three lateral connections were digitized in total following the high ground separating the main channel from the overbank area and spanning a total distance of approximately 50 km. By means of the aforementioned connections, the 1D cross-sections were coupled with the cells of the totally five 2D flow areas digitized. Regarding the 2D mesh, a base cell size of 25 m × 25 m was selected for all 2D areas. Then, the computational mesh was locally refined (12.5 m × 12.5 m cells) at representative locations where more detail was needed, using break lines. This decision was made considering: (a) the resolution of the available terrain data (5 m), which would not allow for a cell size smaller than the terrain resolution; (b) the fact that the area being modeled is primarily characterized by mild terrain without abrupt slopes and, therefore, flow processes can be satisfactorily captured using the selected cell size; and (c) the fact that the selection of a finer resolution would translate into a significant increase in computational burden. The role of break lines in 2D modeling is practically to represent barriers to flow, or areas that affect flow direction, such as high ground. The mesh is typically modified around these locations by reducing the cell size and by aligning cell faces along them in order to accurately capture abrupt changes in terrain. In the present study, the major road and rail networks, levees, part of the drainage network as well as the boundary of four residential areas falling within the modeled area were digitized and represented as break lines. The computational mesh generated based on the above-described discretization covered a total area of approximately 91 km2 and consisted of 157,000 cells. Figure 5 presents a synoptic view of the area modeled and its main features.
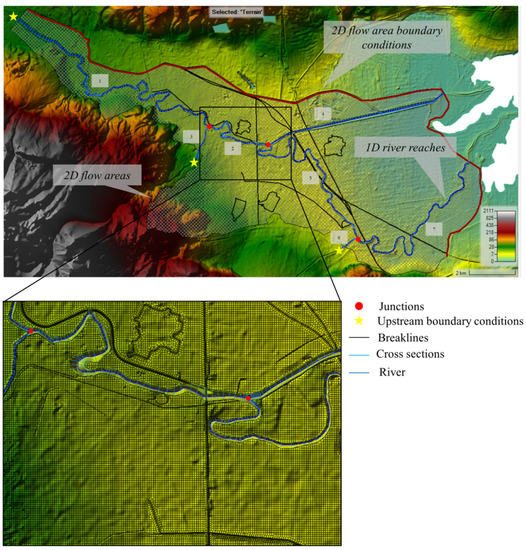
Figure 5.
Synoptic view of the entire area being modeled and its main feature.
As upstream boundary conditions, we applied the flow hydrographs derived from the hydrologic simulation at the outlets of the three examined watersheds, which coincide with the three upper boundaries of the 1D part of the model (most upstream cross-sections of the respective rivers). A baseflow approximately equal to 10% of the peak discharge of each inflow hydrograph was added to each of them to achieve stability in the simulations.
As downstream boundary condition, in all cases (both 1D river and 2D areas) the normal depth was selected, which was computed based on friction slope (assumed to be equal to bed slope) and was set equal to 0.001 for all simulations. The computation interval for the simulation was set at 3 s, leading to a total duration of approximately 4.75 h for the entire time window (from 28 January 2015, 00:00 am to 6 February 2016, 00:00 am) simulated.
Regarding Manning roughness coefficients in the 2D domain, a CORINE Land Cover map was exploited to detect the land uses falling into the model area. The sixteen different land uses identified were reclassified in nine broader land use categories presenting similar roughness characteristics, according to the land use categorization indicated in HEC-RAS 2D User’s Manual [67]. Then, an extended literature review was implemented in an attempt to determine wide ranges of the roughness coefficient value for each reclassified land use category, so as to encompass even relatively great values of the coefficient, which may be the case in 2D shallow flow conditions [67,71,72,73,74,75]. From the published coefficient value ranges, we considered, for each land use, the lowest and the highest coefficient value identified, in order to establish the value ranges exploited in this study. Table 1 presents the initial land use codes and the respective descriptions (according to CORINE), the percentage of the total area being covered by each specific use within the modeled area, the respective area per land use that was detected as flooded through the SAR image, the land use categorization (description and respective code) after the reclassification, and the respective roughness coefficient ranges considered.

Table 1.
Initial and reclassified Land Use (LU) categories and selected roughness coefficient ranges according to the literature.
To establish the roughness coefficient ranges for the main channel (1D part), a segmentation of its total length was performed, assuming that in the upper reaches higher resistance to flow is typically observed compared to the lower ones, which translates into higher roughness coefficient values. The seven river segments into which the main channel was subdivided coincide with the existing river reaches and are illustrated in Figure 5. Each of these river segments was classified in one of the three reach categories considered in this study, i.e., “upper”, “middle”, and “lower” reach category, as described in Table 2.

Table 2.
Representative roughness coefficient values per land use (for the 2D flow areas) and river segment (for the 1D river) applied during the sensitivity analysis.
Given the increased computational time, and in order to maintain the simulations to a reasonable number, the sensitivity analysis was performed by testing five representative values of the roughness coefficient, i.e., the minimum, mean, maximum, and the values corresponding to the 25% and 75% of each established value range. The 2D flow areas and the main channel were examined separately, as follows. For the 2D area, each time a specific land use was tested, all other coefficient values (both for the rest of the land uses and the 1D river reaches) remained stable, being assigned the mean value of their respective value range. Similarly, to examine the influence of the main channel, the five representative coefficient values (min, max, mean, 25%, and 75%), as established per reach class and indicated in Table 2, were tested. During this procedure, all roughness coefficients in the 2D domain remained stable and were assigned the mean value of their respective established value range.
Table 2 presents the representative roughness coefficient values tested for the land uses (2D flow areas) and the three different reach classes (1D river). It should be mentioned that among the existing land uses, we decided to perform the sensitivity analysis only for land uses 2, 3, 4, 5, and 6, taking into account mainly the total area the latter cover within the modeled area along with their proximity to the main channel, which would eventually affect the transfer of flow from the 1D river to the 2D domain and, consequently, the simulation results.
Additionally, the prior knowledge regarding the land use areas which were actually subjected to flood (Table 1), as provided by the satellite image, was also considered, resulting in the exclusion of land uses 1, 7, 8, and 9 from the analysis. These land uses simply maintained a stable Manning coefficient value (equal to the mean value of their established range) during the sensitivity analysis.
During the roughness coefficient sensitivity analysis, all other modeling parameters remained the same. As upstream boundary condition, the initial flow hydrographs, i.e., those derived when the hydrologic simulation of the upstream watersheds was performed considering user-specified values for the model parameters, were applied in all above-described scenarios.
Apart from the effect of the 2D domain and the 1D channel roughness coefficients, the influence of the upstream boundary conditions in the simulation results was also tested. For this purpose, the five indicative flow hydrographs (Figure 4), as derived from the Monte Carlo uncertainty analysis for each of the three upper boundaries of the model, were applied as upstream inflow condition to the respective reaches. For all upstream inflow hydrograph scenarios tested, the roughness coefficient in the 1D river and in all land uses of the 2D areas was set equal to the mean value of each established range.
The results generated from all above-described scenarios were compared against the inundation extent, as extracted from both SAR processing approaches. The ultimate aim was to use the SAR processing result as a reference to detect changes in model response resulting from different uncertainty sources. On a secondary level, we also intended to evaluate the two different SAR processing techniques in terms of their suitability in supporting flood modeling applications.
The results derived from HEC-RAS simulation consisted of the inundation boundary for each examined scenario at exactly the same time with the flood-image acquisition, i.e., 04:30 am UTC. The HEC-RAS-derived inundation boundaries were all exported from HEC-RAS software to ArcGIS for post-processing and comparison with the SAR-derived results.
2.2.4. Comparison–Evaluation
The last stage of the process was implemented in ArcGIS environment and consisted of the post-processing of the inundation results, as obtained from the hydraulic simulations and both SAR processing approaches. All inundation boundaries were converted from raster to polygon features, and their surface area was calculated. Then, the surface areas of intersection and union between each HEC-RAS-derived result and the inundation result derived from each of the two SAR methodologies were computed. The level of coincidence between each simulated scenario and SAR-derived inundation boundary was quantified by using the Critical Success Index (CSI) presented in Equation (11) [10,36,76]:
where Smod is the surface area predicted as flooded by the model, and Sobs is that observed as flooded through the SAR image processing.
The CSI-index ranges between 0 and 100%, with 100 denoting a perfect match between model-predicted and SAR-derived inundated areas.
Moreover, two additional metrics were also incorporated in the analysis, in order to examine the tendency of the model towards either under- or over-prediction. These were the Hit Rate (HR) and the False Alarm (FAR) indices, which are given by Equations (12) and (13), respectively [76]:
Both indices range from 0 to 100%. The Hit Rate expresses the proportion of the SAR-observed inundated area that was also predicted as such by the model, with a value equal to 100 signifying that all of the SAR-derived area was predicted as flooded by the model. On the other hand, the False Alarm index gives an idea of whether the model over-predicts the flood extent, with values of 0 and 100% revealing no false alarms and all false alarms, respectively.
3. Results and Discussion
Figure 6 illustrates the flooded areas for the examined event as extracted from each of the two SAR processing approaches. The spatial extent of both inundation results has been clipped based on the boundary of the HEC-RAS model area to enable comparisons both between each other as well as with the output of the hydraulic simulation. It is observed that the two results reveal significant similarities in terms of the areas being classified as flooded. In most cases, areas detected as flooded by the first approach have been detected as such by the FLOMPY approach as well. However, in the second case, the area that emerged as inundated is almost consistently greater. This has been probably resulted from: (a) the higher sensitivity of the FLOMPY algorithm in relation to the first approach; and (b) the multi-temporal approach integrated in the FLOMPY algorithm, which allows for effective removal of speckle noise without degrading image spatial resolution. This, in turn, leads to a more coherent and spatially continuous flooded area compared to the first approach, which makes use of a traditional despeckling technique. The main discrepancy that occurred between the two results concerns the detection of water along the main channel. In this respect, the first (simplified) approach resulted in partially detecting water within the boundaries of the main channel but only in a very limited part of the total length of the river. Although the methodology has been developed with the aim to also encompass permanent flow in classification, this had not been possible due to the particularly narrow width of the examined river main channel (approximately 10 m in many areas), the further deterioration of spatial resolution that resulted from the filtering process, as well as the dense vegetation covering a great part of the total river length. On the other hand, the FLOMPY approach has not included flow in the main channel at all, due to the nature of the algorithm itself, as it emphasizes detecting changes in backscatter between pre-flood and flood states, and thus, areas which remain the same (permanent flow) in both situations are not included.
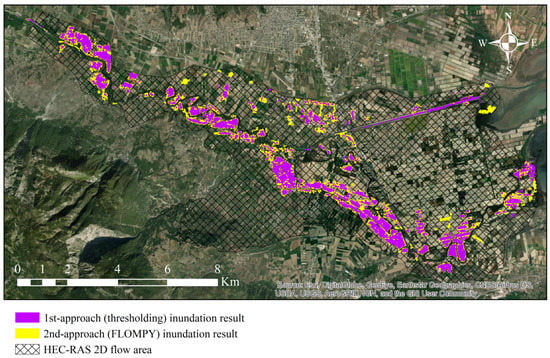
Figure 6.
Inundation boundaries as extracted through the two different SAR processing methodologies.
Given that the area along the main channel was not successfully detected, the two flood extents were finally compared to each other considering only the areas within the 2D domain of HEC-RAS model. This decision was also dictated by the fact that the detection of the permanent flow in this specific case proved to be impossible for C-band and 10 m-resolution satellite data, independently of the utilized flood delineation approach. Therefore, including this area in the comparison would not provide any meaningful conclusion about the relative performance of the two approaches. On this basis, and making use of Equation (11), the percentage of coincidence between the inundation results derived from the two SAR processing methodologies was calculated equal to 51.92%.
Regarding comparisons between HEC-RAS and SAR-derived inundation extents, it should be clarified that flow along the main channel was excluded from HEC-RAS-generated flood maps as well, and the derived results were compared considering only the 2D domain.
Figure 7 presents the results of the sensitivity analysis with respect to variation in roughness coefficient value. The graphs illustrate the changes in the total inundated area (predicted by the model) and the CSI-index of coincidence (Equation (11)) between HEC-RAS result and each of the two SAR processing methodologies, as a function of roughness coefficient in the 2D flow areas (LU 2, 3, 4, 5, and 6) and main channel.
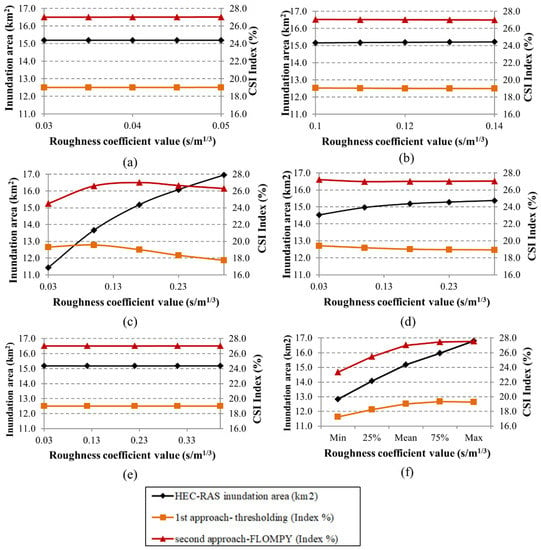
Figure 7.
Inundation area predicted by the model (primary vertical axis) and CSI-index value (%) for each SAR methodology applied (secondary vertical axis) as a function of variation in roughness coefficient value in: (a) land use 2; (b) land use 3; (c) land use 4; (d) land use 5; (e) land use 6; and (f) main channel.
It can be easily observed that the roughness coefficient variation in land uses 2, 3, and 6 exerts, as expected, a negligible impact on both the total inundated area and the CSI-index value, mainly due to the small surface area they cover.
On the other hand, it is clear that the model predictive accuracy (CSI-index value) and total area of inundation, as far as the 2D area is concerned, are almost entirely dependent on land use 4 (Figure 7c) and secondarily on land use 5 (Figure 7d), which is mainly explained by the fact that they together occupy nearly 92% of the total area being modeled. As far as the influence of the 2D domain is concerned, land use 4 causes the greatest variation in model response, with the total area predicted as inundated ranging from approximately 11.4 km2 up to 17 km2, and the respective percentage of coincidence (CSI-index) with the SAR results ranging from 17.7–19.6% and 24.5–27% for each SAR methodology, depending on the selected coefficient value. Surprisingly, an even greater influence concerning CSI-index value is observed when the roughness coefficient within the main channel is varied (Figure 7f). Specifically, even though a more restricted value range than that applied for land use 4 was assumed, variation of roughness coefficient in the main channel between its minimum and maximum values leads to an alteration of index value from 23.4% to 27.5% for the FLOMPY approach (or from 17.3 to 19.4% for the simplified approach). Other recent studies that have exploited the CSI-index to compare HEC-RAS simulation results against satellite imagery-derived flood maps produced index scores of 64% and 66% (after calibration and validation, respectively) [77], between 74.2% and 76.6%, depending on the selected polarization (VV or VA) of the SAR products [78], and between 65% and 95% [79]. Moreover, Nguyen et al. [80], who assimilated SAR-derived flood maps to improve simulation results of a TELEMAC-2D model, reported CSI values ranging between 22% and 63.97% depending on the simulated scenario. Comparatively low index values were finally estimated by Ekeu-wei et al. [81], who calibrated a 2D Caesar-Lisflood hydrodynamic model by exploiting: (a) optical (MODIS) data alone and (b) in combination with SAR data in a vegetation-dominant region. The results demonstrated a low performance of the examined model, which attained a 23.5% and 27.3% CSI score for the optimum roughness coefficient, when the optical and the combined data were considered as reference, respectively. More importantly, Figure 7f reveals that the model predictive performance increases for greater values of the main channel roughness coefficient, contrary to the rest of the cases, i.e., land uses 4 and 5, for which better percentages of coincidence with SAR results occur for roughness coefficient values in the lower or middle areas of the selected value ranges. The greater effect of the main channel compared to the floodplain roughness coefficient was also verified by Lamichhane and Sharma [82], who found that the variation of roughness in the first case led to an 8.97% change in the extent of flooded area against a percentage of hardly 1.49% produced by the variation of roughness coefficient in the floodplains. Afzal et al. [77] also reported that a small increase in manning’s value in the main channel of a 2D HEC-RAS model caused a higher increase in the simulated inundated area, compared to a similar increase in the floodplains’ n values.
Furthermore, Liu et al. [83], who investigated the performance of different hydraulic models with respect to their sensitivity to roughness characterization and model structure, found that LISFLOOD-FP diffusive model and HEC-RAS 2D model showed a greater sensitivity to the channel roughness coefficient as well, while model performance was improved for higher values of the coefficient.
Regarding the different SAR methodologies tested, the results prove that the second approach (FLOMPY algorithm) presents consistently higher percentages of coincidence with model results for all simulated scenarios. This probably indicates its greater suitability for evaluating model response due to the more continuous, and thus, realistic flooded area it yields.
In an effort to further examine the tendency of the model towards either over-prediction or under-prediction of the flooded area, two additional measures of fit, namely the Hit Rate (HR) and the False Alarm ratio (FAR) were estimated and are illustrated in Figure 8a–f.
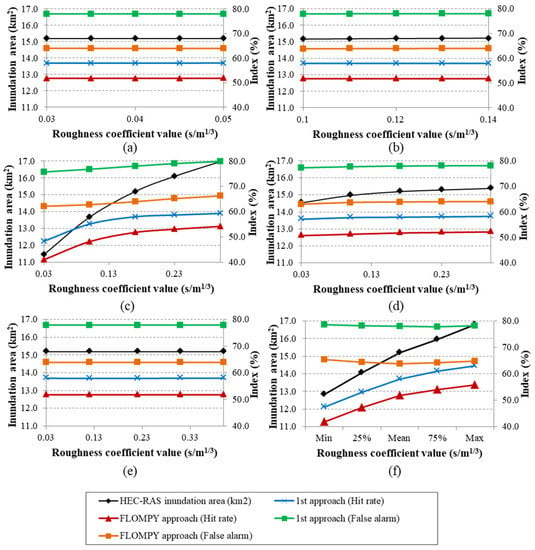
Figure 8.
Inundation area predicted by the model (primary vertical axis) and Hit Rate and False Alarm index values (%) for each SAR methodology applied (secondary vertical axis) as a function of variation in roughness coefficient value in: (a) land use 2; (b) land use 3; (c) land use 4; (d) land use 5; (e) land use 6; and (f) main channel.
The inundated area derived from each of the two SAR processing methodologies was assumed to be the “ground truth”, and the aforementioned indices were computed for each simulated scenario. The HR and FAR indices are significantly affected only by the variation of roughness coefficient in the main channel (Figure 8f) and in the land use 4 (Figure 8c), whereas the rest of the land uses practically exert no impact on the degree of over or under-prediction of the model.
What can be seen from the graphs is that, in all cases, when the FLOMPY result is considered as reference, lower values of both the False Alarm (lower over-prediction of the hydraulic model) and the Hit Rate index emerge compared with when the simplified approach is being considered. This is reasonable since for the simplified SAR processing approach, a smaller inundated area is derived. Hence, when the model is being compared against this area, it looks like it more extensively over-predicts flood.
Likewise, given the smaller inundation extent derived from the first approach, it is easier for the model to reproduce a greater proportion of the SAR-derived flood, and thus, attain higher scores with respect to the Hit rate index.
Depending on the simulated scenario (selected roughness coefficient value), the Hit Rate index ranges from 47.4% to 64% and from 41% to 55.8%, when the first and the FLOMPY approaches are considered as reference, respectively. Correspondingly, the False Alarm ratio varies between 75.6% and 79.8% and between 62.1% and 66.1% for the first and the FLOMPY approaches, respectively. Regarding the main channel (Figure 8f), it is observed that the Hit Rate index increases for higher values of the roughness coefficient, i.e., a greater proportion of the SAR-derived flood is also being captured by the model, without this leading to a simultaneous increase in over-prediction (False Alarm index). This is in agreement with our previously mentioned inference that higher predictive performance (CSI-index) of the model emerges for higher roughness coefficient values in the main channel and thus demonstrates that the optimum coefficient values fall within the upper region (or even further upwards) of the established value range. With regard to the 2D flow area, and specifically the land use 4, as can be seen from the Figure 8c, a rise in roughness coefficient corresponds to simultaneous increase in both HR and FAR indices. However, the Hit Rate index presents a steeper rise compared to the False Alarm index for the first half of the value range, which can be interpreted as a rather positive than negative effect on the overall performance.
Table 3 presents the percentage of coincidence (CSI-index) between SAR-derived results and those extracted from the hydraulic simulation along with the respective Hit Rate (HR) and False Alarm (FAR) indices for each of the five representative inflow hydrograph scenarios simulated. The respective total inundated area is also provided.

Table 3.
Total area of inundation derived from HEC-RAS simulation and percentage of coincidence between SAR-observed and model-predicted inundation results for each SAR processing approach and each input hydrograph utilized.
The simulated inflow hydrograph scenarios reflect the entire range of uncertainty introduced by the hydrologic simulation of the upstream watersheds and consist of the: (a) minimum; (b) mean minus standard deviation; (c) mean; (d) mean plus standard deviation; and the (e) maximum inflow hydrographs. As a general observation, it is shown that the upstream boundary conditions exert a greater influence in the formulation of the final results compared to the variation of roughness coefficient in both the 2D domain and the main channel, causing a percent change in the total flooded area of approximately 81% (i.e., from 11.13 km2 to 20.15 km2). These results are in agreement with our previous study [10] where the response of a simpler 1D hydraulic model as a function of different sources of uncertainty had been investigated. Another study that also confirms the dominant role of input hydrology compared to other components of uncertainty is that of Annis et al. [84], who obtained a 50–220% change in the derived inundation extent by varying input discharge against a 6–9% change by perturbing the roughness coefficient. Other studies that reported similar finding are those of Vojtek et al. [85] and Mosquera-Machado and Ahmad [86]. Specifically, considering the coincidence with FLOMPY results, inflow hydrograph variation produces a range of approximately 5.5% in HEC-RAS model performance, with better percentages emerging for upstream conditions close to the middle–upper inflow scenarios, thus demonstrating a slight underestimation of the initial inflow hydrographs as derived from the hydrologic simulation. In terms of the CSI-index value, it is apparent that the FLOMPY approach shows again a closer similarity with HEC-RAS-derived results, compared to the simplified approach, for all simulated scenarios. H and F indices have a response roughly analogous to the CSI-index, in that they both increase for greater upstream inflow conditions, with the exception that these continue rising even for inflows beyond the “mean plus standard deviation” scenario, where the highest CSI score was identified.
Figure 9a–e presents a qualitative comparison between the SAR-derived (FLOMPY approach) flood extent (depicted in purple) and that derived from the hydraulic simulation (in yellow) for each inflow hydrograph scenario simulated. The common area between the two extents is also illustrated in red.
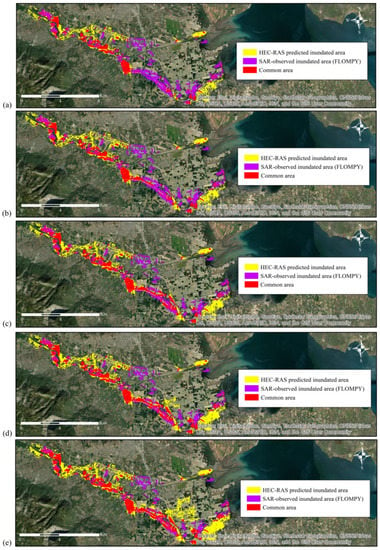
Figure 9.
SAR-observed (FLOMPY approach) and HEC-RAS-predicted inundated areas for the five indicative upstream inflow scenarios generated through the Monte Carlo uncertainty analysis: (a) minimum hydrograph; (b) mean minus standard deviation hydrograph; (c) mean hydrograph; (d) mean plus standard deviation hydrograph; and (e) maximum hydrograph.
With regards to the predictive accuracy of the hydraulic model itself, for the examined event, better results seem to emerge for higher upstream inflow conditions as well as for higher roughness coefficient values in the main channel. Values around the lower–middle areas of roughness coefficient-established ranges for land uses 4 and 5 also contribute to the improvement of the overall model performance.
However, significant uncertainty still remains, which seems not to be related to the upstream conditions and roughness coefficient value. The remaining uncertainty in the simulation results could be associated to some extent with the inaccuracies in terrain representation. Although the effect of terrain spatial resolution and accuracy on the inundation output is not thoroughly examined in this work, this assumption is consistent with the results presented by Lamichhane and Sharma [82], who reported a 35.37% decrease in the total predicted inundated area when precise LIDAR data combined with survey data were exploited, compared to the case when a 30-m DEM was applied. In addition, we estimate that in the present study, model structure also exhibits a great impact on the final results. Although structural uncertainty is often neglected and seems to be a rather unexplored field compared to input data and parametric uncertainties, the former seems to play a dominant role in model results as model complexity increases. As we move from a 1D model to a 1D/2D or 2D representation, input data and parametric uncertainties begin to affect the simulation less, whereas model structure influence increases. This assumption is in agreement with Ghimire et al. [87] and Dimitriadis et al. [88], who found that 1D models tend to be more sensitive to parametric uncertainty compared to a 2D flood model. This is also partially justified by our previous results [10], which showed a much greater response of a quite simpler 1D model to parameter variation (roughness coefficient and input discharge), achieving higher performance scores (up to 65%), although a certain degree of structural uncertainty also existed there. Moreover, the subjective view of the modeler forms an integral part of the structural uncertainty, which is estimated to significantly affect the simulation outputs, especially in complex 1D/2D or 2D hydraulic models, where several modeling decisions should be made (e.g., model area boundary, mesh spatial resolution, representation of structures, etc.).
In particular, and as far as the modeling procedure of the present study is concerned, it was observed that the placement of the 1D/2D connections constitutes a time-consuming procedure where much attention and in some cases a trial-and-error approach are required in order to avoid poorly locating the respective centerlines. Specifically, it is crucial that the lateral structure be placed exactly at the high ground (highest elevation) separating the main channel from the 2D area. When this is not the case, the model may compute a greater amount of flow overtopping the structure and passing to the 2D domain, thus introducing a considerable degree of uncertainty in the results. In fact, the selection of the modeling approach itself, namely between a 1D, 2D, or a coupled 1D/2D model may significantly affect the final output as well. Although the studies focusing on the comparison between 2D and coupled 1D/2D hydraulic models are limited, a recent one undertaken by Ghimire et al. [87] reported that 2D models exhibit better performance compared to 1D/2D ones, while the latter do not actually show any considerable superiority against a 1D model. Moreover, in another study examining the comparative predictive performance of a coupled 1D/2D and a fully 2D model, although the results showed a relatively greater performance of the coupled model for the examined case study, the former was also found to predict approximately 40–50% more flooded area compared to the fully 2D model, which indicates that considerable discrepancies may occur depending on the selected approach [89].
Nevertheless, in the current study, the selection of the 1D/2D approach undoubtedly presented some advantages as well. In particular, it was considered to be more appropriate, compared to a 1D model, for reproducing flow conditions in a complex and highly braided system, as is the one investigated in the current study. Furthermore, in case of using a 1D approach, we could not have dealt with the water overtopping the levees, since in this case water flows in many directions and not in the longitudinal one. On the other hand, the selected approach provided a more efficient alternative in terms of computational burden, compared to a fully 2D model, where the entire domain would need to be modeled through a 2D mesh, thus leading to higher computational times.
A certain amount of uncertainty is inevitably introduced by the SAR satellite data and the processing techniques utilized as well. This is mostly related to the fact that none of the tested methodologies dealt with the case of flooded vegetation, namely high vegetation (e.g., trees) that is not fully submerged by the water, and therefore, the “double bounce” effect causes an increase instead of a decrease in backscatter in these areas. Given the fact that the model area is characterized by high vegetation in the overbank areas next to the main channel at a significant part of its total length, this limitation may have led to an exclusion of these areas from the SAR-derived total inundation extent and, consequently, to a greater discrepancy from the result derived from the simulation. An additional limitation concerns the Sentinel-1 data itself, since C-band does not allow for signal penetration below thick vegetation but only up to the top layers of the canopy, thus hampering water detection in case of densely vegetated areas. Figure 10a-b shows two indicative sub-regions of the study area where SAR processing approaches did not manage to capture flood in areas covered with high dense vegetation (trees) (Figure 10a) and high sparse vegetation (trees and crops) (Figure 10b) next to the main channel.
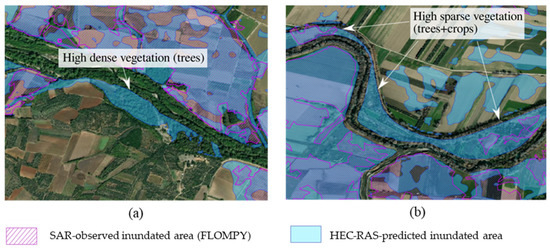
Figure 10.
Vegetated areas next to the main channel where SAR processing techniques did not detect flood: (a) area covered with high dense vegetation (trees); and (b) area covered with high sparse vegetation (trees and crops).
It should be noted that in the present study, although the two SAR-based flood products were exploited as reference to compute the utilized metrics, the focus is rather on investigating model sensitivity, as well as on comparing the derived results and interpreting the resulting discrepancies. We did not intend to calibrate or even evaluate model response since this would mean to neglect the significant uncertainty related to the SAR data and processing techniques.
Finally, a critical issue that should be emphasized is that the present study makes only use of 2D assessment metrics to assess the sensibility and performance of the hydraulic model, since the only available information that could be exploited as reference was the SAR-derived inundation maps. This could be considered as a limitation, since in case in situ observations were available, the comparison of the simulation results against measured water depths through 1D metrics (e.g., RMSE, Maximum Absolute Error, NSE) would enable the examination of model response in a greater detail. It is also worth noting that recent research concentrates on the extraction of remotely-sensed water depth maps by combining SAR-derived inundation extents and high-resolution Digital Elevation Models (e.g., [21,90,91,92]). This is an extremely promising approach that may allow for the calibration and evaluation of flood inundation models also in terms of water depth, even in absence of in situ measurements.
4. Conclusions
The present study attempted to investigate the potential of Sentinel-1 radar data in supporting flood modeling applications. In particular, two different SAR processing approaches were used to extract a flood map, i.e.,: (a) a manual one, where a single-flood image preprocessing is applied, and then a threshold is determined following delineation of training polygons and calculation of their statistics; and (b) an automatic one (FLOMPY algorithm) based on SAR statistical temporal analysis. The utilized approaches were both compared with each other with respect to the resulting inundation boundaries, but they were also exploited as reference for investigating the sensitivity of an integrated 1D/2D hydraulic model with respect to different sources of uncertainty, i.e., variation in the upstream inflow and in the roughness coefficient of the 1D channel and 2D domain. For this purpose, three different metrics, namely the Critical Success Index (CSI), and the Hit Rate (HR) and False Alarm (FAR) indices, along with the change in the total inundated area, were evaluated.
Regarding the effectiveness of the different SAR methodologies in extracting the flood extent for the examined area and flood event, the first approach, acknowledging its simplicity, was considered as adequate to capture the main features of the flooded area and give a quick and rough estimation of its total extent. Its main limitation was the inevitable lack of resolution that resulted from the application of the utilized despeckling technique, which led in some cases to unrealistic discontinuities in the extracted inundation. On the other hand, the second approach proved to be more suitable, mainly due to the multi-temporal analysis incorporated, yielding a more coherent flooded area, closer to that extracted through HEC-RAS. The two results coincided by approximately 52%, with the second one providing a consistently greater flood extent in most areas.
As for the sensitivity analysis undertaken, among the variables tested, it was found that the model response is principally affected by the inflow discharge, and secondarily, by the variation of roughness coefficient in the main channel and the land cover uses 4 (cultivated crops) and 5 (emergent herbaceous wetlands). Higher coincidence (CSI-index) of the hydraulic model with the SAR-derived result emerged: (a) for inflow discharges between the middle–upper area of the uncertainty bounds; (b) for higher roughness coefficient in the main channel; and (c) for coefficient values around the lower–upper areas of the assumed value ranges for land uses 4 and 5.
Additional sources of uncertainty that are believed to affect model predictive performance in comparison with SAR images seem to be associated with inaccuracy in terrain representation as well as with the structural uncertainty inherent in complex hydraulic models. Subjectivity introduced by the user in the different stages of modeling procedure seems to influence more radically model results as the level of complexity increases. Especially for integrated 1D/2D hydraulic models, it was observed that an eventually inaccurate placement of the centerline of the 1D/2D connections by the user may lead to highly ambiguous simulation results. It should be clarified though that the present study does not provide a comprehensive assessment of the comparative advantages or deficiencies of the utilized approach with respect to other models. Within this context and in order to gain a better insight regarding its predictive capability, further investigation of the impact of different modeling approaches (1D or fully 2D) in the same area, as well as in other areas, is required.
Overall, the use of Sentinel-1 products, with respect to the extraction of flood maps, was found to be a valuable tool for supporting flood modeling, as it: (a) provides the modeler with a “rough” prior knowledge of the inundation area rendering the possibility to appropriately adapt modeling decisions and detect unreliable results; (b) serves as a reference base allowing for the detection of changes in model response driven by the variation in selected uncertain parameters; and (c) under certain circumstances, it allows for the evaluation of model performance, acknowledging, however, the uncertainty emerging from the satellite data and the flood mapping technique itself. The derived results would seem to suggest that a flood mapping technique appropriately adapted to the needs of flood modeling applications should be oriented towards statistical multi-temporal approaches to detect changes in backscatter resulting exclusively from flood and at the same time effectively remove the speckle effect. Particular caution should also be given to the limitations the C-band Sentinel-1 data present in areas covered with dense vegetation.
Author Contributions
Conceptualization: I.Z., V.K. and V.A.T.; methodology: I.Z., K.K., V.K. and V.A.T.; software: I.Z.; validation: I.Z., V.K. and V.A.T.; formal analysis: I.Z.; investigation: I.Z.; resources: V.A.T.; data curation: I.Z.; writing—original draft preparation: I.Z.; writing—review and editing: I.Z., K.K., V.K. and V.A.T.; visualization: I.Z.; supervision: V.K. and V.A.T.; project administration: V.A.T.; funding acquisition: I.Z. and V.A.T. All authors have read and agreed to the published version of the manuscript.
Funding
No external funding received.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
All data are presented in the paper.
Acknowledgments
A graduate scholarship to Ioanna Zotou by the Research Committee of the National Technical University of Athens is greatly appreciated. The authors would also like to thank the National Observatory of Athens (NOA) for the provision of the rainfall data utilized in the present study.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Yannopoulos, S.; Eleftheriadou, E.; Mpouri, S.; Giannopoulou, I. Implementing the Requirements of the European Flood Directive: The Case of Ungauged and Poorly Gauged Watersheds. Environ. Process. 2015, 2, 191–207. [Google Scholar] [CrossRef]
- Schlaffer, S.; Chini, M.; Giustarini, L.; Matgen, P. Probabilistic mapping of flood-induced backscatter changes in SAR time series. Int. J. Appl. Earth Obs. Geoinf. 2017, 56, 77–87. [Google Scholar] [CrossRef]
- Li, S.; Sun, D.; Goldberg, M.D.; Sjoberg, B.; Santek, D.; Hoffman, J.P.; DeWeese, M.; Restrepo, P.; Lindsey, S.; Holloway, E. Automatic near real-time flood detection using Suomi-NPP/VIIRS data. Remote Sens. Environ. 2018, 204, 672–689. [Google Scholar] [CrossRef]
- Singh, A.; Sarma, A.K.; Hack, J. Cost-Effective Optimization of Nature-Based Solutions for Reducing Urban Floods Considering Limited Space Availability. Environ. Process. 2020, 7, 297–319. [Google Scholar] [CrossRef]
- Li, Y.; DeLiberty, T. Assessment of Urban Streamflow in Historical Wet and Dry Years Using SWAT across Northwestern Delaware. Environ. Process. 2020, 7, 597–614. [Google Scholar] [CrossRef]
- Budamala, V.; Baburao Mahindrakar, A. Integration of Adaptive Emulators and Sensitivity Analysis for Enhancement of Complex Hydrological Models. Environ. Process. 2020, 7, 1235–1253. [Google Scholar] [CrossRef]
- El Harraki, W.; Ouazar, D.; Bouziane, A.; El Harraki, I.; Hasnaoui, D. Streamflow Prediction Upstream of a Dam Using SWAT and As-sessment of the Impact of Land Use Spatial Resolution on Model Performance. Environ. Process. 2021, 8, 1165–1186. [Google Scholar] [CrossRef]
- Cian, F.; Marconcini, M.; Ceccato, P. Normalized Difference Flood Index for rapid flood mapping: Taking advantage of EO big data. Remote Sens. Environ. 2018, 209, 712–730. [Google Scholar] [CrossRef]
- Pistrika, A.; Tsakiris, G.; Nalbantis, I. Flood Depth-Damage Functions for Built Environment. Environ. Process. 2014, 1, 553–572. [Google Scholar] [CrossRef]
- Zotou, I.; Bellos, V.; Gkouma, A.; Karathanassi, V.; Tsihrintzis, V.A. Using Sentinel-1 imagery to assess predictive performance of a hydraulic model. Water Resour. Manag. 2020, 34, 4415–4430. [Google Scholar] [CrossRef]
- Zhang, B.; Wdowinski, S.; Oliver-Cabrera, T.; Koirala, R.; Jo, M.; Osmanoglu, B. Mapping the extent and magnitude of severe flooding induced by hurricane IRMA with multi-temporal SENTINEL-1 SAR and Insar observations. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2018, 42, 2237–2244. [Google Scholar] [CrossRef]
- Bioresita, F.; Puissant, A.; Stumpf, A.; Malet, J.P. A method for automatic and rapid mapping of water surfaces from sentinel-1 imagery. Remote Sens. 2018, 10, 217. [Google Scholar] [CrossRef]
- Pulvirenti, L.; Pierdicca, N.; Chini, M.; Guerriero, L. An algorithm for operational flood mapping from Synthetic Aperture Radar (SAR) data using fuzzy logic. Nat. Hazards Earth Syst. Sci. 2011, 11, 529–540. [Google Scholar] [CrossRef]
- Pulvirenti, L.; Chini, M.; Pierdicca, N.; Boni, G. Use of SAR data for detecting floodwater in urban and agricultural areas: The role of the interferometric coherence. IEEE Trans. Geosci. Remote Sens. 2015, 54, 1532–1544. [Google Scholar] [CrossRef]
- Di Baldassarre, G.; Schumann, G.; Bates, P.D. A technique for the calibration of hydraulic models using uncertain satellite observations of flood extent. J. Hydrol. 2009, 367, 276–282. [Google Scholar] [CrossRef]
- Alsdorf, D.E.; Rodríguez, E.; Lettenmaier, D.P. Measuring surface water from space. Rev. Geophys. 2007, 45, RG2002. [Google Scholar] [CrossRef]
- Patro, S.; Chatterjee, C.; Singh, R.; Raghuwanshi, N. Hydrodynamic modeling of a large flood-prone river system in India with limited data. Hydrol. Process. 2009, 23, 2774–2791. [Google Scholar] [CrossRef]
- Di Baldassarre, G.; Schumann, G.; Brandimarte, L.; Bates, P.D. Timely low resolution SAR Imagery to support floodplain modeling: A case study review. Surv. Geophys. 2011, 32, 255–269. [Google Scholar] [CrossRef]
- Jung, H.C.; Alsdorf, D.; Moritz, M.; Lee, H.; Vassolo, S. Analysis of the relationship between flooding area and water height in the Logone floodplain. Phys. Chem. Earth Parts A/B/C 2011, 36, 232–240. [Google Scholar] [CrossRef]
- Yan, K.; Di Baldassarre, G.; Solomatine, D. Exploring the potential of SRTM topographic data for flood inundation modelling under uncertainty. J. Hydroinform. 2013, 15, 849–861. [Google Scholar] [CrossRef]
- Scarpino, S.; Albano, R.; Cantisani, A.; Mancusi, L.; Sole, A.; Milillo, G. Multitemporal SAR data and 2D hydrodynamic model flood scenario dynamics assessment. ISPRS Int. J. Geo-Inf. 2018, 7, 105. [Google Scholar] [CrossRef]
- Jacob, X.K.; Bisht, D.S.; Chatterjee, C.; Raghuwanshi, N.S. Hydrodynamic modeling for flood hazard assessment in a data scarce region: A case study of Bharathapuzha river basin. Environ. Model. Assess. 2020, 25, 97–114. [Google Scholar] [CrossRef]
- Logah, F.Y.; Adjei, K.A.; Obuobie, E.; Gyamfi, C.; Odai, S.N. Evaluation and Comparison of Satellite Rainfall Products in the Black Volta Basin. Environ. Process. 2021, 8, 119–137. [Google Scholar] [CrossRef]
- Darko, S.; Adjei, K.A.; Gyamfi, C.; Odai, S.N.; Osei-Wusuansa, H. Evaluation of RFE Satellite Precipitation and its Use in Streamflow Simulation in Poorly Gauged Basins. Environ. Process. 2021, 8, 691–712. [Google Scholar] [CrossRef]
- Akter, T.; Gazi, M.Y.; Mia, M.B. Assessment of Land Cover Dynamics, Land Surface Temperature, and Heat Island Growth in Northwestern Bangladesh Using Satellite Imagery. Environ. Process. 2021, 8, 661–690. [Google Scholar] [CrossRef]
- Wang, Y.; Colby, J.D.; Mulcahy, K.A. An efficient method for mapping flood extent in a coastal floodplain using Landsat TM and DEM data. Int. J. Remote Sens. 2002, 23, 3681–3696. [Google Scholar] [CrossRef]
- Brakenridge, R.; Carlos, H.; Anderson, E.K. River gaging reaches: A strategy for MODIS-based river monitoring. Remote Sens. Environ. Monit. GIS Appl. Geol. II 2003, 4886, 479–486. [Google Scholar]
- Brakenridge, R.; Anderson, E.K.; Nghiem, S.; Caquard, S.; Shabaneh, T.B. Flood warnings, flood disaster assessments, and flood hazard reduction: The roles of orbital remote sensing. In Proceedings of the 30th International Symposium of Remote Sensing and Environment 2003, Honolulu, HI, USA, 10–14 November 2003. [Google Scholar]
- Sandholt, I.; Nyborg, L.; Fog, B.; Lô, M.; Boucum, O.; Rasmussen, K. Remote sensing techniques for flood monitoring in the Senegal River Valley. Dan. J. Geogr. 2003, 103, 71–81. [Google Scholar] [CrossRef]
- Stancalie, G.; Diamandi, A.; Corbus, C.; Catana, S. Application of EO data in flood fore-casting for the Crisuri Basin, Romania. In Flood Risk Management: Hazards, Vulnerability and Mitigation Measures; Springer: Dordrecht, The Netherlands, 2006; pp. 101–113. [Google Scholar]
- Wang, Y. Using Landsat 7 TM data acquired days after a flood event to delineate the maximum flood extent on a coastal floodplain. Int. J. Remote Sens. 2004, 25, 959–974. [Google Scholar] [CrossRef]
- Pulvirenti, L.; Pierdicca, N.; Chini, M.; Guerriero, L. Monitoring flood evolution in vegetated areas using COSMO-SkyMed data: The Tuscany 2009 case study. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2013, 6, 1807–1816. [Google Scholar] [CrossRef]
- Chini, M.; Hostache, R.; Giustarini, L.; Matgen, P.A. Hierarchical split-based approach for parametric thresholding of SAR images: Flood inundation as a test case. IEEE Trans. Geosci. Remote Sens. 2017, 55, 6975–6988. [Google Scholar] [CrossRef]
- Grimaldi, S.; Xu, J.; Li, Y.; Pauwels, V.R.; Walker, J.P. Flood mapping under vegetation using single SAR acquisitions. Remote Sens. Environ. 2020, 237, 111582. [Google Scholar] [CrossRef]
- Horritt, M.S. Calibration of a two-dimensional finite element flood flow model using satellite radar imagery. Water Resour. Res. 2000, 36, 3279–3291. [Google Scholar] [CrossRef]
- Horritt, M.S.; Bates, P.D. Evaluation of 1D and 2D numerical models for predicting river flood inundation. J. Hydrol. 2002, 268, 87–99. [Google Scholar] [CrossRef]
- Horritt, M.S.; Di Baldassarre, G.; Bates, P.D.; Brath, A. Comparing the performance of a 2-D finite element and a 2-D finite volume model of floodplain inundation using airborne SAR imagery. Hydrol. Process. 2007, 21, 2745–2759. [Google Scholar] [CrossRef]
- Schumann, G.J.P.; Hostache, R.; Puech, C.; Hoffmann, L.; Matgen, P.; Pappenberger, F.; Pfister, L. High-resolution 3-D flood information from radar imagery for flood hazard management. IEEE Trans. Geosci. Remote Sens. 2007, 45, 1715–1725. [Google Scholar] [CrossRef]
- Martinis, S.; Fissmer, B.; Rieke, C. Time series analysis of multi-frequency SAR backscatter and bistatic coherence in the context of flood mapping. In Proceedings of the 8th International Workshop on the Analysis of Multitemporal Remote Sensing Images (Multi-Temp) 2015, Annecy, France, 22–24 July 2015; pp. 1–4. [Google Scholar] [CrossRef]
- Bartsch, A.; Trofaier, A.M.; Hayman, G.; Sabel, D.; Schlaffer, S.; Clark, D.B.; Blyth, E. Detection of open water dynamics with ENVISAT ASAR in support of land surface modelling at high latitudes. Biogeosciences 2012, 9, 703–714. [Google Scholar] [CrossRef]
- Chini, M.; Pelich, R.; Pulvirenti, L.; Pierdicca, N.; Hostache, R.; Matgen, P. Sentinel-1 InSAR coherence to detect floodwater in urban areas: Houston and Hurricane Harvey as a test case. Remote Sens. 2019, 11, 107. [Google Scholar] [CrossRef]
- Martinis, S.; Twele, A.; Voigt, S. Towards operational near real-time flood detection using a split-based automatic thresholding procedure on high resolution TerraSAR-X data. Nat. Hazards Earth Syst. Sci. 2009, 9, 303–314. [Google Scholar] [CrossRef]
- Oberstadler, R.; Hönsch, H.; Huth, D. Assessment of the mapping capabilities of ERS-1 SAR data for flood mapping: A case study in Germany. Hydrol. Process. 1997, 11, 1415–1425. [Google Scholar] [CrossRef]
- Townsend, P.A. Mapping seasonal flooding in forested wetlands using multi-temporal Radarsat SAR. Photogramm. Eng. Remote Sens. 2001, 67, 857–864. [Google Scholar]
- Mason, D.C.; Speck, R.; Devereux, B.; Schumann, G.J.P.; Neal, J.C.; Bates, P.D. Flood detection in urban areas using TerraSAR-X. IEEE Trans. Geosci. Remote Sens. 2010, 48, 882–894. [Google Scholar] [CrossRef]
- Matgen, P.; Hostache, R.; Schumann, G.; Pfister, L.; Hoffmann, L.; Savenije, H.H.G. Towards an automated SAR-based flood monitoring system: Lessons learned from two case studies. Phys. Chem. Earth 2011, 36, 241–252. [Google Scholar] [CrossRef]
- Giustarini, L.; Hostache, R.; Matgen, P.; Schuman, G.J.P.; Bates, P.D. A change detection approach to flood mapping in urban areas using TerraSAR-X. IEEE Trans. Geosci. Remote Sens. 2013, 51, 2417–2430. [Google Scholar] [CrossRef]
- Pulvirenti, L.; Chini, M.; Pierdicca, N.; Guerriero, L.; Ferrazzoli, P. Flood monitoring using multi-temporal COSMO-SkyMed data: Image segmentation and signature interpretation. Remote Sens. Environ. 2011, 115, 990–1002. [Google Scholar] [CrossRef]
- Pierdicca, N.; Chini, M.; Pulvirenti, L.; Macina, F. Integrating Physical and Topographic Information into a fuzzy scheme to Map Flooded Area by SAR. Sensors 2008, 8, 4151–4164. [Google Scholar] [CrossRef]
- Twele, A.; Cao, W.; Plank, S.; Martinis, S. Sentinel-1-based flood mapping: A fully automated processing chain. Int. J. Remote Sens. 2016, 37, 2990–3004. [Google Scholar] [CrossRef]
- Westerhoff, R.S.; Kleuskens, M.P.H.; Winsemius, H.C.; Huizinga, H.J.; Brakenridge, G.R.; Bishop, C. Automated global water mapping based on wide-swath orbital synthetic-aperture radar. Hydrol. Earth Syst. Sci. 2013, 17, 651–663. [Google Scholar] [CrossRef]
- Refice, A.; Capolongo, D.; Pasquariello, G.; D’Addabbo, A.; Bovenga, F.; Nutricato, R.; Lovergine, F.P.; Pietranera, L. SAR and InSAR for flood monitoring: Examples with COSMO-SkyMed data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 2711–2722. [Google Scholar] [CrossRef]
- D’Addabbo, A.; Refice, A.; Pasquariello, G.; Lovergine, F.; Capolongo, D.; Manfreda, S. A Bayesian Network for Flood Detection Combining SAR Imagery and Ancillary Data. IEEE Trans. Geosci. Remote Sens. 2016, 54, 3612–3624. [Google Scholar] [CrossRef]
- Bazi, Y.; Bruzzone, L.; Melgani, F. An unsupervised approach based on the generalized Gaussian model to automatic change detection in multitemporal SAR images. IEEE Trans. Geosci. Remote Sens. 2005, 43, 874–887. [Google Scholar] [CrossRef]
- Psomiadis, E. Flash flood area mapping utilising SENTINEL-1 radar data. In Proceedings of the Earth Resources and Environmental Remote Sensing/GIS Applications VII, Edinburgh, UK, 27–29 September 2016. [Google Scholar]
- Uddin, K.; Matin, M.A.; Meyer, F.J. Operational flood mapping using multi-temporal sentinel-1 SAR images: A case study from Bangladesh. Remote Sens. 2019, 11, 1581. [Google Scholar] [CrossRef]
- Gebremichael, E.; Molthan, A.L.; Bell, J.R.; Schultz, L.A.; Hain, C. Flood hazard and risk assessment of extreme weather events using synthetic aperture radar and auxiliary data: A case study. Remote Sens. 2020, 12, 3588. [Google Scholar] [CrossRef]
- Karamvasis, K.; Karathanassi, V. FLOMPY: An Open-Source Toolbox for Floodwater Mapping Using Sentinel-1 Intensity Time Series. Water 2021, 13, 2943. [Google Scholar] [CrossRef]
- Ministry of Environment and Energy of Greece. Available online: https://floods.ypeka.gr/index.php?option=com_content&view=article&id=293&Itemid=785 (accessed on 5 June 2022).
- Copernicus Open Access Hub of the European Space Agency. Available online: https://scihub.copernicus.eu/ (accessed on 13 November 2021).
- US Army Corps of Engineers Hydrologic Engineering Center. Available online: https://www.hec.usace.army.mil/software/hec-hms/ (accessed on 10 February 2022).
- Copernicus Land Monitoring Service. Available online: https://land.copernicus.eu/imagery-in-situ/eu-dem/eu-dem-v1.1 (accessed on 10 November 2021).
- Federal Institute for Geosciences and Natural Resources of Germany. Available online: https://www.bgr.bund.de/EN/Home/homepage_node_en.html (accessed on 10 November 2021).
- Chin, D.A.; Mazumdar, A.; Roy, P.K. Water-Resources Engineering; Prentice Hall: Englewood Cliffs, NJ, USA, 2000; Volume 12. [Google Scholar]
- Qaiser, K.; Yuan, Y.; Lopez, R.D. Urbanization impacts on flooding in the Kansas River Basin and evaluation of wetlands as a mitigation measure. Trans. ASABE 2012, 55, 849–859. [Google Scholar] [CrossRef]
- Dasallas, L.; Kim, Y.; An, H. Case study of HEC-RAS 1D–2D coupling simulation: 2002 Baeksan flood event in Korea. Water 2019, 11, 2048. [Google Scholar] [CrossRef]
- Brunner, G.W. HEC-RAS River Analysis System Hydraulic Reference Manual, Version 6.0; US Army Corps of Engineers Hydrologic Engineering Center: Davis, CA, USA, 2020. [Google Scholar]
- Sarker, S. A Short Review on Computational Hydraulics in the Context of Water Resources Engineering. Open J. Model. Simul. 2022, 10, 1–31. [Google Scholar] [CrossRef]
- Sarker, S. Essence of MIKE 21C (FDM Numerical Scheme): Application on the River Morphology of Bangladesh. Open J. Model. Simul. 2022, 10, 88–117. [Google Scholar] [CrossRef]
- Brunner, G.W. HEC-RAS, River Analysis System Hydraulic Reference Manual, Version 5.0; US Army Corps of Engineers Hydrologic Engineering Center: Davis, CA, USA, 2016. [Google Scholar]
- Huang, Y. Rapid flood risk assessment using GIS technology. Int. J. River Basin Manag. 2009, 7, 3–14. [Google Scholar] [CrossRef]
- Harris County Flood Control District (HCFCD). Two-Dimensional Modeling Guidelines; Harris County Flood Control District (HCFCD): Houston, TX, USA, 2018; Available online: https://www.google.com/search?q=72.+Harris+County+Flood+Control+District+(HCFCD).+Two-Dimensional+Modeling+Guidelines&oq=72.%09Harris+County+Flood+Control+District+(HCFCD).+Two-Dimensional+Modeling+Guidelines&aqs=chrome..69i57.460j0j4&sourceid=chrome&ie=UTF-8 (accessed on 5 December 2022).
- Louisiana Department of Transportation and Development (LA DOTD). Amite River Basin Numerical Model 2019. Available online: https://watershed.la.gov/assets/docs/ARBNM_Project_Report_03252019.pdf (accessed on 5 December 2022).
- Babister, M.; Barton, C. Australian Rainfall and Runoff Revision Project 15: Two Dimensional Modelling in Urban and Rural Floodplains, Stage 1 & 2 Report, P15/S1/009, Engineers Australia, Engineering House 11, National Circuit, Barton ACT 2600, Australia, 2012. Available online: https://arr.ga.gov.au/__data/assets/pdf_file/0019/40573/ARR_Project15_TwoDimensional_Modelling_DraftReport.pdf (accessed on 5 December 2022).
- Davtalab, R.; Mirchi, A.; Harris, R.J.; Troilo, M.X.; Madani, K. Sea Level Rise Effect on Groundwater Rise and Stormwater Retention Pond Reliability. Water 2020, 12, 1129. [Google Scholar] [CrossRef]
- Wing, O.; Bates, P.; Sampson, C.; Smith, A.; Johnson, K.; Erickson, T. Validation of a 30 m resolution flood hazard model of the conterminous United States. Water Resour. Res. 2017, 53, 7968–7986. [Google Scholar] [CrossRef]
- Afzal, M.A.; Ali, S.; Nazeer, A.; Khan, M.I.; Waqas, M.M.; Aslam, R.A.; Cheema, M.J.M.; Nadeem, M.; Saddique, N.; Muzammil, M.; et al. Flood Inundation Modeling by Integrating HEC–RAS and Satellite Imagery: A Case Study of the Indus River Basin. Water 2022, 14, 2984. [Google Scholar] [CrossRef]
- Elkhrachy, I.; Pham, Q.B.; Costache, R.; Mohajane, M.; Rahman, K.U.; Shahabi, H.; Linh, N.T.T.; Anh, D.T. Sentinel-1 remote sensing data and Hydrologic Engineering Centres River Analysis System two-dimensional integration for flash flood detection and modelling in New Cairo City, Egypt. J. Flood Risk Manag. 2021, 14, e12692. [Google Scholar] [CrossRef]
- Pertiwi, A.P.; Roth, A.; Schaffhauser, T.; Bhola, P.K.; Reuß, F.; Stettner, S.; Kuenzer, C.; Disse, M. Monitoring the Spring Flood in Lena Delta with Hydrodynamic Modeling Based on SAR Satellite Products. Remote Sens. 2021, 13, 4695. [Google Scholar] [CrossRef]
- Nguyen, T.H.; Delmotte, A.; Fatras, C.; Kettig, P.; Piacentini, A.; Ricci, S. Validation and improvement of data assimilation for flood hydrodynamic modelling using SAR imagery data. arXiv 2021, arXiv:2109.07470. [Google Scholar]
- Ekeu-wei, I.T.; Blackburn, G.A. Catchment-Scale Flood Modelling in Data-Sparse Regions Using Open-Access Geospatial Technology. ISPRS Int. J. Geo-Inf. 2020, 9, 512. [Google Scholar] [CrossRef]
- Lamichhane, N.; Sharma, S. Effect of input data in hydraulic modeling for flood warning systems. Hydrol. Sci. J. 2018, 63, 938–956. [Google Scholar] [CrossRef]
- Liu, Z.; Merwade, V.; Jafarzadegan, K. Investigating the role of model structure and surface roughness in generating flood inundation extents using one- and two-dimensional hydraulic models. J. Flood Risk Manag. 2019, 12, e12347. [Google Scholar] [CrossRef]
- Annis, A.; Nardi, F.; Volpi, E.; Fiori, A. Quantifying the relative impact of hydrological and hydraulic modelling parameterizations on uncertainty of inundation maps. Hydrol. Sci. J. 2020, 65, 507–523. [Google Scholar] [CrossRef]
- Vojtek, M.; Petroselli, A.; Vojteková, J.; Asgharinia, S. Flood inundation mapping in small and ungauged basins: Sensitivity analysis using the EBA4SUB and HEC-RAS modeling approach. Hydrol. Res. 2019, 50, 1002–1019. [Google Scholar] [CrossRef]
- Mosquera-Machado, S.; Ahmad, S. Flood hazard assessment of Atrato river in Colombia. Water Resour. Manag. 2007, 21, 591–609. [Google Scholar] [CrossRef]
- Ghimire, E.; Sharma, S.; Lamichhane, N. Evaluation of one-dimensional and two-dimensional HEC-RAS models to predict flood travel time and inundation area for flood warning system. ISH J. Hydraul. Eng. 2022, 28, 110–126. [Google Scholar] [CrossRef]
- Dimitriadis, P.; Tegos, A.; Oikonomou, A.; Pagana, V.; Koukouvinos, A.; Mamassis, N.; Koutsoyiannis, D.; Efstratiadis, A. Comparative evaluation of 1D and quasi-2D hydraulic models based on benchmark and real-world applications for uncertainty assessment in flood mapping. J. Hydrology 2016, 534, 478–492. [Google Scholar] [CrossRef]
- Samarasinghe, J.T.; Basnayaka, V.; Gunathilake, M.B.; Azamathulla, H.M.; Rathnayake, U. Comparing Combined 1D/2D and 2D Hydraulic simulations using high-resolution topographic data: Examples from Sri Lanka—Lower Kelani River Basin. Hydrology 2022, 9, 39. [Google Scholar] [CrossRef]
- Cian, F.; Marconcini, M.; Ceccato, P.; Giupponi, C. Flood depth estimation by means of high-resolution SAR images and lidar data. Nat. Hazards Earth Syst. Sci. 2018, 18, 3063–3084. [Google Scholar] [CrossRef]
- Hao, C.; Yunus, A.P.; Subramanian, S.S.; Avtar, R. Basin-wide flood depth and exposure mapping from SAR images and machine learning models. J. Environ. Manag. 2021, 297, 113367. [Google Scholar] [CrossRef] [PubMed]
- Parida, B.R.; Tripathi, G.; Pandey, A.C.; Kumar, A. Estimating floodwater depth using SAR-derived flood inundation maps and geomorphic model in kosi river basin (India). Geocarto Int. 2022, 37, 4336–4360. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).