Influence of Water Depth and Slope on Roughness—Experiments and Roughness Approach for Rain-on-Grid Modeling
Abstract
:1. Introduction
1.1. Modeling Extreme Events
1.2. Aim of the Study
2. Background
2.1. Flow Equations
2.2. Vegetation Resistance
2.3. Conditions for Overland Flow
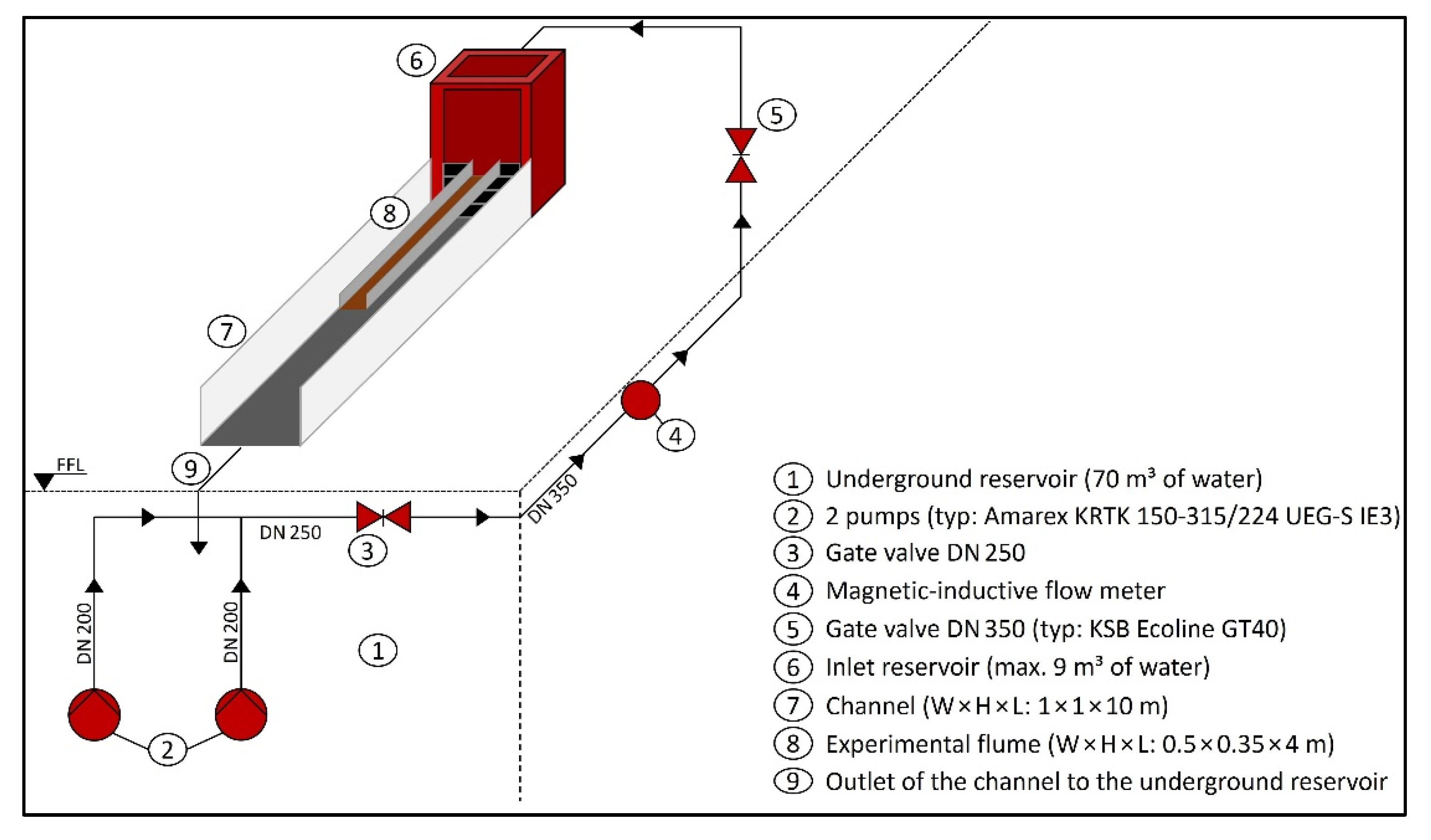
3. Materials and Methods
| Reference | Artificial Grass | Wheat | Cement-Based Coating | Asphaltic Emulsion | Exposed Aggregate Concrete | Aluminum | |
|---|---|---|---|---|---|---|---|
| Description | Nubby blade of grass: length: 2.5 cm height: 1.5 cm predominantly rigid | Dried wheat height: 0.5 m 500 pc./m2 fixed in 3 cm Styrodur and on top: 2 cm cement-based coating predominantly rigid (bending was avoided) | Mixture of masonry mortal and tile adhesive (ratio 1:2) | Grain size: 0–8 mm | Texture: gravel; grain size: 5–20 mm | Plates, 2 mm thick | |
| Installation | Sticked and tightened to a coated plywood plate | 4 separate boxes | 4 separate boxes | 4 separate boxes | 4 pieces | 4 pieces sealed with silicone | |
| Flow condition | Submerged vegetation Submergence: 2.1–7.5 | Emergent vegetation | Submerged Solid surface | Submerged Solid surface | Submerged Solid surface | Submerged Solid surface | |
| Total number of experiments | 149 | 77 | 168 | 119 | 119 | 98 | |
| Q [l/s] | 5–70 | 5–35 | 5–70 | 5–70 | 5–70 | 5–70 | |
| h [cm] | 3.1–11.2 | 1.2–14.3 | 1.0–9.5 | 1.1–7.1 | 1.3–7.5 | 0.9–8.0 | |
| Re | 2.48 × 104– 3.31 × 105 | 2.75 × 104– 1.76 × 105 | 2.78 × 104– 3.75 × 105 | 2.65 × 104– 3.64 × 105 | 2.63 × 104– 3.60 × 105 | 2.92 × 104– 3.74 × 105 | |
| S [%] | 1 | X | X | X | X | X | X |
| 2 | X | X | X | ||||
| 3 | X | X | X | ||||
| 4 | X | X | X | ||||
| 5 | X | X | X | X | X | X | |
| 10 | X | X | X | X | X | X | |
| 15 | X | X | X | X | X | X | |
| 20 | X | X | X | X | X | X | |
| 25 | X | X | X | X | X | ||
| 30 | X | X | X | X | X | X | |
| 35 | X | X | X | X | X | ||
| 40 | X | X | X | X | X | ||
4. Results and Discussion
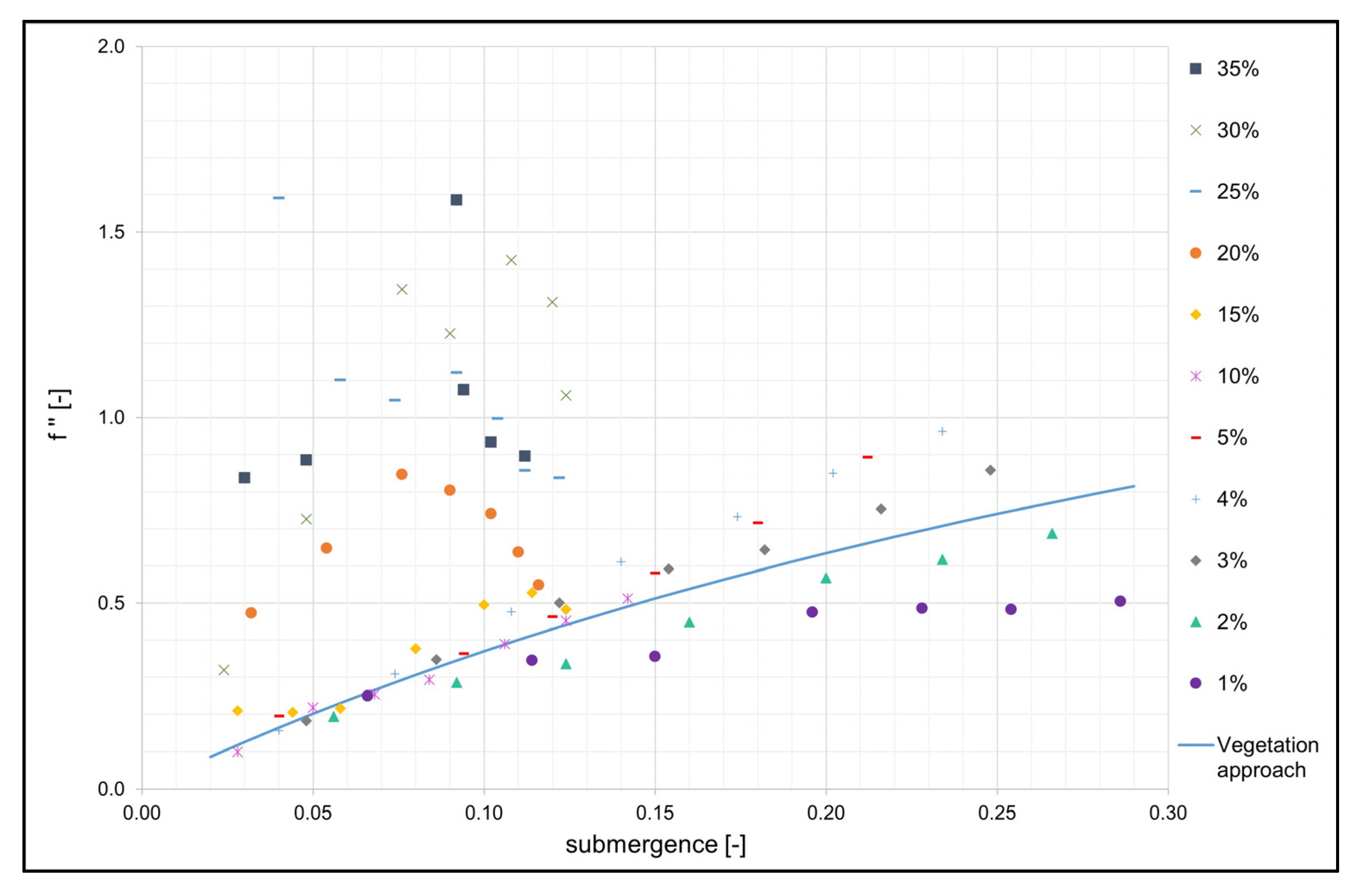
4.1. Consideration of Roughness for Submerged Vegetation
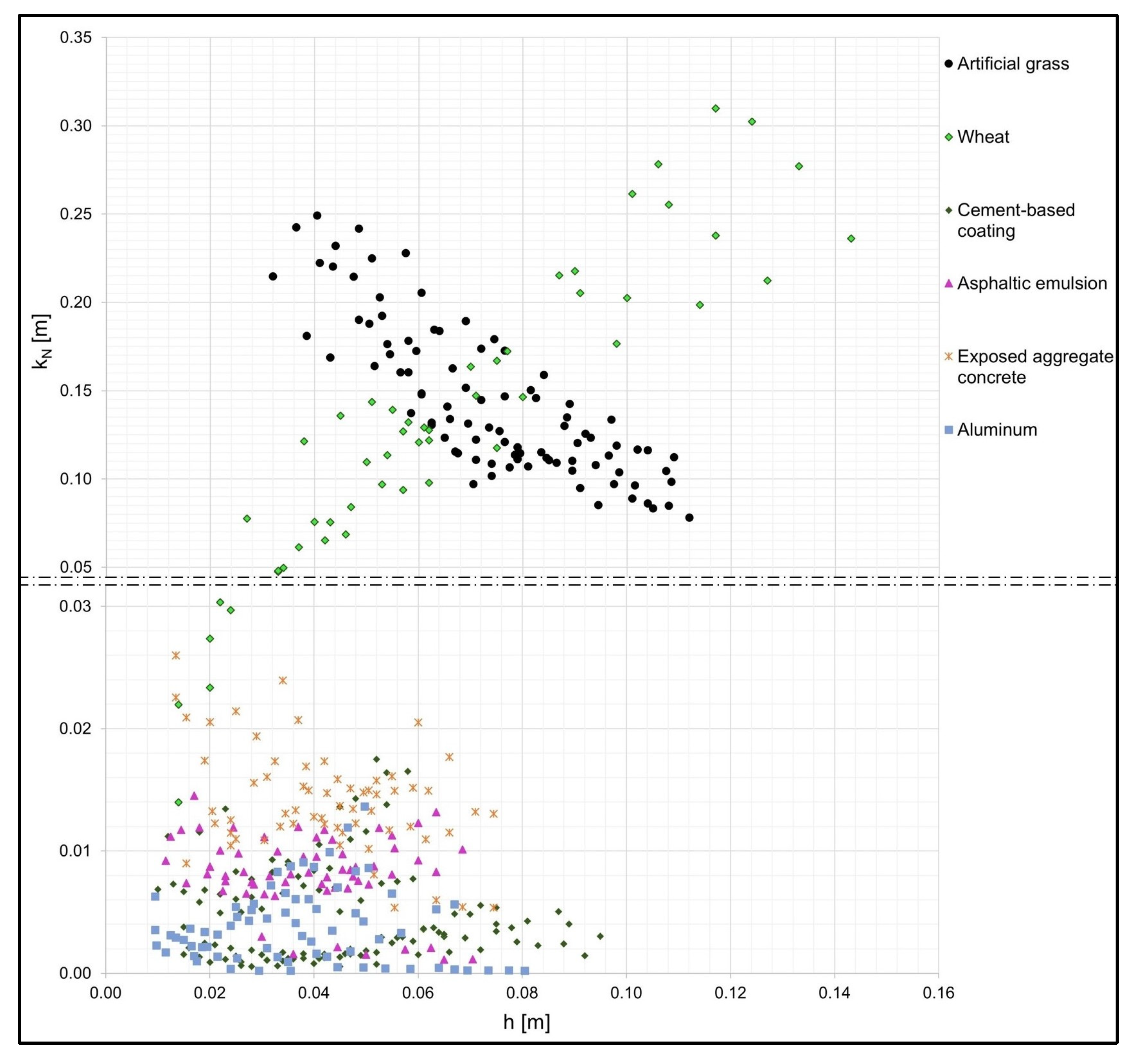
4.1.1. Analyses and Evaluation of Experimental Results
4.1.2. Existing Models
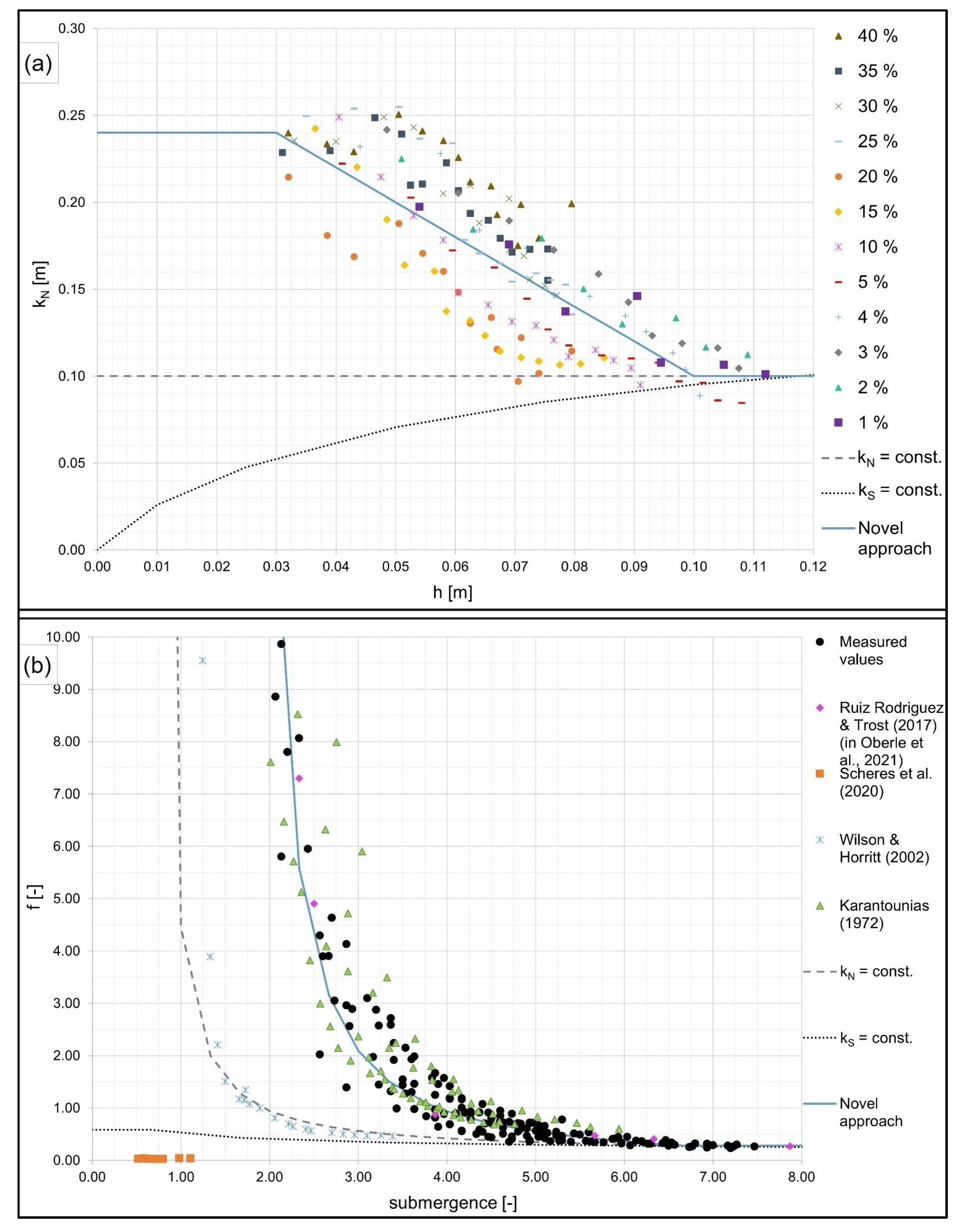
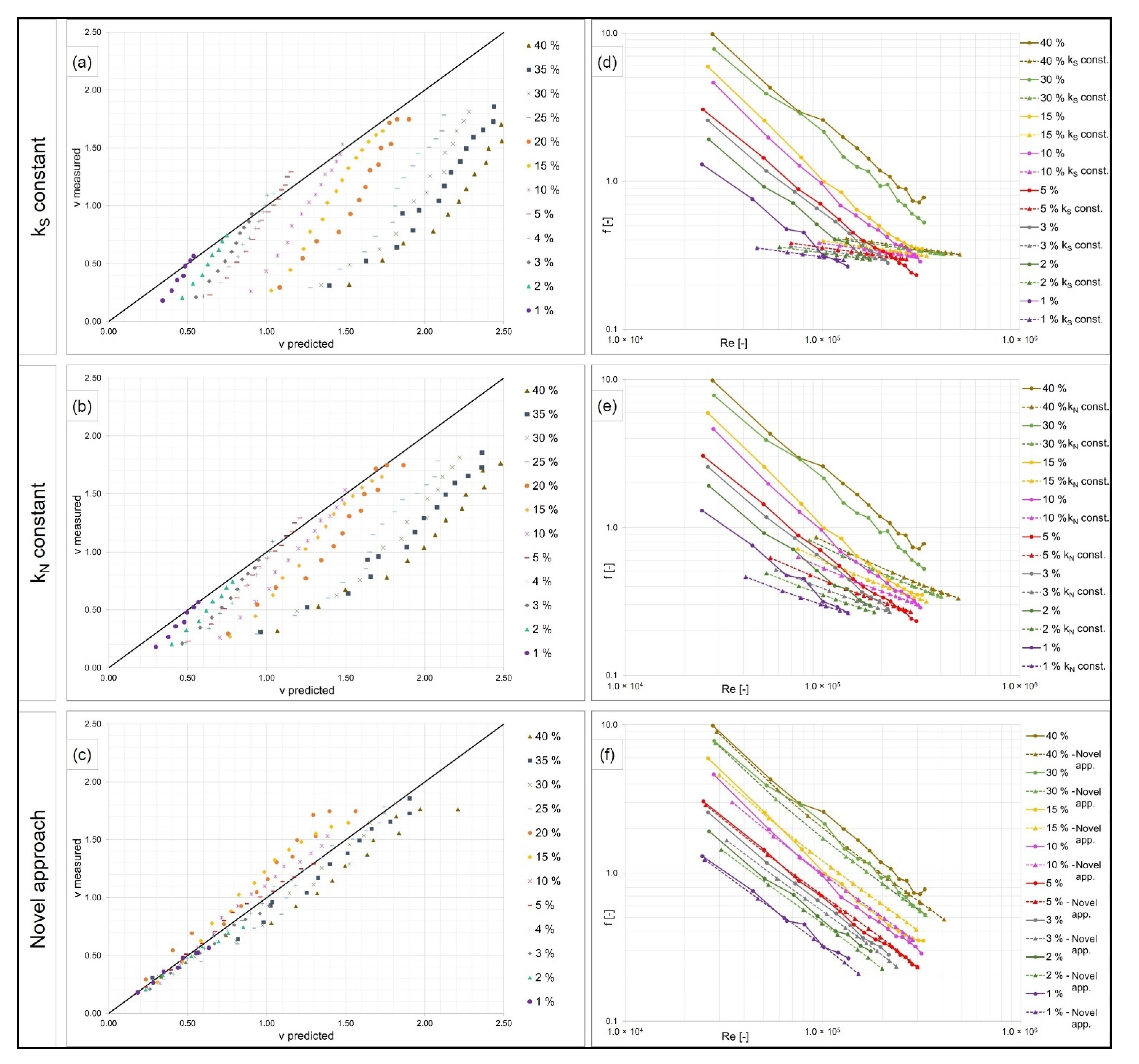
4.1.3. Novel Approach
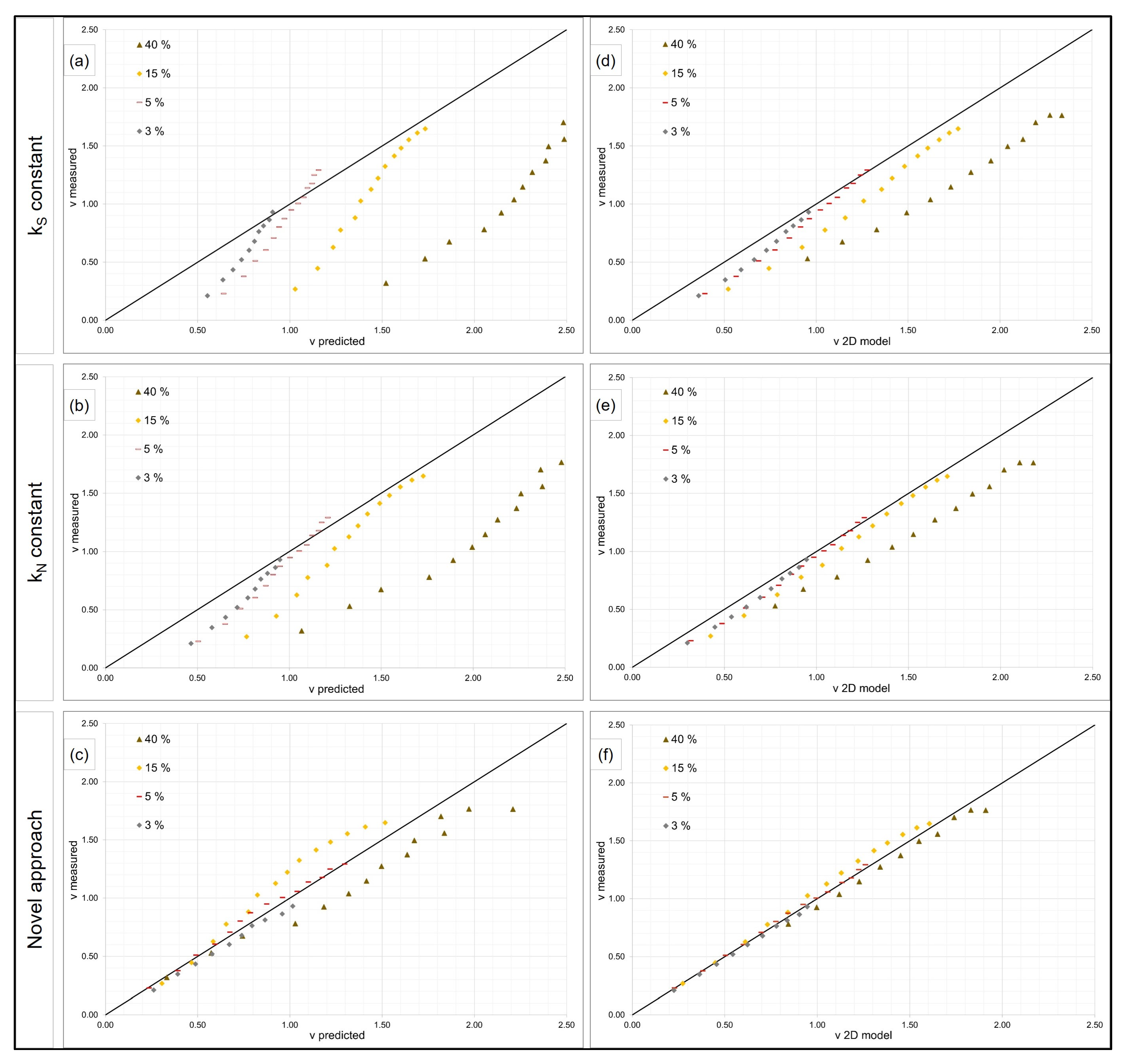
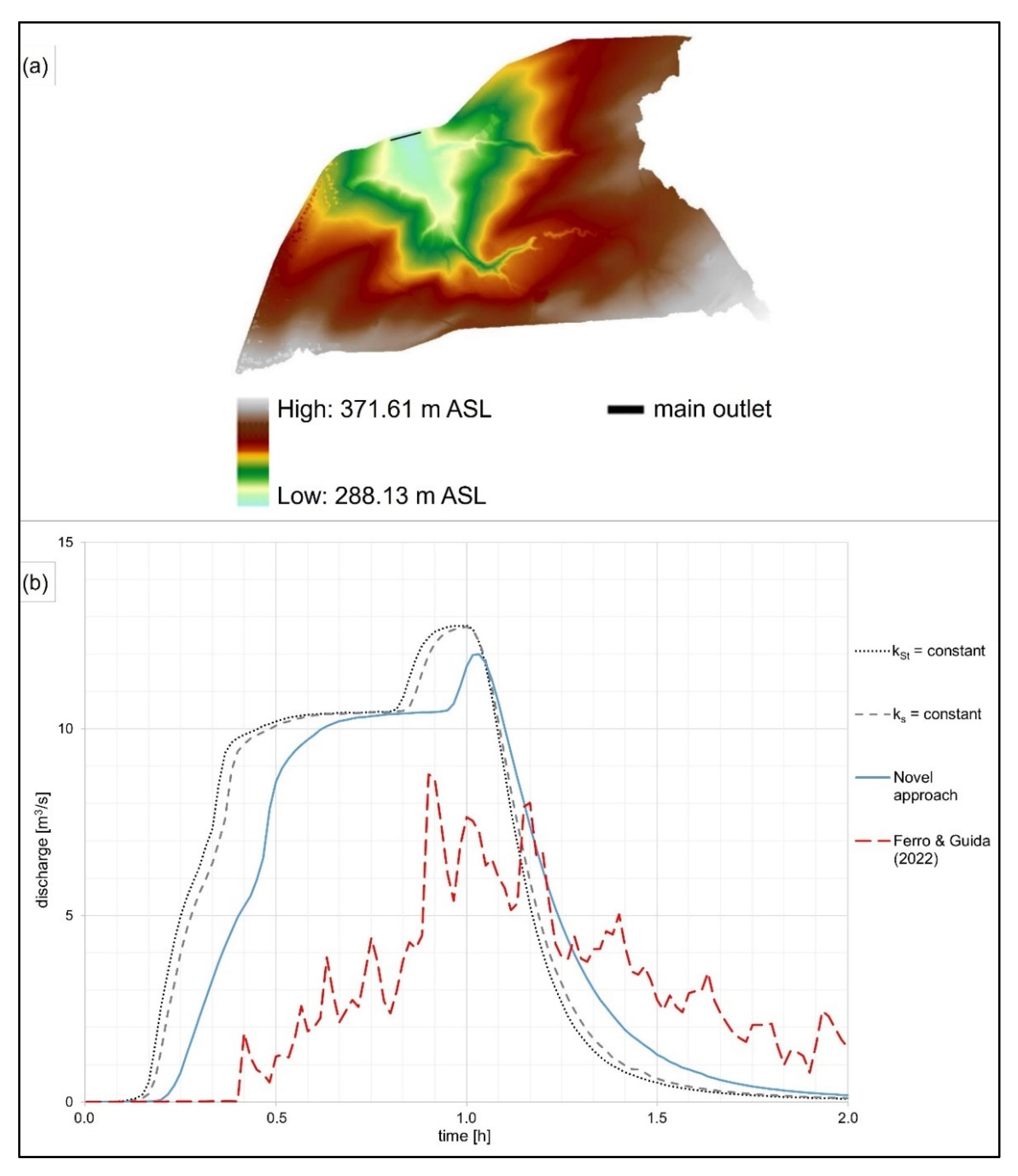
4.1.4. Implementation in a 2D Model
- The novel approach of this study (Equation (4)) with kN as a function of water depth was applied.
- The approach of Ferro and Guida [38] with friction factor f as a function of slope, Reynolds number and Froude number was applied. Here, the calibration factor was 0.21, which fits best to the measured values of high water depth in this study.
4.2. Consideration of Roughness for Emergent Vegetation
4.3. Consideration of Roughness for Solid Surfaces
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Limitations
Notation
| A | Cross-sectional area (m2) |
| CD | Bulk drag coefficient (-) |
| CORR | Corrected |
| DH | Hydraulic diameter (m) |
| dveg | Diameter of the vegetation (m) |
| Dveg | Density of the vegetation (pcs/m2) |
| DEM | Digital elevation model |
| f | Friction factor (Darcy-Weisbach) (-) |
| f′ | Bottom friction factor (-) |
| f″ | Vegetation friction factor (-) |
| Fr | Froude number (-) |
| g | Gravitational acceleration (m/s2) |
| h | Water depth (m) |
| hveg | Vegetation height (m) |
| kN | Equivalent sand-grain roughness (Nikuradse) (m) |
| kS | Strickler roughness coefficient (m1/3/s) |
| pr | Shape coefficient (-) |
| Q | discharge (m³/s) |
| RH | Hydraulic radius (m) |
| Re | Reynolds number (-) |
| RMSE | Root mean square error |
| RoG | Rain-on-Grid |
| S | Channel slope (-) |
| SRTM | Shuttle radar topography mission |
| x | Longitudinal direction along the flume |
| y | Transverse direction of the flume |
| v | Flow velocity (m/s) |
| 2D | Two-dimensional |
References
- IPCC. Summary for Policymakers. In Climate Change 2021: The Physical Science Basis. Contribution of Working Group I to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change; Masson-Delmotte, V., Zhai, P., Pirani, A., Connors, S.L., Péan, C., Berger, S., Caud, N., Chen, Y., Goldfarb, L., Gomis, M.I., et al., Eds.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2021; pp. 3–32. [Google Scholar] [CrossRef]
- Yörük, A.; Sacher, H. Methoden und Qualität von Modellrechnungen für HW-Gefahrenkarten. In Technische Universität Dresden, Institut für Wasserbau und technische Hydromechanik (Ed.): Simulationsverfahren und Modelle für Wasserbau und Wasserwirtschaft. Dresdner Wasserbauliche Mitt. 2014, 50, 55–64. [Google Scholar]
- Caviedes-Vouillème, D.; García-Navarro, P.; Murillo, J. Influence of mesh structure on 2D full shallow water equations and SCS Curve Number simulation of rainfall/runoff events. J. Hydrol. 2012, 448–449, 39–59. [Google Scholar] [CrossRef]
- Bellos, V.; Papageorgaki, I.; Kourtis, I.; Vangelis, H.; Kalogiros, I.; Tsakiris, G. Reconstruction of a flash flood event using a 2D hydrodynamic model under spatial and temporal variability of storm. Nat. Hazards 2020, 101, 711–726. [Google Scholar] [CrossRef]
- Gibson, M.J.; Savic, D.A.; Djordjevic, S.; Chen, A.S.; Fraser, S.; Watson, T. Accuracy and computational efficiency of 2D urban surface flood modelling based on cellular automata. Procedia Eng. 2016, 154, 801–810. [Google Scholar] [CrossRef] [Green Version]
- Barbero, G.; Costabile, P.; Costanzo, C.; Ferraro, D.; Petaccia, G. 2D hydrodynamic approach supporting evaluations of hydrological response in small watersheds: Implications for lag time estimation. J. Hydrol. 2022, 610, 127870. [Google Scholar] [CrossRef]
- Taccone, F.; Antoine, G.; Delestre, O.; Goutal, N. A new criterion for the evaluation of the velocity field for rainfall-runoff modelling using a shallow-water model. Adv. Water Resour. 2020, 140, 103581. [Google Scholar] [CrossRef]
- Abderrezzak, K.E.K.; Paquier, A.; Mignot, E. Modelling flash flood propagation in urban areas using a two-dimensional numerical model. Nat. Hazards 2009, 50, 433–460. [Google Scholar] [CrossRef]
- Huang, W.; Cao, Z.-x.; Qi, W.-j.; Pender, G.; Zhao, K. Full 2D Hydrodynamic Modelling of Rainfall-induced Flash Floods. J. Mt. Sci. 2015, 12, 1203–1218. [Google Scholar] [CrossRef]
- Costabile, P.; Costanzo, C.; Ferraro, D.; Barco, P. Is HEC-RAS 2D accurate enough for storm-event hazard assessment? Lessons learnt from a benchmarking study based on rain-on-grid modelling. J. Hydrol. 2021, 603, 126962. [Google Scholar] [CrossRef]
- Zeiger, S.J.; Hubbart, J.A. Measuring and modeling event-based environmental flows: An assessment of HEC-RAS 2D rain-on-grid simulations. J. Environ. Manag. 2021, 285, 112125. [Google Scholar] [CrossRef]
- García-Pintado, J.; Barberá, G.G.; Erena, M.; Castillo, V.M. Calibration of structure in a distributed forecasting model for a semiarid flash flood: Dynamic surface storage and channel roughness. J. Hydrol. 2009, 377, 165–184. [Google Scholar] [CrossRef]
- David, A.; Schmalz, B. Flood hazard analysis in small catchments: Comparison of hydrological and hydrodynamic approaches by the use of direct rainfall. J. Flood Risk Manag. 2020, 13, e12639. [Google Scholar] [CrossRef]
- Abrahams, A.D.; Parsons, A.J.; Luk, S.-H. Field experiments on the resistance to overland flow on desert hillslopes. In Erosion, Transport and Deposition Processes, Proceedings of the Jerusalem Workshop, Jerusalem, Israel, March–April 1987; IAHS Publications: Wallingford, UK, 1990. [Google Scholar]
- Cea, L.; Legout, C.; Darboux, F.; Esteves, M.; Nord, G. Experimental validation of a 2D overland flow model using high resolution water depth and velocity data. J. Hydrol. 2014, 513, 142–153. [Google Scholar] [CrossRef]
- Augustijn, D.C.M.; Huthoff, F.; van Velzen, E.H. Comparison of vegetation roughness description. In Proceedings of the International Conferences on Fluvial Hydraulics (River Flow), Izmir, Turkey, 3–5 September 2008; pp. 343–350. [Google Scholar]
- Abrahams, A.D.; Parsons, A.J.; Wainwright, J. Resistance to overland flow on semiarid grassland and shrubland hillslopes, Walnut Gulch, southern Ariona. J. Hydrol. 1994, 156, 431–446. [Google Scholar] [CrossRef]
- Huthoff, F.; Augistijn, D.C.M. Hydraulic Resistance of Vegetation: Predictions of Average Flow Velocities Based on a Rigid-Cylinders Analogy; Final Project Report; Planungsmanagement für Auen, University of Twente: Enschede, The Netherlands, 2006. [Google Scholar]
- Prandtl, L., II. Theoretischer Teil. Zur turbulenten Strömung in Rohren und längs Platten. In Ergebnisse der Aerodynamischen Versuchsanstalt zu Göttingen. IV. Lieferung; Dillmann, A., Ed.; Göttinger Klassiker der Strömungsmechanik: Göttingen, Germany, 2009. [Google Scholar] [CrossRef] [Green Version]
- Nikuradse, J. Strömungsgesetze in Rauhen Rohren; VDI: Berlin, Germany, 1933. [Google Scholar]
- Aigner, D.; Bollrich, G. Handbuch der Hydraulik für Wasserbau und Wasserwirtschaft, 1st ed.; Beuth Verlag GmbH: Berlin, Germany, 2015; ISBN 978-3-410-21341-3. [Google Scholar]
- Chow, V.T. Open-Channel Hydraulics; McGraw-Hill Book Company: New York, NY, USA, 1959. [Google Scholar]
- Zanke, U. Hydraulik für Wasserbau, 3rd ed.; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar] [CrossRef]
- Abood, M.M.; Yusuf, B.; Mohammed, T.A.; Ghazali, A.H. Manning Roughness Coefficient for Grass-Lined Channel. Suranaree J. Sci. Technol. 2006, 13, 317–330. [Google Scholar]
- Ferro, V. Assessing flow resistance law in vegetated channels by dimensional analysis and self-similarity. Flow Meas. Instrum. 2019, 69, 101610. [Google Scholar] [CrossRef]
- Gualtieri, P.; De Felice, S.; Pasquino, V.; Doria, G.P. Use of conventional flow resistance equations and a model for the Nikuradse roughness in vegetated flows at high submergence. J. Hydrol. Hydromech. 2018, 66, 107–120. [Google Scholar] [CrossRef] [Green Version]
- Huthoff, F. Theory for flow resistance caused by submerged roughness elements. J. Hydraul. Res. 2012, 50, 10–17. [Google Scholar] [CrossRef]
- Nepf, H.M.; Vivoni, E.R. Flow structure in depth-limited, vegetated flow. J. Geophys. Res. 2000, 105, 28547–28557. [Google Scholar] [CrossRef]
- Tang, X.; Wu, S.; Rahimi, H.; Xue, W.; Lei, Y. Experimental Study of Open Channel Flows with Two Layers Vegetation. In Proceedings of the 2nd International Symposium on Hydraulic Modelling and Measuring Technology Congress, Nanjing, China, 30 May–1 June 2018. [Google Scholar]
- Wang, W.-J.; Peng, W.-Q.; Huai, W.-X.; Katul, G.G.; Liu, X.-B.; Qu, X.-D.; Dong, F. Friction factor for turbulent open channel flow covered by vegetation. Sci. Rep. 2019, 9, 5178. [Google Scholar] [CrossRef] [Green Version]
- Huthoff, F.; Augistijn, D.C.M.; Hulscher, S.J.M.H. Analytical solution of the depth-averaged flow velocity in case of submerged rigid cylindrical vegetation. Water Resour. Res. 2007, 43, W06413. [Google Scholar] [CrossRef] [Green Version]
- Järvelä, J. Determination of flow resistance cause by non-submerged woody vegetation. Int. J. River Basin Manag. 2004, 2, 61–70. [Google Scholar] [CrossRef]
- Vargas-Luna, A.; Crosato, A.; Uijttewaal, W.S.J. Effects of vegetation on flow and sediment transport: Comparative analyses and validation of predicting models. Earth Surf. Process. Landf. 2015, 40, 157–176. [Google Scholar] [CrossRef]
- Ferguson, R. Limits to scale invariance in alluvial rivers. Earth Surf. Process. Landf. 2021, 46, 173–187. [Google Scholar] [CrossRef]
- Baptist, M.J.; Babovic, V.; Rodríguez Uthurburu, J.; Keijzer, M.; Uittenbogaard, R.E.; Mynett, A.; Verwey, A. On inducing equations for vegetation resistance. J. Hydraul. Res. 2007, 45, 435–450. [Google Scholar] [CrossRef]
- Van Velzen, E.H.; Jesse, P.; Cornelissen, P.; Coops, H. Stromingsweerstand Vegetatie in Uiterwaarden; Handboek. Part 1 and 2. RIZA Reports, 2003.028 and 2003.029; Directoraat-Generaal Rijkswaterstaat, RIZA: Arnhem, The Netherlands, 2003. [Google Scholar]
- Schröder, R. Hydraulische Methoden zur Erfassung von Rauheiten; Schriftenreihe des DVWK: Parey, Germany, 1990; Volume 92, ISBN 978-3-490-09297-7. [Google Scholar]
- Ferro, V.; Guida, G. A theoretically-based overland flow resistance law for upland grassland habitats. Catena 2022, 210, 105863. [Google Scholar] [CrossRef]
- Bond, S.; Kirkby, M.J.; Johnston, J.; Crowle, A.; Holden, J. Seasonal vegetation and management influence overland flow velocity and roughness in upland grassland. Hydrol. Process. 2020, 34, 3777–3791. [Google Scholar] [CrossRef]
- Nepf, H.M. Hydrodynamics of vegetated channels. J. Hydraul. Res. 2012, 50, 262–279. [Google Scholar] [CrossRef] [Green Version]
- Polyakov, V.; Stone, J.; Holifield Collins, C.; Nearing, M.A.; Paige, G.; Buono, J.; Gomez-Pond, R.-L. Rainfall simulation experiments in the southwestern USA using the Walnut Gulch Rainfall Simulator. Earth Syst. Sci. Data 2018, 10, 19–26. [Google Scholar] [CrossRef]
- Ferro, V. New Flow-Resistance Law for Steep Mountain Streams Based on Velocity Profile. J. Irrig. Drain. Eng. 2017, 143, 1208. [Google Scholar] [CrossRef]
- Nicosia, A.; Di Stefano, C.; Palmeri, V.; Pampalone, V.; Ferro, V. Flow resistance of overland flow on a smooth bed under simulated rainfall. Catena 2020, 187, 104351. [Google Scholar] [CrossRef]
- Palmeri, V.; Pampalone, V.; Di Stefano, C.; Nicosia, A.; Ferro, V. Experiments for testing soil texture effects on flow resistance in mobile bed rills. Catena 2018, 171, 176–184. [Google Scholar] [CrossRef]
- Carollo, F.G.; Di Stefano, C.; Nicosia, A.; Palmeri, V.; Pampalone, V.; Ferro, V. Flow resistance in mobile bed rills shaped in soils with different texture. Eur. J. Soil Sci. 2021, 72, 2062–2075. [Google Scholar] [CrossRef]
- Di Stefano, C.; Nicosia, A.; Pampalone, V.; Palmeri, V.; Ferro, V. Rill flow resistance law under equilibrium bed-load transport conditions. Hydrol. Process. 2019, 33, 1317–1323. [Google Scholar] [CrossRef]
- Di Stefano, C.; Nicosia, A.; Palmeri, V.; Pampalone, V.; Ferro, V. Comparing flow resistance law for fixed and mobile bed rills. Hydrol. Process. 2019, 33, 3330–3348. [Google Scholar] [CrossRef]
- Di Stefano, C.; Nicosia, A.; Palmeri, V.; Pampalone, V.; Ferro, V. Estimating flow resistance in steep slope rills. Hydrol. Process. 2021, 35, e14296. [Google Scholar] [CrossRef]
- Nicosia, A.; Di Stefano, C.; Pampalone, V.; Palmeri, V.; Ferro, V.; Nearing, M.A. Testing a new rill flow resistance approach using the Water Erosion Prediction Project experimental database. Hydrol. Process. 2019, 33, 616–626. [Google Scholar] [CrossRef]
- Nicosia, A.; Bischetti, G.B.; Chiaradia, E.; Gandolfi, C.; Ferro, V. A full-scale study of Darcy-Weisbach friction factor for channels vegetated by riparian species. Hydrol. Process. 2021, 35, e14009. [Google Scholar] [CrossRef]
- Cheng, N.-S. Representative roughness height of submerged vegetation. Water Resour. Res. 2011, 47, W08517. [Google Scholar] [CrossRef]
- Dunn, C.; López, F.; García, M. Mean Flow and Turbulence in a Laboratory Channel with Simulated Vegetation; Civil Engineering Studies, Hydraulic Engineering Series; University of Illinois: Champaign, IL, USA, 1996. [Google Scholar]
- Murphy, E.; Ghisalberti, M.; Nepf, H. Model and laboratory study of dispersion in flows with submerged vegetation. Water Resour. Res. 2007, 43, W05438. [Google Scholar] [CrossRef]
- Comiti, F.; Mao, L.; Wilcox, A.; Wohl, E.E.; Lenzi, M.A. Field-derived relationships for flow velocity and resistance in high-gradient streams. J. Hydrol. 2007, 340, 48–62. [Google Scholar] [CrossRef]
- Schubert, J.E.; Sanders, B.F.; Smith, M.J.; Wright, N.G. Unstructured mesh generation and landcover-based resistance for hydrodynamic modeling of urban flooding. Adv. Water Resour. 2008, 31, 1603–1621. [Google Scholar] [CrossRef]
- Tyrna, B.; Assmann, A.; Fritsch, K.; Johann, G. Large-scale high-resolution pluvial flood hazard mapping using the raster-based hydrodynamic two-dimensional model FloodAreaHPC. J. Flood Risk Manag. 2018, 11, 1024–1037. [Google Scholar] [CrossRef] [Green Version]
- LUBW Landesanstalt für Umwelt, Messungen und Naturschutz Baden-Württemberg, Publ. Anhänge 1 a, b, c zum Leitfaden Kommunales Starkregenrisikomanagement in Baden-Württemberg. 2020. Available online: https://pudi.lubw.de/detailseite/-/publication/47871 (accessed on 4 December 2022).
- Ruiz Rodriguez, E.; Trost, L. Umgang mit Starkniederschlägen in Hessen. Auszug aus dem 3. Zwischenbericht. KLIMPRAX Starkregen Arbeitspaket 2; Hochschule RheinMain: Wiesbaden, Germany, 2017. [Google Scholar]
- Oberle, P.; Kron, A.; Kerlin, T.; Ruiz Rodriguez, E.; Nestmann, F. Diskussionsbeitrag zur Fließwiderstandsparametrisierung zur Simulation der Oberflächenabflüsse bei Starkregen. WasserWirtschaft 2021, 4, 12–21. [Google Scholar] [CrossRef]
- Scheres, B.; Schüttrumpf, H.; Felder, S. Flow Resistance and Energy Dissipation in Supercritical Air-Water Flows Down Vegetated Chutes. Water Resour. Res. 2020, 56, e2019WR026686. [Google Scholar] [CrossRef] [Green Version]
- Wilson, C.A.M.E.; Horritt, M.S. Measuring the flow resistance of submerged grass. Hydrol. Process. 2002, 16, 2589–2598. [Google Scholar] [CrossRef]
- Karantounias, G. Dünnschichtabfluss auf Stark Geneigter Ebene. Ph.D. Thesis, University Karlsruhe (TH), Karlsruhe, Germany, 1972. [Google Scholar]
- LfU Bayerisches Landesamt für Umwelt, Publ. Handbuch Hydraulische Modellierung. Vorgehensweisen und Standards für die 2-D-hydraulische Modellierung von Fließgewässern in Bayern. 2018. Available online: https://www.bestellen.bayern.de/application/applstarter?APPL=eshop&DIR=eshop&ACTIONxSETVAL(artdtl.htm,APGxNODENR:3779,AARTxNR:lfu_was_00134,AARTxNODENR:351717,USERxBODYURL:artdtl.htm,KATALOG:StMUG,AKATxNAME:StMUG,ALLE:x)=X (accessed on 4 December 2022).
- Software HYDRO_AS-2D, version 5.3.4.; Hydrotec Ingenieurgesellschaft für Wasser und Umwelt mbH: Aachen, Germany, 2022.
- Reference Manual, HYDRO_AS-2D, 2D-Flow Model for Water Management Applications, Version 5.2.5; Hydrotec Ingenieurgesellschaft für Wasser und Umwelt mbH: Aachen, Germany, 2021.
- Albert, A. Schneider–Bautabellen für Ingenieure mit Berechnungshinweisen und Beispielen, 24th ed.; Reguvis: Köln, Germany, 2020; ISBN 978-3-8462-1140-3. [Google Scholar]
- Hinsberger, R.; Biehler, A.; Yörük, A. Influence of Water Depth and Slope on Roughness—Experiments and Roughness Approach for Rain-on-Grid Modeling. Data Repos. 2021. [Google Scholar] [CrossRef]
- Fitt gGmbH, FG Wasser der Htw Saar. Untersuchung der Auswirkungen von Überflutungen Infolge Starkregens für die Gemeinde Eppelborn, Saarbrücken; 2020. Available online: https://www.eppelborn.de/starkregenstudie/ (accessed on 1 December 2022).


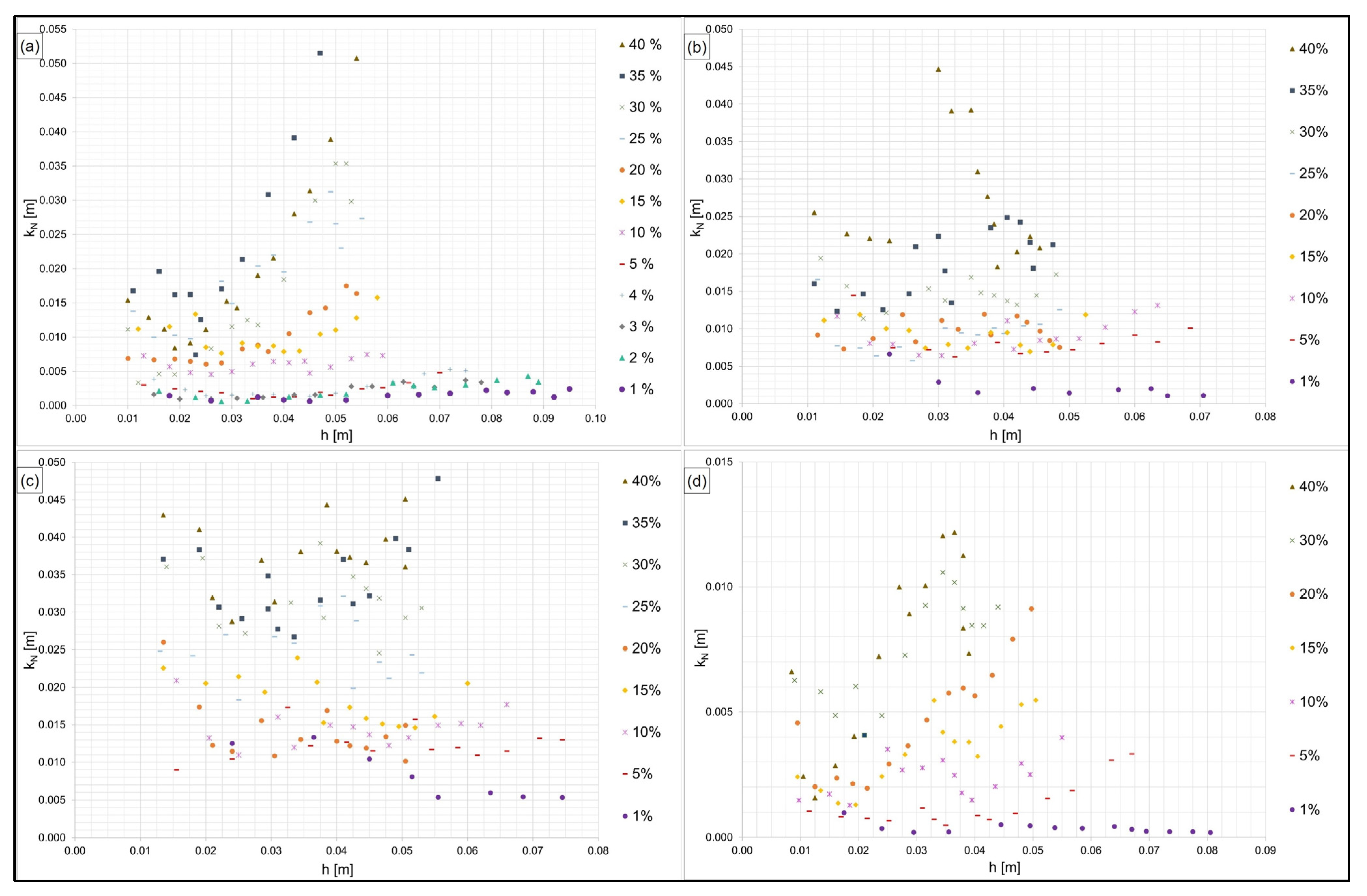
| Surface | Range of Mean kN Values (For S = 2%–S = 20%) | Literature [66] |
|---|---|---|
| Cement-based coating (Figure 10a) | 2.3–10.3 mm (for slope = 1%: kN = 1.4 mm) | Concrete, smooth: kN = 1–6 mm |
| Asphaltic emulsion (Figure 10b) | 8.3–9.7 mm (for slope = 1%: kN = 2.3 mm) | Asphaltic concrete or mastic asphalt: kN = 1.5–2.2 mm |
| Exposed aggregate concrete (Figure 10c) | 12.4–18.4 mm (for slope = 1%: kN = 8.3 mm) | Concrete smooth—rough: kN = 1–20 mm |
| Aluminum (Figure 10d) | 1.3–4.6 mm (for slope = 1%: kN = 0.4 mm) | Steel: kN = 0.04–0.1 mm |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hinsberger, R.; Biehler, A.; Yörük, A. Influence of Water Depth and Slope on Roughness—Experiments and Roughness Approach for Rain-on-Grid Modeling. Water 2022, 14, 4017. https://doi.org/10.3390/w14244017
Hinsberger R, Biehler A, Yörük A. Influence of Water Depth and Slope on Roughness—Experiments and Roughness Approach for Rain-on-Grid Modeling. Water. 2022; 14(24):4017. https://doi.org/10.3390/w14244017
Chicago/Turabian StyleHinsberger, Rebecca, Andreas Biehler, and Alpaslan Yörük. 2022. "Influence of Water Depth and Slope on Roughness—Experiments and Roughness Approach for Rain-on-Grid Modeling" Water 14, no. 24: 4017. https://doi.org/10.3390/w14244017
APA StyleHinsberger, R., Biehler, A., & Yörük, A. (2022). Influence of Water Depth and Slope on Roughness—Experiments and Roughness Approach for Rain-on-Grid Modeling. Water, 14(24), 4017. https://doi.org/10.3390/w14244017






