Sub-Hourly to Daily Rainfall Intensity-Duration-Frequency Estimation Using Stochastic Storm Transposition and Discontinuous Radar Data
Abstract
:1. Introduction
2. Data and Study Area
2.1. Study Area
2.2. Rain Gauges
2.3. Regional Model
2.4. Radar Rainfall
3. Methods
3.1. Stochastic Storm Transposition
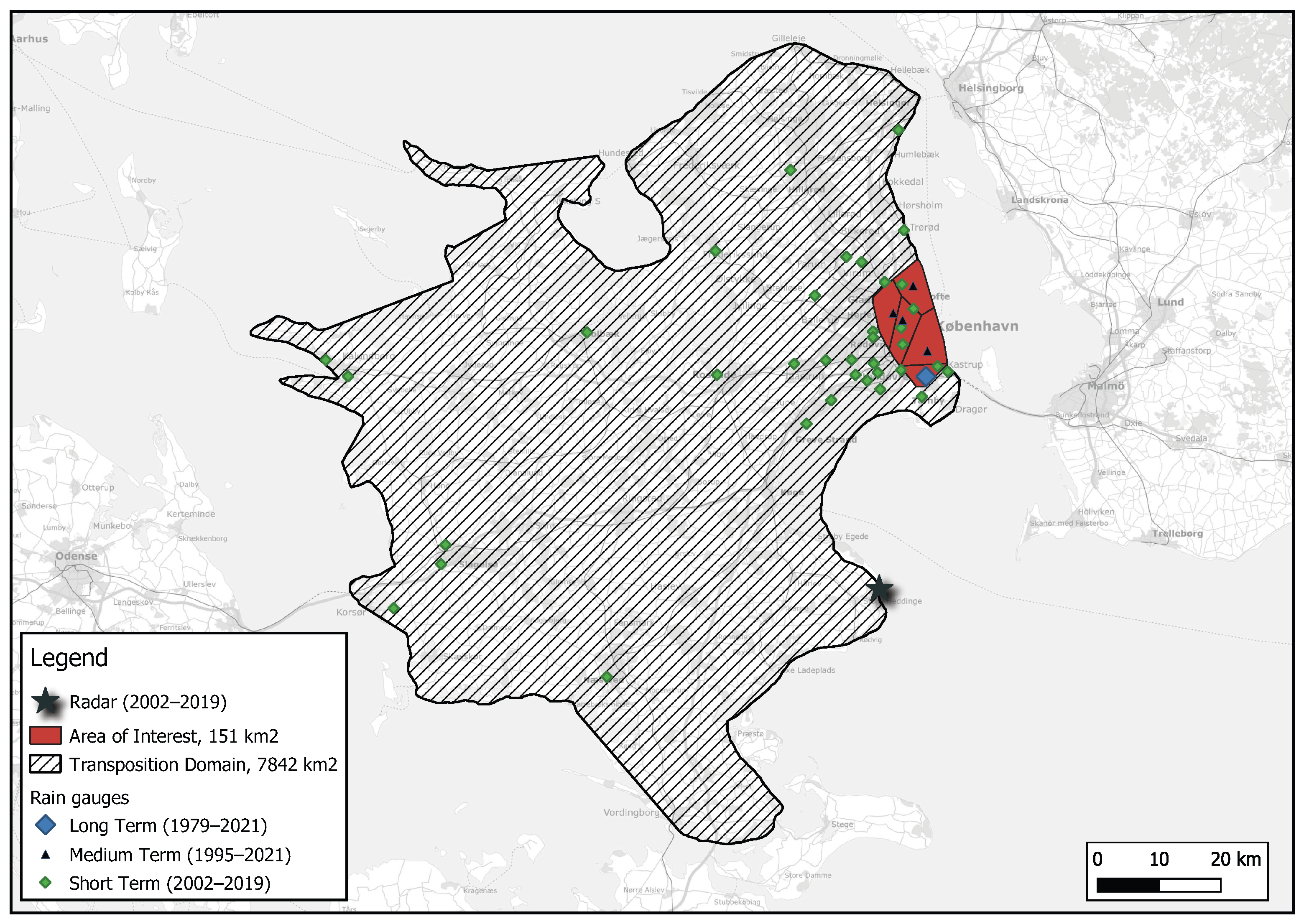
- We specify the island of Zealand (7842 km) as our transposition domain from which rainfall will be resampled, see Figure 1. A prerequisite/assumption for random transposition to the area of interest (151 km) is that the selected domain’s extreme rainfall climatology is homogeneous. This assumption is assessed and discussed in Section 4.1.
- The 500 largest storms at durations: 10, 30, 60, 180, 360, 720, and 1440 min are identified by ranking storms with the same shape and size as the area of interest (Figure 1). This collection of storms is henceforth known as the storm catalog (e.g., 60-minute storm catalog or simply 60-minute catalog). The creation of the storm catalogs is further described in Section 4.2.
- The number of yearly storm occurrences for each duration is assumed to follow a Poisson distribution with a rate parameter: (average 88 storms per year). This derivation will be further explained in Section 4.2.
- From the storm catalog in question (e.g., 60-min), we randomly select a storm. The assumption of homogeneous climatology, within the transposition domain, allows us to stochastically transpose the series of radar images in the x, y directions, since the storm is assumed to have equal likelihood to have appeared anywhere within the domain. Every time step of the radar image series is transposed with the same vector, so the original motion of a rain storm is retained, and only the spatial occurrence is altered.
- Step 4 is repeated k times where k is a random integer drawn from the Poisson distribution explained in step 3. The k storms represent one year of rainfall.
- For each transposed storm in step 4, we compute the t-minute catchment-average/point rainfall depth, for the area/point of interest.
- Steps 4–6 are repeated 1000 times to create 1000 years of synthetic storm events. The 1000 largest values from all of the synthetic years are retained (following a general “partial-duration-series” approach), and IDF values are estimated.
- Steps 4–7 are repeated, for this study, 100 times to quantify the uncertainty of the estimated IDF values.
3.2. Rainfall Statistics
3.3. Pixel-Scale Duration Bias
3.4. Areal Reduction Factors
4. Results and Discussion
4.1. Transposition Domain Selection and Assessment
4.2. Rainfall Catalog Creation
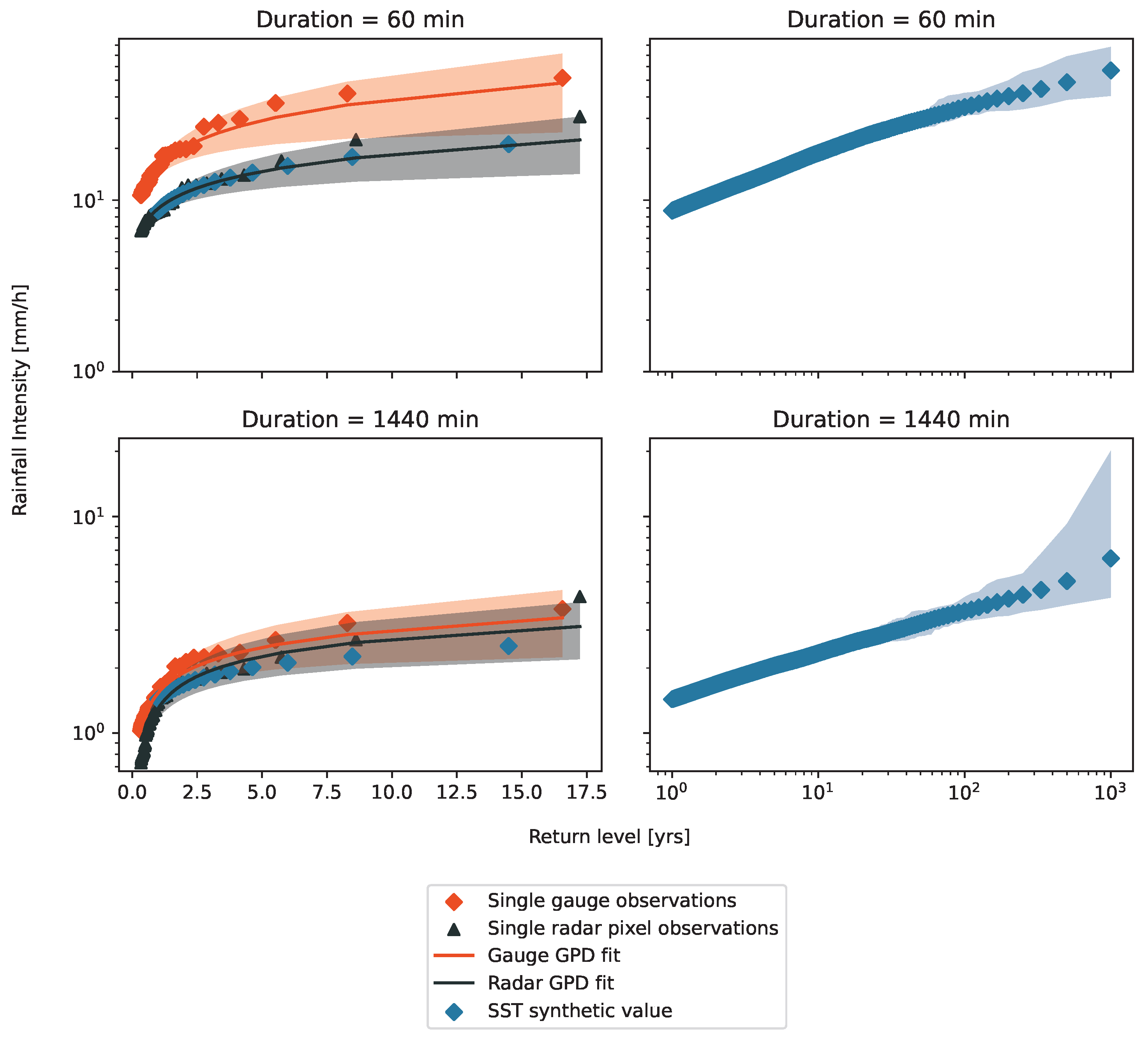
4.3. IDF Curves Based on Empirical Plotting Position, Extreme-Value Distribution Fit, and Comparison to SST
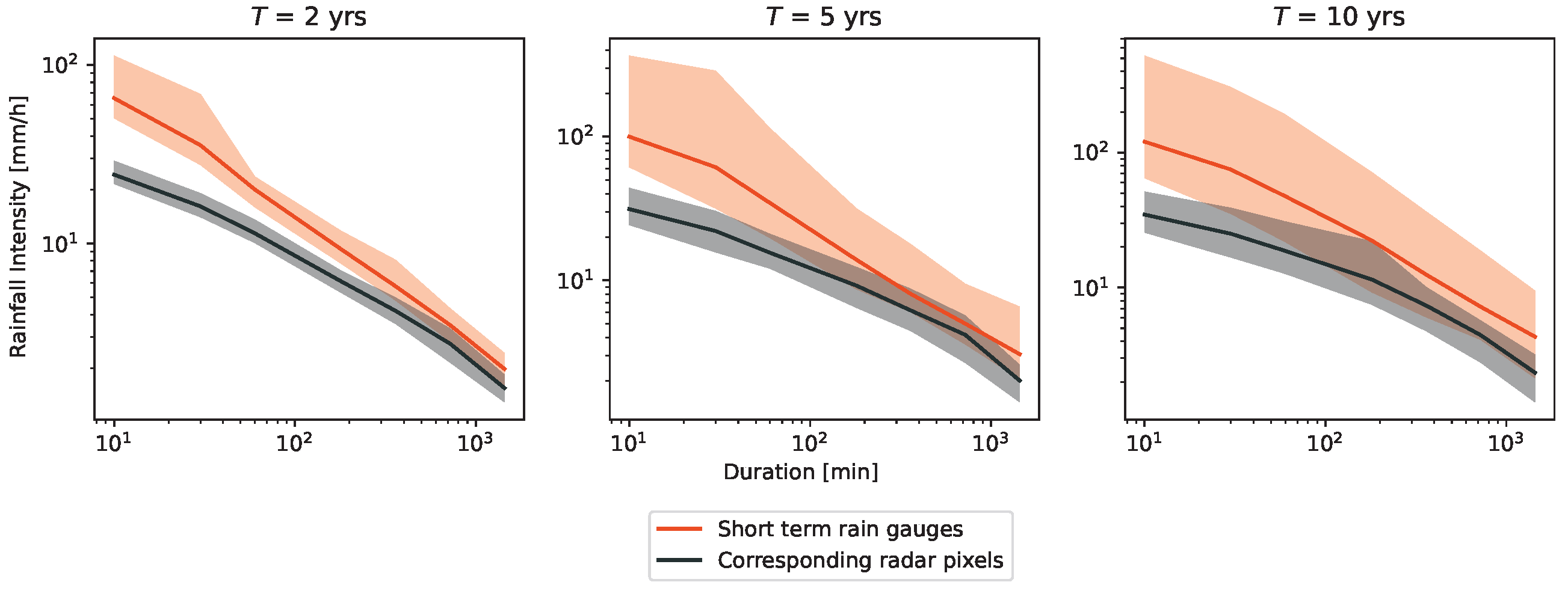
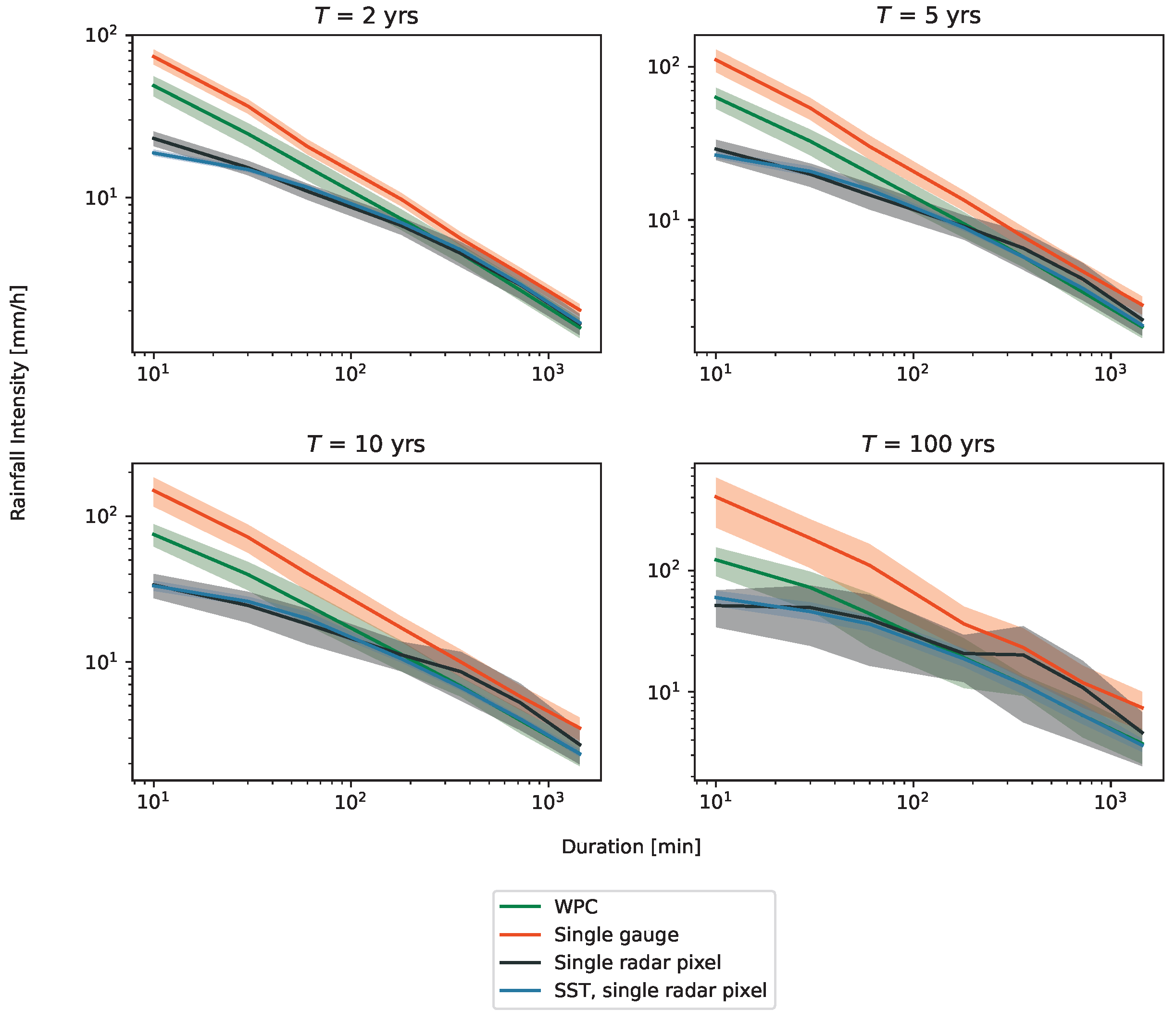
4.4. Point-to-Pixel Comparison of IDF Curves
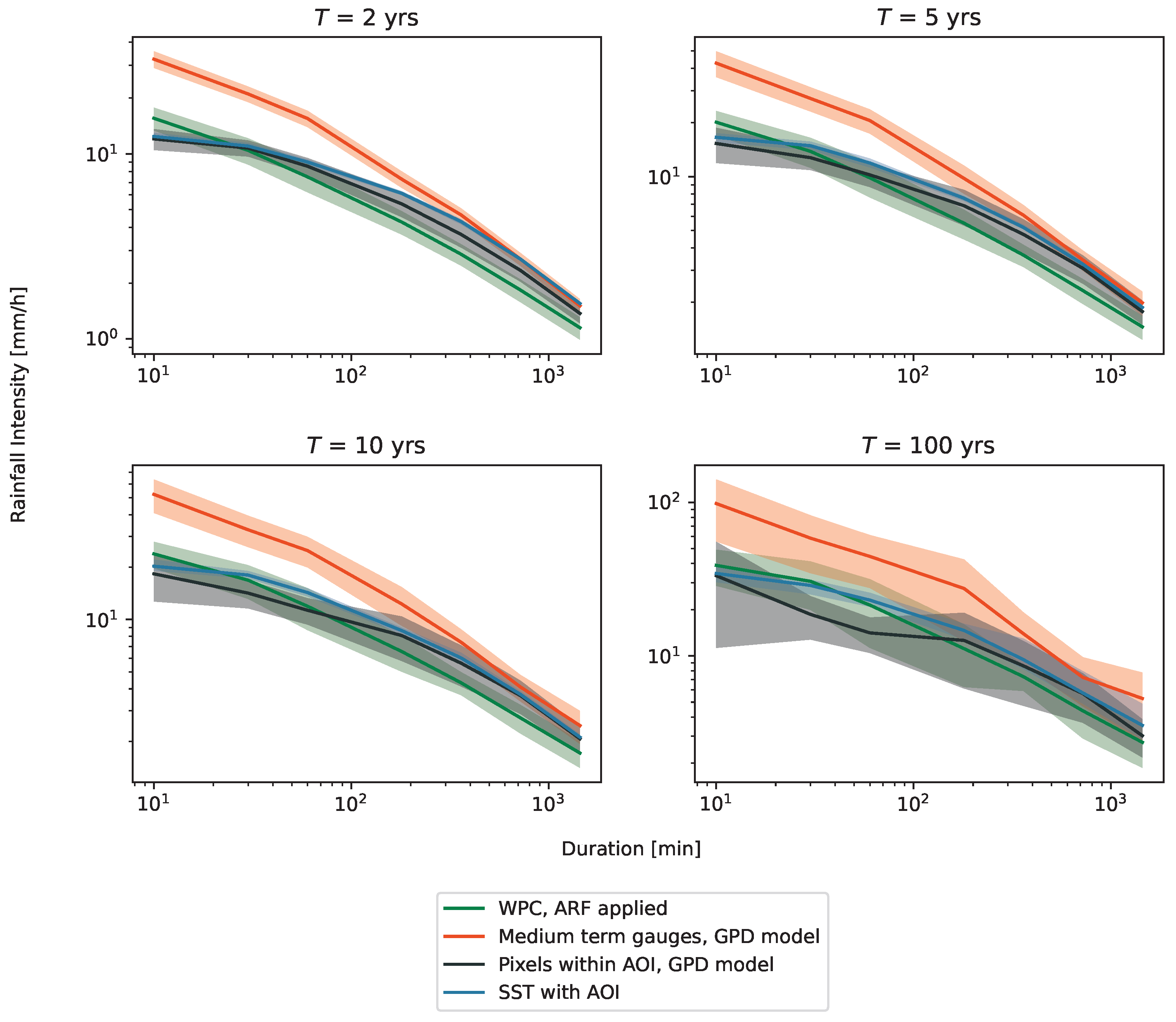
4.5. Catchment-Scale Comparison of IDF Curves
- ARFs are applied to the regional model (WPC) using Equation (5).
- Radar pixels within the AOI are, likewise, used to create an area-mean rainfall time series, and a GPD model is fitted, albeit with significantly more data points than the collection of gauges.
- Instead of only sampling one point for the SST framework, all points within the AOI are used to calculate a catchment average for the randomly generated rainfall event.
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Madsen, H.; Arnbjerg-nielsen, K.; Mikkelsen, P.S. Update of regional intensity–duration–frequency curves in Denmark: Tendency towards increased storm intensities. Atmos. Res. 2009, 92, 343–349. [Google Scholar] [CrossRef]
- Madsen, H.; Mikkelsen, P.S.; Rosbjerg, D.; Harremoës, P. Regional estimation of rainfall intensity-duration-frequency curves using generalized least squares regression of partial duration series statistics. Water Resour. Res. 2002, 38, 21-1–21-11. [Google Scholar] [CrossRef]
- Cristiano, E.; ten Veldhuis, M.; van de Giesen, N. Spatial and temporal variability of rainfall and their effects on hydrological response in urban areas—A review. Hydrol. Earth Syst. Sci. 2017, 21, 3859–3878. [Google Scholar] [CrossRef] [Green Version]
- Kim, C.; Kim, D. Effects of Rainfall Spatial Distribution on the Relationship between Rainfall Spatiotemporal Resolution and Runoff Prediction Accuracy. Water 2020, 12, 846. [Google Scholar] [CrossRef] [Green Version]
- Courty, L.; Rico-Ramirez, M.; Pedrozo-Acuña, A. The Significance of the Spatial Variability of Rainfall on the Numerical Simulation of Urban Floods. Water 2018, 10, 207. [Google Scholar] [CrossRef] [Green Version]
- Ochoa-rodriguez, S.; Wang, L.; Gires, A.; Pina, R.D.; Reinoso-Rondinel, R.; Bruni, G.; Ichiba, A.; Gaitan, S.; Cristiano, E.; van Assel, J.; et al. Impact of spatial and temporal resolution of rainfall inputs on urban hydrodynamic modelling outputs: A multi-catchment investigation. J. Hydrol. 2015, 531, 389–407. [Google Scholar] [CrossRef]
- Gyasi-Agyei, Y. Identification of the Optimum Rain Gauge Network Density for Hydrological Modelling Based on Radar Rainfall Analysis. Water 2020, 12, 1906. [Google Scholar] [CrossRef]
- Einfalt, T.; Arnbjerg-Nielsen, K.; Golz, C.; Jensen, N.; Quirmbach, M.; Vaes, G.; Vieux, B. Towards a roadmap for use of radar rainfall data in urban drainage. J. Hydrol. 2004, 299, 186–202. [Google Scholar] [CrossRef]
- Schleiss, M.; Olsson, J.; Berg, P.; Niemi, T.; Kokkonen, T.; Thorndahl, S.; Nielsen, R.; Nielsen, J.E.; Bozhinova, D.; Pulkkinen, S. The accuracy of weather radar in heavy rain: A comparative study for Denmark, the Netherlands, Finland and Sweden. Hydrol. Earth Syst. Sci. 2019, 24, 3157–3188. [Google Scholar] [CrossRef]
- Thorndahl, S.; Einfalt, T.; Willems, P.; Nielsen, J.E.; ten Veldhuis, M.; Arnbjerg-Nielsen, K.; Rasmussen, M.R.; Molnar, P. Weather radar rainfall data in urban hydrology. Hydrol. Earth Syst. Sci. 2017, 21, 1359–1380. [Google Scholar] [CrossRef]
- Overeem, A.; Buishand, T.A.; Holleman, I.; Uijlenhoet, R. Extreme value modeling of areal rainfall from weather radar. Water Resour. Res. 2010, 46. [Google Scholar] [CrossRef]
- Schaefer, M.G. Regional analyses of precipitation annual maxima in Washington State. Water Resour. Res. 1990, 26, 119–131. [Google Scholar] [CrossRef]
- Madsen, H.; Rasmussen, P.F.; Rosbjerg, D. Comparison of annual maximum series and partial duration series methods for modeling extreme hydrologic events: 1. At-site modeling. Water Resour. Res. 1997, 33, 747–757. [Google Scholar] [CrossRef]
- Madsen, H.; Rosbjerg, D. Generalized least squares and empirical bayes estimation in regional partial duration series index-flood modeling. Water Resour. Res. 1997, 33, 771–781. [Google Scholar] [CrossRef]
- Keifer, C.J.; Chu, H.H. Synthetic Storm Pattern for Drainage Design. J. Hydr. Eng. Div. ASCE 1957, 83, 1332-1–1332-25. [Google Scholar] [CrossRef]
- Rosbjerg, D.; Madsen, H. Initial design of urban drainage systems for extreme rainfall events using intensity-duration-area (IDA) curves and Chicago design storms (CDS). Hydrol. Sci. J. 2019, 64, 1397–1403. [Google Scholar] [CrossRef]
- Sivapalan, M.; Blöschl, G. Transformation of point rainfall to areal rainfall: Intensity-duration-frequency curves. J. Hydrol. 1998, 204, 150–167. [Google Scholar] [CrossRef]
- Rodriguez-iturbe, I.; Mejía, J. On the transformation of point rainfall to areal rainfall. Water Resour. Res. 1974, 10, 729–735. [Google Scholar] [CrossRef]
- Allen, R.J.; Degaetano, A.T. Considerations for the use of radar-derived precipitation estimates in determining return intervals for extreme areal precipitation amounts. J. Hydrol. 2005, 315, 203–219. [Google Scholar] [CrossRef]
- Thorndahl, S.; Nielsen, J.E.; Rasmussen, M. Estimation of Storm-Centred Areal Reduction Factors from Radar Rainfall for Design in Urban Hydrology. Water 2019, 11, 1120. [Google Scholar] [CrossRef]
- Wright, D.B.; Smith, J.A.; Baeck, M.L. Critical Examination of Area Reduction Factors. J. Hydrol. Eng. 2014, 19, 769–776. [Google Scholar] [CrossRef]
- Foufoula-Georgiou, E. A probabilistic storm transposition approach for estimating exceedance probabilities of extreme precipitation depths. Water Resour. Res. 1989, 25, 799–815. [Google Scholar] [CrossRef]
- Wilson, L.L.; Foufoula-Georgiou, E. Regional Rainfall Frequency Analysis via Stochastic Storm Transposition. J. Hydraul. Eng. ASCE 1990, 116, 859–880. [Google Scholar] [CrossRef]
- Wright, D.B.; Smith, J.A.; Villarini, G.; Baeck, M.L. Estimating the frequency of extreme rainfall using weather radar and stochastic storm transposition. J. Hydrol. 2013, 488, 150–165. [Google Scholar] [CrossRef]
- Wright, D.B.; Smith, J.A.; Baeck, M.L. Flood frequency analysis using radar rainfall fields and stochastic storm transposition. Water Resour. Res. 2014, 50, 1592–1615. [Google Scholar] [CrossRef]
- Heiss, W.H.; McGrew, D.L.; Sirmans, D. Nexrad: Next generation weather radar (WSR-88D). Microw. J. 1990, 33, 79. [Google Scholar]
- Opdaterede klimafaktorer og dimensionsgivende regnintensiteter Spildevandskomiteen, Skrift nr. 30 (Updated Climate Factors and Design Rainfall Intensityes Water Pollution Comitee, Guideline no. 30); The Water Pollution Committee of the Society of Danish Engineers, IDA: Copenhagen, Denmark, 2007.
- Madsen, H.; Gregersen, I.B.; Rosbjerg, D.; Arnbjerg-Nielsen, K. Regional frequency analysis of short duration rainfall extremes using gridded daily rainfall data as co-variate. Water Sci. Technol. 2017, 75, 1971–1981. [Google Scholar] [CrossRef]
- Gregersen, I.B.; Madsen, H.; Rosbjerg, D.; Arnbjerg-Nielsen, K. A spatial and nonstationary model for the frequency of extreme rainfall events. Water Resour. Res. 2013, 49, 127–136. [Google Scholar] [CrossRef]
- Thorndahl, S.; Nielsen, J.E.; Rasmussen, M.R. Bias adjustment and advection interpolation of long-term high resolution radar rainfall series. J. Hydrol. 2014, 508, 214–226. [Google Scholar] [CrossRef]
- Thomassen, E.D.; Thorndahl, S.; Andersen, C.B.; Gregersen, I.B.; Arnbjerg-Nielsen, K.; Sørup, H.J.D. Comparing spatial metrics of extreme precipitation between data from rain gauges, weather radar and high-resolution climate model re-analyses. J. Hydrol. 2022, 610, 127915. [Google Scholar] [CrossRef]
- Nielsen, J.E.; Thorndahl, S.; Rasmussen, M.R. A numerical method to generate high temporal resolution precipitation time series by combining weather radar measurements with a nowcast model. Atmos. Res. 2014, 138, 1–12. [Google Scholar] [CrossRef]
- Thejll, P.; Boberg, F.; Schmith, T.; Christiansen, B.; Christensen, O.B.; Madsen, M.S.; Su, J.; Andree, E.; Olsen, S.; Langen, P.L.; et al. Methods Used in the Danish Climate Atlas; DMI Report 21-41; Danish Meteorological Institute: Copenhagen, Denmark, 2021; ISBN 978-87-7478-690-0. [Google Scholar]
- Wright, D.B.; Mantilla, R.; Peters-Lidard, C.D. A remote sensing-based tool for assessing rainfall-driven hazards. Environ. Model. Softw. 2017, 90, 34–54. [Google Scholar] [CrossRef] [Green Version]
- Zhou, Z.; Smith, J.A.; Baeck, M.L.; Wright, D.B.; Smith, B.K.; Liu, S. The impact of the spatiotemporal structure of rainfall on flood frequency over a small urban watershed: An approach coupling stochastic storm transposition and hydrologic modeling. Hydrol. Earth Syst. Sci. 2021, 25, 4701–4717. [Google Scholar] [CrossRef]
- Zhu, Z.; Wright, D.B.; Yu, G. The Impact of Rainfall Space-Time Structure in Flood Frequency Analysis. Water Resour. Res. 2018, 54, 8983–8998. [Google Scholar] [CrossRef]
- WPC. Funktionspraksis for afløbssystemer under regn, skrift nr. 27 (Practice for Drainage Systems during Rain, Guideline no. 27); The Water Pollution Committee of the Society of Danish Engineers, IDA: Copenhagen, Denmark, 2007. [Google Scholar]
- Willems, P.; Olsson, J.; Arnbjerg-Nielsen, K.; Beecham, S.; Pathirana, A.; Gregersen, I.B.; Madsen, H.; Nguyen, V.-T.-V. Impacts of Climate Change on Rainfall Extremes and Urban Drainage Systems; IWA Publishing: London, UK, 2012; ISBN 9781780401263. [Google Scholar]
- Peleg, N.; Marra, F.; Fatichi, S.; Paschalis, A.; Molnar, P.; Burlando, P. Spatial variability of extreme rainfall at radar subpixel scale. J. Hydrol. 2018, 556, 922–933. [Google Scholar] [CrossRef] [Green Version]
- Scharling, M. Climate Grid Denmark—Dataset for Use in Research and Education; Technical Report 12-10; Danish Meteorological Institute: Copenhagen, Denmark, 2012. [Google Scholar]
- Peleg, N.; Ben-asher, M.; Morin, E. Radar subpixel-scale rainfall variability and uncertainty: Lessons learned from observations of a dense rain-gauge network. Hydrol. Earth Syst. Sci. 2013, 17, 2195–2208. [Google Scholar] [CrossRef] [Green Version]
- Wright, D.B.; Kirschbaum, D.B.; Yatheendradas, S. Satellite Precipitation Characterization, Error Modeling, and Error Correction Using Censored Shifted Gamma Distributions. J. Hydrometeorol. 2017, 18, 2801–2815. [Google Scholar] [CrossRef]
- Ciach, G.J.; Morrissey, M.L.; Krajewski, W.F. Conditional Bias in Radar Rainfall Estimation. J. Appl. Meteorol. 2000, 39, 1941–1946. [Google Scholar] [CrossRef]
- Tian, Y.; Huffman, G.J.; Adler, R.F.; Tang, L.; Sapiano, M.; Maggioni, V.; Wu, H. Modeling errors in daily precipitation measurements: Additive or multiplicative? Geophys. Res. Lett. 2013, 40, 2060–2065. [Google Scholar] [CrossRef] [Green Version]
- Bougadis, J.; Adamowski, K. Scaling model of a rainfall intensity-duration-frequency relationship. Hydrol. Process. 2006, 20, 3747–3757. [Google Scholar] [CrossRef]



| Rainfall Duration [min] | 10 | 30 | 60 | 180 | 360 | 720 | 1440 |
|---|---|---|---|---|---|---|---|
| Bias [-] | 1.56 | 1.27 | 1.19 | 1.11 | 1.06 | 1.03 | 1.00 |
| RMSE [mm] | 8.71 | 4.43 | 3.09 | 1.42 | 0.83 | 0.47 | 0.25 |
| MAE [mm] | 4.49 | 2.28 | 1.46 | 0.69 | 0.41 | 0.23 | 0.12 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Andersen, C.B.; Wright, D.B.; Thorndahl, S. Sub-Hourly to Daily Rainfall Intensity-Duration-Frequency Estimation Using Stochastic Storm Transposition and Discontinuous Radar Data. Water 2022, 14, 4013. https://doi.org/10.3390/w14244013
Andersen CB, Wright DB, Thorndahl S. Sub-Hourly to Daily Rainfall Intensity-Duration-Frequency Estimation Using Stochastic Storm Transposition and Discontinuous Radar Data. Water. 2022; 14(24):4013. https://doi.org/10.3390/w14244013
Chicago/Turabian StyleAndersen, Christoffer B., Daniel B. Wright, and Søren Thorndahl. 2022. "Sub-Hourly to Daily Rainfall Intensity-Duration-Frequency Estimation Using Stochastic Storm Transposition and Discontinuous Radar Data" Water 14, no. 24: 4013. https://doi.org/10.3390/w14244013





