Deformation Prediction of Cihaxia Landslide Using InSAR and Deep Learning
Abstract
:1. Introduction
2. Methodology
- Data monitoring is the first step in slope deformation prediction. In this study, we used InSAR to acquire slope deformation data. According to the difference between the two observations, the slope deformation distribution map at different periods can be obtained. We divided the target slope into different zones. In the divided zones, we selected a reference point, and the data of the point were used to represent the deformation of the monitored zone. Thus, the curve of the deformation with time was obtained.
- Model building is the second step in slope deformation prediction. In our research, long short-term memory (LSTM) was adopted in deformation prediction. The attention mechanism was also considered in the LSTM establishment. Then, the additive model was used to build training features. Both the original and generated features were fed to the LSTM model. According to the idea of the model ensemble, the final prediction model was established.
- Model evaluation is the final step in slope deformation prediction. To evaluate the slope deformation model, we used three model evaluation metrics, i.e., root mean square error (RMSE), mean absolute error (MAE), and R-square (R2). The model was built using monitored data from five reference points in the 4# landslide of the Cihaxia hydropower station. Finally, the actual data and test results were compared to evaluate the prediction results. Model evaluation is the final step in slope deformation prediction.
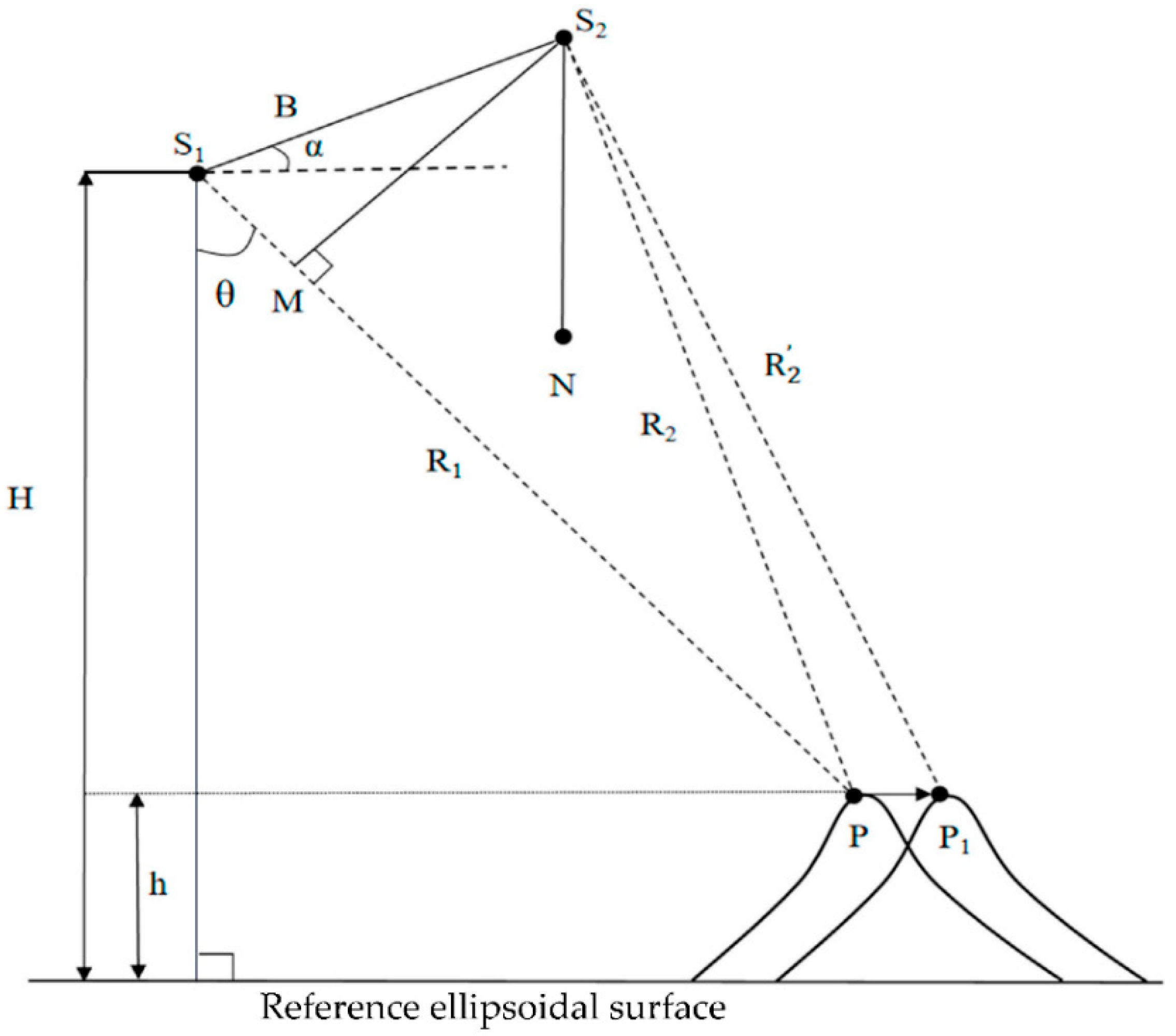
2.1. The Fundamental Principle of InSAR
2.2. ARIMA Model
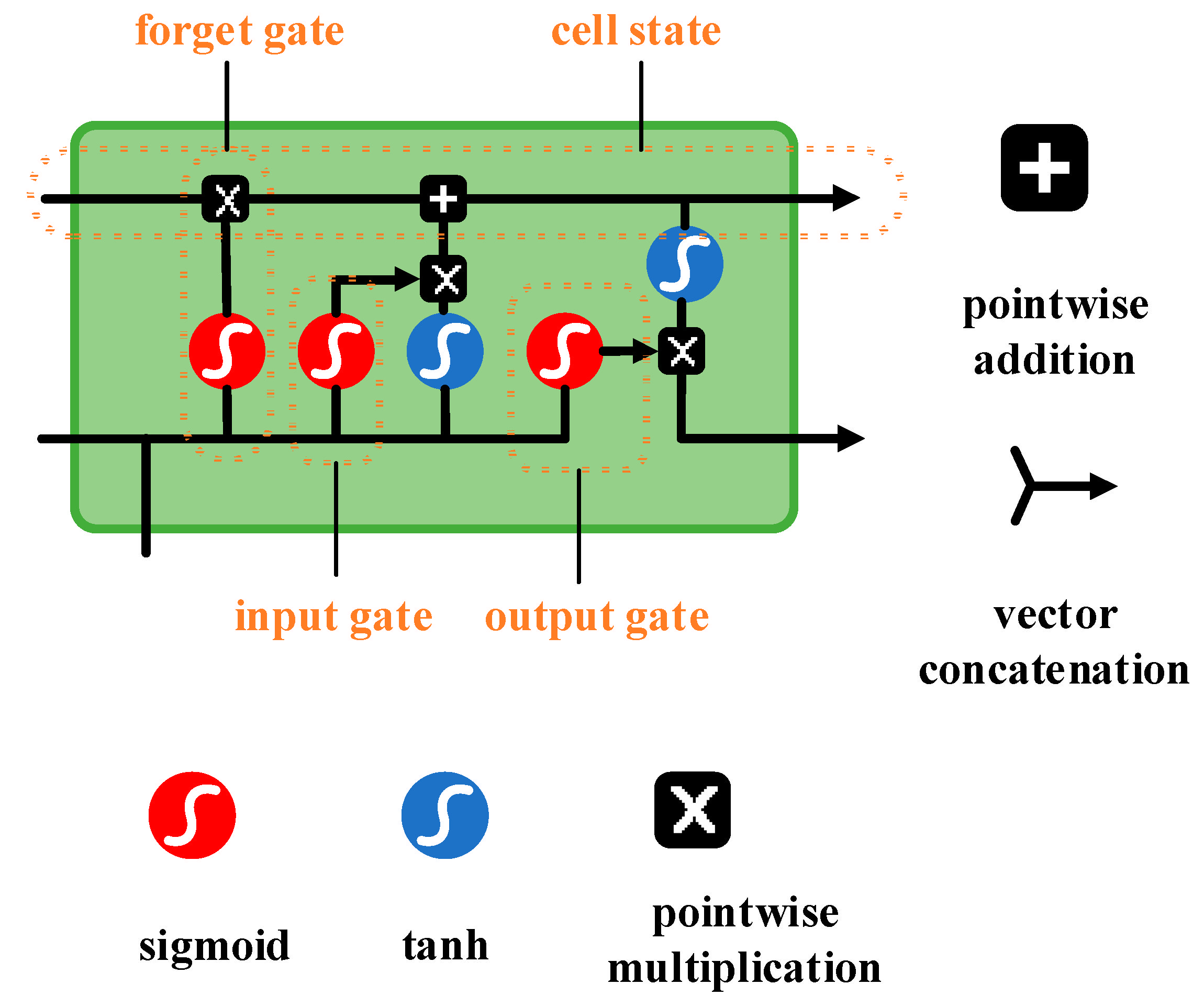
2.3. LSTM-Attention Model
2.4. Attention
2.5. Model Evaluation Metrics
3. Case Study
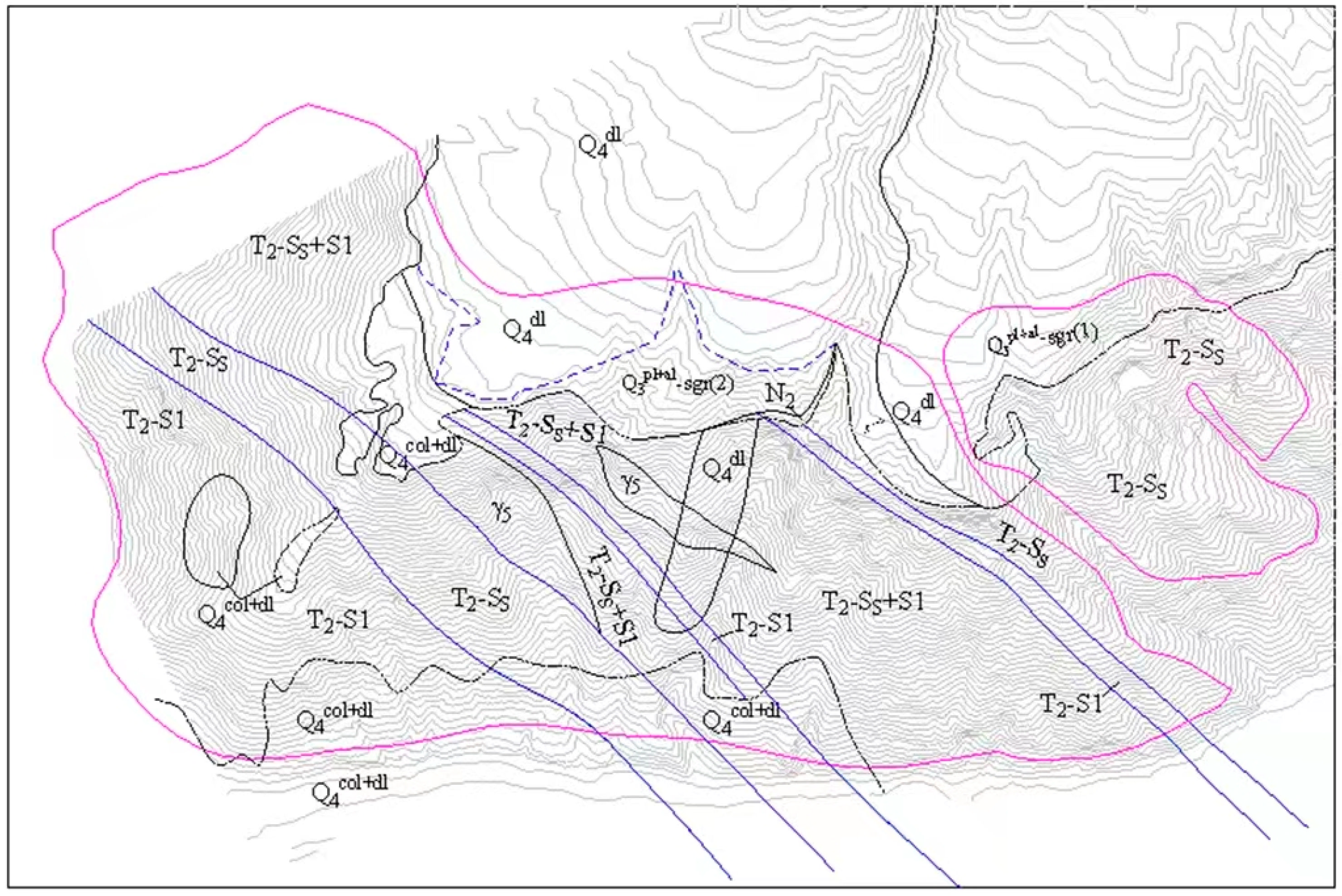
3.1. Engineering Project Review
- T2-Ss is a medium-thin layered sandstone mixed with slate. The sandstone is celadon to gray, medium-to-fine-textured, and layer-structured. The layer has a thickness in the range of 5 cm–25 cm; it is compacted, hard, and weather-resistant.
- T2-Ss + Sl: It is a celadon sandstone mixed up with a gray slate.
- T2-Sl is thin- to ultra-thin layered slate mixed with sandstone. The slate is gray to dark gray, medium-to-fine-textured, and layer-structured. The thickness of the layer is in the range of 0.5 cm–10 cm. The rock is relatively soft and not weather-resistant.
- The intermediate-acid intrusive dike of the Indo-Chinese epoch (γ5) is mainly composed of granite, quartz diorite, and quartzite. It is compacted, hard, and weather-resistant. It intrudes into the rock in the direction of the layer as a dike cutting the T2c stratum.
- The tertiary period Pliocene series (N2) is distributed on the top of the landslide slope, soft, and mainly composed of red-purple aleuropelitic rock. Unconformable contact exists between the stratum and the T2c layer.
- The epipleistocene gravel alluvium (Q3pl+al-sgr (2)) is distributed on the landslide slope far from the flat zone. It is mainly composed of sandstone, quartzite, granite, limestone, and slate. The stratum is dry, compacted, and slightly scattered.
- The holocene slope accumulation gravel soil (Q4dl) is distributed on the top of the landslide slope, which is mainly composed of sandstone and slate. The structure is scattered.
- The holocene avalanche slope accumulation block and rubble (Q4col+dl) is distributed over the bottom of the landslide slope, which is mainly composed of sandstone and slate of different sizes. The structure is scattered.
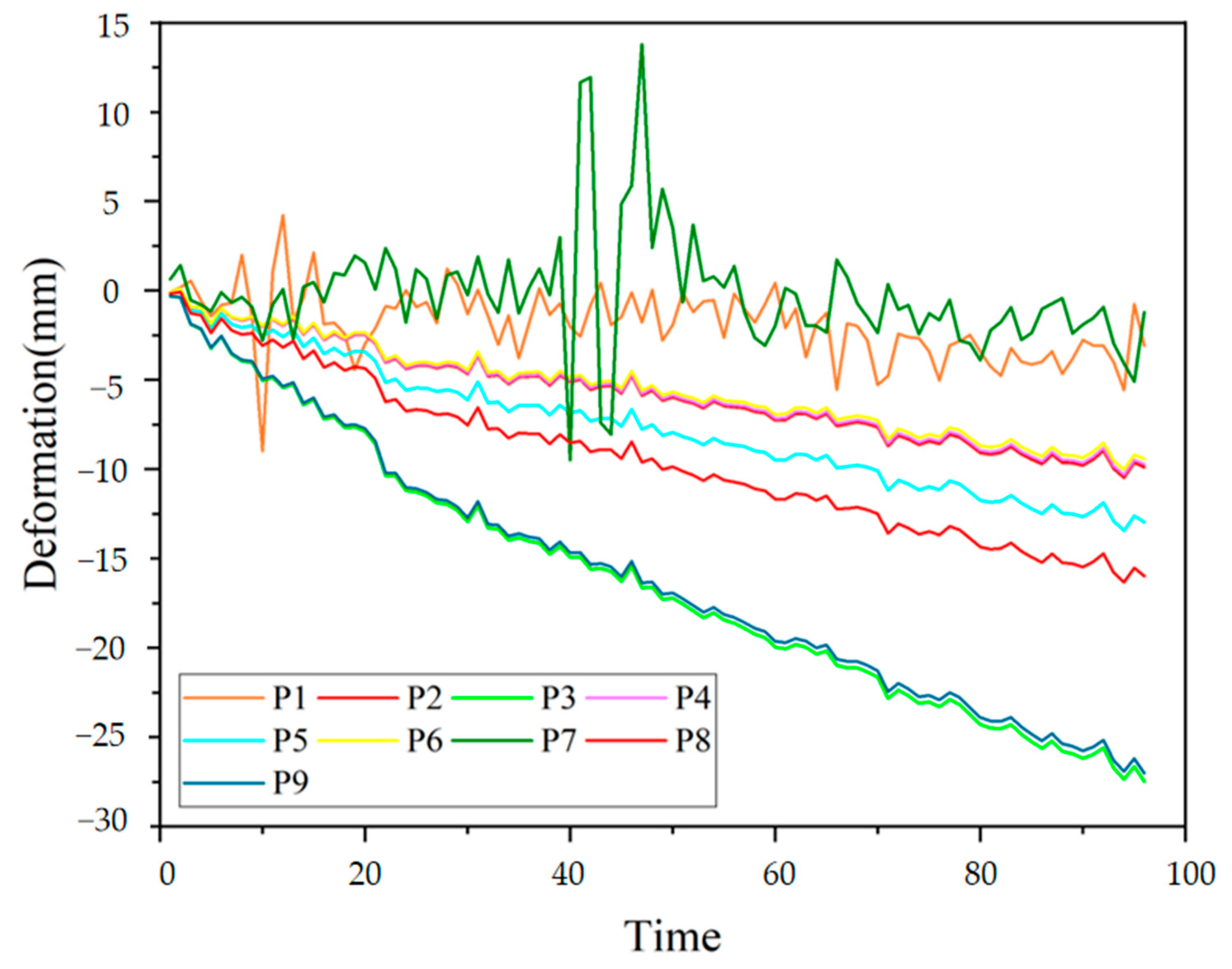
3.2. Slope Deformation Monitoring Using InSAR
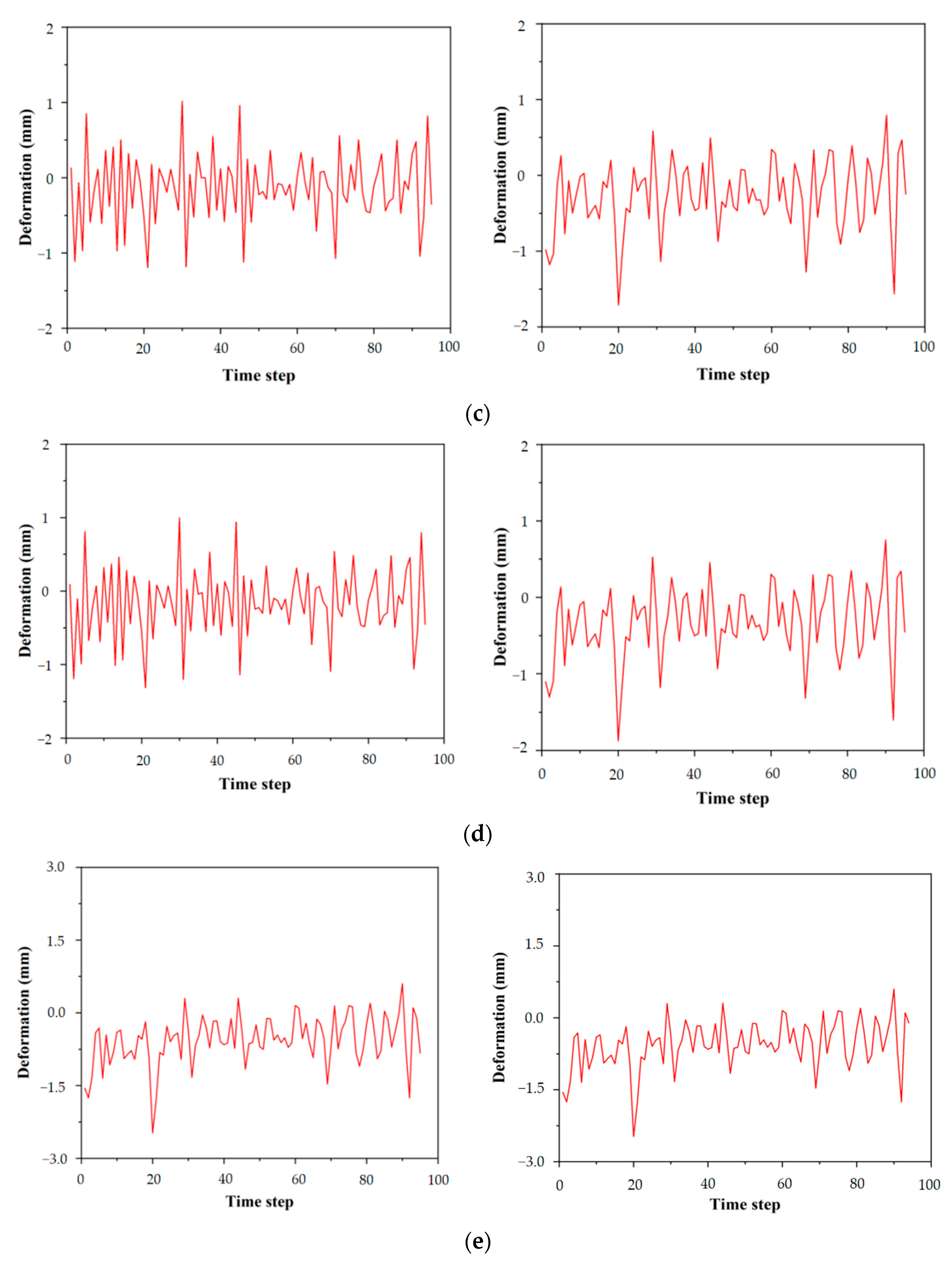
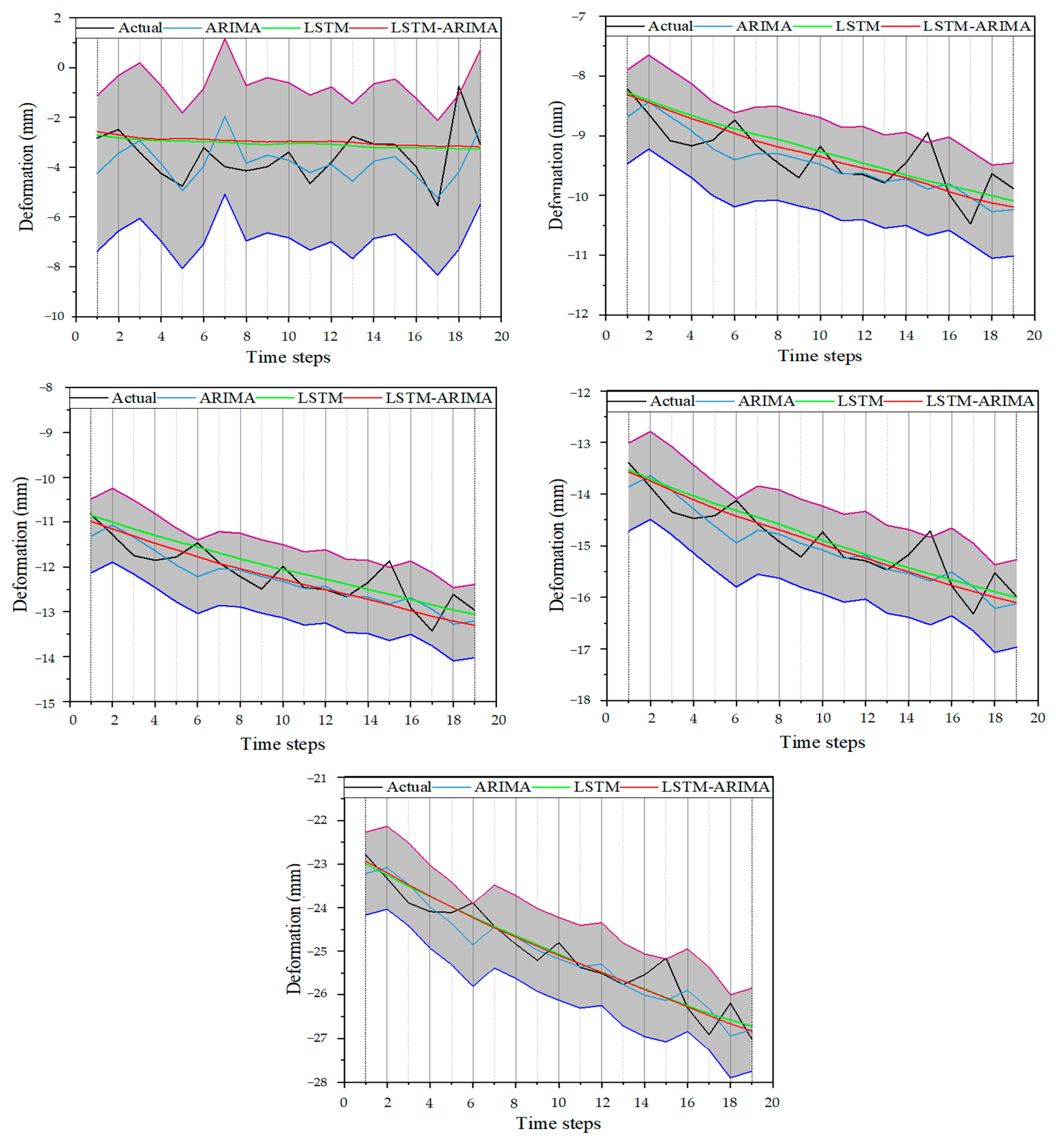
3.3. Experimental Results
3.4. Discussion
4. Conclusions
- The slope deformation was recorded using InSAR, and all the points on the map were recorded. The selected points in different zones were used as the study data. A geological survey provided the engineering details for the composition of the whole slope.
- LSTM predicts the trend in time series data but is insensitive to deviations in data series. Because ARIMA effectively predicts the deviation of stationary sequences, we selected the predictions of ARIMA as new features and added them to the original data as an input to the LSTM. This approach improved the prediction performance of LSTM.
- From the analysis results, the LSTM and LSTM-ARIMA models effectively predicted the slope deformation trend, and for most data points, the LSTM-ARIMA model had minimal RMSE and MAE. Using the ARIMA model to predict the data series yielded a large error, but adding the prediction as a new feature to the original data improved the prediction performance of the ensemble model. In the future, features generated by the ARIMA model can be added to the raw data as pseudo-data to enhance the predictive performance of the model.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhang, Z.; Liu, G.; Wu, S.; Tang, H.; Wang, T.; Li, G.; Liang, C. Rock slope deformation mechanism in the Cihaxia hydropower station, Northwest China. Bull. Eng. Geol. Environ. 2015, 74, 943–958. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, T.; Wu, S.; Tang, H. Rock toppling failure mode influenced by local response to earthquakes. Bull. Eng. Geol. Environ. 2016, 75, 1361–1375. [Google Scholar] [CrossRef]
- Yan, G.; Yin, Y.; Huang, B.; Zhang, Z.; Zhu, S. Formation mechanism and characteristics of the Jinjiling landslide in Wushan in the Three Gorges Reservoir region, China. Landslides 2019, 16, 2087–2101. [Google Scholar] [CrossRef]
- Kim, J.; Kim, Y.; Jeong, S.; Hong, M. Rainfall-induced landslides by deficit field matric suction in unsaturated soil slopes. Environ. Earth Sci. 2017, 76, 1–17. [Google Scholar] [CrossRef]
- Cogan, J.; Gratchev, I. A study on the effect of rainfall and slope characteristics on landslide initiation by means of flume tests. Landslides 2019, 16, 2369–2379. [Google Scholar] [CrossRef]
- Cuomo, S.; Di Perna, A.; Martinelli, M. Modelling the spatio-temporal evolution of a rainfall-induced retrogressive landslide in an unsaturated slope. Eng. Geol. 2021, 294, 106371. [Google Scholar] [CrossRef]
- Castro, J.; Asta, M.P.; Galve, J.P.; Azañón, J.M. Formation of clay-rich layers at the slip surface of slope instabilities: The role of groundwater. Water 2020, 12, 2639. [Google Scholar] [CrossRef]
- Marino, P.; Santonastaso, G.F.; Fan, X.; Greco, R. Prediction of shallow landslides in pyroclastic-covered slopes by coupled modeling of unsaturated and saturated groundwater flow. Landslides 2021, 18, 31–41. [Google Scholar] [CrossRef]
- Marc, V.; Bertrand, C.; Malet, J.-P.; Carry, N.; Simler, R.; Cervi, F. Groundwater—Surface waters interactions at slope and catchment scales: Implications for landsliding in clay-rich slopes. Hydrol. Process. 2017, 31, 364–381. [Google Scholar] [CrossRef]
- Gao, W.W.; Gao, W.; Hu, R.L.; Xu, P.F.; Xia, J.G. Microtremor survey and stability analysis of a soil-rock mixture landslide: A case study in Baidian town, China. Landslides 2018, 15, 1951–1961. [Google Scholar] [CrossRef]
- Zhang, C.; Zhang, M.; Zhang, T.; Dai, Z.; Wang, L. Influence of intrusive granite dyke on rainfall-induced soil slope failure. Bull. Eng. Geol. Environ. 2020, 79, 5259–5276. [Google Scholar] [CrossRef]
- Kim, K.-S.; Jeong, S.-W.; Song, Y.-S.; Kim, M.; Park, J.-Y. Four-year monitoring study of shallow landslide hazards based on hydrological measurements in a weathered granite soil slope in South Korea. Water 2021, 13, 2330. [Google Scholar] [CrossRef]
- Zheng, Y.; Zhu, Z.W.; Li, W.J.; Gu, D.M.; Xiao, W. Experimental research on a novel optic fiber sensor based on OTDR for landslide monitoring. Measurement 2019, 148, 106926. [Google Scholar] [CrossRef]
- Wu, H.; Guo, Y.; Xiong, L.; Liu, W.; Li, G.; Zhou, X. Optical fiber-based sensing, measuring, and implementation methods for slope deformation monitoring: A review. IEEE Sens. J. 2019, 19, 2786–2800. [Google Scholar] [CrossRef]
- Hong, C.-Y.; Zhang, Y.-F.; Li, G.-W.; Zhang, M.-X.; Liu, Z.-X. Recent progress of using Brillouin distributed fiber optic sensors for geotechnical health monitoring. Sens. Actuators A Phys. 2017, 258, 131–145. [Google Scholar] [CrossRef]
- Parente, L.; Chandler, J.H.; Dixon, N. Optimising the quality of an SfM-MVS slope monitoring system using fixed cameras. Photogramm. Rec. 2019, 34, 408–427. [Google Scholar] [CrossRef]
- Li, Q.; Min, G.; Chen, P.; Liu, Y.; Tian, S.; Zhang, D.; Zhang, W. Computer vision-based techniques and path planning strategy in a slope monitoring system using unmanned aerial vehicle. Int. J. Adv. Robot. Syst. 2020, 17, 1729881420904303. [Google Scholar] [CrossRef]
- Li, H.-B.; Li, X.-W.; Li, W.-Z.; Zhang, S.-L.; Zhou, J.-W. Quantitative assessment for the rockfall hazard in a post-earthquake high rock slope using terrestrial laser scanning. Eng. Geol. 2019, 248, 1–13. [Google Scholar] [CrossRef]
- Li, H.-B.; Qi, S.-C.; Yang, X.-G.; Li, X.-W.; Zhou, J.-W. Geological survey and unstable rock block movement monitoring of a post-earthquake high rock slope using terrestrial laser scanning. Rock Mech. Rock Eng. 2020, 53, 4523–4537. [Google Scholar] [CrossRef]
- Sun, Q.; Zhang, L.; Ding, X.; Hu, J.; Li, Z.; Zhu, J. Slope deformation prior to Zhouqu, China landslide from InSAR time series analysis. Remote Sens. Environ. 2015, 156, 45–57. [Google Scholar] [CrossRef]
- Zhang, Y.; Meng, X.; Jordan, C.; Novellino, A.; Dijkstra, T.; Chen, G. Investigating slow-moving landslides in the Zhouqu region of China using InSAR time series. Landslides 2018, 15, 1299–1315. [Google Scholar] [CrossRef]
- Dai, C.; Li, W.; Wang, D.; Lu, H.; Xu, Q.; Jian, J. Active landslide detection based on Sentinel-1 data and InSAR technology in Zhouqu county, Gansu province, Northwest China. J. Earth Sci. 2021, 32, 1092–1103. [Google Scholar] [CrossRef]
- Tang, Y.; Feng, F.; Guo, Z.; Feng, W.; Li, Z.; Wang, J.; Sun, Q.; Ma, H.; Li, Y. Integrating principal component analysis with statistically-based models for analysis of causal factors and landslide susceptibility mapping: A comparative study from the loess plateau area in Shanxi (China). J. Clean. Prod. 2020, 277, 124159. [Google Scholar] [CrossRef]
- Li, S.H.; Wu, L.Z.; Chen, J.J.; Huang, R. Multiple data-driven approach for predicting landslide deformation. Landslides 2020, 17, 709–718. [Google Scholar] [CrossRef]
- Shahabi, H.; Hashim, M.; Ahmad, B.B. Remote sensing and GIS-based landslide susceptibility mapping using frequency ratio, logistic regression, and fuzzy logic methods at the central Zab basin, Iran. Environ. Earth Sci. 2015, 73, 8647–8668. [Google Scholar] [CrossRef]
- Du, S.; Zhang, J.; Li, J.; Su, Q.; Zhu, W.; Chen, Y. The deformation prediction of mine slope surface using PSO-SVM model. TELKOMNIKA Indones. J. Electr. Eng. 2013, 11, 7182–7189. [Google Scholar] [CrossRef]
- Yu, C.; Chen, J. Landslide susceptibility mapping using the slope unit for southeastern Helong City, Jilin Province, China: A comparison of ANN and SVM. Symmetry 2020, 12, 1047. [Google Scholar] [CrossRef]
- Zhang, L.; Shi, B.; Zhu, H.; Yu, X.B.; Han, H.; Fan, X. PSO-SVM-based deep displacement prediction of Majiagou landslide considering the deformation hysteresis effect. Landslides 2021, 18, 179–193. [Google Scholar] [CrossRef]
- Hu, X.; Wu, S.; Zhang, G.; Zheng, W.; Liu, C.; He, C.; Liu, Z.; Guo, X.; Zhang, H. Landslide displacement prediction using kinematics-based random forests method: A case study in Jinping Reservoir Area, China. Eng. Geol. 2021, 283, 105975. [Google Scholar] [CrossRef]
- Sun, D.; Wen, H.; Wang, D.; Xu, J. A random forest model of landslide susceptibility mapping based on hyperparameter optimization using Bayes algorithm. Geomorphology 2020, 362, 107201. [Google Scholar] [CrossRef]
- Chen, H.; Zeng, Z. Deformation prediction of landslide based on improved back-propagation neural network. Cogn. Comput. 2013, 5, 56–62. [Google Scholar] [CrossRef]
- Gordan, B.; Armaghani, D.J.; Hajihassani, M.; Monjezi, M. Prediction of seismic slope stability through combination of particle swarm optimization and neural network. Eng. Comput. 2016, 32, 85–97. [Google Scholar] [CrossRef]
- Javdanian, H.; Pradhan, B. Assessment of earthquake-induced slope deformation of earth dams using soft computing techniques. Landslides 2019, 16, 91–103. [Google Scholar] [CrossRef]
- Zhang, N.; Zhang, W.; Liao, K.; Zhu, H.-H.; Li, Q.; Wang, J. Deformation prediction of reservoir landslides based on a Bayesian optimized random forest-combined Kalman filter. Environ. Earth Sci. 2022, 81, 1–14. [Google Scholar] [CrossRef]
- Deng, L.; Smith, A.; Dixon, N.; Yuan, H. Machine learning prediction of landslide deformation behaviour using acoustic emission and rainfall measurements. Eng. Geol. 2021, 293, 106315. [Google Scholar] [CrossRef]
- Garg, N.; Soni, K.; Saxena, T.; Maji, S. Applications of AutoRegressive Integrated Moving Average (ARIMA) approach in time-series prediction of traffic noise pollution. Noise Control Eng. J. 2015, 63, 182–194. [Google Scholar] [CrossRef] [Green Version]
- Hu, A.Y.; Bao, T.F.; Yang, C.L. LSTM-ARIMA-based Prediction of Dam Deformation: Model and Its Application. J. Yangtze River Sci. Res. Inst. 2020, 37, 64–68. [Google Scholar]
- Chen, H.; Zeng, Z.; Tang, H. Landslide deformation prediction based on recurrent neural network. Neural Process. Lett. 2015, 41, 169–178. [Google Scholar] [CrossRef]
- Yang, B.; Yin, K.; Lacasse, S.; Liu, Z. Time series analysis and long short-term memory neural network to predict landslide displacement. Landslides 2019, 16, 677–694. [Google Scholar] [CrossRef]
- Zhang, W.; Li, H.; Tang, L.; Gu, X.; Wang, L.; Wang, L. Displacement prediction of Jiuxianping landslide using gated recurrent unit (GRU) networks. Acta Geotech. 2022, 17, 1367–1382. [Google Scholar] [CrossRef]
- Wang, J.; Nie, G.; Gao, S.; Wu, S.; Li, H.; Ren, X. Landslide Deformation Prediction Based on a GNSS Time Series Analysis and Recurrent Neural Network Model. Remote Sens. 2021, 13, 1055. [Google Scholar] [CrossRef]
- Jiang, H.; Li, Y.; Zhou, C.; Hong, H.; Glade, T.; Yin, K. Landslide Displacement Prediction Combining LSTM and SVR Algorithms: A Case Study of Shengjibao Landslide from the Three Gorges Reservoir Area. Appl. Sci. 2020, 10, 7830. [Google Scholar] [CrossRef]
- Xing, Y.; Yue, J.; Chen, C. Interval Estimation of Landslide Displacement Prediction Based on Time Series Decomposition and Long Short-Term Memory Network. IEEE Access 2020, 8, 3187–3196. [Google Scholar] [CrossRef]
- Zhang, X.; Zhu, C.; He, M.; Dong, M.; Zhang, G.; Zhang, F. Failure Mechanism and Long Short-Term Memory Neural Network Model for Landslide Risk Prediction. Remote Sens. 2022, 14, 166. [Google Scholar] [CrossRef]
- Xie, P.; Zhou, A.; Chai, B. The Application of Long Short-Term Memory(LSTM) Method on Displacement Prediction of Multifactor-Induced Landslides. IEEE Access 2019, 7, 54305–54311. [Google Scholar] [CrossRef]
- Gao, Y.; Chen, X.; Tu, R.; Chen, G.; Luo, T.; Xue, D. Prediction of Landslide Displacement Based on the Combined VMD-Stacked LSTM-TAR Model. Remote Sens. 2020, 14, 1164. [Google Scholar] [CrossRef]
- Yang, S.; Jin, A.; Nie, W.; Liu, C.; Li, Y. Research on SSA-LSTM-Based Slope Monitoring and Early Warning Model. Sustainability 2022, 14, 10246. [Google Scholar] [CrossRef]


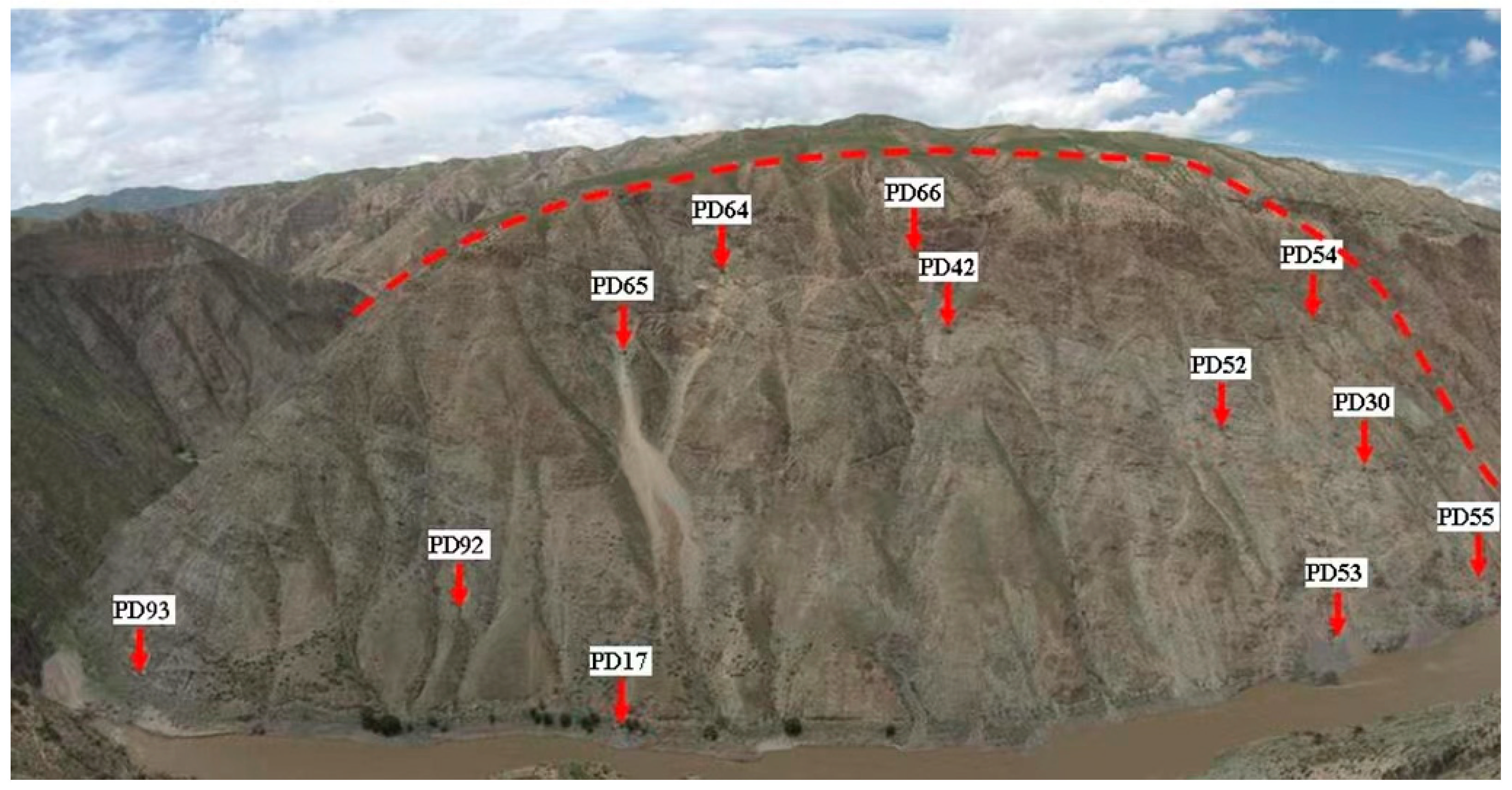
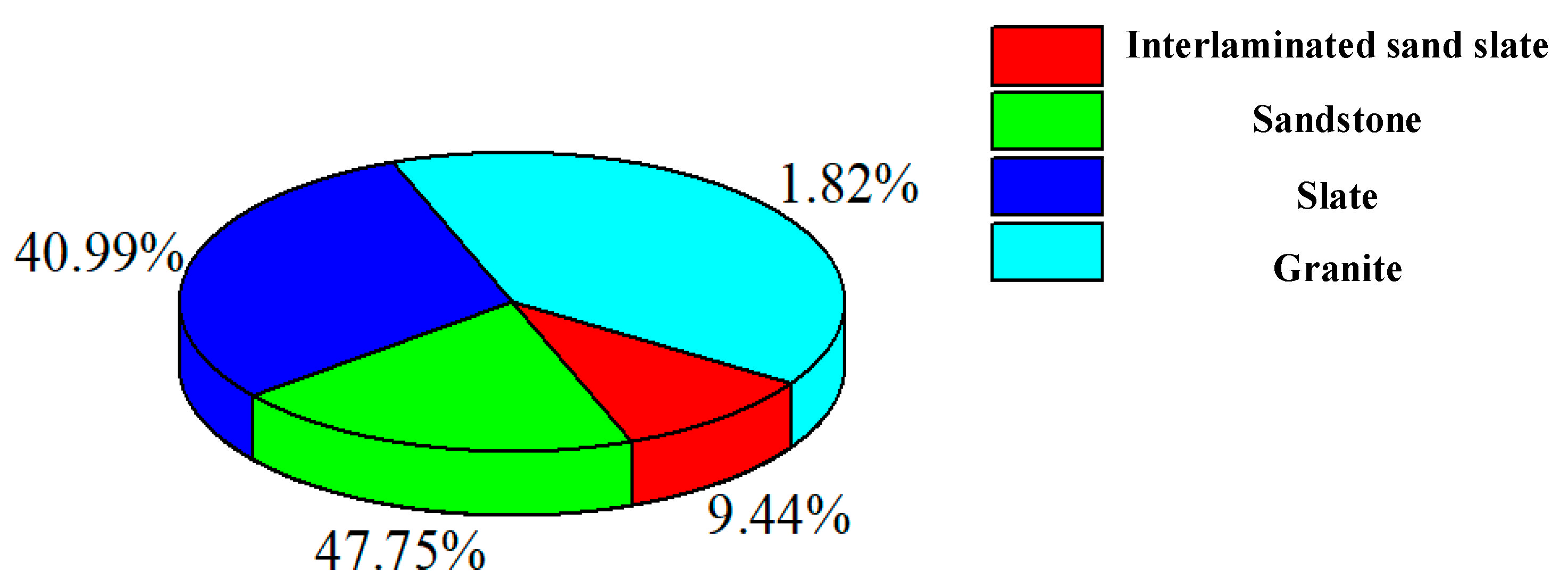





| PD17 | PD55 | ||||
| Chainage (m) | Lithology | Thickness (m) | Chainage (m) | Lithology | Thickness (m) |
| 0–26 | Quaternary system accumulation | 26 | 0–5.6 | Slate | 5.6 |
| 26–32.5 | Slate | 6.5 | 5.6–7.5 | Sandstone | 1.9 |
| 32.5–34.2 | Sandstone | 1.7 | 7.5–8.5 | Slate | 1 |
| 34.2–36.8 | Slate | 2.6 | 8.5–15.5 | Sandstone | 7 |
| 36.8–38.7 | Sandstone | 1.9 | 15.5–21 | Slate | 5.5 |
| 38.7–40 | Slate | 1.3 | 21–22.7 | Sandstone | 1.7 |
| 40–44.2 | Sandstone | 4.2 | 22.7–30.1 | Slate | 7.4 |
| 44.2–46.7 | Slate | 2.5 | 30.1–31.6 | Sandstone | 1.5 |
| 46.7–53 | Sandstone | 6.3 | 31.6–36 | Slate | 4.4 |
| 53–58 | Slate | 5 | 36–38.2 | Sandstone | 2.2 |
| 58–62.5 | Sandstone | 4.5 | 38.2–50.7 | Slate | 12.5 |
| PD42 | 50.7–53.6 | Sandstone | 2.9 | ||
| Chainage (m) | Lithology | Thickness (m) | 53.6–88.4 | Slate | 34.8 |
| 0–14 | Sandstone mixed with slate | 14 | 88.4–89 | Sandstone | 0.6 |
| 14–20.7 | Sandstone mixed with slate | 6.7 | 89–97.4 | Slate | 8.4 |
| 20.723.8 | Slate | 3.1 | 97.4–98.5 | Sandstone | 1.1 |
| 23.8–25.4 | Sandstone | 1.6 | 98.5–98.7 | Slate | 0.2 |
| 25.4–31.3 | Slate | 5.9 | 98.7–100.5 | Sandstone | 1.8 |
| 31.3–36.9 | Sandstone | 5.6 | 100.5–101.4 | Slate | 0.9 |
| 36.9–40 | Slate | 3.1 | 101.4–101.8 | Sandstone | 0.4 |
| 40–42.8 | Sandstone | 2.8 | 101.8–102 | Slate | 0.2 |
| 42.8–45.8 | Slate | 3 | 102–102.5 | Sandstone | 0.5 |
| 45.8–71 | Sandstone | 25.2 | 102.5–104.5 | Slate | 2 |
| 71–73.1 | Slate | 2.1 | 104.5–109.4 | Sandstone | 4.9 |
| 73.1–82.4 | Sandstone | 9.3 | 109.4–113.9 | Slate | 4.5 |
| 82.4–85.5 | Sandstone mixed with slate | 3.1 | 113.9–122.7 | Sandstone | 8.8 |
| 85.5–93 | Slate | 7.5 | 122.7–125.7 | Slate | 3 |
| 93–96.3 | Sandstone | 3.3 | 125.7–127.4 | Sandstone | 1.7 |
| 96.3–99.5 | Slate | 3.2 | PD66 | ||
| 99.5–117.2 | Sandstone | 17.7 | Chainage (m) | Lithology | Thickness (m) |
| PD65 | 0–6 m | Sandstone | 6 | ||
| Chainage (m) | Lithology | Thickness (m) | 6–18 m | Slate | 12 |
| 0–26.5 m | Sandstone | 26.5 | 18–27 m | Sandstone | 9 |
| 26.5–40 m | Slate | 13.5 | 27–33 m | Slate | 6 |
| 40–60 m | Sandstone | 20 | 33–46 m | Sandstone | 13 |
| 60–63 m | Slate | 3 | 46–50 m | Granite | 4 |
| 63–84 m | Sandstone | 21 | 50–56 m | Sandstone | 6 |
| 84–108 m | Slate | 24 | 56–64 m | Slate | 8 |
| 108–114 m | Sandstone | 6 | 64–70 m | Sandstone | 6 |
| 114–119 m | Slate | 5 | 70–73 m | Slate | 3 |
| 119–123 m | Sandstone | 4 | 73–87 m | Sandstone | 14 |
| 123–128 m | Slate | 5 | 87–103 m | Slate | 16 |
| 128–135 m | Sandstone | 7 | 103–107 m | Sandstone | 4 |
| 135–150 m | Granite | 15 | 107–113 m | Slate | 6 |
| 150–160 m | Slate | 10 | 113–131.5 m | Sandstone | 18.5 |
| 160–164 m | Sandstone | 4 | PD52 | ||
| PD64 | Chainage (m) | Lithology | Thickness (m) | ||
| Chainage (m) | Lithology | Thickness (m) | 0–12 m | Slate | 12 |
| 0–8 m | Slate | 8 | 12–45 m | Sandstone | 33 |
| 8–16 m | Sandstone | 8 | 45–48 m | Slate | 3 |
| 16–27 m | Slate | 11 | 48–51 m | Sandstone | 3 |
| 27–35.5 m | Sandstone | 8.5 | 51–60 m | Slate | 9 |
| 35.5–71 m | Slate | 35.5 | 60–67 m | Sandstone | 7 |
| 71–75 m | Sandstone | 4 | 67–83 m | Slate | 16 |
| 75–76.5 m | Slate | 1.5 | 83–88 m | Sandstone | 5 |
| 76.5–92 m | Sandstone | 15.5 | 88–131 m | Slate | 43 |
| 92–98 m | Slate | 6 | 131–138 m | Sandstone | 7 |
| 98–101 m | Sandstone | 3 | 138–150.6 m | Slate | 12.6 |
| 101–112.5 m | Slate | 11.5 | PD30 | ||
| 112.5–116 m | Sandstone | 3.5 | Chainage (m) | Lithology | Thickness (m) |
| 116–122 m | Slate | 6 | 0–56 m | Sandstone mixed with slate | 56 |
| 122–131 m | Sandstone | 9 | 56–89 m | Sandstone | 33 |
| 131–133 m | Slate | 2 | 89–93.5 m | Sandstone mixed with slate | 4.5 |
| 133–134 m | Sandstone | 1 | 93.5–136 m | Sandstone | 42.5 |
| 134–136 m | Slate | 2 | 136–150 | Sandstone mixed with slate | 14 |
| 136–148 m | Sandstone | 12 | 150–166 | Sandstone | 16 |
| Models | Points | RMSE | MAE | R2 |
|---|---|---|---|---|
| ARIMA | Point 1 | 1.148 | 0.820 | −0.309 |
| Point 2 | 0.390 | 0.312 | 0.396 | |
| Point 5 | 0.405 | 0.323 | 0.555 | |
| Point 8 | 0.419 | 0.330 | 0.658 | |
| Point 9 | 0.459 | 0.361 | 0.831 | |
| LSTM | Point 1 | 1.127 | 0.866 | −0.295 |
| Point 2 | 0.367 | 0.314 | 0.542 | |
| Point 5 | 0.375 | 0.317 | 0.678 | |
| Point 8 | 0.341 | 0.283 | 0.792 | |
| Point 9 | 0.332 | 0.260 | 0.916 | |
| LSTM-ARIMA | Point 1 | 1.165 | 0.894 | −0.324 |
| Point 2 | 0.347 | 0.289 | 0.617 | |
| Point 5 | 0.355 | 0.272 | 0.738 | |
| Point 8 | 0.336 | 0.261 | 0.806 | |
| Point 9 | 0.333 | 0.258 | 0.919 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Li, S.; Li, B. Deformation Prediction of Cihaxia Landslide Using InSAR and Deep Learning. Water 2022, 14, 3990. https://doi.org/10.3390/w14243990
Wang Y, Li S, Li B. Deformation Prediction of Cihaxia Landslide Using InSAR and Deep Learning. Water. 2022; 14(24):3990. https://doi.org/10.3390/w14243990
Chicago/Turabian StyleWang, Yuxiao, Shouyi Li, and Bin Li. 2022. "Deformation Prediction of Cihaxia Landslide Using InSAR and Deep Learning" Water 14, no. 24: 3990. https://doi.org/10.3390/w14243990
APA StyleWang, Y., Li, S., & Li, B. (2022). Deformation Prediction of Cihaxia Landslide Using InSAR and Deep Learning. Water, 14(24), 3990. https://doi.org/10.3390/w14243990





