Saturated Hydraulic Conductivity Estimation Using Artificial Intelligence Techniques: A Case Study for Calcareous Alluvial Soils in a Semi-Arid Region
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area and Data
2.2. Machine Learning Methods
2.2.1. Artificial Neural Networks
2.2.2. Deep Learning
2.2.3. Decision Tree
2.2.4. Random Forest
2.3. Selected Inputs and Model Development
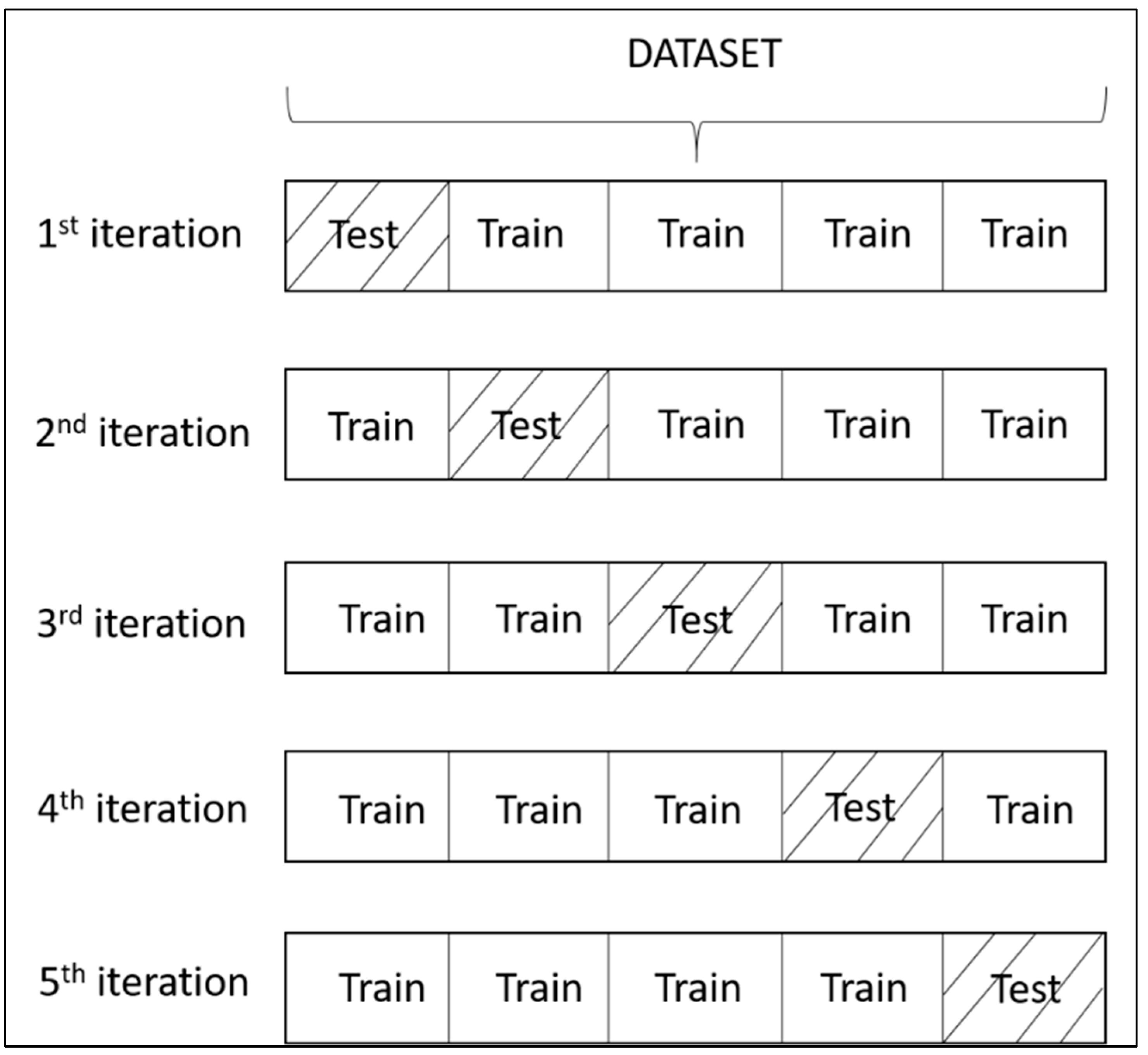
2.4. Performance Evaluation
3. Results
3.1. Adjustment of Input Variables
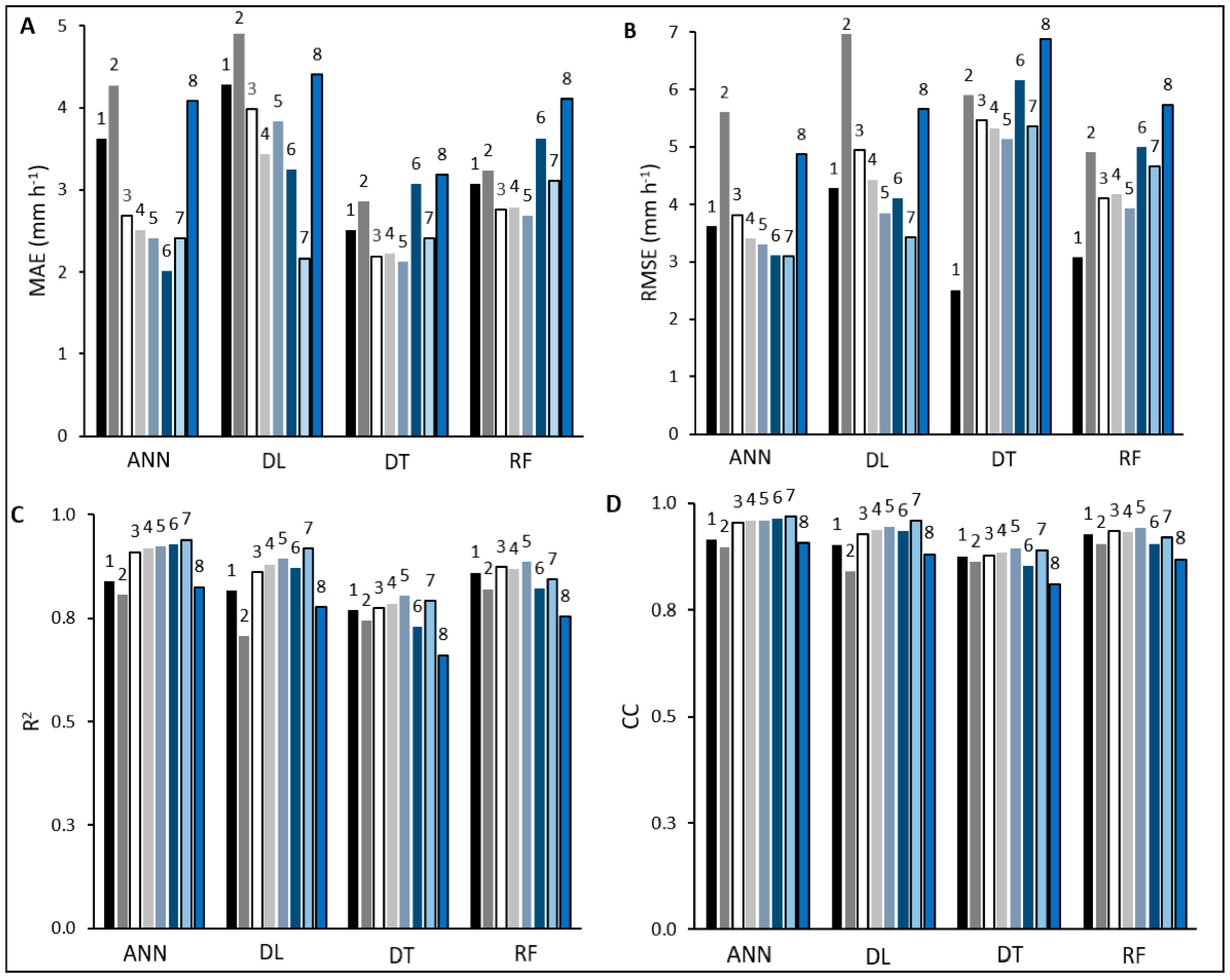
3.2. Performance of Machine Learning Methods
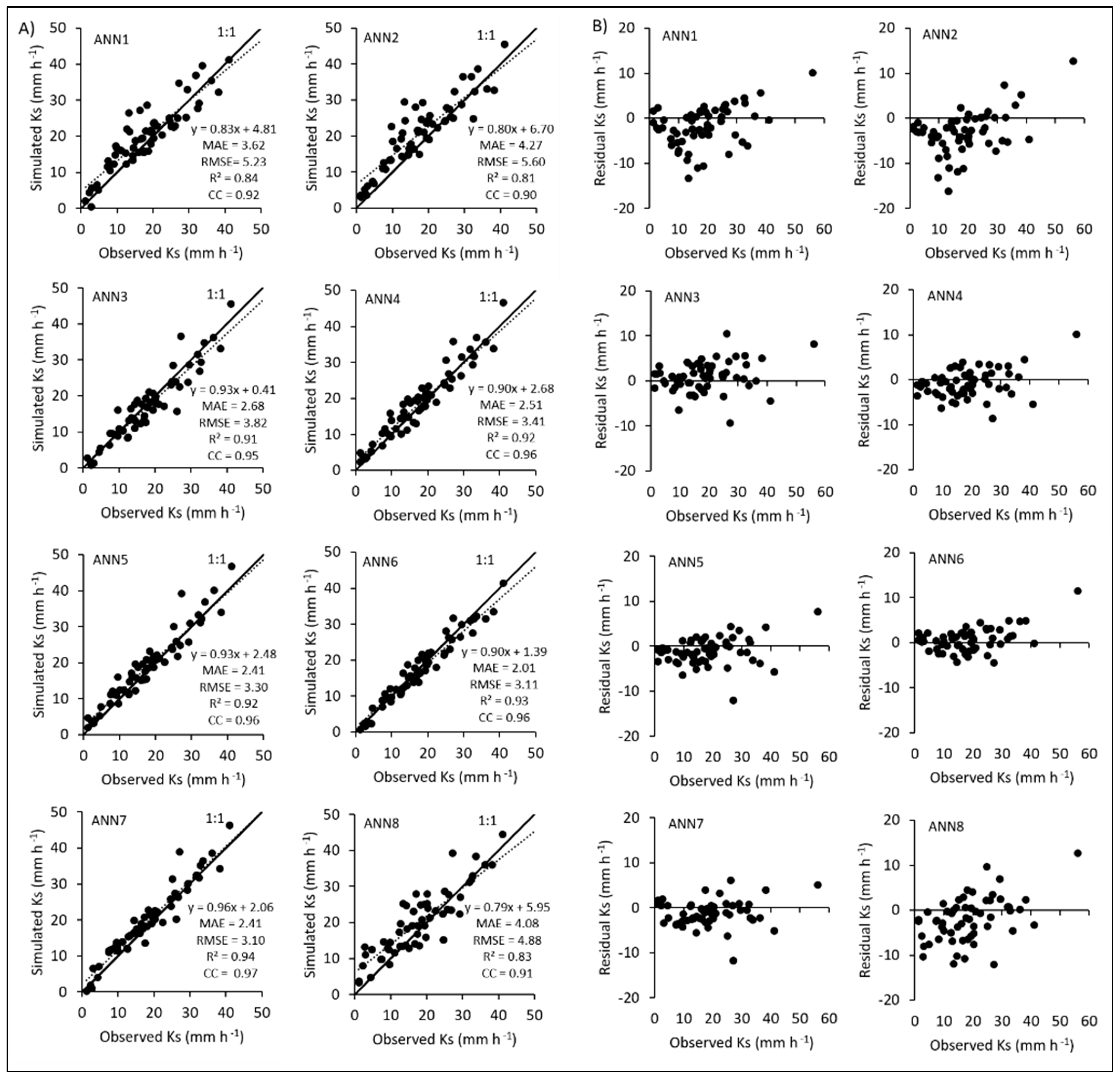
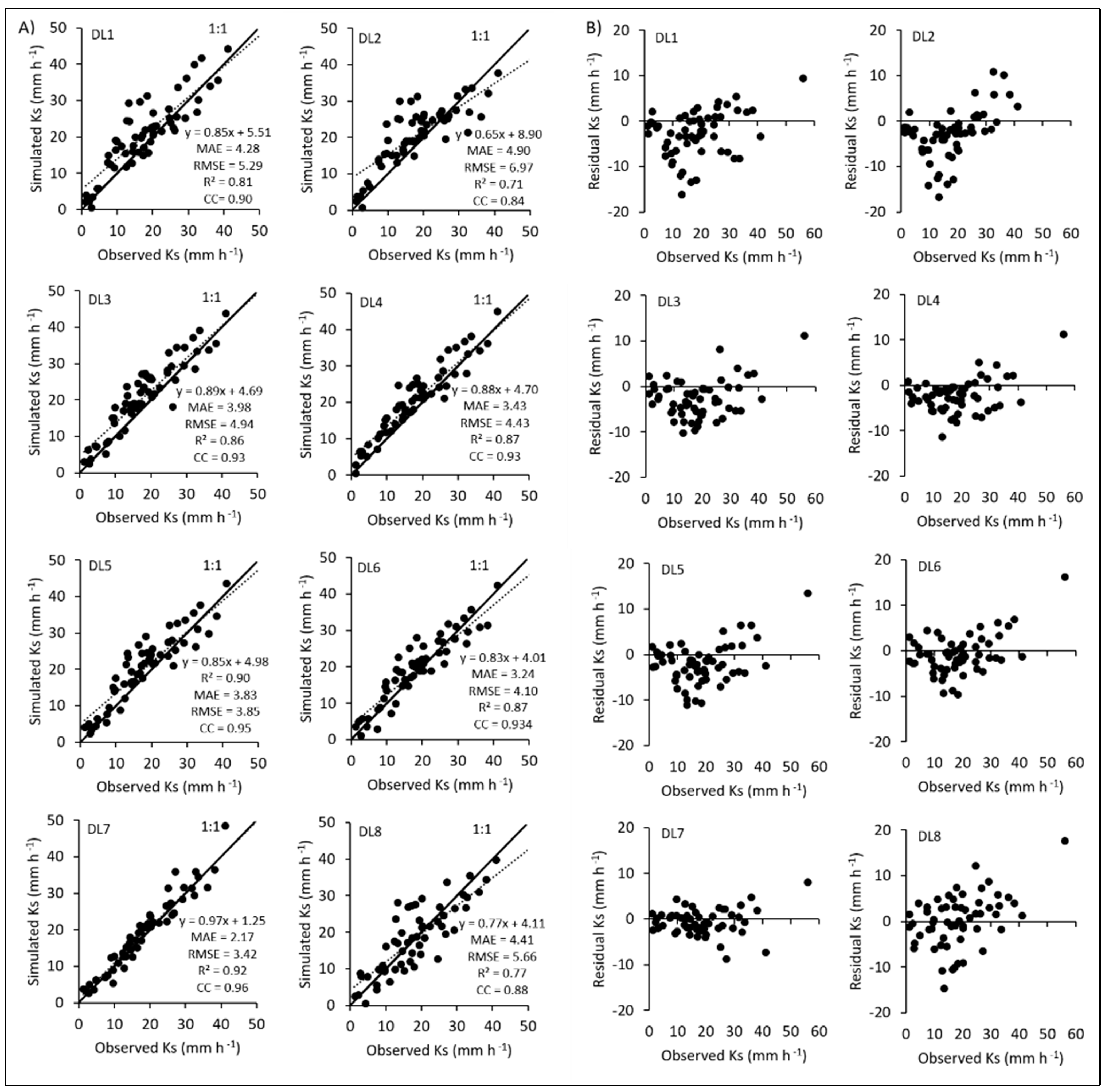
3.3. Performances of Neural-Network-Based Machine Learning Methods
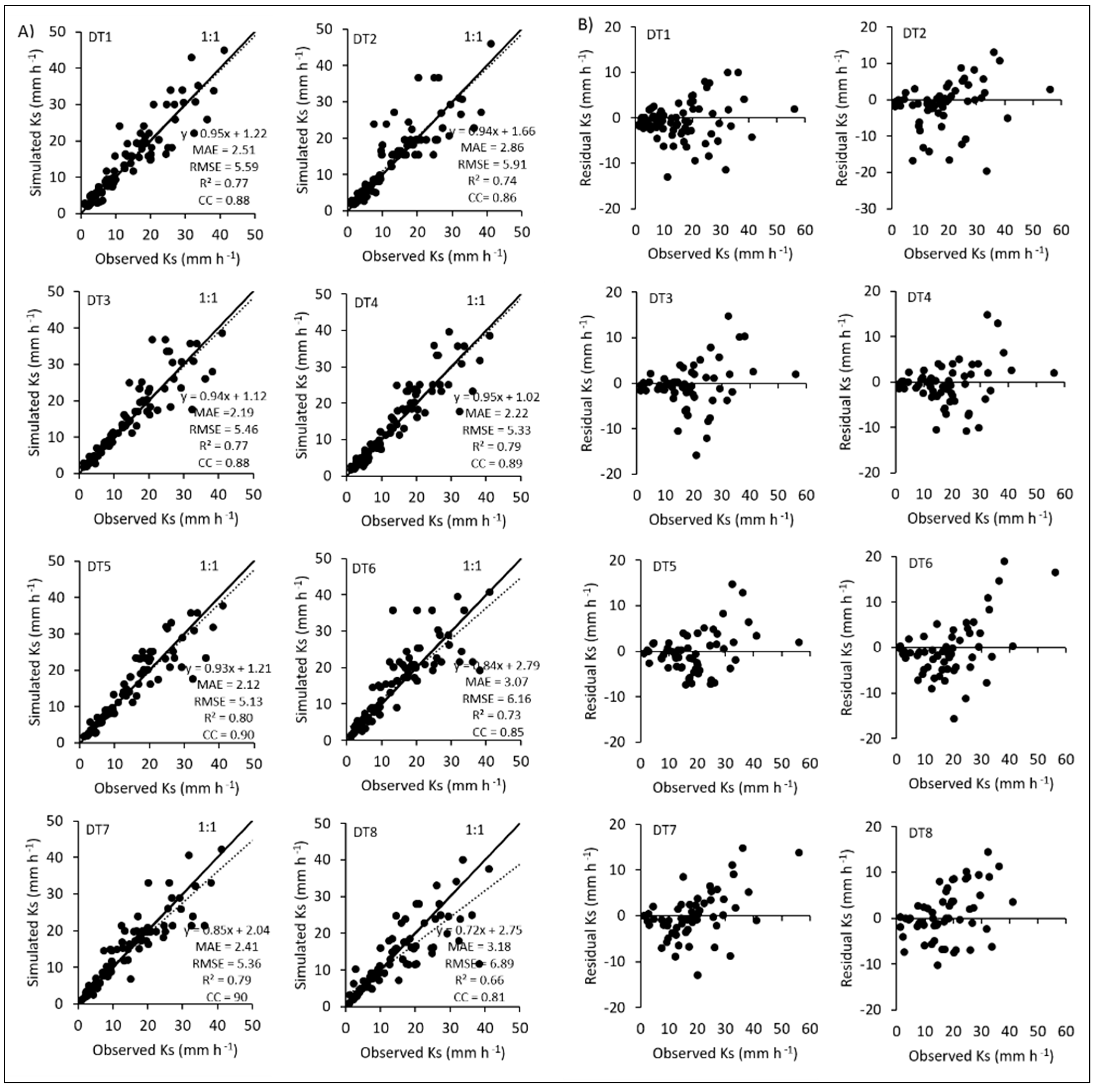
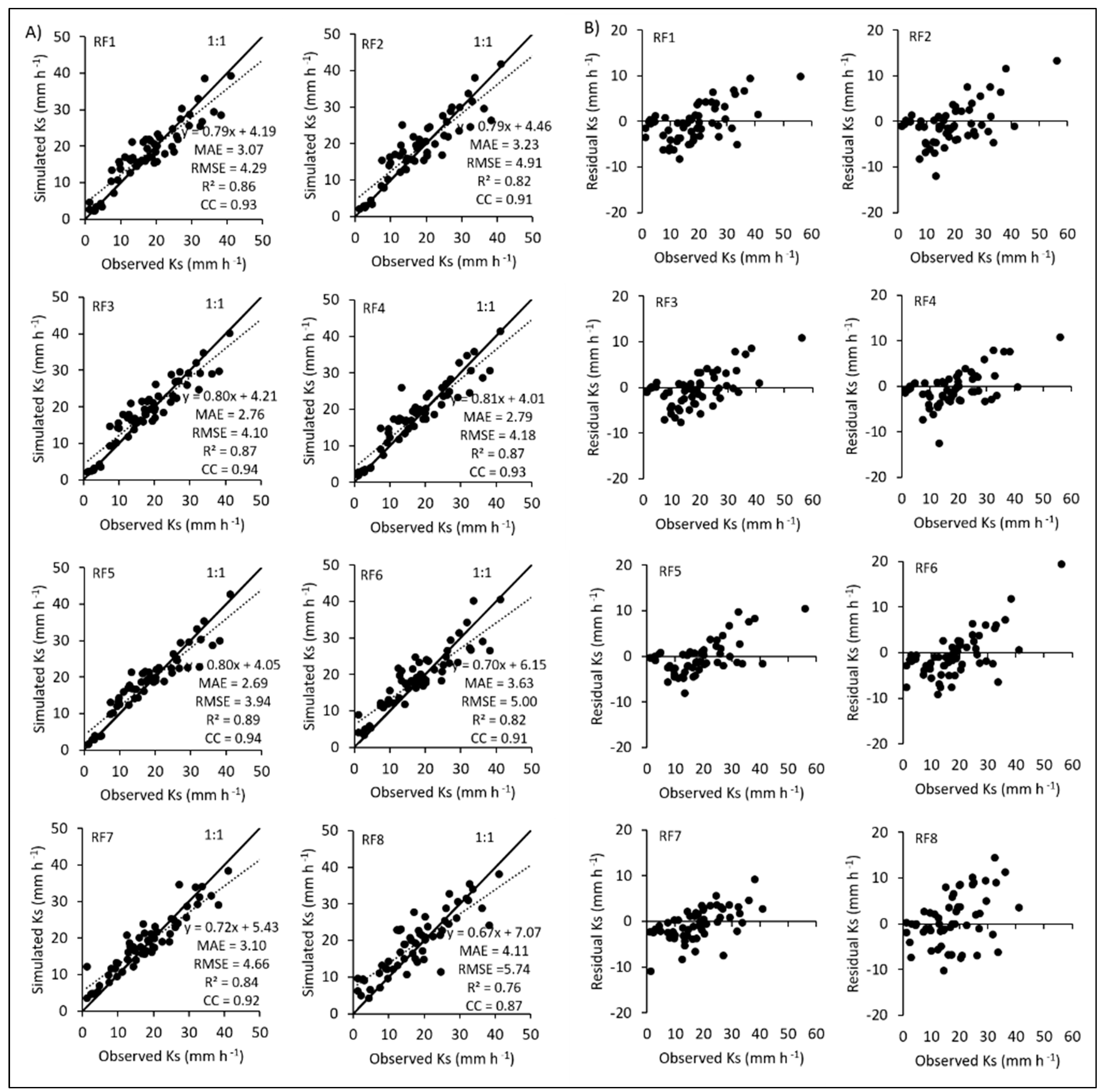
3.4. Performances of Tree-Based Machine Learning Methods
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Stenitzer, E.; Diestel, H.; Zenker, T.; Schwartengräber, R. Assessment of Capillary Rise from Shallow Groundwater by the Simulation Model SIMWASER Using Either Estimated Pedotransfer Functions or Measured Hydraulic Parameters. Water Resour. Manag. 2007, 21, 1567–1584. [Google Scholar] [CrossRef]
- Zhang, Y.; Schaap, M.G. Estimation of saturated hydraulic conductivity with pedotransfer functions: A review. J. Hydrol. 2019, 575, 1011–1030. [Google Scholar] [CrossRef]
- Ghosh, B.; Pekkat, S. An Appraisal on the Interpolation Methods Used for Predicting Spatial Variability of Field Hydraulic Conductivity. Water Resour. Manag. 2019, 33, 2175–2190. [Google Scholar] [CrossRef]
- Tayfur, G.; Nadiri, A.A.; Moghaddam, A.A. Supervised Intelligent Committee Machine Method for Hydraulic Conductivity Estimation. Water Resour. Manag. 2014, 28, 1173–1184. [Google Scholar] [CrossRef]
- Tzimopoulos, C.D.; Sakellariou-Makrantonaki, M. A new analytical model to predict the hydraulic conductivity of unsaturated soils. Water Resour. Manag. 1996, 10, 397–414. [Google Scholar] [CrossRef]
- van Genuchten, M.T. A Closed-form Equation for Predicting the Hydraulic Conductivity of Unsaturated Soils. Soil Sci. Soc. Am. J. 1980, 44, 892–898. [Google Scholar] [CrossRef]
- Brooks, R.H.; Corey, A.T. Hydraulic properties of porous media and their relation to drainage design. Trans. ASAE 1964, 7, 26–28. [Google Scholar]
- Rawls, J.W.; Gimenez, D.; Grossman, R. Use of soil texture, bulk density, and slope of the water retention curve to predict saturated hydraulic conductivity. Trans. ASAE 1998, 41, 983–988. [Google Scholar] [CrossRef]
- Mermoud, A.; Xu, D. Comparative analysis of three methods to generate soil hydraulic functions. Soil Tillage Res. 2006, 87, 89–100. [Google Scholar] [CrossRef]
- Rawls, W.J.; Brakensiek, D.L. Estimation of Soil Water Retention and Hydraulic Properties. In Unsaturated Flow in Hydrologic Modeling: Theory and Practice; Morel-Seytoux, H.J., Ed.; Springer: Dordrecht, The Netherlands, 1989; pp. 275–300. [Google Scholar] [CrossRef]
- Saxton, K.E. Estimating Generalized Soil-water Characteristics from Texture. Soil Sci. Soc. Am. J. 1986, 50, 1031–1036. [Google Scholar] [CrossRef]
- Saxton, K.E.; Rawls, W.J. Soil Water Characteristic Estimates by Texture and Organic Matter for Hydrologic Solutions. Soil Sci. Soc. Am. J. 2006, 70, 1569–1578. [Google Scholar] [CrossRef]
- Wagner, B.; Tarnawski, V.R.; Stöckl, M. Evaluation of pedotransfer functions predicting hydraulic properties of soils and deeper sediments. J. Plant Nutr. Soil Sci. 2004, 167, 236–245. [Google Scholar] [CrossRef]
- Ahuja, L.R.; Naney, J.W.; Green, R.E.; Nielsen, D.R. Macroporosity to Characterize Spatial Variability of Hydraulic Conductivity and Effects of Land Management. Soil Sci. Soc. Am. 1984, 48, 699–702. [Google Scholar] [CrossRef]
- Bourazanis, G.; Katsileros, A.; Kosmas, C.; Kerkides, P. The effect of treated municipal wastewater and fresh water on saturated hydraulic conductivity of a clay-loamy soil. Water Resour. Manag. 2016, 30, 2867–2880. [Google Scholar] [CrossRef]
- Cosby, B.J.; Hornberger, G.M.; Clapp, R.B.; Ginn, T.R. A Statistical Exploration of the Relationships of Soil Moisture Characteristics to the Physical Properties of Soils. Water Resour. Res. 1984, 20, 682–690. [Google Scholar] [CrossRef]
- Van Genuchten, M.; Leij, F.; Yates, S. The RETC Code for Quantifying the Hydraulic Functions of Unsaturated Soils; US Salinity Laboratory US Department of Agriculture, Agricultural Research Service: Riverside, CA, USA, 1991. [Google Scholar]
- Klopp, H.W.; Arriaga, F.A.; Daigh, A.L.M.; Bleam, W.F. Development of functions to predict soil hydraulic properties that account for solution sodicity and salinity. Catena 2021, 204, 105389. [Google Scholar] [CrossRef]
- Minasny, B.; Hopmans, J.W.; Harter, T.; Eching, S.O.; Tuli, A.; Denton, M.A. Neural Networks Prediction of Soil Hydraulic Functions for Alluvial Soils Using Multistep Outflow Data. Soil Sci. Soc. Am. J. 2004, 68, 417–429. [Google Scholar] [CrossRef]
- Rogiers, B.; Mallants, D.; Batelaan, O.; Gedeon, M.; Huysmans, M.; Dassargues, A. Estimation of Hydraulic Conductivity and Its Uncertainty from Grain-Size Data Using GLUE and Artificial Neural Networks. Math. Geosci. 2012, 44, 739–763. [Google Scholar] [CrossRef]
- Zuo, Y.; He, K. Evaluation and Development of Pedo-Transfer Functions for Predicting Soil Saturated Hydraulic Conductivity in the Alpine Frigid Hilly Region of Qinghai Province. Agronomy 2021, 11, 1581. [Google Scholar] [CrossRef]
- Araya, S.N.; Ghezzehei, T.A. Using Machine Learning for Prediction of Saturated Hydraulic Conductivity and Its Sensitivity to Soil Structural Perturbations. Water Resour. Res. 2019, 55, 5715–5737. [Google Scholar] [CrossRef]
- Naganna, S.R.; Deka, P.C. Artificial intelligence approaches for spatial modeling of streambed hydraulic conductivity. Acta Geophys. 2019, 67, 891–903. [Google Scholar] [CrossRef]
- Sihag, P.; Esmaeilbeiki, F.; Singh, B.; Ebtehaj, I.; Bonakdari, H. Modeling unsaturated hydraulic conductivity by hybrid soft computing techniques. Soft Comput. 2019, 23, 12897–12910. [Google Scholar] [CrossRef]
- Kashani, H.M.; Ghorbani, M.A.; Shahabi, M.; Naganna, S.R.; Diop, L. Multiple AI model integration strategy—Application to saturated hydraulic conductivity prediction from easily available soil properties. Soil Tillage Res. 2020, 196, 104449. [Google Scholar] [CrossRef]
- Kalumba, M.; Bamps, B.; Nyambe, I.; Dondeyne, S.; van Orshoven, J. Development and functional evaluation of pedotransfer functions for soil hydraulic properties for the Zambezi River Basin. Eur. J. Soil Sci. 2021, 72, 1559–1574. [Google Scholar] [CrossRef]
- Morshedi, A.; Sameni, A.M. Hydraulic conductivity of calcareous soils as affected by salinity and sodicity. I. Effect of concentration and composition of leaching solution and type and amount of clay minerals of tested soils. Commun. Soil Sci. Plant Anal. 2000, 31, 51–67. [Google Scholar] [CrossRef]
- Amer, A.M.M.; Logsdon, S.D.; Davis, D. Prediction of hydraulic conductivity as related to pore size distribution in unsaturated soils. Soil Sci. 2009, 174, 508–515. [Google Scholar] [CrossRef]
- Fernández-Ugalde, O.; Virto, I.; Bescansa, P.; Imaz, M.J.; Enrique, A.; Karlen, D.L. No-tillage improvement of soil physical quality in calcareous, degradation-prone, semiarid soils. Soil Tillage Res. 2009, 106, 29–35. [Google Scholar] [CrossRef]
- Khodaverdiloo, H.; Homaee, M.; van Genuchten, M.T.; Dashtaki, S.G. Deriving and validating pedotransfer functions for some calcareous soils. J. Hydrol. 2011, 399, 93–99. [Google Scholar] [CrossRef]
- Kabir, E.B.; Bashari, H.; Bassiri, M.; Mosaddeghi, M.R. Effects of land-use/cover change on soil hydraulic properties and pore characteristics in a semi-arid region of central Iran. Soil Tillage Res. 2020, 197, 104478. [Google Scholar] [CrossRef]
- Mozaffari, H.; Moosavi, A.A.; Sepaskhah, A.R. Land use-dependent variation of near-saturated and saturated hydraulic properties in calcareous soils. Environ. Earth Sci. 2021, 80, 769. [Google Scholar] [CrossRef]
- Şeker, C.; Özaytekin, H.H.; Gümüş, İ.; Karaarslan, E.; Ummahan, K. Çumra Ovasında Önemli ve Yaygın Üç Toprak Serisinin Toprak Kalite İndislerinin Belirlenmesi, Proje Raporu; Proje No: 112O314; Program Kodu: Konya, Turkey, 2016. (In Turkish) [Google Scholar]
- Yamaç, S.S.; Şeker, C.; Negiş, H. Evaluation of machine learning methods to predict soil moisture constants with different combinations of soil input data for calcareous soils in a semi arid area. Agric. Water Manag. 2020, 234, 106121. [Google Scholar] [CrossRef]
- Kottek, M.; Grieser, J.; Beck, C.; Rudolf, B.; Rubel, F. World map of the Köppen-Geiger climate classification updated. Meteorol. Z. 2006, 15, 259–263. [Google Scholar] [CrossRef] [PubMed]
- MGM. Meteoroloji Genel Müdürlüğü. 2015. Available online: https://www.mgm.gov.tr/ (accessed on 15 October 2022).
- Bahçeci, İ.; Dinç, N.; Tarı, A.F.; Ağar, A.İ.; Sönmez, B. Water and salt balance studies, using SaltMod, to improve subsurface drainage design in the Konya–Çumra Plain, Turkey. Agric. Water Manag. 2006, 85, 261–271. [Google Scholar] [CrossRef]
- Driessen, P.M.; Meester, T.D. Soils of the Çumra Area, Turkey; Pudoc: Wageningen, The Netherlands, 1969. [Google Scholar]
- Topraksu. Konya Kapalı Havzası Toprakları; Toprak Etüdleri ve Haritalama Dairesi Topak Etüdleri Fen Heyeti Md; Ankara Yayın: Ankara, Turkeys, 1978; p. 288. [Google Scholar]
- Gee, G.W.; Bauder, J.; Klute, A. Methods of Soil Analysis, Part 1, Physical and Mineralogical Methods; Soil Science Society of America Book Series; American Society of Agronomy, Inc. and Soil Science Society of America, Inc.: Madison, WI, USA, 1986; pp. 383–411. [Google Scholar]
- Blake, G.R.; Hartge, K.H. Bulk density. In Methods of Soil Analysis, Part 1-Physical and Mineralogical Methods, 2nd ed.; Klute, A., Ed.; Agronomy Monograph 9; American Society of Agronomy-Soil Science Society of America: Madison, WI, USA, 1986; Volume 9, pp. 363–382. [Google Scholar]
- Blake, G.R.; Hartge, K.H. Particle density. In Methods of Soil Analysis, Part 1-Physical and Mineralogical Methods, 2nd ed.; Klute, A., Ed.; Agronomy Monograph 9; American Society of Agronomy-Soil Science Society of America: Madison, WI, USA, 1986; Volume 9, pp. 377–382. [Google Scholar]
- Cassel, D.K.; Nielsen, D.R. Field Capacity and Available Water Capacity. In Methods of Soil Analysis; AWE International: Dorset, UK, 1986; pp. 901–926. [Google Scholar] [CrossRef]
- Moebius-Clune, B.; Moebius-Clune, D.; Gugino, B.; Idowu, O.; Schindelbeck, R.; Ristow, A.; van Es, H.; Thies, J.; Shayler, H.; McBride, M.; et al. Comprehensive Assessment of Soil Health—The Cornell Framework, 3.2 ed.; Cornell University: Ithaca, NY, USA, 2016. [Google Scholar]
- Mclean, E.O. Soil pH and Lime Requirement. In Methods of Soil Analysis; AWE International: Dorset, UK, 1983; pp. 199–224. [Google Scholar] [CrossRef]
- Wright, A.F.; Bailey, J.S. Organic carbon, total carbon, and total nitrogen determinations in soils of variable calcium carbonate contents using a Leco CN-2000 dry combustion analyzer. Commun. Soil Sci. Plant. Anal. 2001, 32, 3243–3258. [Google Scholar] [CrossRef]
- Ferreira, L.B.; da Cunha, F.F.; de Oliveira, R.A.; Fernandes Filho, E.I. Estimation of reference evapotranspiration in Brazil with limited meteorological data using ANN and SVM—A new approach. J. Hydrol. 2019, 572, 556–570. [Google Scholar] [CrossRef]
- Gurney, K. An Introduction to Neural Networks; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Reis, M.M.; da Silva, A.J.; Zullo Junior, J.; Tuffi Santos, L.D.; Azevedo, A.M.; Lopes, É.M.G. Empirical and learning machine approaches to estimating reference evapotranspiration based on temperature data. Comput. Electron. Agric. 2019, 165, 104937. [Google Scholar] [CrossRef]
- Yamaç, S.S. Reference evapotranspiration estimation with kNN and ANN models using different climate input combinations in the semi-arid environment. J. Agric. Sci. 2021, 27, 129–137. [Google Scholar]
- Dechter, R. Learning while searching in constraint-satisfaction problems. In Proceedings of the fifth National Conference on Artificial Intelligence (AAAI-86), Philadelphia, PA, USA, 11–15 August 1986; pp. 178–185. [Google Scholar]
- de Lucas, P.O.E.; Alves, M.A.; de Silva, P.C.L.E.; Guimarães, F.G. Reference evapotranspiration time series forecasting with ensemble of convolutional neural networks. Comput. Electron. Agric. 2020, 177, 105700. [Google Scholar] [CrossRef]
- Kamilaris, A.; Prenafeta-Boldú, F.X. Deep learning in agriculture: A survey. Comput. Electron. Agric. 2018, 147, 70–90. [Google Scholar] [CrossRef]
- Saggi, M.K.; Jain, S. Reference evapotranspiration estimation and modeling of the Punjab Northern India using deep learning. Comput. Electron. Agric. 2019, 156, 387–398. [Google Scholar] [CrossRef]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef] [PubMed]
- Özgür, A.; Yamaç, S.S. Modelling of Daily Reference Evapotranspiration Using Deep Neural Network in Different Climates. arXiv 2020, arXiv:abs/200601760. Available online: https://arxivorg/abs/200601760 (accessed on 15 October 2022).
- Liu, S.; McGree, J.; Ge, Z.; Xie, Y. 2—Classification methods. In Computational and Statistical Methods for Analysing Big Data with Applications; Liu, S., McGree, J., Ge, Z., Xie, Y., Eds.; Academic Press: Cambridge, MA, USA, 2016. [Google Scholar]
- Safavian, S.R.; Landgrebe, D. A survey of decision tree classifier methodology. IEEE Trans. Syst. Man. Cybern. 1991, 21, 660–674. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Yamaç, S.S. Artificial intelligence methods reliably predict crop evapotranspiration with different combinations of meteorological data for sugar beet in a semiarid area. Agric. Water Manag. 2021, 254, 106968. [Google Scholar] [CrossRef]
- Gocić, M.; Motamedi, S.; Shamshirband, S.; Petković, D.; Ch, S.; Hashim, R.; Arif, M. Soft computing approaches for forecasting reference evapotranspiration. Comput. Electron. Agric. 2015, 113, 164–173. [Google Scholar] [CrossRef]
- Arya, L.M.; Leij, F.J.; Shouse, P.J.; van Genuchten, M.T. Relationship between the hydraulic conductivity function and the particle-size distribution. Soil Sci. Soc. Am. 1999, 67, 373. [Google Scholar] [CrossRef]
- Frenkel, H.; Levy, G.; Fey, M. Clay dispersion and hydraulic conductivity of clay-sand mixtures as affected by the addition of various anions. Clays Clay 1992, 40, 515–521. [Google Scholar] [CrossRef]
- Park, E.-J.; Smucker, A.J.M. Saturated Hydraulic Conductivity and Porosity within Macroaggregates Modified by Tillage. Soil Sci. Soc. Am. J. 2005, 69, 38–45. [Google Scholar] [CrossRef]
- Lu, J. Chapter 6—Identification of Forensic Information from Existing Conventional Site-Investigation Data. In Introduction to Environmental Forensics, 3rd ed.; Murphy, B.L., Morrison, R.D., Eds.; Academic Press: San Diego, CA, USA, 2015; pp. 149–164. [Google Scholar] [CrossRef]
- Shaykewich, C.F.; Zwarich, M.A. Relationships between soil physical constants and soil physical components of some manitoba soils. Can. J. Soil Sci. 1968, 48, 199–204. [Google Scholar] [CrossRef]
- Abdulwahhab, Q. Determination of the Effects of Lime, Organic Matter and Soil Compaction on Some Hydrodynamic Properties of Different Textured Soils. Ph.D. Thesis, Department of Soil Science and Plant Nutrition, Institute of Science, Selcuk University, Konya, Turkey, 2020. [Google Scholar]
- Agyare, W.A.; Park, S.J.; Vlek, P.L.G. Artificial Neural Network Estimation of Saturated Hydraulic ConductivityAll rights reserved. No part of this periodical may be reproduced or transmitted in any form or by any means, electronic or mechanical, including photocopying, recording, or any information storage and retrieval system, without permission in writing from the publisher. Vadose Zone J. 2007, 6, 423–431. [Google Scholar] [CrossRef]
- Parasuraman, K.; Elshorbagy, A.; Si, B.C. Estimating Saturated Hydraulic Conductivity In Spatially Variable Fields Using Neural Network Ensembles. Soil Sci. Soc. Am. J. 2006, 70, 1851–1859. [Google Scholar] [CrossRef]


| Parameters | Abbreviations | Units | Methods | References |
|---|---|---|---|---|
| Soil texture (Clay, Silt, Sand) | - | % | Bouyoucos hydrometer method | [40] |
| Bulk density | Pb | g cm−3 | Core method (50 * 51 mm core samples) | [41] |
| Particle density | Ps | g cm−3 | Pycnometer method | [42] |
| Field capacity | FC | cm3 cm−3 | Pressure plate apparatus at 0.33 bars | [43] |
| Permanent wilting point | PWP | cm3 cm−3 | Pressure plate apparatus at 15 bars | |
| Available water capacity | AWC | cm3 cm−3 | ||
| Aggregate stability | AS | % | Cornell Sprinkle Infiltrometer | [44] |
| Penetration resistance | PR | PSI | Digital penetrometer (Eijkelkamp) | |
| Lime content | L | % | Scheibler Calcimeter 1:3 acid/water | [45] |
| Organic carbon | OC | % | Dry combustion C and N analyzer | [46] |
| Sand | Silt | Clay | Pb | FC | PWP | P | EP | AS | PR | Lime | OC | Ks1 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Silt | −0.288 *** | ||||||||||||
| Clay | −0.923 *** | −0.104 ns | |||||||||||
| Pb | 0.471 *** | −0.161 *** | −0.424 *** | ||||||||||
| FC | −0.809 *** | 0.133 ns | 0.787 *** | −0.504 *** | |||||||||
| PWP | −0.772 *** | 0.015 ns | 0.796 *** | −0.496 *** | 0.893 *** | ||||||||
| P | −0.487 *** | 0.143 * | 0.448 *** | −0.974 *** | 0.510 *** | 0.496 *** | |||||||
| MP | 0.273 *** | −0.001 ns | −0.283 *** | −0.565 *** | −0.414 *** | −0.321 *** | 0.563 *** | ||||||
| AS | −0.385 *** | 0.122 * | 0.350 *** | −0.412 *** | 0.211 *** | 0.219 *** | 0.395 *** | 0.212 *** | |||||
| PR | 0.335 *** | −0.260 *** | −0.244 *** | 0.464 *** | −0.392 *** | −0.361 *** | −0.459 *** | −0.106 ns | −0.186 *** | ||||
| Lime | −0.542 *** | −0.138 * | 0.619 *** | −0.080 ns | 0.263 *** | 0.320 *** | 0.122 * | −0.138 * | 0.206 *** | 0.069 ns | |||
| OC | −0.398 *** | −0.059 ns | 0.436 *** | −0.185 *** | 0.253 *** | 0.369 *** | 0.196 *** | −0.034 ns | 0.273 *** | 0.001 ns | 0.341 *** | ||
| Ks1 | 0.391 *** | −0.187 *** | −0.331 *** | −0.131 * | −0.313 *** | −0.237 *** | 0.113 ns | 0.430 *** | −0.080 ns | −0.036 ns | −0.302 *** | −0.195 *** | |
| Ks2 | 0.548 *** | −0.392 *** | −0.411 *** | −0.255 *** | −0.537 *** | −0.386 *** | 0.226 *** | 0.788 *** | 0.009 ns | 0.059 ns | −0.223 *** | −0.061 ns | 0.559 *** |
| Combination Numbers | Machine Learning Models | Input Combinations | |||
|---|---|---|---|---|---|
| 1 | ANN1 | DL1 | DT1 | RF1 | Sand, EP |
| 2 | ANN2 | DL2 | DT2 | RF2 | Clay, EP |
| 3 | ANN3 | DL3 | DT3 | RF3 | Sand, Clay, EP |
| 4 | ANN4 | DL4 | DT4 | RF4 | Sand, Clay, EP, FC |
| 5 | ANN5 | DL5 | DT5 | RF5 | Sand, Clay, EP, Pb |
| 6 | ANN6 | DL6 | DT6 | RF6 | Sand, Clay, EP, FC, Pb, PWP, P, Lime |
| 7 | ANN7 | DL7 | DT7 | RF7 | Sand, Silt, Clay, FC, Pb, PWP |
| 8 | ANN8 | DL8 | DT8 | RF8 | Sand, Clay, Pb, OC |
| Sand (%) | Silt (%) | Clay (%) | Pb (Mg m−3) | FC (cm3 cm−3) | PWP (cm3 cm−3) | P (cm3 cm−3) | EP (cm3 cm−3) | AS (%) | PR (PSI) | Lime (%) | OC (%) | Ks1 (mm h−1) | Ks2 (mm h−1) | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Maximum | 66.40 | 40.00 | 79.57 | 1.75 | 0.42 | 0.29 | 0.59 | 0.31 | 61.01 | 434 | 41.50 | 2.30 | 24.45 | 58.91 |
| Minimum | 5.43 | 11.60 | 21.10 | 1.09 | 0.14 | 0.09 | 0.35 | 0.00 | 3.15 | 60 | 6.47 | 0.29 | 0.00 | 0.88 |
| Mean | 28.24 | 24.41 | 47.36 | 1.31 | 0.28 | 0.17 | 0.51 | 0.15 | 21.74 | 198 | 15.96 | 0.85 | 5.083 | 17.21 |
| Standard deviation | 13.91 | 5.38 | 13.39 | 0.12 | 0.05 | 0.05 | 0.04 | 0.07 | 11.04 | 70.16 | 6.79 | 0.30 | 5.095 | 11.35 |
| Variation coefficient | 49.25 | 22.05 | 28.27 | 9.32 | 18.82 | 26.26 | 8.79 | 49.34 | 50.78 | 35.49 | 42.51 | 35.35 | 100.24 | 65.93 |
| Skewness | 0.59 | −0.06 | 0.10 | 0.57 | −0.06 | 0.32 | −0.57 | −0.13 | 0.58 | 0.71 | 0.66 | 1.38 | 1.50 | 0.86 |
| Kurtosis | −0.52 | −0.23 | −0.66 | 0.12 | −0.57 | −0.63 | 0.08 | −0.88 | −0.05 | 0.12 | 0.12 | 3.37 | 1.94 | 0.68 |
| Method | MAE | RMSE | R2 | CC |
|---|---|---|---|---|
| (mm h−1) | (mm h−1) | |||
| ANN1 | 3.617 | 5.230 | 0.838 | 0.915 |
| ANN2 | 4.272 | 5.603 | 0.806 | 0.897 |
| ANN3 | 2.684 | 3.817 | 0.910 | 0.954 |
| ANN4 | 2.512 | 3.411 | 0.920 | 0.959 |
| ANN5 | 2.411 | 3.301 | 0.924 | 0.961 |
| ANN6 | 2.015 | 3.109 | 0.929 | 0.964 |
| ANN7 | 2.407 | 3.096 | 0.940 | 0.970 |
| ANN8 | 4.081 | 4.876 | 0.825 | 0.908 |
| DL1 | 4.283 | 5.285 | 0.816 | 0.903 |
| DL2 | 4.898 | 6.965 | 0.707 | 0.840 |
| DL3 | 3.977 | 4.936 | 0.861 | 0.928 |
| DL4 | 3.427 | 4.428 | 0.880 | 0.938 |
| DL5 | 3.833 | 3.853 | 0.894 | 0.945 |
| DL6 | 3.244 | 4.099 | 0.872 | 0.934 |
| DL7 | 2.167 | 3.423 | 0.919 | 0.959 |
| DL8 | 4.407 | 5.655 | 0.776 | 0.881 |
| Method | MAE | RMSE | R2 | CC |
|---|---|---|---|---|
| (mm h−1) | (mm h−1) | |||
| DT1 | 2.508 | 5.586 | 0.769 | 0.876 |
| DT2 | 2.860 | 5.905 | 0.744 | 0.862 |
| DT3 | 2.193 | 5.459 | 0.774 | 0.879 |
| DT4 | 2.223 | 5.333 | 0.785 | 0.886 |
| DT5 | 2.121 | 5.130 | 0.804 | 0.896 |
| DT6 | 3.074 | 6.163 | 0.729 | 0.852 |
| DT7 | 2.410 | 5.358 | 0.791 | 0.889 |
| DT8 | 3.179 | 6.886 | 0.661 | 0.811 |
| RF1 | 3.072 | 4.290 | 0.860 | 0.927 |
| RF2 | 3.229 | 4.912 | 0.820 | 0.906 |
| RF3 | 2.760 | 4.099 | 0.874 | 0.935 |
| RF4 | 2.789 | 4.178 | 0.869 | 0.932 |
| RF5 | 2.685 | 3.936 | 0.887 | 0.942 |
| RF6 | 3.626 | 4.998 | 0.822 | 0.906 |
| RF7 | 3.104 | 4.663 | 0.844 | 0.919 |
| RF8 | 4.106 | 5.736 | 0.755 | 0.869 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yamaç, S.S.; Negiş, H.; Şeker, C.; Memon, A.M.; Kurtuluş, B.; Todorovic, M.; Alomair, G. Saturated Hydraulic Conductivity Estimation Using Artificial Intelligence Techniques: A Case Study for Calcareous Alluvial Soils in a Semi-Arid Region. Water 2022, 14, 3875. https://doi.org/10.3390/w14233875
Yamaç SS, Negiş H, Şeker C, Memon AM, Kurtuluş B, Todorovic M, Alomair G. Saturated Hydraulic Conductivity Estimation Using Artificial Intelligence Techniques: A Case Study for Calcareous Alluvial Soils in a Semi-Arid Region. Water. 2022; 14(23):3875. https://doi.org/10.3390/w14233875
Chicago/Turabian StyleYamaç, Sevim Seda, Hamza Negiş, Cevdet Şeker, Azhar M. Memon, Bedri Kurtuluş, Mladen Todorovic, and Gadir Alomair. 2022. "Saturated Hydraulic Conductivity Estimation Using Artificial Intelligence Techniques: A Case Study for Calcareous Alluvial Soils in a Semi-Arid Region" Water 14, no. 23: 3875. https://doi.org/10.3390/w14233875
APA StyleYamaç, S. S., Negiş, H., Şeker, C., Memon, A. M., Kurtuluş, B., Todorovic, M., & Alomair, G. (2022). Saturated Hydraulic Conductivity Estimation Using Artificial Intelligence Techniques: A Case Study for Calcareous Alluvial Soils in a Semi-Arid Region. Water, 14(23), 3875. https://doi.org/10.3390/w14233875










