Stability of Braced Excavation Underneath Crossing Underground Large Pressurized Pipelines
Abstract
:1. Introduction
2. Project Overview
2.1. The Excavation Project
2.2. Excavation Support System
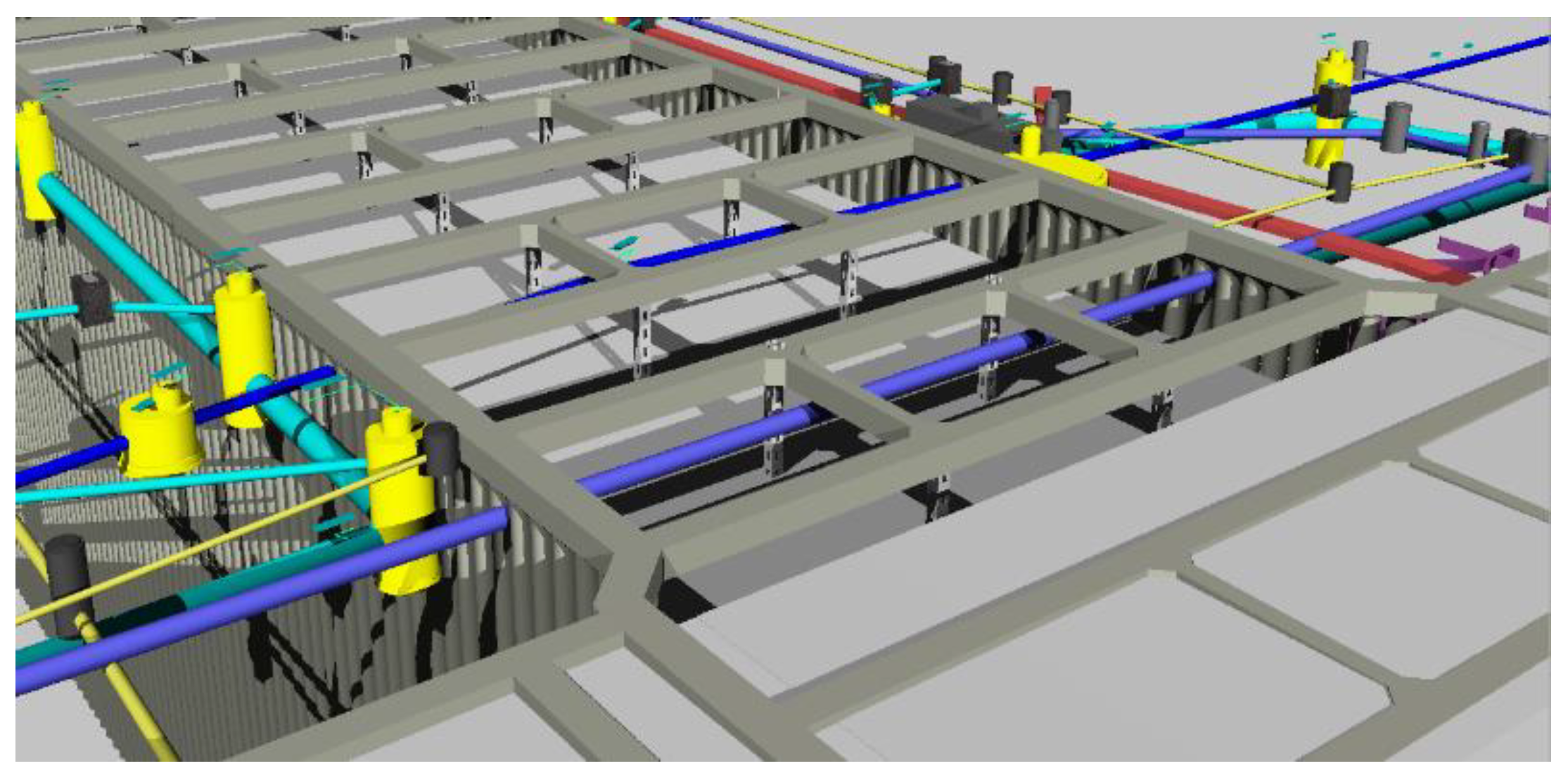
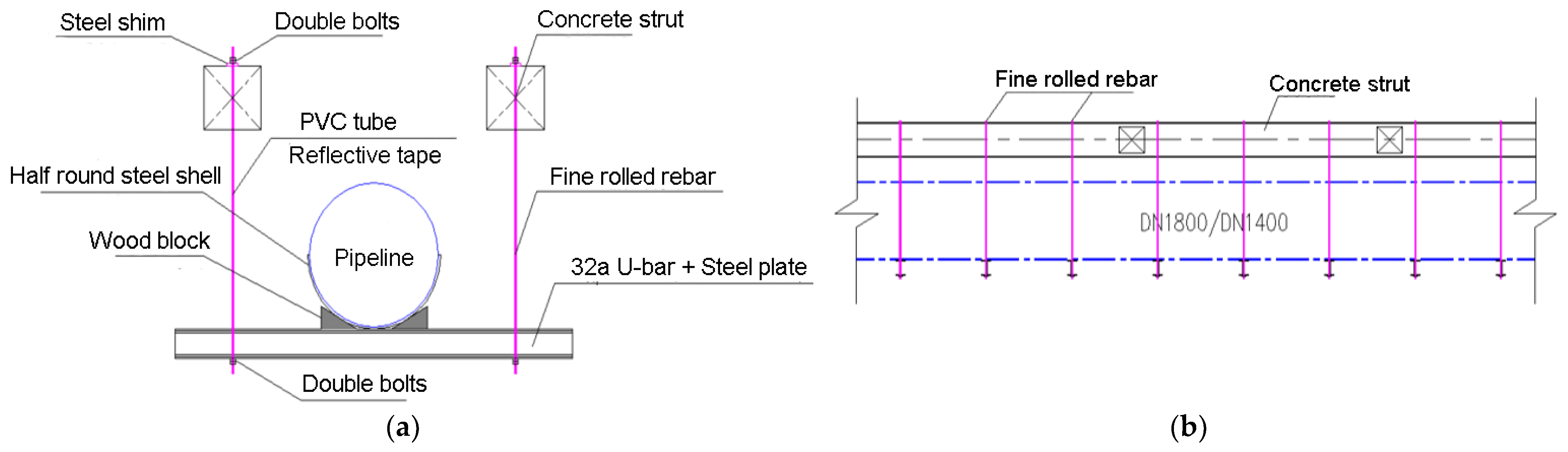
2.3. Pipeline Suspension Structure
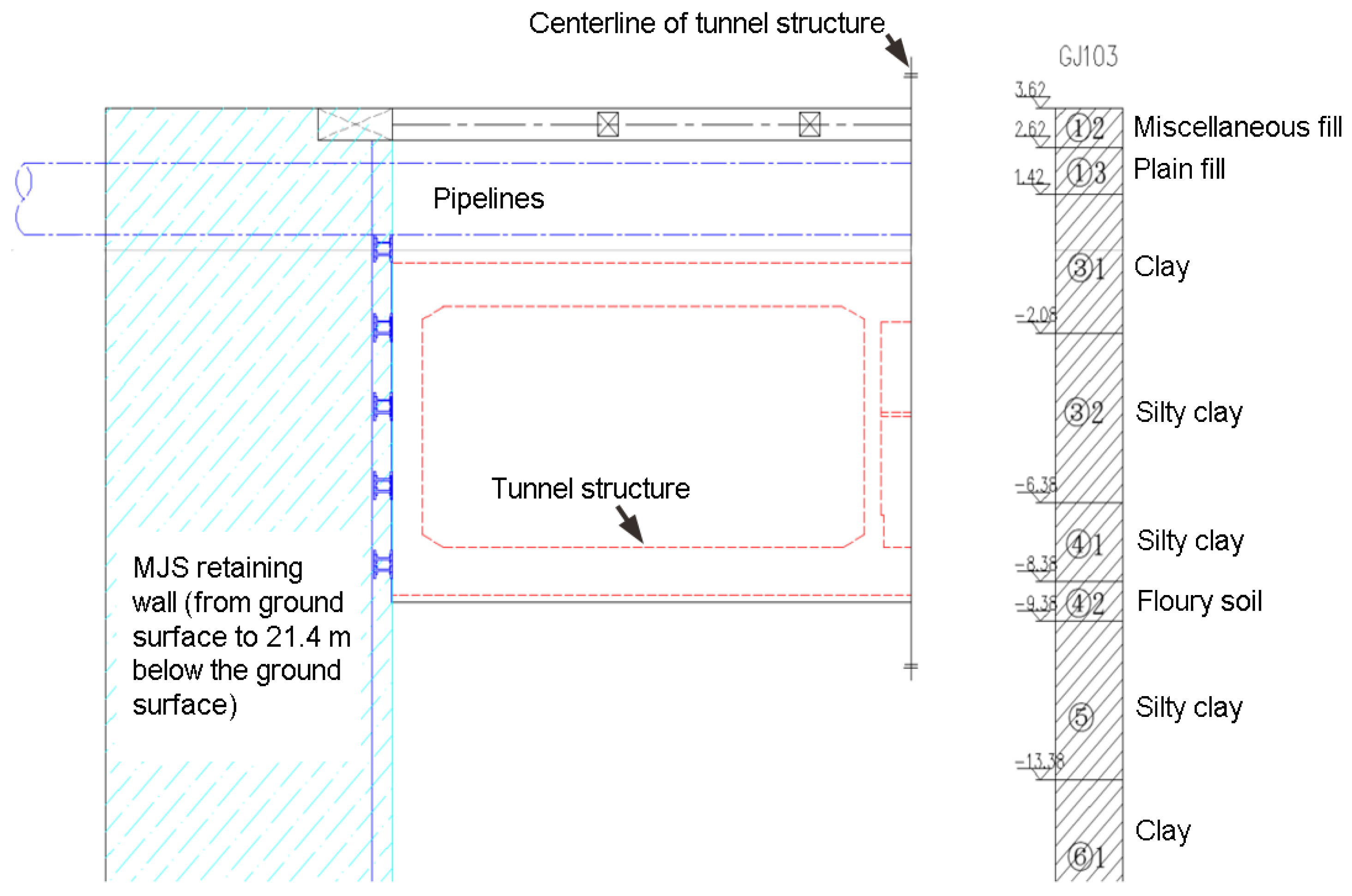
2.4. Geological and Hydrologic Conditions
3. Numerical Modelling
3.1. Finite Element Analysis Software
3.2. Meshing and Boundary Conditions
3.3. Parameters Used for Finite Element Analysis
3.4. Excavation Sequence Simulation
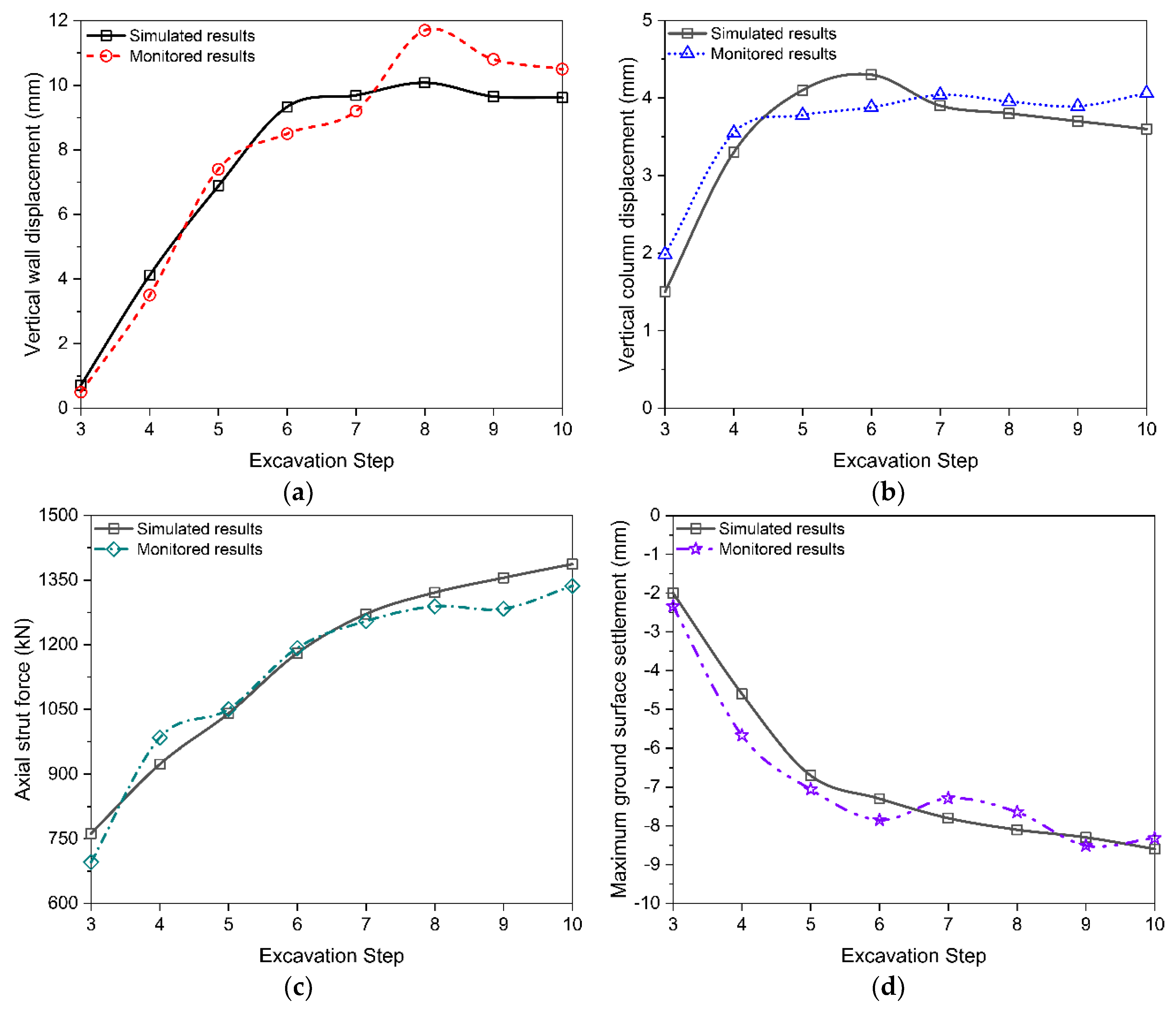
4. Validation of Finite Element Method
5. Results and Discussion
5.1. Deformation Characteristics of Diaphragm Wall and MJS Retaining Wall
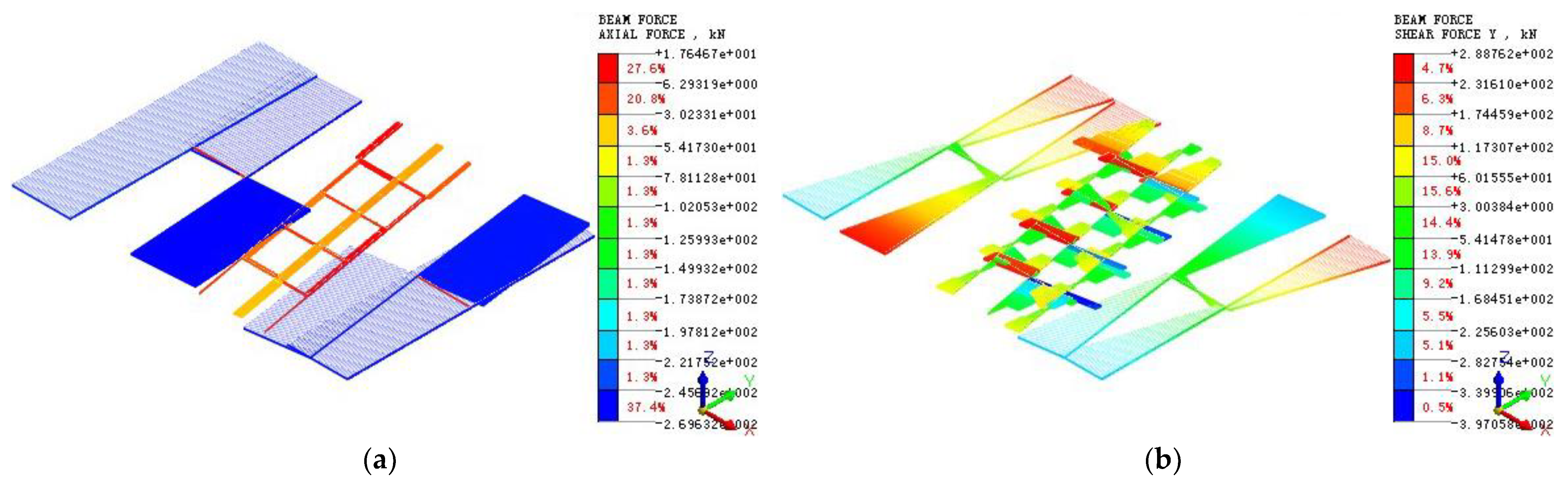
5.2. Distribution of Internal Forces in Concrete Strut
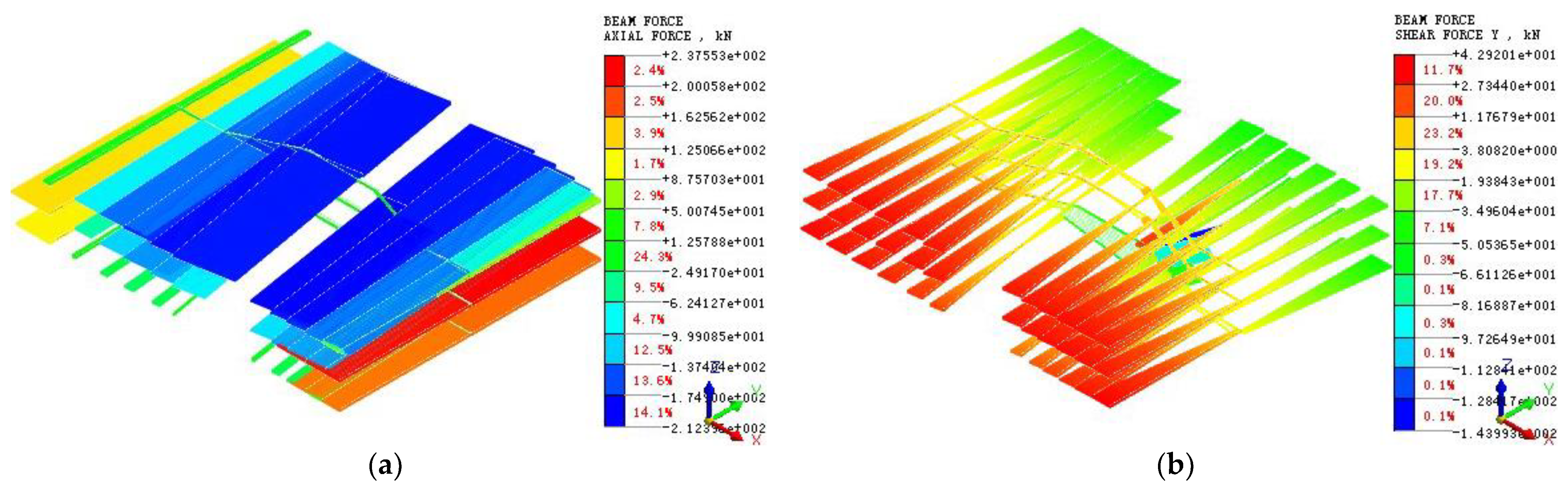
5.3. Distribution of Internal Forces in Steel Strut
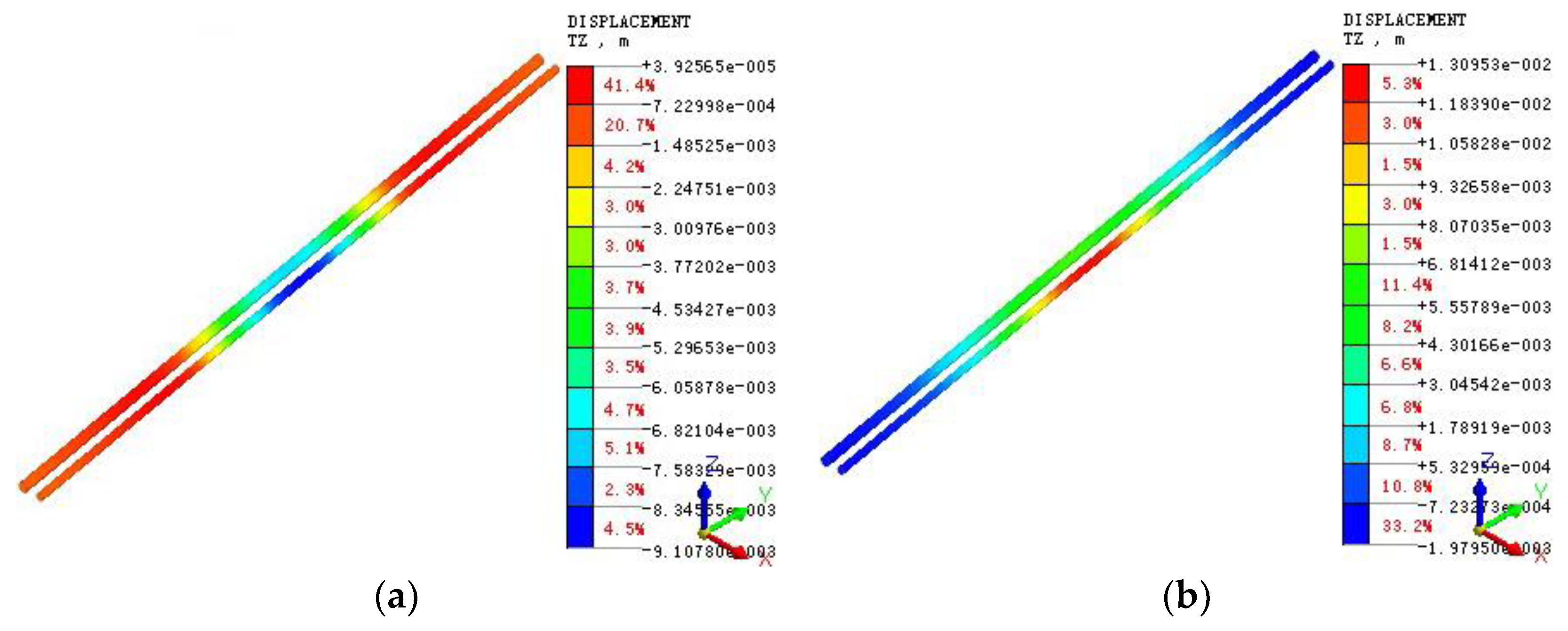
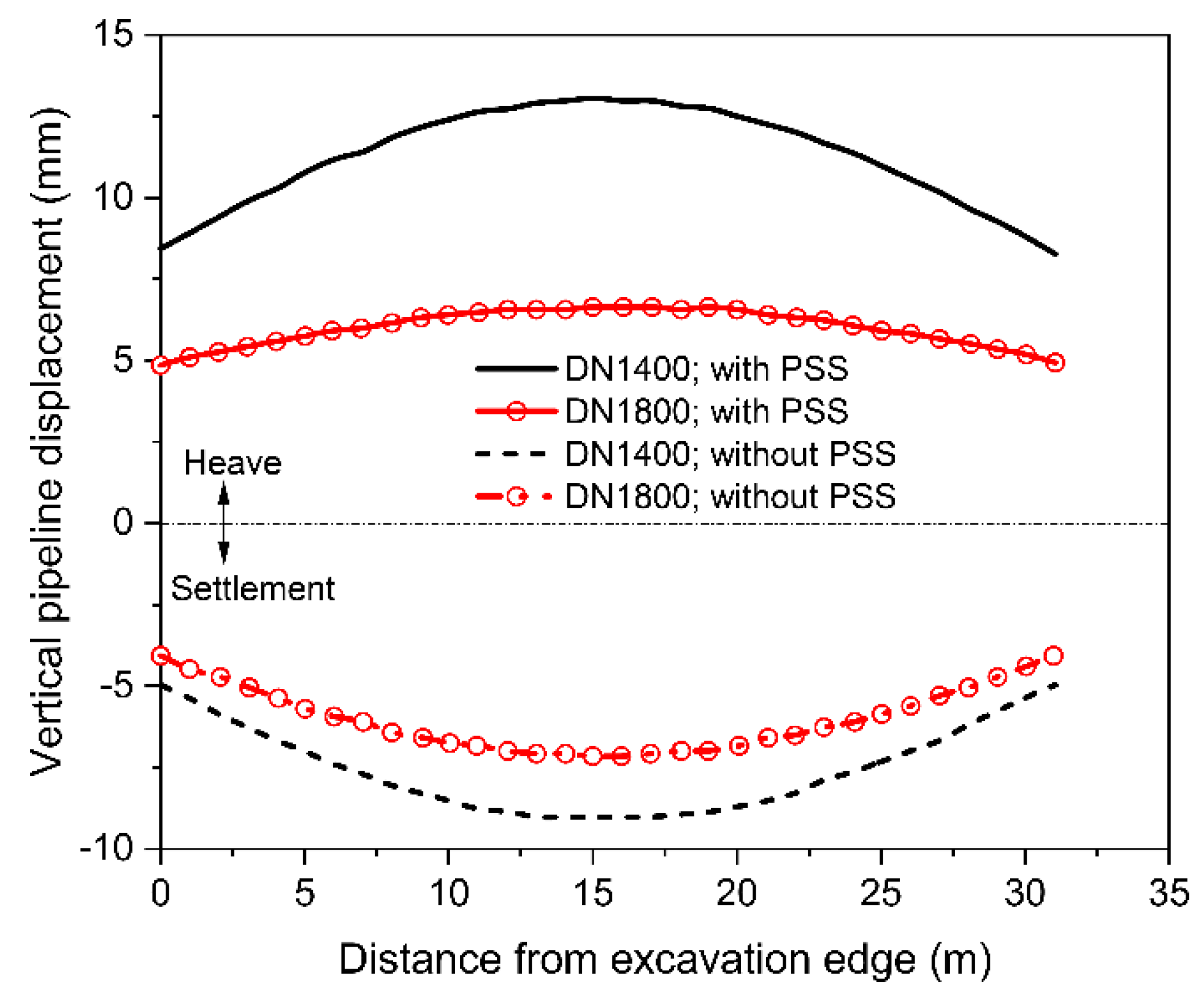
5.4. Vertical Displacements of Pipelines
5.5. Discussion of Supporting Effect of Pipeline Suspension Structure (PSS)
6. Conclusions
- (1)
- Both the diaphragm wall and the MJS retaining wall have a tendency to deform towards the excavation with proceeding the Excavation Step. The deformation of these walls constantly increases with an increase in the excavation depth.
- (2)
- When the final excavation depth is reached, the distribution of the shear forces in the Y and Z directions along the axis of the concrete strut is in a linear manner, while the distribution of the bending moments in the Y and Z directions is in a symmetric manner.
- (3)
- At the final excavation depth, the shear force in the Y direction is of linear distribution along the axis of the steel strut, and the distribution of the bending moments in both Y and Z directions is almost symmetric with regard to the middle of the steel strut. The magnitude of the maximum shear force in the Z direction is negligible compared to the magnitude of the maximum shear force in the Y direction.
- (4)
- With an increase in the excavation depth, the heave of the pipelines increases due to an increase in the basal heave of the excavation. The maximum heave of pipeline DN1400 is 1 mm greater than that of pipeline DN1800, which may be attributed to the lighter weight of pipeline DN1400.
- (5)
- The installation of the pipeline suspension structure is beneficial for the structural integrity and the safety of the pipelines during both the construction phase and the operational phase of the tunnel. This benefit is obtained by implementing conveniently the operation that the elevation of the pipeline suspension structure cork base is stably lowered during the construction period.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Tan, Y.; Lu, Y.; Wang, D. Deep excavation of the Gate of the Orient in Suzhou stiff clay: Composite earth retaining systems and dewatering plans. J. Geotech. Geoenviron. Eng. 2018, 144, 05017009. [Google Scholar] [CrossRef]
- Oztoprak, S.; Cinicioglu, S.F.; Oztorun, N.K.; Alhan, C. Impact of neighbouring deep excavation on high-rise sun plaza building and its surrounding. Eng. Fail. Anal. 2020, 111, 104495. [Google Scholar] [CrossRef]
- Tan, Y.; Wei, B.; Zhou, X.; Diao, Y. Lessons learned from construction of Shanghai metro stations: Importance of quick excavation, prompt propping, timely casting, and segmented construction. J. Perform. Constr. Facil. 2015, 29, 04014096. [Google Scholar] [CrossRef]
- Li, D.; Yan, C. Building deformation prediction based on ground surface settlements of metro-station deep excavation. Adv. Civ. Eng. 2018, 2018, 6050353. [Google Scholar] [CrossRef]
- Liu, B.; Xu, W.; Zhang, D.; Zhang, Q. Deformation behaviors and control indexes of metro-station deep excavations based on case histories. Tunn. Undergr. Space Technol. 2022, 122, 104400. [Google Scholar] [CrossRef]
- Shi, H.; Jia, Z.; Wang, T.; Cheng, Z.; Zhang, D.; Bai, M.; Yu, K. Deformation characteristics and optimization design for large-scale deep and circular foundation pit partitioned excavation in a complex environment. Buildings 2022, 12, 1292. [Google Scholar] [CrossRef]
- Hou, Y.M.; Wang, J.H.; Zhang, L.L. Finite-element modeling of a complex deep excavation in Shanghai. Acta Geotech. 2009, 4, 7–16. [Google Scholar] [CrossRef]
- Li, M.-G.; Chen, J.-J.; Xu, A.-J.; Xia, X.-H.; Wang, J.-H. Case study of innovative top-down construction method with channel-type excavation. J. Constr. Eng. Manag. 2014, 140, 05014003. [Google Scholar] [CrossRef]
- Whittle, A.J.; Hashash, Y.M.A.; Whitman, R.V. Analysis of deep excavation in Boston. J. Geotech. Eng. 1993, 119, 69–90. [Google Scholar] [CrossRef]
- Huang, X.; Schweiger, H.F.; Huang, H. Influence of deep excavations on nearby existing tunnels. Int. J. Geomech. 2013, 13, 170–180. [Google Scholar] [CrossRef]
- Wang, J.; Xiang, H.; Yan, J. Numerical simulation of steel sheet pile support structures in foundation pit excavation. Int. J. Geomech. 2019, 19, 05019002. [Google Scholar] [CrossRef]
- Issa, U.; Saeed, F.; Miky, Y.; Alqurashi, M.; Osman, E. Hybrid AHP-fuzzy TOPSIS approach for selecting deep excavation support system. Buildings 2022, 12, 295. [Google Scholar] [CrossRef]
- Hong, L.; Chen, L.; Wang, X. Reliability analysis of serviceability limit state for braced excavation considering multiple failure modes in spatially variable soil. Buildings 2022, 12, 722. [Google Scholar] [CrossRef]
- Gong, X.-n.; Zhang, X.-c. Excavation collapse of Hangzhou subway station in soft clay and numerical investigation based on orthogonal experiment method. J. Zhejiang Univ.-SCI A 2012, 13, 760–767. [Google Scholar] [CrossRef]
- He, L.; Liu, Y.; Bi, S.; Wang, L.; Broggi, M.; Beer, M. Estimation of failure probability in braced excavation using Bayesian networks with integrated model updating. Undergr. Space 2020, 5, 315–323. [Google Scholar] [CrossRef]
- Do, T.-N.; Ou, C.-Y.; Chen, R.-P. A study of failure mechanisms of deep excavations in soft clay using the finite element method. Comput. Geotech. 2016, 73, 153–163. [Google Scholar] [CrossRef]
- Chen, R.P.; Li, Z.C.; Chen, Y.M.; Ou, C.Y.; Hu, Q.; Rao, M. Failure investigation at a collapsed deep excavation in very sensitive organic soft clay. J. Perform. Constr. Facil. 2015, 29, 04014078. [Google Scholar] [CrossRef]
- Tan, Y.; Lu, Y. Forensic diagnosis of a leaking accident during excavation. J. Perform. Constr. Facil. 2017, 31, 04017061. [Google Scholar] [CrossRef]
- Hu, Q.; Xu, X.B.; Huang, T.M.; Lu, S.Q. Collapse of a deep excavation and its reconstruction in soft soil of Nanjing, China. Proc. Inst. Civ. Eng.-Forensic Eng. 2021, 174, 1–7. [Google Scholar] [CrossRef]
- Liu, G.B.; Ng, C.W.W.; Wang, Z.W. Observed performance of a deep multistrutted excavation in Shanghai soft clays. J. Geotech. Geoenviron. Eng. 2005, 131, 1004–1013. [Google Scholar] [CrossRef]
- Masini, L.; Gaudio, D.; Rampello, S.; Romani, E. Observed performance of a deep excavation in the historical center of Rome. J. Geotech. Geoenviron. Eng. 2021, 147, 05020015. [Google Scholar] [CrossRef]
- Cheng, K.; Xu, R.; Ying, H.; Gan, X.; Zhang, L.; Liu, S. Observed performance of a 30.2 m deep-large basement excavation in Hangzhou soft clay. Tunn. Undergr. Space Technol. 2021, 111, 103872. [Google Scholar] [CrossRef]
- Zhang, R.; Wu, C.; Goh, A.T.C.; Böhlke, T.; Zhang, W. Estimation of diaphragm wall deflections for deep braced excavation in anisotropic clays using ensemble learning. Geosci. Front. 2021, 12, 365–373. [Google Scholar] [CrossRef]
- Guo, P.; Lei, G.; Luo, L.; Gong, X.; Wang, Y.; Li, B.; Hu, X.; Hu, H. Soil creep effect on time-dependent deformation of deep braced excavation. Adv. Mater. Sci. Eng. 2022, 2022, 5655592. [Google Scholar] [CrossRef]
- Guo, P.; Gong, X.; Wang, Y. Displacement and force analyses of braced structure of deep excavation considering unsymmetrical surcharge effect. Comput. Geotech. 2019, 113, 103102. [Google Scholar] [CrossRef]
- Chen, H.; Li, J.; Yang, C.; Feng, C. A theoretical study on ground surface settlement induced by a braced deep excavation. Eur. J. Environ. Civ. Eng. 2022, 26, 1897–1916. [Google Scholar] [CrossRef]
- Liu, J.; Shi, C.; Lei, M.; Cao, C.; Lin, Y. Improved analytical method for evaluating the responses of a shield tunnel to adjacent excavations and its application. Tunn. Undergr. Space Technol. 2020, 98, 103339. [Google Scholar] [CrossRef]
- Guo, P.; Liu, F.; Lei, G.; Li, X.; Zhu, C.; Wang, Y.; Lu, M.; Cheng, K.; Gong, X. Predicting response of constructed tunnel to adjacent excavation with dewatering. Geofluids 2021, 2021, 5548817. [Google Scholar] [CrossRef]
- Zhang, D.-M.; Xie, X.-C.; Li, Z.-L.; Zhang, J. Simplified analysis method for predicting the influence of deep excavation on existing tunnels. Comput. Geotech. 2020, 121, 103477. [Google Scholar] [CrossRef]
- Kung, G.T.C.; Juang, C.H.; Hsiao, E.C.L.; Hashash, Y.M.A. Simplified model for wall deflection and ground-surface settlement caused by braced excavation in clays. J. Geotech. Geoenviron. Eng. 2007, 133, 731–747. [Google Scholar] [CrossRef]
- Ou, C.-Y.; Hsieh, P.-G. A simplified method for predicting ground settlement profiles induced by excavation in soft clay. Comput. Geotech. 2011, 38, 987–997. [Google Scholar] [CrossRef]
- Hu, B.; Li, X.; Huang, D. Safety risk analysis and protective control of existing pipelines affected by deep pit excavation in metro construction. Model. Simul. Eng. 2019, 2019, 3643808. [Google Scholar] [CrossRef] [Green Version]
- Jiang, N.; Zhu, B.; He, X.; Zhou, C.; Luo, X.; Wu, T. Safety assessment of buried pressurized gas pipelines subject to blasting vibrations induced by metro foundation pit excavation. Tunn. Undergr. Space Technol. 2020, 102, 103448. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhang, M.; Zhao, Q. A simplified analysis for deformation behavior of buried pipelines considering disturbance effects of underground excavation in soft clays. Arab. J. Geosci. 2015, 8, 7771–7785. [Google Scholar] [CrossRef]
- Kog, Y.C. Buried pipeline response to braced excavation movements. J. Perform. Constr. Facil. 2010, 24, 235–241. [Google Scholar] [CrossRef]
- Linehan, P.W.; Longinow, A.; Dowding, C.H. Pipe response to pile driving and adjacent excavation. J. Geotech. Eng. 1992, 118, 300–316. [Google Scholar] [CrossRef]
- Tan, Y.; Lu, Y. Responses of shallowly buried pipelines to adjacent deep excavations in Shanghai soft ground. J. Pipeline Syst. Eng. Pract. 2018, 9, 05018002. [Google Scholar] [CrossRef]
- Chen, H.; Li, J.; Li, L. Performance of a zoned excavation by bottom-up technique in Shanghai soft soils. J. Geotech. Geoenviron. Eng. 2018, 144, 05018003. [Google Scholar] [CrossRef]








| Pipeline | Material | Cover Depth (m) | Diameter (m) | Wall Thickness (mm) | Internal Pressure (MPa) |
|---|---|---|---|---|---|
| DN1800 | steel | 1.45–1.55 | 1.8 | 16 | 0.3 |
| DN1400 | steel | 1.60–1.74 | 1.4 | 14 | 0.2 |
| Soil Layer Number | Thickness (m) | Unit Weight (kN/m3) | Elasticity Modulus (MPa) | Poisson’s Ratio (-) | Friction Angle (°) | Cohesion (kPa) |
|---|---|---|---|---|---|---|
| ①2 | 1 | 18.5 | 3.5 | 0.23 | 12 | 5 |
| ①3 | 1.2 | 19 | 4 | 0.2 | 10 | 12 |
| ③1 | 3.5 | 19.3 | 25 | 0.3 | 16.0 | 33.1 |
| ③2 | 4.3 | 18.6 | 20 | 0.33 | 17.0 | 19.8 |
| ④1 | 2 | 18.8 | 22 | 0.36 | 19.2 | 19.6 |
| ④2 | 1 | 18.4 | 30 | 0.25 | 17.7 | 17.2 |
| ⑤ | 4 | 18.5 | 20 | 0.33 | 15.9 | 39.4 |
| ⑥1 | 9.5 | 19.8 | 20 | 0.3 | 18.5 | 17.6 |
| Structure | Unit Weight (kN/m3) | Elastic Modulus (MPa) | Poisson’s Ratio (-) | Remark |
|---|---|---|---|---|
| Diaphragm wall | 25 | 3 × 104 | 0.2 | Thickness = 0.6 m; Depth = 25 m |
| MJS wall | 20 | 1 × 104 | 0.2 | From ground surface to −21.4 m |
| CISB pile | 20 | 3 × 104 | 0.2 | Diameter = 0.8 m; Length = 30 or 38 m |
| Ring beam | 25 | 3 × 104 | 0.2 | Sectional dimension = 1 m × 0.8 m |
| Concrete strut | 25 | 3 × 104 | 0.2 | Sectional dimension = 0.8 m × 0.8 m |
| Steel strut | 78.5 | 2 × 105 | 0.25 | Diameter = 609 mm; Wall thick. = 16 mm |
| Lattice column | 78.5 | 2 × 105 | 0.25 | Longitudinal interval = 6 m |
| Cork base | 78.5 | 2 × 105 | 0.25 | Using 32a U-bar |
| Fine rolled rebar | 78.5 | 2 × 105 | 0.25 | Diameter = 25 mm |
| Monitored Item | Device Used | Version |
|---|---|---|
| Horizontal disp. at diaphragm wall top | Total station instrument | TCRA1201 |
| Vertical disp. at diaphragm wall top | Total station instrument | TCRA1201 |
| Pipeline displacements | Total station instrument | TCRA1201 |
| Ground surface settlements | Single-point settling meter | YH02-A20 |
| Axial forces in struts | Vibrating string-type steel bar meter | GJJ10 |
| Groundwater level | Pneumatic water level gauge | YH04-A06 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, F.; Guo, P.; Geng, N.; Mao, L.; Lin, F.; Zhao, Y.; Lin, H.; Wang, Y. Stability of Braced Excavation Underneath Crossing Underground Large Pressurized Pipelines. Water 2022, 14, 3867. https://doi.org/10.3390/w14233867
Li F, Guo P, Geng N, Mao L, Lin F, Zhao Y, Lin H, Wang Y. Stability of Braced Excavation Underneath Crossing Underground Large Pressurized Pipelines. Water. 2022; 14(23):3867. https://doi.org/10.3390/w14233867
Chicago/Turabian StyleLi, Fangang, Panpan Guo, Ningning Geng, Lei Mao, Feng Lin, Yanlin Zhao, Hang Lin, and Yixian Wang. 2022. "Stability of Braced Excavation Underneath Crossing Underground Large Pressurized Pipelines" Water 14, no. 23: 3867. https://doi.org/10.3390/w14233867
APA StyleLi, F., Guo, P., Geng, N., Mao, L., Lin, F., Zhao, Y., Lin, H., & Wang, Y. (2022). Stability of Braced Excavation Underneath Crossing Underground Large Pressurized Pipelines. Water, 14(23), 3867. https://doi.org/10.3390/w14233867










