Future Rainfall Erosivity over Iran Based on CMIP5 Climate Models
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Climate Models
2.3. Downscaling Methods
2.4. Estimation of Rainfall-Runoff Erosivity (R-Factor)
2.5. Yearly Erosivity Density Ratio
2.6. Examination of R-Factor Performance
3. Results
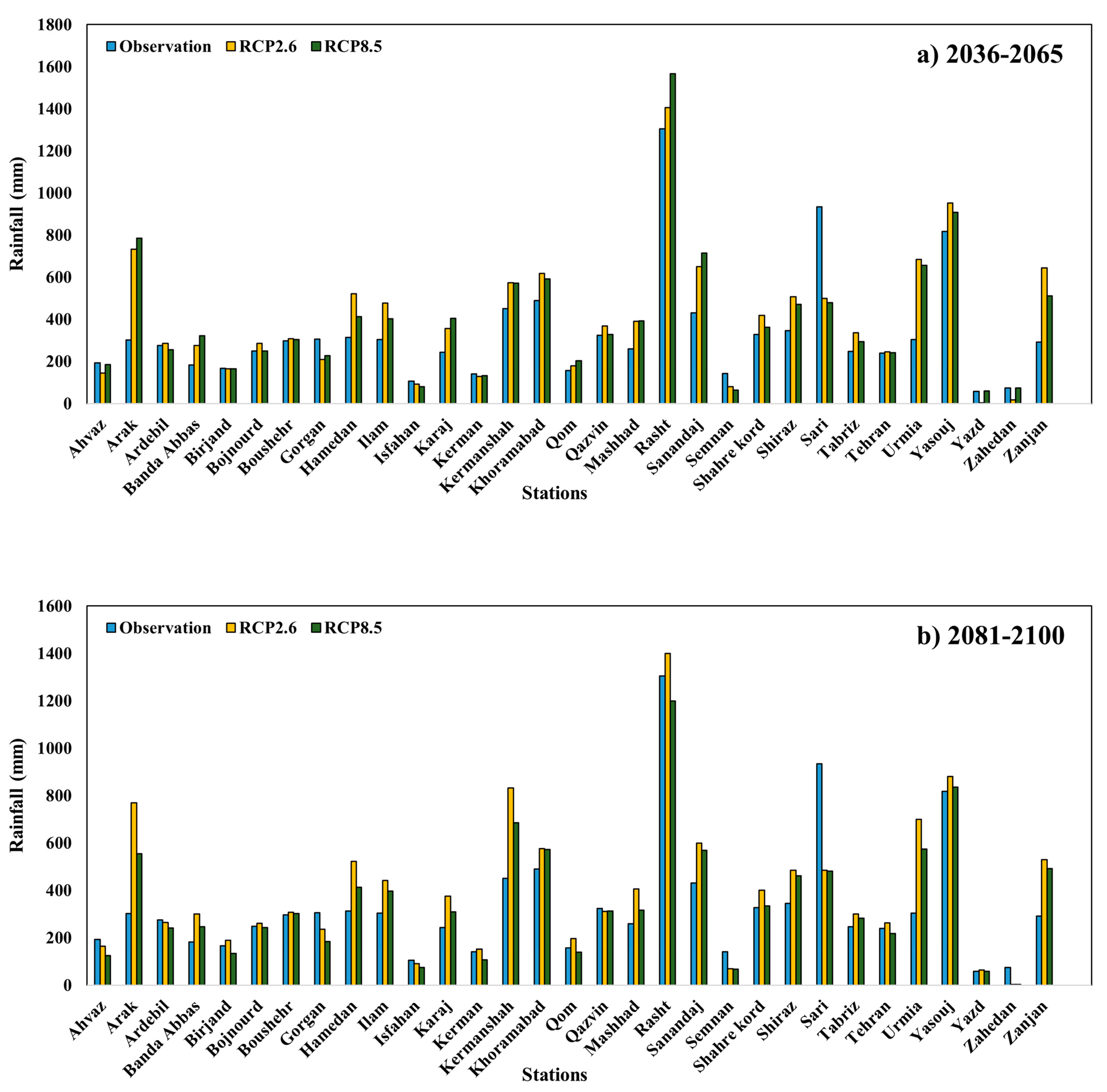
3.1. Analysis of Future Precipitation
3.2. Precipitation Prediction under Climate Change
3.3. Spatial Distribution of R-Factor Erosivity in Current and Future Periods
3.4. The Prediction of R-Factor under Climate Change
4. Discussion and Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Talchabhadel, R.; Nakagawa, H.; Kawaike, K.; Prajapati, R. Evaluating the rainfall erosivity (R-factor) from daily rainfall data: An application for assessing climate change impact on soil loss in Westrapti River basin, Nepal. Model. Earth Syst. Environ. 2020, 6, 1741–1762. [Google Scholar] [CrossRef]
- Jackson, R.B.; Saunois, M.; Bousquet, P.; Canadell, J.G.; Poulter, B.; Stavert, A.R.; Bergamaschi, P.; Niwa, Y.; Segers, A.; Tsuruta, A. Increasing anthropogenic methane emissions arise equally from agricultural and fossil fuel sources. Environ. Res. Lett. 2020, 15, 071002. [Google Scholar] [CrossRef]
- Shin, J.-Y.; Kim, K.R.; Ha, J.-C. Seasonal forecasting of daily mean air temperatures using a coupled global climate model and machine learning algorithm for field-scale agricultural management. Agric. For. Meteorol. 2020, 281, 107858. [Google Scholar] [CrossRef]
- Pandey, D. Agricultural Sustainability and Climate Change Nexus. In Contemporary Environmental Issues and Challenges in Era of Climate Change; Springer: Singapore, 2020; pp. 77–97. [Google Scholar]
- Chen, X.; Zhu, H.; Yan, B.; Shutes, B.; Xing, D.; Banuelos, G.; Cheng, R.; Wang, X. Greenhouse gas emissions and wastewater treatment performance by three plant species in subsurface flow constructed wetland mesocosms. Chemosphere 2020, 239, 124795. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Ayyub, B.M. Electricity System Assessment and Adaptation to Rising Temperatures in a Changing Climate Using Washington Metro Area as a Case Study. J. Infrastruct. Syst. 2020, 26, 04020017. [Google Scholar] [CrossRef]
- Siegert, M.; Alley, R.B.; Rignot, E.; Englander, J.; Corell, R. Twenty-first century sea-level rise could exceed IPCC projections for strong-warming futures. One Earth 2020, 3, 691–703. [Google Scholar] [CrossRef]
- Konapala, G.; Mishra, A.K.; Wada, Y.; Mann, M.E. Climate change will affect global water availability through compounding changes in seasonal precipitation and evaporation. Nat. Commun. 2020, 11, 3044. [Google Scholar] [CrossRef]
- Schädler, M.; Buscot, F.; Klotz, S.; Reitz, T.; Durka, W.; Bumberger, J.; Merbach, I.; Michalski, S.G.; Kirsch, K.; Remmler, P.; et al. Investigating the consequences of climate change under different land-use regimes: A novel experimental infrastructure. Ecosphere 2019, 10, e02635. [Google Scholar] [CrossRef]
- Barton, M.G.; Terblanche, J.S.; Sinclair, B.J. Incorporating temperature and precipitation extremes into process-based models of African lepidoptera changes the predicted distribution under climate change. Ecol. Model. 2019, 394, 53–65. [Google Scholar] [CrossRef]
- Nearing, M.A.; Pruski, F.F.; O’Neal, M.R. Expected climate change impacts on soil erosion rates: A review. J. Soil Water Conserv. 2004, 59, 43–50. [Google Scholar]
- Simonneaux, V.; Cheggour, A.; Deschamps, C.; Mouillot, F.; Cerdan, O.; Le Bissonnais, Y. Land use and climate change effects on soil erosion in a semi-aridmountainous watershed (High Atlas, Morocco). J. Arid Environ. 2015, 122, 64–75. [Google Scholar] [CrossRef]
- Morán-Ordóñez, A.; Duane, A.; Gil-Tena, A.; De Cáceres, M.; Aquilué, N.; Guerra, C.A.; Geijzendorffer, I.R.; Fortin, M.; Brotons, L. Future impact of climate extremes in the Mediterranean: Soil erosion projections when fire and extreme rainfall meet. Land Degrad. Dev. 2020, 31, 3040–3054. [Google Scholar] [CrossRef]
- Gafforov, K.S.; Bao, A.; Rakhimov, S.; Liu, T.; Abdullaev, F.; Jiang, L.; Durdiev, K.; Duulatov, E.; Rakhimova, M.; Mukanov, Y. The assessment of climate change on rainfall-runoff erosivity in the Chirchik–Akhangaran Basin, Uzbekistan. Sustainability 2020, 12, 3369. [Google Scholar] [CrossRef]
- Kastridis, A.; Stathis, D.; Sapountzis, M.; Theodosiou, G. Insect outbreak and long-term post-fire effects on soil erosion editerraneanean suburban forest. Land 2022, 11, 911. [Google Scholar] [CrossRef]
- de Almeida, W.S.; Seitz, S.; de Oliveira, L.F.C.; de Carvalho, D.F. Duration and intensity of rainfall events with the same erosivity change sediment yield and runoff rates. Int. Soil Water Conserv. Res. 2021, 9, 69–75. [Google Scholar] [CrossRef]
- Kinnell, P.; Yu, B. CLIGEN as a weather generator for predicting rainfall erosion using USLE based modelling systems. Catena 2020, 194, 104745. [Google Scholar] [CrossRef]
- Grillakis, M.G.; Polykretis, C.; Alexakis, D.D. Past and projected climate change impacts on rainfall erosivity: Advancing our knowledge for the eastern Mediterranean island of Crete. Catena 2020, 193, 104625. [Google Scholar] [CrossRef]
- Liu, Y.; Zhao, W.; Liu, Y.; Pereira, P. Global rainfall erosivity changes between 1980 and 2017 based on an erosivity model using daily precipitation data. Catena 2020, 194, 104768. [Google Scholar] [CrossRef]
- Riquetti, N.B.; Mello, C.R.; Beskow, S.; Viola, M.R. Rainfall erosivity in South America: Current patterns and future perspectives. Sci. Total. Environ. 2020, 724, 138315. [Google Scholar] [CrossRef]
- Nasidi, N.M.; Wayayok, A.; Abdullah, A.F.; Kassim, M.S.M. Spatio-temporal dynamics of rainfall erosivity due to climate change in Cameron Highlands, Malaysia. Model. Earth Syst. Environ. 2021, 7, 1847–1861. [Google Scholar] [CrossRef]
- Almagro, A.; Oliveira, P.T.; Nearing, M.A.; Hagemann, S. Projected climate change impacts in rainfall erosivity over Brazil. Sci. Rep. 2017, 7, 8130. [Google Scholar] [CrossRef]
- Xu, Y.; Sun, H.; Ji, X. Spatial-temporal evolution and driving forces of rainfall erosivity in a climatic transitional zone: A case in Huaihe River Basin, eastern China. Catena 2021, 198, 104993. [Google Scholar] [CrossRef]
- Azhdari, Z.; Sardooi, E.R.; Bazrafshan, O.; Zamani, H.; Singh, V.P.; Saravi, M.M.; Ramezani, M. Impact of climate change on net primary production (NPP) in south Iran. Environ. Monit. Assess. 2020, 192, 409. [Google Scholar] [CrossRef] [PubMed]
- Chakrabortty, R.; Pradhan, B.; Mondal, P.; Pal, S.C. The use of RUSLE and GCMs to predict potential soil erosion associated with climate change in a monsoon-dominated region of eastern India. Arab. J. Geosci. 2020, 13, 1073. [Google Scholar] [CrossRef]
- Sadeghi, S.H.R.; Hazbavi, Z. Trend analysis of the rainfall erosivity index at different time scales in Iran. Nat. Hazards 2015, 77, 383–404. [Google Scholar] [CrossRef]
- Fiedler, S.; Crueger, T.; D’Agostino, R.; Peters, K.; Becker, T.; Leutwyler, D.; Paccini, L.; Burdanowitz, J.; Buehler, S.A.; Cortes, A.U.; et al. Simulated Tropical Precipitation Assessed across Three Major Phases of the Coupled Model Intercomparison Project (CMIP). Mon. Weather Rev. 2020, 148, 3653–3680. [Google Scholar] [CrossRef]
- Emori, S.; Taylor, K.; Hewitson, B.; Zermoglio, F.; Juckes, M.; Lautenschlager, M.; Stockhause, M. CMIP5 Data Provided at the IPCC Data Distribution Centre. In Fact Sheet of the Task Group on Data and Scenario Support for Impact and Climate Analysis (TGICA) of The Intergovernmental Panel on Climate Change (IPCC); IPCC: Geneva, Switzerland, 2016. [Google Scholar]
- Aghakhaniafshar, A.; Hasanzadeh, Y.; Pourreza-Bilondi, A.A.B.M. Seasonal changes of precipitation and temperature of mountainous watersheds in future periods with approach of fifth report of Intergovernmental Panel on Climate Change (case study: Kashafrood Watershed Basin). J. Water Soil 2016, 30, 1718–1732. [Google Scholar]
- Burke, E.J.; Zhang, Y.; Krinner, G. Evaluating permafrost physics in the Coupled Model Intercomparison Project 6 (CMIP6) models and their sensitivity to climate change. Cryosphere 2020, 14, 3155–3174. [Google Scholar] [CrossRef]
- Colorado-Ruiz, G.; Cavazos, T.; Salinas, J.A.; De Grau, P.; Ayala, R. Climate change projections from Coupled Model Intercomparison Project phase 5 multi-model weighted ensembles for Mexico, the North American monsoon, and the mid-summer drought region. Int. J. Clim. 2018, 38, 5699–5716. [Google Scholar] [CrossRef]
- Wandres, M.; Pattiaratchi, C.; Hemer, M.A. Projected changes of the southwest Australian wave climate under two atmospheric greenhouse gas concentration pathways. Ocean Model. 2017, 117, 70–87. [Google Scholar] [CrossRef]
- Sánchez-García, D.; Bienvenido-Huertas, D.; Pulido-Arcas, J.A.; Rubio-Bellido, C. Analysis of Energy Consumption in Different European Cities: The Adaptive Comfort Control Implemented Model (ACCIM) Considering Representative Concentration Pathways (RCP) Scenarios. Appl. Sci. 2020, 10, 1513. [Google Scholar] [CrossRef]
- Zhang, Y.; You, Q.; Chen, C.; Ge, J. Impacts of climate change on streamflows under RCP scenarios: A case study in Xin River Basin, China. Atmospheric Res. 2016, 178–179, 521–534. [Google Scholar] [CrossRef]
- Gupta, A.S.; Jourdain, N.; Brown, J.N.; Monselesan, D. Climate Drift in the CMIP5 Models. J. Clim. 2013, 26, 8597–8615. [Google Scholar] [CrossRef]
- Tranu, L. Projections of changes in productivity of major agricultural crops in the Republic of Moldova according to CMIP5 ensemble of 21 GCMs for RCP2. 6, RCP4. 5 and RCP8. 5 scenarios. Sci. Pap. Ser. A Agron. 2016, 59, 431–440. [Google Scholar]
- Balov, M.N.; Altunkaynak, A. Spatio-temporal evaluation of various global circulation models in terms of projection of different meteorological drought indices. Environ. Earth Sci. 2020, 79, 126. [Google Scholar] [CrossRef]
- Akinsanola, A.; Ajayi, V.; Adejare, A.; Adeyeri, O.; Gbode, I.; Ogunjobi, K.; Nikulin, G.; Abolude, A. Evaluation of rainfall simulations over West Africa in dynamically downscaled CMIP5 global circulation models. Theor. Appl. Climatol. 2017, 132, 437–450. [Google Scholar] [CrossRef]
- Shrestha, S.; Bach, T.V.; Pandey, V.P. Climate change impacts on groundwater resources in Mekong Delta under repre-sentative concentration pathways (RCPs) scenarios. Environ. Sci. Policy 2016, 61, 1–13. [Google Scholar] [CrossRef]
- Adeniyi, M.O. The consequences of the IPCC AR5 RCPs 4.5 and 8.5 climate change scenarios on precipitation in West Africa. Clim. Chang. 2016, 139, 245–263. [Google Scholar] [CrossRef]
- Murakami, H.; Vecchi, G.; Villarini, G.; Delworth, T.; Gudgel, R.; Underwood, S.; Yang, X.; Zhang, W.; Lin, S.-J. Seasonal Forecasts of Major Hurricanes and Landfalling Tropical Cyclones using a High-Resolution GFDL Coupled Climate Model. J. Clim. 2016, 29, 7977–7989. [Google Scholar] [CrossRef]
- Gallina, V.; Torresan, S.; Zabeo, A.; Rizzi, J.; Carniel, S.; Sclavo, M.; Pizzol, L.; Marcomini, A.; Critto, A. Assessment of Climate Change Impacts in the North Adriatic Coastal Area. Part II: Consequences for Coastal Erosion Impacts at the Regional Scale. Water 2019, 11, 1300. [Google Scholar] [CrossRef]
- Zhu, Q.; Yang, X.; Ji, F.; Liu, D.L.; Yu, Q. Extreme rainfall, rainfall erosivity, and hillslope erosion in Australian Alpine region and their future changes. Int. J. Clim. 2019, 40, 1213–1227. [Google Scholar] [CrossRef]
- Nourani, V.; Paknezhad, N.J.; Sharghi, E.; Khosravi, A. Estimation of prediction interval in ANN-based multi-GCMs downscaling of hydro-climatologic parameters. J. Hydrol. 2019, 579, 124226. [Google Scholar] [CrossRef]
- Kimiagar, V.; Fattahi, E.; Alimohammadi, S. Analyzing effect of different statistical downscaling methods on the predicted streamflow in Karaj dam basin under climate change effect. J. Clim. Res. 2020, 1398, 17–31. [Google Scholar]
- Meresa, H.; Murphy, C.; Fealy, R.; Golian, S. Uncertainties and their interaction in flood risk assessment with climate change. Hydrol. Earth Syst. Sci. Discuss. 2020, 2020, 1–35. [Google Scholar] [CrossRef]
- Wootten, A.M.; Dixon, K.W.; Adams-Smith, D.J.; McPherson, R.A. Statistically downscaled precipitation sensitivity to gridded observation data and downscaling technique. Int. J. Clim. 2021, 41, 980–1001. [Google Scholar] [CrossRef]
- Van Uytven, E.; Wampers, E.; Wolfs, V.; Willems, P. Evaluation of change factor-based statistical downscaling methods for impact analysis in urban hydrology. Urban Water J. 2020, 17, 785–794. [Google Scholar] [CrossRef]
- Dixon, K.; Adams-Smith, D.; Lanzante, J. On the Sensitivity of 21st Century Spring Plant Phenology Projections to the Choice Of Statistical Downscaling Method. In Proceedings of the EGU General Assembly Conference, Virtual, 4–8 May 2020; Abstracts. p. 3776. [Google Scholar]
- Maqsoom, A.; Aslam, B.; Hassan, U.; Kazmi, Z.A.; Sodangi, M.; Tufail, R.F.; Farooq, D. Geospatial Assessment of Soil Erosion Intensity and Sediment Yield Using the Revised Universal Soil Loss Equation (RUSLE) Model. ISPRS Int. J. Geo-Inf. 2020, 9, 356. [Google Scholar] [CrossRef]
- Albut, S. Determination of R Factor in Revised Universal Soil Loss Equation (RUSLE) With Open Sources Geographical Information System (GIS) Software. J. Multidiscip. Eng. Sci. Technol. 2020, 7, 12507–12510. [Google Scholar]
- Nehaï, S.A.; Guettouche, M.S. Soil loss estimation using the revised universal soil loss equation and a GIS-based model: A case study of Jijel Wilaya, Algeria. Arab. J. Geosci. 2020, 13, 152. [Google Scholar] [CrossRef]
- Yue, T.; Xie, Y.; Yin, S.; Yu, B.; Miao, C.; Wang, W. Effect of time resolution of rainfall measurements on the erosivity factor in the USLE in China. Int. Soil Water Conserv. Res. 2020, 8, 373–382. [Google Scholar] [CrossRef]
- Girmay, G.; Moges, A.; Muluneh, A. Estimation of soil loss rate using the USLE model for Agewmariayam Watershed, northern Ethiopia. Agric. Food Secur. 2020, 9, 9. [Google Scholar] [CrossRef]
- Azari, M.; Oliaye, A.; Nearing, M.A. Expected climate change impacts on rainfall erosivity over Iran based on CMIP5 climate models. J. Hydrol. 2021, 593, 125826. [Google Scholar] [CrossRef]
- Panagos, P.; Borrelli, P.; Meusburger, K.; Yu, B.; Klik, A.; Lim, K.J.; Yang, J.E.; Ni, J.; Miao, C.; Chattopadhyay, N.; et al. Global rainfall erosivity assessment based on high-temporal resolution rainfall records. Sci. Rep. 2017, 7, 4175. [Google Scholar] [CrossRef] [PubMed]
- Duulatov, E.; Chen, X.; Amanambu, A.C.; Ochege, F.U.; Orozbaev, R.; Issanova, G.; Omurakunova, G. Projected Rainfall Erosivity Over Central Asia Based on CMIP5 Climate Models. Water 2019, 11, 897. [Google Scholar] [CrossRef]
- Margiorou, S.; Kastridis, A.; Sapountzis, M. Pre/Post-Fire Soil Erosion and Evaluation of Check-Dams Effectiveness in Mediterranean Suburban Catchments Based on Field Measurements and Modeling. Land 2022, 11, 1705. [Google Scholar] [CrossRef]
- Singh, J.; Knapp, H.V.; Arnold, J.G.; Demissie, M. Hydrological modeling of the Iroquois river watershed using HSPF and SWAT. J. Am. Water Resour. Assoc. 2005, 41, 343–360. [Google Scholar] [CrossRef]
- Samadi, S.; Sagareswar, G.; Tajiki, M. Comparison of General Circulation Models: Methodology for selecting the best GCM in Kermanshah Synoptic Station, Iran. Int. J. Glob. Warm. 2010, 2, 347–365. [Google Scholar] [CrossRef]
- Keteklahijani, V.K.; Alimohammadi, S.; Fattahi, E. Predicting changes in monthly streamflow to Karaj dam res-ervoir, Iran, in climate change condition and assessing its uncertainty. Ain Shams Eng. J. 2019, 10, 669–679. [Google Scholar] [CrossRef]
- Zarghami, M.; Abdi, A.; Babaeian, I.; Hassanzadeh, Y.; Kanani, R. Impacts of climate change on runoffs in East Azerbaijan, Iran. Glob. Planet. Chang. 2011, 78, 137–146. [Google Scholar] [CrossRef]
- Azimi Sardari, M.R.A.; Bazrafshan, O.; Panagopoulos, T.; Sardooi, E.R. Modeling the Impact of Climate Change and Land Use Change Scenarios on Soil Erosion at the Minab Dam Watershed. Sustainability 2019, 11, 3353. [Google Scholar] [CrossRef]
- Sharafati, A.; Pezeshki, E. A strategy to assess the uncertainty of a climate change impact on extreme hydrological events in the semi-arid Dehbar catchment in Iran. Theor. Appl. Climatol. 2019, 139, 389–402. [Google Scholar] [CrossRef]
- Litschert, S.; Theobald, D.; Brown, T. Effects of climate change and wildfire on soil loss in the Southern Rockies Ecoregion. Catena 2014, 118, 206–219. [Google Scholar] [CrossRef]
- Amanambu, A.C.; Li, L.; Egbinola, C.N.; Obarein, O.A.; Mupenzi, C.; Chen, D. Spatio-temporal variation in rain-fall-runoff erosivity due to climate change in the Lower Niger Basin, West Africa. Catena 2019, 172, 324–334. [Google Scholar] [CrossRef]
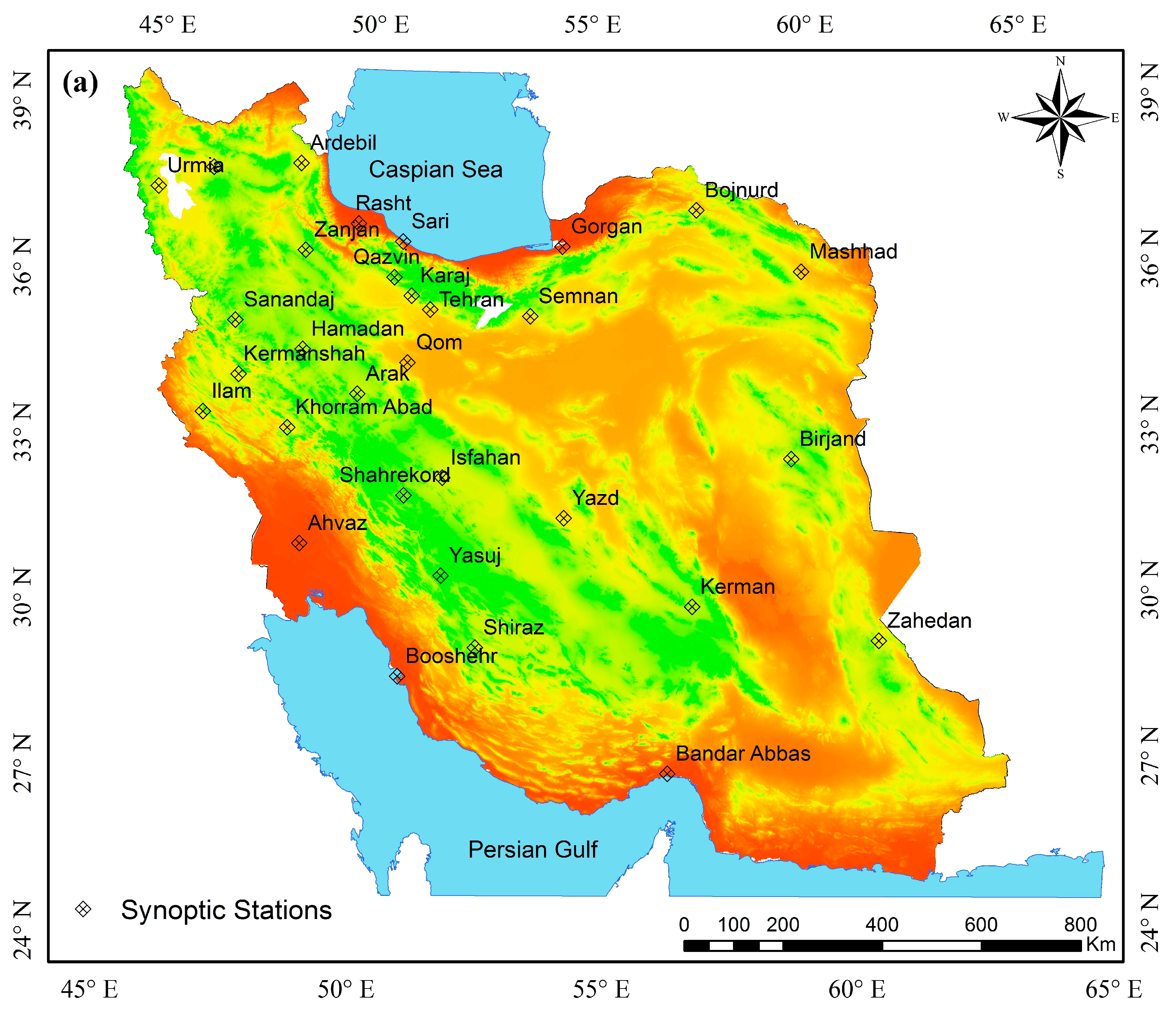
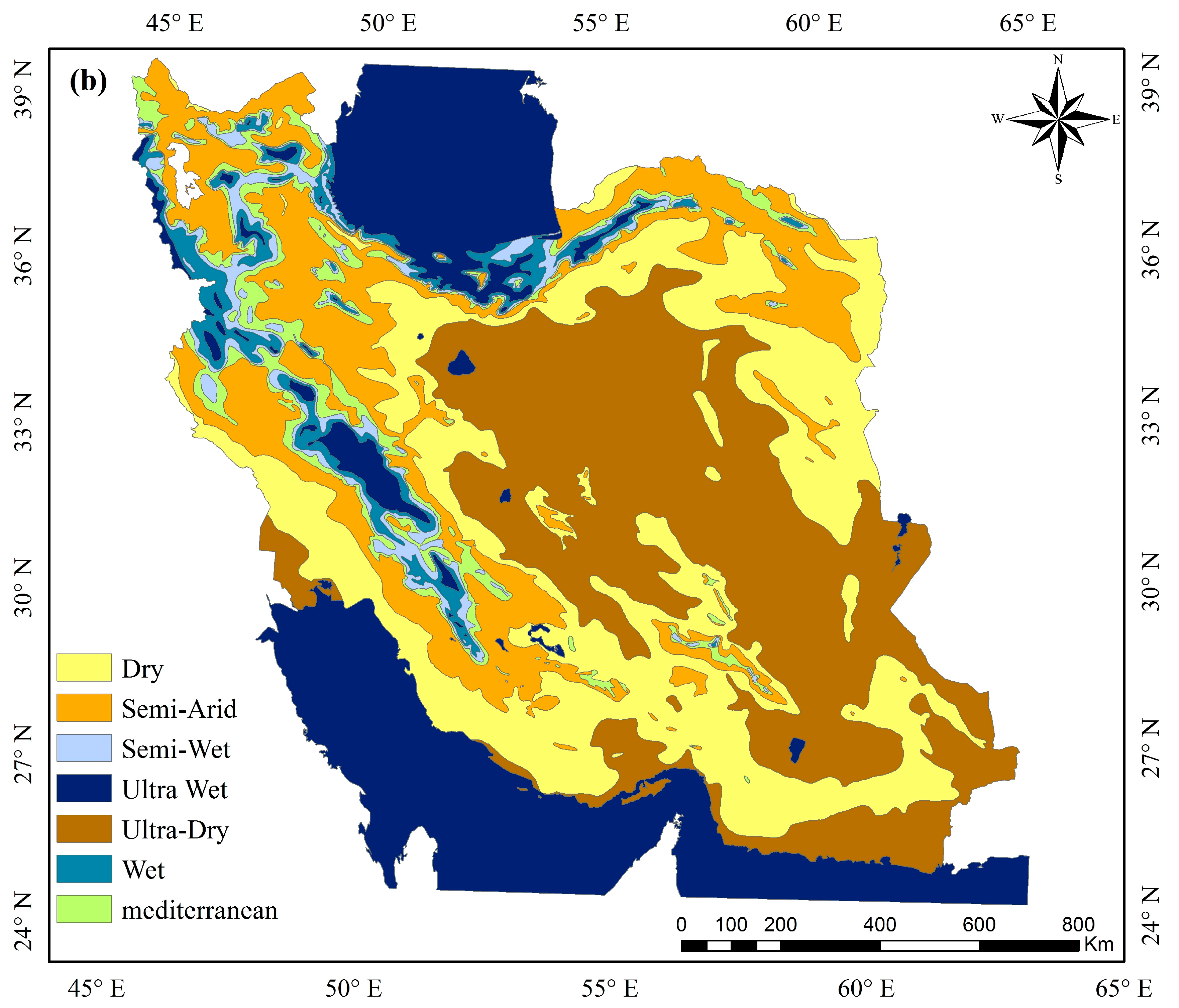



| Station | Elevation | Longitude | Latitude |
|---|---|---|---|
| Ahvaz | 22.5 | 48°40′ | 31°20′ |
| Arak | 1708 | 49°46′ | 34°06′ |
| Ardebil | 1332 | 48°17′ | 38°15′ |
| Banda Abbas | 9.8 | 56°22′ | 27°13′ |
| Birjand | 1491 | 59°12′ | 32°52′ |
| Bojnourd | 1112 | 57°16′ | 37°28′ |
| Boushehr | 19.6 | 50°50′ | 28°59′ |
| Gorgan | 13.3 | 54°16′ | 36°51′ |
| Hamedan | 1679 | 48°43′ | 35°12′ |
| Ilam | 1337 | 46°26′ | 33°38′ |
| Isfahan | 1550 | 51°40′ | 32°37′ |
| Karaj | 1312 | 50°54′ | 35°55′ |
| Kerman | 1753 | 56°58′ | 30°15′ |
| Kermanshah | 1318 | 47°09′ | 34°24′ |
| Khoramabad | 1147 | 48°17′ | 33°26′ |
| Qom | 877 | 50°51′ | 32°42′ |
| Qazvin | 1279 | 50°03′ | 36°15′ |
| Mashhad | 999 | 59°38′ | 36°16′ |
| Rasht | 36.7 | 49°39′ | 37°12′ |
| Sanandaj | 1373 | 47°00′ | 35°20′ |
| Semnan | 1130 | 53°33′ | 35°35′ |
| Shahre kord | 2048 | 50°51′ | 32°17′ |
| Shiraz | 1484 | 52°36′ | 29°32′ |
| Sari | 23 | 53°00′ | 36°33′ |
| Tabriz | 1361 | 46°17′ | 38°50′ |
| Tehran | 1190 | 51°19′ | 35°41′ |
| Urmia | 1315 | 45°05′ | 37°32′ |
| Yasouj | 1831 | 51°41′ | 30°50′ |
| Yazd | 1273 | 54°17′ | 31°54′ |
| Zahedan | 1370 | 60°33′ | 29°28′ |
| Zanjan | 1663 | 48°29′ | 36°41′ |
| Scenarios | Radiative Forcing | Concentration of Carbon Dioxide(ppm) | Temperature (C°) | Pathway |
|---|---|---|---|---|
| RCP2.6 | 3 W/m2 | 490–530 | 1.5 | Peak and Decline |
| RCP4.5 | 4.5 W/m2 | 580–720 | 2.4 | Stabilization without overshoot pathway |
| RCP6 | 6 W/m2 | 720–1000 | 3 | Stabilization without overshoot pathway |
| RCP8.5 | 8.5 W/m2 | 4.8 | Rising radiative forcing pathway |
| Models | Institute | Resolution |
|---|---|---|
| CSIRO-Mk3.6.0 | Commonwealth Scientific and Industrial Research Organization (CSIRO), Canberra, Australia | 1.88° × 1.88° |
| CCSM4 | National Center for Atmospheric Research (NSAR), Boulder, CO, USA | 1.25° × 0.94° |
| GFDL-ESM2g | Geophysical Fluid Dynamics Laboratory (NOAA), Princeton, NJ, USA | 2.00° × 2.02° |
| HadGEM2-es | Met Office Hadley Center (MOHC), Exeter, UK | 1.88° × 1.25° |
| Station | Model | RMSE | RMSE/SD < 0.65 | MAE | Station | RMSE | RMSE/SD < 0.65 | MAE |
|---|---|---|---|---|---|---|---|---|
| Ardebil | GFDL-ESM2g | 10.64 | 0.43 | 8.32 | Hamedan | 15.57 | 0.29 | 12.33 |
| HadGEM2-es | 69.39 | 2.83 | 38.15 | 42.06 | 0.78 | 136.63 | ||
| CSIRO-Mk3.6.0 | 10.1 | 0.41 | 8.31 | 29.03 | 0.54 | 21.73 | ||
| CCSM4 | 10.33 | 0.42 | 8.31 | 20.76 | 0.38 | 14.17 | ||
| SD observed | 24.5 | - | - | - | 54 | - | - | |
| Arak | GFDL-ESM2g | 10.28 | 0.27 | 6.76 | Ilam | 38.5 | 0.44 | 62.58 |
| HadGEM2-es | 260.71 | 6.95 | 89.92 | 54.5 | 0.63 | 161.13 | ||
| CSIRO-Mk3.6.0 | 10.4 | 0.28 | 14.38 | 10.11 | 0.12 | 8.3 | ||
| CCSM4 | 11.44 | 0.31 | 8.54 | 136.74 | 1.57 | 49.44 | ||
| SD observed | 37.5 | - | - | - | 87 | - | - | |
| Urmia | GFDL-ESM2g | 15.64 | 0.12 | 11.82 | Karaj | 10.56 | 0.10 | 7.1 |
| HadGEM2-es | 270.27 | 2.05 | 88.4 | 19.09 | 0.19 | 12.79 | ||
| CSIRO-Mk3.6.0 | 11.2 | 0.08 | 11.95 | 8.6 | 0.09 | 12.66 | ||
| CCSM4 | 12.84 | 0.10 | 9.24 | 9.06 | 0.09 | 4.97 | ||
| SD observed | 132 | - | - | - | 101 | - | - | |
| Bandar abbas | GFDL-ESM2g | 18.76 | 0.18 | 11.94 | Kerman | 8 | 0.14 | 4.97 |
| HadGEM2-es | 108.99 | 1.04 | 45.63 | 11.5 | 0.20 | 7.57 | ||
| CSIRO-Mk3.6.0 | 20.1 | 0.19 | 14.14 | 7.2 | 0.12 | 6.98 | ||
| CCSM4 | 20.36 | 0.19 | 12.14 | 8.46 | 0.15 | 5.04 | ||
| SD observed | 105 | - | - | - | 58 | - | - | |
| Birjand | GFDL-ESM2g | 7.32 | 0.42 | 3.82 | Kermanshah | 41.24 | 0.21 | 17.54 |
| HadGEM2-es | 24.84 | 1.42 | 14.66 | 73.45 | 0.37 | 21.32 | ||
| CSIRO-Mk3.6.0 | 6.53 | 0.37 | 5.08 | 24 | 0.12 | 11.25 | ||
| CCSM4 | 7.04 | 0.40 | 4.02 | 25.11 | 0.13 | 17.58 | ||
| SD observed | 17.5 | - | - | - | 198 | - | - | |
| Bojnourd | GFDL-ESM2g | 11.52 | 0.18 | 7.78 | Khorram abad | 8.05 | 0.06 | 4.97 |
| HadGEM2-es | 22.27 | 0.34 | 15.18 | 11.5 | 0.09 | 7.57 | ||
| CSIRO-Mk3.6.0 | 10.9 | 0.17 | 8.89 | 11.2 | 0.08 | 6.98 | ||
| CCSM4 | 21.76 | 0.33 | 15.82 | 8.46 | 0.06 | 5.04 | ||
| SD observed | 65 | - | - | - | 135 | - | - | |
| Boushehr | GFDL-ESM2g | 83.75 | 0.88 | 142.12 | Ahvaz | 25.24 | 0.20 | 16.4 |
| HadGEM2-es | 70.3 | 0.74 | 287.07 | 85.45 | 0.68 | 36.35 | ||
| CSIRO-Mk3.6.0 | 19.17 | 0.20 | 16.2 | 29.04 | 0.23 | 21.25 | ||
| CCSM4 | 34.3 | 0.36 | 34.3 | 29.49 | 0.24 | 17.58 | ||
| SD observed | 95 | - | - | - | 125 | - | - | |
| Shahre kord | GFDL-ESM2g | 2.65 | 0.10 | 16.15 | Yasuj | 1.44 | 0.06 | 16.19 |
| HadGEM2-es | 6.36 | 0.24 | 52.17 | 6.36 | 0.25 | 75.17 | ||
| CSIRO-Mk3.6.0 | 9.6 | 0.36 | 7.65 | 5.4 | 0.22 | 15.65 | ||
| CCSM4 | 5.6 | 0.21 | 12.85 | 5.68 | 0.23 | 10.82 | ||
| SD observed | 27 | - | - | - | 25 | - | - | |
| Isfahan | GFDL-ESM2g | 5.67 | 0.16 | 4.13 | Mashahd | 58.55 | 2.34 | 34.05 |
| HadGEM2-es | 64.61 | 1.82 | 29.48 | 10.96 | 0.44 | 8.94 | ||
| CSIRO-Mk3.6.0 | 5.1 | 0.14 | 3.62 | 7.8 | 0.31 | 11.51 | ||
| CCSM4 | 5.86 | 0.17 | 4.73 | 8.88 | 0.36 | 7.51 | ||
| SD observed | 35.5 | - | - | - | 25 | - | - | |
| Qom | GFDL-ESM2g | 11.11 | 0.13 | 7.15 | Sanandaj | 41.45 | 0.92 | 17.15 |
| HadGEM2-es | 16.2 | 0.19 | 15.12 | 68.85 | 1.53 | 22.41 | ||
| CSIRO-Mk3.6.0 | 19.52 | 0.23 | 15.65 | 21.2 | 0.47 | 13.89 | ||
| CCSM4 | 8.56 | 0.10 | 7.85 | 22.11 | 0.49 | 16.75 | ||
| SD observed | 84 | - | - | - | 45 | - | - | |
| Qazvin | GFDL-ESM2g | 7.25 | 0.12 | 7.8 | Semnan | 6.58 | 0.14 | 5.15 |
| HadGEM2-es | 9.59 | 0.15 | 12.65 | 6.4 | 0.14 | 36.65 | ||
| CSIRO-Mk3.6.0 | 7.75 | 0.12 | 8.81 | 5.1 | 0.11 | 3.62 | ||
| CCSM4 | 6.71 | 0.11 | 8.91 | 5.21 | 0.11 | 4.51 | ||
| SD observed | 63 | - | - | - | 47 | - | - | |
| Gorgan | GFDL-ESM2g | 13.39 | 0.23 | 9.58 | Shiraz | 3.52 | 0.05 | 19.19 |
| HadGEM2-es | 29.95 | 0.52 | 19.35 | 9.98 | 0.15 | 25.17 | ||
| CSIRO-Mk3.6.0 | 24.59 | 0.42 | 16.5 | 1.2 | 0.02 | 7.85 | ||
| CCSM4 | 13.39 | 0.23 | 11.4 | 7.61 | 0.12 | 11.12 | ||
| SD observed | 58 | - | - | - | 65 | - | - |
| Station | Regression Equations | R2 | RMSE | SD | RMSE/SD < 0.65 | MAE |
|---|---|---|---|---|---|---|
| Ahvaz | R = 0.111P + 5.50 | 0.68 | 0.6 | 1.2 | 0.5 | 0.08 |
| Arak | R = −0.4406P + 4.9161 | 0.55 | 0.29 | 2.33 | 0.12446352 | 0.08 |
| Ardebil | R = −2.6982P2 + 4.423P + 2.29 | 0.87 | 0.26 | 2.65 | 0.09811321 | 0.04 |
| Banda Abbas | R = −0.5223P + 7.15 | 0.85 | 1.12 | 2.68 | 0.41791045 | 0.13 |
| Birjand | R = −1.2727P + 5.69 | 0.69 | 0.8 | 2.9 | 0.27586207 | 0.15 |
| Bojnourd | R = 0.6157P + 3.53 | 0.71 | 0.58 | 3.2 | 0.18125 | 0.11 |
| Boushehr | R = −3.401P2 + 6.329P + 5.63 | 0.85 | 2.21 | 5.6 | 0.39464286 | 0.23 |
| Gorgan | R = −0.3555P + 4.25 | 0.9 | 0.16 | 2.5 | 0.064 | 0.03 |
| Hamedan | R = 0.2458P + 4.10 | 0.91 | 0.34 | 3.96 | 0.08585859 | 0.07 |
| Ilam | R = −0.6888P + 2.19 | 0.84 | 0.66 | 4.5 | 0.14666667 | 1.41 |
| Isfahan | R = −0.2607P + 5.44 | 0.69 | 0.4 | 3.5 | 0.11428571 | 0.04 |
| Karaj | R = 0.1628P + 4.59 | 0.54 | 0.35 | 2.1 | 0.16666667 | 0.07 |
| Kerman | R = −3.1598P + 6.53 | 0.65 | 0.64 | 2.15 | 0.29767442 | 0.09 |
| Kermanshah | R = −0.0102P + 4.64 | 0.78 | 0.28 | 3.1 | 0.09032258 | 0.05 |
| Khoramabad | R = −0.2267P + 4.93 | 0.64 | 0.27 | 2.1 | 0.12857143 | 0.05 |
| Qom | R = −35.975P2 + 27.186P − 3.1351 | 0.81 | 0.99 | 2.7 | 0.36666667 | 0.89 |
| Qazvin | R = 0.0469P + 4.3155 | 0.63 | 0.23 | 3.2 | 0.071875 | 0.08 |
| Mashhad | R = −0.128P + 4.67 | 0.9 | 0.31 | 2.5 | 0.124 | 0.06 |
| Rasht | R = −1.2644P + 4.18 | 0.58 | 3.84 | 6.3 | 0.60952381 | 0.05 |
| Sanandaj | R = 0.0737P + 4.3091 | 0.84 | 0.79 | 3.01 | 0.26245847 | 0.15 |
| Semnan | R = −0.5948P + 4.99 | 0.52 | 0.56 | 2.2 | 0.25454545 | 0.1 |
| Shahre kord | R = −0.2402P + 5.07 | 0.67 | 0.32 | 2 | 0.16 | 0.004 |
| Shiraz | R = −0.174P + 5.7783 | 0.66 | 0.62 | 2 | 0.31 | 0.09 |
| Sari | R = 0.0328P + 3.99 | 0.81 | 0.31 | 2 | 0.155 | 0.06 |
| Tabriz | R = −1.2084P + 5.21 | 0.82 | 0.59 | 2 | 0.295 | 0.11 |
| Tehran | R = −0.1245P + 4.37 | 0.63 | 0.3 | 2 | 0.15 | 0.08 |
| Urmia | R = −0.1517P + 4.45 | 0.45 | 0.36 | 2 | 0.18 | 0.07 |
| Yasouj | R = 0.0694P + 4.96 | 0.57 | 0.49 | 2 | 0.245 | 0.07 |
| Yazd | R = −5.2782P + 6.3442 | 0.71 | 2.53 | 2 | 1.265 | 0.49 |
| Zahedan | R = −2.1561P + 6.7889 | 0.58 | 1.22 | 2 | 0.61 | 0.15 |
| Zanjan | R = 0.2839P + 3.5779 | 0.69 | 0.41 | 2 | 0.205 | 0.08 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Farokhzadeh, B.; Bazrafshan, O.; Singh, V.P.; Choobeh, S.; Mohseni Saravi, M. Future Rainfall Erosivity over Iran Based on CMIP5 Climate Models. Water 2022, 14, 3861. https://doi.org/10.3390/w14233861
Farokhzadeh B, Bazrafshan O, Singh VP, Choobeh S, Mohseni Saravi M. Future Rainfall Erosivity over Iran Based on CMIP5 Climate Models. Water. 2022; 14(23):3861. https://doi.org/10.3390/w14233861
Chicago/Turabian StyleFarokhzadeh, Behnoush, Ommolbanin Bazrafshan, Vijay P. Singh, Sepide Choobeh, and Mohsen Mohseni Saravi. 2022. "Future Rainfall Erosivity over Iran Based on CMIP5 Climate Models" Water 14, no. 23: 3861. https://doi.org/10.3390/w14233861
APA StyleFarokhzadeh, B., Bazrafshan, O., Singh, V. P., Choobeh, S., & Mohseni Saravi, M. (2022). Future Rainfall Erosivity over Iran Based on CMIP5 Climate Models. Water, 14(23), 3861. https://doi.org/10.3390/w14233861








