Optimization of a Laboratory Rainfall Simulator to Be Representative of Natural Rainfall
Abstract
:1. Introduction
2. Materials and Methods
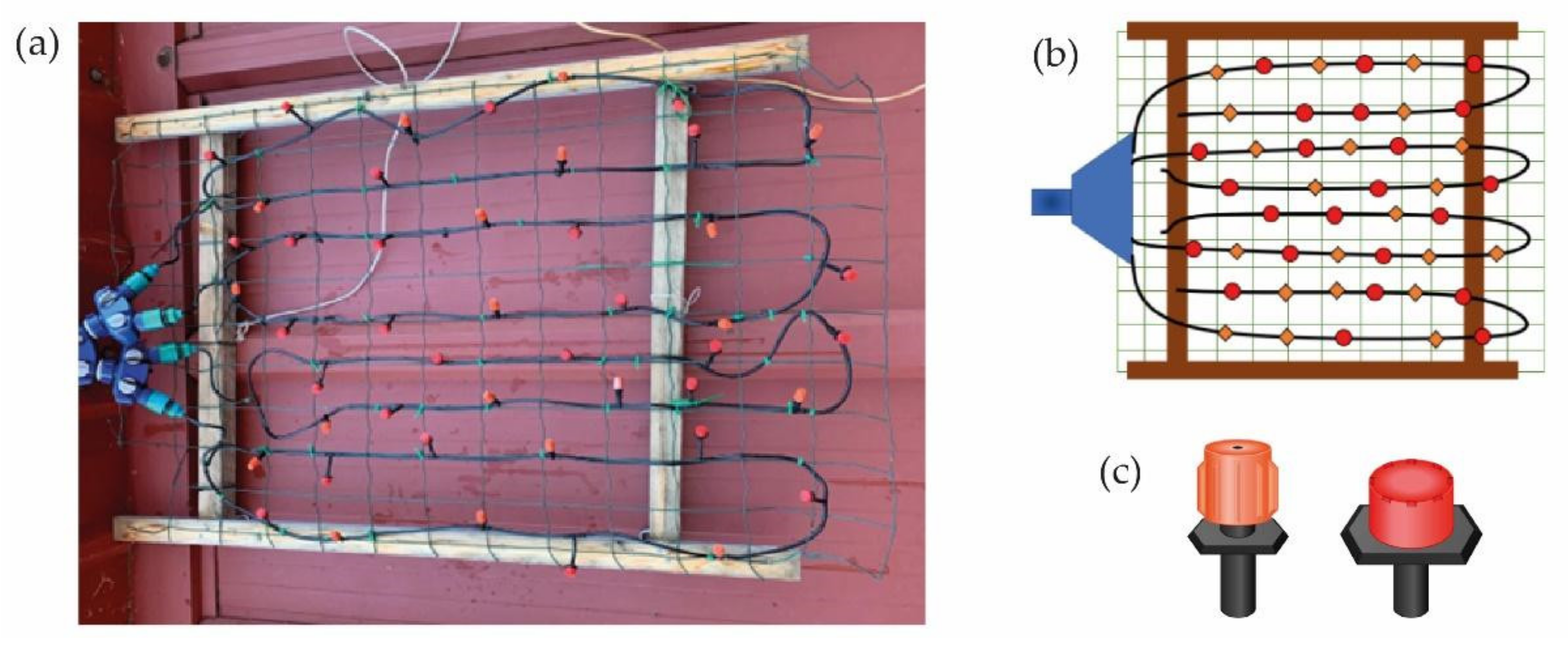
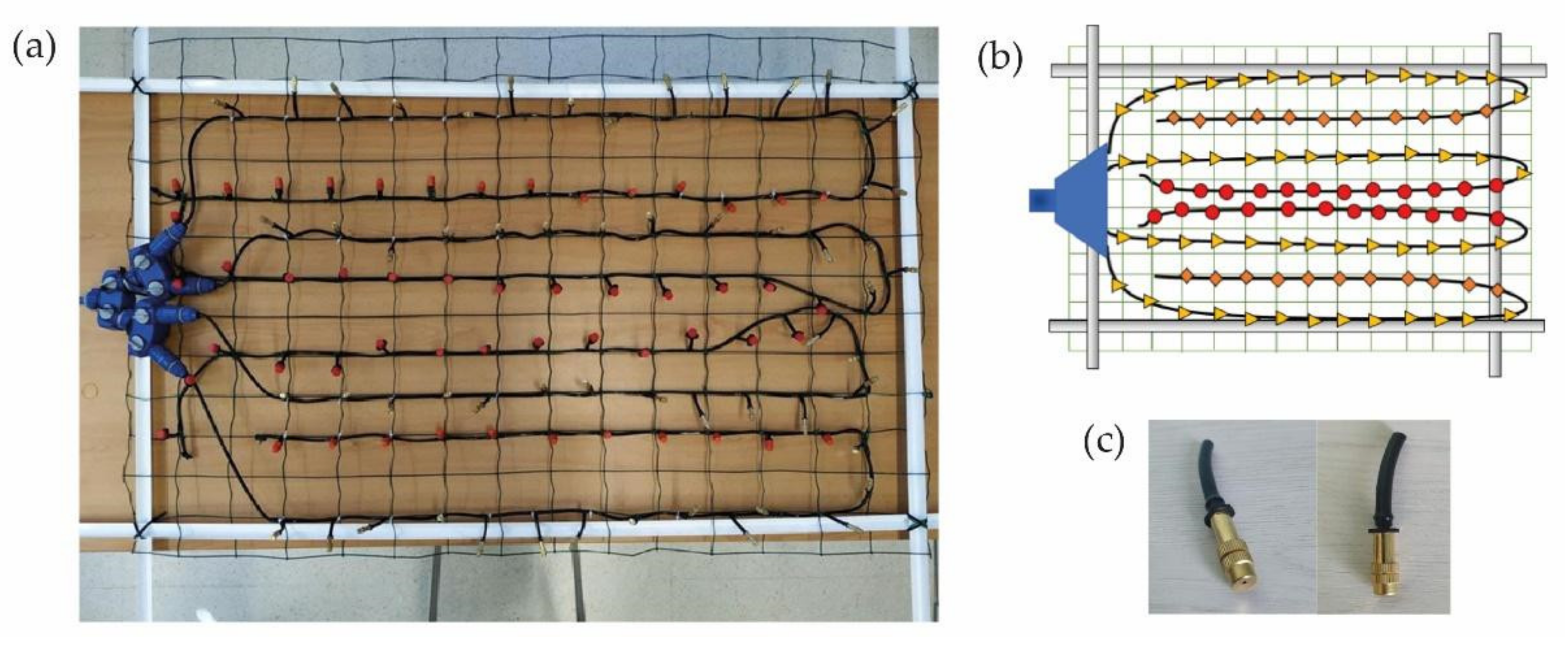
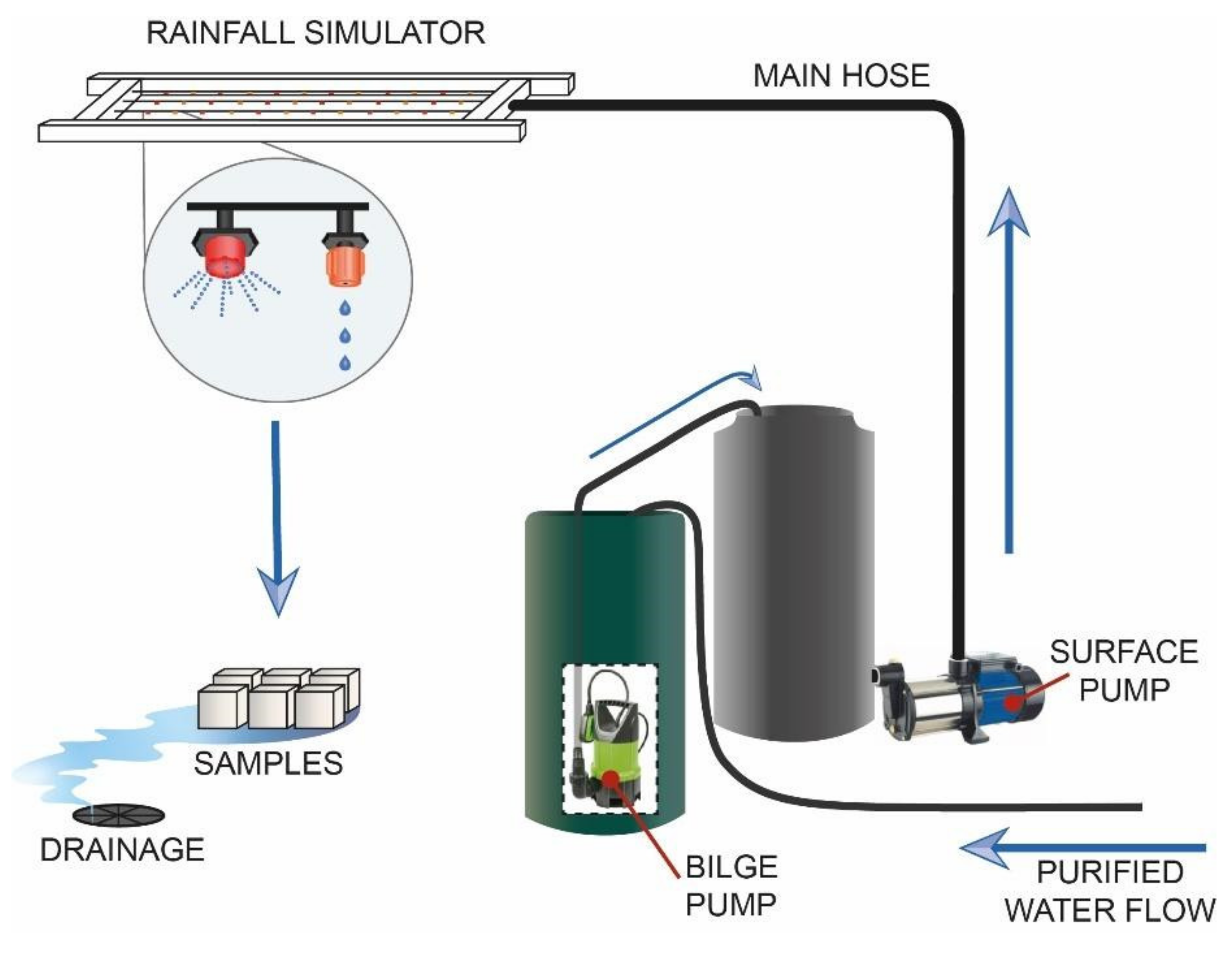
2.1. Simulator Structure Design
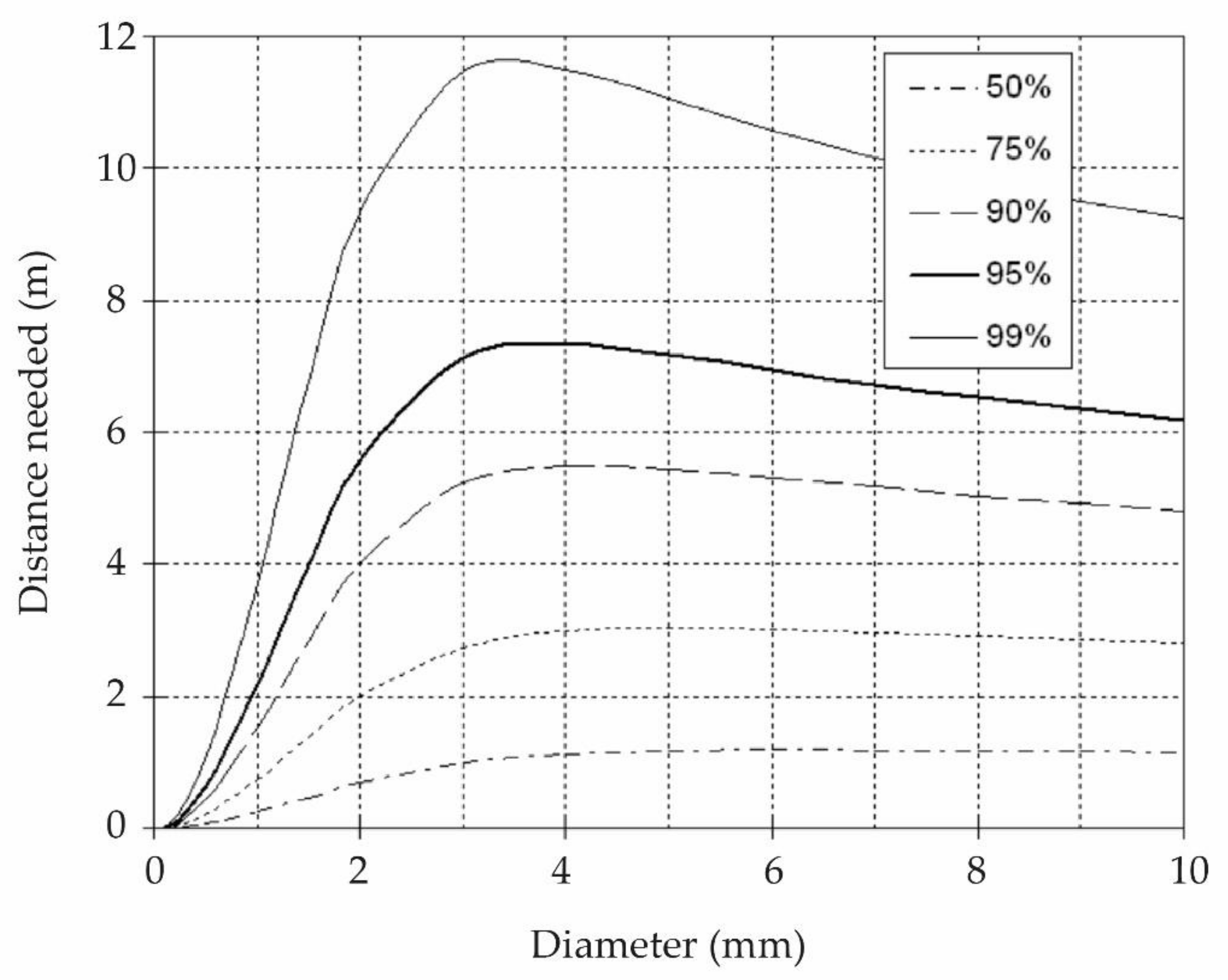
2.2. Rainfall Simulator Calibration
3. Results
Christiansen Uniformity Coefficient Results
4. Discussion
5. Conclusions
- Achieving a spectrum of mini sprinklers with droppers that produce droplet sizes similar to natural droplet sizes.
- Analyzing the distance required by a droplet to reach terminal velocity.
- Appropriate location that provides sufficient height to reach terminal velocity.
- Keeping the simulator sheltered from wind currents that may disperse water droplets.
- Versatility of the simulator to represent rainfall in different seasons, regions, or even in polluted atmospheres.
- Searching for homogeneity of results using the CUC.
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Mastoi, D. Design and Construction of Rainfall Simulator for Determination of Erosion. Doctoral Thesis, Sindh Agriculture University, Tando Jam, Pakistan, 2022. [Google Scholar] [CrossRef]
- Mhaske, S.N.; Pathak, K.; Basak, A. A Comprehensive Design of Rainfall Simulator for the Assessment of Soil Erosion in the Laboratory. Catena 2019, 172, 408–420. [Google Scholar] [CrossRef]
- Vergni, L.; Todisco, F.; Vinci, A. Setup and Calibration of the Rainfall Simulator of the Masse Experimental Station for Soil Erosion Studies. Catena 2018, 167, 448–455. [Google Scholar] [CrossRef]
- Lassu, T.; Seeger, M.; Peters, P.; Keesstra, S.D. The Wageningen Rainfall Simulator: Set-up and Calibration of an Indoor Nozzle-Type Rainfall Simulator for Soil Erosion Studies. Land Degrad. Dev. 2015, 26, 604–612. [Google Scholar] [CrossRef]
- Aksoy, H.; Unal, N.E.; Cokgor, S.; Gedikli, A.; Yoon, J.; Koca, K.; Inci, S.B.; Eris, E. A Rainfall Simulator for Laboratory-Scale Assessment of Rainfall-Runoff-Sediment Transport Processes over a Two-Dimensional Flume. Catena 2012, 98, 63–72. [Google Scholar] [CrossRef]
- Iserloh, T.; Fister, W.; Seeger, M.; Willger, H.; Ries, J.B. A Small Portable Rainfall Simulator for Reproducible Experiments on Soil Erosion. Soil Tillage Res. 2012, 124, 131–137. [Google Scholar] [CrossRef]
- Stroosnijder, L. Measurement of Erosion: Is It Possible? Catena 2005, 64, 162–173. [Google Scholar] [CrossRef]
- Cerdá, A. Simuladores de Lluvia y Su Aplicación En Geomorfología: Estado de La Cuestión. Cuad. Investig. Geogr./Geogr. Res. Lett. 1999, 25, 45–84. [Google Scholar] [CrossRef] [Green Version]
- Navas, A.; Alberto, F.; Machín, J.; Galán, A. Design and operation of a rainfall simulator for field studies of runoff and soil erosion. Soil Technol. 1990, 3, 385–397. [Google Scholar] [CrossRef] [Green Version]
- Meyer, L.D. Simulation of Rainfall for Soil Erosion Research. Trans. ASAE 1965, 8, 63–65. [Google Scholar] [CrossRef]
- González-Campelo, D.; Fernández-Raga, M.; Gómez-Gutiérrez, Á.; Guerra-Romero, M.I.; González-Domínguez, J.M. Extraordinary Protective Efficacy of Graphene Oxide over the Stone-Based Cultural Heritage. Adv. Mater. Interfaces 2021, 8, 2101012. [Google Scholar] [CrossRef]
- Perakis, P.; Schellewald, C.; Kebremariam, K.F.; Theoharis, T. Simulating Erosion on Cultural Heritage Monuments. In Proceedings of the 20th International Conference on Cultural Heritage and New Technologies (CHNT20), Vienna, Austria, 2–4 November 2015; Volume 17. [Google Scholar]
- Emmerich, W.E.; Cox, J.R. Hydrologic Characteristics Immediately after Seasonal Burning on Introduced and Native Grasslands. J. Range Manag. 1992, 45, 476. [Google Scholar] [CrossRef]
- Wang, X.; Liu, Z.; Chen, H. Investigating Flood Impact on Crop Production under a Comprehensive and Spatially Explicit Risk Evaluation Framework. Agriculture 2022, 12, 484. [Google Scholar] [CrossRef]
- Sharpley, A.; Kleinman, P. Effect of Rainfall Simulator and Plot Scale on Overland Flow and Phosphorus Transport. J. Environ. Qual. 2003, 32, 2172–2179. [Google Scholar] [CrossRef] [Green Version]
- Tamošiūnaitė, M.; Tamošiūnas, S.; Daukšas, V.; Tamošiūnienė, M.; Žilinskas, M. Prediction of Electromagnetic Waves Attenuation Due to Rain in the Localities of Lithuania. Elektron. Elektrotech. 2010, 105, 9–12. [Google Scholar]
- Nnadi, E.; Newman, A.; Duckers, L.; Coupe, S.; Charlesworth, S. Design and Validation of a Test Rig to Simulate High Rainfall Events for Infiltration Studies of Permeable Pavement Systems. J. Irrig. Drain. Eng. 2012, 138, 1333–1339. [Google Scholar] [CrossRef]
- Ngezahayo, E.; Burrow, M.; Ghataora, G. Calibration of the Simple Rainfall Simulator for Investigating Soil Erodibility in Unpaved Roads. Int. J. Civ. Infrastruct. 2021, 4, 144–156. [Google Scholar] [CrossRef]
- Nielsen, K.T.; Moldrup, P.; Thorndahl, S.; Nielsen, J.E.; Duus, L.B.; Rasmussen, S.H.; Uggerby, M.; Rasmussen, M.R. Automated Rainfall Simulator for Variable Rainfall on Urban Green Areas. Hydrol. Process. 2019, 33, 3364–3377. [Google Scholar] [CrossRef] [Green Version]
- Yakubu, M.L.; Yusop, Z. Adaptability of Rainfall Simulators as a Research Tool on Urban Sealed Surfaces—A Review. Hydrol. Sci. J. 2017, 62, 996–1012. [Google Scholar] [CrossRef]
- Menezes Sanchez Macedo, P.; Ferreira Pinto, M.; Alves Sobrinho, T.; Schultz, N.; Altamir Rodrigues Coutinho, T.; Fonseca de Carvalho, D. A Modified Portable Rainfall Simulator for Soil Erosion Assessment under Different Rainfall Patterns. J. Hydrol. 2021, 596, 126052. [Google Scholar] [CrossRef]
- Zambon, N.; Johannsen, L.L.; Strauss, P.; Dostal, T.; Zumr, D.; Cochrane, T.A.; Klik, A. Splash Erosion Affected by Initial Soil Moisture and Surface Conditions under Simulated Rainfall. Catena 2021, 196, 104827. [Google Scholar] [CrossRef]
- Regmi, T.P.; Thompson, A.L. Rainfall Simulator for Laboratory Studies. Appl. Eng. Agric. 2000, 16, 641–647. [Google Scholar] [CrossRef]
- Monjo, R. Measure of Rainfall Time Structure Using the Dimensionless N-Index. Clim. Res. 2016, 67, 71–86. [Google Scholar] [CrossRef] [Green Version]
- Fernández-Raga, M.; Fraile, R.; Keizer, J.J.; Varela, M.E.; Castro, A.; Palencia, C.; Calvo, A.I.; Koenders, J.; Liliana, R.; Marqués, D.C. The Kinetic Energy of Rain Measured with an Optical Disdrometer: An Application to Splash Erosion. Atmos. Res. 2010, 96, 225–240. [Google Scholar] [CrossRef]
- Hudson, N.W. Soil Conservation; B.T. Batsford LTD: London, UK, 1971; ISBN 10: 0813823722. [Google Scholar]
- Laws, J.O. Measurements of the Fall-Velocity of Water-Drops and Raindrops. Eos Trans. Am. Geophys. Union 1941, 22, 709–921. [Google Scholar] [CrossRef]
- Živanović, N.; Rončević, V.; Spasić, M.; Ćorluka, S.; Polovina, S. Construction and Calibration of a Portable Rain Simulator Designed for the in Situ Research of Soil Resistance to Erosion. Soil Water Res. 2022, 17, 158–169. [Google Scholar] [CrossRef]
- Bubenzer, G.D. Rainfall Characteristics Important for Simulation; Department of Agriculture, Science and Education Administration: Tucson, AZ, USA, 1979; Volume 10, pp. 22–35. [Google Scholar]
- Van Boxel, J. Numerical Model for the Fall Speed of Rain Drops in a Rain Fall Simulator. I.C.E. Spec. Rep. 1998, 1, 77–85. [Google Scholar]
- Beard, K.V.; Prupacher, H.R. A Determination of the Terminal Velocity and Drag of Small Water Drops by Means of a Wind Tunnel. J. Atmos. Sci. 1969, 26, 1066–1072. [Google Scholar] [CrossRef]
- Gunn, R.; Kinzer, G.D. The Terminal Velocity of Fall for Water Droplets in Stagnant Air. J. Meteorol. 1949, 8, 249–253. [Google Scholar] [CrossRef]
- ASABE. Design and Installation of Micro-Irrigation Systems; American Society of Agricultural Engineers: St. Joseph, MI, USA, 1994. [Google Scholar]
- Fernández-Raga, M.; Palencia, C.; Keesstra, S.; Jordán, A.; Fraile, R.; Angulo-Martínez, M.; Cerdá, A. Splash Erosion: A Review with Unanswered Questions. Earth-Sci. Rev. 2017, 171, 463–477. [Google Scholar] [CrossRef] [Green Version]
- Glossary of Meteorology Rain. Gloss. Meteorol. 2000. Available online: https://glossary.ametsoc.org/wiki/Rain (accessed on 20 November 2022).
- Fernandez-Raga, M.; Castro, A.; Marcos, E.; Palencia, C.; Fraile, R. Weather Types and Rainfall Microstructure in Leon, Spain. Int. J. Climatol. 2017, 37, 1834–1842. [Google Scholar] [CrossRef]
- Fernández-Raga, M.; Castro, A.; Palencia, C.; Calvo, A.; Fraile, R. Rain Events on 22 October 2006 in León (Spain): Drop Size Spectra. Atmos. Res. 2009, 93, 619–635. [Google Scholar] [CrossRef]
- Vinci, A.; Todisco, F.; Vergni, L.; Torri, D. A Comparative Evaluation of Random Roughness Indices by Rainfall Simulator and Photogrammetry. Catena 2020, 188, 104468. [Google Scholar] [CrossRef]
- Todisco, F.; Vergni, L.; Vinci, A.; Torri, D. Infiltration and Bulk Density Dynamics with Simulated Rainfall Sequences. Catena 2022, 218, 106542. [Google Scholar] [CrossRef]

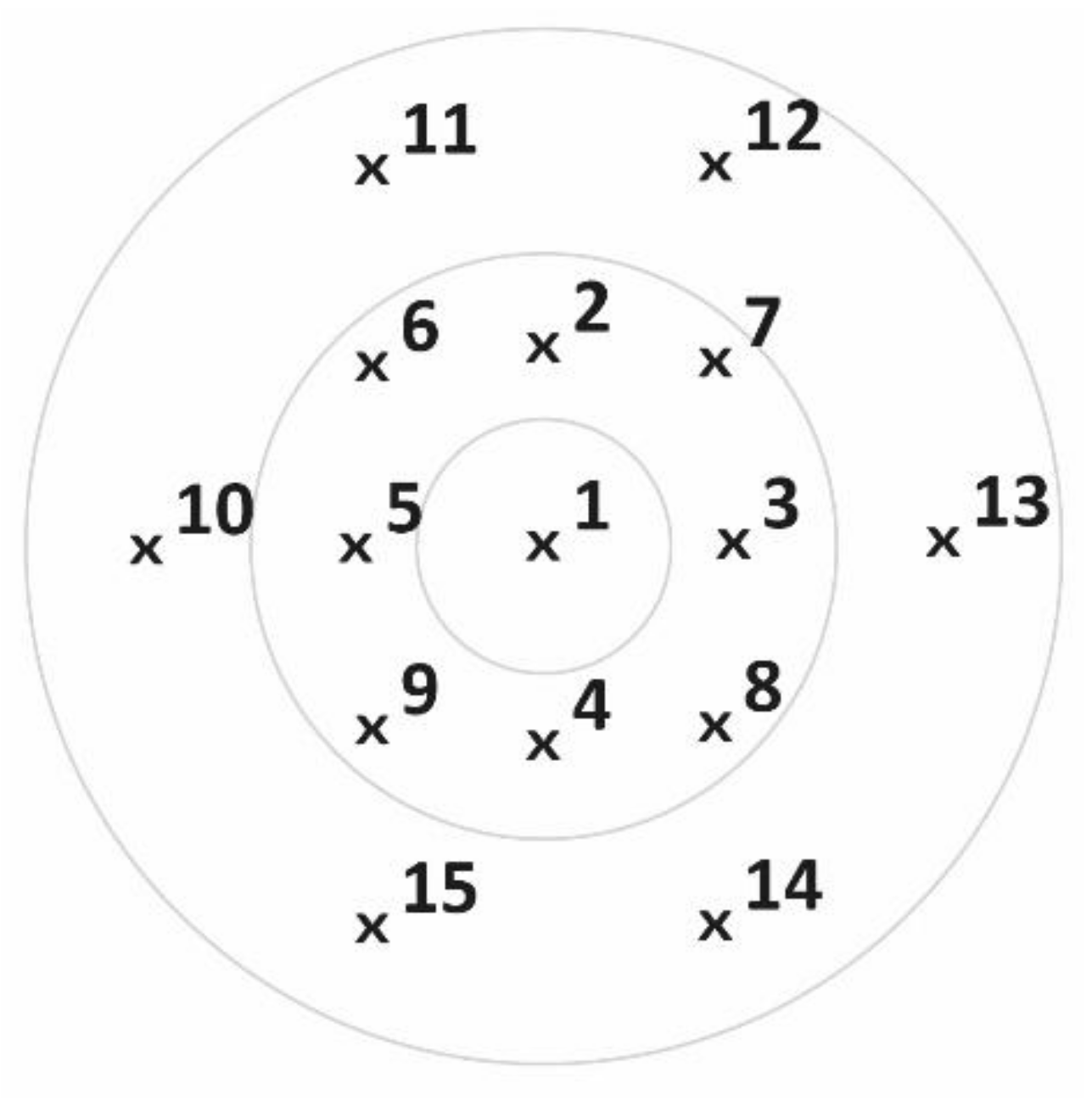

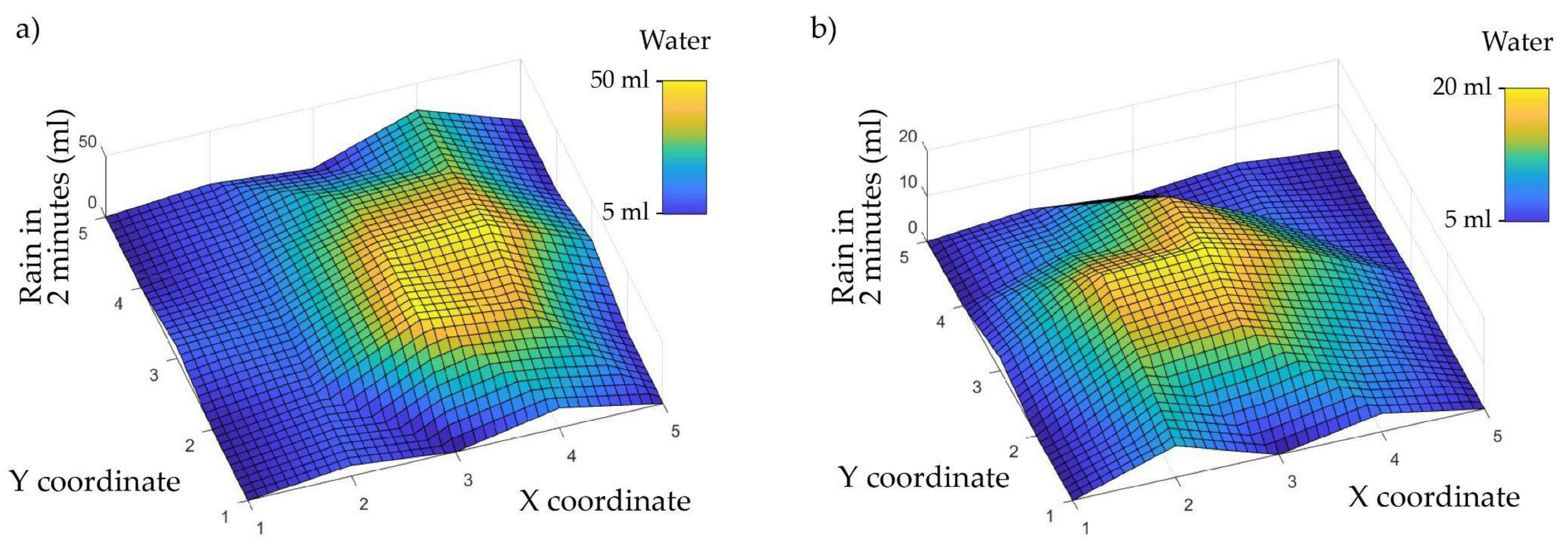
| Container No. | Test 1 (mL) | Test 2 (mL) | Test 3 (mL) | Test 4 (mL) | Mean (mL) |
|---|---|---|---|---|---|
| 1 | 41 | 44 | 51 | 53 | 47 |
| 2 | 46 | 40 | 57 | 58 | 50 |
| 3 | 52 | 39 | 55 | 55 | 50 |
| 4 | 36 | 22 | 38 | 32 | 32 |
| 5 | 14 | 11 | 13 | 16 | 14 |
| 6 | 8 | 11 | 10 | 10 | 10 |
| 7 | 37 | 43 | 41 | 38 | 40 |
| 8 | 39 | 29 | 34 | 39 | 35 |
| 9 | 9 | 10 | 14 | 11 | 11 |
| 10 | 11 | 10 | 13 | 6 | 10 |
| 11 | 8 | 10 | 9 | 8 | 9 |
| 12 | 18 | 10 | 18 | 16 | 16 |
| 13 | 18 | 12 | 19 | 18 | 17 |
| 14 | 35 | 20 | 29 | 26 | 28 |
| 15 | 5 | 4 | 10 | 9 | 7 |
| Container No. | Test 1 (mL) | Test 2 (mL) | Test 3 (mL) | Test 4 (mL) | Mean (mL) |
|---|---|---|---|---|---|
| 1 | 16 | 17 | 19 | 17 | 17 |
| 2 | 15 | 14 | 12 | 14 | 14 |
| 3 | 10 | 10 | 11 | 12 | 11 |
| 4 | 15 | 12 | 14 | 16 | 14 |
| 5 | 14 | 16 | 17 | 15 | 16 |
| 6 | 12 | 12 | 13 | 10 | 12 |
| 7 | 7 | 6 | 8 | 7 | 7 |
| 8 | 5 | 2 | 2 | 5 | 4 |
| 9 | 9 | 6 | 5 | 7 | 7 |
| 10 | 4 | 3 | 3 | 3 | 3 |
| 11 | 6 | 7 | 7 | 8 | 7 |
| 12 | 3 | 4 | 5 | 5 | 4 |
| 13 | 2 | 1 | 1 | 1 | 1 |
| 14 | 5 | 1 | 1 | 1 | 2 |
| 15 | 1 | 4 | 1 | 3 | 2 |
| CLASSIFICATION | CUC (%) |
|---|---|
| Excellent | >90 |
| Good | 80–90 |
| Fair | 70–80 |
| Poor | 60–70 |
| Unacceptable | <60 |
| Cont.* 1 | Cont. 2 | Cont. 3 | Cont. 4 | Cont. 5 | Cont. 6 | Cont. 7 | Cont. 8 | Cont. 9 | Cont. 10 | Cont. 11 | Cont. 12 | Cont. 13 | Cont. 14 | Cont.15 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| CUC-W | 89.9 | 85.6 | 88.8 | 84.4 | 88.9 | 91.0 | 94.3 | 89.4 | 86.4 | 80.0 | 91.4 | 87.5 | 85.8 | 83.6 | 64.3 |
| CUC-A | 94.9 | 93.6 | 93.0 | 91.2 | 93.5 | 92.6 | 92.9 | 57.1 | 81.5 | 88.5 | 92.9 | 82.4 | 70.0 | 25.0 | 44.4 |
| CLASSIFICATION | L/m2/h |
|---|---|
| Light | <3.5 |
| Moderate | 2.5–7.6 |
| Heavy | 7.6–50 |
| Torrential | >50 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fernández-Raga, M.; Rodríguez, I.; Caldevilla, P.; Búrdalo, G.; Ortiz, A.; Martínez-García, R. Optimization of a Laboratory Rainfall Simulator to Be Representative of Natural Rainfall. Water 2022, 14, 3831. https://doi.org/10.3390/w14233831
Fernández-Raga M, Rodríguez I, Caldevilla P, Búrdalo G, Ortiz A, Martínez-García R. Optimization of a Laboratory Rainfall Simulator to Be Representative of Natural Rainfall. Water. 2022; 14(23):3831. https://doi.org/10.3390/w14233831
Chicago/Turabian StyleFernández-Raga, María, Indira Rodríguez, Pablo Caldevilla, Gabriel Búrdalo, Almudena Ortiz, and Rebeca Martínez-García. 2022. "Optimization of a Laboratory Rainfall Simulator to Be Representative of Natural Rainfall" Water 14, no. 23: 3831. https://doi.org/10.3390/w14233831
APA StyleFernández-Raga, M., Rodríguez, I., Caldevilla, P., Búrdalo, G., Ortiz, A., & Martínez-García, R. (2022). Optimization of a Laboratory Rainfall Simulator to Be Representative of Natural Rainfall. Water, 14(23), 3831. https://doi.org/10.3390/w14233831










