Smooth Spatial Modeling of Extreme Mediterranean Precipitation
Abstract
:1. Introduction
2. Study Area and Data
2.1. Rainfall Station Data
2.2. CHIRPS Data Set
2.3. Inter-Covariate Correlation Analysis
3. Statistical Methods
3.1. Extreme Value Theory
3.2. Smooth Spatial Modeling for Extremes
3.2.1. Generalized Linear Models
3.2.2. Artificial Neural Networks
- Shuffle the data set randomly.
- Split the data set into k = 10 folds.
- For each fold:
- –
- Define that fold as the validation data set.
- –
- Define the remaining folds as the training data set.
- –
- Fit the model on the training set and evaluate on the validation set.
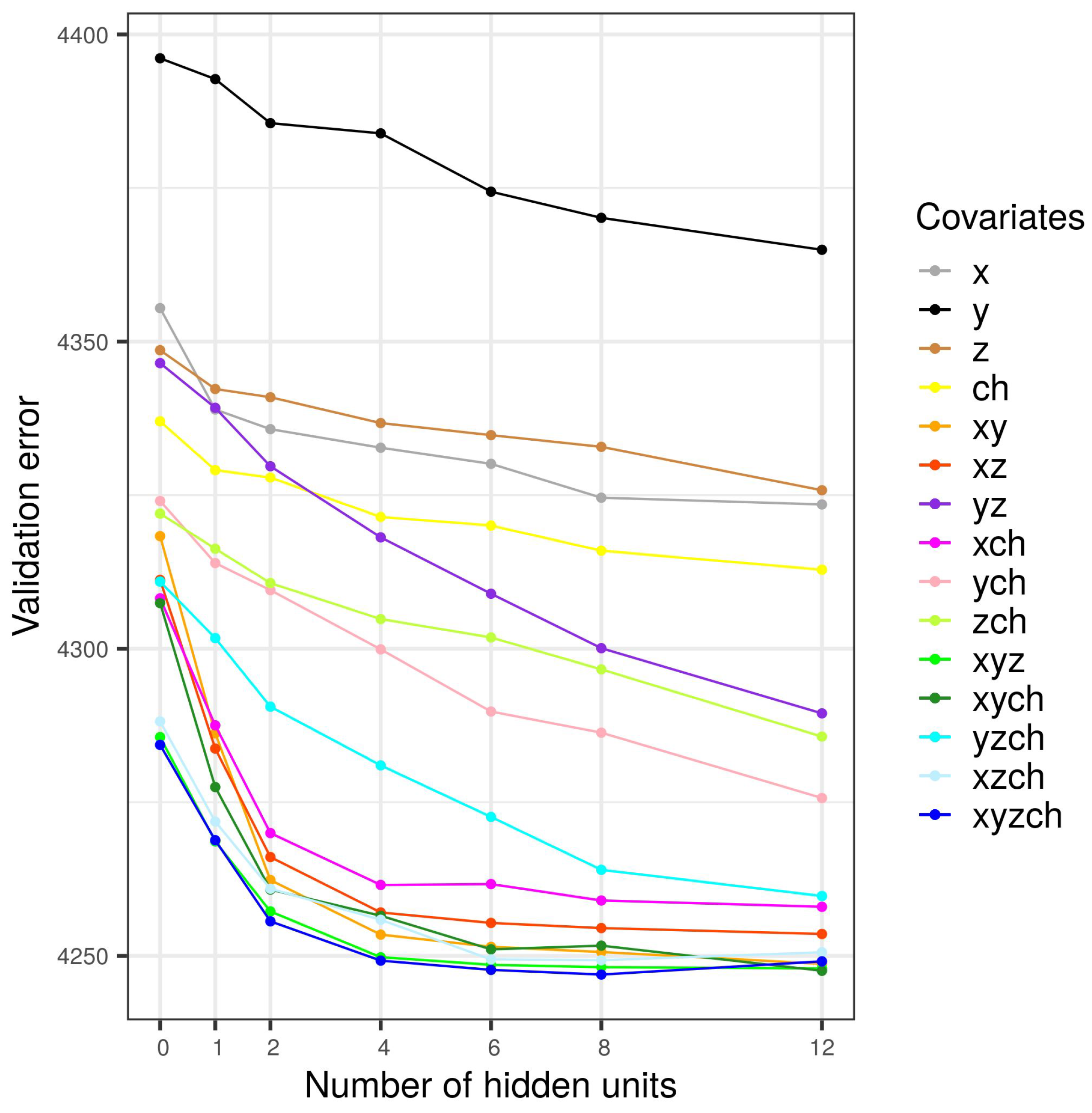
- The error is calculated as the average of the error over all validation sets. The optimal number of hidden units corresponds to the minimum of errors.
4. Results
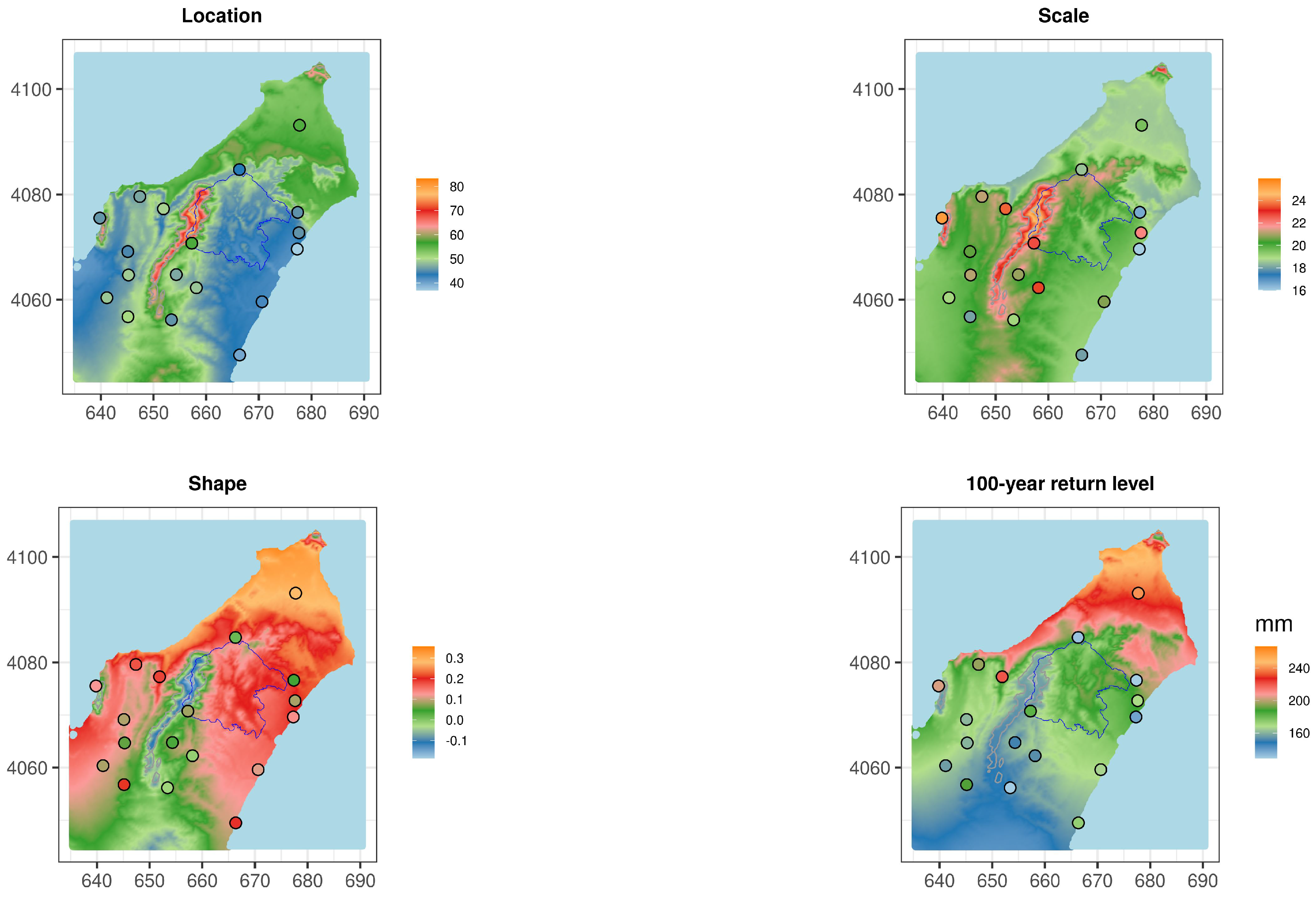
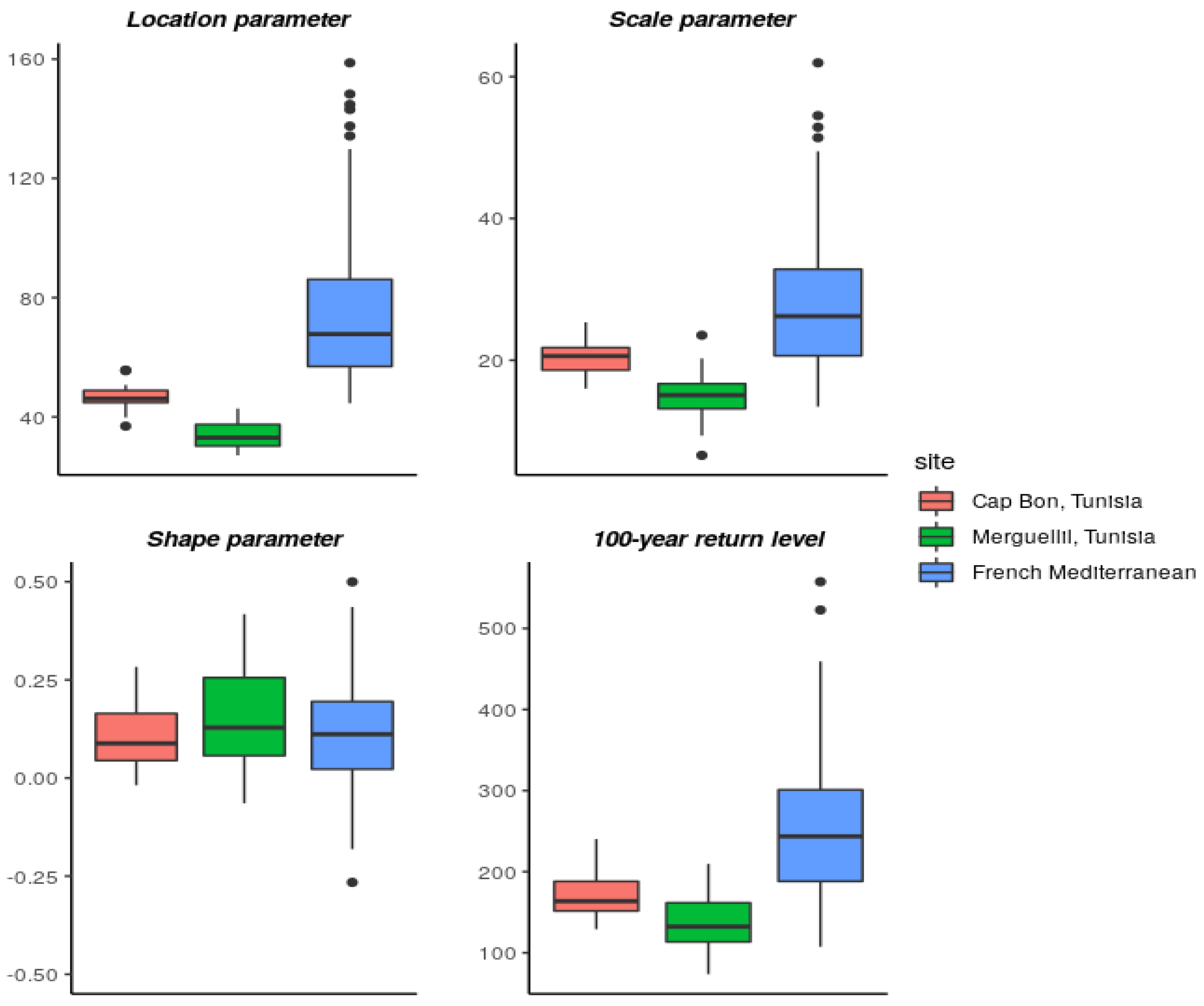
4.1. Pointwise GEV Parameters Estimation
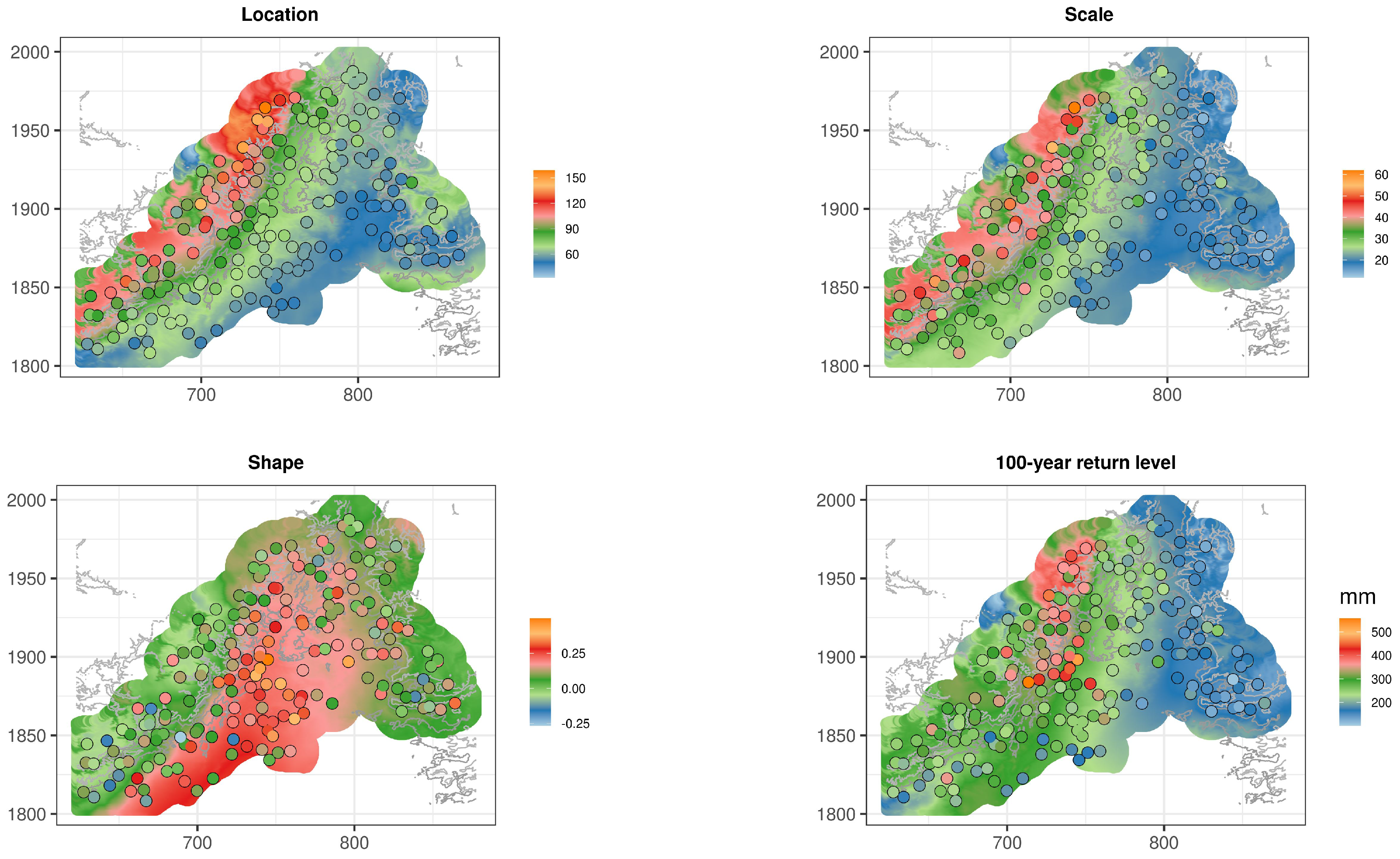
4.2. Spatial GEV Parameters Estimation
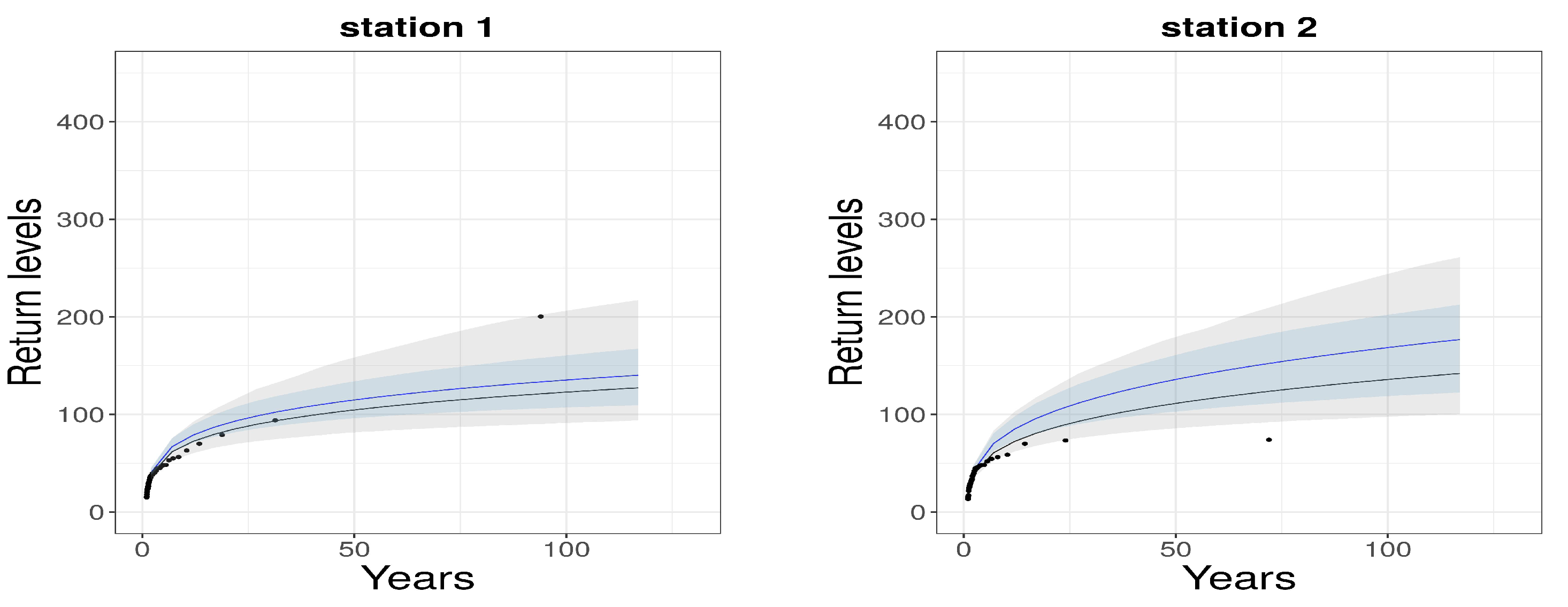
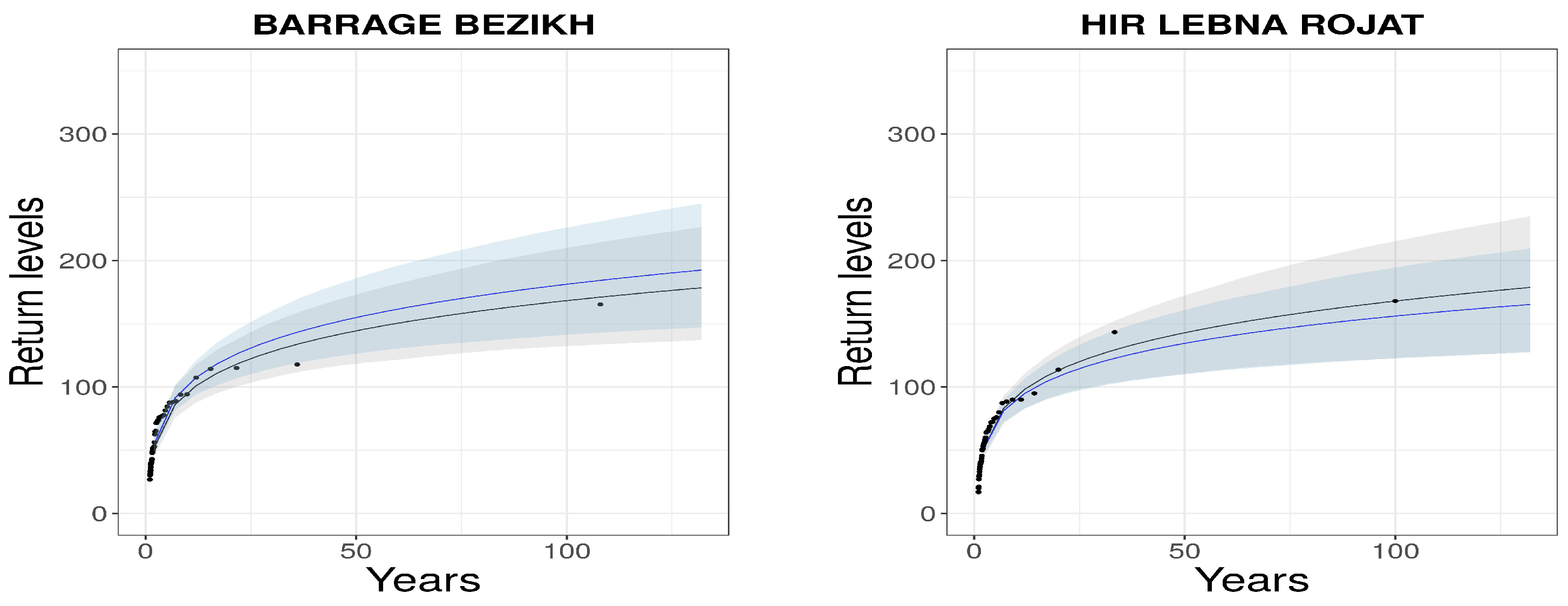
4.3. Model Evaluation
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix A.1. Estimation of the GEV Parameters Using ANN on the Tunisian Sites

Appendix A.2. 10-Fold Cross-Validation Results
References
- Gaume, E.; Borga, M.; Llassat, M.; Maouche, S.; Lang, M.; Diakakis, M. Sub-chapter 1.3.4. Mediterranean extreme floods and flash floods. In The Mediterranean Region under Climate Change; Collection Synthèses; IRD Editions: Marseille, France, 2016; pp. 133–144. [Google Scholar] [CrossRef]
- Leduc, C.; Ammar, S.B.; Favreau, G.; Beji, R.; Virrion, R.; Lacombe, G.; Tarhouni, J.; Aouadi, C.; Chelli, B.Z.; Jebnoun, N.; et al. Impacts of hydrological changes in the Mediterranean zone: Environmental modifications and rural development in the Merguellil catchment, central Tunisia/Un Ex. D’évolution Hydrol. En Méditerranée: Impacts Des Modif. Environnementales Et Du Développement Agric. Dans Le Bassin-Versant Du Merguellil (Tunisie Cent. Hydrol. Sci. J. 2007, 52, 1162–1178. [Google Scholar] [CrossRef]
- Hmidi, N.; Fehri, N.; Baccar, A. Inondation devastatrice dans la ville de Soliman (Tunisie): Cas de sa zone industrielle lors de l’événement pluviométrique du 22 septembre 2018. In Le Changement Climatique, la Variabilité et les Risques Climatiques; AIC: Aix-en-Provence, France, 2019; p. 199. [Google Scholar]
- Brunet, P.; Bouvier, C.; Neppel, L. Retour d’expérience sur les crues des 6 et 7 octobre 2014 à Montpellier-Grabels (Hérault, France): Caractéristiques hydro-météorologiques et contexte historique de l’épisode. Physio-Géo 2018, 12, 43–59. [Google Scholar] [CrossRef]
- Katz, R.W.; Parlange, M.B.; Naveau, P. Statistics of extremes in hydrology. Adv. Water Resour. 2002, 25, 1287–1304. [Google Scholar] [CrossRef] [Green Version]
- Coles, S. An Introduction to Statistical Modeling of Extreme Values; Springer Series in Statistics; Springer: Berlin/Heidelberg, Germany, 2001. [Google Scholar] [CrossRef]
- Vicente-Serrano, S.M.; Saz-Sánchez, M.A.; Cuadrat, J.M. Comparative analysis of interpolation methods in the middle Ebro Valley (Spain): Application to annual precipitation and temperature. Clim. Res. 2003, 24, 161–180. [Google Scholar] [CrossRef] [Green Version]
- Li, J.; Heap, A.D. A Review of Spatial Interpolation Methods for Environmental Scientists; Geoscience Australia: Canberra, Australia, 2008; p. 154.
- Kumar Adhikary, S.; Muttil, N.; Gokhan Yilmaz, A. Ordinary kriging and genetic programming for spatial estimation of rainfall in the Middle Yarra River catchment, Australia. Hydrol. Res. 2016, 47, 1182–1197. [Google Scholar] [CrossRef]
- Feki, H.; Slimani, M.; Cudennec, C. Incorporating elevation in rainfall interpolation in Tunisia using geostatistical methods. Hydrol. Sci. J. 2012, 57, 1294–1314. [Google Scholar] [CrossRef]
- Feki, H.; Slimani, M.; Cudennec, C. Geostatistically based optimization of a rainfall monitoring network extension: Case of the climatically heterogeneous Tunisia. Hydrol. Res. 2017, 48, 514–541. [Google Scholar] [CrossRef]
- Ceresetti, D.; Ursu, E.; Carreau, J.; Anquetin, S.; Creutin, J.D.; Gardes, L.; Girard, S.; Molinié, G. Evaluation of classical spatial-analysis schemes of extreme rainfall. Nat. Hazards Earth Syst. Sci. 2012, 12, 3229–3240. [Google Scholar] [CrossRef]
- Shepard, D. A two-dimensional interpolation function for irregularly-spaced data. In Proceedings of the 1968 23rd ACM National Conference, New York, NY, USA, 27–29 August 1968; ACM Press: New York, NY, USA, 1968; pp. 517–524. [Google Scholar] [CrossRef]
- Goovaerts, P. Geostatistical approaches for incorporating elevation into the spatial interpolation of rainfall. J. Hydrol. 2000, 228, 113–129. [Google Scholar] [CrossRef]
- Blanchet, J.; Lehning, M. Mapping snow depth return levels: Smooth spatial modeling versus station interpolation. Hydrol. Earth Syst. Sci. 2010, 14, 2527–2544. [Google Scholar] [CrossRef] [Green Version]
- Neppel, L.; Arnaud, P.; Borchi, F.; Carreau, J.; Garavaglia, F.; Lang, M.; Paquet, E.; Renard, B.; Soubeyroux, J.; Veysseire, J. Résultats du projet Extraflo sur la comparaison des méthodes d’estimation des pluies extrêmes en France. Houille Blanche-Rev. Int. L’eau 2014, 2, 14–19. [Google Scholar] [CrossRef] [Green Version]
- Chowdhury, M.; Alouani, A.; Hossain, F. Comparison of ordinary kriging and artificial neural network for spatial mapping of arsenic contamination of groundwater. Stoch. Environ. Res. Risk Assess. 2010, 24, 1–7. [Google Scholar] [CrossRef]
- Bishop, C.M. Pattern Recognition and Machine Learning; Information Science and Statistics; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Carreau, J.; Toulemonde, G. Extra-parametrized extreme value copula: Extension to a spatial framework. Spat. Stat. 2020, 40, 100410. [Google Scholar] [CrossRef] [Green Version]
- Tramblay, Y.; Neppel, L.; Carreau, J.; Najib, K. Non-stationary frequency analysis of heavy rainfall events in southern France. Hydrol. Sci. J. 2013, 58, 280–294. [Google Scholar] [CrossRef]
- Panthou, G.; Vischel, T.; Lebel, T.; Blanchet, J.; Quantin, G.; Ali, A. Extreme rainfall in West Africa: A regional modeling. Water Resour. Res. 2012, 48, 8. [Google Scholar] [CrossRef]
- Šraj, M.; Viglione, A.; Parajka, J.; Blöschl, G. The influence of non-stationarity in extreme hydrological events on flood frequency estimation. J. Hydrol. Hydromech. 2016, 64, 426–437. [Google Scholar] [CrossRef] [Green Version]
- Villarini, G.; Smith, J.; Serinaldi, F.; Ntelekos, A.; Schwarz, U. Analyses of extreme flooding in Austria over the period 1951–2006. Int. J. Climatol. 2012, 32, 1178–1192. [Google Scholar] [CrossRef]
- Aissaoui-Fqayeh, I.; El-Adlouni, S.; Ouarda, T.B.M.J.; St-Hilaire, A. Non-stationary lognormal model development and comparison with the non-stationary GEV model. Hydrol. Sci. J. 2009, 54, 1141–1156. [Google Scholar] [CrossRef]
- Wagner, P.D.; Fiener, P.; Wilken, F.; Kumar, S.; Schneider, K. Comparison and evaluation of spatial interpolation schemes for daily rainfall in data scarce regions. J. Hydrol. 2012, 464, 388–400. [Google Scholar] [CrossRef]
- Slimani, M.; Cudennec, C.; Feki, H. Structure du gradient pluviométrique de la transition Méditerranée-Sahara en Tunisie: Déterminants géographiques et saisonnalité/Structure Rainfall Gradient Mediterranean-Sahara Transit. Tunisia: Geogr. Determ. Seas. Hydrol. Sci. J. 2007, 52, 1088–1102. [Google Scholar] [CrossRef]
- Raymond, F. and Ullmann, A.; Tramblay, Y.; Drobinski, P.; Camberlin, P. Evolution of Mediterranean extreme dry spells during the wet season under climate change. Reg. Environ. Chang. 2019, 19, 2339–2351. [Google Scholar] [CrossRef]
- Joly, D.; Brossard, T.; Cardot, H.; Cavailhes, J.; Hilal, M.; Wavresky, P. Les types de climats en France, une construction spatiale. Cybergeo 2010, 501, 34–42. [Google Scholar] [CrossRef]
- Pujol, N.; Neppel, L.; Sabatier, R. Approche régionale pour la détection de tendances dans des séries de précipitations de la région méditerranéenne française. Comptes Rendus Geosci. 2007, 339, 651–658. [Google Scholar] [CrossRef]
- Lacombe, G.; Cappelaere, B.; Leduc, C. Hydrological impact of water and soil conservation works in the Merguellil catchment of central Tunisia. J. Hydrol. 2008, 359, 210–224. [Google Scholar] [CrossRef]
- Funk, C.; Peterson, P.; Landsfeld, M.; Pedreros, D.; Verdin, J.; Shukla, S.; Husak, G.; Rowland, J.; Harrison, L.; Hoell, A.; et al. The climate hazards infrared precipitation with stations-a new environmental record for monitoring extremes. Sci. Data 2015, 2, 150066. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Fisher, R.A.; Tippett, L.H.C. Limiting forms of the frequency distribution of the largest or smallest member of a sample. Math. Proc. Camb. Philos. Soc. 1928, 24, 180–190. [Google Scholar] [CrossRef]
- Pujol, N.; Neppel, L.; Sabatier, R. Regional tests for trend detection in maximum precipitation series in the French Mediterranean region. Hydrol. Sci. J. 2007, 52, 956–973. [Google Scholar] [CrossRef]
- Cooley, D.; Nychka, D.; Naveau, P. Bayesian Spatial Modeling of Extreme Precipitation Return Levels. J. Am. Stat. Assoc. 2007, 102, 824–840. [Google Scholar] [CrossRef]
- Hosking, J. L-moments: Analysis and Estimation of Distribution us sing Linear Combinations of Order Statistics. J. R. Stat. Soc. Ser. B Methodol. 1990, 52, 105–124. [Google Scholar] [CrossRef]
- Hosking, J.R.M.; Wallis, J.R. Regional Frequency Analysis: An Approach Based on L-Moments, 1st ed.; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar] [CrossRef]
- McCullagh, P. Generalized Linear Models; Routledge: London, UK, 2019. [Google Scholar]
- Chandler, R. On the use of generalized linear models for interpreting climate variability. Environmetrics 2005, 16, 699–715. [Google Scholar] [CrossRef]
- Yan, Z.; Bate, S.; Chandler, R.E.; Isham, V.; Wheater, H. An Analysis of Daily Maximum Wind Speed in Northwestern Europe Using Generalized Linear Models. J. Clim. 2002, 15, 2073–2088. [Google Scholar] [CrossRef]
- McCullagh, P.; Nelder, J.A. Generalized Linear Models; Monographs on statistics and applied probability; Chapman and Hall: New York, NY, USA, 1989. [Google Scholar]
- Yee, T.W.; Stephenson, A. Vector generalized linear and additive extreme value models. Extremes 2007, 10, 1–19. [Google Scholar] [CrossRef]
- Herath, H.; Chadalawada, J.; Babovic, V. Hydrologically informed machine learning for rainfall–runoff modelling: Towards distributed modelling. Hydrol. Earth Syst. Sci. 2021, 25, 4373–4401. [Google Scholar] [CrossRef]
- Jiang, S.; Zheng, Y.; Wang, C.; Babovic, V. Uncovering flooding mechanisms across the contiguous United States through interpretive deep learning on representative catchments. Water Resour. Res. 2022, 58, e2021WR030185. [Google Scholar] [CrossRef]
- Mezghani, A.; Hingray, B. A combined downscaling-disaggregation weather generator for stochastic generation of multisite hourly weather variables over complex terrain: Development and multi-scale validation for the Upper Rhone River basin. J. Hydrol. 2009, 377, 245–260. [Google Scholar] [CrossRef]
- Carreau, J.; Mhenni, N.; Huard, F.; Neppel, L. Exploiting the spatial pattern of daily precipitation in the analog method for regional temporal disaggregation. J. Hydrol. 2019, 568, 780–791. [Google Scholar] [CrossRef]
- Li, X.; Meshgi, A.; Wang, X.; Zhang, J.; Tay, S.H.X.; Pijcke, G.; Manocha, N.; Ong, M.; Nguyen, M.; Babovic, V. Three resampling approaches based on method of fragments for daily-to-subdaily precipitation disaggregation. Int. J. Climatol. 2018, 38, e1119–e1138. [Google Scholar] [CrossRef]
- Mélèse, V.; Blanchet, J.; Creutin, J. A Regional Scale-Invariant Extreme Value Model of Rainfall Intensity-Duration-Area-Frequency Relationships. Water Resour. Res. 2019, 55, 5539–5558. [Google Scholar] [CrossRef]
- Ulrich, J.; Jurado, O.; Peter, M.; Scheibel, M.; Rust, H. Estimating IDF Curves Consistently over Durations with Spatial Covariates. Water 2020, 12, 3119. [Google Scholar] [CrossRef]
- Fatichi, S.; Ivanov, V.; Caporali, E. Simulation of future climate scenarios with a weather generator. Adv. Water Resour. 2011, 34, 448–467. [Google Scholar] [CrossRef]
- Li, X.; Babovic, V. A new scheme for multivariate, multisite weather generator with inter-variable, inter-site dependence and inter-annual variability based on empirical copula approach. Clim. Dyn. 2019, 52, 2247–2267. [Google Scholar] [CrossRef]

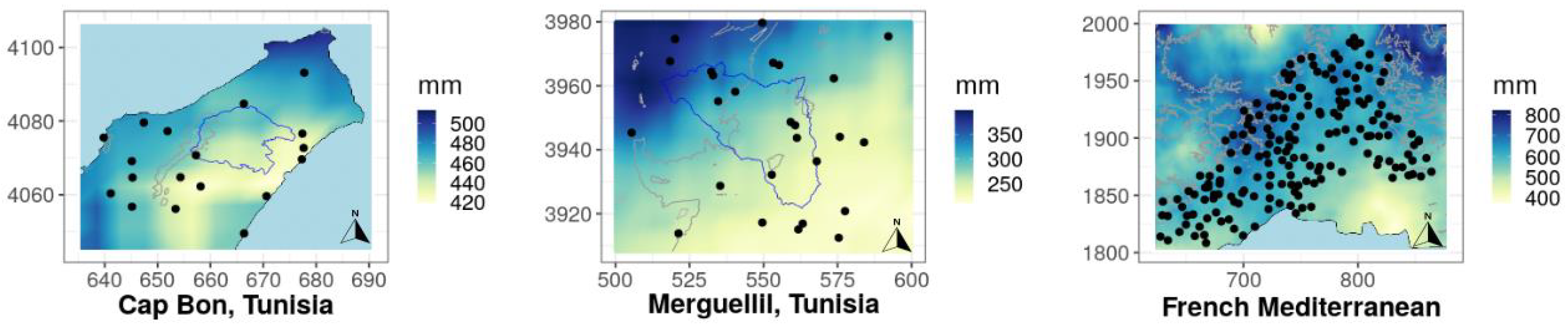


| Covariate | French Mediterranean | Merguellil | Lebna |
|---|---|---|---|
| x | 4341.18 | 488.39 | 364.70 |
| y | 4382.88 | 488.36 | 367.07 |
| z | 4341.94 | 488.46 | 366.97 |
| chirps | 4326.7 | 488.56 | 365.08 |
| (x,y) | 4305.67 | 487.34 | 361.42 |
| (x,z) | 4301.3 | 487.21 | 364.51 |
| (y,z) | 4340.35 | 488.63 | 363.98 |
| (x,chirps) | 4296.11 | 486.64 | 364.42 |
| (y,chirps) | 4313.43 | 487.00 | 364.65 |
| (z,chirps) | 4314.11 | 487.50 | 363.04 |
| (x,y,z) | 4275.84 | 486.52 | 360.75 |
| (x,y,chirps) | 4295.64 | 486.93 | 360.91 |
| (y,z,chirps) | 4301.79 | 487.46 | 361.89 |
| (x,z,chirps) | 4277.24 | 486.60 | 362.39 |
| (x,y,z,chirps) | 4274.04 | 486.55 | 361.25 |
| Site | GLM Covariate | ANN Covariate | Number of Hidden Units |
|---|---|---|---|
| French Mediterranean | (x,y,z,chirps) | (x,y,z,chirps) | 4 |
| Merguellil | (x,y,z) | (y,chirps) | 1 |
| Lebna | (x,y,z) | (y,z) | 1 |
| Site | Negative Log-Likelihood | Kolmogorov–Smirnov |
|---|---|---|
| French Mediterranean | 72.67% | 74.35% |
| Merguellil | 61.53% | 65.38% |
| Lebna | 61.1% | 61.1% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hammami, H.; Carreau, J.; Neppel, L.; Elasmi, S.; Feki, H. Smooth Spatial Modeling of Extreme Mediterranean Precipitation. Water 2022, 14, 3782. https://doi.org/10.3390/w14223782
Hammami H, Carreau J, Neppel L, Elasmi S, Feki H. Smooth Spatial Modeling of Extreme Mediterranean Precipitation. Water. 2022; 14(22):3782. https://doi.org/10.3390/w14223782
Chicago/Turabian StyleHammami, Hela, Julie Carreau, Luc Neppel, Sadok Elasmi, and Haifa Feki. 2022. "Smooth Spatial Modeling of Extreme Mediterranean Precipitation" Water 14, no. 22: 3782. https://doi.org/10.3390/w14223782






