Topological Analysis and Application of Urban Drainage Network
Abstract
1. Introduction
- A data sorting method for urban drainage networks is proposed, emphasizing the flow direction in the drainage network system, and the basic principle that is needed to follow in topology building of urban drainage networks is discussed.
- According to the connection relationship of the network topology relationship, we trace the potential drainage outfall for each drainage node and use the control area of the node with the same potential drainage information as a subcatchment.
- The allocation ratio of the rainwater between subcatchments is calibrated dynamically with a hydrodynamic model and then applied to further hydrological analysis.
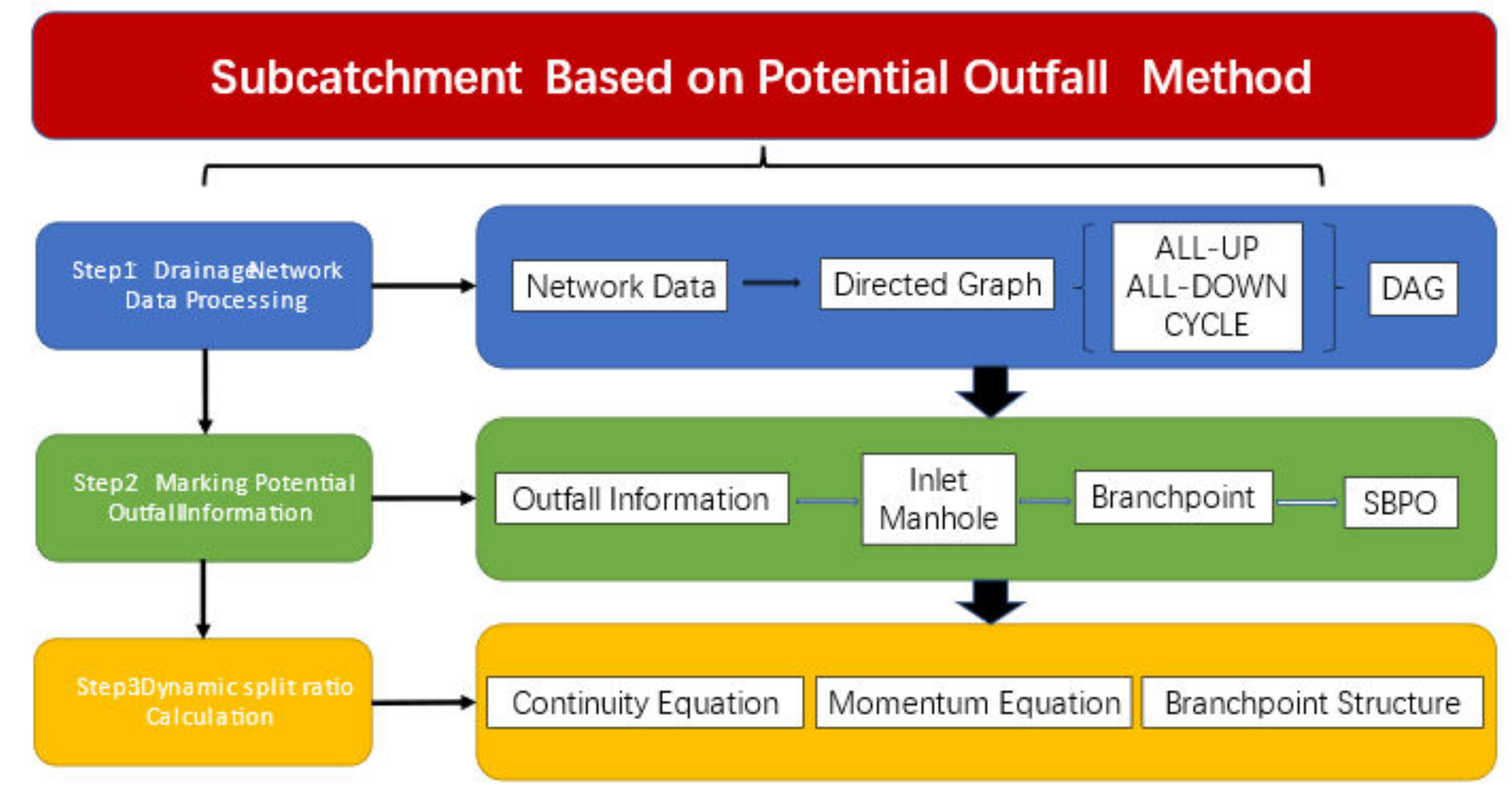
2. Methodology
2.1. Drainage Network Data Combing Method Based on Potential Outfall
2.1.1. Correction of Flow Direction
- , a set of vertices;
- , a set of edges, which are ordered pairs of vertices.
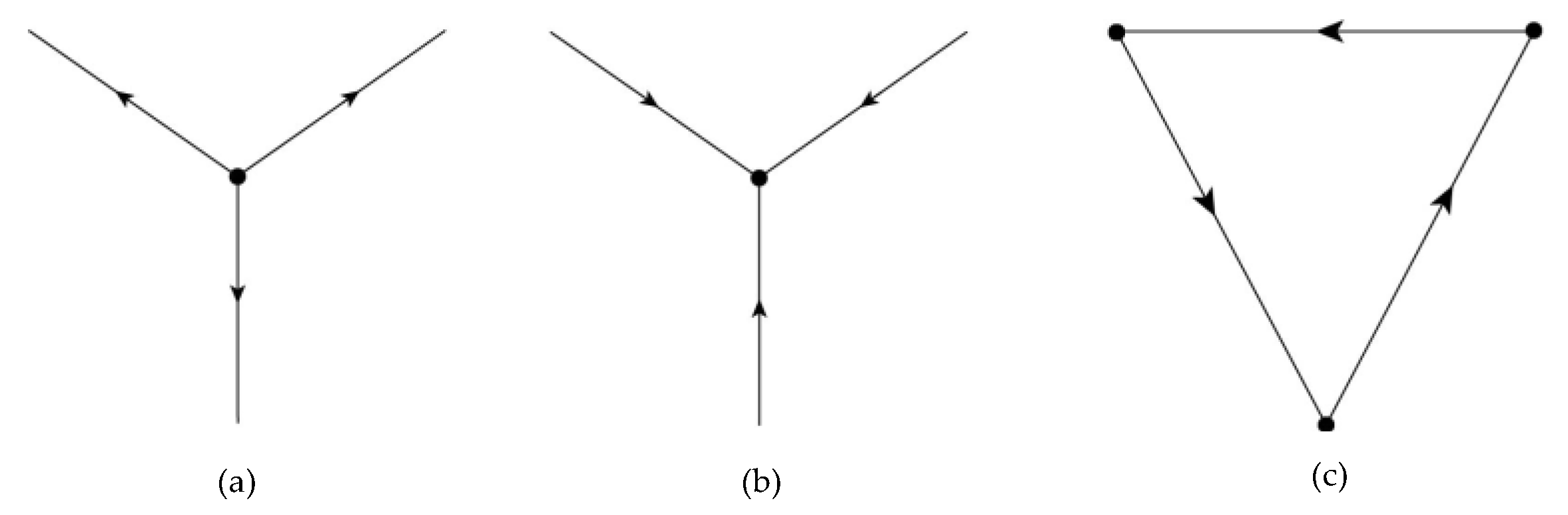
- We name structure (a) as an “All-up” node, which is defined as a point upstream of several pipeline but not downstream of any pipeline. For such points, we should warn against it and only retain it after confirming that it is actually correct.
- We name structure (b) as “ALL-down” node. The definition of such a node is that the point is downstream of several pipelines, but not upstream of any pipeline. When such a node appears, an error should be prompted, because such a node will not appear in reality, and the inflow of the node needs to have a reasonable place to go.
- We name structure (c) “Cycle”, which is the same as the definition of cycle in graph theory. Starting from a node in this structure, it can return to itself according to the direction of the pipelines. Such structures make no sense when only gravity is driving them.
2.1.2. Topology Analysis
- Analyze the in-degree and out-degree of each node.
- The node in-degree = 0 (no upstream), defined as type = 0, which is usually rain grate or household pipe entrance;
- The node in-degree > 0 and out degree > 0 (not the starting point or end point of the drainage network), defined as type = 1, which is generally a manhole;
- The node out-degree = 0 (without downstream), defined as type = 2, which is generally an outlet mouth or an inlet of a sewage plant.
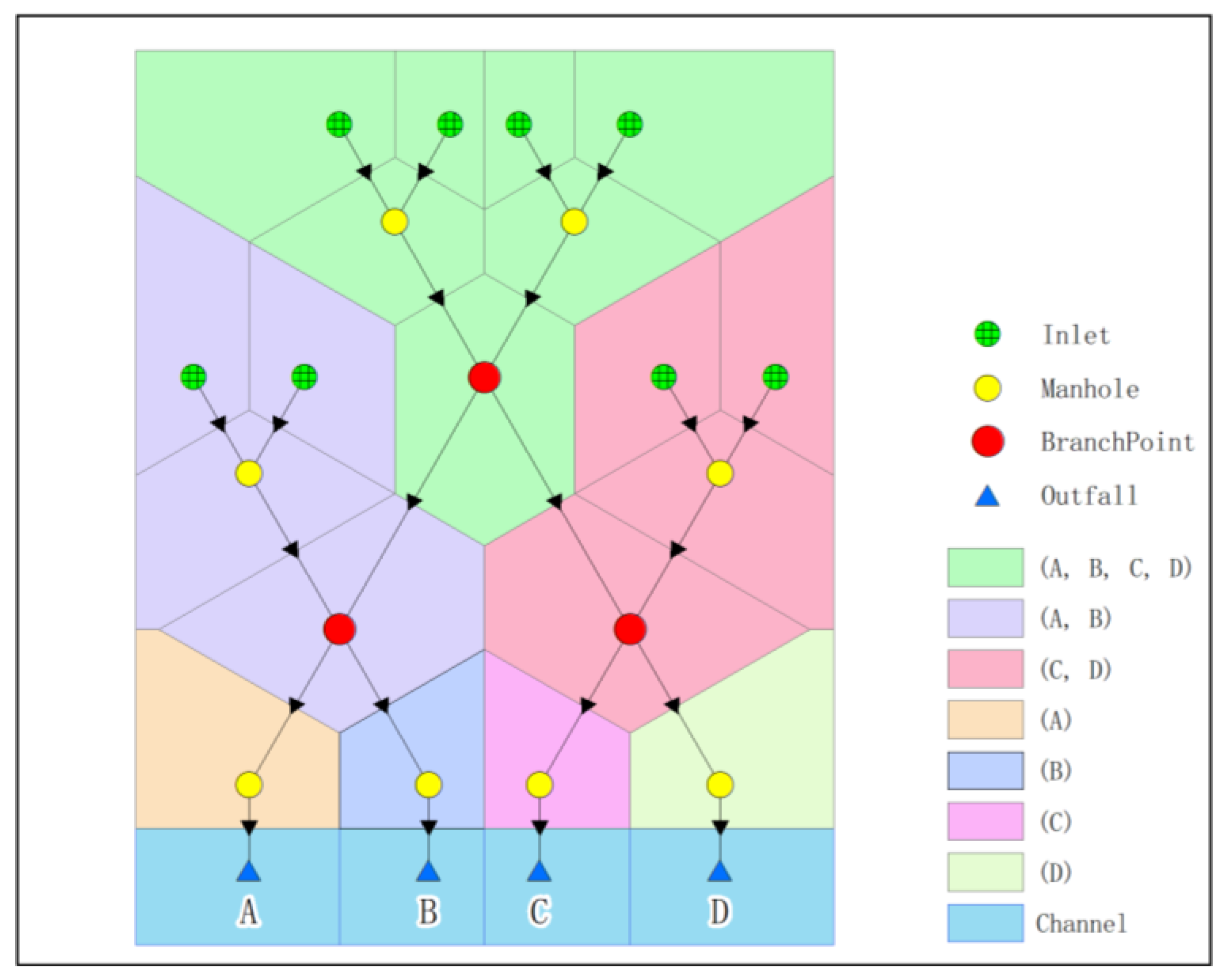
- Mark potential outfall information.
- If a point type is 2, then its outfall information is marked by its own number;
- If a point type is not 2, the downstream of the point is retrieved according to the topological relationship, and the drainage outfall information of the downstream node is returned for recursion;
- Classification—Nodes with the same outfall information are defined as homogeneous nodes.
2.2. Subcatchment Based on Network Connectivity
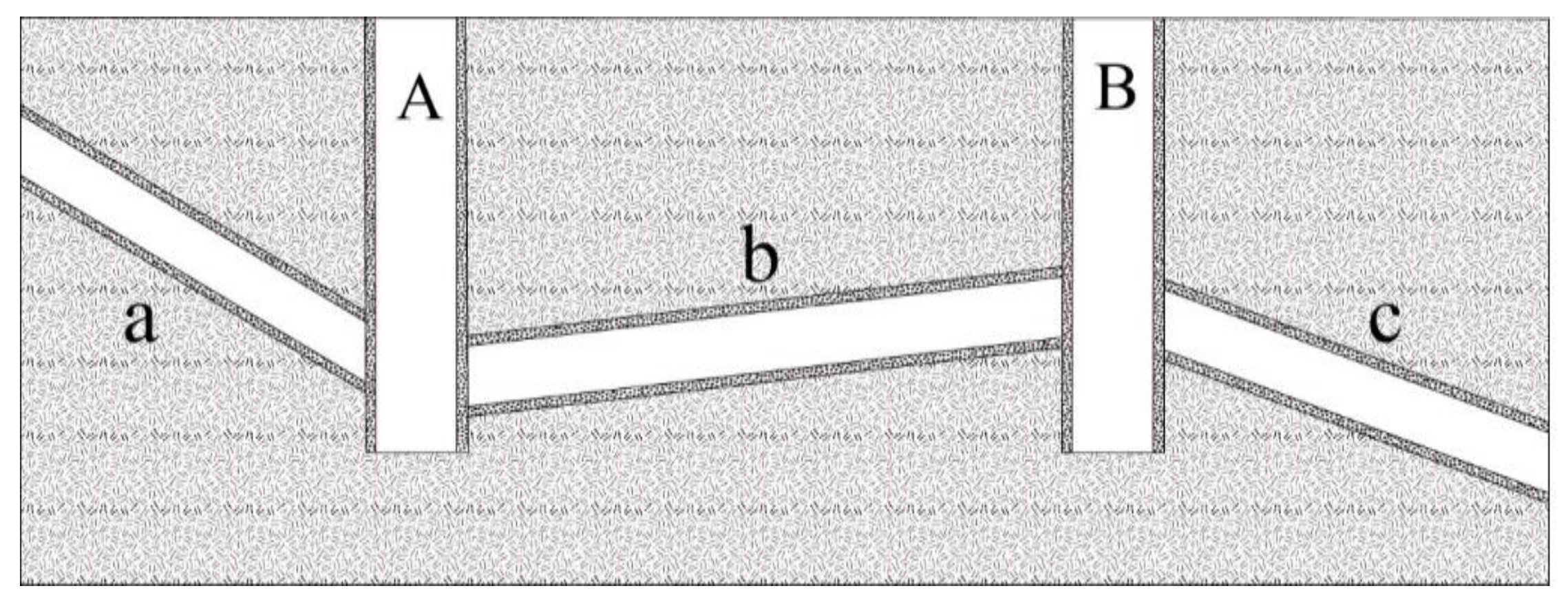
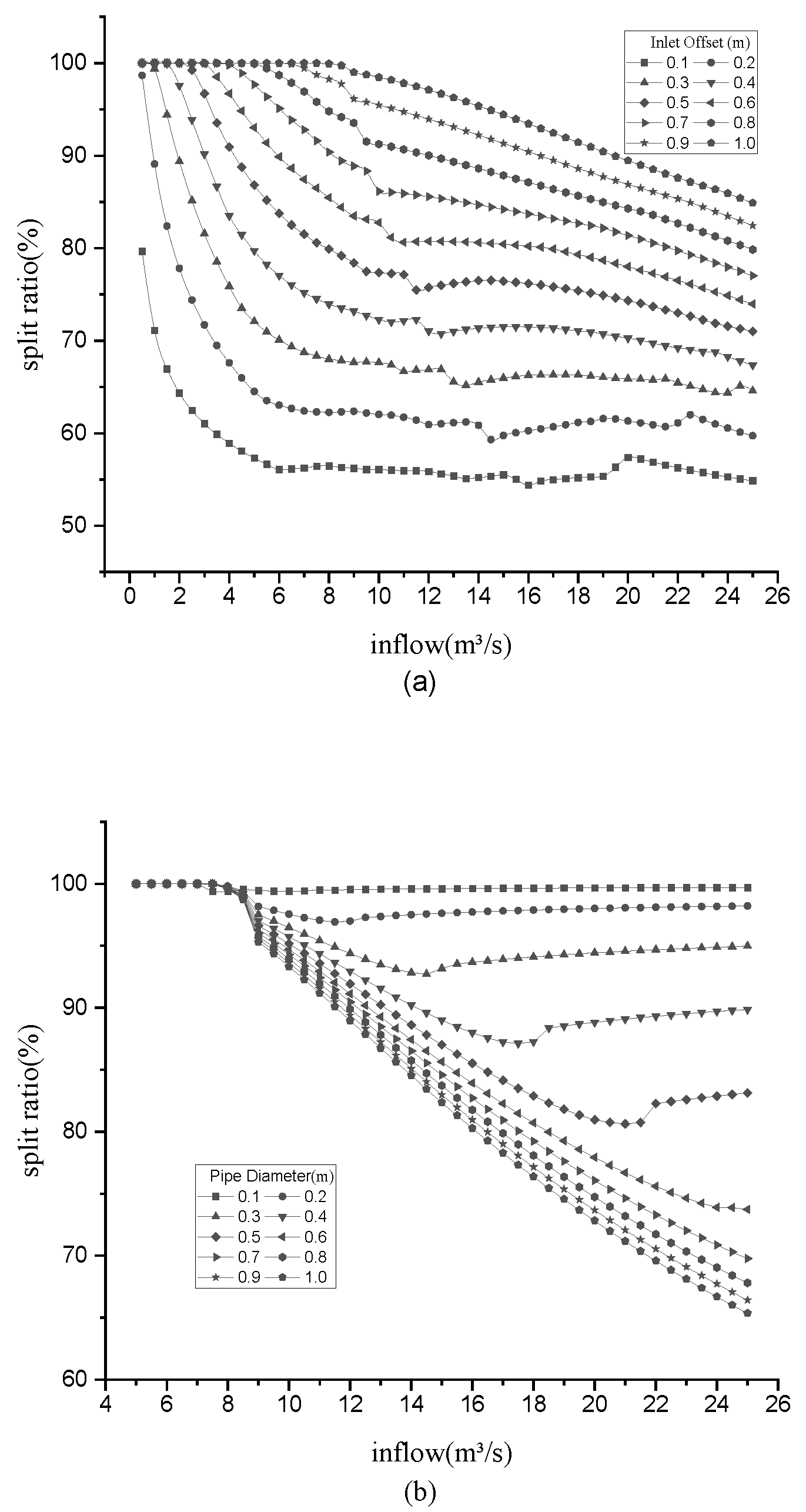
2.3. Dynamic Split Ratio at Branchpoint of Bifurcation Tube
- = distance (ft);
- = time (sec);
- = flow cross-sectional area (ft2);
- = flow rate (cfs);
- = hydraulic head of water in the conduit () (ft);
- = conduit invert elevation (ft);
- = conduit water depth (ft);
- = friction slope (head loss per unit length);
- = acceleration of gravity (ft/sec2).
- = percentage of a pipe to the total discharge of a branch;
- = flow rate of the two pipes at the inlet.
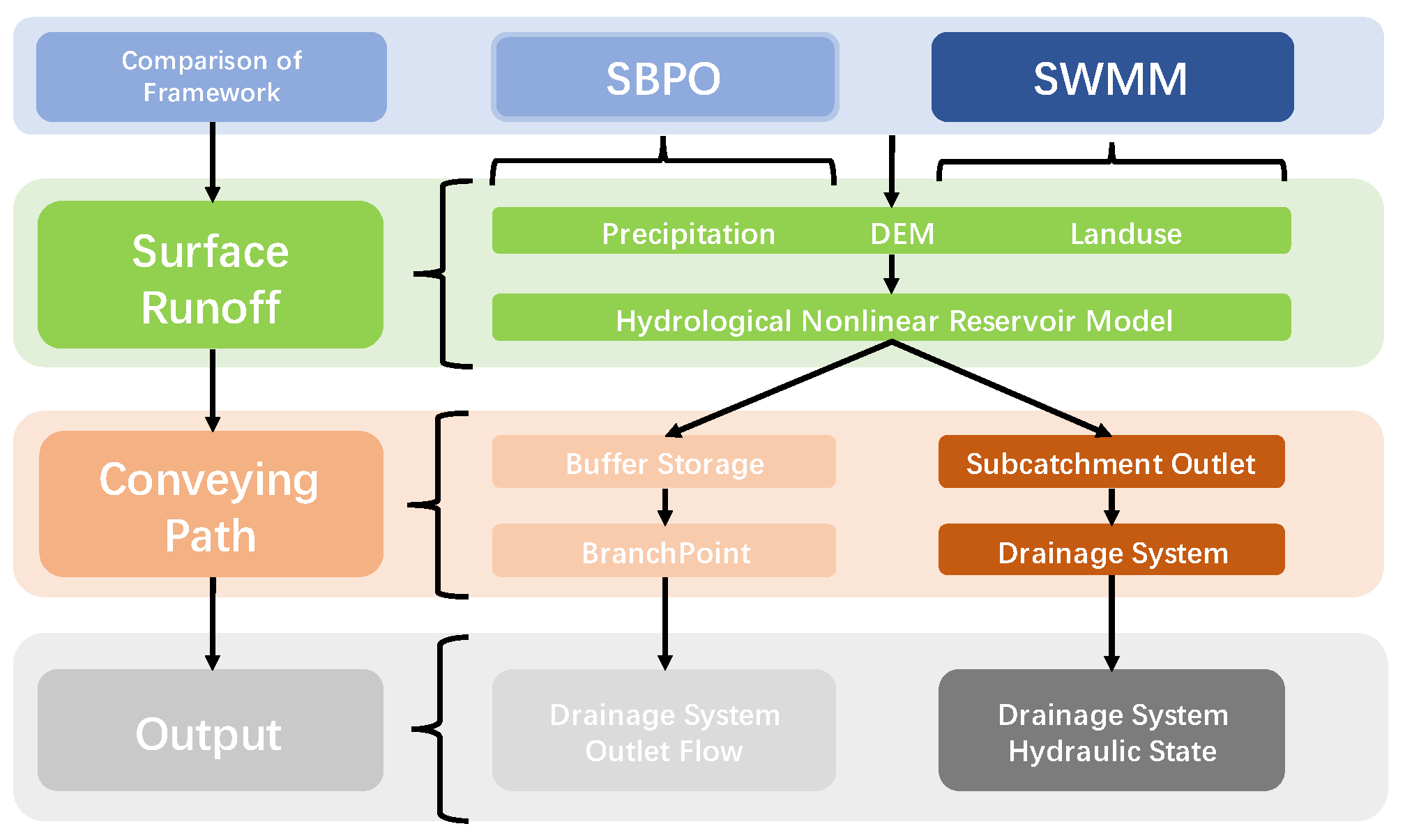
2.4. SBPO Modeling Method Details
- = reservoir water depth (ft);
- = rate of rainfall (ft/s);
- = surface evaporation rate (ft/s);
- = infiltration rate (ft/s);
- = runoff rate (ft/s).
- = cross sectional area (m2);
- = the water level (m);
- = runoff rate (m3/s);
- = discharge rate (m3/s).
3. Study Area and Scenario Design
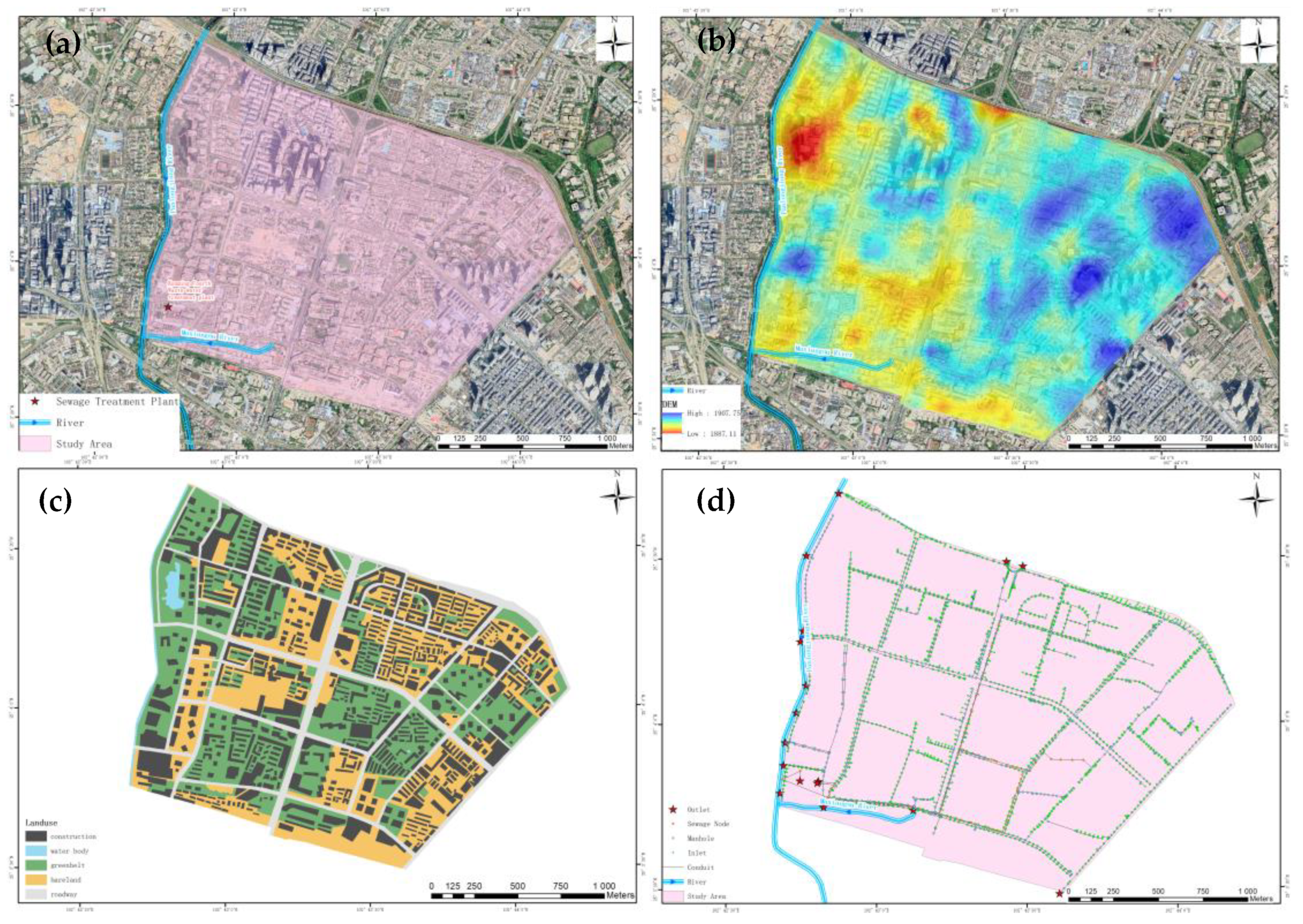
3.1. Study Area
3.2. Scenario Design
4. Results
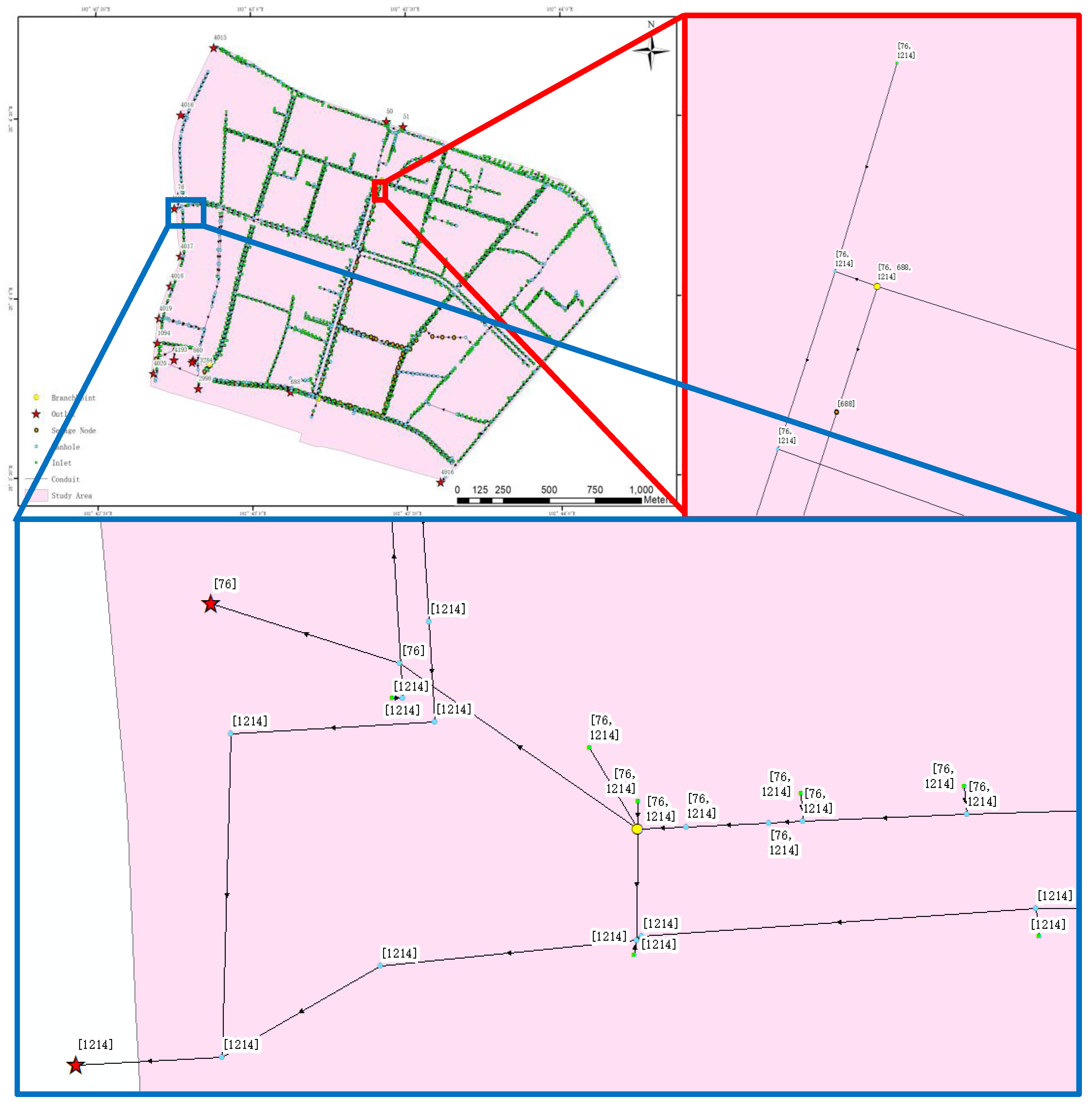
4.1. Results of Drainage System Topology Combing and Subcatchment Based on Potential Outfall
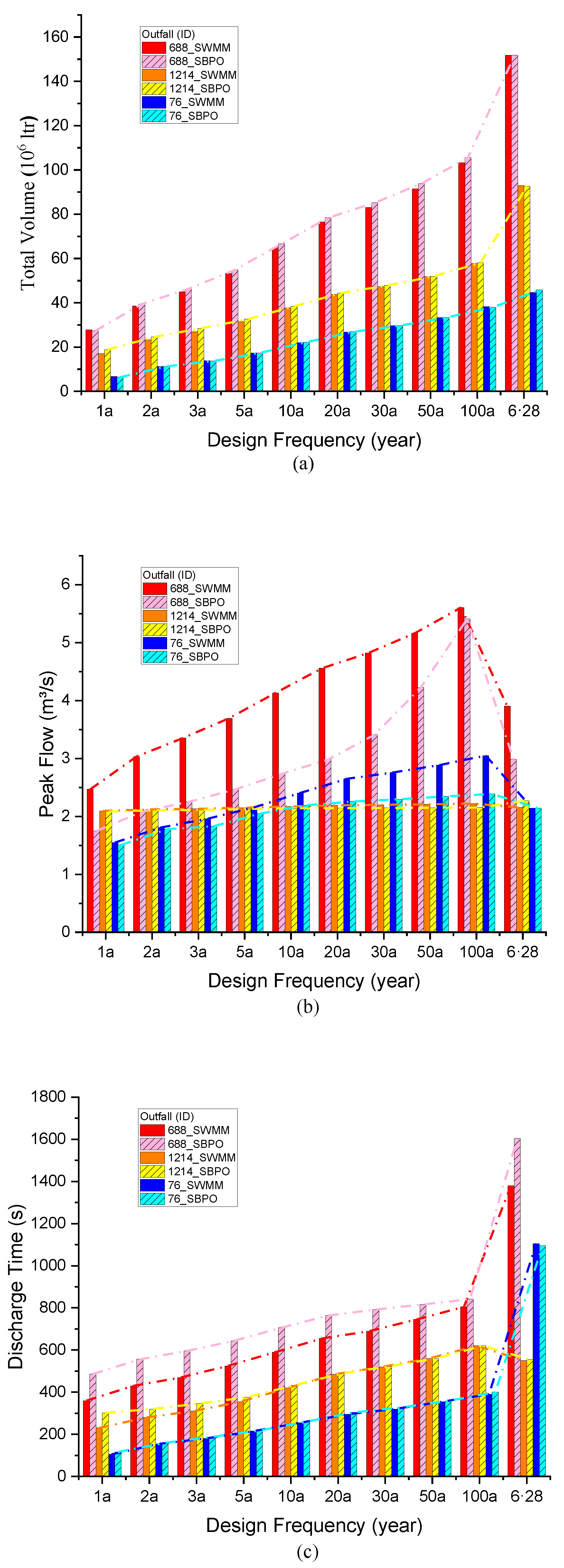
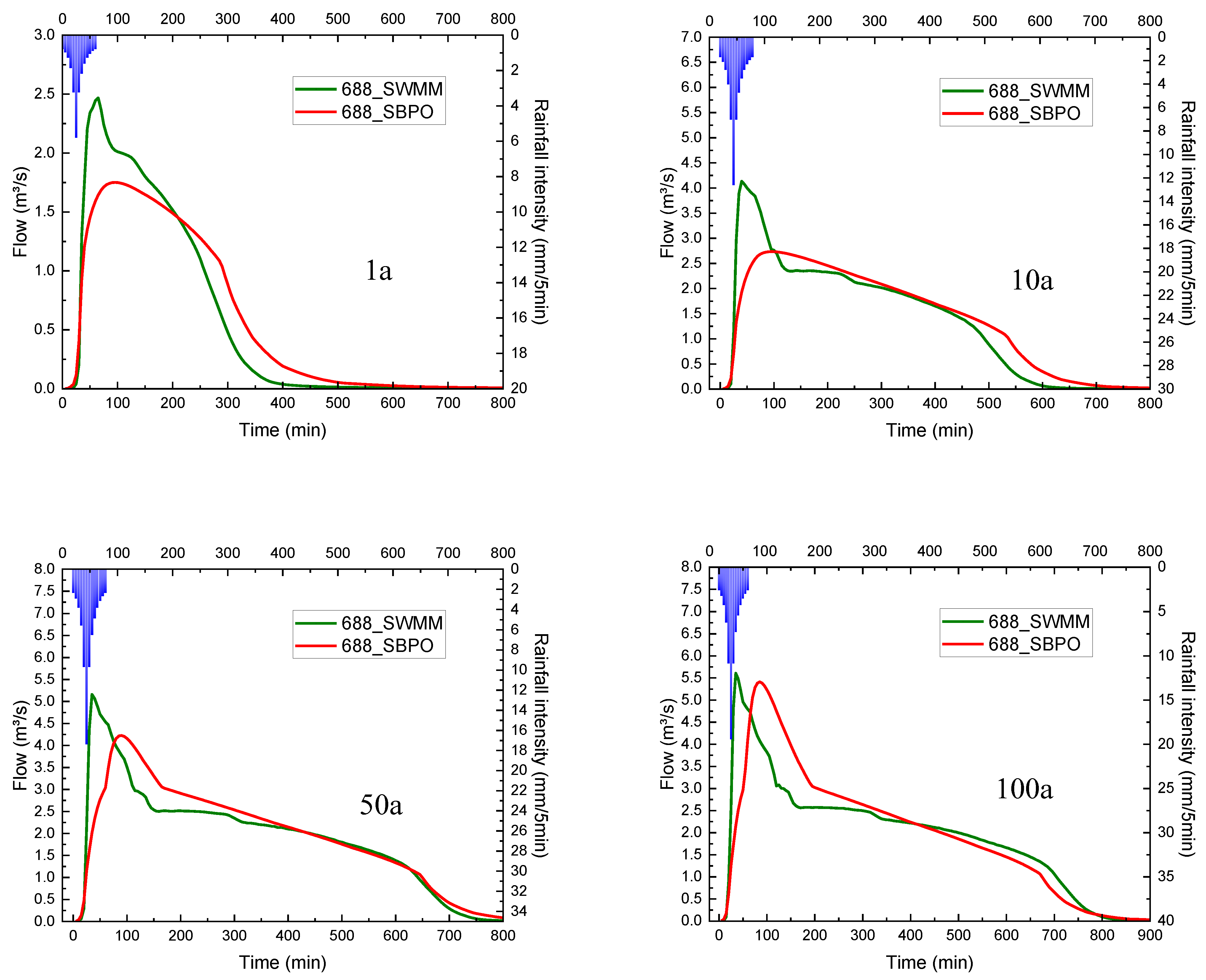
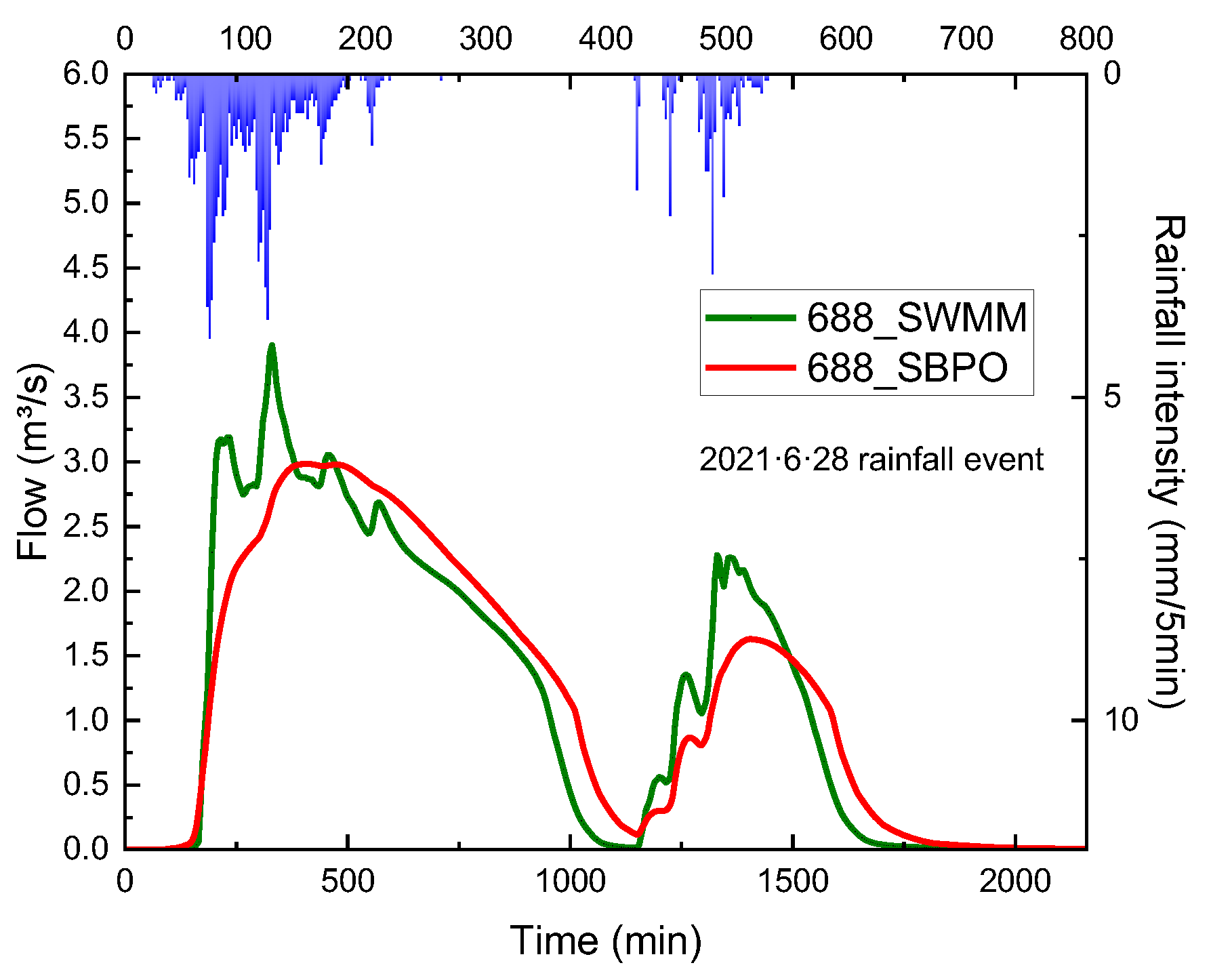
4.2. Result of Outfalls’ Total Inflow
5. Discussion
5.1. Basic Drainage Network Data Processing
5.2. Application of Potential Outfall Information Based on Network Node
6. Conclusions
- The point-line relationship of the drainage network system is generalized to a directed graph, and the topological relationship of the drainage network can be quickly and effectively sorted into the DAG diagram of the outfall leading to the river or sewage by changing and correcting the partial structures such as “ALL-DOWN”, “ALL-UP” and “CYCLE” defined by the in-out degree. This can greatly simplify the difficulty of sorting out the intricate underground drainage network data in urban areas.
- By tracing the network upstream from the outfall with the correct representation of the flow direction, the researchers can retrieve the potential outfall at each node of the network system. The relative independence of the drainage network system can be explained by clustering the drainage network system from this perspective. The branchpoint points defined by the potential outfall information are the key to water exchange between subcatchment areas and the keynote of overflow analysis in the combined sewer area.
- The SBPO modeling method is highly consistent with the SWMM of a high-resolution drainage network in terms of drainage outfall volume. Under the SBPO method, the time of computing the peak discharge and discharge duration can significantly reduce with the buffer effect of the storage on the drainage network system.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| Parameter Set | SPBO | SWMM | ||
|---|---|---|---|---|
| Ruoff-generation | Sub-catchment | Area, Width, Slope, Imperv, N-inperv, N-perv, Dstore-Imperv, Dstore-Perv, OUTLET | ||
| Runoff-conveying | Drainage Network | Faraway Branchpoint | Near Branchpoint | Node: Invert EI MAX. Depth Initial Depth Surcharge Depth Ponded Area |
| Topological information: Inlet Node, Outlet Node | Node: Invert EI MAX. Depth Initial Depth Surcharge Depth Ponded Area | |||
| Conduit: Inlet Node Outlet Node Shape MAX. depth Length Roughless InletOffset OutletOffset InitialFlow | Conduit: Inlet Node Outlet Node Shape MAX. depth Length Roughless InletOffset OutletOffset InitialFlow | |||
References
- Allen, M.R.; Ingram, W.J. Constraints on Future Changes in Climate and the Hydrologic Cycle. Nature 2002, 419, 228–232. [Google Scholar] [CrossRef] [PubMed]
- Kharin, V.V.; Zwiers, F.W.; Zhang, X.; Wehner, M. Changes in Temperature and Precipitation Extremes in the CMIP5 Ensemble. Clim. Change 2013, 119, 345–357. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, Y.; He, R.; Hu, Q.; Song, X. Discussion on the urban flood and waterlogging and causes analysis in China. Adv. Water Sci. 2016, 27, 485–491. [Google Scholar] [CrossRef]
- Xu, Z.; Chen, H.; Ren, M.; Cheng, T. Progress on disaster mechanism and risk assessment of urban flood/waterlogging disasters in China. Adv. Water Sci. 2020, 31, 713–724. [Google Scholar] [CrossRef]
- Ganeshan, M.; Murtugudde, R.; Imhoff, M.L. A Multi-City Analysis of the UHI-Influence on Warm Season Rainfall. Urban Clim. 2013, 6, 1–23. [Google Scholar] [CrossRef]
- Kaufmann, R.K.; Seto, K.C.; Schneider, A.; Liu, Z.; Zhou, L.; Wang, W. Climate Response to Rapid Urban Growth: Evidence of a Human-Induced Precipitation Deficit. J. Clim. 2007, 20, 2299–2306. [Google Scholar] [CrossRef]
- Shepherd, J.M.; Burian, S.J. Detection of Urban-Induced Rainfall Anomalies in a Major Coastal City. Earth Interact. 2003, 7, 1–17. [Google Scholar] [CrossRef]
- Bounoua, L.; Zhang, P.; Mostovoy, G.; Thome, K.; Masek, J.; Imhoff, M.; Shepherd, M.; Quattrochi, D.; Santanello, J.; Silva, J.; et al. Impact of Urbanization on US Surface Climate. Environ. Res. Lett. 2015, 10, 084010. [Google Scholar] [CrossRef]
- Shao, W.; Su, X.; Lu, J.; Liu, J.; Yang, Z.; Cao, Y.; Yang, Z.; Wang, K. The Application of Big Data in the Analysis of the Impact of Urban Floods: A Case Study of Qianshan River Basin. J. Phys. Conf. Ser. 2021, 1955, 012061. [Google Scholar] [CrossRef]
- Su, X.; Shao, W.; Liu, J.; Jiang, Y.; Wang, K. Dynamic Assessment of the Impact of Flood Disaster on Economy and Population under Extreme Rainstorm Events. Remote Sens. 2021, 13, 3924. [Google Scholar] [CrossRef]
- Xu, Z.X.; Ye, C.L. Simulation of urban flooding/waterlogging processes:Principle, models and prospects. J. Hydraul. Eng. 2021, 52, 381–392. [Google Scholar] [CrossRef]
- Zhou, J.; Liu, Y.; Guo, H.; He, D. Combining the SWAT Model with Sequential Uncertainty Fitting Algorithm for Streamflow Prediction and Uncertainty Analysis for the Lake Dianchi Basin, China: Swat with Sufi-2 for Streamflow Prediction and Uncertainty Analysis. Hydrol. Process. 2014, 28, 521–533. [Google Scholar] [CrossRef]
- Rahman, K.U.; Shang, S.; Shahid, M.; Wen, Y. Hydrological Evaluation of Merged Satellite Precipitation Datasets for Streamflow Simulation Using SWAT: A Case Study of Potohar Plateau, Pakistan. J. Hydrol. 2020, 587, 125040. [Google Scholar] [CrossRef]
- Leng, M.; Yu, Y.; Wang, S.; Zhang, Z. Simulating the Hydrological Processes of a Meso-Scale Watershed on the Loess Plateau, China. Water 2020, 12, 878. [Google Scholar] [CrossRef]
- Zhang, H.; Wang, B.; Liu, D.L.; Zhang, M.; Leslie, L.M.; Yu, Q. Using an Improved SWAT Model to Simulate Hydrological Responses to Land Use Change: A Case Study of a Catchment in Tropical Australia. J. Hydrol. 2020, 585, 124822. [Google Scholar] [CrossRef]
- GironAs, J.; Roesner, L.A.; Rossman, L.A.; Davis, J. A New Applications Manual for the Storm Water Management Model (SWMM). Environ. Model. Softw. 2010, 25, 813–814. [Google Scholar] [CrossRef]
- Krebs, G.; Kokkonen, T.; Valtanen, M.; Setälä, H.; Koivusalo, H. Spatial Resolution Considerations for Urban Hydrological Modelling. J. Hydrol. 2014, 512, 482–497. [Google Scholar] [CrossRef]
- Babaei, S.; Ghazavi, R.; Erfanian, M. Urban Flood Simulation and Prioritization of Critical Urban Sub-Catchments Using SWMM Model and PROMETHEE II Approach. Phys. Chem. Earth Parts A/B/C 2018, 105, 3–11. [Google Scholar] [CrossRef]
- Cheng, T.; Xu, Z.; Hong, S.; Song, S. Flood Risk Zoning by Using 2D Hydrodynamic Modeling: A Case Study in Jinan City. Math. Probl. Eng. 2017, 2017, 5659197. [Google Scholar] [CrossRef]
- Sidek, L.M.; Jaafar, A.S.; Majid, W.H.A.W.A.; Basri, H.; Marufuzzaman, M.; Fared, M.M.; Moon, W.C. High-Resolution Hydrological-Hydraulic Modeling of Urban Floods Using InfoWorks ICM. Sustainability 2021, 13, 10259. [Google Scholar] [CrossRef]
- Zhang, H.; Wu, W.; Hu, C.; Hu, C.; Li, M.; Hao, X.; Liu, S. A Distributed Hydrodynamic Model for Urban Storm Flood Risk Assessment. J. Hydrol. 2021, 600, 126513. [Google Scholar] [CrossRef]
- Guo, J. Urban Flood Mitigation and Stormwater Management; CRC Press: Boca Raton, FL, USA, 2017; p. 589. ISBN 978-1-315-26991-7. [Google Scholar]
- Wang, X.; Xia, J.; Dong, B.; Hou, J.; Li, Q. Simulation of urban flood using the SWMM with the hierarchical catchment partition method. Adv. Water Sci. 2022, 33, 196–207. [Google Scholar] [CrossRef]
- Duke, G.D.; Kienzle, S.W.; Johnson, D.L.; Byrne, J.M. Incorporating Ancillary Data to Refine Anthropogenically Modified Overland Flow Paths. Hydrol. Process. 2006, 20, 1827–1843. [Google Scholar] [CrossRef]
- Kayembe, A.; Mitchell, C.P.J. Determination of Subcatchment and Watershed Boundaries in a Complex and Highly Urbanized Landscape. Hydrol. Process. 2018, 32, 2845–2855. [Google Scholar] [CrossRef]
- Yang, Q.; Dai, Q.; Han, D.; Zhu, X.; Zhang, S. Impact of the Storm Sewer Network Complexity on Flood Simulations According to the Stroke Scaling Method. Water 2018, 10, 645. [Google Scholar] [CrossRef]
- Miller, J.D.; Kim, H.; Kjeldsen, T.R.; Packman, J.; Grebby, S.; Dearden, R. Assessing the Impact of Urbanization on Storm Runoff in a Peri-Urban Catchment Using Historical Change in Impervious Cover. J. Hydrol. 2014, 515, 59–70. [Google Scholar] [CrossRef]
- Hagberg, A.A.; Schult, D.A.; Swart, P.J. Exploring Network Structure, Dynamics, and Function Using Network X; Los Alamos National Lab. (LANL): Los Alamos, NM, USA, 2008; p. 5. [Google Scholar]
- Krueger, E.; Klinkhamer, C.; Urich, C.; Zhan, X.; Rao, P.S.C. Generic Patterns in the Evolution of Urban Water Networks: Evidence from a Large Asian City. Phys. Rev. E 2017, 95, 032312. [Google Scholar] [CrossRef]
- Yazdani, A.; Jeffrey, P. Complex Network Analysis of Water Distribution Systems. Chaos 2011, 21, 016111. [Google Scholar] [CrossRef]
- Strahler, A.N. Quantitative Analysis of Watershed Geomorphology. Trans. Am. Geophys. Union 1957, 38, 913–920. [Google Scholar] [CrossRef]
- Sitzenfrei, R. Stochastic Generation of Urban Water Systems for Case Study Analysis; Innsbruck University Press: Innsbruck, Austria, 2012; p. 231. [Google Scholar]
- Xu, G.; Lian, J. Changes of the entropy, the entropy production and the rate of energy dissipation in river adjustment. Adv. Water Sci. 2004, 15, 1–5. [Google Scholar] [CrossRef]
- Reply of The State Council on the Implementation Plan of New Urbanization during the 14th Five-Year Plan Period; Bulletin of The State Council of the People’s Republic of China: Beijing, China, 2022; p. 23.
- McDonnell, B.; Ratliff, K.; Tryby, M.; Wu, J.; Mullapudi, A. PySWMM: The Python Interface to Stormwater Management Model (SWMM). J. Open Source Softw. 2020, 5, 2292. [Google Scholar] [CrossRef]
- Arnell, V.; Harremoës, P.; Jensen, M.; Johansen, N.B.; Niemczynowicz, J. Review of Rainfall Data Application for Design and Analysis. Water Sci. Technol. 1984, 16, 1–45. [Google Scholar] [CrossRef]
- Madsen, H.; Mikkelsen, P.S.; Rosbjerg, D.; Harremoës, P. Regional Estimation of Rainfall Intensity-Duration-Frequency Curves Using Generalized Least Squares Regression of Partial Duration Series Statistics: Regional Estimation of Rainfall Idf Curves. Water Resour. Res. 2002, 38, 21-1–21-11. [Google Scholar] [CrossRef]
- Park, S.Y.; Lee, K.W.; Park, I.H.; Ha, S.R. Effect of the Aggregation Level of Surface Runoff Fields and Sewer Network for a SWMM Simulation. Desalination 2008, 226, 328–337. [Google Scholar] [CrossRef]
- McGrath, G.; Kaeseberg, T.; Reyes Silva, J.D.; Jawitz, J.W.; Blumensaat, F.; Borchardt, D.; Mellander, P.; Paik, K.; Krebs, P.; Rao, P.S.C. Network Topology and Rainfall Controls on the Variability of Combined Sewer Overflows and Loads. Water Resour. Res. 2019, 55, 9578–9591. [Google Scholar] [CrossRef]
- Cleveland, T.G.; Luong, T.; Thompson, D.B. Water Subdivision for Modeling. In Proceedings of the World Environmental and Water Resources Congress 2009, Kansas City, MI, USA, 12 May 2009; pp. 1–10. [Google Scholar]
- Lungariya, P.; Katharotiya, N.; Mehta, D.; Waikhom, S. Analysis of Continuous Water Distribution in Surat City Using Epanet: A Case Study. GRD J. Eng. Recent Adv. Civ. Eng. Glob. Sustain. 2016, 2455–5703. [Google Scholar]
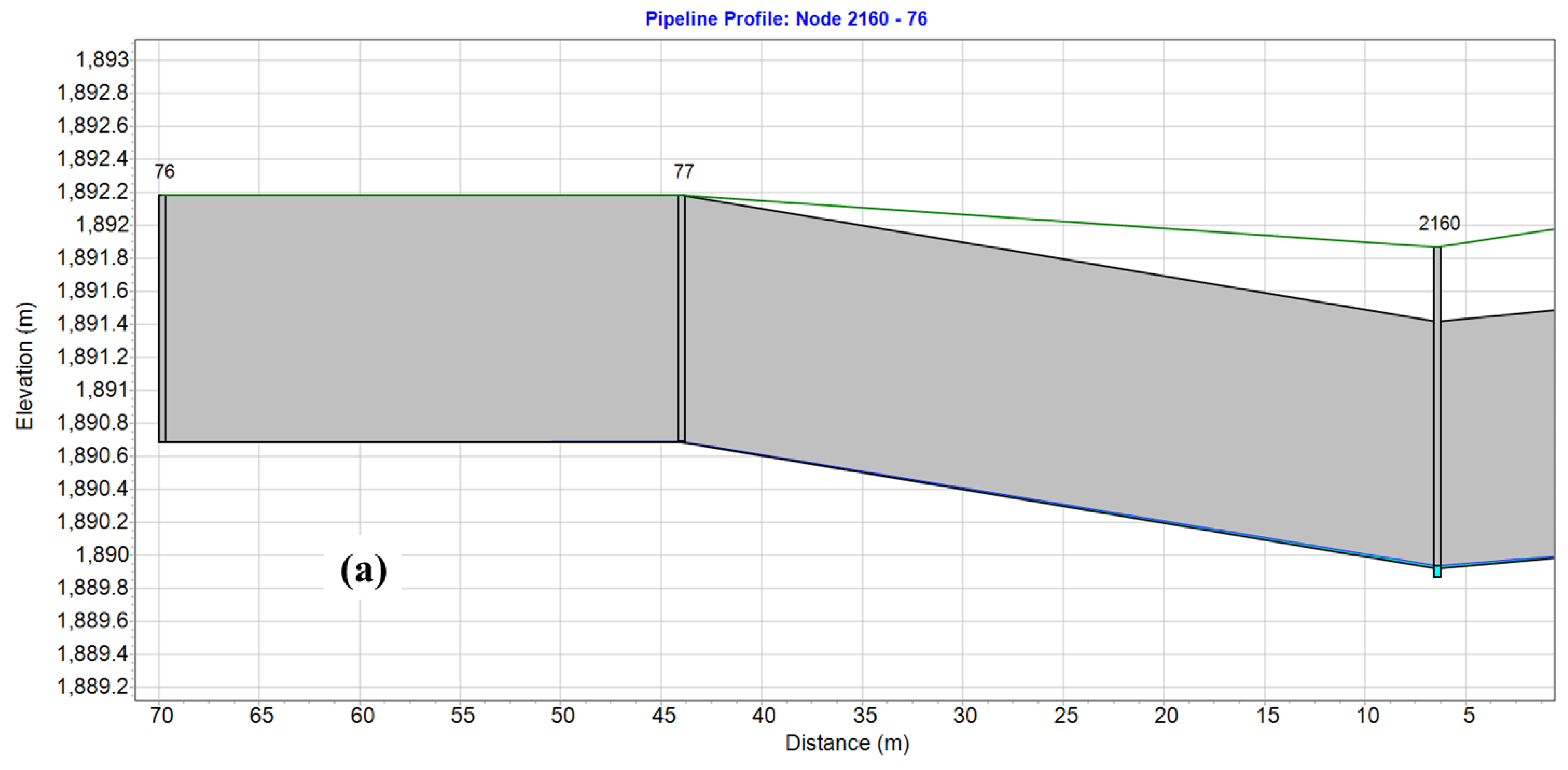
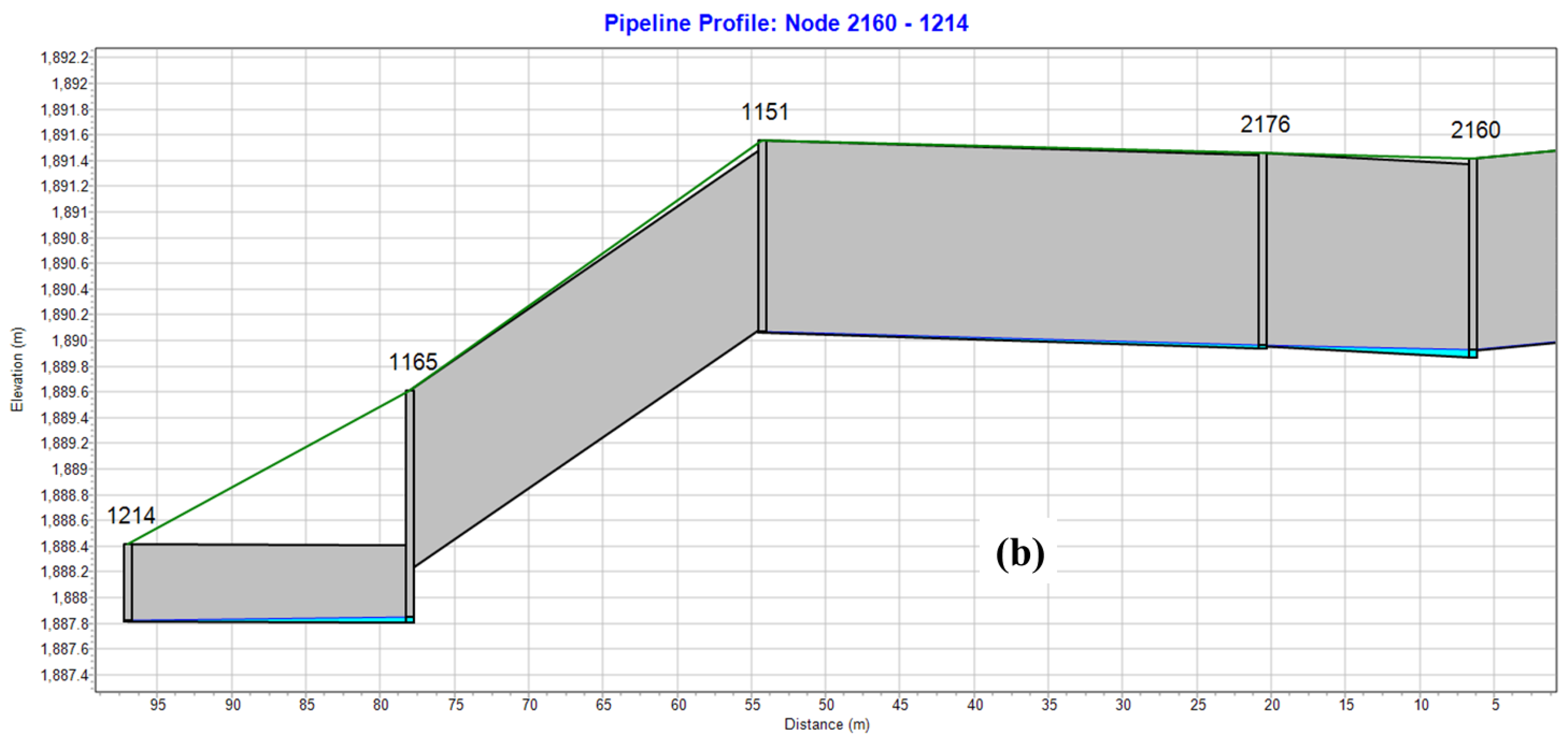
| Design Frequency (a) | The Total Rainfall (mm) | The Biggest Rain Density (mm/5 min) |
|---|---|---|
| 1 | 24.953 | 5.805 |
| 2 | 33.778 | 7.858 |
| 3 | 38.940 | 9.059 |
| 5 | 45.442 | 10.571 |
| 10 | 54.267 | 12.624 |
| 20 | 63.091 | 14.677 |
| 30 | 68.252 | 15.878 |
| 50 | 74.755 | 17.39 |
| 100 | 83.579 | 19.443 |
| Potential Outfall | Area (ha) | Length of Conduits (m) | Number of Nodes | Number of Potential Outfalls | Combined System |
|---|---|---|---|---|---|
| (688) | 143.5 | 19,697.853 | 1146 | 1 | YES |
| (76, 1214) | 103.9 | 14,906.404 | 1020 | 2 | YES |
| (2998) | 20.01 | 2775.734 | 86 | 1 | YES |
| (688, 860, 4193) | 19.04 | 1061.384 | 69 | 3 | YES |
| (4916) | 16.13 | 2223.359 | 164 | 1 | NO |
| (51) | 15.08 | 3090.572 | 235 | 1 | NO |
| (76, 688, 1214) | 14.82 | 2725.267 | 219 | 3 | YES |
| (4015) | 11.02 | 1117.715 | 95 | 1 | NO |
| (50) | 7.202 | 994.165 | 122 | 1 | NO |
| (1214) | 5.414 | 800.299 | 55 | 1 | YES |
| (4016) | 5.067 | 783.716 | 32 | 1 | NO |
| (688, 3284) | 3.903 | 49.525 | 59 | 2 | YES |
| (4017) | 3.815 | 563.841 | 26 | 1 | NO |
| (1094) | 1.681 | 656.529 | 16 | 1 | NO |
| (4018) | 1.153 | 145.865 | 14 | 1 | NO |
| (4020) | 0.897 | 81.848 | 9 | 1 | NO |
| Computing Time (s) | Design Frequency | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 1a | 2a | 3a | 5a | 10a | 20a | 30a | 50a | 100a | MEAN | |
| SWMM | 273 | 280 | 288 | 290 | 291 | 296 | 290 | 302 | 311 | 291.22 |
| SBPO | 62 | 60 | 65 | 78 | 80 | 86 | 91 | 93 | 98 | 79.22 |
| Improve Efficiency (%) | 77.29 | 78.57 | 77.43 | 73.10 | 72.51 | 70.95 | 68.62 | 69.21 | 68.49 | 72.91 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ren, H.; Liu, S.; Li, M.; Zhang, H.; Wang, H.; Hao, X.; Cui, J. Topological Analysis and Application of Urban Drainage Network. Water 2022, 14, 3732. https://doi.org/10.3390/w14223732
Ren H, Liu S, Li M, Zhang H, Wang H, Hao X, Cui J. Topological Analysis and Application of Urban Drainage Network. Water. 2022; 14(22):3732. https://doi.org/10.3390/w14223732
Chicago/Turabian StyleRen, Hancheng, Shu Liu, Min Li, Hongping Zhang, Huiying Wang, Xiaoli Hao, and Jie Cui. 2022. "Topological Analysis and Application of Urban Drainage Network" Water 14, no. 22: 3732. https://doi.org/10.3390/w14223732
APA StyleRen, H., Liu, S., Li, M., Zhang, H., Wang, H., Hao, X., & Cui, J. (2022). Topological Analysis and Application of Urban Drainage Network. Water, 14(22), 3732. https://doi.org/10.3390/w14223732






