1. Introduction
The East Australian Current (EAC) is one of the most important current systems in the South Pacific Ocean. It carries huge amount of warm water from low latitudes to high latitudes, significantly affecting the local climate (Bowen et al., 2006 [
1]; Speich et al., 2002 [
2]). Besides, located at a crossroad between the Pacific and the Indian Oceans, the EAC also affects the material transport across the basins (Ridgway and Godfrey, 1997 [
3]). Therefore, it is of great importance to study the dynamic processes of the multi-scale circulation variability in the EAC region. Compared to the other western boundary currents, the EAC is less explored, especially in terms of its eddy–mean flow interaction (Imawaki et al., 2013 [
4]).
The EAC occupies a region of complex ocean dynamics characterized by current bifurcations and eddy shedding (
Figure 1). The EAC is formed at 10–15° S, and it gradually intensifies poleward (Ridgway and Dunn, 2003 [
5]). At about 32° S, the EAC separates into two branches: one, referred to as the southward EAC extension, and the other, the eastward Tasman Front, due to a combined effect of nonlinear flow instabilities and upper-ocean-topographic coupling (Tilburg et al., 2001 [
6]). Based on historical hydrographic observations and expendable bathythermograph data, Ridgway and Godfrey (1997 [
3]) firstly showed the seasonal variation in the EAC, with an amplitude of 6 Sv, weaker in austral winter and stronger in austral summer. Subsequent studies also revealed significant seasonal variations of the EAC’s southward transport (Cetina-Heredia et al., 2014 [
7]) and its cross-shelf transport (Schaeffer et al., 2014 [
8]) by using in situ and satellite data, as well as model outputs. The stronger EAC in austral summer is associated with higher eddy kinetic energy (EKE) in this region (Qiu and Chen, 2004 [
9]) and a southward shift of the EAC separation latitude (Ypma et al., 2016 [
10]). Nevertheless, by using Argo data and satellite altimeter observations, Zilberman et al. (2018) [
11] suggested that the EAC transport reaches its peak in March (21.6 ± 1.4 Sv), much earlier than previous studies. All these studies reveal the complex ocean dynamics of the seasonal variability in the EAC.
Although the EAC is recognized to be the weakest western boundary current in the ocean, its regional mesoscale eddy activities are comparable with those in the Gulf Stream and the Kuroshio, and play a vital role in the EAC system (Mata et al., 2006 [
12]). By using satellite altimeter observations, previous studies have found significant oscillations in the EAC transport with periods between 90 and 180 days, and suggested that it is associated with eddy activities in this region (Bowen et al., 2005 [
13]; Mata et al., 2006 [
12]; Wilkin and Zhang, 2007 [
14]). Based on observations and model outputs, eddy shedding activities in the EAC separation latitude have been explored (Everett et al., 2012 [
15]), and the result reveals that these eddies have a major impact on the entrainment and connectivity of plankton and fish populations. Besides, van Sebille et al. (2012) [
16] found that the detached eddies could move southward and eventually enter the Indian Ocean, affecting the heat and mass transport between the ocean basins. In addition to these shedding eddies, previous studies also found significant eddy activities in the southwest Pacific (Bowen et al., 2006 [
1]), which are related to the baroclinic instability along the South Pacific Subtropical Countercurrent (Qiu and Chen, 2004; Travis and Qiu, 2017 [
17]).
Previous research has focused on the seasonal variability in the EAC, especially the southward EAC transport, but less attention has been paid to how these seasonal variations of circulation impact on the mesoscale eddy activities along the EAC path. As the EAC varies with season, its horizontal velocity shear and its separation latitude all fluctuate. All these changes could modify the stability of the EAC system, affecting potentially the mesoscale eddy-shedding activities. To explore this modification, both satellite altimeter observations and outputs from a global eddy-permitting ECCO2 state estimate are used in this study. The goal is to detect the intra-seasonal eddy modulations along the EAC path and to quantify the related dynamical processes on the seasonal time scale.
3. Verification of ECCO2 Simulation
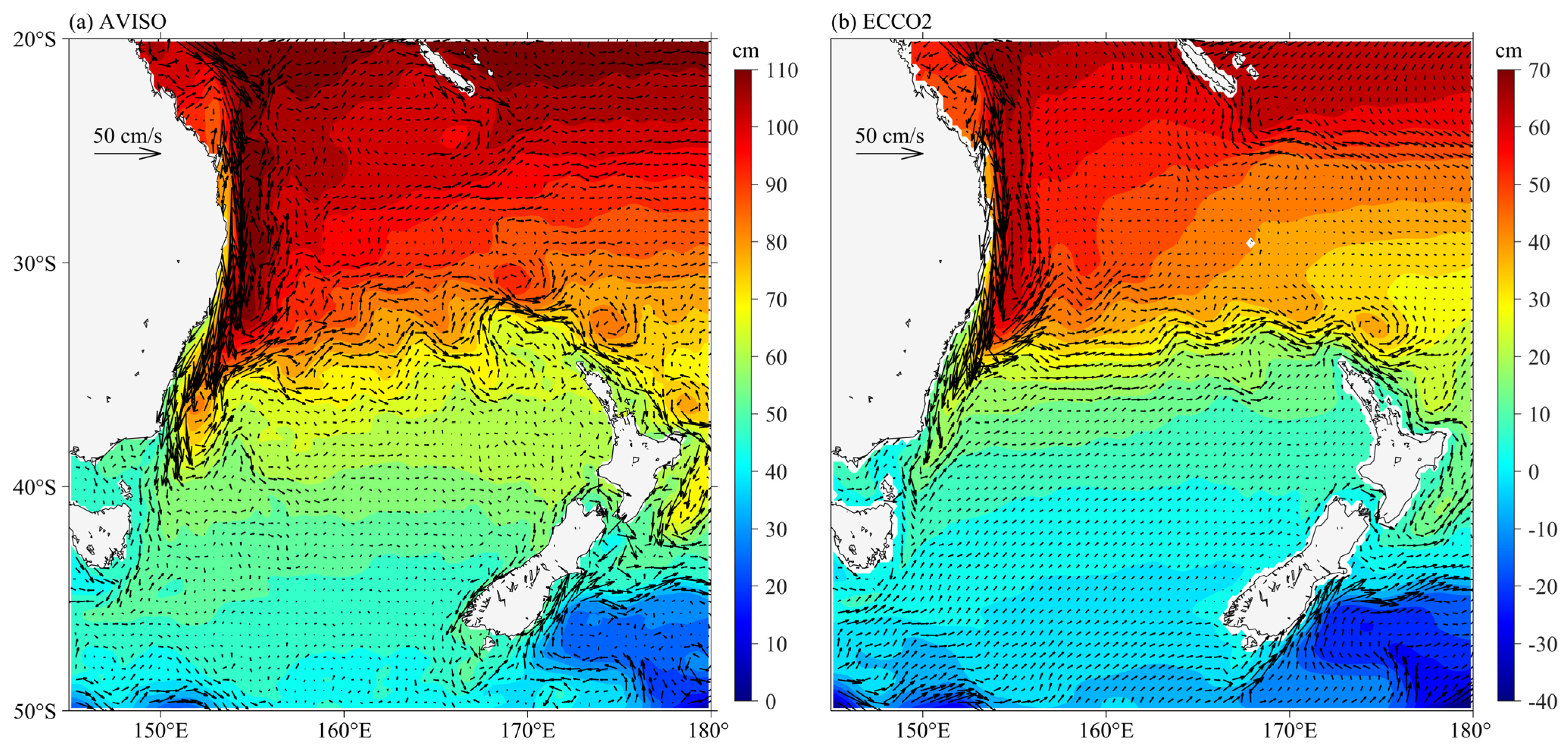
Before using the ECCO2 state estimate to study the dynamic processes governing the EKE signals in the EAC region, it is important to assess the accuracy of ECCO2 outputs against the satellite altimetry observations. As shown in
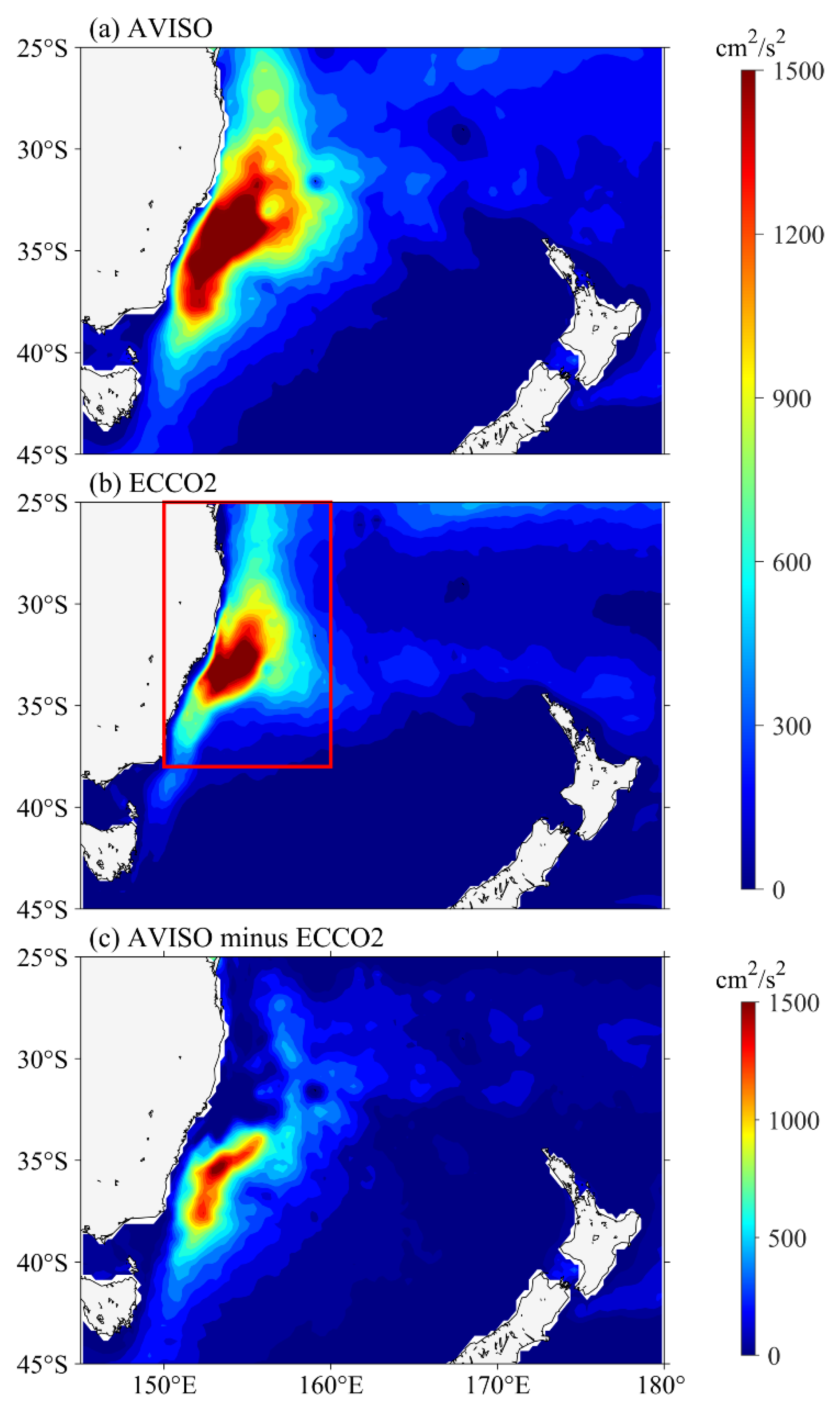
Figure 1, both SSH fields and surface circulations of ECCO2 state estimate match well that of AVISO data, which shows strong current retroflections associated with the positive SSH anomalies at about 37° S, and the meandering Tasman Front associated with the distinct SSH gradients along 34° S. Such good agreement is partially due to the assimilation of AVISO data in ECCO2 state estimate. In addition, we compared the time-mean surface EKE distributions in the EAC region, which are calculated from both AVISO data and ECCO2 outputs (
Figure 2). The result indicates that the ECCO2 state estimate can simulate EKE signals along the EAC. Both AVISO and ECCO2 results show high EKE in the 150–160° E, 25–38° S (red box in
Figure 2), around the EAC separation latitude, although the EKE signals from the ECCO2 outputs are relatively weaker to the south of 35° S. We also compared the observed and simulated EKE time series averaged in the high EKE region (red box in
Figure 2) as a function of calendar months (
Figure 3). It can be seen that both time series show an annual cycle that is strong in austral summer and weak in austral winter. Given these agreements, we believe the ECCO2 state estimate is reliable enough to explore the seasonal variation of EKE along the EAC.
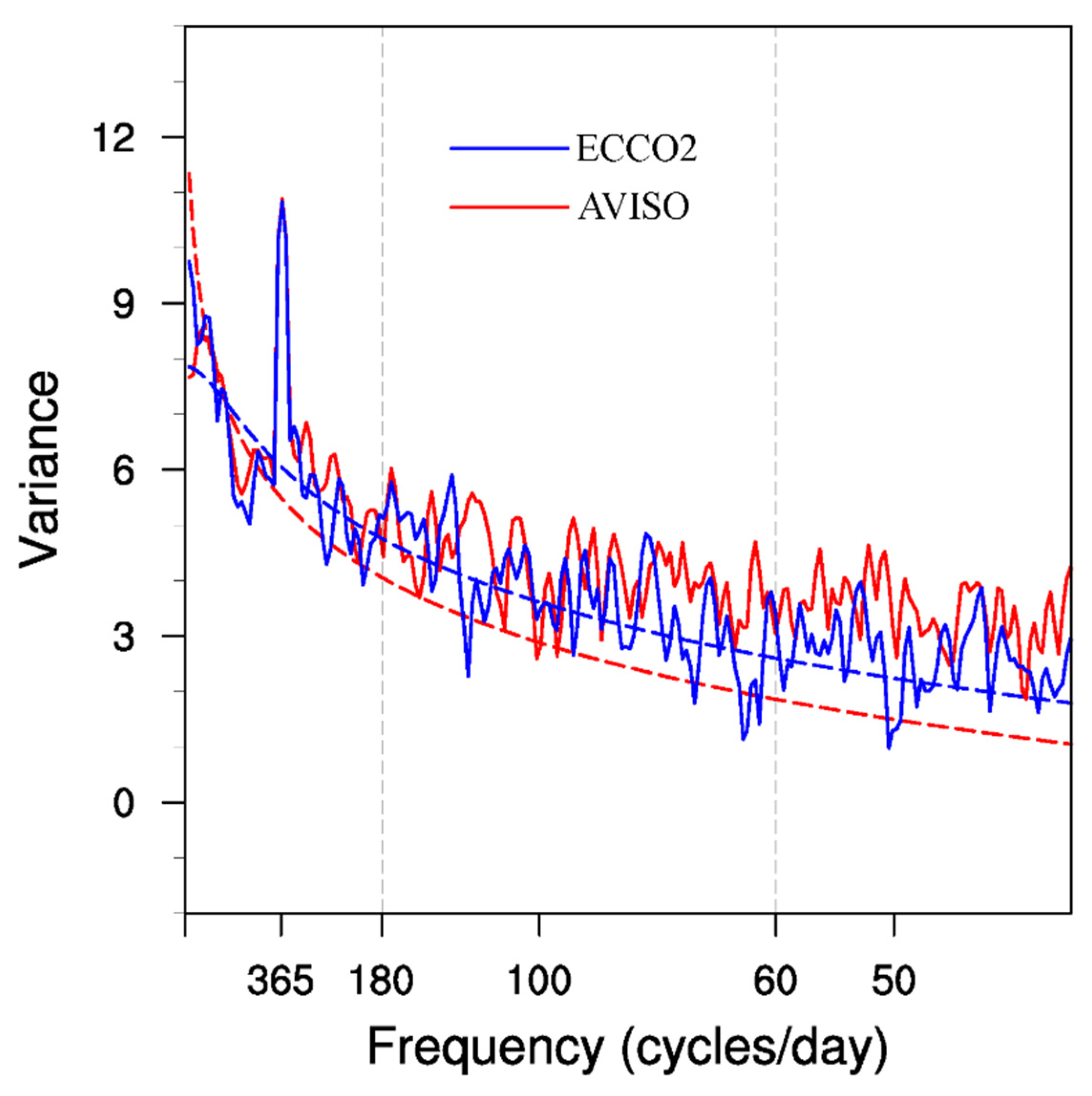
To better focus on the mesoscale signals, we calculated the variance-preserved power spectra of sea level anomalies along the EAC (red box in
Figure 2) from the AVISO data and ECCO2 state estimate. As shown in
Figure 4, in addition to the prominent annual period signals at 365 days, both observed and simulated results show significant intra-seasonal signals with periods at 60–180 days. To better focus on the intra-seasonal signals, we separate the velocity u into two parts, as follows:
where,
and
denote the 180-day low-pass filtered velocity time series and 60–180-day bandpass filtered velocity time series, respectively. In this paper, a 4-order Butterworth filter is used to extract intra-seasonal signals.
4. Seasonal EKE Modulation along the EAC
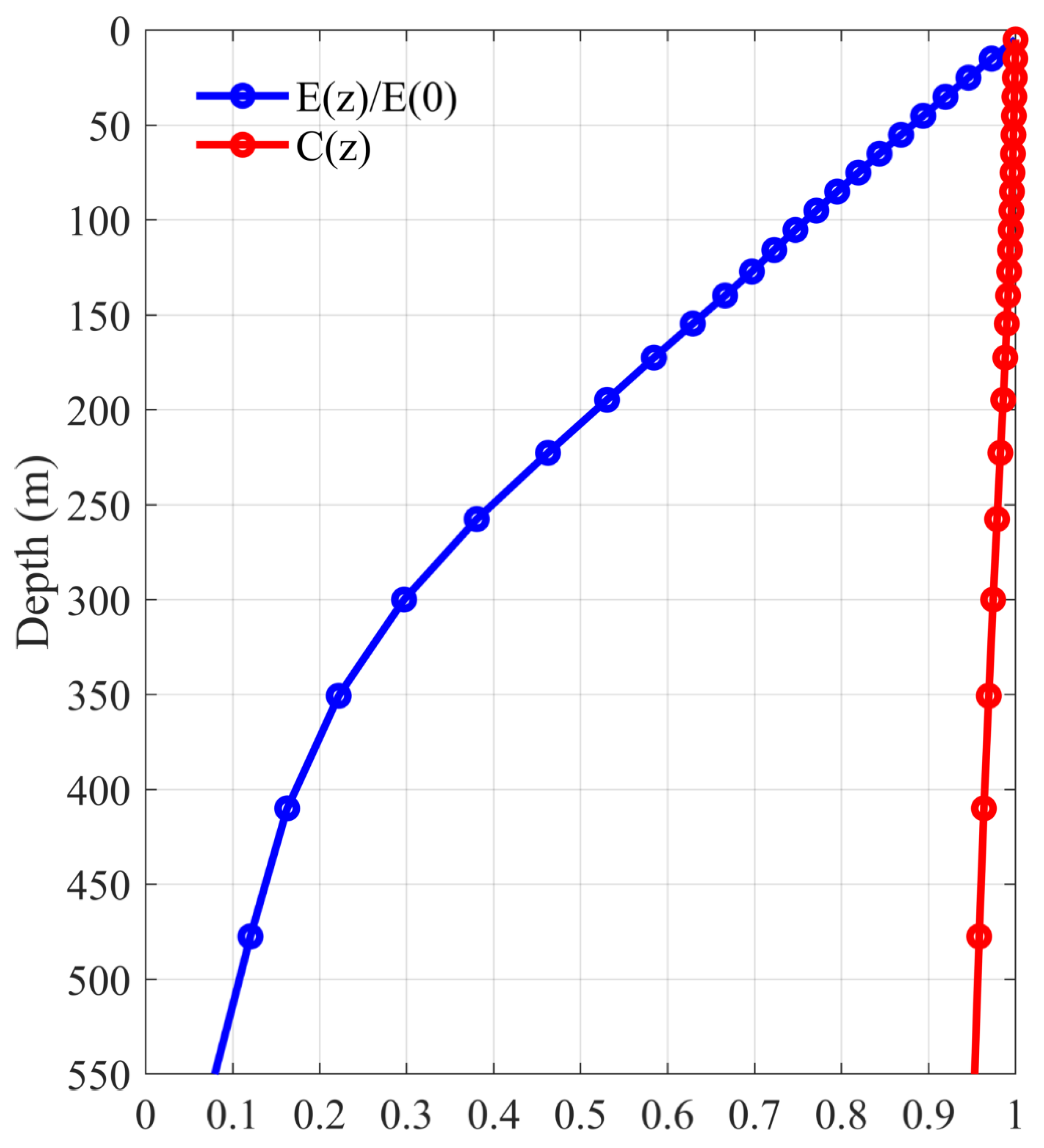
To explore the seasonal variation of EKE along the EAC, it is first necessary to determine the vertical structure of the EKE. To do so, we calculated the EKE time series at different depths from the ECCO2 outputs, referred to as
E(
t,
z), which is spatial averaged in the chosen region (red box in
Figure 2). As shown in
Figure 5, the blue line represents the ratio of EKE at different depths to EKE at the surface: 〈
E(
t,
z)〉/〈
E(
t, 0)〉, where 〈 〉 represent the time mean result. It can be seen that the EKE ratio decreases rapidly with depth. At about 500 m, the EKE value is only 10 percent the size of surface EKE. The red line represents the correlation coefficient between the EKE time series at different depths and the surface time series, which is calculated as follows:
where,
is the regression coefficients. Here, C(z) represents the correlation between EKE time series at different depth z and the surface EKE time series. It can be seen that C(z) is greater than 0.9 over the full upper 500 m layer. This indicates that the temporal variation of EKE at different depth is similar to that at the surface. Given the ratio and correlation between
E(
t, 0) and
E(
t,
z) at different depth, we focus below on the EKE variations in the upper 500 m layer.
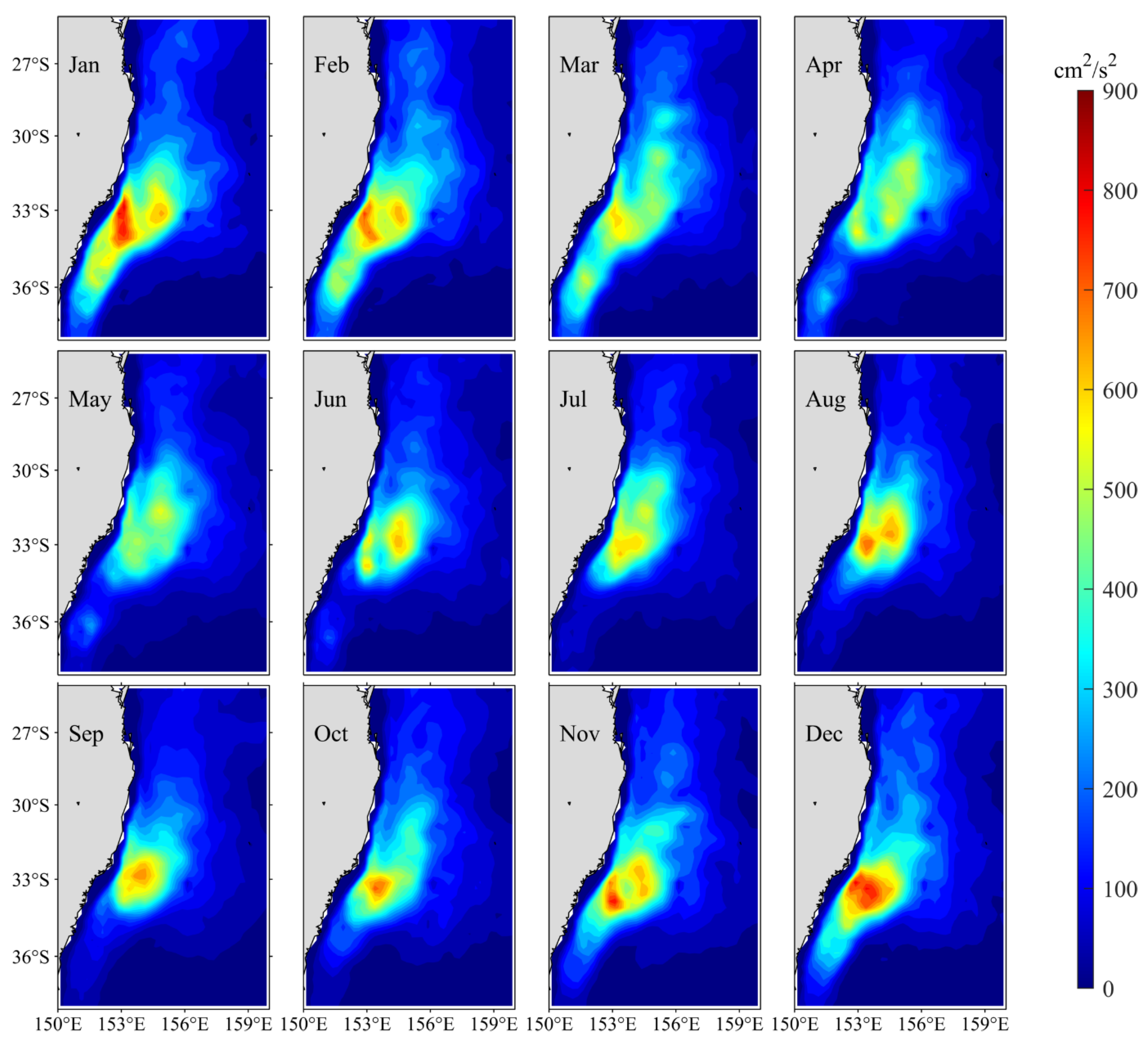
Figure 6 shows the monthly distribution of EKE along the EAC averaged in the upper 500 m, which is calculated by using 60–180-day bandpass filtered
and
based on Equation (1). The EKE is relatively larger around the EAC separation latitude, and shows a well-defined annual cycle. The EKE is largest in austral summer from December to February, with the maximum value area extends to south about 36° S. After February, the EKE decreases gradually and the maximum value area shrinks similarly. Both the EKE and the maximum value area reach their minima in June.
In Figure 9, we plot the mesoscale EKE time series (black line) in the 150–160° E, 25–38° S as a function of calendar months. With a maximum (152 cm2/s2) in January and a minimum (110 cm2/s2) in September, the seasonality of EKE along the EAC is clearly dominated by the local EKE signals around the EAC separation latitude.
5. Processes Governing the Seasonal EKE Variability
In order to elucidate the dynamic processes behind the seasonal variation of EKE, we calculated the barotropic and baroclinic eddy energy conversion rates, which are defined as follows (Chen et al., 2015 [
19]; Yang et al., 2020 [
20]):
where,
and
are the 60–180-day bandpass filtered horizontal velocity anomalies, and
and
denote the background horizontal currents (including time–mean flows) with time scales longer than 180 days. Similarly,
and
are the 60–180-day bandpass filtered potential density and vertical velocity anomalies,
g is the gravitational acceleration (
g = 9.8 m/s
2),
is the background potential density (
= 1025 kg/m
3). It should be noted that the barotropic conversion rate (BTR) represents the conversion process between EKE and mean kinetic energy (MKE). A positive BTR represents the conversion of energy from the MKE to the EKE, and reflects barotropic instability of the background mean flow. The baroclinic conversion rate (BCR) represents the transformation between eddy potential energy (EPE) and EKE. A positive baroclinic conversion rate represents the energy transformation from EPE to EKE as a result of baroclinic instability.
Figure 7 shows the monthly mean barotropic conversion rate (BTR) distributions averaged in the upper 500 m. the BTR is larger along the EAC path, especially around the EAC separation latitude. In addition, the BTR shows a clear seasonal variation. Starting from June, positive BTR signals increase in magnitude gradually until February and weaken steadily after March. Along with the seasonal evolution of the BTR, the maximum value area of positive BTR expands southward in austral winter and shrinks northward in austral summer. This seasonal variation of BTR matches favorably with the evolution in mesoscale EKE signals along the EAC (recall
Figure 6).
Figure 9 plots the BTR time series (red solid line) as a function of calendar months, which are averaged within 150–160° E, 25–38° S region. The BTR is largest in March (1.2 × 10−4 cm2/s3) and smallest in September (0.4 × 10−4 cm2/s3). It can be seen that the seasonal variation of BTR is similar to the seasonal cycle of EKE, except for the drop-out value in February. Over all, this result reveals the high correlation between EKE and BTR.
We also calculated the BCR variation in this study.
Figure 8 shows the monthly distributions of the BCR averaged in the upper 500 m layer. Like BTR, the large BCR values are also concentrated in the EAC separation region. Moreover, BCRs are largely positive along the coast and negative in the offshore sea, forming a dipole structure. Overall, the BCR values are much smaller than BTR. The red dash line in
Figure 9 shows the BCR time series in the 150–160° E, 25–38° S region as a function of calendar months. It is largest (0.19 × 10
−4 cm
2/s
3) in August and smallest (0.04 × 10
−4 cm
2/s
3) in February, which is opposite to the seasonal BTR variation. In general, the seasonal variation of BCR is much smaller than that of BTR, indicating the leading role of barotropic instability in the EAC’s EKE evolution.
6. Discussion and Summary
To better understand the dynamic processes of eddy–mean flow interaction in the EAC region, we also analyze the seasonal variation of the 180-day low-passed EAC (
Figure 10). The EAC is strong in the coastal region, and the northward EAC countercurrent is formed at about 33° S. Due to the existence of countercurrent, the anticyclonic recirculation is formed in the offshore sea, further promoting the generation of eddies in the offshore sea. It can be seen that the anticyclonic recirculation is strongest in January, and the southern end of the recirculation can reach to about 35° S. From February, the anticyclonic recirculation begins to weaken, and it almost disappears in June, accompanied by a less sharp angle of retroflection. From July, the anticyclonic recirculation gradually increases as the season progresses, reaching its peak in January in the following year, completing the annual cycle. In addition, it is clear that the southward mean EAC shows an annual cycle, which is stronger in austral summer and weaker in austral winter. To visualize the variation more intuitively, we also calculated the time series of the EAC velocity averaged in the upper 500 m layer as a function of months, which is shown in
Figure 9 (green line). The result reveals that the spatial averaged EAC velocity reaches its peak in January (12.9 cm/s) and its trough in June (7.9 cm/s), which is the same as the seasonal BTR variation (red solid line). In summary, barotropic instability of the background mean circulation is associated with the EAC strength in this region. In austral summer, the larger EAC velocity promotes a stronger anticyclonic recirculation around the EAC separation latitude and favors the barotropic instability of the mean flow, and vice versa in austral winter.
The occurrence of barotropic instability usually requires strong horizontal shear of the background mean flow. To further confirm our above conclusion, we calculated the lateral rate of strain (refer to as LRS in the following) as follows (Rocha et al., 2016 [
21]), which can quantitatively characterize the magnitude of horizontal velocity shear:
where,
and
represent the 180-day low-pass filtering velocities.
Figure 11 shows the monthly LRS anomaly distributions in the upper 500 m layer, which have subtracted the annual mean value. In general, the seasonal evolution of LRS is similar to the seasonal variation of the EAC mean flow, which further validates our above conclusion.
In summary, the seasonal variation of EKE along the EAC and the related dynamic processes are examined in this paper. Our result reveals that the evolution of EKE is mainly controlled by the barotrophic instability of the EAC. In austral summer, the stronger southward-extending EAC promotes the formation of the anticyclonic recirculation, which favors the barotropic instability of the mean flow, elevating the regional EKE level. All these processes are reversed in austral winter. Meanwhile, it can be seen in
Figure 10 that the EAC separation latitude also shifts north–south with seasons, which agrees well with the previous study (Oke et al., 2019 [
22]). Extending the previous study, our result reveals that the barotropic instability is mainly controlled by the strength of the EAC. At the same time, it can be noticed that the EKE from ECCO2 state estimate is a litter weaker than that from AVISO data, which may relate to the eddy-permitting resolution (0.25° × 0.25°) of the ECCO2 state estimate. Thus, a high-resolution ocean state estimate is needed in the future to more accurately capture the magnitude of the EKE variations.
Based on global eddy databases (Chelton et al., 2007 [
23]; Chelton et al., 2011 [
24], Everett et al., 2012 [
15]) emphasized the vital roles of eddies in this region, known as the “Eddy Avenue”, whose eddy transport can explain 46% of the total southward volume transport (Cetina-Heredia et al., 2014 [
7]). Considering the wrapping capacity of mesoscale eddies, more in situ observations and high-resolution modeling studies are needed to understand the impact of eddy-shedding activities on inter-basin heat/fresh water transport and their impact on ecologies in the Southern Ocean.