Study on Water Vertical Infiltration Characteristics and Water Content Simulation of Sandstone Overlying Loess
Abstract
:1. Introduction
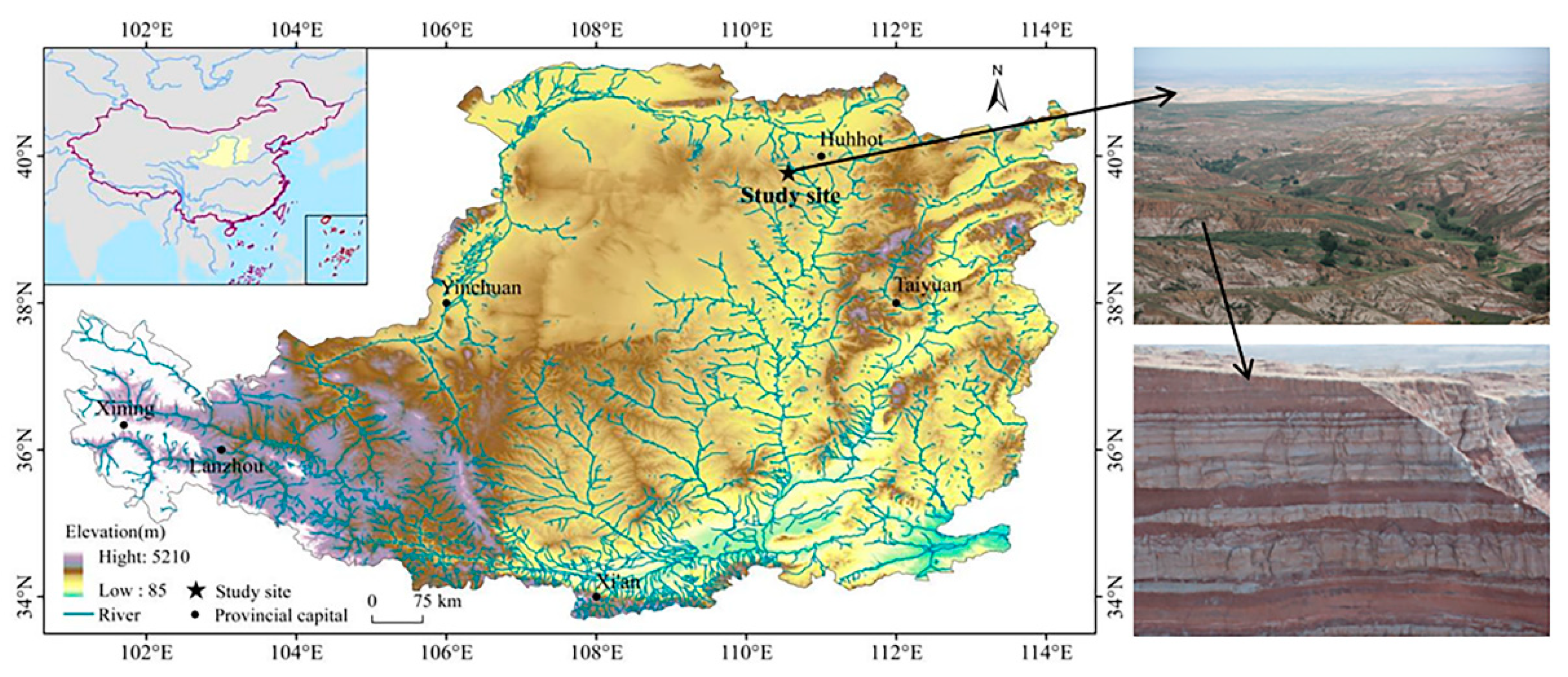
2. Materials and Methods
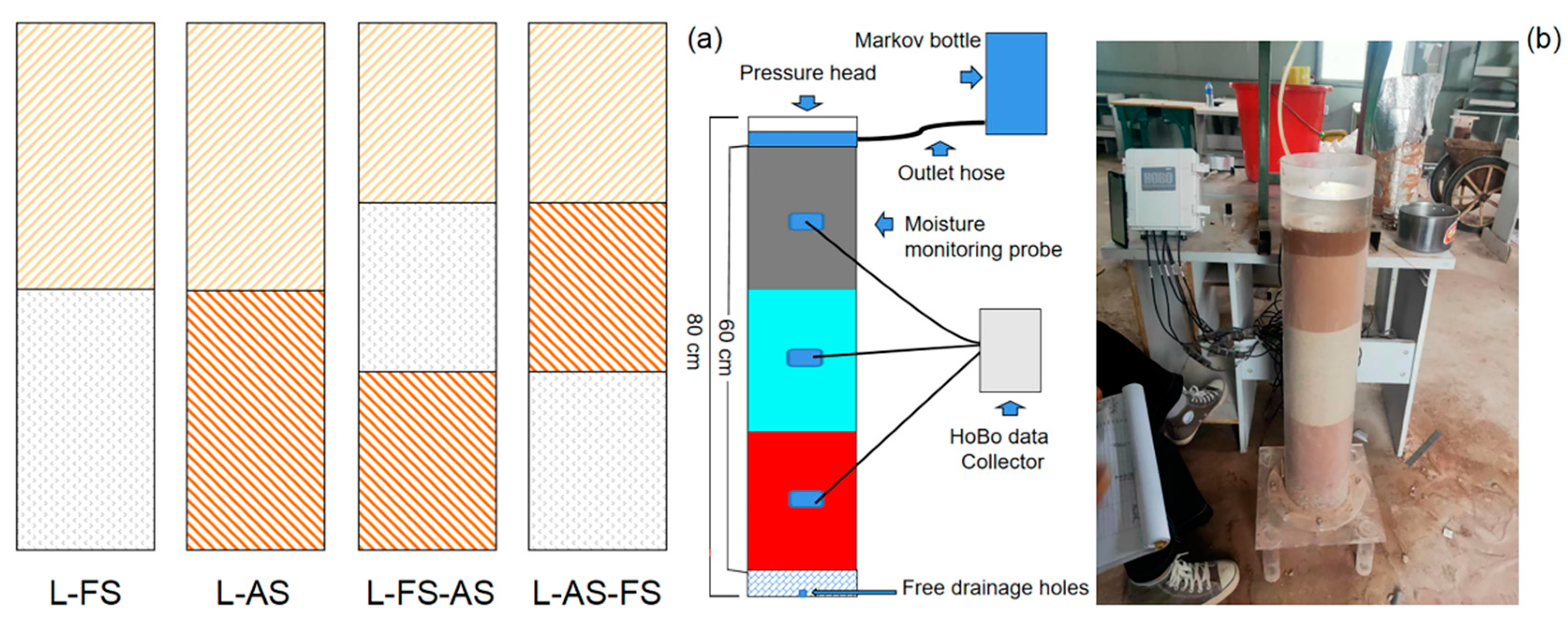
2.1. Experimental Design
2.2. Model Principle
2.3. Accuracy of the Verification Parameters
3. Results
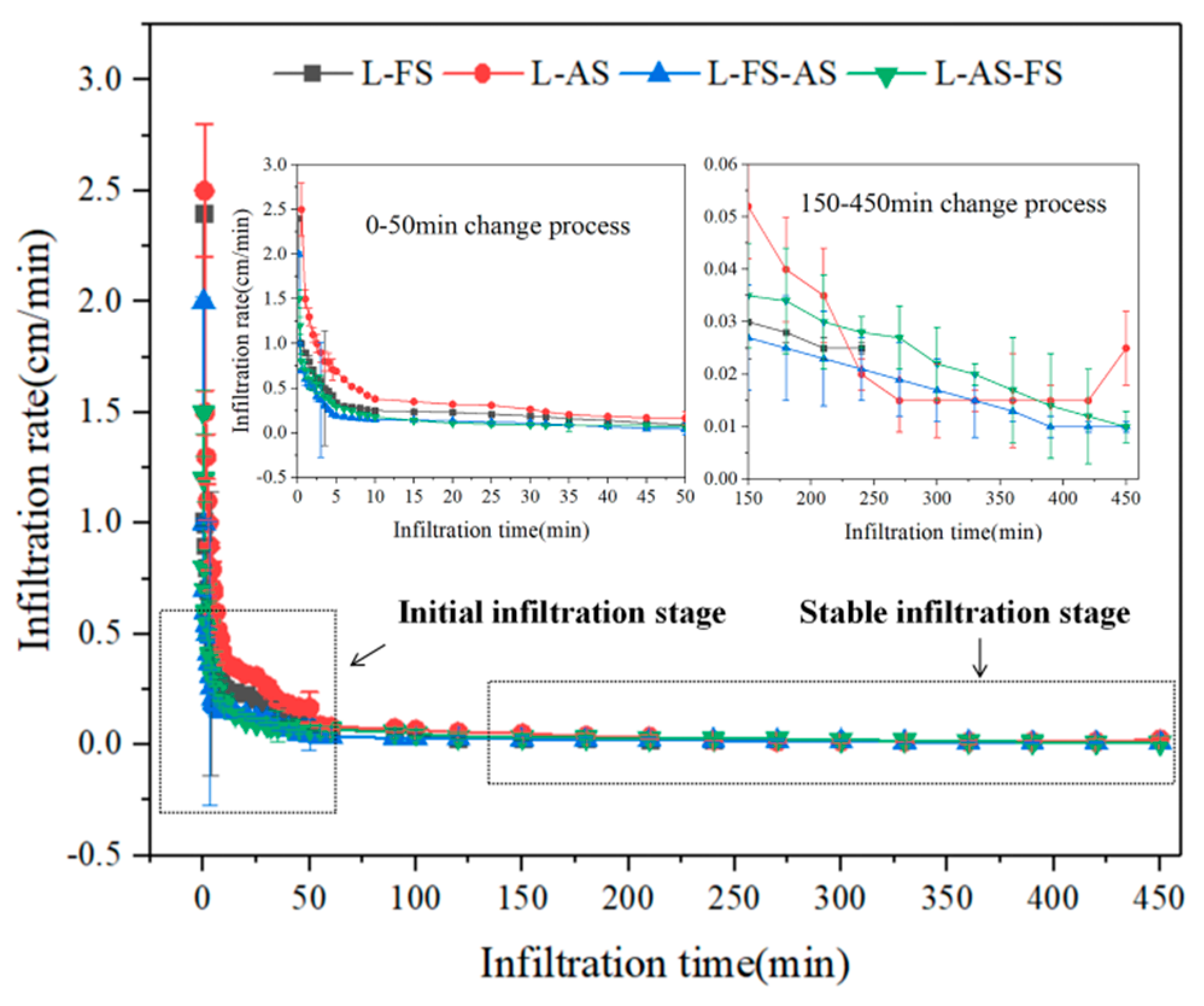
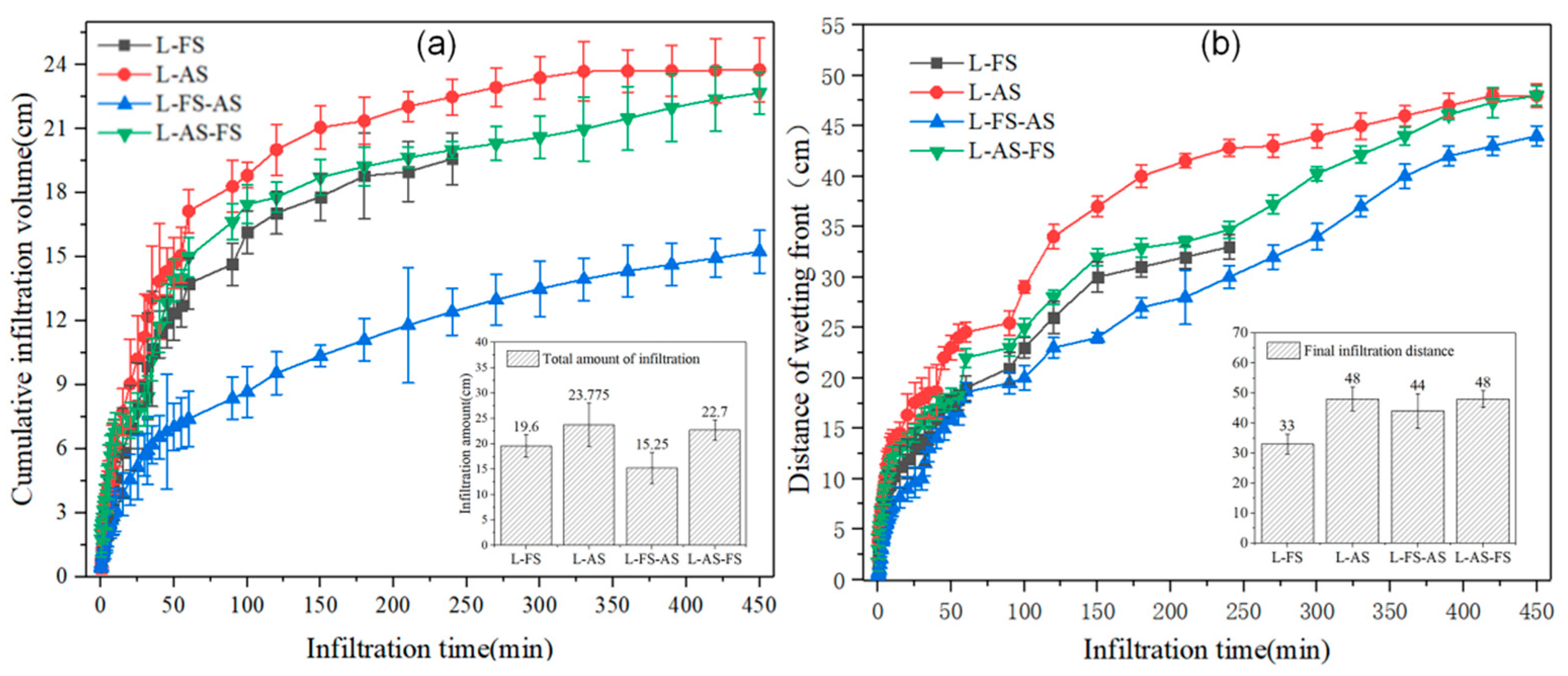
3.1. Characteristics of Water Infiltration in Loess–Sandstone Structures
3.2. Simulation of Water Movement in Loess-Sandstone Structure
3.2.1. Determination and Inversion of Hydraulic Parameter of Soil
3.2.2. Establishment of Spatial and Temporal Information and Setting Boundary Conditions
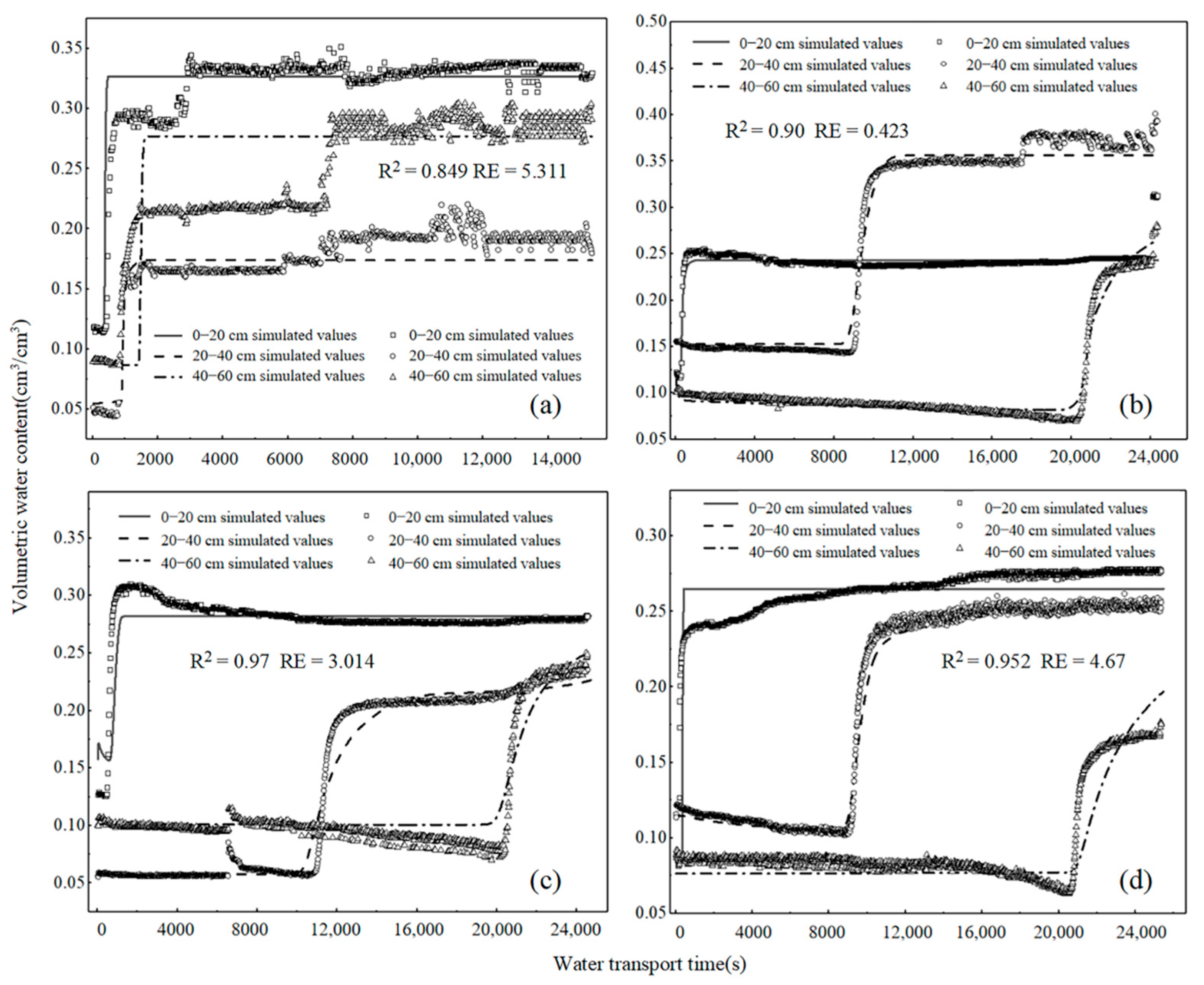
3.2.3. Simulation and Accuracy Verification of Moisture Transport in Loess-Overlaid Sandstone
4. Discussion
4.1. Influencing Factors of Water Infiltration in Loess-Overlaid Sandstone
4.2. Role of Infiltration in Loess-Overlaid Sandstone in Hydraulic Erosion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Morbidelli, R.; Corradini, C.; Saltalippi, C.; Flammini, A.; Dari, J.; Govindaraju, R.S. A New Conceptual Model for Slope-Infiltration. Water 2019, 11, 678. [Google Scholar] [CrossRef] [Green Version]
- Shen, Z.; Liu, K.; Wu, Z.; Liu, J.; Qi, K.; Niu, X.; Wang, G.; Yao, W. Transformation of Raindrop characteristics (Nov 24, 2015) of natural rainfall of Yellow River basin. IOP Conf. Series: Earth Environ. Sci. 2018, 113, 012014. [Google Scholar] [CrossRef]
- Guo, Y.; Liu, S.; Baetz, B.W. Probabilistic rainfall-runoff transformation considering both infiltration and saturation excess runoff generation processes. Water Resour. Res. 2012, 48. [Google Scholar] [CrossRef] [Green Version]
- Shoaib, M.; Shamseldin, A.Y.; Melville, B.W. Comparative study of different wavelet based neural network models for rainfall–runoff modeling. J. Hydrol. 2014, 515, 47–58. [Google Scholar] [CrossRef]
- Zongjie, L.; Zongxing, L.; Qi, F.; Xufeng, W.; Yanhu, M.; Huijuan, X.; Ling-Ling, S.; Juan, G.; Baijuan, Z.; Wende, G.; et al. Hydrological effects of multiphase water transformation in Three-River Headwaters Region, China. J. Hydrol. 2021, 601, 126662. [Google Scholar] [CrossRef]
- Marquart, A.; Eldridge, D.J.; Geissler, K.; Lobas, C.; Blaum, N. Interconnected effects of shrubs, invertebrate-derived macropores and soil texture on water infiltration in a semi-arid savanna rangeland. Land Degrad Dev. 2020, 31, 2307–2318. [Google Scholar] [CrossRef]
- Foley, J.; Loch, R.; Glanville, S.; Connolly, R. Effects of tillage, stubble and rainfall energy on infiltration. Soil Tillage Res. 1991, 20, 45–55. [Google Scholar] [CrossRef]
- Sun, Z. Effect of Soft Rock Amendment on Soil Moisture and Water Storage in Mu Us Sandy Land. IOP Conf. Series: Mater. Sci. Eng. 2018, 381, 012044. [Google Scholar] [CrossRef]
- Szejba, D.; Cymes, I.; Szatylowicz, J.; Szymczyk, S. An impact of drainage system on soil water conditions at Lidzbark Warminski experimental site. Biologia 2009, 64, 565–569. [Google Scholar] [CrossRef]
- Ryzhenko, B.N.; Sidkina, E.S.; Cherkasova, E.V. Thermodynamic modeling of water-rock systems to evaluate their generative potential for hydrocarbons. Geochem. Int. 2015, 53, 825–837. [Google Scholar] [CrossRef]
- Belyaeva, T.A.; Bobrov, P.P.; Kroshka, E.S.; Lapina, A.S.; Rodionova, O.V. The effect of very low water content on the complex dielectric permittivity of clays, sand-clay and sand rocks. Meas. Sci. Technol. 2016, 28, 014005. [Google Scholar] [CrossRef]
- Yuan, L.H.; Fan, G.S. The Experiment Study on the Soil Infiltration Characteristics of Yumenkou Water Pumping Station Irrigation District of Regional Scale. Appl. Mech. Mater. 2013, 316, 661–664. [Google Scholar] [CrossRef]
- Morel-Seytoux, H.J.; Meyer, P.; Nachabe, M.; Tourna, J.; van Genuchten, M.; Lenhard, R.J. Parameter Equivalence for the Brooks-Corey and Van Genuchten Soil Characteristics: Preserving the Effective Capillary Drive. Water Resour. Res. 1996, 32, 1251–1258. [Google Scholar] [CrossRef]
- Mbagwu, J. Testing the goodness of fit of infiltration models for highly permeable soils under different tropical soil management systems. Soil Tillage Res. 1995, 34, 199–205. [Google Scholar] [CrossRef]
- Al Maimuri, N.M.L. Applicability of Horton model and recharge evaluation in irrigated arid Mesopotamian soils of Hashimiya, Iraq. Arab. J. Geosci. 2018, 11, 610. [Google Scholar] [CrossRef]
- Haowen, X.; Yawen, W.; Luping, W.; Weilin, L.; Wenqi, Z.; Hong, Z.; Yichen, Y.; Jun, L. Comparing simulations of green roof hydrological processes by SWMM and HYDRUS-1D. Water Supply 2019, 20, 130–139. [Google Scholar] [CrossRef]
- Shelia, V.; Šimůnek, J.; Boote, K.; Hoogenbooom, G. Coupling DSSAT and HYDRUS-1D for simulations of soil water dynamics in the soil-plant-atmosphere system. J. Hydrol. Hydromechanics 2018, 66, 232–245. [Google Scholar] [CrossRef] [Green Version]
- González, M.G.; Ramos, T.B.; Carlesso, R.; Paredes, P.; Petry, M.T.; Martins, J.D.; Aires, N.P.; Pereira, L.S. Modelling soil water dynamics of full and deficit drip irrigated maize cultivated under a rain shelter. Biosyst. Eng. 2015, 132, 1–18. [Google Scholar] [CrossRef] [Green Version]
- Okamoto, K.; Sakai, K.; Nakamura, S.; Cho, H.; Nakandakari, T.; Ootani, S. Optimal Choice of Soil Hydraulic Parameters for Simulating the Unsaturated Flow: A Case Study on the Island of Miyakojima, Japan. Water 2015, 7, 5676–5688. [Google Scholar] [CrossRef] [Green Version]
- Trafimow, D. The intelligibility of r or r2 as an effect size statistic: Dichotomous variables. Front. Psychol. 2015, 6, 294. [Google Scholar] [CrossRef]
- Romero-Padilla, J.M.; Han, C.-P. Estimation of variance in bivariate normal distribution after the preliminary test of homogeneity. Commun. Stat. -Theory Methods 2016, 46, 1290–1305. [Google Scholar] [CrossRef] [Green Version]
- Valdes-Abellan, J.; Pachepsky, Y.; Martinez, G. MATLAB algorithm to implement soil water data assimilation with the Ensemble Kalman Filter using HYDRUS. MethodsX 2018, 5, 184–203. [Google Scholar] [CrossRef] [PubMed]
- Su, L.; Li, M.; Wang, Q.; Zhou, B.; Shan, Y.; Duan, M.; Sun, Y.; Ning, S. Algebraic model for one-dimensional horizontal water flow with arbitrary initial soil water content. Soil Res. 2021, 59, 511–524. [Google Scholar] [CrossRef]
- Grant, S.A.; Jabro, J.D.; Fritton, D.D.; Baker, D.E. A stochastic model of infiltration which simulates “macropore” soil water flow. Water Resour. Res. 1991, 27, 1439–1446. [Google Scholar] [CrossRef]
- Elshafei, Y.Z.; Aldarby, A.M. Bulk-Density in Relation to Infiltration Capacity of Loam Soils. Arab Gulf. J. Sci. Res. 1991, 9, 55–69. [Google Scholar]
- Li, H.; Fan, G. The Quantitative Relation of Stable Infiltration Rates between the Pressured and Non-pressured Water Infiltration in Unsaturated Soils. J. Irrig. Drain. 2010, 29, 17–21. [Google Scholar]
- Noborio, K.; Mclnnes, K.J.; Heilman, J.L. Measurements of cumulative infiltration and wetting front location by time domain reflectometry. Soil Sci. 1996, 161, 480–483. [Google Scholar] [CrossRef]
- Zhao, L.; Wang, L.; Liang, X.; Wang, J.; Wu, F. Soil Surface Roughness Effects on Infiltration Process of a Cultivated Slopes on the Loess Plateau of China. Water Resour. Manag. 2013, 27, 4759–4771. [Google Scholar] [CrossRef]
- Hardie, M.; Deurer, M.; Doyle, R.; Lisson, S.; Cotching, W.; Mattern, K. Development of Unstable Flow and Reduced Hydraulic Conductivity due to Water Repellence and Restricted Drainage. Vadose Zone J. 2012, 11, vzj2011.0099. [Google Scholar] [CrossRef]
- Najm, M.R.A.; Stewart, R.D.; Di Prima, S.; Lassabatere, L. A Simple Correction Term to Model Infiltration in Water-Repellent Soils. Water Resour. Res. 2021, 57, 2. [Google Scholar] [CrossRef]
- Sawhney, B.L.; Parlange, J.-Y. Two-Dimensional Water Infiltration from a Trench in Unsaturated Soil. Sci. Soc. Am. J. 1974, 38, 867. [Google Scholar] [CrossRef]
- Dong, Q.G.; Han, J.C.; Zhang, Y.; Li, N.; Lei, N.; Sun, Z.H.; Du, Y.C.; He, J. Water Infiltration of Covering Slils With Different Textures and Bulk Densities in Gravel Mulched Areas. Appl. Ecol. Envrion. Res. 2019, 17, 14039–14052. [Google Scholar]
- Chen, L.; Fei, L.; Liu, L.; Wang, Z.; Zhong, Y. Effects of Soil Initial Water Content on Transport Characteristics of Free Infiltration Water and Nitrogen Under Film Hole Irrigation with Muddy Water. J. Soil Water Conser. 2018, 32, 58–66. [Google Scholar]
- He, J.; Bai, D.; Guo, L.; Wang, X. Study on influence factors of vertical tube emitter’s infiltration characteristics. J. Xi’an Univ. Technol. 2017, 32, 354–358. [Google Scholar]
- Guo, S.; Shao, Y.; Zhang, T.; Zhu, D.Z.; Zhang, Y. Physical Modeling on Sand Erosion around Defective Sewer Pipes under the Influence of Groundwater. J. Hydraul. Eng. 2013, 139, 1247–1257. [Google Scholar] [CrossRef]
- Grieve, I.C.; Davidson, D.A.; Bruneau, P.M. Effects of liming on void space and aggregation in an upland grassland soil. Geoderma 2005, 125, 39–48. [Google Scholar] [CrossRef]
- Xu, Y.; Cui, G. Influence of spectral characteristics of the Earth’s surface radiation on the greenhouse effect: Principles and mechanisms. Atmospheric Environ. 2020, 244, 117908. [Google Scholar] [CrossRef]
- Mingalev, I.V.; Fedotova, E.A.; Orlov, K.G. Parameterization of the Infrared Molecular Absorption in the Earth’s Lower and Middle Atmosphere. Atmospheric Ocean. Opt. 2018, 31, 582–589. [Google Scholar] [CrossRef]
- Badro, J.; Aubert, J.; Hirose, K.; Nomura, R.; Blanchard, I.; Borensztajn, S.; Siebert, J. Magnesium Partitioning Between Earth’s Mantle and Core and its Potential to Drive an Early Exsolution Geodynamo. Geophys. Res. Lett. 2018, 45, 13240–13248. [Google Scholar] [CrossRef]
- Bryan, R.; Rockwell, D. Water table control on rill initiation and implications for erosional response. Geomorphology 1998, 23, 151–169. [Google Scholar] [CrossRef]
- Kinnell, P. Applying the RUSLE and the USLE-M on hillslopes where runoff production during an erosion event is spatially variable. J. Hydrol. 2014, 519, 3328–3337. [Google Scholar] [CrossRef]
- Han, S.; Yang, Y.; Fan, T.; Xiao, D.; Moiwo, J.P. Precipitation-runoff processes in Shimen hillslope micro-catchment of Taihang Mountain, north China. Hydrol. Process. 2011, 26, 1332–1341. [Google Scholar] [CrossRef]
- Chang, C.-M.; Yeh, H.-D. Spectral analysis of temporal non-stationary rainfall-runoff processes. J. Hydrol. 2018, 559, 84–88. [Google Scholar] [CrossRef]
- O’Loughlin, G.; Huber, W.; Chocat, B. Rainfall-runoff processes and modelling. J. Hydraul. Res. 1996, 34, 733–751. [Google Scholar] [CrossRef]
- Schertxer, D.; Tchiguirinskaia, I.; Lovejoy, S.; Hubert, P.; Bendjoudi, H.; Larcheveque, M. Discussion of “Evidence of chaos in the rainfall-runoff process” Which chaos in the rainfall-runoff process? Hydrol. Sci. J. 2002, 47, 139–148. [Google Scholar]
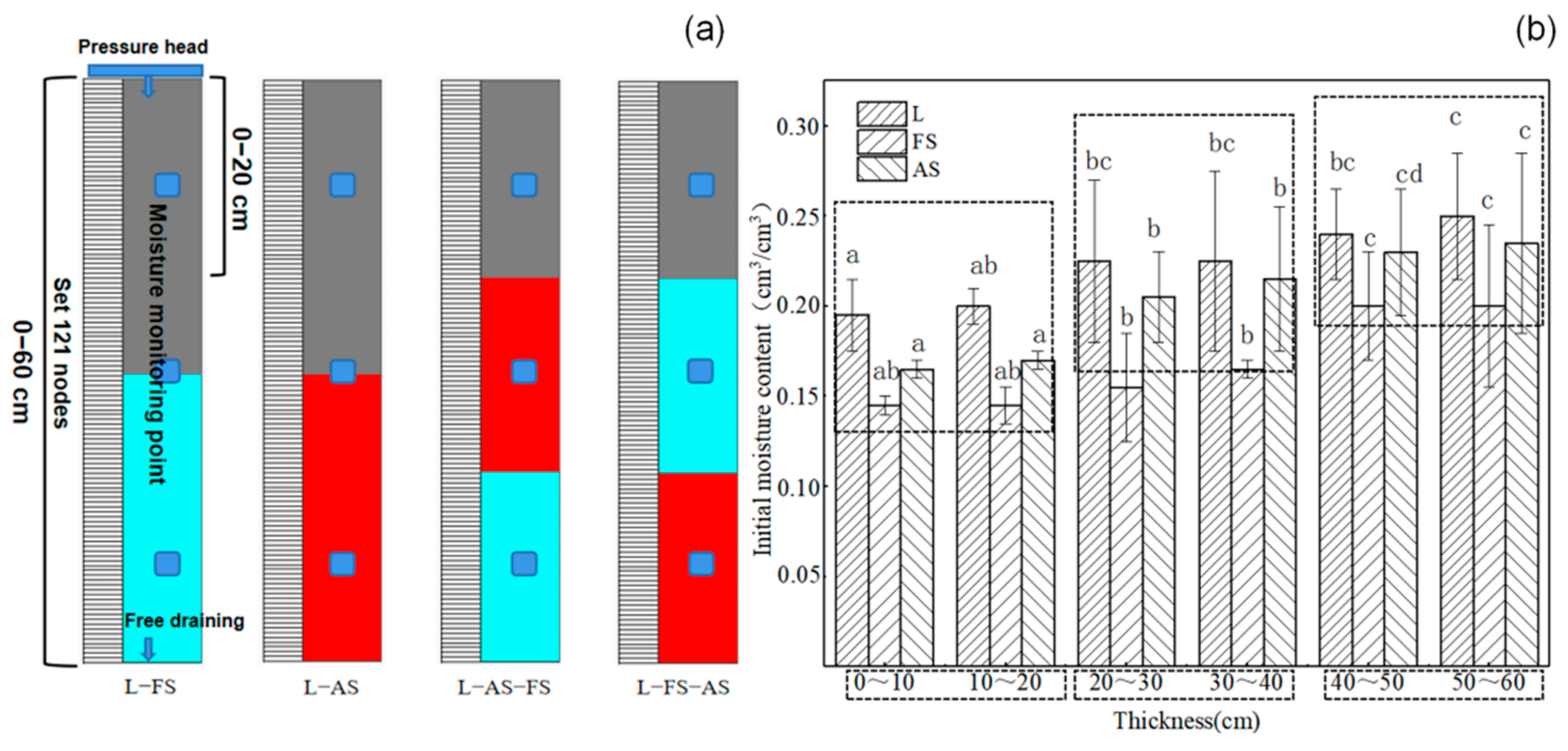
| Type | Bulk Density (g·cm−3) | Mechanical Composition Content (%) | Initial Moisture Content (cm3·cm−3) | Total Porosity (%) | ||
|---|---|---|---|---|---|---|
| Clay <0.002 mm | Powder 0.05~0.002 mm | Sand 0.050~2.00 mm | ||||
| L | 1.36 ± 0.09 | 23.62 ± 2.54 | 29.06 ± 1.14 | 65.02 ± 5.55 | 0.25 ± 0.04 | 40.48 ± 2.11 |
| FS | 1.68 ± 0.1 | 11.72 ± 1.36 | 5.88 ± 2.41 | 82.4 ± 7.12 | 0.27 ± 0.21 | 30.66 ± 3.45 |
| AS | 1.54 ± 0.13 | 27.21 ± 2.21 | 13.89 ± 5.01 | 58.9 ± 4.31 | 0.31 ± 0.07 | 37.4 ± 0.98 |
| Type | Initial Infiltration Rate (cm·min−1) | Stable Infiltration Rate (cm·min−1) |
|---|---|---|
| L–FS | 0.65 | 0.025 |
| L–AS | 0.91 | 0.03 |
| L–FS–AS | 0.47 | 0.01 |
| L–AS–FS | 0.53 | 0.015 |
| Type | Location of Interlayer Transition Plane | Time (min) | |
|---|---|---|---|
| Double layer structure | L–FS | 30 cm | 195 |
| L–AS | 30 cm | 175 | |
| Three layer structure | L–FS–AS | 20 cm | 120 |
| 40 cm | 420 | ||
| L–AS–FS | 20 cm | 100 | |
| 40 cm | 330 | ||
| Type | Depth (cm) | θx (cm3·cm−3) | θs (cm3·cm−3) | α (cm−1) | n | Ks (cm/s) |
|---|---|---|---|---|---|---|
| L | 0–20 | 0.0362 | 0.2629 | 0.02528 | 1.329 | 0.00513 |
| 20–40 | 0.0311 | 0.24 | 0.04528 | 1.213 | 8.15 × 10−4 | |
| 40–60 | 0.0332 | 0.256 | 0.04525 | 1.229 | 1.15 × 10−4 | |
| FS | 0–20 | 0.031 | 0.2626 | 0.0332 | 1.6508 | 0.00753 |
| 20–40 | 0.028 | 0.2724 | 0.02938 | 1.6508 | 0.00301 | |
| 40–60 | 0.031 | 0.1995 | 0.0332 | 1.4508 | 1.38 × 10−4 | |
| AS | 0–20 | 0.068 | 0.3412 | 0.01166 | 1.243 | 2.07 × 10−4 |
| 20–40 | 0.038 | 0.2286 | 0.01416 | 1.257 | 2.35 × 10−4 | |
| 40–60 | 0.033 | 0.3122 | 0.02136 | 1.145 | 1.56 × 10−4 |
| Type | Depth (cm ) | θx (cm3·cm−3 ) | θs (cm3·cm−3 ) | α (cm−1 ) | n | Ks (cm/s) |
|---|---|---|---|---|---|---|
| L–FS | 0–20 | 0.04795 | 0.3271 | 0.06071 | 1.438 | 0.00803 |
| 20–40 | 0.038 | 0.2808 | 0.05166 | 1.543 | 0.0576 | |
| 40–60 | 0.028 | 0.2799 | 0.05166 | 1.543 | 0.0221 | |
| L–AS | 0–20 | 0.05795 | 0.2833 | 0.03528 | 1.696 | 0.00639 |
| 20–40 | 0.038 | 0.3562 | 0.0423 | 1.427 | 6.92 × 10−4 | |
| 40–60 | 0.035 | 0.4786 | 0.01899 | 6.408 | 4.49 × 10−4 | |
| L–FS–AS | 0–20 | 0.05795 | 0.265 | 0.0922 | 1.929 | 0.00518 |
| 20–40 | 0.045 | 0.2724 | 0.02938 | 1.75 | 0.00301 | |
| 40–60 | 0.033 | 0.332 | 0.05155 | 1.584 | 0.005 | |
| L–AS–FS | 0–20 | 0.05795 | 0.2824 | 0.03149 | 1.849 | 0.00538 |
| 20–40 | 0.038 | 0.2306 | 0.02863 | 4.31 | 2.91 × 10−4 | |
| 40–60 | 0.035 | 0.2802 | 0.03541 | 1.589 | 1.96 × 10−4 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dong, X.; Qin, F.; Li, L.; Yang, Z.; Li, Y.; Wu, Y. Study on Water Vertical Infiltration Characteristics and Water Content Simulation of Sandstone Overlying Loess. Water 2022, 14, 3716. https://doi.org/10.3390/w14223716
Dong X, Qin F, Li L, Yang Z, Li Y, Wu Y. Study on Water Vertical Infiltration Characteristics and Water Content Simulation of Sandstone Overlying Loess. Water. 2022; 14(22):3716. https://doi.org/10.3390/w14223716
Chicago/Turabian StyleDong, Xiaoyu, Fucang Qin, Long Li, Zhenqi Yang, Yan Li, and Yihan Wu. 2022. "Study on Water Vertical Infiltration Characteristics and Water Content Simulation of Sandstone Overlying Loess" Water 14, no. 22: 3716. https://doi.org/10.3390/w14223716
APA StyleDong, X., Qin, F., Li, L., Yang, Z., Li, Y., & Wu, Y. (2022). Study on Water Vertical Infiltration Characteristics and Water Content Simulation of Sandstone Overlying Loess. Water, 14(22), 3716. https://doi.org/10.3390/w14223716







