Towards Understanding Factors Affecting Arsenic, Chromium, and Vanadium Mobility in the Subsurface
Abstract
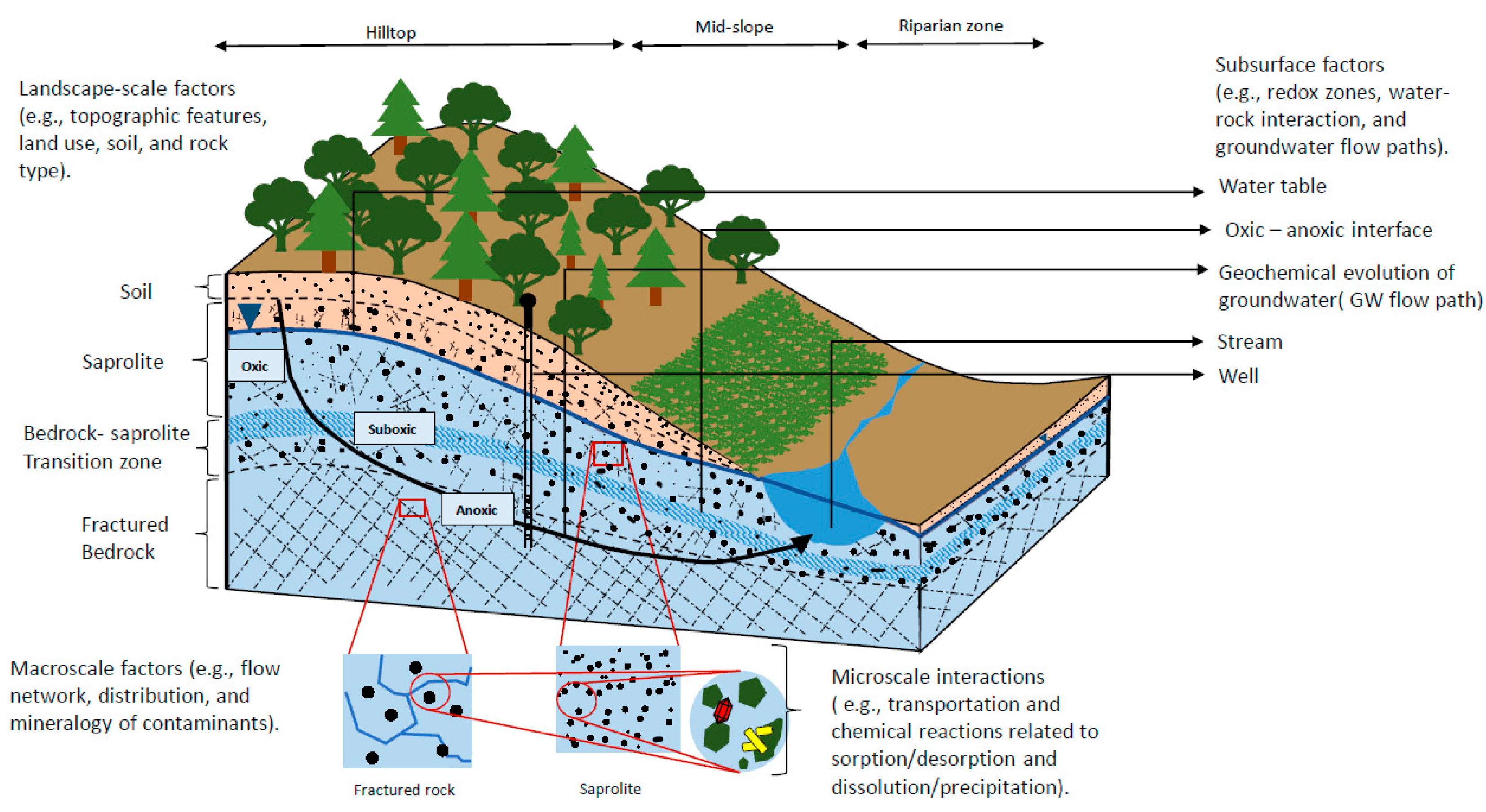
:1. Introduction
2. Framing Subsurface Hydrogeochemical Processes
2.1. Groundwater Flow and Its Relationship to Chemical Evolution
2.2. Limitations and Challenges
3. Mineralogical Sources of Geogenic Contamination
3.1. Arsenic
3.2. Chromium
3.3. Vanadium
3.4. Challenges
4. Biogeochemical Processes
4.1. Redox Controls on Speciation
4.2. Redox Transformations
4.3. Sorption and Desorption Reactions
4.4. Challenges
5. Measurement Methods
6. Mechanistic Modeling
6.1. Fundamental Concepts
6.2. Modeling Metal(loid)s
6.3. Batch Models
6.4. Microscale Models
6.5. Macroscale Models
6.6. Conceptual Illustration: Bimolecular Reactive Transport
6.7. Challenges
7. Outlook and Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- LaFayette, G.N.; Knappett, P.S.K.; Li, Y.; Loza-Aguirre, I.; Polizzotto, M.L. Geogenic sources and chemical controls on fluoride release to groundwater in the Independence Basin, Mexico. Appl. Geochem. 2020, 123, 104787. [Google Scholar] [CrossRef]
- Pichler, T.; Renshaw, C.E.; Sültenfuß, J. Geogenic As and Mo groundwater contamination caused by an abundance of domestic supply wells. Appl. Geochem. 2017, 77, 68–79. [Google Scholar] [CrossRef]
- Borch, T.; Kretzschmar, R.; Kappler, A.; Van Cappellen, P.; Ginder-Vogel, M.; Voegelin, A.; Campbell, K. Biogeochemical redox processes and their impact on contaminant dynamics. Environ. Sci. Technol. 2010, 44, 15–23. [Google Scholar] [CrossRef]
- Vinson, D.S.; McIntosh, J.C.; Dwyer, G.S.; Vengosh, A. Arsenic and other oxyanion-forming trace elements in an alluvial basin aquifer: Evaluating sources and mobilization by isotopic tracers (Sr, B, S, O, H, Ra). Appl. Geochem. 2011, 26, 1364–1376. [Google Scholar] [CrossRef]
- Wright, M.T.; Belitz, K. Factors Controlling the Regional Distribution of Vanadium in Groundwater. Groundwater 2010, 48, 515–525. [Google Scholar] [CrossRef]
- Wright, M.T.; Stollenwerk, K.G.; Belitz, K. Assessing the solubility controls on vanadium in groundwater, northeastern San Joaquin Valley, CA. Appl. Geochem. 2014, 48, 41–52. [Google Scholar] [CrossRef]
- Oze, C.; Bird, D.K.; Fendorf, S. Genesis of hexavalent chromium from natural sources in soil and groundwater. Proc. Natl. Acad. Sci. USA 2007, 104, 6544–6549. [Google Scholar] [CrossRef] [Green Version]
- Hug, S.J.; Winkel, L.H.E.; Voegelin, A.A.; Berg, M.; Johnson, C.A. Arsenic and Other Geogenic Contaminants in Groundwater—A Global Challenge. Chimia 2020, 74, 524. [Google Scholar] [CrossRef]
- Gillispie, E.C.; Austin, R.E.; Rivera, N.A.; Bolich, R.; Duckworth, O.W.; Bradley, P.; Amoozegar, A.; Hesterberg, D.; Polizzotto, M.L. Soil Weathering as an Engine for Manganese Contamination of Well Water. Environ. Sci. Technol. 2016, 50, 9963–9971. [Google Scholar] [CrossRef]
- Ying, S.C.; Schaefer, M.V.; Cock-Esteb, A.; Li, J.; Fendorf, S. Depth Stratification Leads to Distinct Zones of Manganese and Arsenic Contaminated Groundwater. Environ. Sci. Technol. 2017, 51, 8926–8932. [Google Scholar] [CrossRef]
- Smith, A.H.; Lingas, E.O.; Rahman, M. Contamination of drinking-water by arsenic in Bangladesh: A public health emergency. Bull. World Health Organ. 2000, 78, 1093–1103. [Google Scholar]
- Ayotte, J.D.; Medalie, L.; Qi, S.L.; Backer, L.C.; Nolan, B.T. Estimating the High-Arsenic Domestic-Well Population in the Conterminous United States. Environ. Sci. Technol. 2017, 51, 12443–12454. [Google Scholar] [CrossRef] [Green Version]
- Ravenscroft, P.; Brammer, H.; Richards, K. Arsenic Pollution: A Global Synthesis; Wiley: New York, NY, USA, 2009. [Google Scholar] [CrossRef]
- Farkhondeh, T.; Samarghandian, S.; Azimi-Nezhad, M. The role of arsenic in obesity and diabetes. J. Cell. Physiol. 2019, 234, 12516–12529. [Google Scholar] [CrossRef]
- Coyte, R.M.; McKinley, K.L.; Jiang, S.; Karr, J.; Dwyer, G.S.; Keyworth, A.J.; Davis, C.C.; Kondash, A.J.; Vengosh, A. Occurrence and distribution of hexavalent chromium in groundwater from North Carolina, USA. Sci. Total Environ. 2020, 711, 135135. [Google Scholar] [CrossRef]
- Coyte, R.M.; Vengosh, A. Factors Controlling the Risks of Co-occurrence of the Redox-Sensitive Elements of Arsenic, Chromium, Vanadium, and Uranium in Groundwater from the Eastern United States. Environ. Sci. Technol. 2020, 54, 4367–4375. [Google Scholar] [CrossRef]
- Smith, S.M. National Geochemical Database—Reformatted Data from the National Uranium Resource Evaluation (NURE) Hydrogeochemical and Stream Sediment Reconnaissance (HSSR) Program. Available online: http://mrdata.usgs.gov/nure/sediment/ (accessed on 29 September 2022).
- Vengosh, A.; Coyte, R.; Karr, J.; Harkness, J.S.; Kondash, A.J.; Ruhl, L.S.; Merola, R.B.; Dywer, G.S. Origin of Hexavalent Chromium in Drinking Water Wells from the Piedmont Aquifers of North Carolina. Environ. Sci. Technol. Lett. 2016, 3, 409–414. [Google Scholar] [CrossRef]
- Oze, C.; Fendorf, S.; Bird, D.K.; Coleman, R.G. Chromium geochemistry in serpentinized ultramafic rocks and serpentine soils from the Franciscan complex of California. Am. J. Sci. 2004, 304, 67–101. [Google Scholar] [CrossRef]
- Ścibior, A.; Pietrzyk, Ł.; Plewa, Z.; Skiba, A. Vanadium: Risks and possible benefits in the light of a comprehensive overview of its pharmacotoxicological mechanisms and multi-applications with a summary of further research trends. J. Trace Elem. Med. Biol. 2020, 61, 126508. [Google Scholar] [CrossRef]
- Gustafsson, J.P. Vanadium geochemistry in the biogeosphere—Speciation, solid-solution interactions, and ecotoxicity. Appl. Geochem. 2019, 102, 1–25. [Google Scholar] [CrossRef]
- Watt, J.A.J.; Burke, I.T.; Edwards, R.A.; Malcolm, H.M.; Mayes, W.M.; Olszewska, J.P.; Pan, G.; Graham, M.C.; Heal, K.V.; Rose, N.L.; et al. Vanadium: A Re-Emerging Environmental Hazard. Environ. Sci. Technol. 2018, 52, 11973–11974. [Google Scholar] [CrossRef]
- Bundschuh, J.; Niazi, N.K.; Alam, M.A.; Berg, M.; Herath, I.; Tomaszewska, B.; Maity, J.P.; Ok, Y.S. Global arsenic dilemma and sustainability. J. Hazard. Mater. 2022, 436, 129197. [Google Scholar] [CrossRef]
- Shaji, E.; Santosh, M.; Sarath, K.V.; Prakash, P.; Deepchand, V.; Divya, B.V. Arsenic contamination of groundwater: A global synopsis with focus on the Indian Peninsula. Geosci. Front. 2021, 12, 101079. [Google Scholar] [CrossRef]
- Huang, L.; Wu, H.; van der Kuijp, T.J. The health effects of exposure to arsenic-contaminated drinking water: A review by global geographical distribution. Int. J. Environ. Health Res. 2015, 25, 432–452. [Google Scholar] [CrossRef]
- Fitts, C.R. Groundwater Science, 2nd ed.; Academic Press: Cambridge, MA, USA, 2013. [Google Scholar]
- Daniel, C.C.; Dahlen, P.R. Preliminary Hydrogeologic Assessment and Study Plan for a Regional Ground-Water Resource Investigation of the Blue Ridge and Piedmont Provinces of North Carolina; Water-Resources Investigations Report 2002-4105; US Department of the Interior, US Geological Survey: Reston, VA, USA, 2002. [CrossRef]
- McMahon, P.B.; Chapelle, F.H. Redox Processes and Water Quality of Selected Principal Aquifer Systems. Groundwater 2008, 46, 259–271. [Google Scholar] [CrossRef]
- Lindsey, B.; Zimmerman, T.; Chapman, M.; Cravotta, C.; Szabo, Z. Water Quality in the Principal Aquifers of the Piedmont, Blue Ridge, and Valley and Ridge Regions, Eastern United States, 1993–2009; US Geological Survey: Reston, VA, USA, 2015. [CrossRef] [Green Version]
- Chapelle, F.H. Ground-Water Microbiology and Geochemistry, 2nd ed.; Wiley: New York, NY, USA, 2000. [Google Scholar]
- Clark, I.; Fritz, P.F. Environmental Isotopes in Hydrology; Lewis Publishers: Lewis, UK, 1998. [Google Scholar]
- Vinson, D.S.; Vengosh, A.; Hirschfeld, D.; Dwyer, G.S. Relationships between radium and radon occurrence and hydrochemistry in fresh groundwater from fractured crystalline rocks, North Carolina (USA). Chem. Geol. 2009, 260, 159–171. [Google Scholar] [CrossRef] [Green Version]
- Wanty, R.B.; Goldhaber, M.B. Thermodynamics and kinetics of reactions involving vanadium in natural systems: Accumulation of vanadium in sedimentary rocks. Geochim. Cosmochim. Acta 1992, 56, 1471–1483. [Google Scholar] [CrossRef]
- Stumm, W.; Morgan, J.J. Aquatic Chemistry, 3rd ed.; Wiley: New York, NY, USA, 1996. [Google Scholar]
- Lu, P.; Zhu, C. Arsenic Eh–pH diagrams at 25 °C and 1 bar. Environ. Earth Sci. 2011, 62, 1673–1683. [Google Scholar] [CrossRef]
- Eby, G.N. Principles of Environmental Geochemistry; Waveland Press: Long Grove, IL, USA, 2004. [Google Scholar]
- Pallud, C.; Masue-Slowey, Y.; Fendorf, S. Aggregate-scale spatial heterogeneity in reductive transformation of ferrihydrite resulting from coupled biogeochemical and physical processes. Geochim. Cosmochim. Acta 2010, 74, 2811–2825. [Google Scholar] [CrossRef]
- Wilmoth, J.L. Redox Heterogeneity Entangles Soil and Climate Interactions. Sustainability 2021, 13, 10084. [Google Scholar] [CrossRef]
- Kim, D.; Miranda, M.L.; Tootoo, J.; Bradley, P.; Gelfand, A.E. Spatial modeling for groundwater arsenic levels in North Carolina. Environ. Sci. Technol. 2011, 45, 4824–4831. [Google Scholar] [CrossRef] [Green Version]
- Connolly, C.T.; Stahl, M.O.; DeYoung, B.A.; Bostick, B.C. Surface Flooding as a Key Driver of Groundwater Arsenic Contamination in Southeast Asia. Environ. Sci. Technol. 2022, 56, 928–937. [Google Scholar] [CrossRef]
- Kazakis, N.; Kantiranis, N.; Voudouris, K.S.; Mitrakas, M.; Kaprara, E.; Pavlou, A. Geogenic Cr oxidation on the surface of mafic minerals and the hydrogeological conditions influencing hexavalent chromium concentrations in groundwater. Sci. Total Environ. 2015, 514, 224–238. [Google Scholar] [CrossRef]
- McMahon, P.B.; Belitz, K.; Reddy, J.E.; Johnson, T.D. Elevated Manganese Concentrations in United States Groundwater, Role of Land Surface–Soil–Aquifer Connections. Environ. Sci. Technol. 2019, 53, 29–38. [Google Scholar] [CrossRef]
- McMahon, P.B.; Chapelle, F.H.; Bradley, P.M. Evolution of Redox Processes in Groundwater. In Aquatic Redox Chemistry; American Chemical Society: Washington, DA, USA, 2011; Volume 1071, pp. 581–597. [Google Scholar]
- Zhang, Z.; Furman, A. Soil redox dynamics under dynamic hydrologic regimes—A review. Sci. Total Environ. 2021, 763, 143026. [Google Scholar] [CrossRef]
- Riedel, T.; Kübeck, C.; Quirin, M. Legacy nitrate and trace metal (Mn, Ni, As, Cd, U) pollution in anaerobic groundwater: Quantifying potential health risk from “the other nitrate problem”. Appl. Geochem. 2022, 139, 105254. [Google Scholar] [CrossRef]
- FAO and UNEP. Global Assessment of Soil Pollution: Report; FAO and UNEP: Rome, Italy, 2021. [Google Scholar]
- Zhu, C.; Burden, D.S. Mineralogical compositions of aquifer matrix as necessary initial conditions in reactive contaminant transport models. J. Contam. Hydrol. 2001, 51, 145–161. [Google Scholar] [CrossRef]
- Nickson, R.; McArthur, J.; Burgess, W.; Ahmed, K.M.; Ravenscroft, P.; Rahmanñ, M. Arsenic poisoning of Bangladesh groundwater. Nature 1998, 395, 338. [Google Scholar] [CrossRef]
- Herath, I.; Vithanage, M.; Bundschuh, J.; Maity, J.P.; Bhattacharya, P. Natural Arsenic in Global Groundwaters: Distribution and Geochemical Triggers for Mobilization. Curr. Pollut. Rep. 2016, 2, 68–89. [Google Scholar] [CrossRef]
- Majzlan, J.; Drahota, P.; Filippi, M. Parageneses and Crystal Chemistry of Arsenic Minerals. Rev. Mineral. Geochem. 2014, 79, 17–184. [Google Scholar] [CrossRef]
- Leonardi, G.; Gnagnarella, P.; Fletcher, T. Intake of inorganic arsenic from food in Hungary, Romania and Slovakia. In Arsenic Research and Global Sustainability, Proceedings of the Sixth International Congress on Arsenic in the Environment (As2016), Stockholm, Sweden, 19–23 June 2016; CRC Press: Boca Raton, FL, USA, 2016; pp. 316–317. [Google Scholar] [CrossRef]
- Smedley, P.L.; Kinniburgh, D.G. A review of the source, behaviour and distribution of arsenic in natural waters. Appl. Geochem. 2002, 17, 517–568. [Google Scholar]
- Morales-Simfors, N.; Bundschuh, J.; Herath, I.; Inguaggiato, C.; Caselli, A.T.; Tapia, J.; Choquehuayta, F.E.A.; Armienta, M.A.; Ormachea, M.; Joseph, E.; et al. Arsenic in Latin America: A critical overview on the geochemistry of arsenic originating from geothermal features and volcanic emissions for solving its environmental consequences. Sci. Total Environ. 2020, 716, 135564. [Google Scholar] [CrossRef] [PubMed]
- Welch, A.H.; Westjohn, D.B.; Helsel, D.R.; Wanty, R.B. Arsenic in Ground Water of the United States: Occurrence and Geochemistry. Groundwater 2000, 38, 589–604. [Google Scholar] [CrossRef]
- Barnhart, J. Occurrences, uses, and properties of chromium. Regul. Toxicol. Pharmacol. 1997, 26, S3–S7. [Google Scholar] [CrossRef] [PubMed]
- Chrysochoou, M.; Theologou, E.; Bompoti, N.; Dermatas, D.; Panagiotakis, I. Occurrence, Origin and Transformation Processes of Geogenic Chromium in Soils and Sediments. Curr. Pollut. Rep. 2016, 2, 224–235. [Google Scholar] [CrossRef] [Green Version]
- Kelepertzis, E.; Galanos, E.; Mitsis, I. Origin, mineral speciation and geochemical baseline mapping of Ni and Cr in agricultural topsoils of Thiva Valley (central Greece). J. Geochem. Explor. 2013, 125, 56–68. [Google Scholar] [CrossRef]
- Saputro, S.; Yoshimura, K.; Matsuoka, S.; Takehara, K.; Narsito; Aizawa, J.; Tennichi, Y. Speciation of dissolved chromium and the mechanisms controlling its concentration in natural water. Chem. Geol. 2014, 364, 33–41. [Google Scholar] [CrossRef]
- Ball, J.W.; Izbicki, J.A. Occurrence of hexavalent chromium in ground water in the western Mojave Desert, California. Appl. Geochem. 2004, 19, 1123–1135. [Google Scholar] [CrossRef]
- Yang, B.; He, J.; Zhang, G.; Guo, J. Chapter 3—Vanadium mineral resources. In Vanadium; Yang, B., He, J., Zhang, G., Guo, J., Eds.; Elsevier: Amsterdam, The Netherlands, 2021; pp. 33–58. [Google Scholar] [CrossRef]
- Kelley, K.D.; Scott, C.; Polyak, D.E.; Kimball, B.E. Vanadium; Professional Paper 1802-U; U.S. Geological Survey: Reston, VA, USA, 2017; 48p. [CrossRef]
- Huang, J.-H.; Huang, F.; Evans, L.; Glasauer, S. Vanadium: Global (bio)geochemistry. Chem. Geol. 2015, 417, 68–89. [Google Scholar] [CrossRef]
- Chermak, J.A.; Schreiber, M.E. Mineralogy and trace element geochemistry of gas shales in the United States: Environmental implications. Int. J. Coal Geol. 2014, 126, 32–44. [Google Scholar] [CrossRef]
- Shaheen, S.M.; Alessi, D.S.; Tack, F.M.G.; Ok, Y.S.; Kim, K.-H.; Gustafsson, J.P.; Sparks, D.L.; Rinklebe, J. Redox chemistry of vanadium in soils and sediments: Interactions with colloidal materials, mobilization, speciation, and relevant environmental implications—A review. Adv. Colloid Interface Sci. 2019, 265, 1–13. [Google Scholar] [CrossRef]
- Minelli, L.; Veschetti, E.; Giammanco, S.; Mancini, G.; Ottaviani, M. Vanadium in Italian waters: Monitoring and speciation of V(IV) and V(V). Microchem. J. 2000, 67, 83–90. [Google Scholar] [CrossRef]
- Fischel, J.S.; Fischel, M.H.; Sparks, D.L. Advances in Understanding Reactivity of Manganese Oxides with Arsenic and Chromium in Environmental Systems. In Advances in the Environmental Biogeochemistry of Manganese Oxides; American Chemical Society: Washington, DC, USA, 2015; Volume 1197, pp. 1–27. [Google Scholar]
- Tang, Y.; Webb, S.M.; Estes, E.R.; Hansel, C.M. Chromium(iii) oxidation by biogenic manganese oxides with varying structural ripening. Environ. Sci. Process. Impacts 2014, 16, 2127–2136. [Google Scholar] [CrossRef] [PubMed]
- Thompson, A.K.; Monti, M.M.; Gribble, M.O. Co-Occurrence of Metal Contaminants in United States Public Water Systems in 2013–2015. Int. J. Environ. Res. Public Health 2021, 18, 7884. [Google Scholar] [CrossRef] [PubMed]
- Bethke, C.M. Geochemical and Biogeochemical Reaction Modeling, 3rd ed.; Cambridge University Press: Cambridge, UK, 2022. [Google Scholar]
- Adriano, D.C. Trace Elements in Terrestrial Environments, 2nd ed.; Springer: New York, NY, USA, 2001. [Google Scholar]
- Rai, D.; Eary, L.E.; Zachara, J.M. Environmental chemistry of chromium. Sci. Total Environ. 1989, 86, 15–23. [Google Scholar] [CrossRef]
- Oscarson, D.W.; Huang, P.M.; Defosse, C.; Herbillon, A. Oxidative power of Mn(IV) and Fe(III) oxides with respect to As(III) in terrestrial and aquatic environments. Nature 1981, 291, 50–51. [Google Scholar] [CrossRef]
- Keimowitz, A.R.; Mailloux, B.J.; Wovkulich, K.; Harkness, J.; Ross, J.M.; Chillrud, S.N. Manganese redox buffering limits arsenic release from contaminated sediments, Union Lake, New Jersey. Appl. Geochem. 2017, 77, 24–30. [Google Scholar] [CrossRef]
- Liang, J.; Huang, X.; Yan, J.; Li, Y.; Zhao, Z.; Liu, Y.; Ye, J.; Wei, Y. A review of the formation of Cr(VI) via Cr(III) oxidation in soils and groundwater. Sci. Total Environ. 2021, 774, 145762. [Google Scholar] [CrossRef]
- Abernathy, M.J.; Schaefer, M.V.; Vessey, C.J.; Liu, H.; Ying, S.C. Oxidation of V(IV) by Birnessite: Kinetics and Surface Complexation. Environ. Sci. Technol. 2021, 55, 11703–11712. [Google Scholar] [CrossRef]
- Kotaś, J.; Stasicka, Z. Chromium occurrence in the environment and methods of its speciation. Environ. Pollut. 2000, 107, 263–283. [Google Scholar] [CrossRef]
- O’Loughlin, E.J.; Boyanov, M.I.; Kemner, K.M. Reduction of Vanadium(V) by Iron(II)-Bearing Minerals. Minerals 2021, 11, 316. [Google Scholar] [CrossRef]
- Grundl, T.J.; Haderlein, S.; Nurmi, J.T.; Tratnyek, P.G. Introduction to Aquatic Redox Chemistry. In Aquatic Redox Chemistry; American Chemical Society: Washington, DA, USA, 2011; Volume 1071, pp. 1–14. [Google Scholar]
- Masuda, H. Arsenic cycling in the Earth’s crust and hydrosphere: Interaction between naturally occurring arsenic and human activities. Prog. Earth Planet. Sci. 2018, 5, 68. [Google Scholar] [CrossRef]
- Kruger, M.C.; Bertin, P.N.; Heipieper, H.J.; Arsène-Ploetze, F. Bacterial metabolism of environmental arsenic—Mechanisms and biotechnological applications. Appl. Microbiol. Biotechnol. 2013, 97, 3827–3841. [Google Scholar] [CrossRef] [PubMed]
- Gutiérrez-Corona, J.F.; Romo-Rodríguez, P.; Santos-Escobar, F.; Espino-Saldaña, A.E.; Hernández-Escoto, H. Microbial interactions with chromium: Basic biological processes and applications in environmental biotechnology. World J. Microbiol. Biotechnol. 2016, 32, 191. [Google Scholar] [CrossRef] [PubMed]
- Sowers, T.D.; Harrington, J.M.; Polizzotto, M.L.; Duckworth, O.W. Sorption of arsenic to biogenic iron (oxyhydr)oxides produced in circumneutral environments. Geochim. Cosmochim. Acta 2017, 198, 194–207. [Google Scholar] [CrossRef] [Green Version]
- Ying, S.C.; Kocar, B.D.; Fendorf, S. Oxidation and competitive retention of arsenic between iron- and manganese oxides. Geochim. Cosmochim. Acta 2012, 96, 294–303. [Google Scholar] [CrossRef]
- Strawn, D.G.; Bohn, H.L.; O’Connor, G.A. Soil Chemistry; John Wiley & Sons, Incorporated: Somerset, UK, 2015. [Google Scholar]
- Frau, F.; Biddau, R.; Fanfani, L. Effect of major anions on arsenate desorption from ferrihydrite-bearing natural samples. Appl. Geochem. 2008, 23, 1451–1466. [Google Scholar] [CrossRef]
- Neupane, G.; Donahoe, R.J.; Arai, Y. Kinetics of competitive adsorption/desorption of arsenate and phosphate at the ferrihydrite–water interface. Chem. Geol. 2014, 368, 31–38. [Google Scholar] [CrossRef]
- Marzi, M.; Towfighi, H.; Shahbazi, K.; Farahbakhsh, M.; Rinklebe, J.; Lima, E.C. Adsorption and desorption characteristics of arsenic in calcareous soils as a function of time; equilibrium and thermodynamic study. Environ. Sci. Pollut. Res. 2022. [Google Scholar] [CrossRef]
- Currell, M.; Cartwright, I.; Raveggi, M.; Han, D. Controls on elevated fluoride and arsenic concentrations in groundwater from the Yuncheng Basin, China. Appl. Geochem. 2011, 26, 540–552. [Google Scholar] [CrossRef]
- Scanlon, B.R.; Nicot, J.P.; Reedy, R.C.; Kurtzman, D.; Mukherjee, A.; Nordstrom, D.K. Elevated naturally occurring arsenic in a semiarid oxidizing system, Southern High Plains aquifer, Texas, USA. Appl. Geochem. 2009, 24, 2061–2071. [Google Scholar] [CrossRef]
- Wang, S.; Mulligan, C.N. Effect of natural organic matter on arsenic release from soilsand sediments into groundwater. Environ. Geochem. Health 2006, 28, 197–214. [Google Scholar] [CrossRef] [PubMed]
- Cui, J.; Jing, C. A review of arsenic interfacial geochemistry in groundwater and the role of organic matter. Ecotoxicol. Environ. Saf. 2019, 183, 109550. [Google Scholar] [CrossRef] [PubMed]
- Kent, D.B.; Davis, J.A.; Anderson, L.C.D.; Rea, B.A. Transport of Chromium and Selenium in a Pristine Sand and Gravel Aquifer: Role of Adsorption Processes. Water Resour. Res. 1995, 31, 1041–1050. [Google Scholar] [CrossRef]
- Pyrzyńska, K.; Wierzbicki, T. Determination of vanadium species in environmental samples. Talanta 2004, 64, 823–829. [Google Scholar] [CrossRef]
- Martínez-Bravo, Y.; Roig-Navarro, A.F.; López, F.J.; Hernández, F. Multielemental determination of arsenic, selenium and chromium(VI) species in water by high-performance liquid chromatography-inductively coupled plasma mass spectrometry. J. Chromatogr. A 2001, 926, 265–274. [Google Scholar] [CrossRef]
- Sarzanini, C.; Bruzzoniti, M.C. Metal species determination by ion chromatography. TrAC Trends Anal. Chem. 2001, 20, 304–310. [Google Scholar] [CrossRef]
- Chen, Z.; Mahmudur Rahman, M.; Naidu, R. Speciation of vanadium by anion-exchange chromatography with inductively coupled plasma mass spectrometry and confirmation of vanadium complex formation using electrospray mass spectrometry. J. Anal. At. Spectrom. 2007, 22, 811–816. [Google Scholar] [CrossRef]
- Kilibarda, N.; Afton, S.E.; Harrington, J.M.; Yan, F.; Levine, K.E. Rapid speciation and determination of vanadium compounds using ion-pair reversed-phase ultra-high-performance liquid chromatography inductively coupled plasma-sector field mass spectrometry. J. Chromatogr. A 2013, 1304, 121–126. [Google Scholar] [CrossRef]
- Roberts, L.C.; Hug, S.J.; Dittmar, J.; Voegelin, A.; Saha, G.C.; Ali, M.A.; Badruzzaman, A.B.M.; Kretzschmar, R. Spatial Distribution and Temporal Variability of Arsenic in Irrigated Rice Fields in Bangladesh. 1. Irrigation Water. Environ. Sci. Technol. 2007, 41, 5960–5966. [Google Scholar] [CrossRef]
- Wendelken, S.; Smith, G.; Munch, D.; Zaffiro, A.; Zimmerman, M. Method 218.7: Determination of Hexavalent Chromium in Drinking Water by Ion Chromatography with Post-Column Derivatization and UV–Visible Spectroscopic Detection; Version 1.0; U.S. EPA Office of Water: Washington, DC, USA, 2011.
- Laul, J.C. Neutron activation analysis of geological materials. At. Energy Rev. 1979, 17, 603–695. [Google Scholar]
- Koeberl, C. Instrumental neutron activation analysis of geochemical and cosmochemical samples: A fast and reliable method for small sample analysis. J. Radioanal. Nucl. Chem. 1993, 168, 47–60. [Google Scholar] [CrossRef]
- Chen, M.; Ma, L.Q. Comparison of Four USEPA Digestion Methods for Trace Metal Analysis Using Certified and Florida Soils. J. Environ. Qual. 1998, 27, 1294–1300. [Google Scholar] [CrossRef]
- Agazzi, A.; Pirola, C. Fundamentals, methods and future trends of environmental microwave sample preparation. Microchem. J. 2000, 67, 337–341. [Google Scholar] [CrossRef]
- Santelli, R.E.; Cassella, R.J.; Arruda, M.A.Z.; Nóbrega, J.A. Modern Strategies for Environmental Sample Preparation and Analysis. In Environmental Geochemistry in Tropical and Subtropical Environments; Drude de Lacerda, L., Santelli, R.E., Duursma, E.K., Abrão, J.J., Eds.; Springer: Berlin Heidelberg, Germany, 2004; pp. 37–68. [Google Scholar] [CrossRef]
- Shan, X.; Chen, B. Evaluation of sequential extraction for speciation of trace metals in model soil containing natural minerals and humic acid. Anal. Chem. 1993, 65, 802–807. [Google Scholar] [CrossRef]
- Gleyzes, C.; Tellier, S.; Astruc, M. Fractionation studies of trace elements in contaminated soils and sediments: A review of sequential extraction procedures. TrAC Trends Anal. Chem. 2002, 21, 451–467. [Google Scholar] [CrossRef]
- Scheinost, A.C.; Kretzschmar, R.; Pfister, S.; Roberts, D.R. Combining Selective Sequential Extractions, X-ray Absorption Spectroscopy, and Principal Component Analysis for Quantitative Zinc Speciation in Soil. Environ. Sci. Technol. 2002, 36, 5021–5028. [Google Scholar] [CrossRef]
- Cui, Y.; Weng, L. Interpretation of heavy metal speciation in sequential extraction using geochemical modelling. Environ. Chem. 2015, 12, 163–173. [Google Scholar] [CrossRef] [Green Version]
- Kelly, S.D.; Hesterberg, D.; Ravel, B. Analysis of Soils and Minerals Using X-ray Absorption Spectroscopy. In Methods of Soil Analysis; Ulery, A.L., Drees, L.R., Eds.; Soil Science Society of America: Madison, WI, USA, 2008. [Google Scholar]
- Ellison, E.; Mayhew, L.; Miller, H.; Templeton, A. Quantitative microscale Fe redox imaging by multiple energy X-ray fluorescence mapping at the Fe K pre-edge peak. Am. Mineral. 2020, 105, 1812–1829. [Google Scholar] [CrossRef]
- Bear, J. Dynamics of Fluids in Porous Media; Elsevier: New York, NY, USA, 1972. [Google Scholar]
- De Marsily, G. Quantitative Hydrogeology: Groundwater Hydrology for Engineers; Academic Press: San Diego, CA, USA, 1986. [Google Scholar]
- Gray, W.G.; Miller, C.T. Introduction to the Thermodynamically Constrained Averaging Theory for Porous Medium Systems; Springer: Cham, Switzerland, 2014. [Google Scholar]
- Berkowitz, B.; Dror, I.; Hansen, S.K.; Scher, H. Measurements and models of reactive transport in geological media. Rev. Geophys. 2016, 54, 930–986. [Google Scholar] [CrossRef] [Green Version]
- Miller, C.T.; Valdés-Parada, F.J.; Wood, B.D. A Pedagogical Approach to the Thermodynamically Constrained Averaging Theory. Transp. Porous Media 2017, 119, 585–609. [Google Scholar] [CrossRef]
- Boso, F.; Battiato, I. Homogenizability conditions for multicomponent reactive transport. Adv. Water Resour. 2013, 62, 254–265. [Google Scholar] [CrossRef]
- Molins, S.; Trebotich, D.; Steefel, C.I.; Shen, C. An investigation of the effect of pore scale flow on average geochemical reaction rates using direct numerical simulation. Water Resour. Res. 2012, 48, W03527. [Google Scholar] [CrossRef] [Green Version]
- Liu, M.; Shabaninejad, M.; Mostaghimi, P. Impact of mineralogical heterogeneity on reactive transport modelling. Comput. Geosci. 2017, 104, 12–19. [Google Scholar] [CrossRef]
- Bowers, C.A.; Miller, C.T. Generalized Newtonian fluid flow in porous media. Phys. Rev. Fluids 2021, 6, 123302. [Google Scholar] [CrossRef]
- Hauswirth, S.C.; Bowers, C.A.; Fowler, C.P.; Schultz, P.B.; Hauswirth, A.D.; Weigand, T.; Miller, C.T. Modeling cross model non-Newtonian fluid flow in porous media. J. Contam. Hydrol. 2020, 235, 103708. [Google Scholar] [CrossRef] [PubMed]
- Weigand, T.M.; Miller, C.T. Microscale modeling of nondilute flow and transport in porous medium systems. Phys. Rev. E 2020, 102, 033104. [Google Scholar] [CrossRef]
- Weigand, T.M.; Schultz, P.B.; Giffen, D.H.; Farthing, M.W.; Crockett, A.; Kelley, C.T.; Gray, W.G.; Miller, C.T. Modeling Nondilute Species Transport Using the Thermodynamically Constrained Averaging Theory. Water Resour. Res. 2018, 54, 6656–6682. [Google Scholar] [CrossRef]
- Yekta, A.; Salinas, P.; Hajirezaie, S.; Amooie, M.A.; Pain, C.C.; Jackson, M.D.; Jacquemyn, C.; Soltanian, M.R. Reactive transport modeling in heterogeneous porous media with dynamic mesh optimization. Comput. Geosci. 2021, 25, 357–372. [Google Scholar] [CrossRef]
- Donado, L.D.; Sanchez-Vila, X.; Dentz, M.; Carrera, J.; Bolster, D. Multicomponent reactive transport in multicontinuum media. Water Resour. Res. 2009, 45, W11402. [Google Scholar] [CrossRef] [Green Version]
- Tartakovsky, A.M.; Panzeri, M.; Tartakovsky, G.D.; Guadagnini, A. Uncertainty Quantification in Scale-Dependent Models of Flow in Porous Media. Water Resour. Res. 2017, 53, 9392–9401. [Google Scholar] [CrossRef]
- Edery, Y.; Porta, G.M.; Guadagnini, A.; Scher, H.; Berkowitz, B. Characterization of Bimolecular Reactive Transport in Heterogeneous Porous Media. Transp. Porous Media 2016, 115, 291–310. [Google Scholar] [CrossRef]
- Naftaly, A.; Dror, I.; Berkowitz, B. Measurement and modeling of engineered nanoparticle transport and aging dynamics in a reactive porous medium. Water Resour. Res. 2016, 52, 5473–5491. [Google Scholar] [CrossRef]
- Crevillén-García, D.; Leung, P.K.; Rodchanarowan, A.; Shah, A.A. Uncertainty Quantification for Flow and Transport in Highly Heterogeneous Porous Media Based on Simultaneous Stochastic Model Dimensionality Reduction. Transp. Porous Media 2019, 126, 79–95. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Menke, H.P.; Andrew, M.G.; Blunt, M.J.; Bijeljic, B. Reservoir condition imaging of reactive transport in heterogeneous carbonates using fast synchrotron tomography—Effect of initial pore structure and flow conditions. Chem. Geol. 2016, 428, 15–26. [Google Scholar] [CrossRef] [Green Version]
- Dentz, M.; Le Borgne, T.; Englert, A.; Bijeljic, B. Mixing, spreading and reaction in heterogeneous media: A brief review. J. Contam. Hydrol. 2011, 120–121, 1–17. [Google Scholar] [CrossRef] [PubMed]
- Nissan, A.; Berkowitz, B. Reactive Transport in Heterogeneous Porous Media Under Different Péclet Numbers. Water Resour. Res. 2019, 55, 10119–10129. [Google Scholar] [CrossRef]
- Rubin, Y. Applied Stochastic Hydrogeology; Oxford University Press: New York, NY, USA, 2003. [Google Scholar]
- Bruning, K.; Miller, C.T. Toward a New Generation of Two-Fluid Flow Models Based on the Thermodynamically-Constrained Averaging Theory. Water 2019, 11, 2260. [Google Scholar] [CrossRef] [Green Version]
- Steefel, C.I.; Appelo, C.A.J.; Arora, B.; Jacques, D.; Kalbacher, T.; Kolditz, O.; Lagneau, V.; Lichtner, P.C.; Mayer, K.U.; Meeussen, J.C.L.; et al. Reactive transport codes for subsurface environmental simulation. Comput. Geosci. 2015, 19, 445–478. [Google Scholar] [CrossRef] [Green Version]
- Gramling, C.M.; Harvey, C.F.; Meigs, L.C. Reactive Transport in Porous Media: A Comparison of Model Prediction with Laboratory Visualization. Environ. Sci. Technol. 2002, 36, 2508–2514. [Google Scholar] [CrossRef]
- Gurung, D.; Ginn, T.R. Mixing Ratios With Age: Application to Preasymptotic One-Dimensional Equilibrium Bimolecular Reactive Transport in Porous Media. Water Resour. Res. 2020, 56, e2020WR027629. [Google Scholar] [CrossRef]
- Benson, D.A.; Aquino, T.; Bolster, D.; Engdahl, N.; Henri, C.V.; Fernàndez-Garcia, D. A comparison of Eulerian and Lagrangian transport and non-linear reaction algorithms. Adv. Water Resour. 2017, 99, 15–37. [Google Scholar] [CrossRef] [Green Version]
- Cheng, H.; Hu, Y.; Luo, J.; Xu, B.; Zhao, J. Geochemical processes controlling fate and transport of arsenic in acid mine drainage (AMD) and natural systems. J. Hazard. Mater. 2009, 165, 13–26. [Google Scholar] [CrossRef] [PubMed]
- Nordstrom, D.K. Worldwide Occurrences of Arsenic in Ground Water. Science 2002, 296, 2143–2145. [Google Scholar] [CrossRef]
- Nordstrom, D.K.; Blowes, D.W.; Ptacek, C.J. Hydrogeochemistry and microbiology of mine drainage: An update. Appl. Geochem. 2015, 57, 3–16. [Google Scholar] [CrossRef]
- Palanichamy, J.; Schüttrumpf, H.; Köngeter, J.; Becker, T.; Palani, S. Simulation of ammonium and chromium transport in porous media using coupling scheme of a numerical algorithm and a stochastic algorithm. Water Sci. Technol. 2009, 59, 1577–1584. [Google Scholar] [CrossRef] [PubMed]
- Sadiq, M. Arsenic chemistry in soils: An overview of thermodynamic predictions and field observations. Water Air Soil Pollut. 1997, 93, 117–136. [Google Scholar] [CrossRef]
- Peng, C.; Crawshaw, J.P.; Maitland, G.C.; Trusler, J.P.M. Kinetics of calcite dissolution in CO2-saturated water at temperatures between (323 and 373) K and pressures up to 13.8 MPa. Chem. Geol. 2015, 403, 74–85. [Google Scholar] [CrossRef] [Green Version]
- Xu, J.; Fan, C.; Teng, H.H. Calcite dissolution kinetics in view of Gibbs free energy, dislocation density, and pCO2. Chem. Geol. 2012, 322–323, 11–18. [Google Scholar] [CrossRef]
- Han, J.; Ro, H.-M. Interpreting competitive adsorption of arsenate and phosphate on nanosized iron (hydr)oxides: Effects of pH and surface loading. Environ. Sci. Pollut. Res. 2018, 25, 28572–28582. [Google Scholar] [CrossRef]
- Limousin, G.; Gaudet, J.P.; Charlet, L.; Szenknect, S.; Barthès, V.; Krimissa, M. Sorption isotherms: A review on physical bases, modeling and measurement. Appl. Geochem. 2007, 22, 249–275. [Google Scholar] [CrossRef]
- Parkhurst, D.L.; Appelo, C.A.J. Description of Input and Examples for PHREEQC Version 3: A Computer Program for Speciation, Batch-reaction, One-Dimensional Transport, and Inverse Geochemical Calculations; USGS: Reston, VA, USA, 2013.
- Damiani, L.H.; Kosakowski, G.; Glaus, M.A.; Churakov, S.V. A framework for reactive transport modeling using FEniCS–Reaktoro: Governing equations and benchmarking results. Comput. Geosci. 2020, 24, 1071–1085. [Google Scholar] [CrossRef]
- Thoenen, T.; Hummel, W.; Berner, U.; Curti, E. The PSI/Nagra Chemical Thermodynamic Database. Nuclear Energy and Safety Research Department Laboratory for Waste Management (LES); Paul Scherrer Institute: Würenlingen, Switzerland, 2014. [Google Scholar]
- Yetkin, E.F.; Pişkin, Ş. Sensitivity of computational fluid dynamics simulations against soft errors. Computing 2021, 103, 2687–2709. [Google Scholar] [CrossRef]
- Bradford, S.A.; Torkzaban, S.; Shapiro, A. A Theoretical Analysis of Colloid Attachment and Straining in Chemically Heterogeneous Porous Media. Langmuir 2013, 29, 6944–6952. [Google Scholar] [CrossRef] [PubMed]
- Atchley, A.L.; Maxwell, R.M.; Navarre-Sitchler, A.K. Using streamlines to simulate stochastic reactive transport in heterogeneous aquifers: Kinetic metal release and transport in CO2 impacted drinking water aquifers. Adv. Water Resour. 2013, 52, 93–106. [Google Scholar] [CrossRef]
- Chen, L.; Wang, M.; Kang, Q.; Tao, W. Pore scale study of multiphase multicomponent reactive transport during CO2 dissolution trapping. Adv. Water Resour. 2018, 116, 208–218. [Google Scholar] [CrossRef]
- Municchi, F.; Di Pasquale, N.; Dentz, M.; Icardi, M. Heterogeneous Multi-Rate mass transfer models in OpenFOAM®. Comput. Phys. Commun. 2021, 261, 107763. [Google Scholar] [CrossRef]
- Sole-Mari, G.; Bolster, D.; Fernàndez-Garcia, D. A Closer Look: High-Resolution Pore-Scale Simulations of Solute Transport and Mixing through Porous Media Columns. Transp. Porous Media 2022. [Google Scholar] [CrossRef]
- Boso, F.; Bellin, A.; Dumbser, M. Numerical simulations of solute transport in highly heterogeneous formations: A comparison of alternative numerical schemes. Adv. Water Resour. 2013, 52, 178–189. [Google Scholar] [CrossRef]
- Porta, G.M.; Chaynikov, S.; Thovert, J.-F.; Riva, M.; Guadagnini, A.; Adler, P.M. Numerical investigation of pore and continuum scale formulations of bimolecular reactive transport in porous media. Adv. Water Resour. 2013, 62, 243–253. [Google Scholar] [CrossRef]
- Tartakovsky, A.M.; Trask, N.; Pan, K.; Jones, B.; Pan, W.; Williams, J.R. Smoothed particle hydrodynamics and its applications for multiphase flow and reactive transport in porous media. Comput. Geosci. 2016, 20, 807–834. [Google Scholar] [CrossRef] [Green Version]
- Sin, I.; Corvisier, J. Multiphase Multicomponent Reactive Transport and Flow Modeling. Rev. Mineral. Geochem. 2019, 85, 143–195. [Google Scholar] [CrossRef]
- Greenshields, C.J. Openfoam User Guide; OpenFOAM Foundation Ltd.: London, UK, 2019. [Google Scholar]
- Rolle, M.; Sprocati, R.; Masi, M.; Jin, B.; Muniruzzaman, M. Nernst-Planck-based Description of Transport, Coulombic Interactions, and Geochemical Reactions in Porous Media: Modeling Approach and Benchmark Experiments. Water Resour. Res. 2018, 54, 3176–3195. [Google Scholar] [CrossRef] [Green Version]
- Tian, Z.; Wang, J. Lattice Boltzmann simulation of dissolution-induced changes in permeability and porosity in 3D CO2 reactive transport. J. Hydrol. 2018, 557, 276–290. [Google Scholar] [CrossRef]
- Bandopadhyay, A.; Le Borgne, T.; Méheust, Y.; Dentz, M. Enhanced reaction kinetics and reactive mixing scale dynamics in mixing fronts under shear flow for arbitrary Damköhler numbers. Adv. Water Resour. 2017, 100, 78–95. [Google Scholar] [CrossRef] [Green Version]
- Patel, R.A.; Perko, J.; Jacques, D.; De Schutter, G.; Van Breugel, K.; Ye, G. A versatile pore-scale multicomponent reactive transport approach based on lattice Boltzmann method: Application to portlandite dissolution. Phys. Chem. Earth Parts A/B/C 2014, 70–71, 127–137. [Google Scholar] [CrossRef]
- Saaltink, M.W.; Carrera, J.; Ayora, C. On the behavior of approaches to simulate reactive transport. J. Contam. Hydrol. 2001, 48, 213–235. [Google Scholar] [CrossRef]
- Hiorth, A.; Jettestuen, E.; Cathles, L.M.; Madland, M.V. Precipitation, dissolution, and ion exchange processes coupled with a lattice Boltzmann advection diffusion solver. Geochim. Cosmochim. Acta 2013, 104, 99–110. [Google Scholar] [CrossRef]
- Benson, D.A.; Pankavich, S.; Bolster, D. On the separate treatment of mixing and spreading by the reactive-particle-tracking algorithm: An example of accurate upscaling of reactive Poiseuille flow. Adv. Water Resour. 2019, 123, 40–53. [Google Scholar] [CrossRef] [Green Version]
- Engdahl, N.B.; Benson, D.A.; Bolster, D. Lagrangian simulation of mixing and reactions in complex geochemical systems. Water Resour. Res. 2017, 53, 3513–3522. [Google Scholar] [CrossRef]
- Paster, A.; Bolster, D.; Benson, D.A. Connecting the dots: Semi-analytical and random walk numerical solutions of the diffusion–reaction equation with stochastic initial conditions. J. Comput. Phys. 2014, 263, 91–112. [Google Scholar] [CrossRef]
- Sole-Mari, G.; Fernàndez-Garcia, D.; Rodríguez-Escales, P.; Sanchez-Vila, X. A KDE-Based Random Walk Method for Modeling Reactive Transport With Complex Kinetics in Porous Media. Water Resour. Res. 2017, 53, 9019–9039. [Google Scholar] [CrossRef]
- Engdahl, N.B.; Aquino, T. Considering the utility of backward-in-time simulations of multi-component reactive transport in porous media. Adv. Water Resour. 2018, 119, 17–27. [Google Scholar] [CrossRef]
- Schopf, S.O.; Hartwig, A.; Fritsching, U.; Mädler, L. Imbibition into Highly Porous Layers of Aggregated Particles. Transp. Porous Media 2017, 119, 119–141. [Google Scholar] [CrossRef]
- Van Lopik, J.H.; Snoeijers, R.; van Dooren, T.C.G.W.; Raoof, A.; Schotting, R.J. The Effect of Grain Size Distribution on Nonlinear Flow Behavior in Sandy Porous Media. Transp. Porous Media 2017, 120, 37–66. [Google Scholar] [CrossRef] [Green Version]
- Li, L.; Ma, W. Experimental Study on the Effective Particle Diameter of a Packed Bed with Non-Spherical Particles. Transp. Porous Media 2011, 89, 35–48. [Google Scholar] [CrossRef]
- Kang, Q.; Chen, L.; Valocchi, A.J.; Viswanathan, H.S. Pore-scale study of dissolution-induced changes in permeability and porosity of porous media. J. Hydrol. 2014, 517, 1049–1055. [Google Scholar] [CrossRef]
- Radu, F.A.; Pop, I.S. Newton method for reactive solute transport with equilibrium sorption in porous media. J. Comput. Appl. Math. 2010, 234, 2118–2127. [Google Scholar] [CrossRef] [Green Version]
- Tartakovsky, A.M.; de Anna, P.; Le Borgne, T.; Balter, A.; Bolster, D. Effect of spatial concentration fluctuations on effective kinetics in diffusion-reaction systems. Water Resour. Res. 2012, 48, W02526. [Google Scholar] [CrossRef] [Green Version]
- Undheim, O.; Andersson, H.I.; Berge, E. Non-Linear, Microscale Modelling of the Flow Over Askervein Hill. Bound.-Layer Meteorol. 2006, 120, 477–495. [Google Scholar] [CrossRef]
- Lian, Y.P.; Dallmann, J.; Sonin, B.; Roche, K.R.; Packman, A.I.; Liu, W.K.; Wagner, G.J. Double Averaging Analysis Applied to a Large Eddy Simulation of Coupled Turbulent Overlying and Porewater Flow. Water Resour. Res. 2021, 57, e2021WR029918. [Google Scholar] [CrossRef]
- Hanjalić, K.; Launder, B.E. Reassessment of modeling turbulence via Reynolds averaging: A review of second-moment transport strategy. Phys. Fluids 2021, 33, 091302. [Google Scholar] [CrossRef]
- Gray, W.G.; Bruning, K.; Miller, C.T. Non-hysteretic functional form of capillary pressure in porous media. J. Hydraul. Res. 2019, 57, 747–759. [Google Scholar] [CrossRef]
- McClure, J.E.; Armstrong, R.T.; Berrill, M.A.; Schlüter, S.; Berg, S.; Gray, W.G.; Miller, C.T. Geometric state function for two-fluid flow in porous media. Phys. Rev. Fluids 2018, 3, 084306. [Google Scholar] [CrossRef]
- Miller, C.T.; Bruning, K.; Talbot, C.L.; McClure, J.E.; Gray, W.G. Nonhysteretic Capillary Pressure in Two-Fluid Porous Medium Systems: Definition, Evaluation, Validation, and Dynamics. Water Resour. Res. 2019, 55, 6825–6849. [Google Scholar] [CrossRef]
- Tartakovsky, D.M.; Dentz, M.; Lichtner, P.C. Probability density functions for advective-reactive transport with uncertain reaction rates. Water Resour. Res. 2009, 45, W07414. [Google Scholar] [CrossRef]
- Perez, L.J.; Hidalgo, J.J.; Dentz, M. Upscaling of Mixing-Limited Bimolecular Chemical Reactions in Poiseuille Flow. Water Resour. Res. 2019, 55, 249–269. [Google Scholar] [CrossRef]
- Gillespie, D.T. The chemical Langevin equation. J. Chem. Phys. 2000, 113, 297–306. [Google Scholar] [CrossRef]
- Mayer, K.U.; Benner, S.G.; Blowes, D.W. Process-based reactive transport modeling of a permeable reactive barrier for the treatment of mine drainage. J. Contam. Hydrol. 2006, 85, 195–211. [Google Scholar] [CrossRef]
- Hayes, R.E.; Afacan, A.; Boulanger, B.; Shenoy, A.V. Modelling the flow of power law fluids in a packed bed using a volume-averaged equation of motion. Transp. Porous Media 1996, 23, 175–196. [Google Scholar] [CrossRef]
- Carrera, J.; Saaltink, M.W.; Soler-Sagarra, J.; Wang, J.; Valhondo, C. Reactive Transport: A Review of Basic Concepts with Emphasis on Biochemical Processes. Energies 2022, 15, 925. [Google Scholar] [CrossRef]
- Massoudieh, A.; Dentz, M. Upscaling non-linear reactive transport in correlated velocity fields. Adv. Water Resour. 2020, 143, 103680. [Google Scholar] [CrossRef]
- Miller, C.T.; Gray, W.G.; Schrefler, B.A. A continuum mechanical framework for modeling tumor growth and treatment in two- and three-phase systems. Arch. Appl. Mech. 2022, 92, 461–489. [Google Scholar] [CrossRef] [PubMed]
- Noiriel, C.; Steefel, C.I.; Yang, L.; Bernard, D. Effects of pore-scale precipitation on permeability and flow. Adv. Water Resour. 2016, 95, 125–137. [Google Scholar] [CrossRef] [Green Version]
- Jakobsen, R.; Kazmierczak, J.; Sø, H.U.; Postma, D. Spatial Variability of Groundwater Arsenic Concentration as Controlled by Hydrogeology: Conceptual Analysis Using 2-D Reactive Transport Modeling. Water Resour. Res. 2018, 54, 10,254–10,269. [Google Scholar] [CrossRef] [Green Version]
- Goovaerts, P.; AvRuskin, G.; Meliker, J.; Slotnick, M.; Jacquez, G.; Nriagu, J. Geostatistical modeling of the spatial variability of arsenic in groundwater of southeast Michigan. Water Resour. Res. 2005, 41, W07013. [Google Scholar] [CrossRef]
- Parkhurst, D.L.; Kipp, K.L.; Charlton, S.R. PHAST Version 2-A Program for Simulating Groundwater Flow, Solute Transport, and Multicomponent Geochemical Reactions; Techniques and Methods 6-A35; US Geological Survey: Reston, VA, USA, 2010. [Google Scholar] [CrossRef]
- Nikolaidis, N.P.; Dobbs, G.M.; Lackovic, J.A. Arsenic removal by zero-valent iron: Field, laboratory and modeling studies. Water Res. 2003, 37, 1417–1425. [Google Scholar] [CrossRef]
- Rawson, J.; Prommer, H.; Siade, A.; Carr, J.; Berg, M.; Davis, J.A.; Fendorf, S. Numerical Modeling of Arsenic Mobility during Reductive Iron-Mineral Transformations. Environ. Sci. Technol. 2016, 50, 2459–2467. [Google Scholar] [CrossRef] [Green Version]
- Pillai, K.; Raizada, A. Modeling Transport and Adsorption of Arsenic Ions in Iron-Oxide Laden Porous Media. Part I: Theoretical Developments. Water 2021, 13, 779. [Google Scholar] [CrossRef]




Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Peel, H.R.; Balogun, F.O.; Bowers, C.A.; Miller, C.T.; Obeidy, C.S.; Polizzotto, M.L.; Tashnia, S.U.; Vinson, D.S.; Duckworth, O.W. Towards Understanding Factors Affecting Arsenic, Chromium, and Vanadium Mobility in the Subsurface. Water 2022, 14, 3687. https://doi.org/10.3390/w14223687
Peel HR, Balogun FO, Bowers CA, Miller CT, Obeidy CS, Polizzotto ML, Tashnia SU, Vinson DS, Duckworth OW. Towards Understanding Factors Affecting Arsenic, Chromium, and Vanadium Mobility in the Subsurface. Water. 2022; 14(22):3687. https://doi.org/10.3390/w14223687
Chicago/Turabian StylePeel, Hannah R., Fatai O. Balogun, Christopher A. Bowers, Cass T. Miller, Chelsea S. Obeidy, Matthew L. Polizzotto, Sadeya U. Tashnia, David S. Vinson, and Owen W. Duckworth. 2022. "Towards Understanding Factors Affecting Arsenic, Chromium, and Vanadium Mobility in the Subsurface" Water 14, no. 22: 3687. https://doi.org/10.3390/w14223687







