1. Introduction
Water distribution systems (WDS) are spatially extensive; hence, they are vulnerable to ‘accidents’. At large, accidents causing problems with the physical integrity of WDS can cause substantial economic loss and environmental damage, but their direct threat to human health is limited. On the contrary, accidents involving a contaminant intrusion in WDS cause drinking-water quality deterioration and could induce acute or chronic health risks to the water consumers.
For any contaminant not prevailing within the distribution pipe environment [
1] to reach consumer taps, intrusion(s) (accidental or intentional) should happen, either at the treatment plants or within the distribution network domain (reservoirs, tanks, pipes). Although backflow preventers impede contaminant entry into the pipes from the outside, they are not prevalent at every pipe joint, and if they exist, they might not always be functioning. Presumably, due to the integrity flaws in WDS and/or its components malfunctioning in contamination prevention [
2], several accidental and intentional contaminant intrusion events in WDS have been reported in the past [
3,
4].
An Online Contaminant Monitoring System (OCMS) employing water quality (WQ) sensors is generally admitted [
5] as the primary tool to minimize contaminant intrusion impacts. An OCMS is designed to detect unexpected events of drinking-water contamination and furnish knowledge on the contamination event-location of contamination with the WDS domain and intrusion characteristics (contaminant type, intrusion time and duration, concentration, and mass intrusion rate). In fact, designing an OCMS is one of the most explored problems in WDS security enhancement through modeling [
6,
7,
8,
9,
10].
Due to cost constraints, WQ sensors cannot be placed at every node of a WDS; hence, the available resources must be optimally deployed. This motivated the development of countless methodologies to allocate a limited number of sensors within a distribution network optimally. The pioneering work in this direction is attributed to Lee et al. [
11]. These researchers solved the WQ sensor placement problem using mixed-integer linear programming and assuming steady-state hydraulic conditions within the network. The maximum demand coverage was selected as their objective function. Afterward, Harmant et al. [
12] improved the WQ sensor placement methodology by including water quality and considering unsteady hydraulic conditions. With the evolution of heuristic optimization, Al-Zahrani and Moeid [
13] employed genetic algorithms to solve the same problem formulation. Following the work of Lee et al. [
11], Kessler et al. [
14] added an all-shortest path algorithm to the coverage problem and constructed a pollution matrix. The pollution matrix comprised data on the nodes contaminated by multiple possible contamination events. These researchers defined the contaminated node as a node in which the contaminant concentration is above a predefined threshold value. Later on, Ostfeld and Salomons [
9] expanded this study and introduced a randomized pollution matrix which holds binary information about a set of randomly generated multiple contaminant intrusion locations and times. This was applied to determine whether a system node is contaminated during a specific random contaminant intrusion event. Although numerous studies were reported on further altering, expanding, and improving the methodologies above-mentioned and applying them to several probable contamination scenarios in different WDS [
7,
8,
15,
16,
17,
18], the benchmark in this field of study is the battle of the water sensor networks (BWSN) conference held in Cincinnati in the year 2006 [
19]. The BWSN conference compared fifteen approaches to optimal WQ sensor placement in WDS, and these approaches primarily evaluated four objectives: (1) the time of detection; (2) the affected population prior to detection; (3) consumption of contaminated water prior to detection; and (4) likelihood of detection.
The extensive research efforts in WQ sensor network placement modeling have resulted in the development of several tools. TEVA-SPOT, developed by the U. S. Environmental Protection Agency, Sandia National Laboratories, Argonne National Laboratory, and the University of Cincinnati [
20], is a widely applied tool for developing an OCMS. After implementing an OCMS in a WDS, communication occurs via a Supervisory Control and Data Acquisition (SCADA) system.
Nevertheless, as WDS is vulnerable to accidents, the OCMS and the associated SCADA system are susceptible to malfunctioning by natural causes or cyber-physical attacks. The malfunctioning could result in (1) OCMS giving erroneous predictions, (2) OCMS being entirely non-functional and giving no predictions, and (3) OCMS being partially functional. Although the above three likely scenarios resulting in full or partial deactivation of OCMS components are critical in governing its reliability, surprisingly, the WQ sensor network placement studies evaluating these scenarios have not yet been reported. In this direction, the current study attempts to close this gap in the state-of-the-art by developing a methodology for assessing the consequence of an OCMS and/or the associated SCADA system becoming only partly operational due to a cyber-physical attack. The study’s findings would advance the state-of-the-art to enhance the procedure of placing an OCMS in WDS and assist the decision makers in water utilities and regulators to identify the critical sensors in an OCMS that necessitates increased security under possible cyber-physical attacks.
2. Materials and Methods
2.1. Methodology
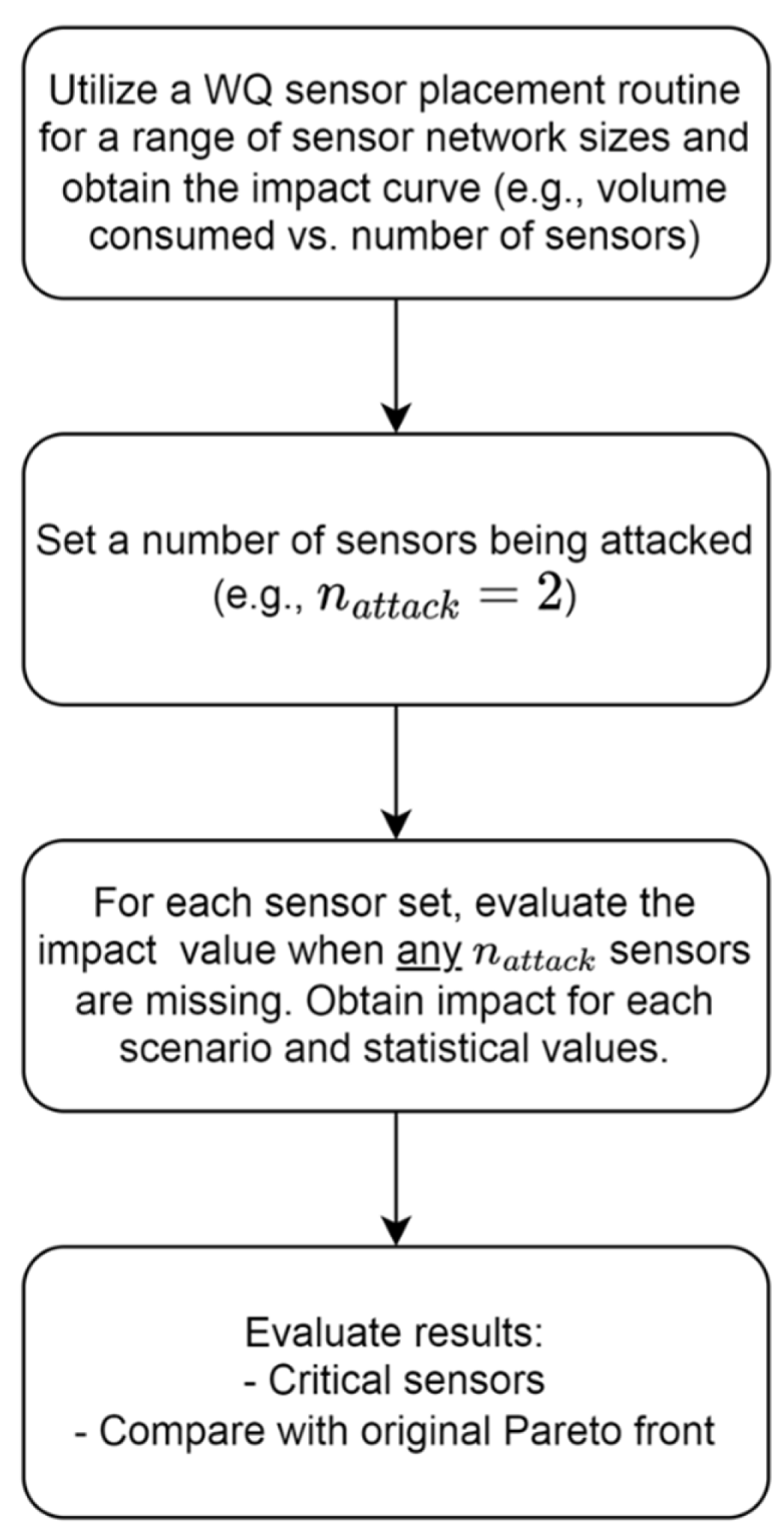
The detailed methodology adopted in this study is schematically represented in
Figure 1. The first step involves utilizing TEVA-SPOT to design an OCMS and develop the impact curve (i.e., the relation between the number of sensors deployed vs. the mean impact of possible contamination). The designing of an OCMS involves deciding on the optimal locations of placing a predefined number of WQ sensors (
) within a distribution network to minimize contaminant intrusion impacts. In this regard, the objective function was selected as the mean volume of consumption of contaminated water before detection (Equation (1)).
where:
= volume of contaminated water consumed before detection (m
3);
= contaminant intrusion scenario index;
= set of contaminant intrusion scenarios;
= node index;
= set of demand nodes;
= time index;
= set of time steps for which node
receives contaminated water;
= actual quantity of contaminated water supplied to node
at time
(m
3/s); and
= time-step width (s).
Once the OCMS was designed, the impact curve signifying the relationship between the mean volume of contaminated water consumed by the water consumers before detection of contaminant intrusion and the number of WQ sensors was generated. On generating the impact curves, it was assumed that there is no time delay in the WQ sensors for detecting contamination and that the WDS’s operator response to contaminant-intrusion detection is instantaneous. In other words, the WQ sensors are activated instantly with contamination detection, and contaminant spread is controlled simultaneously by remedial measures such as the actuation of flushing units or by public notification to stop consuming water.
The second step of the methodology involves simulating cyber-physical attack scenarios and analyzing the designed OCMS performance under possible malfunctioning of its components. As already mentioned, we are limiting to the case that the OCMS is partly functional after the attack, i.e., only those WQ sensors that have been attacked are entirely not giving out any signals (WQ predictions), and the remaining ones are fully operational. Though we could have accounted for the case in which the WQ sensors that were attacked are ‘operational’ but give out erroneous signals, we decided not to consider this because this might require advancing the methodology to distinguish between erroneous and proper signals. However, it could be noted that the proposed methodology is fully applicable even under such a case once the WQ sensor(s) giving out erroneous signals are pinpointed. Under a cyber-physical attack, only WQ sensors would be functional within the OCMS.
The third step comprises assessing the impact value (mean volume of contaminated water consumed by the water consumers before detection of contaminant intrusion) when a predefined number () of WQ sensors within the OCMS are under cyber-physical attack. This step involves determining all the possible combinations of functional WQ sensors. As the only information known is the value and further whereabouts (locations) of the WQ sensors that could be non-operational are unknown, the number of possible sets of operational sensors is determined as . For example, for and values six and two, respectively, 360 possible combinations of operational WQ sensors would evolve, and all of them are individually considered to calculate the impact values.
The fourth and final step includes interpreting the results to demarcate the critical sensors and assess the overall reliability of an OCMS during a cyber-physical attack. For every value, impact values would be generated. From the generated sets of impact values, six values (minimum, 25th percentile, median, 75th percentile, maximum, and mean) are specifically picked to evaluate the effects of the cyber-physical attack on the reliability of contamination detection by the designed OCMS. The maximum impact value corresponds to the case when the in-effect OCMS with only the number of WQ sensors under operation is not adequate to timely detect the contaminant intrusion incident. Therefore, those WQ sensors that may fall within the set of WQ sensors of length , subjected to cyber-physical attack, that gives out the maximum impact value could be deemed as the most critical WQ sensors within the OCMS.
2.2. Test Problem
The test problem studied is the C-Town WDS (
Figure 2), one of the benchmark networks employed in WDS engineering. This network, consisting of 429 pipes and 388 demand nodes, is based on a real-world, medium-sized network [
21]. The WDS consists of five pressure zones, each controlled by one or two water tanks. In total, the network has seven tanks (T1 to T7), whose water level controls the operations of one valve. The network has 11 pumps, and they are spread across five pumping stations (S1 to S5). The pumping station S1 draws water from the only source and delivers it to Tank T1 and several demand nodes. The remaining four pumping stations pump the water from the lower elevation zone to four higher elevation zones, each controlled by water tanks.
In this study, we varied between 1 and 11 sensors and assumed that the number of sensors subjected to cyber-physical () was two. We also analyzed an additional scenario with three WQ sensors under cyber-physical attack ( = 3) for the OCMS designed with = 6 to perceive the effects of on the reliability of an OCMS under partial operational conditions. The cyber-physical attack scenario is not evaluated for the OCMS design with = 1, 2, and 3. Furthermore, for designed OCMS with > 8, the number of possible combinations to evaluate under a cyber-physical attack becomes very high (>181,440 combinations). Only 50,000 combinations were randomly selected to handle the computational complexity under such cases.
3. Results and Discussion
3.1. Design of OCMS
The TEVA-SPOT was applied to decide the optimal locations of placing the WQ sensors within the considered distribution network for minimizing the volume of contaminated water consumed during a contaminant intrusion event (Equation (1)). Diverse OCMS designs corresponding to
= 1, 3, …, 11 were evolved by operating a total of 2328 contaminant intrusion scenarios for each
, i.e., six different contaminant intrusion scenarios corresponding to the time of intrusion for 388 demand nodes of the Test problem. Increasing the value of
from 1 to 11 enabled us to explore the effects of the successive increase in the WQ sensors’ number on minimizing the contaminant intrusion impacts. The spatial distribution of the WQ sensors for the case with
= 5 and 6 is illustrated in
Figure 3.
As can be seen from
Figure 3, some similarities are apparent between the two designs. The locations corresponding to nodes J109, J239, J352, and J67 emerged as the optimal locations for WQ sensor placement in both the OCMS designs corresponding to
= 5 and 6. However, instead of node J492, J131 and J385 came out as the optimal locations for WQ sensor placement when the
value was increased from five to six. Altogether, the OCMS designs obtained revealed its high sensitivity to the
value.
3.2. Determination of Impact Values
The variations of the impact values determined for different OCMS designs (corresponding to
= 2, 3, …, 11) versus the number of WQ sensors (
Figure 4 and
Table 1) exposed the significant impact of the
value on any OCMS performance. In the absence of an OCMS within the distribution network, the mean impact value during contamination intrusion was estimated as 10,138 m
3 (
Table 1). Introducing an OCMS with only one WQ sensor was found capable of reducing the above value to 2161 m
3, i.e., by ~79%. Introducing an additional WQ sensor further reduced the impact value by 95%. Simultaneously, the stage-wise reduction (between adding one WQ sensor and adding two WQ sensors within the distribution network) in the impact value decreased from 95 to 76%.
Intriguingly, the subsequent introduction of WQ sensors (increase in the
values) failed to engender comparable effects corresponding to adding only two WQ sensors within the network. As seen in
Figure 4, even though the overall reduction in the impact value improved from 95 to 98% by increasing the
value from 2 to 3, the stage-wise reduction dropped to 69%. Likewise, a steady drop in the stage-wise reduction in the impact values was evident with the subsequent increase in the
values. Beyond
= 5, the variations in the overall reduction in the impact value remained almost unnoticeable. The consequent effects of minimizing the extent of contaminant spread within the C-Town network also became nearly constant (
Figure 4). Therefore, for the test problem analyzed, an OCMS design with
= 5 could be considered ‘best’ to minimize contaminant intrusion impacts. However, as previously mentioned, such a conclusion is classically made only by making a tradeoff between the impact values and the cost of implementing and operating an OCMS. Moreover, this study attempts to explore the implications of factors such as the reliability of an OCMS under cyber-physical attacks towards making these conclusions.
3.3. Evaluating the Cyber-Physical Attack Scenarios
The impact values obtained by considering cyber-physical attack scenarios corresponding to
= 2 are detailed in
Table 1.
Figure 5 also schematically illustrates the variations in the impact values corresponding to scenarios under which the designed OCMS with
= 4, 5, 6, 7, and 8 are subjected to cyber-physical attacks, and the number of available WQ sensors within the OCMS is reduced to 2, 3, 4, 5, and 6, respectively.
Intriguingly, after analyzing 12 different combinations of operational WQ sensors, a ~21 times increase in the mean impact value was detected when the OCMS design with
= 4 was subjected to a cyber-physical attack. As seen in
Figure 5, the maximum impact value (2706 m
3) was almost 111% greater than the mean value. For the OCMS design with
= 5, although the magnitude of the mean impact value obtained under a cyber-physical attack was lower than the case with
= 4, the relative increment in the value (~25 times) was more substantial. Furthermore, the maximum impact value for the OCMS design with
= 5 obtained after analyzing 60 possible combinations of operational WQ sensors was found to be ~188% higher than the mean value. However, similar to the mean impact value, this value (2631 m
3) was also lower than that obtained for the OCMS design with
= 4. Nevertheless, the relative decrease in the mean and maximum impact values for the OCMS design with
= 5 from that with
= 4 was estimated as ~29 and ~3%, respectively. Similar outcomes were derived when 360 different possible combinations of cyber-physical attack scenarios were analyzed for the OCMS design with
= 6.
Relative to the OCMS with
= 6, the OCMS with
= 7 was observed to be more resilient to the malfunctioning of the WQ sensors. As seen in
Table 1 and
Figure 5, the mean impact value under the cyber-physical attack scenario was 13 times higher than that under the absence of the same for the OCMS with
= 7. Even though the reduction in the mean impact value is not very noteworthy compared to the case of OCMS with
= 6, the decrease in the maximum value appeared relatively significant. The maximum impact value obtained for the OCMS with
= 6 under a cyber-physical attack was 2624 m
3. On the contrary, the same value found for the OCMS with
= 7 (after considering 2520 cyber-physical attack scenarios) was ~68% lower (i.e., 835 m
3).
This shows that although not many changes are attributable between the performances of the two OCMS designs with
= 6 and 7 under normal conditions (absence of a cyber-physical attack), significant variations appear when the WQ sensors’ malfunction is accounted for under possible cyber-physical attacks. Increasing the WQ sensors’ number from 7 to 8 also significantly improved minimizing the contamination spread during a contaminant intrusion concurrently under a cyber-physical attack (
Table 1 and
Figure 5). Overall, the results stress the importance of considering cyber-physical attacks and potential malfunctioning of the OCMS components in designing and evaluating the OCMS in WDS.
3.4. Identifying Critical WQ Sensors in an OCMS
Each cyber-physical attack scenario analyzed signifies the case of only
WQ sensors out of
within the OCMS being operational.
Figure 6 schematically illustrates the variations in the impact values over the 360 cyber-physical attack scenarios (possible combinations of four WQ sensors out of six) considered for the designed OCMS with
= 6. The values were found to vary between 60 and 2624 m
3, with 525 m
3 and 464 m
3 as the mean and median values, respectively.
Both the minimum (60 m3) and maximum (2624 m3) impact values were repeated 24 times (out of 360). From a closer look, the WQ sensors at locations J67 and J352 were absent in all numbers of operational WQ sensor combinations that gave out the maximum value. Similarly, in all 24 combinations where we obtained the minimum value, the WQ sensors at the above two locations were present. This indicated the significance of these two WQ sensors in governing the performance of the designed OCMS. Their presence or absence dictated the celerity with which the OCMS detected a contaminant intrusion scenario within the Test problem with four available WQ sensors. Thus, from the results obtained, J67 and J352 can be demarcated as the critical WQ sensors corresponding to the designed OCMS with = 6.
However, it may be noted that the critical WQ sensors for other OCMS designs corresponding to different values could be entirely dissimilar. Hence, making a general conclusion about the critical locations of WQ sensors within the C-Town network would be illogical. Since fully securing the OCMS against any form of cyber-physical attacks is essentially impossible, the above-mentioned straightforward approach could enable water utility managers to recognize the critical locations of the WQ sensors and introduce additional security measures to prevent their malfunctioning and improve the overall reliability of the OCMS system.
3.5. Determining the Optimal Number of WQ Sensors in an OCMS
Figure 7 gives an overall depiction of all the scenarios analyzed—with and without cyber-physical attacks. The results indicate an alarming increase in the spread of contamination during a cyber-physical attack. For example, from analyzing 2328 scenarios for the designed OCMS with four WQ sensors, the maximum volume of contaminated water consumed before detecting a contaminant intrusion within the C-Town network was estimated as 729 m
3. However, this value increased ~3.7 times during a cyber-physical attack scenario. Intriguingly, for the designed OCMS with
= 5 and 6, the relative increase in the maximum impact values was much higher (~6.6 and ~8.4 times, respectively). Moreover, the decline in the curves representing the variations in the maximum impact value versus the number of WQ sensors was also found to be entirely different for the cases with and without cyber-physical attacks (
Figure 7).
Nevertheless, a peculiar decline in the curves mentioned above was observed when the number of WQ sensors was increased beyond six. The maximum impact value under a cyber-physical attack scenario for an OCMS designed with seven WQ sensors was found to be 338 m
3. This value was only ~2.7 times higher than the value obtained under a normal scenario and was much lower than that obtained with
= 6. As expected, the extent of contaminant spread declined with increasing the number of WQ sensors within the distribution network beyond seven. However, beyond the
value 8, increasing the number of WQ sensors failed to induce significant differences in the maximum impact value (
Figure 7). Between
= 8 and 9, the relative decline in the maximum impact value under cyber-physical attack scenario was obtained as just 1.6%. Between
= 9 and 10, this figure further dropped to a mere 0.2%. These results signify that even with 10 WQ sensors, the volume of contaminated water that could be consumed before detecting a contaminant intrusion under a cyber-physical attack might be as high as ~576 m
3. This number is startling because, in the absence of a cyber-physical attack, the maximum volume of contaminated water that could be consumed before detecting a contaminant intrusion would be only ~397 m
3, with just five WQ sensors optimally placed. With eight sensors, this value could even be reduced to 277 m
3, i.e., almost half of that obtained under a cyber-physical attack (with eight operating WQ sensors out of ten).
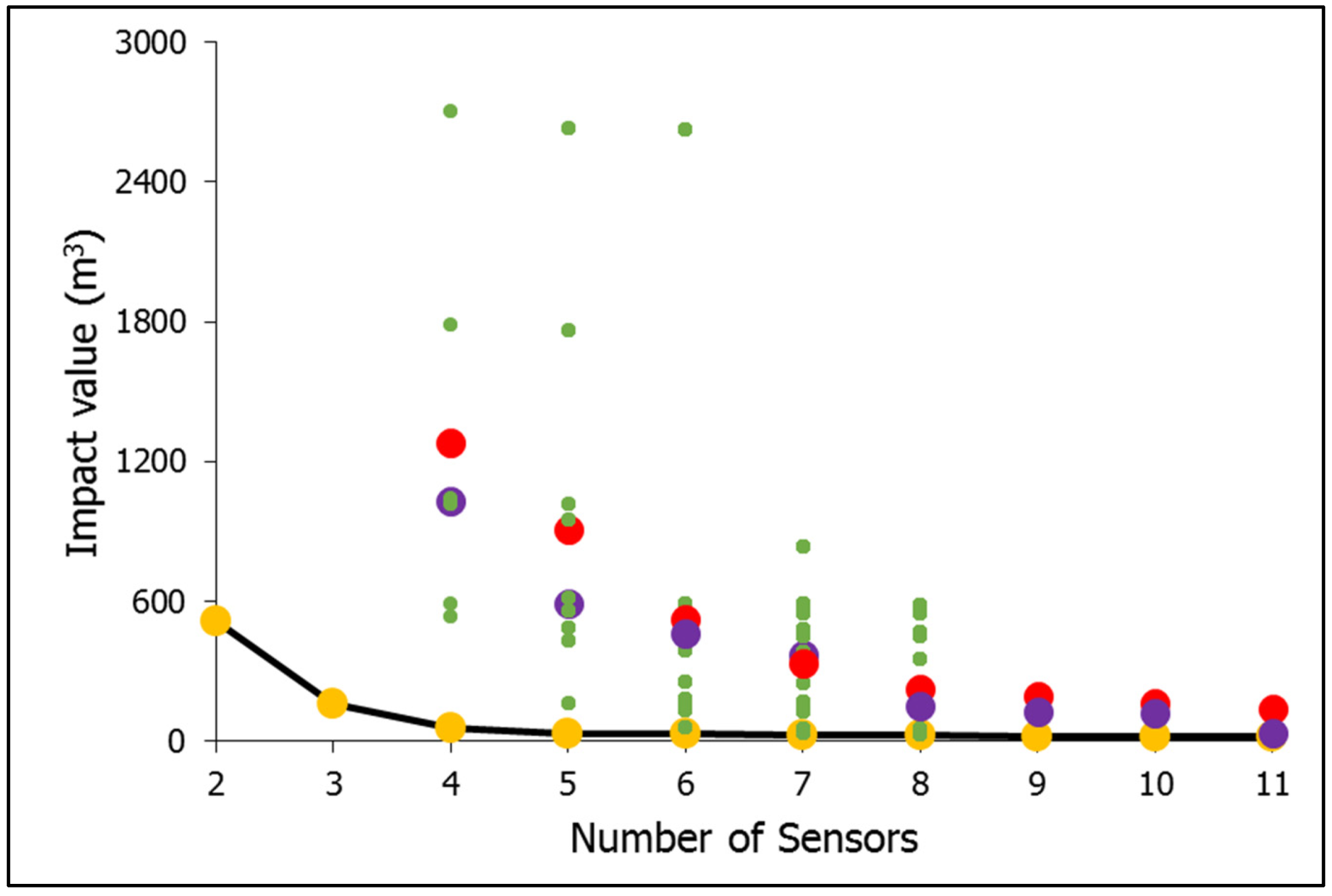
Thus, from a detailed analysis of the results, it can be concluded that under cyber-physical attacks and potential malfunctioning of the WQ sensors, it is virtually impossible to minimize the spread of contamination beyond a certain degree if the OCMS is designed following a conventional approach (overlooking the scenarios of WQ sensors operation being compromised). Altogether, from the results, eight can be interpreted as the number of sensors that need to be placed within the C-Town network to minimize contamination spread. However, this figure cannot be deemed optimal because the OCMS designs corresponding to > 11 were not analyzed under cyber-physical attacks. Moreover, the results discussed above only correspond to the scenarios of only two WQ sensors being attacked.
Figure 8 schematically illustrates the variations in the statistical values obtained for the designed OCMS with
= 6 when the
value was increased from 2 to 3. A substantial increase in the impact values was evident when 120 different scenarios were analyzed with three WQ sensors malfunctioning instead of two (
Figure 8). The mean impact value increased from 30 m
3 under no cyber-physical attack to 1054 m
3 when only three (out of six) were functional under contaminant intrusion events. This was almost twice what we obtained when four (out of six) were operational. In total, these results signify the importance of considering different cyber-physical attack scenarios in analyzing the reliability of the OCMS designed with the traditional approach using the TEVA-SPOT. Moreover, these results imply that the inference on the optimal number of WQ sensors required for an OCMS can be arrived at only by making a cost–benefit tradeoff by interpreting the designs obtained concurrently varying the
and
values within valid ranges.
3.6. Defining the Reliability of an OCMS Subjected to Cyber-Physical Attacks
Carefully looking at the mean and median impact values (
Figure 7) provides some interesting insights into the performance of designed OCMS under cyber-physical attack scenarios. As seen in
Figure 7, the mean impact values were found to be greater than the corresponding median values for almost all the OCMS designs. Even under normal scenarios, the same trend was observed. For example, for the designed OCMS with
= 1, the mean impact value under a normal scenario was obtained as 2161 m
3. However, the corresponding median value was only 35 m
3. This shows that the mean impact value estimated from diverse contaminant intrusion scenarios is entirely controlled by the outliers, specifically the maximum impact values. Comparing the other statistical figures (25th percentile = 6 m
3 and 75th percentile = 451 m
3, respectively) also proves that under the majority of the scenarios, the impact value is much lower than the mean impact value. These results stress the significance of recognizing critical sensor locations within a designed OCMS.
An associated question would be which statistical value among the mean and median of the impact values would be pragmatic to better interpret and analyze the reliability of a designed OCMS under cyber-physical attacks. We presume that considering only the mean of the impact values obtained under scenarios with and without attack would only give an incomplete picture of the performance of the OCMS. Similarly, only accounting for the median of the impact values might not reflect the worst-case settings with respect to contaminant spread as well. Towards formulating reliability indices, the best approach would be accounting for all of the five statistical values (as shown in
Figure 8) along with the mean. However, this could over-complicate the formulation. Moreover, this could constrain its applicability in an optimization model for designing the WQ sensor locations. Therefore, considering all the above aspects, we propose a straightforward reliability index formulation that considers both the mean and median impact values (Equations (2)–(4)) that can be easily incorporated as a constraint or a penalty variable in the objective function.
where:
and
= reliability index values corresponding to mean and median impact values for an OCMS subjected to cyber-physical attack;
= effective reliability index;
and
= mean and median impact values obtained under a normal scenario; and
and
= mean and median impact values corresponding to a cyber-physical attack scenario.
The value is a function of and for a specific WDS. Its value equal to 1 signifies that the designed OCMS is fully reliable and performs without any flaw, even under a cyber-physical attack. On the contrary, higher values indicate that the capability of an OCMS to minimize contaminant intrusion impacts is significantly affected by the malfunctioning of number of WQ sensors.
Since the mean impact values are susceptible to outliers, is expected to reflect more on the cases where the critical sensors are malfunctioning. Therefore, we believe that taking the sum of both and in Equation (4) is expected to incorporate the overall effects of cyber-physical attacks on WQ sensors in a better way.
4. Conclusions
In this study, we have developed and demonstrated a methodology for evaluating the impacts of cyber-physical attacks on a designed OCMS, partially malfunctioning its components and compromising its functionality. Varied OCMS designs corresponding to the number of WQ sensors varying between 1 and 11 were developed by analyzing 2328 contaminant intrusion scenarios for the well-tested C-Town network using TEVA-SPOT, one of the widely applied tools for optimally deciding sensor locations. Minimizing the volume of contaminated water consumed during a contaminant intrusion event was adopted as the objective function.
From a superficial interpretation of the results, an OCMS design with five fully operational WQ sensors arrived as the ‘best’ to minimize contaminant intrusion impacts. The maximum volume of contaminated water that could be consumed before detecting a contaminant intrusion was determined as 397 m3. Significant variations in the predictions on contaminant spread within the distribution network became apparent when scenarios corresponding to possible cyber-physical attacks and malfunctioning of any two random WQ sensors were accounted for. The obtained results signified that even with ten WQ sensors, the volume of contaminated water that could be consumed before detecting a contaminant intrusion under a cyber-physical attack might be as high as 576 m3. The simulation outcomes also established that under cyber-physical attacks, it is virtually unattainable to minimize the spread of contamination beyond a certain degree if the OCMS is designed overlooking the scenarios of WQ sensor operation being compromised partially/fully.
A detailed look into the results also highlighted that the presence or absence of specific WQ sensors is vital in dictating the celerity with which the OCMS could detect a contaminant intrusion scenario within the C-Town network. A straightforward approach for demarcating these locations within the distribution network was derived and explained. In addition, we have also proposed a simple reliability index formulation that can be incorporated easily into the sensor-placement optimization problem to evolve OCMS designs with enhanced reliability against cyber-physical attacks. Altogether, the findings of the presented study could be deemed beneficial in examining the performance of sensor networks under accidental/intentional malfunctioning, providing valuable information for decision makers in water utilities and regulators, and enhancing the planning and development of WDS operation [
22].