Intermittency of Rock Fractured Surfaces: A Power Law
Abstract
:1. Introduction
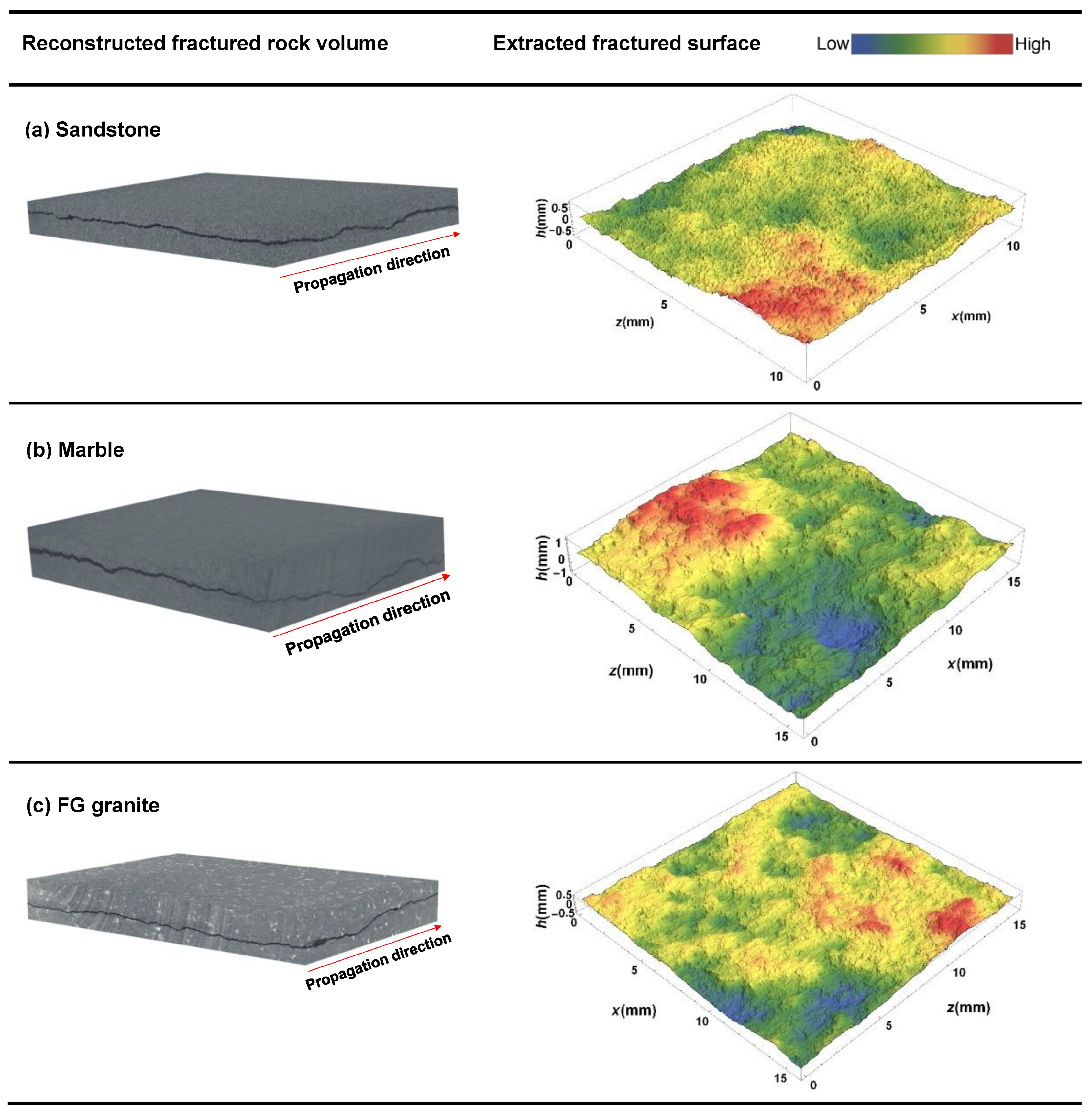
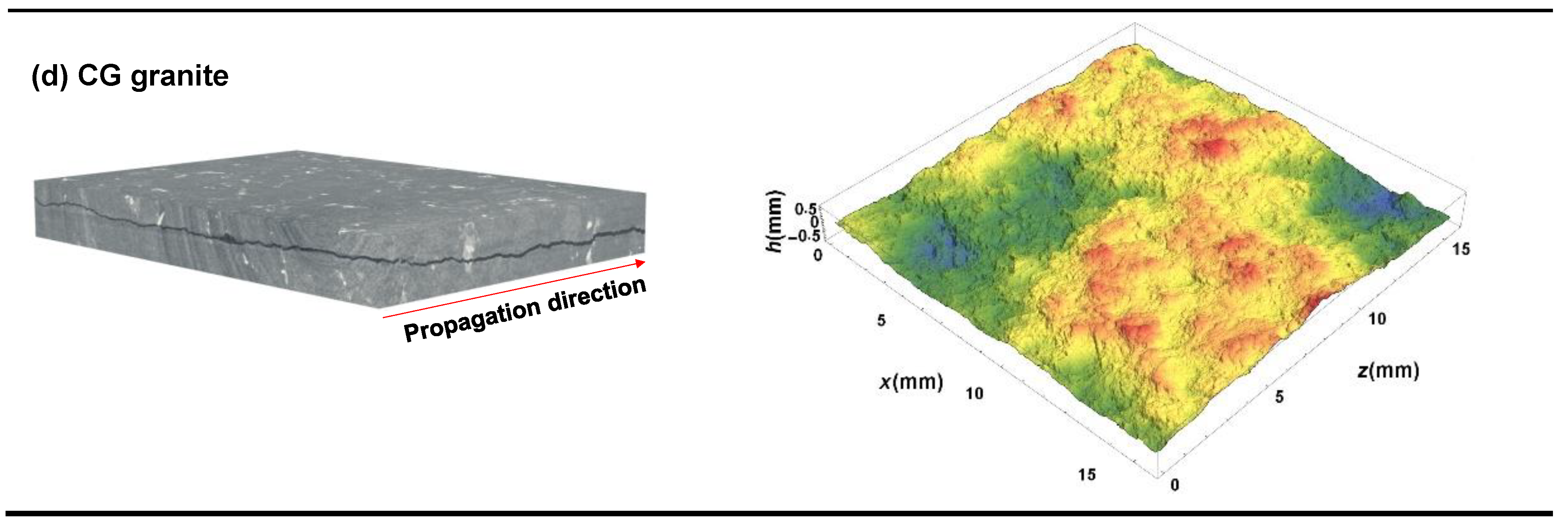
2. Materials and Methods
3. Results and Discussions
3.1. Roughness Correlation
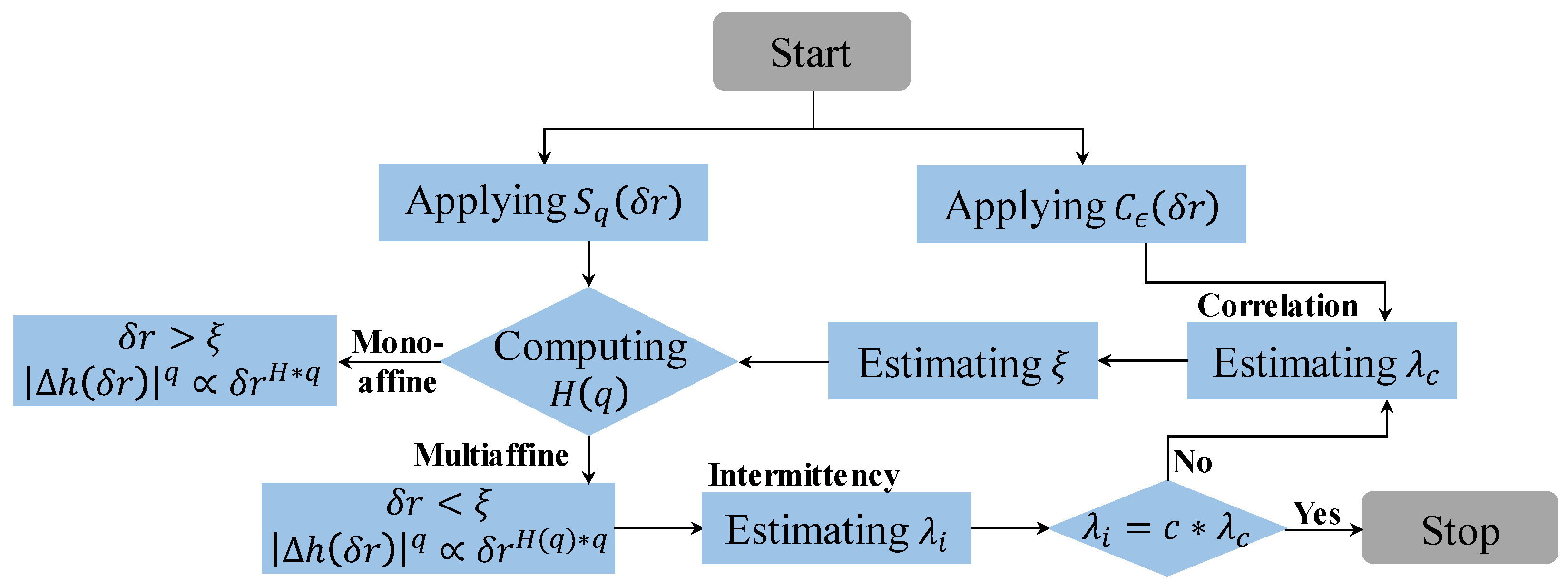
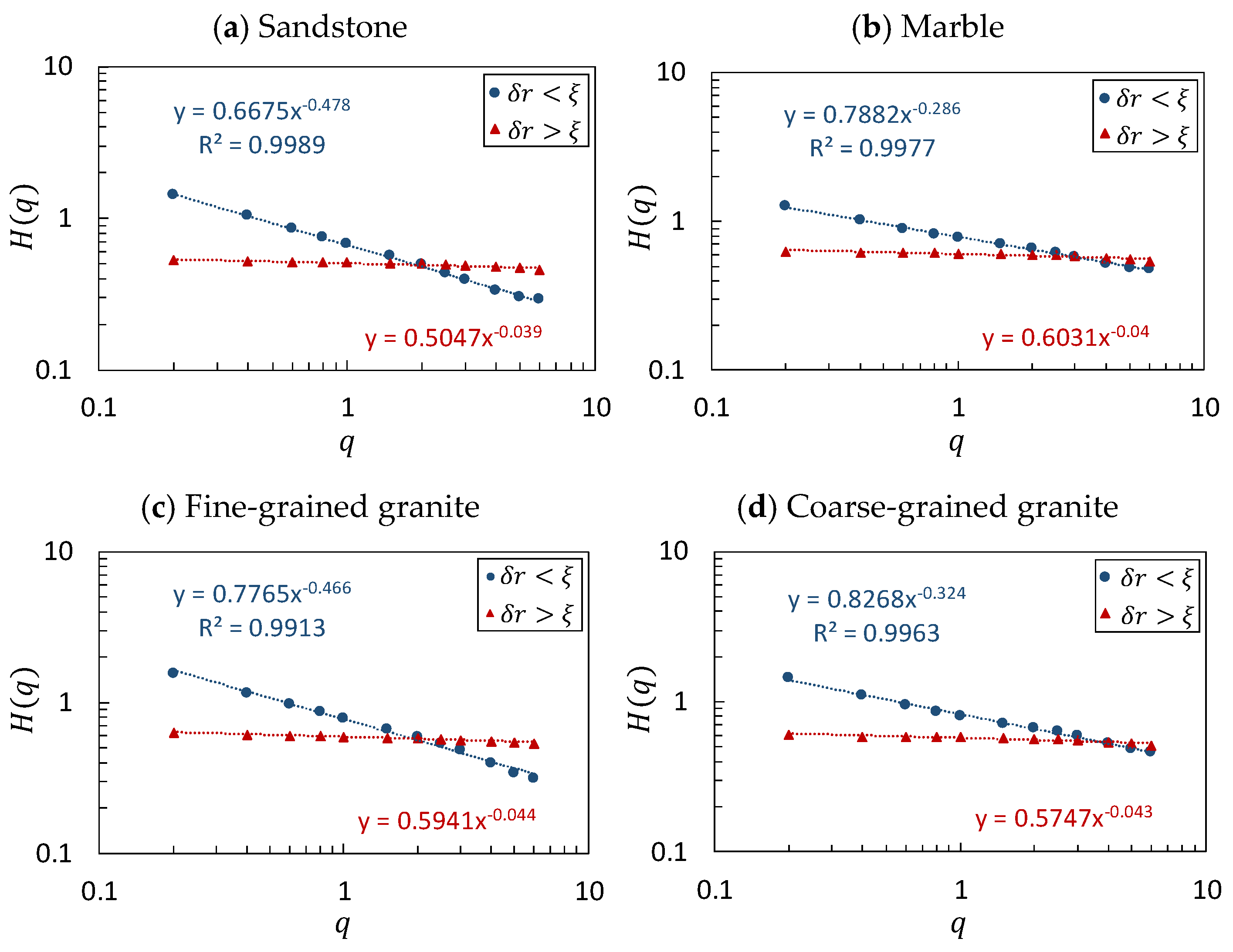
3.2. Multifractality of Roughness
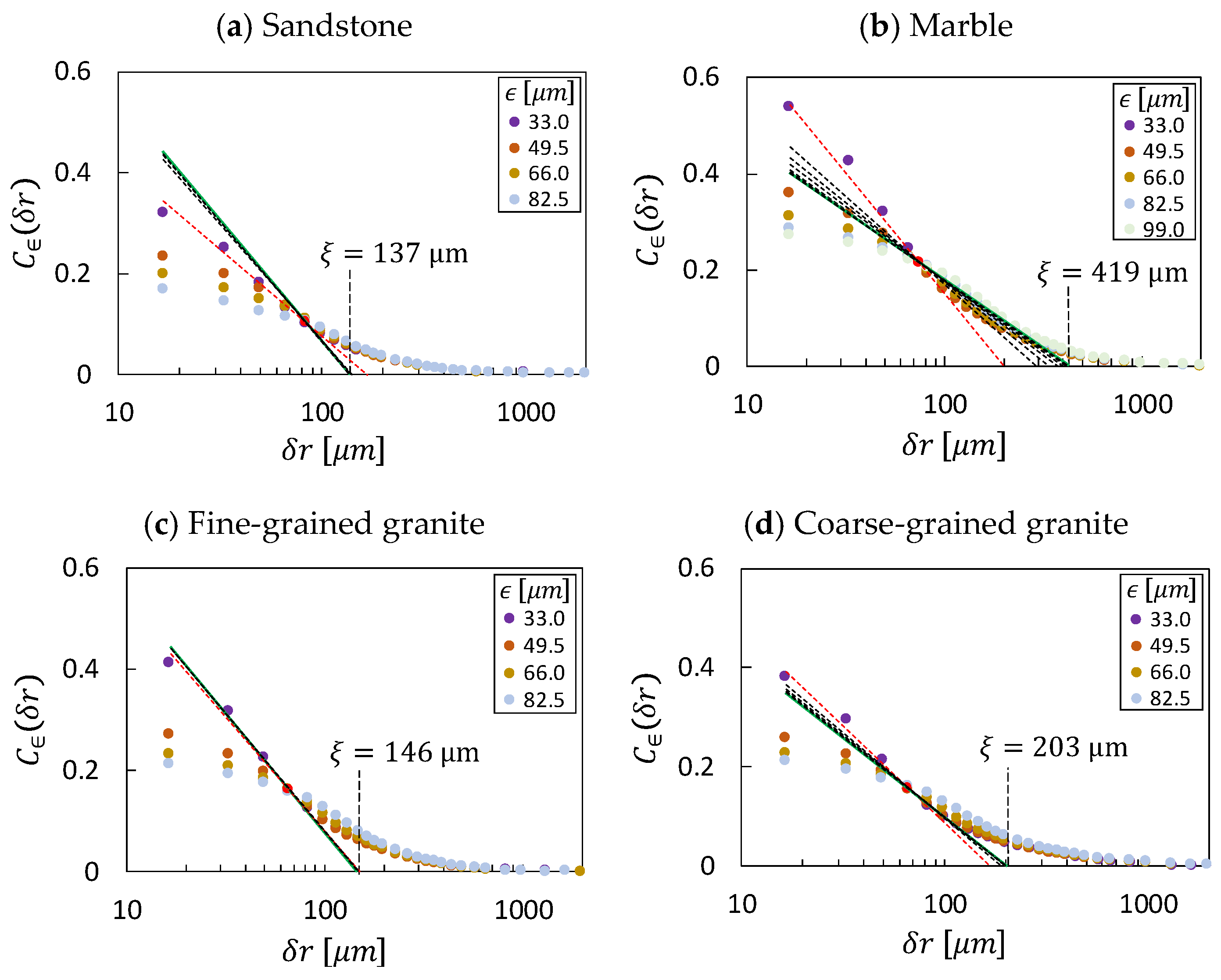
3.3. Determining the Cut-Off Length
3.4. Limitations and Future Work
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Barton, N.; Choubey, V. The shear strength of rock joints in theory and practice. Rock Mech. Rock Eng. 1977, 10, 1–54. [Google Scholar] [CrossRef]
- Pyrak-Nolte, L.; Nolte, D. Approaching a universal scaling relationship between fracture stiffness and fluid flow. Nat Commun 2016, 7, 10663. [Google Scholar] [CrossRef] [Green Version]
- Magsipoc, E.; Zhao, Q.; Grasselli, G. 2D and 3D Roughness Characterization. Rock Mech. Rock Eng. 2020, 53, 1495–1519. [Google Scholar] [CrossRef]
- Sornette, D. Critical Phenomena in Natural Sciences; Springer: Berlin, Germany, 2004. [Google Scholar]
- Alava, M.J.; Nukala, P.K.; Zapperi, S. Statistical models of fracture. Adv. Phys. 2006, 55, 349–476. [Google Scholar] [CrossRef] [Green Version]
- Gjerden, K.S.; Stormo, A.; Hansen, A. Universality Classes in Constrained Crack Growth. Phys. Rev. Lett. 2013, 111, 135502. [Google Scholar] [CrossRef] [PubMed]
- Shekhawat, A.; Zapperi, S.; Sethna, J.P. From Damage Percolation to Crack Nucleation Through Finite Size Criticality. Phys. Rev. Lett. 2013, 110, 185505. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Aligholi, S. Evaluating Rock Physics–Fracture Mechanics Relationship by Quantifying Fracture Process Zone. Ph.D. Thesis, Monash University, Victoria, Australia, 2022. [Google Scholar] [CrossRef]
- Barenblatt, G.I. The mathematical theory of equilibrium cracks in brittle fracture. Adv. Appl. Mech. 1962, 7, 55–129. [Google Scholar]
- Aligholi, S.; Ponson, L.; Torabi, A.R.; Zhang, Q.B. A new methodology inspired from the theory of critical distances for determination of inherent tensile strength and fracture toughness of rock materials. Int. J. Rock Mech. Min. Sci. 2022, 152, 105073. [Google Scholar] [CrossRef]
- Barabasi, A.L.; Bourbonnais, R.; Jensen, M.; Kertész, J.; Vicsek, T.; Zhang, Y.C. Multifractality of growing surfaces. Phys. Rev. A 1992, 45, R6951. [Google Scholar] [CrossRef] [PubMed]
- Davis, A.; Marshak, A.; Wiscombe, W.; Cahalan, R. Multifractal characterizations of nonstationarity and intermittency in geophysical fields: Observed, retrieved, or simulated. J. Geophys. Res. Atmos. 1994, 99, 8055–8072. [Google Scholar] [CrossRef]
- Mazeran, P.; Odoni, L.; Loubet, J. Curvature radius analysis for scanning probe microscopy. Surf. Sci. 2005, 585, 25–37. [Google Scholar] [CrossRef]
- Vernede, S.; Ponson, L.; Bouchaud, J.P. Turbulent fracture surfaces: A footprint of damage percolation? Phys. Rev. Lett. 2015, 114, 215501. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Santucci, S.; Maloy, K.J.; Delaplace, A.; Mathiesen, J.; Hansen, A.; Bakke, J.O.H.; Schmittbuhl, J.; Vanel, L.; Ray, P. Statistics of fracture surfaces. Phys. Rev. E 2007, 75, 016104. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Barabasi, A.L.; Szepfalusy, P.; Vicsek, T. Multifractal spectra of multi-affine functions. Phys. A 1991, 178, 17. [Google Scholar] [CrossRef]
- Peng, C.K.; Havlin, S.; Stanley, H.E.; Goldberger, A.L. Quantification of scaling exponents and crossover phenomena in nonstationary heartbeat time series. Chaos 1995, 5, 82–87. [Google Scholar] [CrossRef] [PubMed]
- Bacry, E.; Delour, J.; Muzy, J.F. Multifractal random walk. Phys. Rev. E 2001, 64, 026103. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Flandrin, P. On the spectrum of fractional Brownian motions. IEEE Trans. Inf. Theory 1989, 35, 197–199. [Google Scholar] [CrossRef]
- Martin, W.; Flandrin, P. Wigner-Ville spectral analysis of nonstationary processes. IEEE Trans. Acoust. Speech Signal Process. 1985, 33, 1461–1470. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aligholi, S.; Khandelwal, M. Intermittency of Rock Fractured Surfaces: A Power Law. Water 2022, 14, 3662. https://doi.org/10.3390/w14223662
Aligholi S, Khandelwal M. Intermittency of Rock Fractured Surfaces: A Power Law. Water. 2022; 14(22):3662. https://doi.org/10.3390/w14223662
Chicago/Turabian StyleAligholi, Saeed, and Manoj Khandelwal. 2022. "Intermittency of Rock Fractured Surfaces: A Power Law" Water 14, no. 22: 3662. https://doi.org/10.3390/w14223662






