A Linear Programming Model for Operational Optimization of Agricultural Activity Considering a Hydroclimatic Forecast—Case Studies for Western Bahia, Brazil
Abstract
:1. Introduction
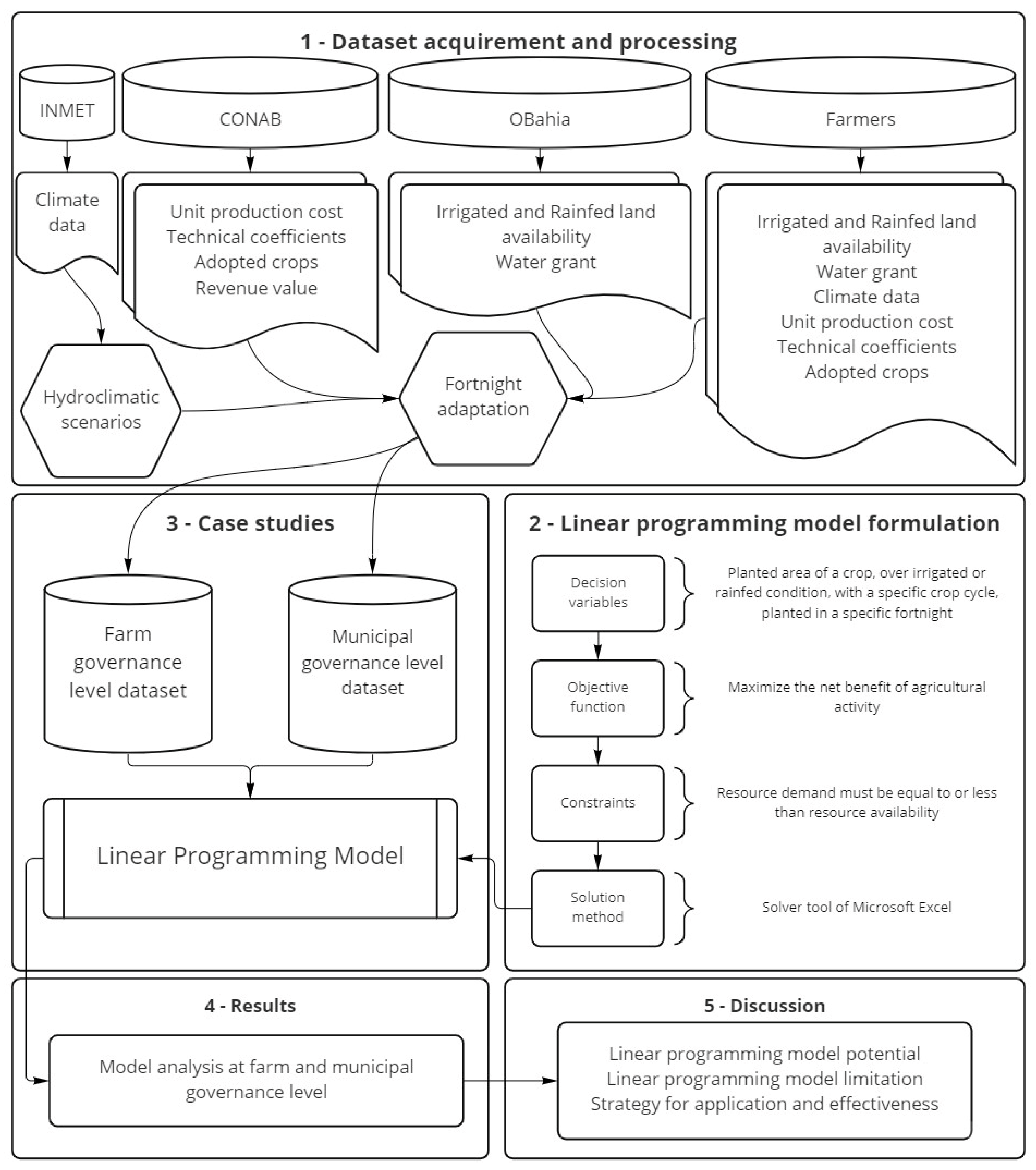
2. Materials and Methods
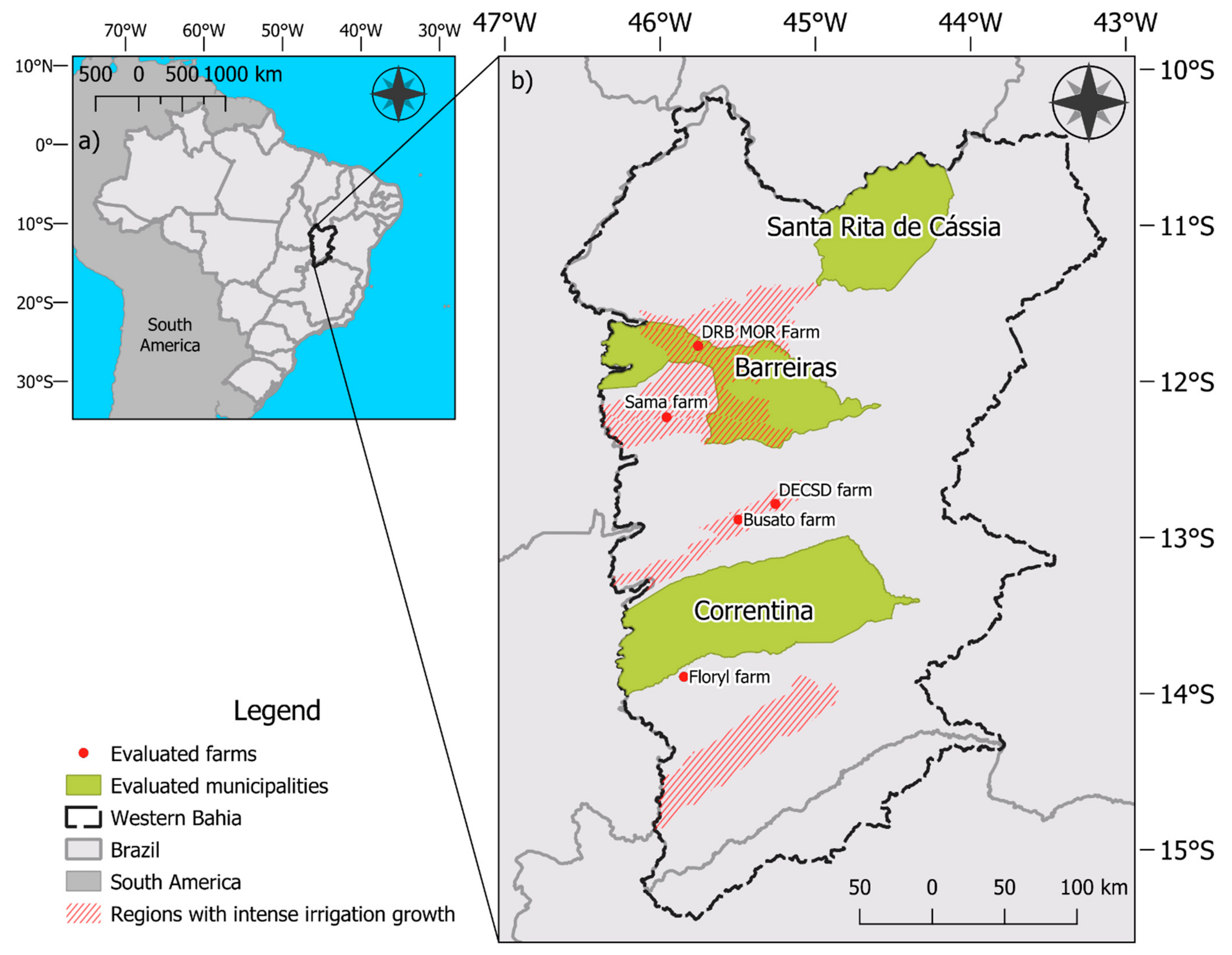
2.1. Region Description
2.2. Dataset Acquisition and Processing
2.3. LPM Formulation
2.3.1. Decision Variables
2.3.2. Objective Function
2.3.3. Constraints and Solution Method
3. Case Studies
3.1. Farms and Municipalities Characterization
3.2. Crop Characterization
3.3. Model’s Constraints Setup
4. Results
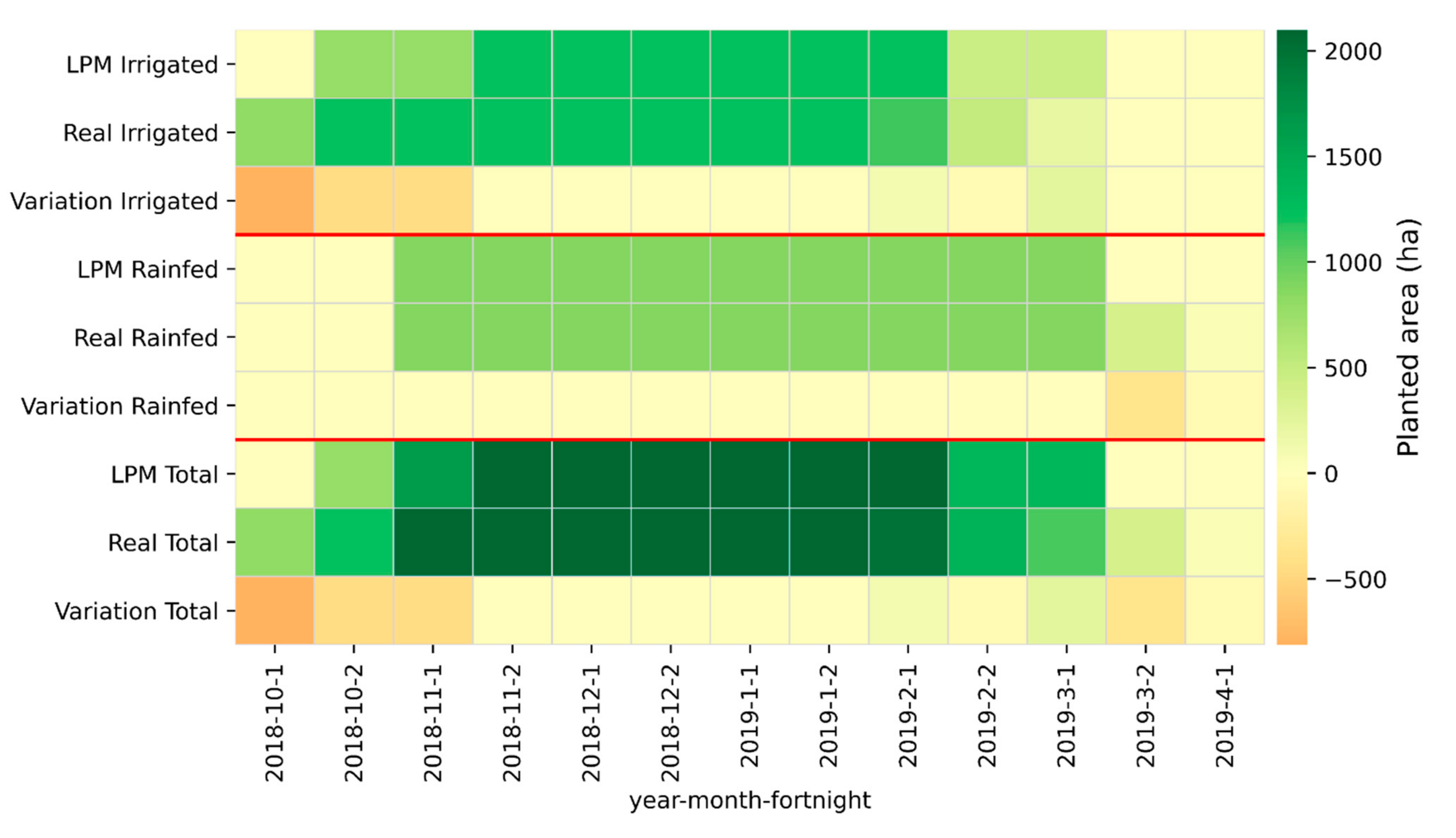
4.1. LPM Application at Farms
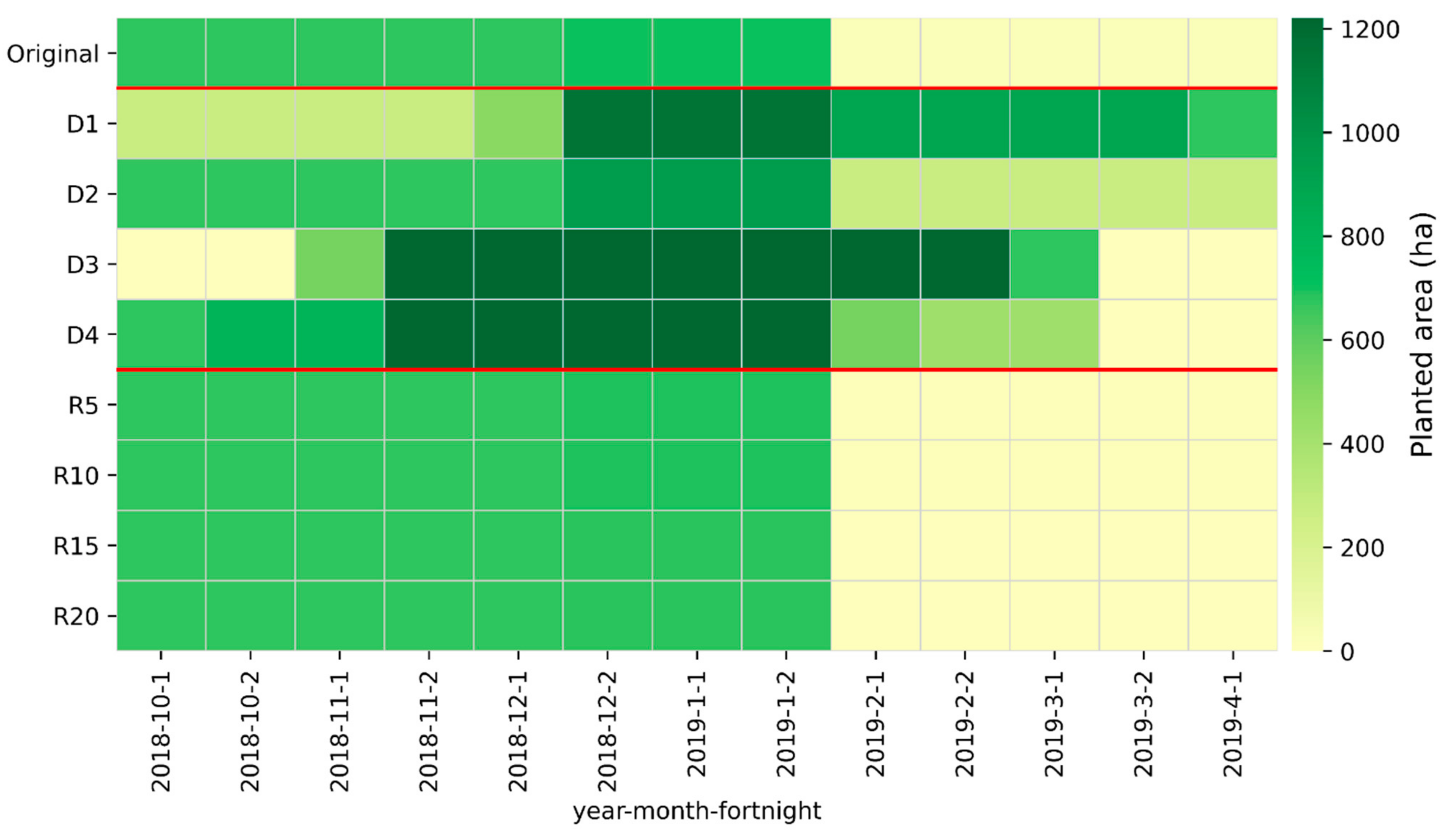
4.2. LPM Application at Municipalities
5. Discussion
Strategy for LPM Effectiveness
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- World Economic Forum. The Global Risks Report 2020; World Economic Forum: Geneva, Swizetzerland, 2020; ISBN 9782940631247. [Google Scholar]
- Department of Economic and Social Affairs of United Nations. World Population Prospects 2019; United Nations, Ed.; United Nations: New York, NY, USA, 2019; ISBN 9789211483161. [Google Scholar]
- IPCC. Summary for Policymakers. In Climate Change 2021: The Physical Science Basis. Contribution of Working Group I to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK, 2021. [Google Scholar]
- WWAP. The United Nations World Water Development Report 2016: Water and Jobs; UNESCO: Paris, France, 2016; ISBN 9789231001550. [Google Scholar]
- Pacific Institute Water Conflict Chronology. Available online: https://www.worldwater.org/conflict/map/ (accessed on 10 June 2022).
- Rawlins, J. Political economy of water reallocation in South Africa: Insights from the Western Cape water crisis. Water Secur. 2019, 6, 100029. [Google Scholar] [CrossRef]
- Muñoz, A.A.; Klock-Barría, K.; Alvarez-Garreton, C.; Aguilera-Betti, I.; González-Reyes, Á.; Lastra, J.A.; Chávez, R.O.; Barría, P.; Christie, D.; Rojas-Badilla, M.; et al. Water crisis in petorca basin, Chile: The combined effects of a mega-drought and water management. Water 2020, 12, 648. [Google Scholar] [CrossRef]
- Varisco, D. Pumping Yemen Dry: A History of Yemen’s Water Crisis. Hum. Ecol. 2019, 47, 317–329. [Google Scholar] [CrossRef]
- Shan, V.; Singh, S.K.; Haritash, A.K. Water Crisis in the Asian Countries: Status and Future Trends. In Resilience, Response, and Risk in Water Systems; Springer: Singapore, 2020; pp. 173–194. [Google Scholar] [CrossRef]
- Gilbert, N. How to avert a global water crisis. Nature 2010. [Google Scholar] [CrossRef]
- Dias, L.C.P.; Pimenta, F.M.; Santos, A.B.; Costa, M.H.; Ladle, R.J. Patterns of land use, extensification, and intensification of Brazilian agriculture. Glob. Chang. Biol. 2016, 22, 2887–2903. [Google Scholar] [CrossRef]
- AIBA. Dados e Pesquisa: Região Oeste. Available online: https://aiba.org.br/regiao-oeste/ (accessed on 25 January 2021).
- AIBA. Atlas do Oeste da Bahia; AIBA: Barreiras, Brazil, 2019. [Google Scholar]
- Pousa, R.; Costa, M.H.; Pimenta, F.M.; Fontes, V.C.; Castro, M. Climate change and intense irrigation growth in Western Bahia, Brazil: The urgent need for hydroclimatic monitoring. Water 2019, 11, 933. [Google Scholar] [CrossRef]
- Abrahão, G.M.; Costa, M.H. Evolution of rain and photoperiod limitations on the soybean growing season in Brazil: The rise (and possible fall) of double-cropping systems. Agric. For. Meteorol. 2018, 256, 32–45. [Google Scholar] [CrossRef]
- Mantovani, E.C.; da Silva Júnior, A.G.; Costa, M.H.; Marques, E.A.G.; da Silva Júnior, G.C.; Pruski, F.F. Relatório Técnico Final: Estudo do Potencial Hídrico da Região Oeste da Bahia: Quantificação e Monitoramento da Disponibilidade dos Recursos do Aquífero Urucuia e Superficiais nas Bacias dos rios Grande, Corrente e Carinhanha; UFV: Viçosa, Brazil, 2019. [Google Scholar]
- Pimenta, F.M.; Silva, M.L.; Castro, M.; Fontes, V.C.; Costa, M.H. OBahia—Western Bahia Map Server. 2020. Available online: https://www.escavador.com/sobre/7173300/fernando-martins-pimenta (accessed on 12 May 2022).
- Zhang, C.; Guo, P. An inexact CVaR two-stage mixed-integer linear programming approach for agricultural water management under uncertainty considering ecological water requirement. Ecol. Indic. 2018, 92, 342–353. [Google Scholar] [CrossRef]
- Ma, T.; Wang, J.; Liu, Y.; Sun, H.; Gui, D.; Xue, J. A mixed integer linear programming method for optimizing layout of irrigated pumping well in Oasis. Water 2019, 11, 1185. [Google Scholar] [CrossRef]
- Sheibani, H.; Shourian, M. Determining optimum reliability for supplying agricultural demand downstream of a reservoir using an explicit method with an economic objective function. Water Resour. Econ. 2019, 26, 100131. [Google Scholar] [CrossRef]
- Aljanabi, A.A.; Mays, L.W.; Fox, P. Optimization model for agricultural reclaimed water allocation using mixed-integer nonlinear programming. Water 2018, 10, 1291. [Google Scholar] [CrossRef]
- Chen, S.; Xu, J.; Li, Q.; Tan, X.; Nong, X. A copula-based interval-bistochastic programming method for regional water allocation under uncertainty. Agric. Water Manag. 2019, 217, 154–164. [Google Scholar] [CrossRef]
- Freire-González, J.; Decker, C.A.; Hall, J.W. A linear programming approach towater allocation during a drought. Water 2018, 10, 363. [Google Scholar] [CrossRef]
- Fu, J.; Zhong, P.A.; Zhu, F.; Chen, J.; Wu, Y.N.; Xu, B. Water resources allocation in transboundary river based on asymmetric Nash-Harsanyi Leader-Follower game model. Water 2018, 10, 270. [Google Scholar] [CrossRef]
- Fu, Q.; Li, L.; Li, M.; Li, T.; Liu, D.; Cui, S. A simulation-based linear fractional programming model for adaptable water allocation planning in the main stream of the Songhua River basin, China. Water 2018, 10, 627. [Google Scholar] [CrossRef]
- Jin, L.; Fu, H.; Kim, Y.; Long, J.; Huang, G. A Bi-objective pseudo-interval T2 linear programming approach and its application towater resources management under uncertainty. Water 2018, 10, 1545. [Google Scholar] [CrossRef]
- Veintimilla-Reyes, J.; De Meyer, A.; Cattrysse, D.; Tacuri, E.; Vanegas, P.; Cisneros, F.; Van Orshoven, J. MILP for optimizing water allocation and reservoir location: A case study for the Machángara river basin, Ecuador. Water 2019, 11, 1011. [Google Scholar] [CrossRef]
- Bekchanov, M.; Ringler, C.; Bhaduri, A.; Jeuland, M. Optimizing irrigation efficiency improvements in the Aral Sea Basin. Water Resour. Econ. 2016, 13, 30–45. [Google Scholar] [CrossRef]
- Zhao, J.; Li, M.; Guo, P.; Zhang, C.; Tan, Q. Agricultural water productivity oriented water resources allocation based on the coordination of multiple factors. Water 2017, 9, 490. [Google Scholar] [CrossRef]
- Suo, M.; Wu, P.; Zhou, B. An integrated method for interval multi-objective planning of a water resource system in the eastern part of Handan. Water 2017, 9, 528. [Google Scholar] [CrossRef]
- Li, M.; Fu, Q.; Singh, V.P.; Liu, D. An interval multi-objective programming model for irrigation water allocation under uncertainty. Agric. Water Manag. 2018, 196, 24–36. [Google Scholar] [CrossRef]
- Li, M.; Fu, Q.; Singh, V.P.; Liu, D.; Li, T.; Zhou, Y. Managing agricultural water and land resources with tradeoff between economic, environmental, and social considerations: A multi-objective non-linear optimization model under uncertainty. Agric. Syst. 2020, 178, 102685. [Google Scholar] [CrossRef]
- Zhang, F.; Guo, S.; Liu, X.; Wang, Y.; Engel, B.A.; Guo, P. Towards sustainable water management in an arid agricultural region: A multi-level multi-objective stochastic approach. Agric. Syst. 2020, 182, 102848. [Google Scholar] [CrossRef]
- Niu, G.; Zheng, Y.; Han, F.; Qin, H. The nexus of water, ecosystems and agriculture in arid areas: A multiobjective optimization study on system efficiencies. Agric. Water Manag. 2019, 223, 105697. [Google Scholar] [CrossRef]
- IBGE. Produção Agrícola Municipal. Available online: https://sidra.ibge.gov.br/tabela/5457 (accessed on 9 June 2022).
- Pimenta, F.M.; Speroto, A.T.; Costa, M.H.; Dionizio, E.A. Historical changes in land use and suitability for future agriculture expansion in Western Bahia, Brazil. Remote Sens. 2021, 13, 1088. [Google Scholar] [CrossRef]
- MAPA INMET. Available online: https://portal.inmet.gov.br/ (accessed on 19 August 2020).
- CONAB Série Histórica das Safras. Available online: https://www.conab.gov.br/info-agro/safras/serie-historica-das-safras (accessed on 25 January 2021).
- CONAB Preços Agrícolas, da Sociobio e da Pesca. Available online: http://sisdep.conab.gov.br/precosiagroweb/ (accessed on 20 January 2021).
- Vanderbei, R.J. Linear Programming. In International Series in Operations Research & Management Science, 4th ed.; Hillier, F.S., Ed.; Springer: Berlin/Heidelberg, Germany, 2014; Volume 196, ISBN 9781461476290. [Google Scholar]
- Luenberger, D.G.; Ye, Y. Linear and Nonlinear Programming, 4th ed.; Price, C.C., Zhu, J., Hillier, F.S., Eds.; Springer: Cham, Switzerland, 2016; Volume 228, ISBN 978-3-319-18841-6. [Google Scholar]
- CONAB. Calendário de Plantio e Colheita de Grãos no Brasil 2019; CONAB: Brasilia, Brazil, 2019. [Google Scholar]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop Evapotranspiration (Guidelines for Computing Crop Water Requirements); FAO: Rome, Italy, 1998; Volume 300, p. D05109. [Google Scholar]
- Santos, I.S.; Mantovani, E.C.; Venancio, L.P.; da Cunha, F.F.; Aleman, C.C. Controlled water stress in agricultural crops in Brazilian Cerrado. Biosci. J. 2020, 36, 886–895. [Google Scholar] [CrossRef]
- Bullock, D.G. Crop rotation. CRC Crit. Rev. Plant Sci. 1992, 11, 309–326. [Google Scholar] [CrossRef]
- G1 Grupo Invade Fazendas e Incendeia Galpão em Protesto no Oeste da Bahia. 2017. Available online: https://g1.globo.com/bahia/noticia/grupo-invade-fazendas-e-incendeia-galpao-em-protesto-no-oeste-da-bahia.ghtml (accessed on 7 July 2020).
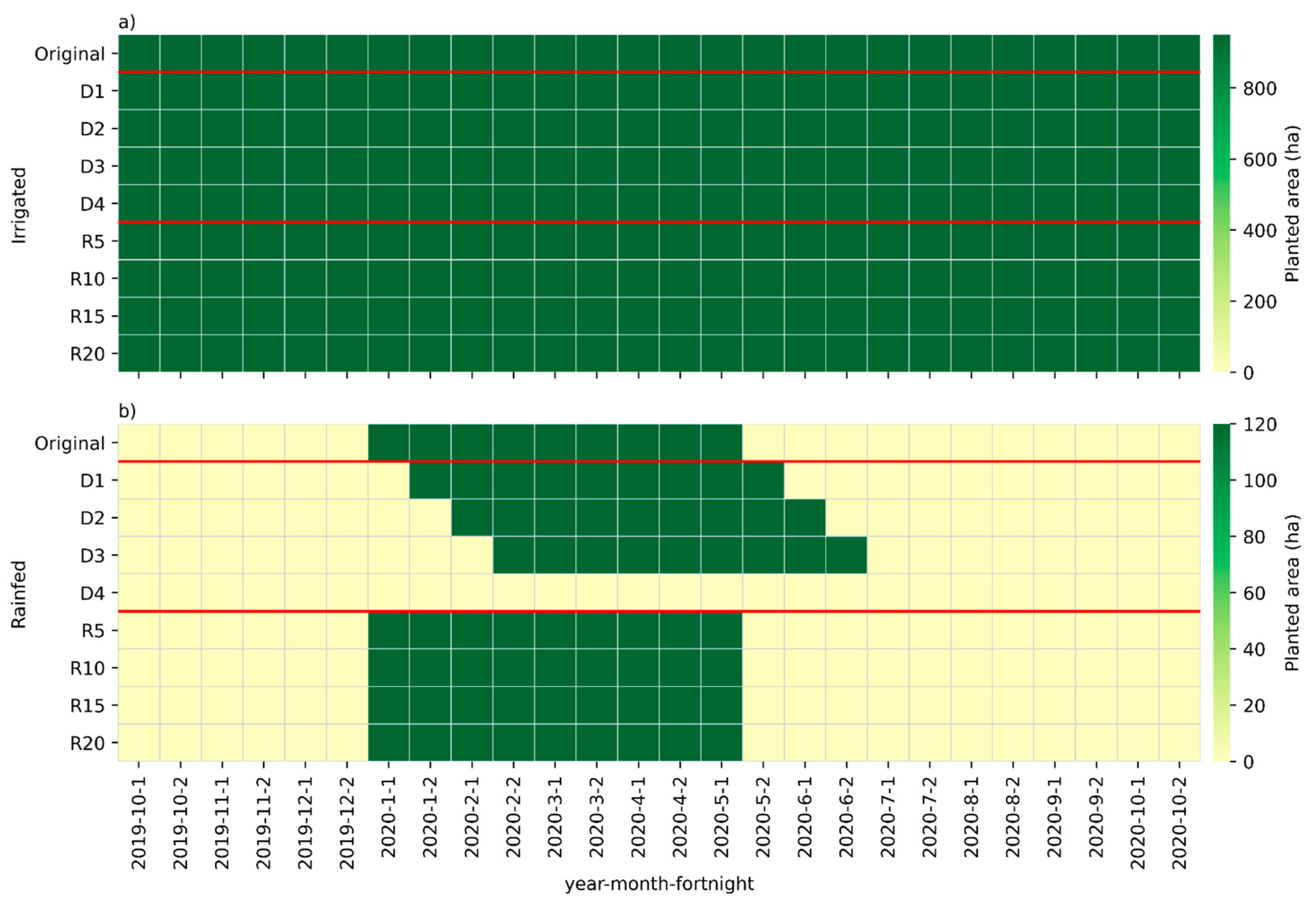
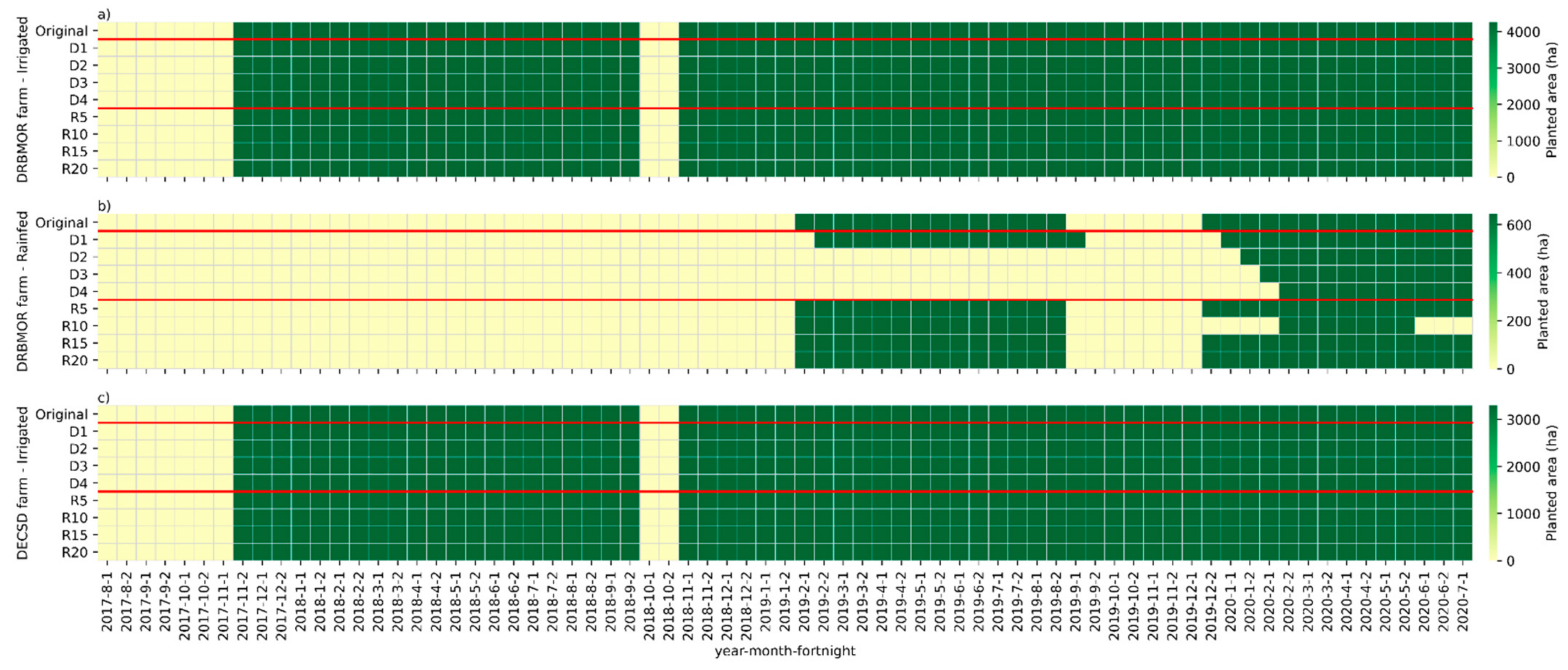
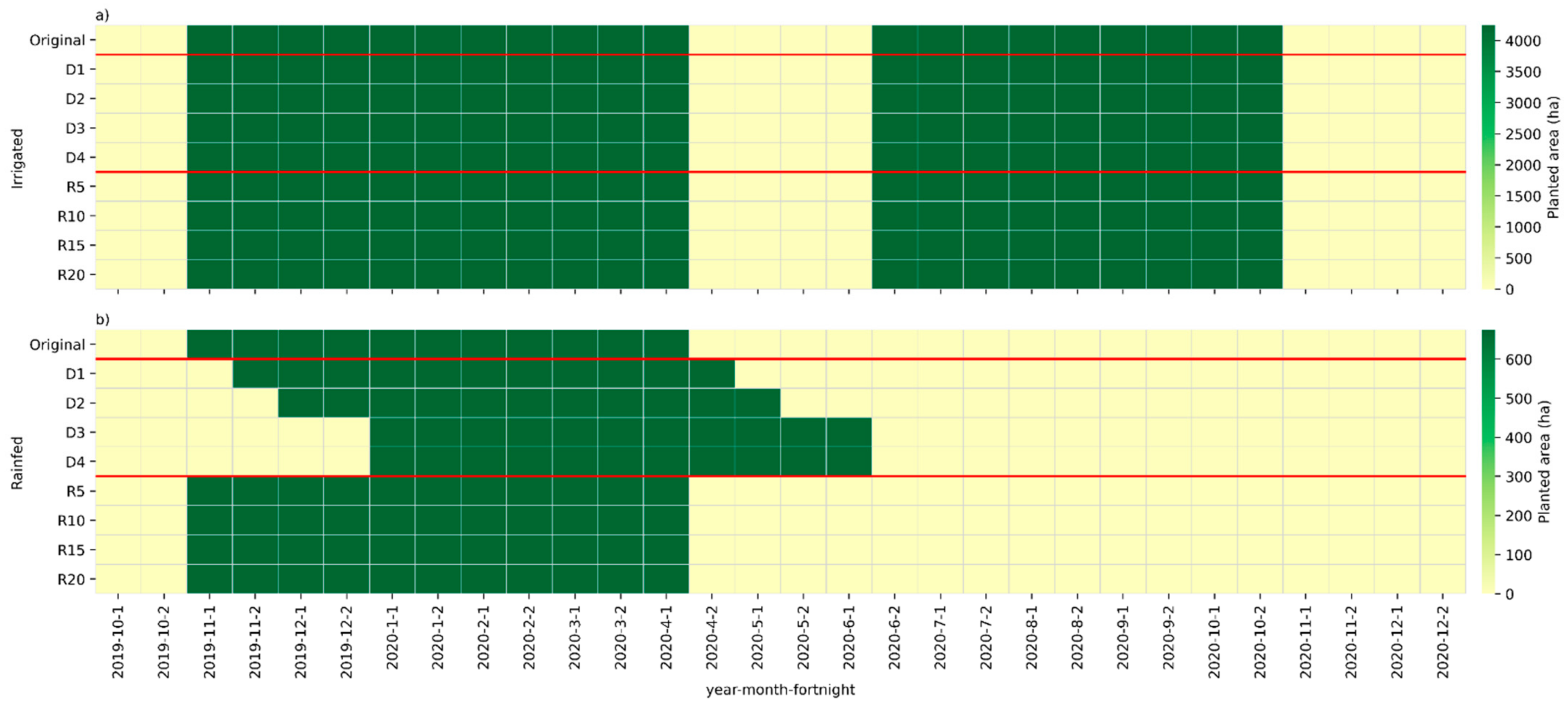
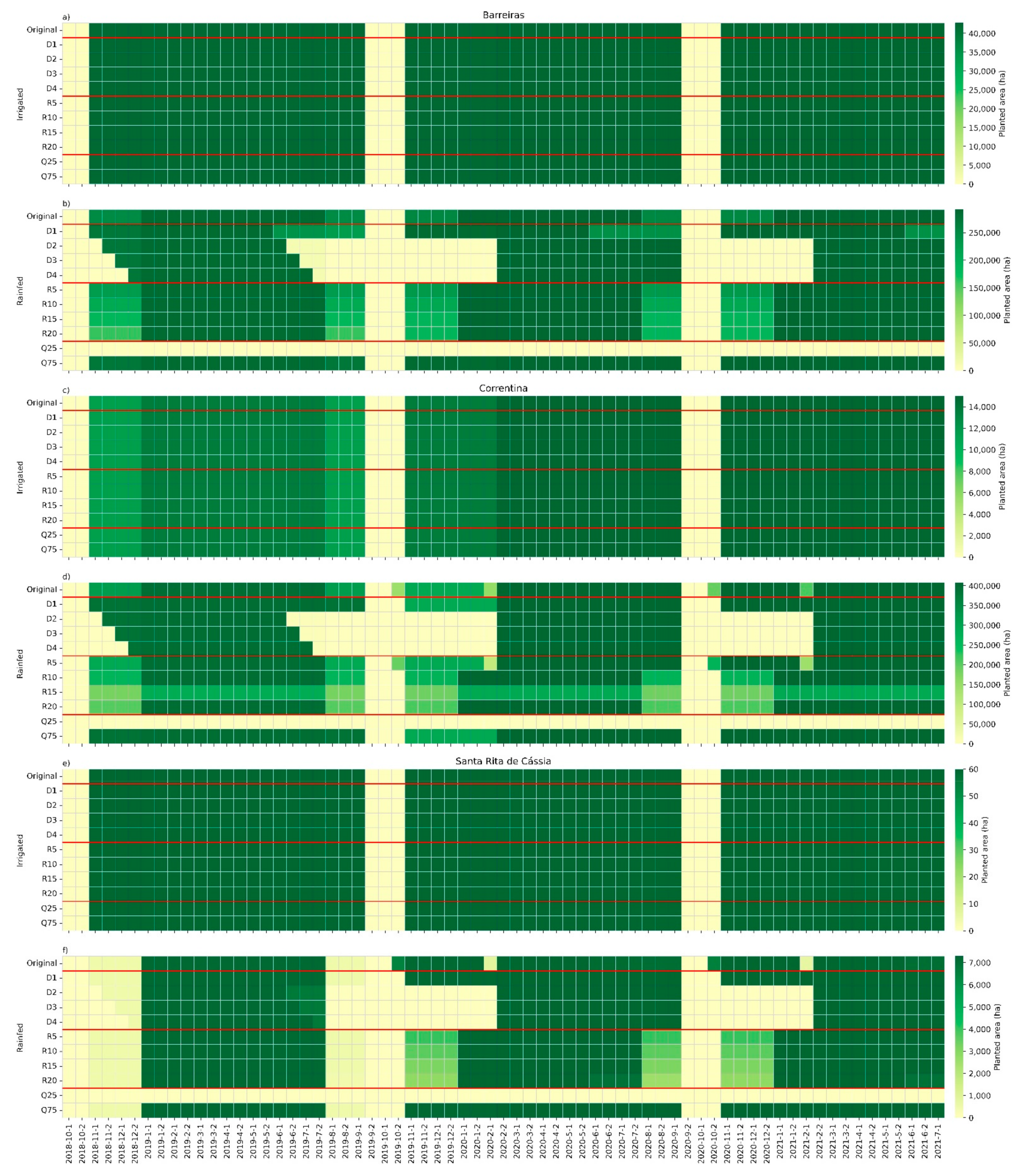
| Farm or Municipality | Irrigated Area | Rainfed Area | Water Grant | Evaluated Crop | Season | Labor Availability | Tractor Availability | Truck Availability | Sprayer Availability | Harvester Availability |
|---|---|---|---|---|---|---|---|---|---|---|
| (Hectares) | (Hectares) | (m³ day−1) | (h day−1) | (h day−1) | (h day−1) | (h day−1) | (h day−1) | |||
| Sama f | 1221.10 | 878.50 | 39,297.50 | Soybean | 2018/19 | 160 | 16 | 16 | 32 | 16 |
| Floryl f | 950.00 | 120.00 | 68,437.00 | Maize 1−2; Soybean | 2019/20 | Not applicable | ||||
| DRB MOR f | 4267.00 | 646.00 | 101,760.00 | Cotton; Bean 1−2; Maize 1−2; Soybean; Wheat | 2017 aw; 2017 ss; 2018 aw; 2018 ss; 2019 aw; 2019 ss | |||||
| DECDS f | 3299.00 | 0.00 | 156,552.00 | |||||||
| Busato f | 4246.80 | 676.00 | 23,240.00 | Cotton; Maize 1−2; Soybean | 2019/20 | |||||
| Barreiras m | 42,760.00 | 291,948.00 | 4,586,256.52 | Cotton; Bean 1−2; Maize 1−2; Soybean | 2018 ss; 2019 aw; 2019 ss; 2020 aw; 2020 ss; 2021 aw | |||||
| Correntina m | 15,008.00 | 408,022.00 | 2,444,307.23 | |||||||
| Santa Rita de Cássia m | 60.00 | 7293.00 | 44,000.00 | |||||||
| Farm or Municipality | Minimum ETo | Maximum ETo | Minimum Rainfall | Maximum Rainfall |
|---|---|---|---|---|
| (mm fortnight−1) | (mm fortnight−1) | (mm fortnight−1) | (mm fortnight−1) | |
| Sama f | 45.2 | 96.9 | 0.0 | 172.8 |
| Floryl f | 42.7 | 86.7 | 0.0 | 142.8 |
| DRB MOR f | 46.2 | 107.5 | 0.0 | 142.8 |
| DECDS f | 43.1 | 89.9 | 0.0 | 232.2 |
| Busato f | 41.1 | 94.7 | 0.0 | 168.8 |
| Barreiras m | 54.7 | 88.6 | 0.2 | 103.7 |
| Correntina m | 54.5 | 84.8 | 0.2 | 108.7 |
| Santa Rita de Cássia m | 59.0 | 91.6 | 0.0 | 101.5 |
| Crop | Cycle Type | Cycle Duration | Initial Kc | Average Kc | Final Kc | Kr [44] | Range Sowing Time |
|---|---|---|---|---|---|---|---|
| (Fortnight, or 15 Days) | (Fortnight–Month) [42] | ||||||
| Soybean | short | 8 | 0.60 | 0.70 | 0.80 | 0.80 | 1–10 to 2–02 |
| average | 9 | ||||||
| long | 10 | ||||||
| Maize 1st season | average | 9 | 0.65 | 1.00 | 0.60 | 0.88 | 1–10 to 2–02 |
| long | 12 | 0.60 | 0.50 | ||||
| Maize 2nd Season | average | 9 | 0.65 | 1.00 | 0.60 | 0.88 | 1–05 to 2–06 |
| long | 12 | 0.60 | 0.50 | ||||
| Cotton | long | 14 | 0.50 | 0.90 | 0.38 | 0.80 | 1–11 to 2–02 |
| Bean 1st season | average | 7 | 0.70 | 1.20 | 0.60 | 0.87 | 1–10 to 2–02 |
| Bean 2nd season | average | 7 | 0.70 | 1.20 | 0.60 | 0.87 | 1–04 to 2–06 |
| Wheat | average | 8 | 0.70 | 1.20 | 0.40 | 0.85 | 1–08 to 2–09 |
| Analysis | Farms | Municipalities | ||||||
|---|---|---|---|---|---|---|---|---|
| Sama | Floryl | DRB MOR | DECSD | Busato | Barreiras | Correntina | Santa Rita de Cássia | |
| Original | Ia; Ra; CwdI | - | - | - | - | Ia; Ra; CwdI; CwdR | Ia; Ra; CwdI; CwdR | Ia; Ra; CwdI; CwdR |
| Irrigated original | Ia; CwdI; L; M | Ia; CwdI | Ia; CwdI | Ia; CwdI | Ia; CwdI | Ia; CwdI | Ia; CwdI | Ia; CwdI |
| Irrigated rain delay | ||||||||
| Irrigated rain reduction | ||||||||
| Rainfed original | Ra; CwdR; L; M | Ra; CwdR | Ra; CwdR | - | Ra; CwdR | Ra; CwdR | Ra; CwdR | Ra; CwdR |
| Rainfed rain delay | ||||||||
| Rainfed rain reduction | ||||||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Boninsenha, I.; Mantovani, E.C.; Costa, M.H.; da Silva Júnior, A.G. A Linear Programming Model for Operational Optimization of Agricultural Activity Considering a Hydroclimatic Forecast—Case Studies for Western Bahia, Brazil. Water 2022, 14, 3625. https://doi.org/10.3390/w14223625
Boninsenha I, Mantovani EC, Costa MH, da Silva Júnior AG. A Linear Programming Model for Operational Optimization of Agricultural Activity Considering a Hydroclimatic Forecast—Case Studies for Western Bahia, Brazil. Water. 2022; 14(22):3625. https://doi.org/10.3390/w14223625
Chicago/Turabian StyleBoninsenha, Igor, Everardo Chartuni Mantovani, Marcos Heil Costa, and Aziz Galvão da Silva Júnior. 2022. "A Linear Programming Model for Operational Optimization of Agricultural Activity Considering a Hydroclimatic Forecast—Case Studies for Western Bahia, Brazil" Water 14, no. 22: 3625. https://doi.org/10.3390/w14223625








