Performance Analysis of an Eductor-Based Membrane Distillation Unit
Abstract
:1. Introduction
2. Technology and Mechanism Description
2.1. Eductor
2.2. Mechanism of Membrane Distillation (MD)
2.2.1. Heat Transfer
2.2.2. Mass Transfer Mechanism
3. Eductor-Based Membrane Distillation
3.1. Concept Discussion
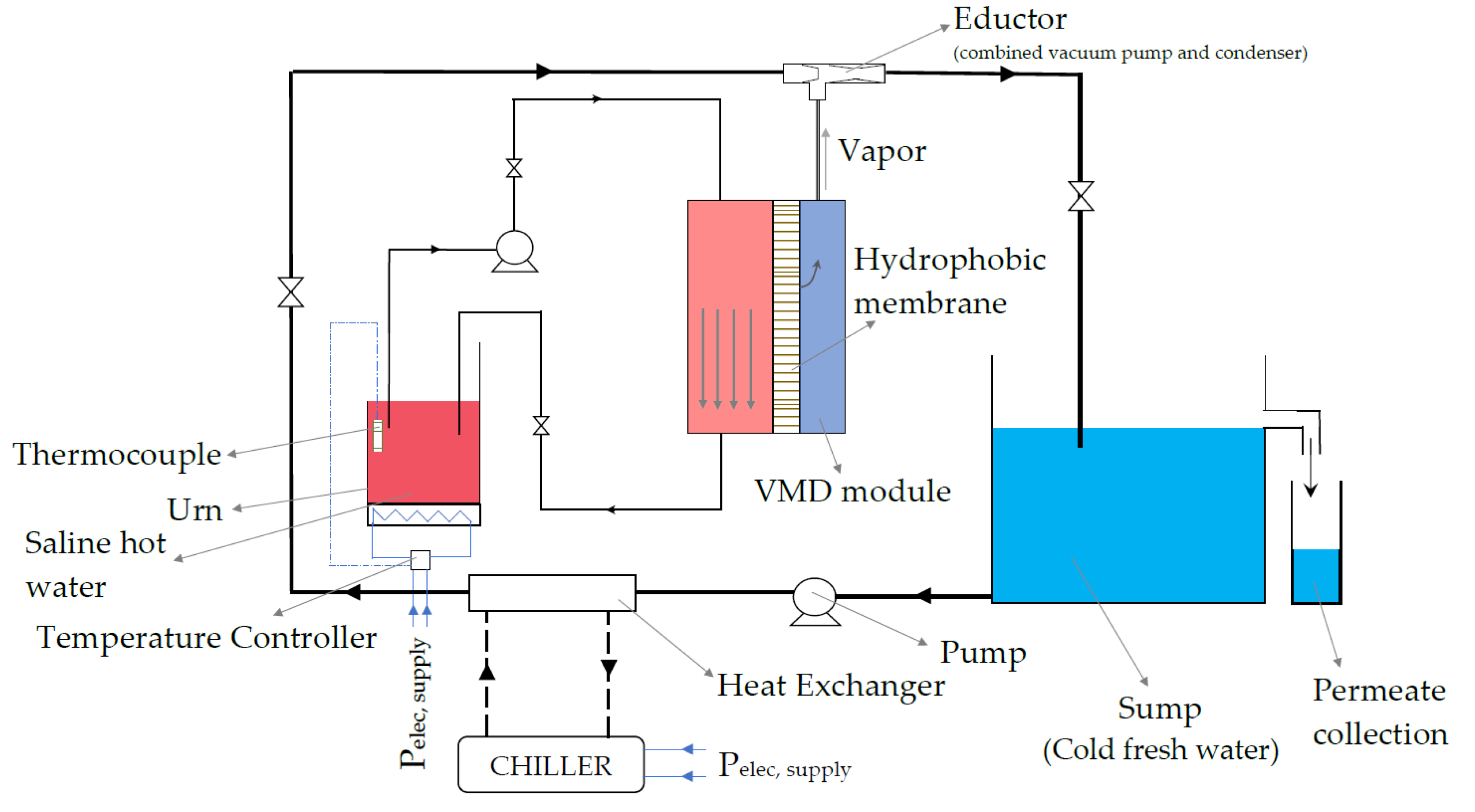
3.2. Experimental Set-Up Description
4. Results and Discussion
4.1. Capacity Assessment of the Eductor
4.2. Performance of Desalination Module
4.2.1. Impact of Feed Temperature
4.2.2. Impact of Feedwater Flow Rate
4.3. Performance of the Eductor
5. Practicality of Modified Eductor Based VMD (E-MD)
6. Sensitivity Analysis
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Boretti, A.; Rosa, L. Reassessing the projections of the World Water Development Report. NPJ Clean Water 2019, 1–6. [Google Scholar] [CrossRef] [Green Version]
- Darre, N.C.; Toor, G.S. Desalination of Water: A Review. Curr. Pollut. Rep. 2018, 4, 104–111. [Google Scholar] [CrossRef]
- Ibrahim, A.G.; Rashad, A.M.; Dincer, I. Exergoeconomic analysis for cost optimization of a solar distillation system. Sol. Energy 2017, 151, 22–32. [Google Scholar] [CrossRef]
- El-Dessouky, H.; Ettouney, H. Introduction. In Fundamentals of Salt-Water Desalination; Elsevier Science B.V.: Amsterdam, The Netherlands, 2002. [Google Scholar]
- Tal, A. The Desalination Debate—Lessons Learned Thus Far. Environ. Sci. Policy Sustain. Dev. 2011, 53, 34–48. [Google Scholar] [CrossRef]
- Curto, D.; Franzitta, V.; Guercio, A. A review of the Water Desalination Technologies. Appl. Sci. 2021, 11, 670. [Google Scholar] [CrossRef]
- Alkaisi, A.; Mossad, R.; Barforoush, A.-S. A Review of the Water Desalination Systems Integrated with Renewable Energy. Energy Procedia 2017, 110, 268–274. [Google Scholar] [CrossRef]
- Ma, Q.; Lu, H. Wind energy technologies integrated with desalination systems: Review and state-of-the-art. Desalination 2011, 277, 274–280. [Google Scholar] [CrossRef]
- Altmann, T.; Das, R. Process improvement of sea water reverse osmosis (SWRO) and subsequent decarbonization. Desalination 2021, 499, 114791. [Google Scholar] [CrossRef]
- Sideman, S.; Moalem-Maron, D. Direct contact condensation. Adv. Heat Transf. 1982, 15, 227–281. [Google Scholar]
- Zhang, Z.; Chong, D.; Yan, J. Modeling and experimental investigation on water-driven steam injector for waste heat recovery. Appl. Therm. Eng. 2012, 40, 189–197. [Google Scholar] [CrossRef]
- Han, Y.; Wang, X.; Yuen, A.C.Y.; Li, A.; Guo, L.; Yeoh, G.H.; Tu, J. Characterization of choking flow behaviors inside steam ejectors based on the ejector refrigeration system. Int. J. Refrig. 2020, 113, 29307. [Google Scholar] [CrossRef]
- Camacho, M.L.; Dumee, L.; Zhang, J.; Li, J.; Duke, M.; Gomez, J.; Gray, S. Advances in membrane distillation for water de-salination and purification applications. Water 2013, 5, 94–196. [Google Scholar] [CrossRef] [Green Version]
- Manawi, Y.M.; Kharaisheh, A.K.; Fard, A.K.; Benyahia, F.; Adham, S. Effect of operatonal parameters on distillate flux in direct contact membrane distillation (DCMD): Comparison between experimental and model predicted performance. Desalination 2014, 336 (Suppl. C), 110–120. [Google Scholar] [CrossRef]
- EI-Bourawi, M.S.; Ding, A.; Ma, R.; Khayet, M. A framework for better understanding membrane distillation seperation process. J. Membr. Sci. 2006, 285, 4–29. [Google Scholar] [CrossRef]
- Koo, J.; Han, J.; Sohn, J.; Lee, S.; Hwang, T.-M. Experimental comparison of direct contact membrane distillation (DCMD) with vacuum membrane distillation (VMD). Desalination Water Treat. 2013, 51, 6299–6309. [Google Scholar] [CrossRef]
- Khayet, M.; Matsuura, T. Membrane Distillation: Principles and Applications; Elsevier: Amsterdam, The Netherlands, 2011. [Google Scholar]
- Andrjesdóttir, Ó.; Ong, C.L.; Nabavi, M.; Paredes, S.; Khalil, A.S.G.; Michel, B.; Poulikakos, D. An experimentally optimized model for heat and mass transfer in direct contact membrane distillation. Int. J. Heat Mass Transf. 2013, 66, 855–867. [Google Scholar] [CrossRef]
- Qtaishat, M.; Matsuura, T.; Kruczek, B.; Khayet, M. Heat and mass transfer analysis in direct contact membrane distillation. Desalination 2008, 219, 272–292. [Google Scholar] [CrossRef]
- Lawson, K.W.; Lloyd, D.R. Membrane distillation. J. Membr. Sci. 1997, 124, 1–25. [Google Scholar] [CrossRef]
- Garcia-Payo, M.C.; Izquierdo-Gil, M.A. Thermal resistance technique for measuring the thermal conductivity of thin microporous membranes. J. Phys. D Appl. Phys. 2004, 37, 3008–3016. [Google Scholar] [CrossRef]
- Schofield, R.W.; Fane, A.G.; Fell, C.J. Heat and mass transfer in membrane distillation. J. Membr. Sci. 1987, 33, 299–313. [Google Scholar] [CrossRef]
- Nayar, K.G.; Sharqawy, M.H.; Banchik, L.D.; Lienhard, J.H.V. Thermophysical properties of seawater: A review and new correlations that include pressure dependence. Desalination 2016, 390, 1–24. [Google Scholar] [CrossRef]
- Ve, Q.L.; Koirala, R.; Bawahab, M.; Faqeha, H.; Do, M.C.; Nguyen, Q.L.; Date, A.; Akbarzedeh, A. Experimental investigation of the effect of the spacer and operating conditions on mass transfer in direct contact membrane distillation. Desalination 2021, 500, 114. [Google Scholar] [CrossRef]
- Aas, G.A.; Mea, A.; Ha, S.A.; Masa, A.M.A. Effect of different salts on mass transfer coefficient and inorganic fouling of TFC membranes. J. Membr. Sci. Technol. 2017, 7, 100175. [Google Scholar] [CrossRef]
- Boudinar, M.B.; Hanbury, W.T.; Avlonitis, S. Numerical simulation and optimisation of spiral-wound modules. Desalination 1992, 86, 273–290. [Google Scholar] [CrossRef]
- Mengual, J.I.; Khayet, M.; Godino, M.P. Heat and mass transfer in vacuum membrane distillation. Int. J. Heat Mass Transf. 2004, 47, 865–875. [Google Scholar] [CrossRef]
- Kim, Y.-D.; Kim, Y.-B.; Woo, S.-Y. Detailed modeling and simulation of an out-in configuration vacuum membrane distillation process. Water Res. 2018, 132, 23–33. [Google Scholar] [CrossRef]
- Bhuyan, D. Direct and indirect contact film-wise as well as dropwise condensation of water vapour with and without non-condensable gas-A review. Int. Res. J. Eng. Technol. 2020, 7, 10. [Google Scholar]













| Mass Transfer Mechanism | MD Coefficient (Bm) | Eq No. | Condition |
|---|---|---|---|
| Molecular diffusion | (25) | Kn < 0.01 | |
| Combined Knudsen-molecular diffusion | (26) | 0.01 < Kn < 1 | |
| Knudsen flow model | (27) | Kn > 1 | |
| Mass Transfer Mechanism | MD Coefficient (Bm) | Eq No. | Condition |
|---|---|---|---|
| Viscous flow model | (28) | Kn < 0.01 | |
| Combined Knudsen-viscous mechanism | (29) | 0.01 < Kn < 10 | |
| Knudsen flow model | (30) | Kn > 10 |
| Particular | Description | Units | Symbols |
|---|---|---|---|
| Membrane Module | |||
| Width | 2 | mm | W |
| Length | 180 | mm | L |
| Breadth | 180 | mm | B |
| Membrane | |||
| Material | PTFE | ||
| Pore size | 0.22 | µm | dp |
| Thickness | 190–240 | µm | δt |
| Porosity | 80 | % | |
| Eductor | |||
| Inlet diameter | 12 | mm | Ded,in |
| Outlet diameter | 12 | mm | Ded,out |
| Suction diameter | 12 | mm | Ded,suc |
| Eductor length | 114 | mm | Led |
| Particular | Description | Units | Symbols |
|---|---|---|---|
| Membrane Module operating parameter | |||
| Feed flow | 5.02 | LPM | Qf,in |
| Feed temperature | 50, 60, 70 & 80 (+/−2) | °C | Tf |
| Eductor operating parameter | |||
| Eductor inflow | 4.85 | LPM | Qe,in |
| Eductor inlet Temperature | 15 | °C | Te,in |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Koirala, R.; Ve, Q.L.; Rupakheti, E.; Inthavong, K.; Date, A. Performance Analysis of an Eductor-Based Membrane Distillation Unit. Water 2022, 14, 3624. https://doi.org/10.3390/w14223624
Koirala R, Ve QL, Rupakheti E, Inthavong K, Date A. Performance Analysis of an Eductor-Based Membrane Distillation Unit. Water. 2022; 14(22):3624. https://doi.org/10.3390/w14223624
Chicago/Turabian StyleKoirala, Ravi, Quoc Linh Ve, Eliza Rupakheti, Kiao Inthavong, and Abhijit Date. 2022. "Performance Analysis of an Eductor-Based Membrane Distillation Unit" Water 14, no. 22: 3624. https://doi.org/10.3390/w14223624
APA StyleKoirala, R., Ve, Q. L., Rupakheti, E., Inthavong, K., & Date, A. (2022). Performance Analysis of an Eductor-Based Membrane Distillation Unit. Water, 14(22), 3624. https://doi.org/10.3390/w14223624








