Effects of Nonlinearity on Velocity, Acceleration and Pressure Gradient in Free-Stream Zone of Solitary Wave over Horizontal Bed—An Experimental Study
Abstract
:1. Introduction
2. Experimental Set-Up and Instrumentation
2.1. Wave Flume and Coordinate System
2.2. Wave Gauge, HSPIV, and Flow Observation
2.3. Experimental Conditions
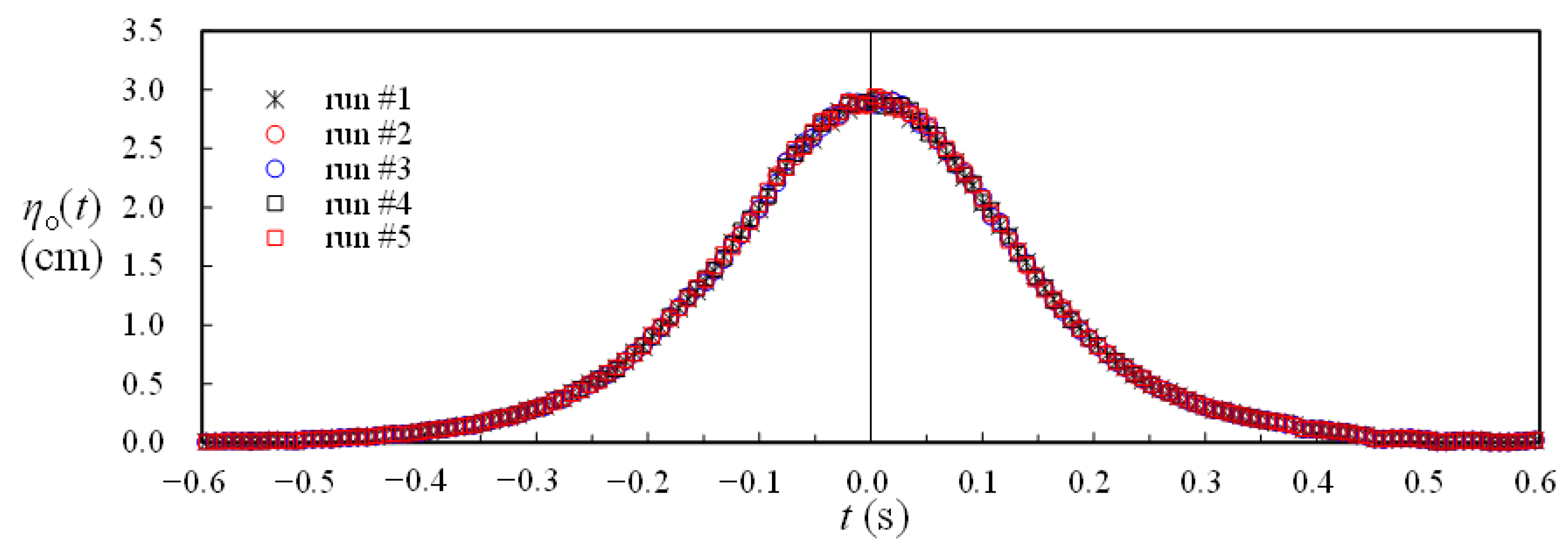
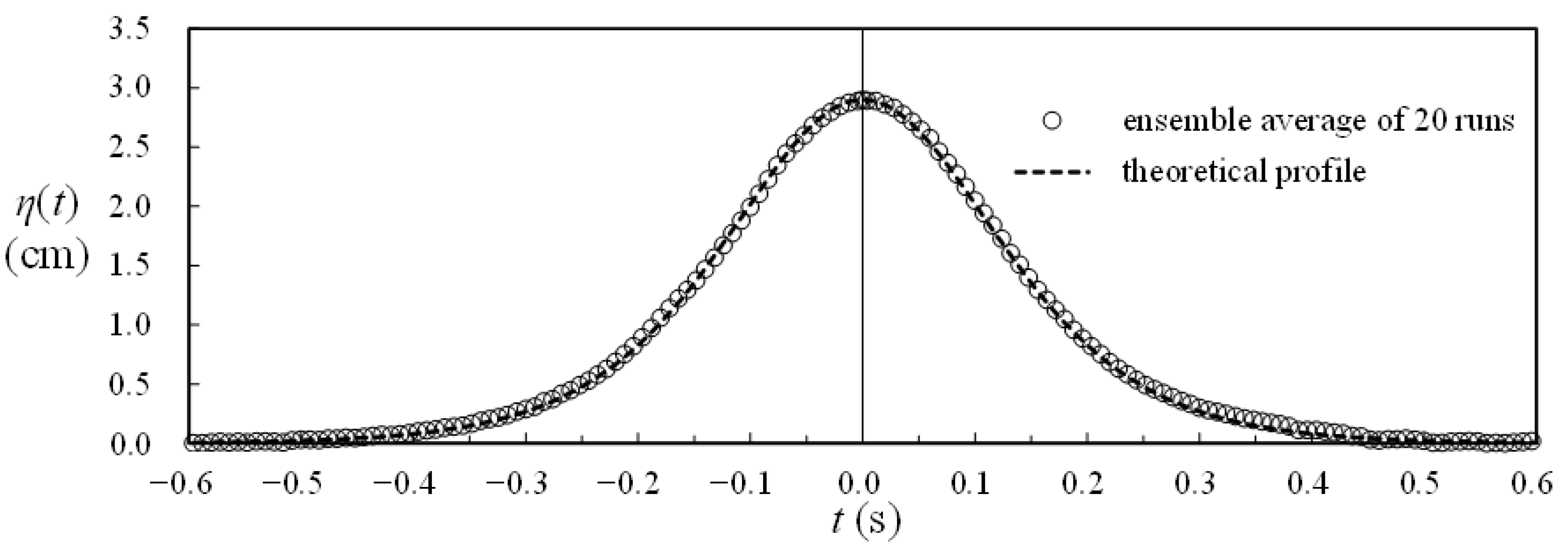
3. Validation Tests
4. Results and Discussion
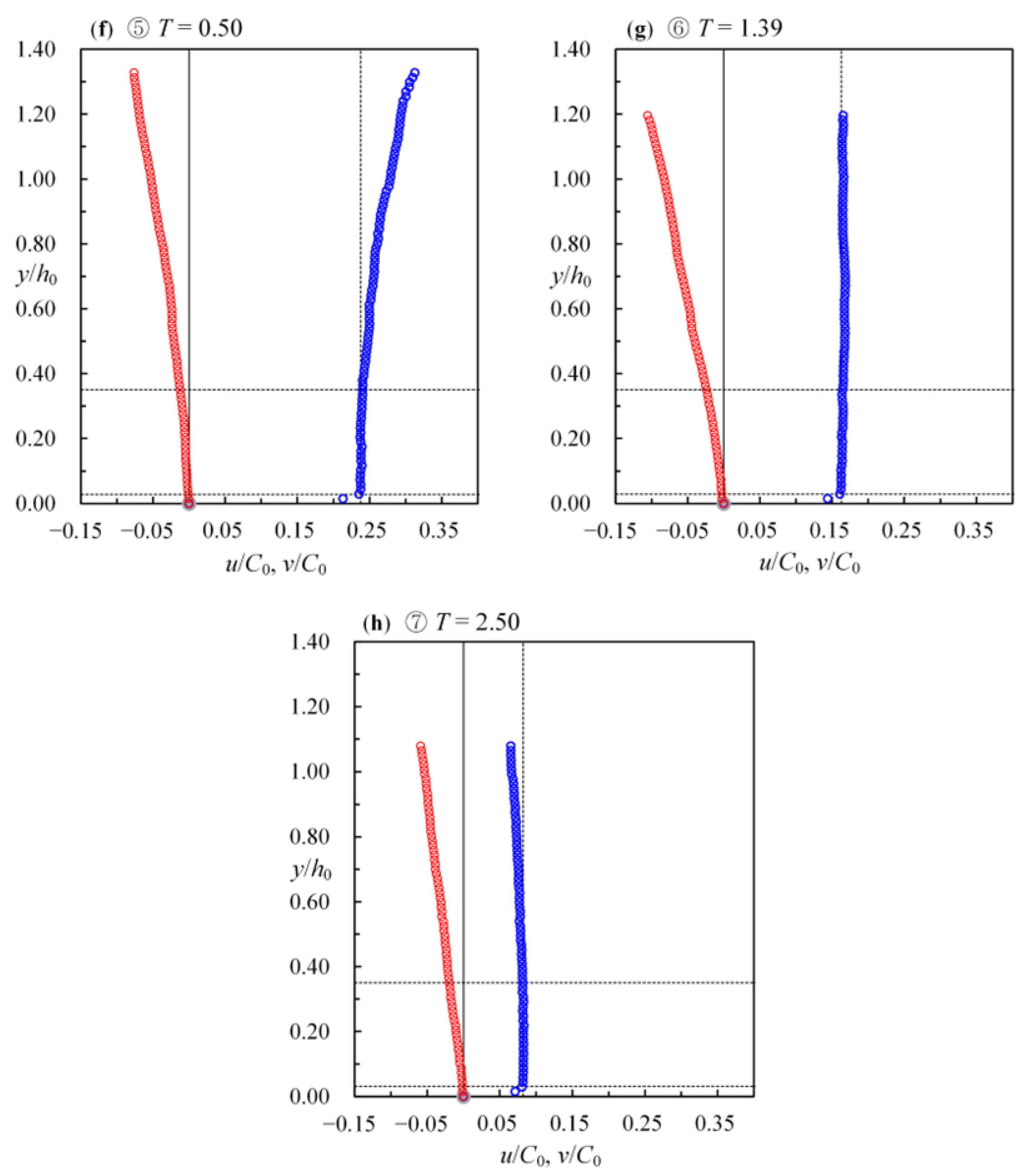
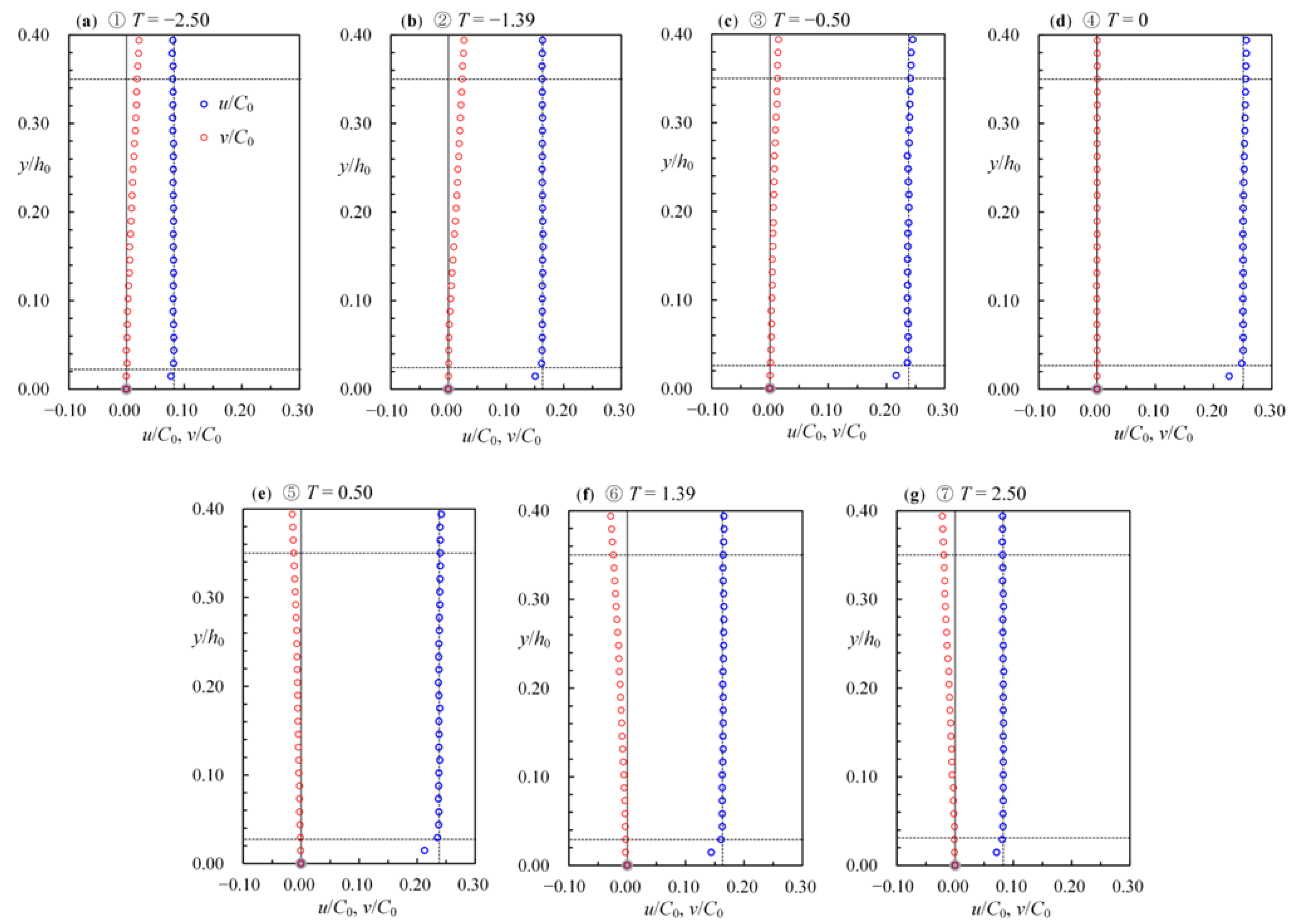
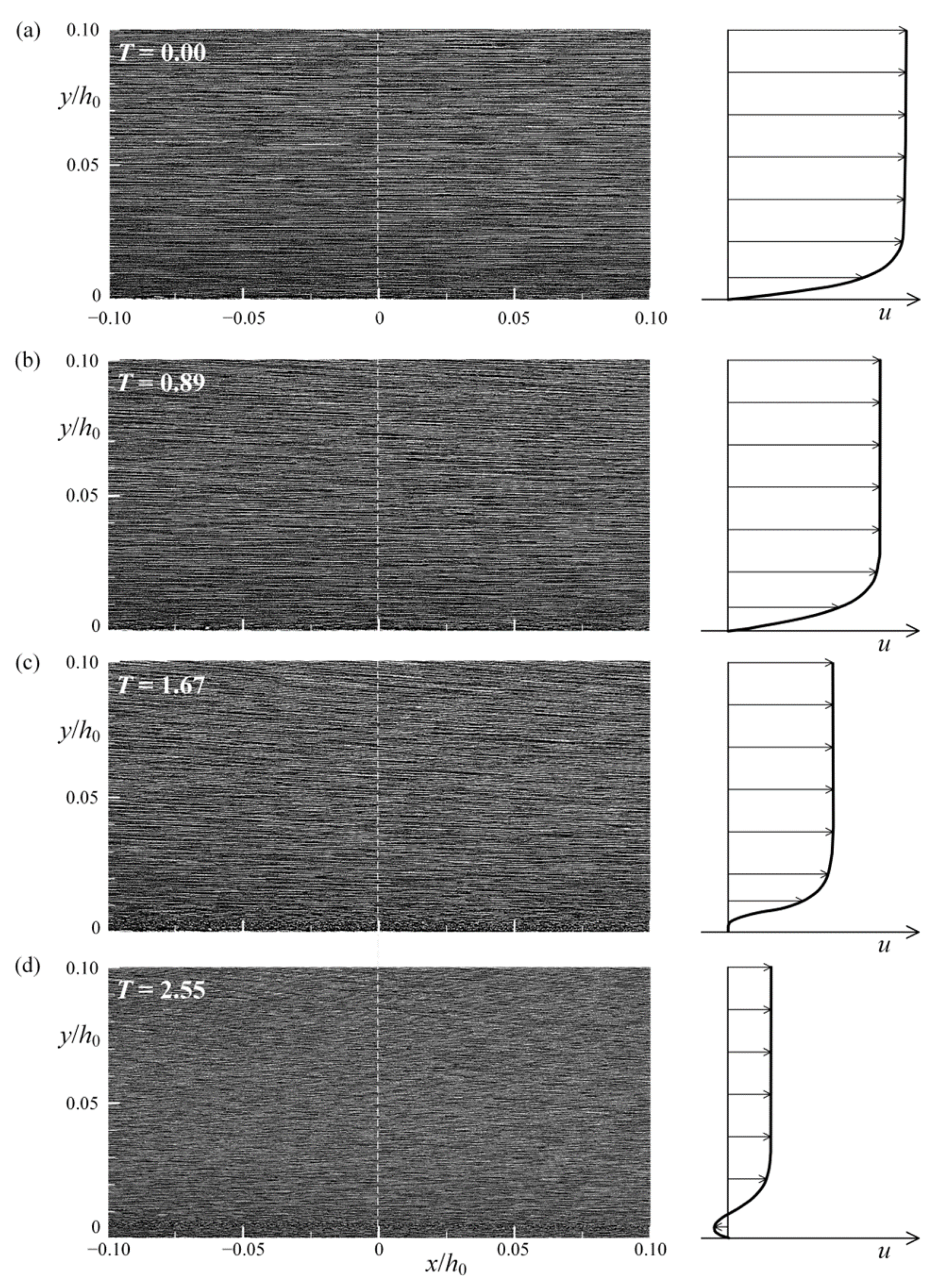
4.1. Elucidation of FSZs from Velocity Profiles
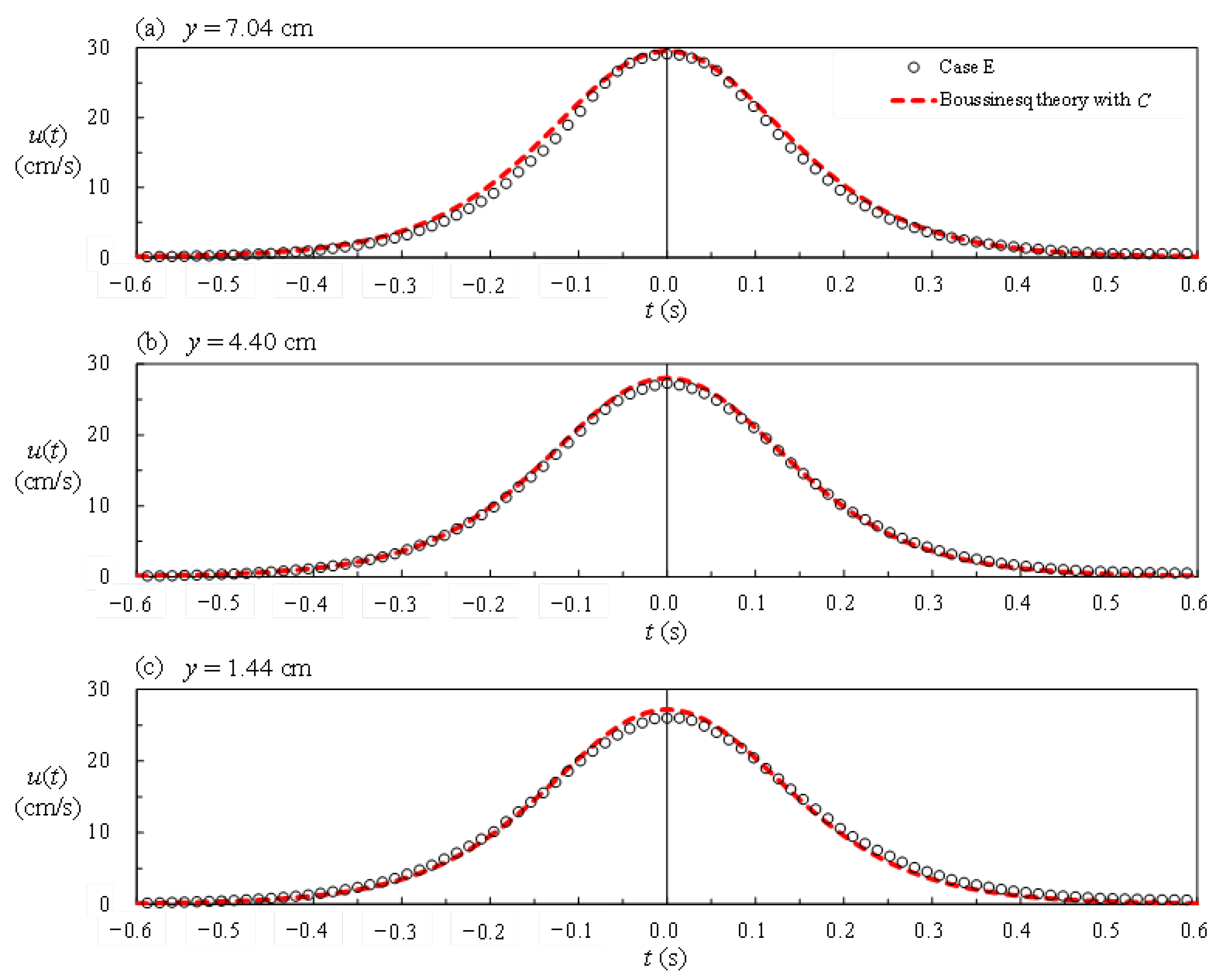
4.2. Nonlinear Effect on Free Surface Elevation and Free-Stream Velocity
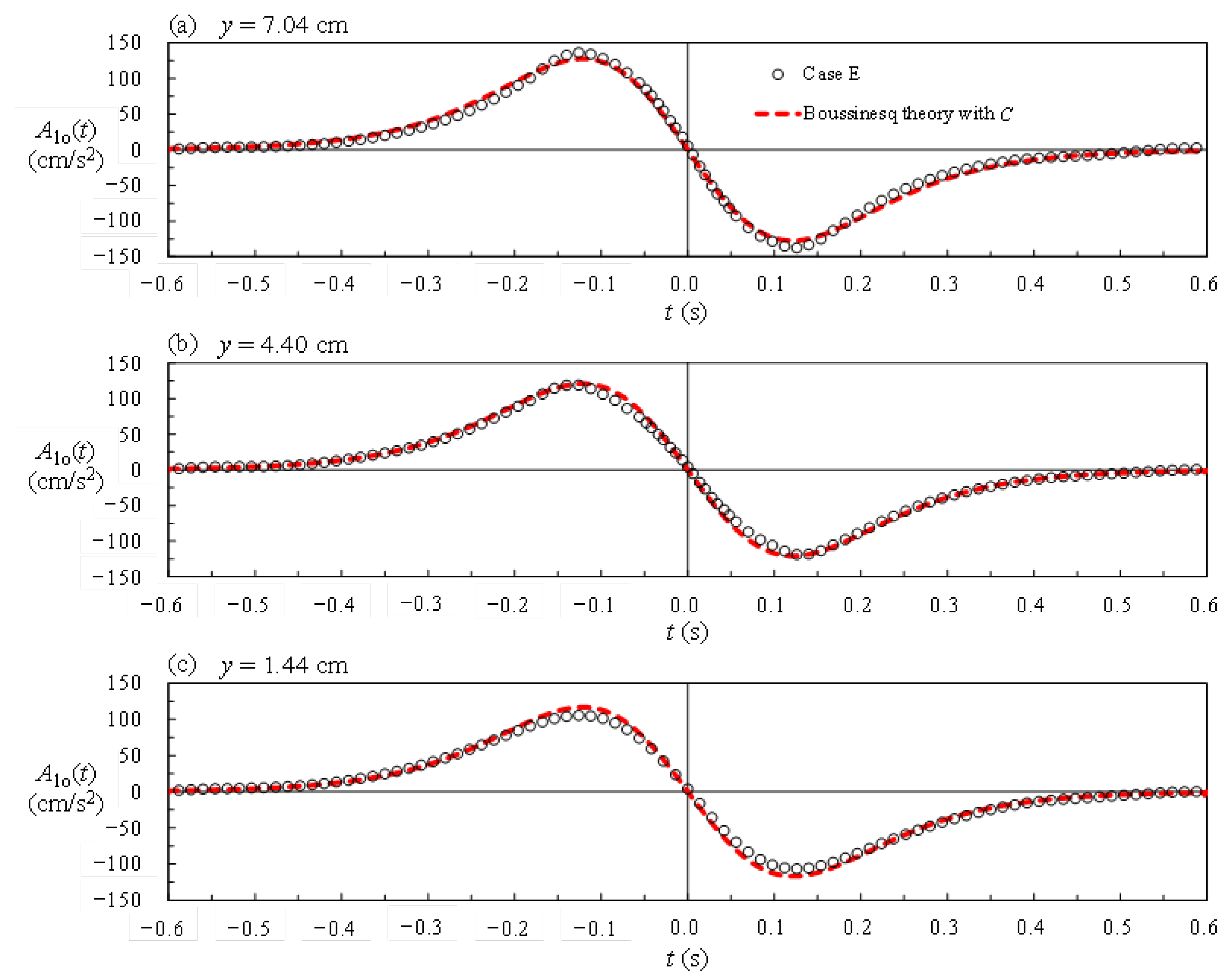
4.3. Nonlinear Effect on Local and Convective Accelerations in FSZ
4.4. Nonlinear Effect on Pressure Gradient in FSZ
= −[Alo(t) + Aco(t)].
= Po(t)
5. Conclusions
- For all the cases exclusive of Case E, the FSZs are positioned between y/h0 = (0.035–0.055) and (0.335–0.366), nearly identical to those between y/h0 = 0.05 and 0.350 in Case E.
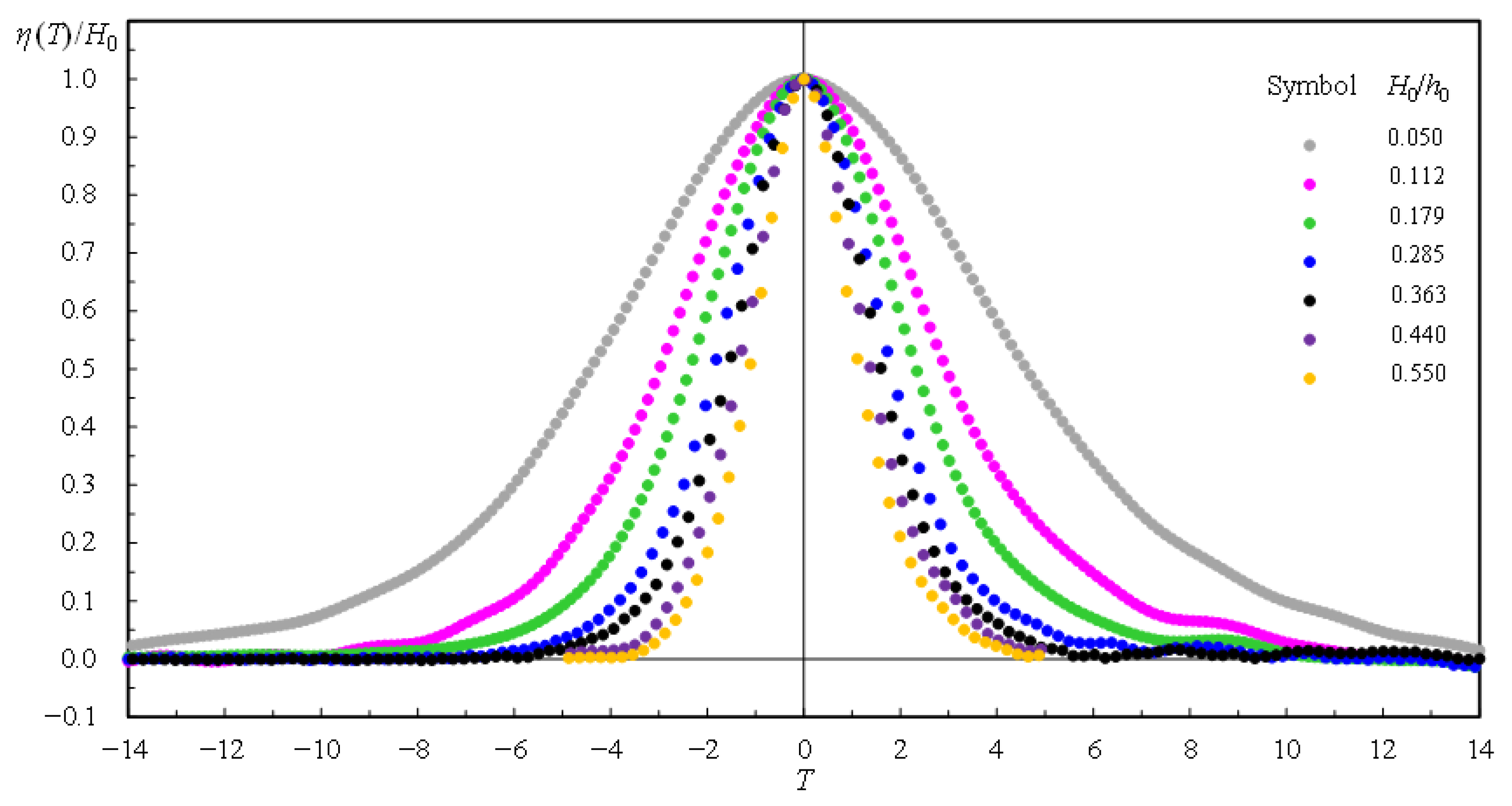
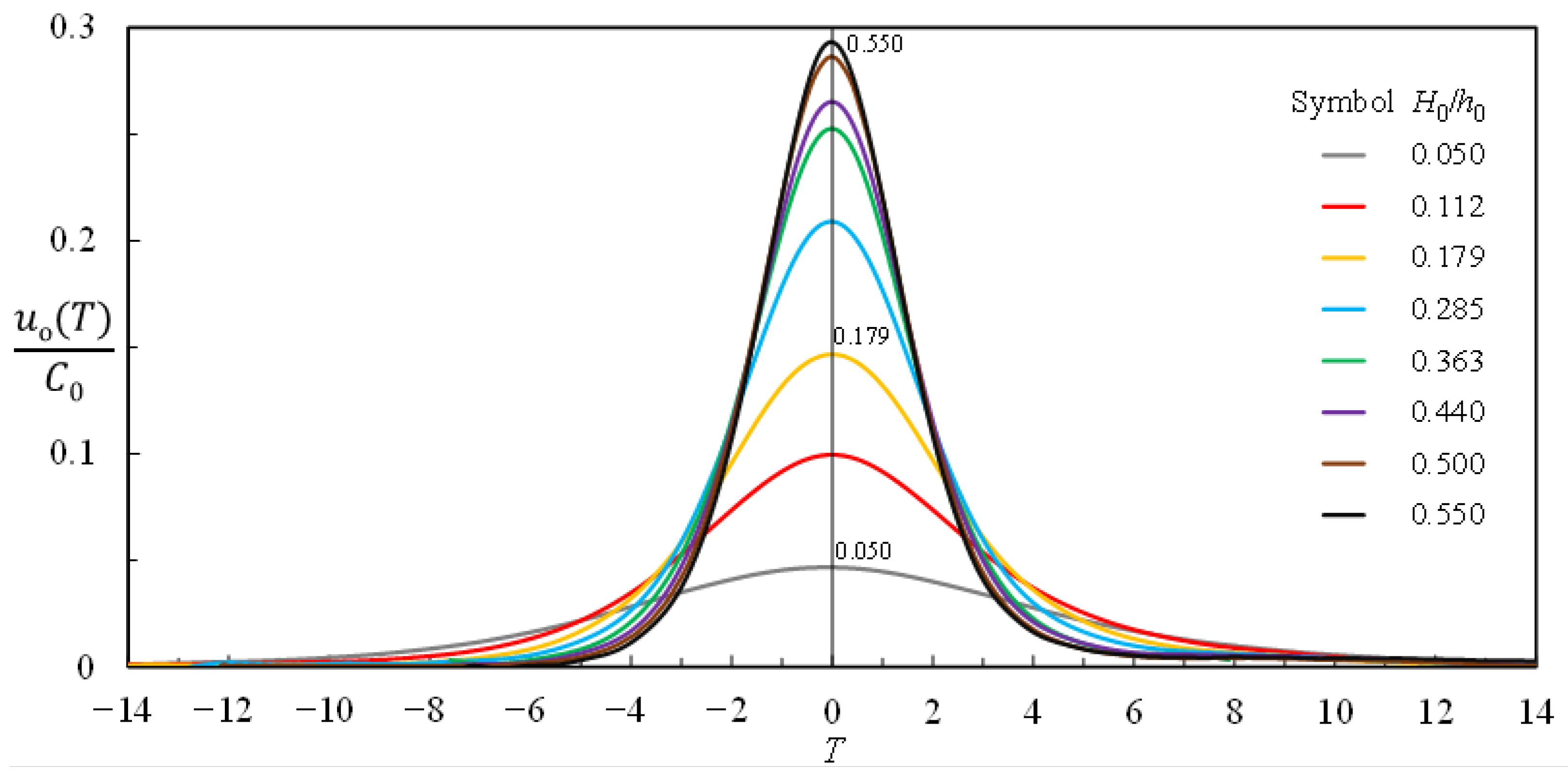
- If H0/h0 increases, the dimensionless free surface elevation, η(T)/H0, and the dimensionless free stream velocity, uo(T)/C0, become more concentrated around T = 0 with a narrower symmetric bell-shape, exhibiting shorter time taken to generate a complete wave motion. This trend indicates that the change of ascending or descending free surface elevation per unit (dimensionless) time becomes greater in magnitude.
- For −6.00 ≤ T < 0 and 0 < T ≤ 6.00, the dimensionless free-stream velocity, [uo(T)/C0], increases from near zero to a maximum and decreases from the maximum to about zero, highlighting the temporal acceleration and deceleration in the FSZ.
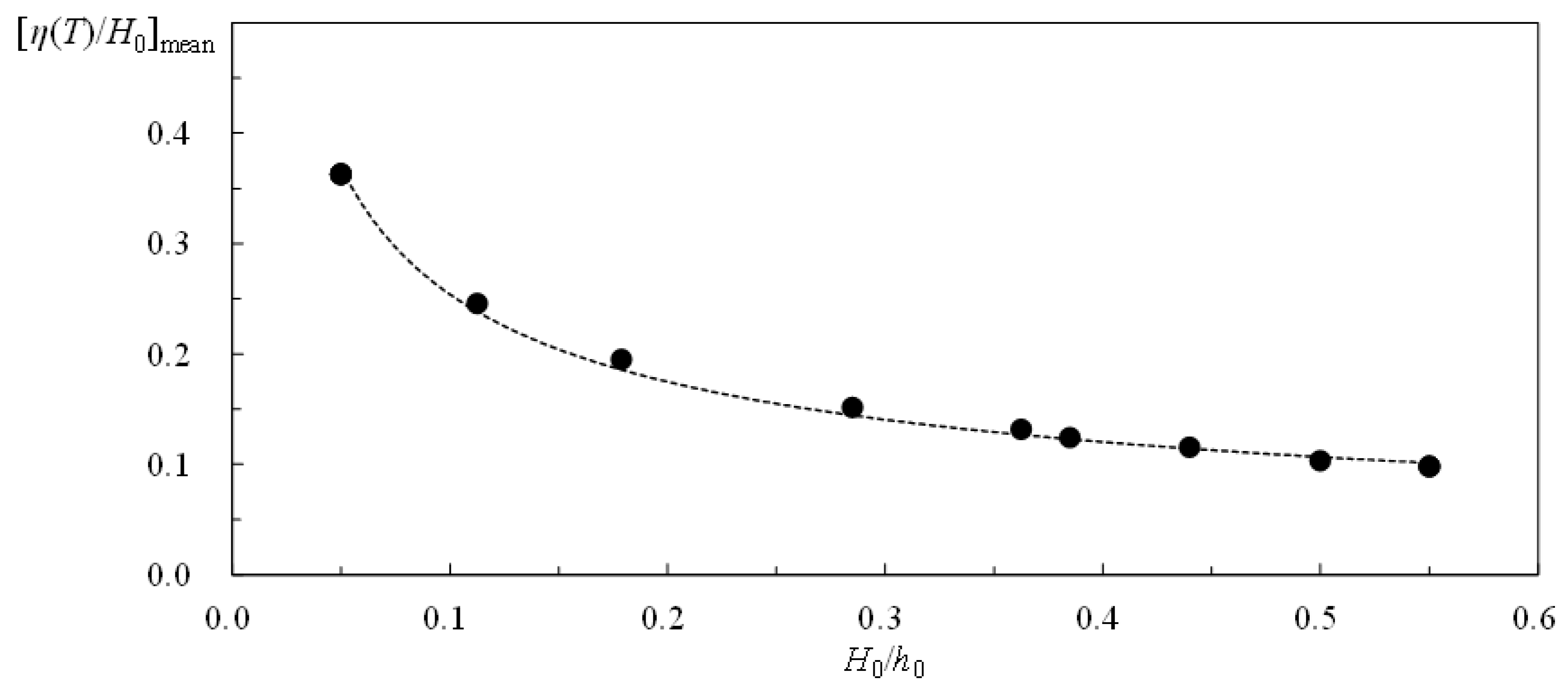
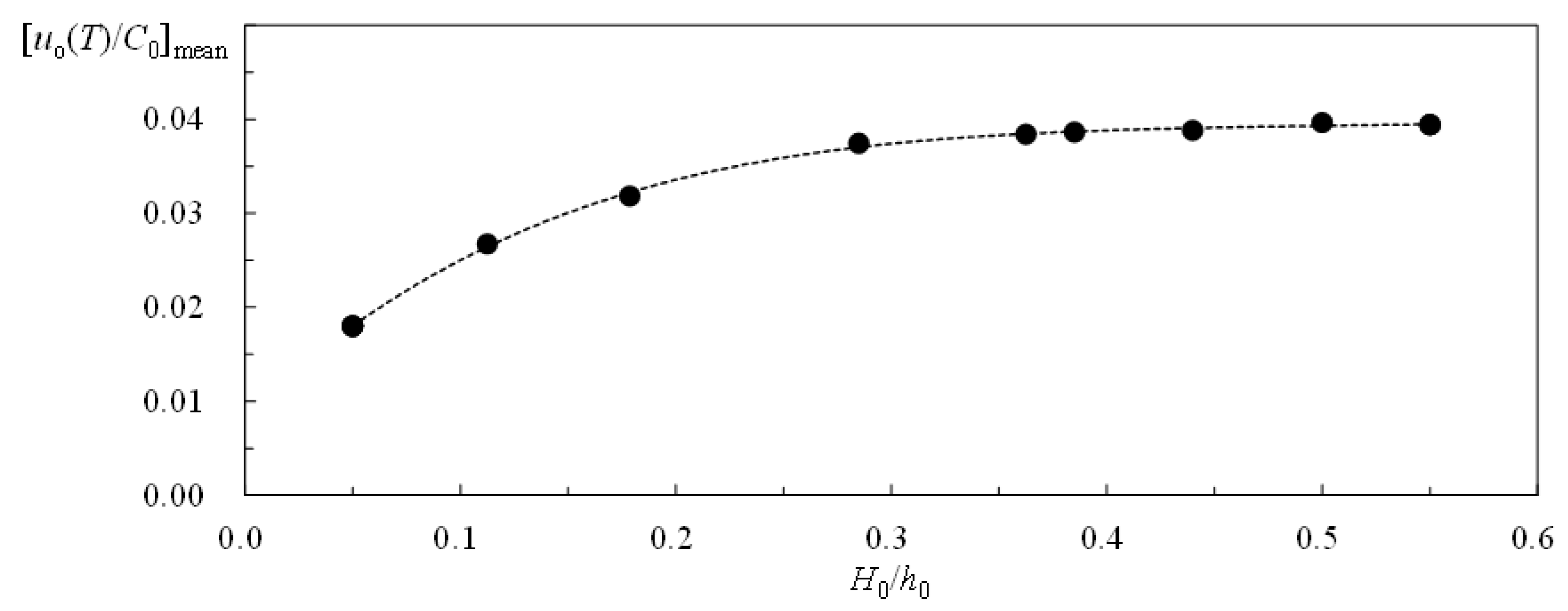
- The relationship between [uo/C0]max and H0/h0 is uniquely expressed in Equation (3), stating that the former gets large with an increasing H0/h0. For H0/h0 = 0.179, 0.363 and 0.550, the values of [uo/C0]max are about 3.10, 5.32, and 6.20 times that (= 0.0473) for H0/h0 = 0.050. This trend demonstrates the nonlinear effect on [uo/C0]max.
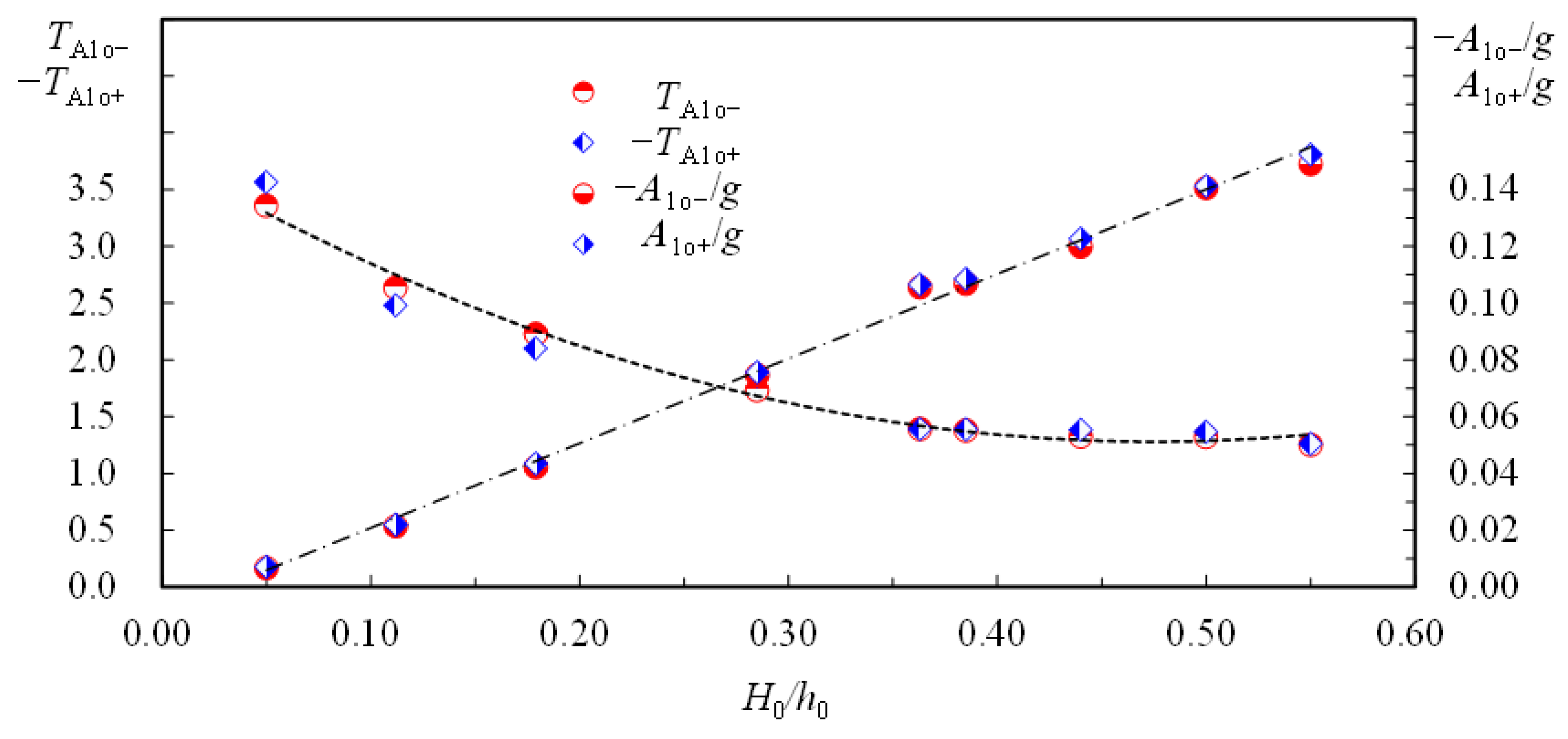
- The dimensionless local acceleration, Alo/g, is positive for −6.00 ≤ T < 0 and negative for 0 < T ≤ 6.00. At T = 0 with wave crest intersecting the SMS, Alo/g is equal to zero and the free-stream velocity reaches its maximum.
- The magnitudes of positive and negative maxima in the dimensionless local acceleration, Alo+/g and Alo−/g (≈ −Alo+/g), increase linearly, and the counterparts of the dimensionless characteristic time TAlo+ (< 0)and TAlo− (> 0) decrease with an increase in H0/h0. For H0/h0 = 0.179, 0.363 and 0.550, the values of Alo+/g are about 6.11, 15.14 and 21.45 times that (= 0.0071) for H0/h0 = 0.050, indicating the nonlinear effect on Alo+/g and Alo−/g.
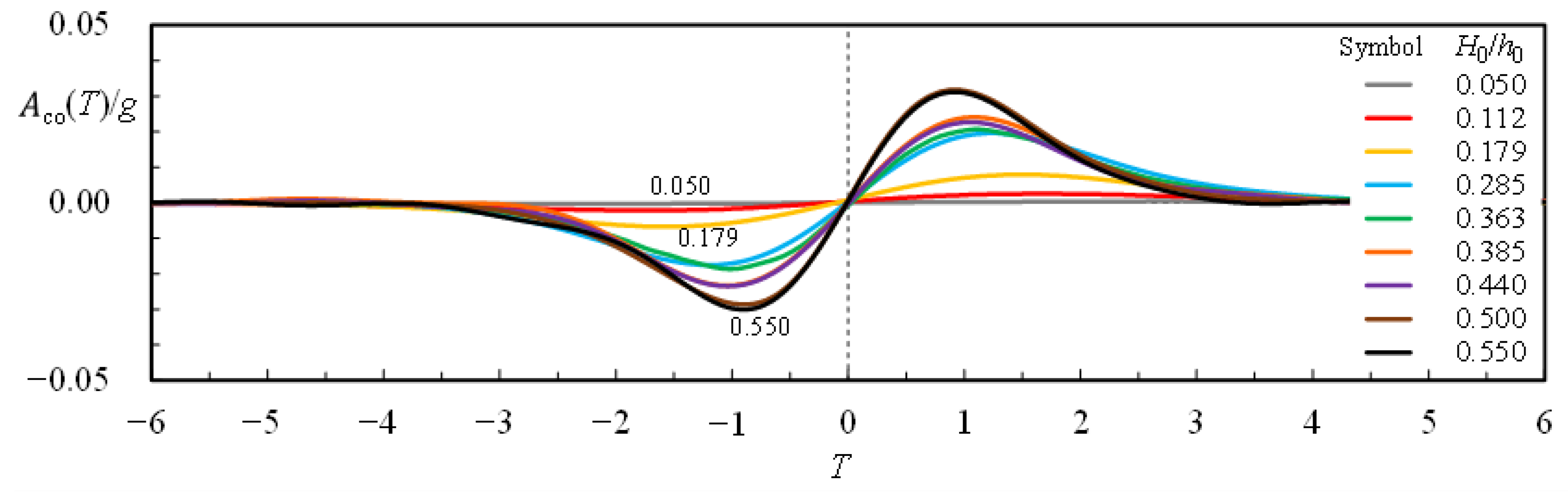
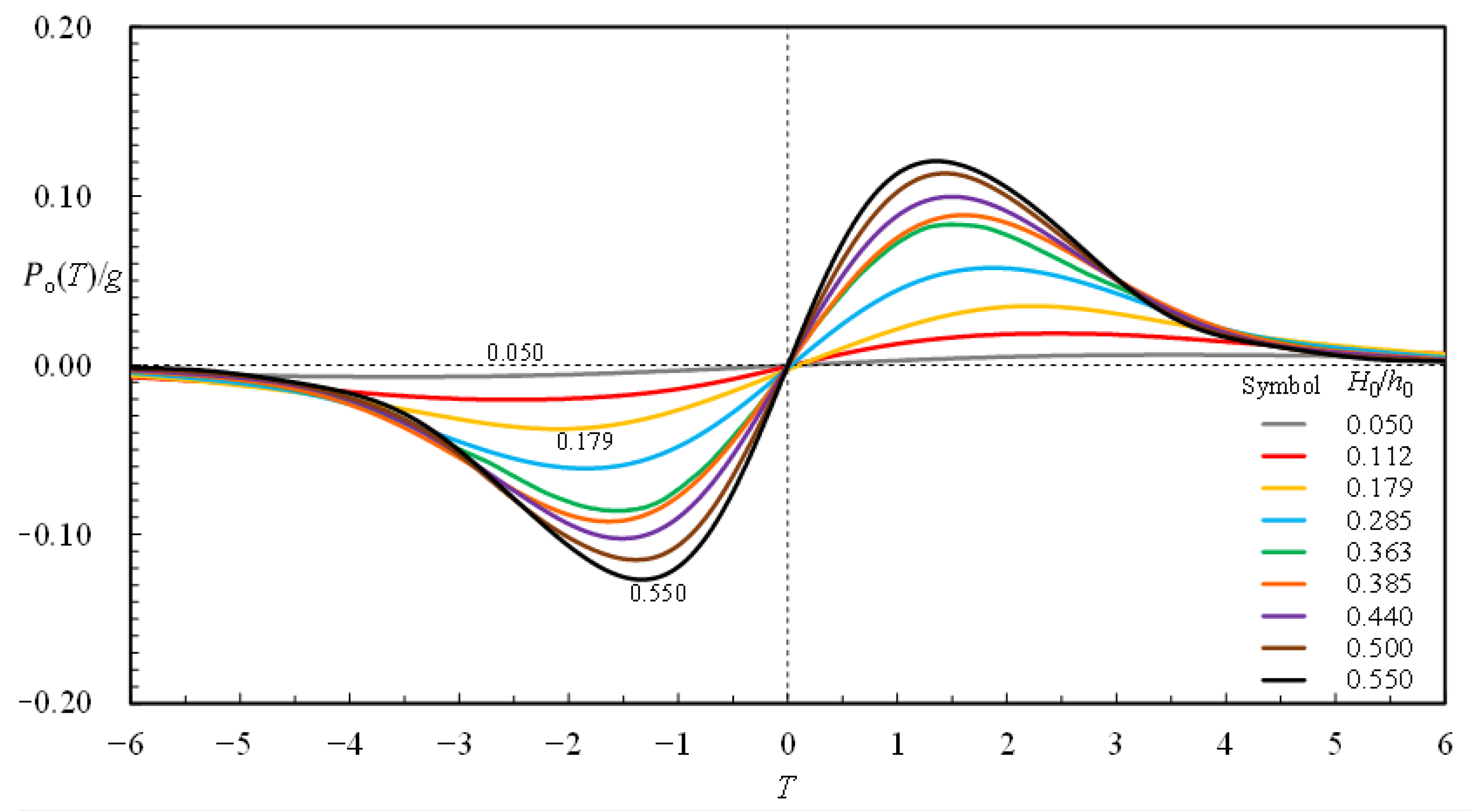
- The magnitudes of negative and positive maxima in the dimensionless convective acceleration, Aco−/g, and Aco+/g, increase when H0/h0 increases. However, their magnitudes are about 1/22.0–1/4.3 times those of Alo+/g and Alo−/g. With the magnitude of Aco(T)/g being much smaller than that of Alo(T)/g, the contribution to the dimensionless pressure gradient, Po(T)/g (= −[Alo(T) + Aco(T)]/g), is thus governed mainly by Alo(T)/g.
- Po(T)/g decreases from near zero to Po_/g (< 0) for −6.00 ≤ T ≤ TPo− or from Po+/g (≈ −Po_/g > 0) to about zero for TPo+ ≤ T ≤ 6.00, exhibiting an increase in the favorable pressure gradient or decrease in the adverse pressure gradient in the FSZ. Moreover, it increases from Po_/g, via 0, to Po+/g for TPo− ≤ T < 0, T = 0, and 0 < T ≤ TPo+, indicating the change from favorable, via zero, to an adverse pressure gradient.
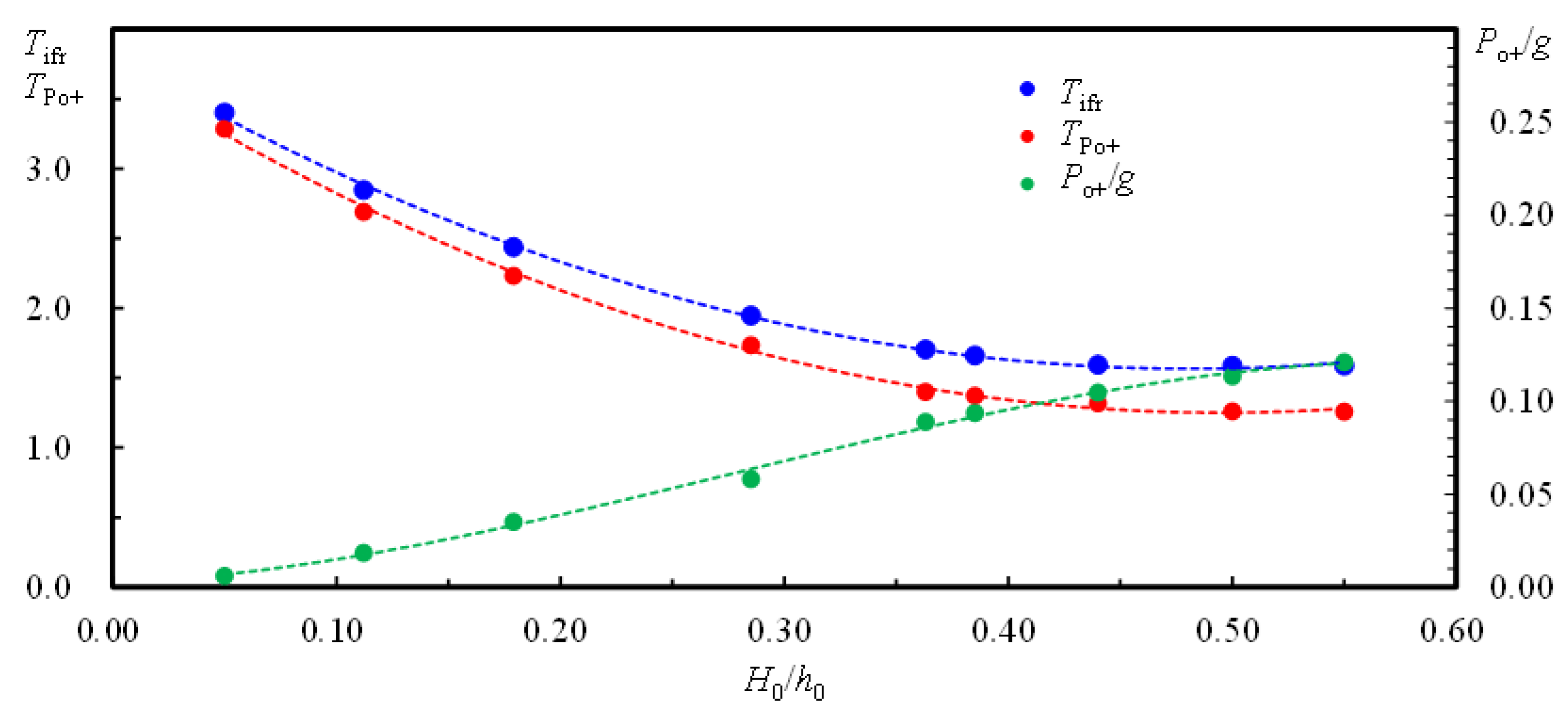
- With an increase in H0/h0, Po+/g increases but TPo+ decreases. For H0/h0 = 0.179, 0.363 and 0.550, the values of Po+/g are about 5.74, 14.54 and 19.84 times that (= 0.0061) for H0/h0 = 0.050, showing the strong nonlinear effect on Po(T)/g and Po+/g.
- For each case, the incipient flow reversal occurs immediately after the maximum adverse pressure gradient. Namely, TPo+ is slightly less than Tifr. Further, Tifr decreases if H0/h0 increases, which accentuates the nonlinear effect on the incipient flow reversal right above the bed.
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Russell, J.S. On Waves; The British Association for the Advancement of Science: London, UK, 1844; pp. 311–390. [Google Scholar]
- Keulegan, G.H. Gradual damping of solitary waves. J. Res. 1948, 40, 487–498. [Google Scholar] [CrossRef]
- Grue, J.; Pelinovsky, E.N.; Frustus, D.; Talipova, T.; Kharif, C. Formation of undular bores and solitary waves in the Strait of Malacca caused by the 26 December 2004 Indian Ocean Tsunami. J. Geophys. Res. 2008, 113, C005008. [Google Scholar] [CrossRef]
- Madsen, P.A.; Fuhrman, D.R.; Schaffer, H.A. On the solitary wave paradigm for tsunami. J. Geophys. Res. 2008, 113, C12012. [Google Scholar] [CrossRef]
- El, G.A.; Grimshaw, R.H.; Tiong, W.K. Transformation of a shoaling undular bore. J. Fluid Mech. 2012, 709, 371–395. [Google Scholar] [CrossRef] [Green Version]
- Grilli, S.T.; Harris, J.C.; Shi, F.; Kirby, J.T.; Tajalli Bakhah, T.S.; Estibals, E.; Tehranirad, B. Numerical modeling of coastal tsunami dissipation and impact. In Proceedings of the 33rd International Conference on Coastal Engineering, Santander, Spain, 1–6 July 2012. [Google Scholar]
- Boussinesq, J. Theorie des ondes et des remous qui se propagent le long d’un canal rectangulaire horizontal, en communiquant au liquide contenu dans ce canal de vitesses sensiblement parreilles de la surface au fond. J. Math. Pures Appl. 1872, 17, 55–108. [Google Scholar]
- McCowan, J. On the solitary waves. Philos. Mag. 1891, 32, 45–58. [Google Scholar] [CrossRef] [Green Version]
- Munk, W.H. The solitary wave theory and its applications to surf problems. Ann. N.Y. Acad. Sci. 1949, 51, 376–424. [Google Scholar] [CrossRef]
- Synolakis, C.E. The runup of solitary waves. J. Fluid Mech. 1987, 185, 523–545. [Google Scholar] [CrossRef]
- Liu, P.L.-F.; Park, Y.S.; Cowen, E.A. Boundary layer flow and bed shear stress under a solitary wave. J. Fluid Mech. 2007, 574, 449–463. [Google Scholar] [CrossRef]
- Gavrilyuk, S.; Liapidevskii, V.; Chesnokov, A. Spilling breakers in shallow depth- applications to Favre waves and to the shoaling and breaking of solitary waves. J. Fluid Mech. 2016, 808, 441–468. [Google Scholar] [CrossRef]
- Grimshaw, R. The solitary waves in water of variable depth (part 2). J. Fluid Mech. 1971, 46, 611–622. [Google Scholar] [CrossRef]
- Fenton, J. A ninth-order solution for the solitary waves. J. Fluid Mech. 1971, 53, 257–271. [Google Scholar] [CrossRef]
- Higuera, P.; Liu, P.L.-F.; Lin, C.; Wong, W.Y.; Kao, M.J. Laboratory-scale swash flows generated by a non-breaking solitary wave on a steep slope. J. Fluid Mech. 2018, 847, 186–227. [Google Scholar] [CrossRef]
- Aly, A.M. Incompressible smoothed particle hydrodynamics simulations on free surface flows. Int. J. Ind. Math. 2015, 7, 99–106. [Google Scholar]
- Lee, J.J.; Skjelbreia, J.E.; Raichlen, F. Measurement of velocities in solitary waves. J. Waterw. Port Coast. Ocean. Eng. 1982, 109, 200–218. [Google Scholar] [CrossRef]
- Lin, C.; Yu, S.M.; Wong, W.Y.; Tzeng, G.W.; Kao, M.J.; Yeh, P.H.; Raikar, R.V.; Yang, J.; Tsai, C.P. Velocity characteristics in boundary layer flow caused by solitary wave traveling over horizontal bottom. Exp. Therm. Fluid Sci. 2016, 76, 238–252. [Google Scholar] [CrossRef]
- Lin, C.; Kao, M.J.; Yang, J.; Raikar, R.V.; Yuan, J.M.; Hsieh, S.C. Particle acceleration and pressure gradient in a solitary wave traveling over a horizontal bed. AIP Adv. 2020, 10, 115210. [Google Scholar] [CrossRef]
- Lin, C.; Kao, M.J.; Yang, J.; Raikar, R.V.; Yuan, J.M.; Hsieh, S.C. Similarity and Froude number similitude in kinematic and hydrodynamic features of solitary waves over horizontal bed. Processes 2021, 9, 1420. [Google Scholar] [CrossRef]
- Lin, C.; Yeh, P.H.; Hseih, S.C.; Shih, Y.N.; Lo, L.F.; Tsai, C.P. Pre-breaking internal velocity field induced by a solitary wave propagating over a 1:10 slope. Ocean. Eng. 2014, 80, 1–12. [Google Scholar] [CrossRef]
- Lin, C.; Yeh, P.H.; Kao, M.J.; Yu, M.H.; Hseih, S.C.; Chang, S.C.; Wu, T.R.; Tsai, C.P. Velocity fields inside near-bottom and boundary layer flow in prebreaking zone of solitary wave propagating over a 1:10 slope. J. Waterw. Port Coast. Ocean. Eng. 2015, 141, 04014038. [Google Scholar] [CrossRef]
- Lin, C.; Kao, M.J.; Tzeng, G.W.; Wong, W.Y.; Yang, J.; Raikar, R.V.; Wu, T.R.; Liu, P.L.-F. Study on flow fields of boundary-layer separation and hydraulic jump during rundown motion of shoaling solitary wave. J. Earthq. Tsunami 2015, 9, 1540002. [Google Scholar] [CrossRef]
- Lin, C.; Wong, W.Y.; Kao, M.J.; Tsai, C.P.; Hwung, H.H.; Wu, Y.T.; Raikar, R.V. Evolution of velocity field and vortex structure during run-down of solitary wave over very steep beach. Water 2018, 10, 1713. [Google Scholar] [CrossRef]
- Lin, C.; Wong, W.Y.; Raikar, R.V.; Hwung, H.H.; Tsai, C.P. Characteristics of accelerations and pressure gradient during run-down of solitary wave over very steep beach–a case study. Water 2019, 11, 523. [Google Scholar] [CrossRef] [Green Version]
- Lin, C.; Kao, M.J.; Raikar, R.V.; Yuan, J.M.; Yang, J.; Chuang, P.Y.; Syu, J.M.; Pan, W.C. Novel similarities in the free-surface profiles and velocities of solitary waves traveling over a very steep beach. Phys. Fluids 2020, 32, 083601. [Google Scholar] [CrossRef]
- Lin, C.; Kao, M.J.; Yuan, J.M.; Raikar, R.V.; Wong, W.Y.; Yang, J.; Yang, R.Y. Features of the flow velocity and pressure gradient of an undular bore on a horizontal bed. Phys. Fluids 2020, 32, 043603. [Google Scholar]
- Goring, D.G. Tsunami: The Propagation of Long Waves onto a Shelf; Technical Report No. KH-R-38; W.M. Keck Laboratory of Hydraulics and Water Resources, California Institute of Technology: Pasadena, CA, USA, 1978. [Google Scholar]
- Adrain, R.J.; Westerweel, J. Particle Image Velocimetry; Cambridge University Press: New York, NY, USA, 2011. [Google Scholar]
- Cowen, E.A.; Monismith, S.G. A hybrid digital particle tracking velocimetry technique. Exp. Fluids 1997, 22, 199–211. [Google Scholar] [CrossRef]
- Dean, R.G.; Dalrymple, R.A. Water Wave Mechanics for Engineers and Scientists; World Scientific Publishing Co. Pte. Ltd.: Hackensack, NJ, USA, 1991. [Google Scholar]
- Chang, K.A.; Liu, P.L.F. Pseudo turbulence in PIV breaking wave measurements. Exp. Fluids 2000, 29, 331–338. [Google Scholar] [CrossRef]
- Daily, J.W.; Harleman, D.R.F. Fluid Dynamics; Addison-Wesley Publishing Company, Inc.: Boston, MA, USA, 1966. [Google Scholar]
- Munson, B.R.; Young, D.L.; Okiishi, T.H. Fundamentals of Fluid Mechanics; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2006. [Google Scholar]
- Jensen, A.; Pedersen, G.K.; Wood, D.J. An experimental study of wave run-up at a steep beach. J. Fluid Mech. 2003, 486, 161–188. [Google Scholar] [CrossRef]







| Case | H0 (cm) | H0/h0 * | C (cm/s) | C0 (cm/s) | C0/C | Framing Rate of HSPIV (Hz) | Framing Rate of FV (Hz) | Size (cm × cm) (Length × Width) |
|---|---|---|---|---|---|---|---|---|
| A | 0.40 | 0.050 | 88.59 | 90.78 | 1.025 | 1600 | 30 | 2.05 × 1.15 |
| B | 0.90 | 0.112 | 88.59 | 93.44 | 1.055 | 2500 | 50 | 2.05 × 1.15 |
| C | 1.43 | 0.179 | 88.59 | 96.18 | 1.086 | 2500 | 50 | 2.05 × 1.15 |
| D | 2.28 | 0.285 | 88.59 | 100.42 | 1.134 | 2500 | 100 | 2.05 × 1.15 |
| E | 2.90 | 0.363 | 88.59 | 103.41 | 1.167 | 500 | - | 16.80 × 16.80 (HSPIV) |
| 1000 | - | 2.00 × 1.00 (HSPIV) | ||||||
| - | 100 | 2.05 × 1.15 (FV) | ||||||
| F | 3.08 | 0.385 | 88.59 | 104.26 | 1.177 | 2500 | 100 | 2.05 × 1.15 |
| G | 3.52 | 0.440 | 88.59 | 106.31 | 1.200 | 2500 | 100 | 2.11 × 1.18 |
| H | 4.00 | 0.500 | 88.59 | 108.50 | 1.225 | 2000 | - | 2.11 × 1.18 |
| I | 4.40 | 0.550 | 88.59 | 110.29 | 1.245 | 2500 | 100 | 2.11 × 1.18 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, C.; Kao, M.-J.; Yang, J.; Yuan, J.-M.; Hsieh, S.-C. Effects of Nonlinearity on Velocity, Acceleration and Pressure Gradient in Free-Stream Zone of Solitary Wave over Horizontal Bed—An Experimental Study. Water 2022, 14, 3609. https://doi.org/10.3390/w14223609
Lin C, Kao M-J, Yang J, Yuan J-M, Hsieh S-C. Effects of Nonlinearity on Velocity, Acceleration and Pressure Gradient in Free-Stream Zone of Solitary Wave over Horizontal Bed—An Experimental Study. Water. 2022; 14(22):3609. https://doi.org/10.3390/w14223609
Chicago/Turabian StyleLin, Chang, Ming-Jer Kao, James Yang, Juan-Ming Yuan, and Shih-Chun Hsieh. 2022. "Effects of Nonlinearity on Velocity, Acceleration and Pressure Gradient in Free-Stream Zone of Solitary Wave over Horizontal Bed—An Experimental Study" Water 14, no. 22: 3609. https://doi.org/10.3390/w14223609
APA StyleLin, C., Kao, M.-J., Yang, J., Yuan, J.-M., & Hsieh, S.-C. (2022). Effects of Nonlinearity on Velocity, Acceleration and Pressure Gradient in Free-Stream Zone of Solitary Wave over Horizontal Bed—An Experimental Study. Water, 14(22), 3609. https://doi.org/10.3390/w14223609








