Degradation of Emerging Pollutants by Photocatalysis: Radiation Modeling and Kinetics in Packed-Bed Reactors
Abstract
:1. Introduction
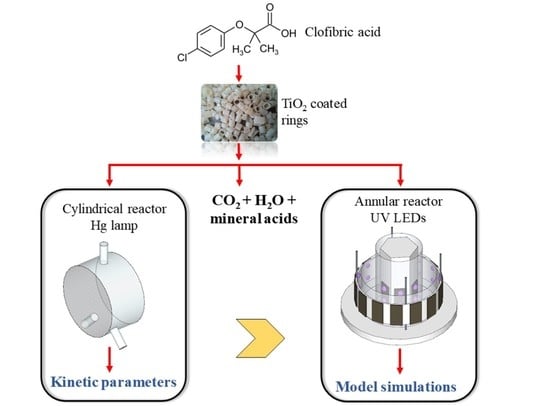
2. Employed Strategy
- 1-
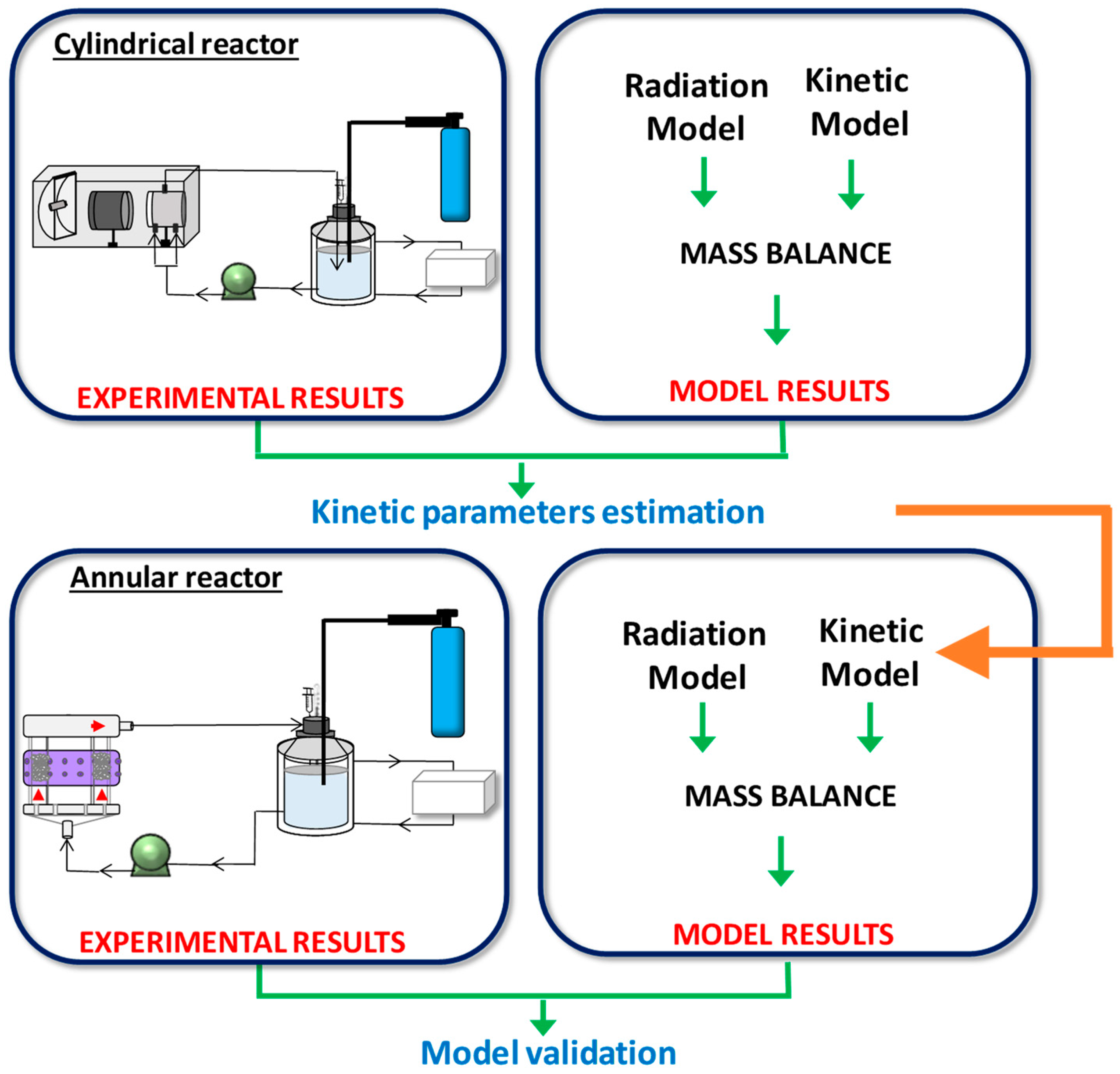
- Intrinsic kinetic parameters were first obtained in a simple, cylindrical reactor (CR) irradiated from one end by a mercury lamp. To accomplish this, a kinetic model to represent the photocatalytic degradation of the pollutant CA was developed. The expression of the CA degradation rate includes the value of the local surface rate of photon absorption (LSRPA or ). Therefore, a 1-D radiation model was solved to obtain the LSRPA distribution inside the reactor. Then, the mass balance of CA was set in order to predict the evolution of the pollutant in the system. Finally, the values of the intrinsic kinetic parameters were obtained by applying an optimization algorithm to adjust model simulations to experimental data.
- 2-
- The second stage involved the use of the kinetic parameters found in the first reactor to predict the performance of the second one: an annular reactor (AR) illuminated by UV-LEDs. This task involved the resolution of the mass balance for CA, using the kinetic expression obtained in the CR, and the calculation of the LSRPA. Due to its particular configuration and illumination arrangement, a 3-D radiation model was developed to calculate the LSRPA in the AR. Finally, simulation results were compared with experimental data in order to validate the modeling procedure.
3. Experimental Devices
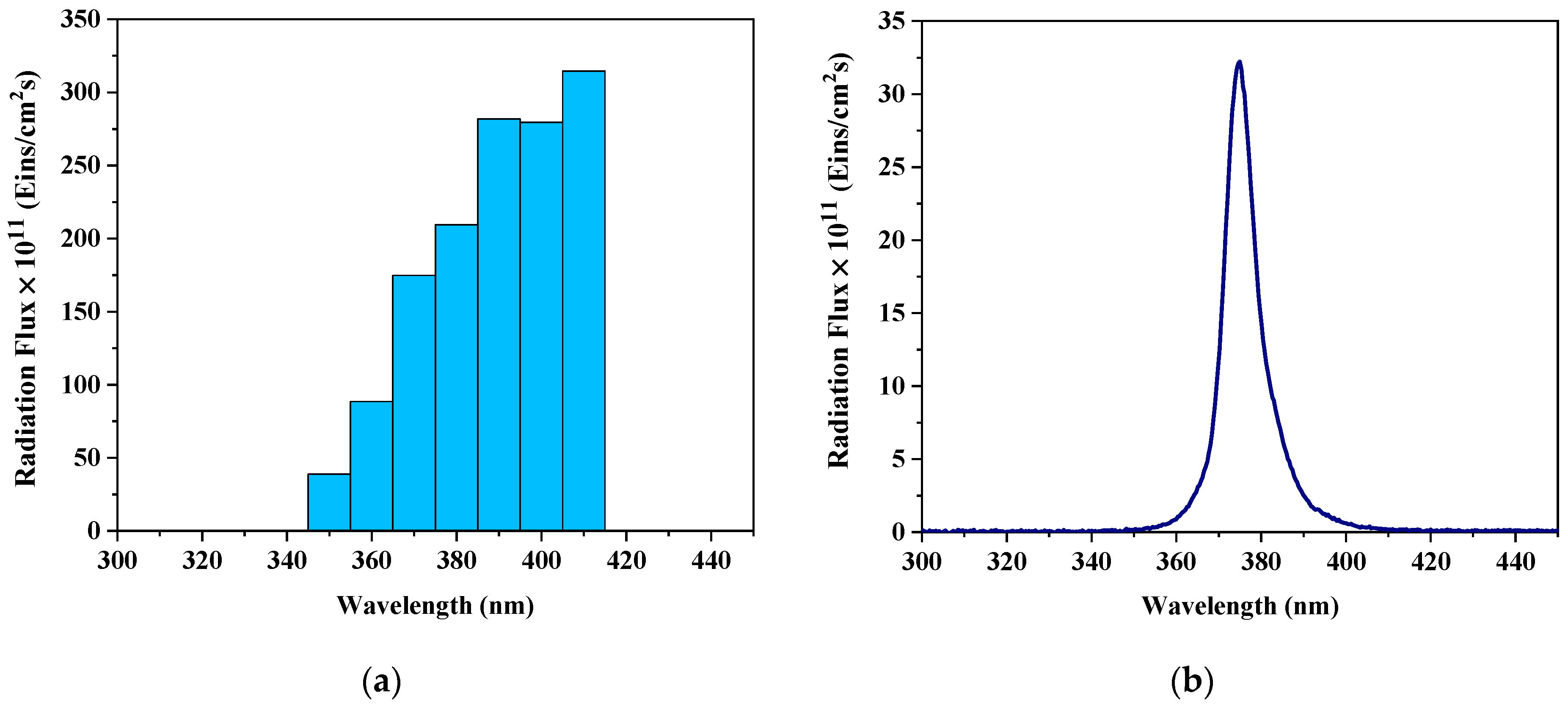
3.1. Reactors and Irradiation Sources
3.2. Recycling Setup
3.3. Catalyst Immobilization
4. Experimental Assays
5. Reactor Modeling
5.1. Mass Balance
5.2. Kinetic Model
5.3. Local Surface Rate of Photon Absorption (LSRPA)
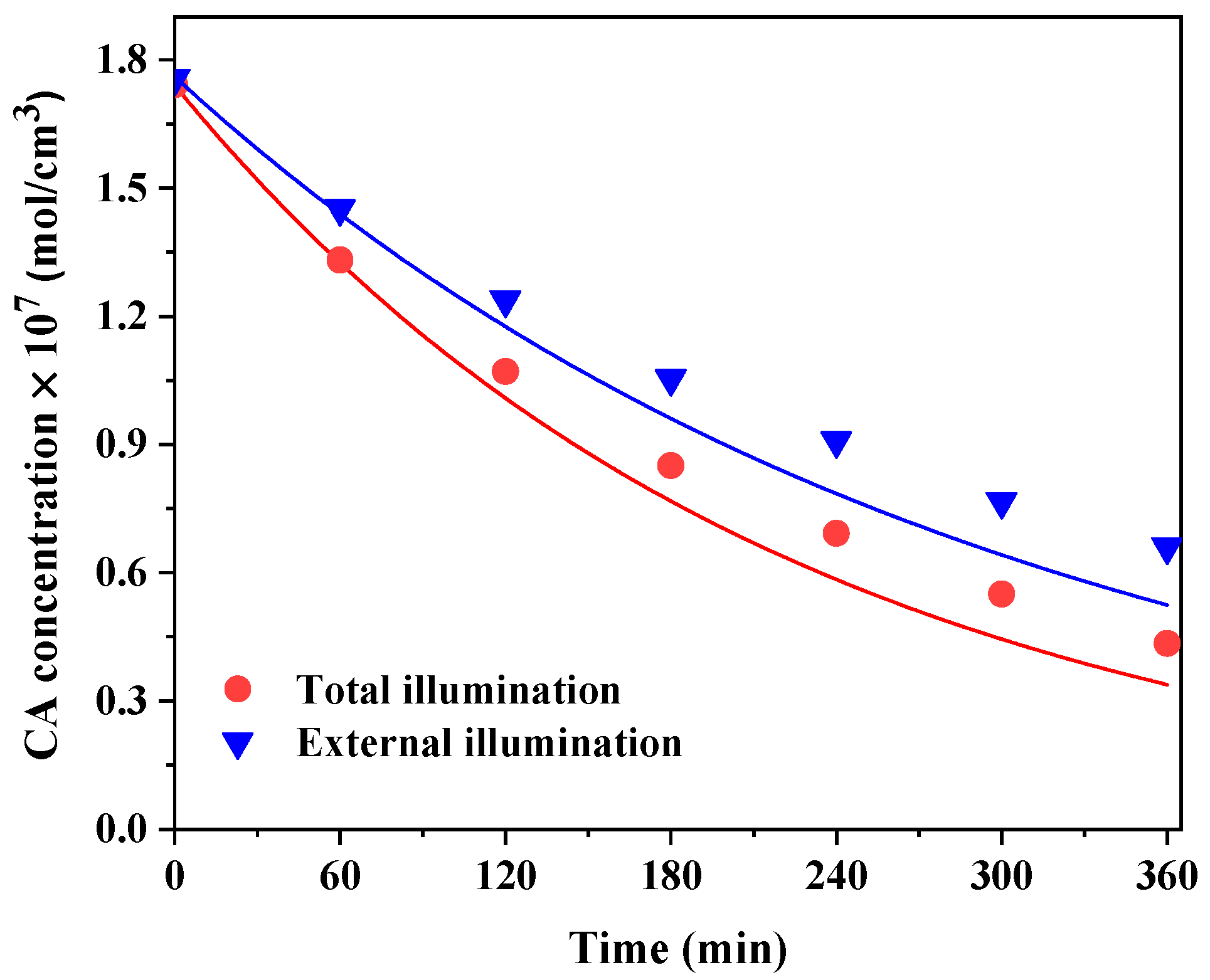
6. Results and Discussion
6.1. LSRPA Distribution
6.2. Kinetic Simulations
7. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lee, B.C.Y.; Lim, F.Y.; Loh, W.H.; Ong, S.L.; Hu, J. Emerging Contaminants: An Overview of Recent Trends for Their Treatment and Management Using Light-Driven Processes. Water 2021, 13, 2340. [Google Scholar] [CrossRef]
- Saravanan, A.; Senthil Kumar, P.; Jeevanantham, S.; Anubha, M.; Jayashree, S. Degradation of toxic agrochemicals and pharmaceutical pollutants: Effective and alternative approaches toward photocatalysis. Environ. Pollut. 2022, 1, 118844. [Google Scholar] [CrossRef]
- Ahmed, S.; Saleem, F.; Khan, F.S.A.; Mubarak, N.M.; Khalid, M.; Tan, Y.; Mazari, S.A.; Karri, R.R.; Abdullah, E.C. Emerging pollutants and their removal using visible-light responsive photocatalysis—A comprehensive review. J. Environ. Chem. Eng. 2021, 6, 106643. [Google Scholar] [CrossRef]
- Alfano, O.M.; Cassano, A.E. Scaling-Up of Photoreactors: Applications to Advanced Oxidation Processes. In Advances in Chemical Engineering, 1st ed.; De Lasa, H.I., Rosales, B.S., Eds.; Academic Press: Burlington, MA, USA, 2009; pp. 229–287. [Google Scholar]
- Toepfer, B.; Gora, A.; Li Puma, G. Photocatalytic oxidation of multicomponent solutions of herbicides: Reaction kinetics analysis with explicit photon absorption effects. App. Catal. B 2006, 68, 171–180. [Google Scholar] [CrossRef]
- Moreira, R.P.M.; Li Puma, G. Multiphysics Computational Fluid-Dynamics (CFD) Modeling of Annular Photocatalytic Reactors by the Discrete Ordinates Method (DOM) and the Six-Flux Model (SFM) and Evaluation of the Contaminant Intrinsic Kinetics Constants. Catal. Today 2021, 361, 77–84. [Google Scholar] [CrossRef]
- Bayarri, B.; Giménez, J.; Curcó, D.; Esplugas, S. Absorbed radiation and kinetic model in photocatalysis by TiO2. Int. J. Chem. React. Eng. 2022, 20, 3–15. [Google Scholar] [CrossRef]
- Satuf, M.L.; Brandi, R.J.; Cassano, A.E.; Alfano, O.M. Scaling-up of slurry reactors for the photocataytic degradation of 4-chlorophenol. Catal. Today 2007, 129, 110–117. [Google Scholar] [CrossRef]
- Casado, C.; Marugán, J.; Timmers, R.; Muñoz, M.; van Grieken, R. Comprehensive multiphysics modeling of photocatalytic processes by computational fluid dynamics based on intrinsic kinetic parameters determined in a differential photoreactor. Chem. Eng. J. 2017, 310, 368–380. [Google Scholar] [CrossRef] [Green Version]
- Imoberdorf, G.E.; Irazoqui, H.A.; Alfano, O.M.; Cassano, A.E. Scaling-up from first principles of a photocatalytic reactor for air pollution remediation. Chem. Eng. Sci. 2007, 62, 793–804. [Google Scholar] [CrossRef]
- Grcic, I.; Koprivanac, N.; Li Puma, G. Modeling the photocatalytic oxidation of carboxylic acids on aqueous TiO2 suspensions and on immobilized TiO2-chitosan thin films in different reactor geometries irradiated by UVA or UVC light sources. Chem. Eng. J. 2021, 422, 130104. [Google Scholar] [CrossRef]
- Martín-Sómer, M.; Pablos, C.; van Grieken, R.; Marugán, J. Influence of light distribution on the performance of photocatalytic reactors: LED vs mercury lamps. Appl. Catal. B 2017, 215, 1–7. [Google Scholar] [CrossRef]
- Wang, Q.; Xiao, M.; Peng, Z.; Zhang, C.; Du, X.; Wang, Z.; Wang, W. Visible LED photocatalysis combined with ultrafiltration driven by metal-free oxygen-doped graphitic carbon nitride for sulfamethazine degradation. J. Hazard. Mat. 2022, 439, 129632. [Google Scholar] [CrossRef] [PubMed]
- Manassero, A.; Satuf, M.L.; Alfano, O.M. Photocatalytic degradation of an emerging pollutant by TiO2-coated glass rings: A kinetic study. Environ. Sci. Pollut. Res. 2017, 24, 6031–6039. [Google Scholar] [CrossRef]
- Manassero, A.; Alfano, O.M.; Satuf, M.L. Radiation modeling and performance evaluation of a UV-LED photocatalytic reactor for water treatment. J. Photochem. Photobiol. A 2022, 436, 114367. [Google Scholar] [CrossRef]
- van Grieken, R.; Marugán, J.; Sordo, C.; Pablos, C. Comparison of the photocatalytic disinfection of E. coli suspensions in slurry, wall and fixed-bed reactors. Catal. Today 2009, 144, 48–54. [Google Scholar] [CrossRef]
- Murov, S.L.; Carmichael, I.; Hug, G.L. Handbook of Photochemistry, 2nd ed.; Marcel Dekker: New York, NY, USA, 1993. [Google Scholar]
- Dordio, A.; Estêvão Candeias, A.; Pinto, A.; Teixeira da Costa, C.; Palace Carvalho, A. Preliminary media screening for application in the removal of clofibric acid, carbamazepine and ibuprofen by SSF-constructed wetlands. Ecol. Eng. 2009, 35, 290–302. [Google Scholar] [CrossRef]
- Mills, A.; Davies, R. Photomineralisation of 4-chlorophenol sensitised by titanium dioxide: A study of the intermediates. J. Photochem. Photobiol. A 1993, 70, 183–191. [Google Scholar] [CrossRef]
- Theurich, J.; Lindner, M.; Bahnemann, D.W. Photocatalytic degradation of 4-chlorophenol in aerated aqueous titanium dioxide suspensions: A kinetic and mechanistic study. Langmuir 1996, 12, 6368–6376. [Google Scholar] [CrossRef]
- Pelizzetti, E.; Minero, C. Mechanism of the photo-oxidative degradation of organic pollutants over TiO2 particles. Electrochim. Acta 1993, 38, 47–55. [Google Scholar] [CrossRef]
- Almquist, C.B.; Biswas, P. A mechanistic approach to modeling the effect of dissolved oxygen in photo-oxidation reactions on titanium dioxide in aqueous systems. Chem. Eng. Sci. 2001, 56, 3421–3430. [Google Scholar] [CrossRef]
- Dijkstra, M.F.J.; Panneman, H.J.; Winkelman, J.G.M. Modeling the photocatalytic degradation of formic acid in a reactor with immobilized catalyst. Chem. Eng. Sci. 2022, 57, 4895–4907. [Google Scholar] [CrossRef] [Green Version]
- Turchi, C.S.; Ollis, D.F. Photocatalytic degradation of organic water contaminants: Mechanisms involving hydroxyl radical attack. J. Catal. 1990, 122, 178–190. [Google Scholar] [CrossRef]
- Terzian, R.; Serpone, N.; Minero, C.; Pelizzetti, E.; Hidaka, H. Kinetic studies in heterogeneous photocatalysis 4. The ph tomineralization of a hydroquinone and a catechol. Photochem. Photobiol. A 1990, 55, 243–249. [Google Scholar] [CrossRef]
- Satuf, M.L.; Brandi, R.J.; Cassano, A.E.; Alfano, O.M. Quantum efficiencies of 4-chlorophenol photocatalytic degradation and mineralization in a well-mixed slurry reactor. Ind. Eng. Chem. Res. 2007, 46, 43–51. [Google Scholar] [CrossRef]
- Manassero, A.; Satuf, M.L.; Alfano, O.M. Kinetic modeling of the photocatalytic degradation of clofibric acid in a slurry reactor. Environ. Sci. Pollut. Res. 2015, 22, 926–937. [Google Scholar] [CrossRef] [PubMed]
- Alfano, O.M.; Cabrera, M.I.; Cassano, A.E. Photocatalytic reactions involving hydroxyl radical attack. J. Catal. 1997, 172, 370–379. [Google Scholar] [CrossRef]
- Chen, D.; Li, F.; Ray, A.K. External and internal mass transfer effect on photocatalytic degradation. Catal. Today 2001, 66, 475–485. [Google Scholar] [CrossRef]
- Ould-Mame, S.M.; Zahraa, O.; Bouchy, M. Photocatalytic degradation of salicylic acid on fixed TiO2 -Kinetic studies. Int. J. Photoenergy 2000, 2, 59–66. [Google Scholar] [CrossRef] [Green Version]
- Cloteaux, A.; Gérardin, F.; Thomas, D.; Midoux, N.; André, J.C. Fixed bed photocatalytic reactor for formaldehyde degradation: Experimental and modeling study. Chem. Eng. J. 2014, 249, 121–129. [Google Scholar] [CrossRef]
- Onda, K.; Sada, E.; Murase, Y. Liquid-side mass transfer coefficients in packed towers. AIChE J. 1959, 5, 235–239. [Google Scholar] [CrossRef]




| Photoreactor | ||
|---|---|---|
| Characteristics | Cylindrical | Annular |
| Main dimensions | Length = 2.75 cm Diameter = 5.0 cm | Length = 4.0 cm Inner diameter = 6.5 cm Outer diameter = 10.5 cm |
| Reactor volume | 54 mL | 214 mL |
| Total system volume | 1000 mL | 600 mL |
| Irradiation source | One mercury lamp | 40 UV-LED lamps |
| Lamp emission range | 350–410 nm | 360–390 nm |
| Number of rings | 310 | 900 |
| Catalytic area | 487 cm2 | 1414 cm2 |
| Irradiation | From one side | Internal and external |
| Distance between lamps and irradiated windows | 33 cm | Internal LEDs = 0.3 cm External LEDs = 0.6 cm |
| Irradiated window area | 19.6 cm2 | Inner = 81.6 cm2 Outer = 131.8 cm2 |
| Photoreactor | ||
|---|---|---|
| Variable | Cylindrical | Annular |
| Initial CA concentration, CCA,0 [mol/cm3] | 0.93 × 10−7 | (0.93, 1.87, 2.34) × 10−7 |
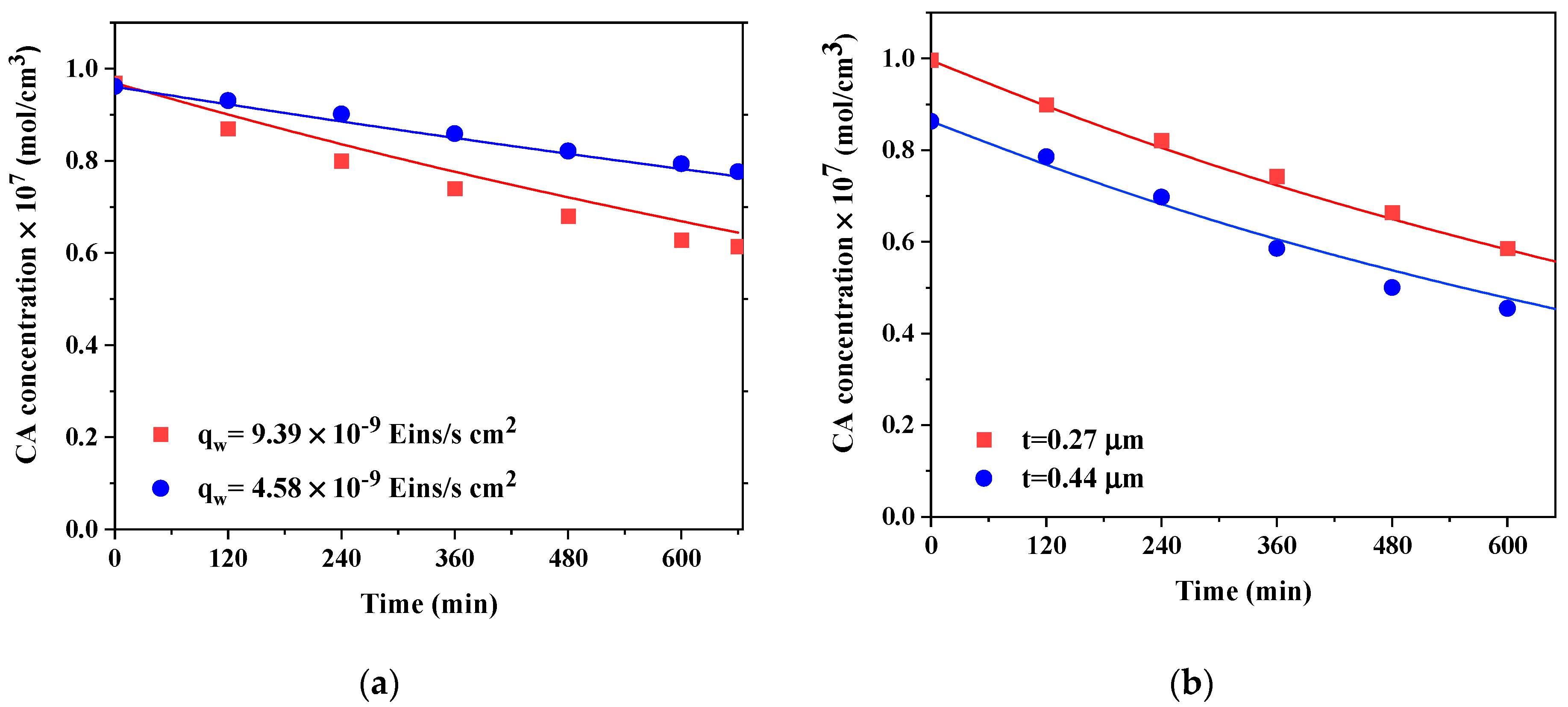
| Incident radiation fluxes, [Eins/(s cm2)] | (15.2, 9.39, 4.58) × 10−9 | (2.29, 2.94, 3.34) × 10−9 |
| Thickness of TiO2 film, [µm] | 0.27, 0.44 | 0.27, 3.24 |
| Step | Reaction | Reaction Rate |
|---|---|---|
| Activation | rgs | |
| Recombination | ||
| Electron trapping | ||
| Hole trapping | ||
| Hydroxyl radical attack |
| Characteristics | Cylindrical Reactor | Annular Reactor |
|---|---|---|
| Spatial dimension | 1D | 3D |
| Number of spatial cells | 103 | 106 |
| Coordinate system for photon location | Cartesian: x | Cylindrical:,, |
| Coordinate system for photon direction | Polar: θ | Spherical:,, |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Manassero, A.; Alfano, O.M.; Satuf, M.L. Degradation of Emerging Pollutants by Photocatalysis: Radiation Modeling and Kinetics in Packed-Bed Reactors. Water 2022, 14, 3608. https://doi.org/10.3390/w14223608
Manassero A, Alfano OM, Satuf ML. Degradation of Emerging Pollutants by Photocatalysis: Radiation Modeling and Kinetics in Packed-Bed Reactors. Water. 2022; 14(22):3608. https://doi.org/10.3390/w14223608
Chicago/Turabian StyleManassero, Agustina, Orlando Mario Alfano, and María Lucila Satuf. 2022. "Degradation of Emerging Pollutants by Photocatalysis: Radiation Modeling and Kinetics in Packed-Bed Reactors" Water 14, no. 22: 3608. https://doi.org/10.3390/w14223608