Covariance-Based Selection of Parameters for Particle Filter Data Assimilation in Soil Hydrology
Abstract
:1. Introduction
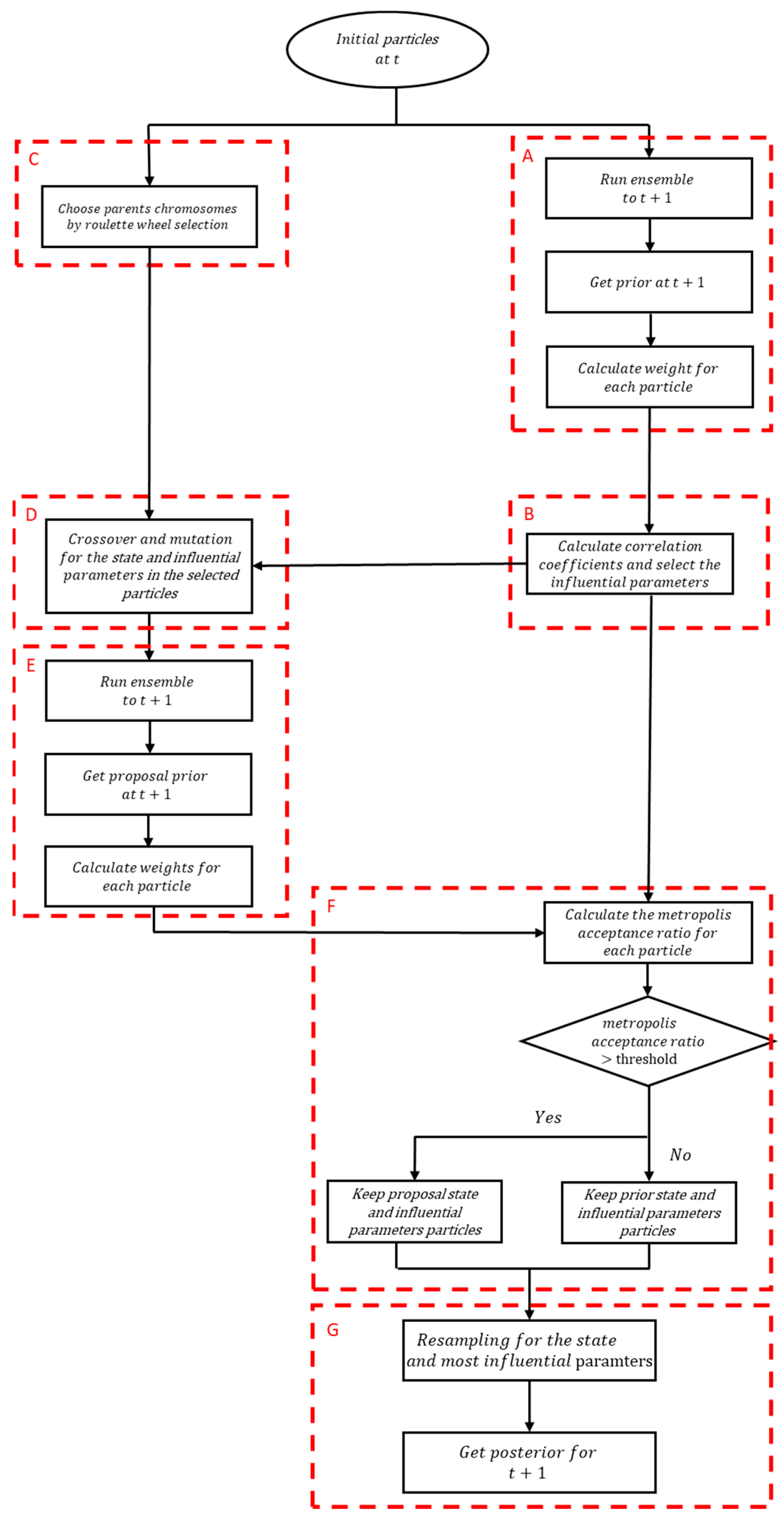
2. Methods
2.1. Particle Filtering
2.2. Correlation Analysis
3. Case Studies
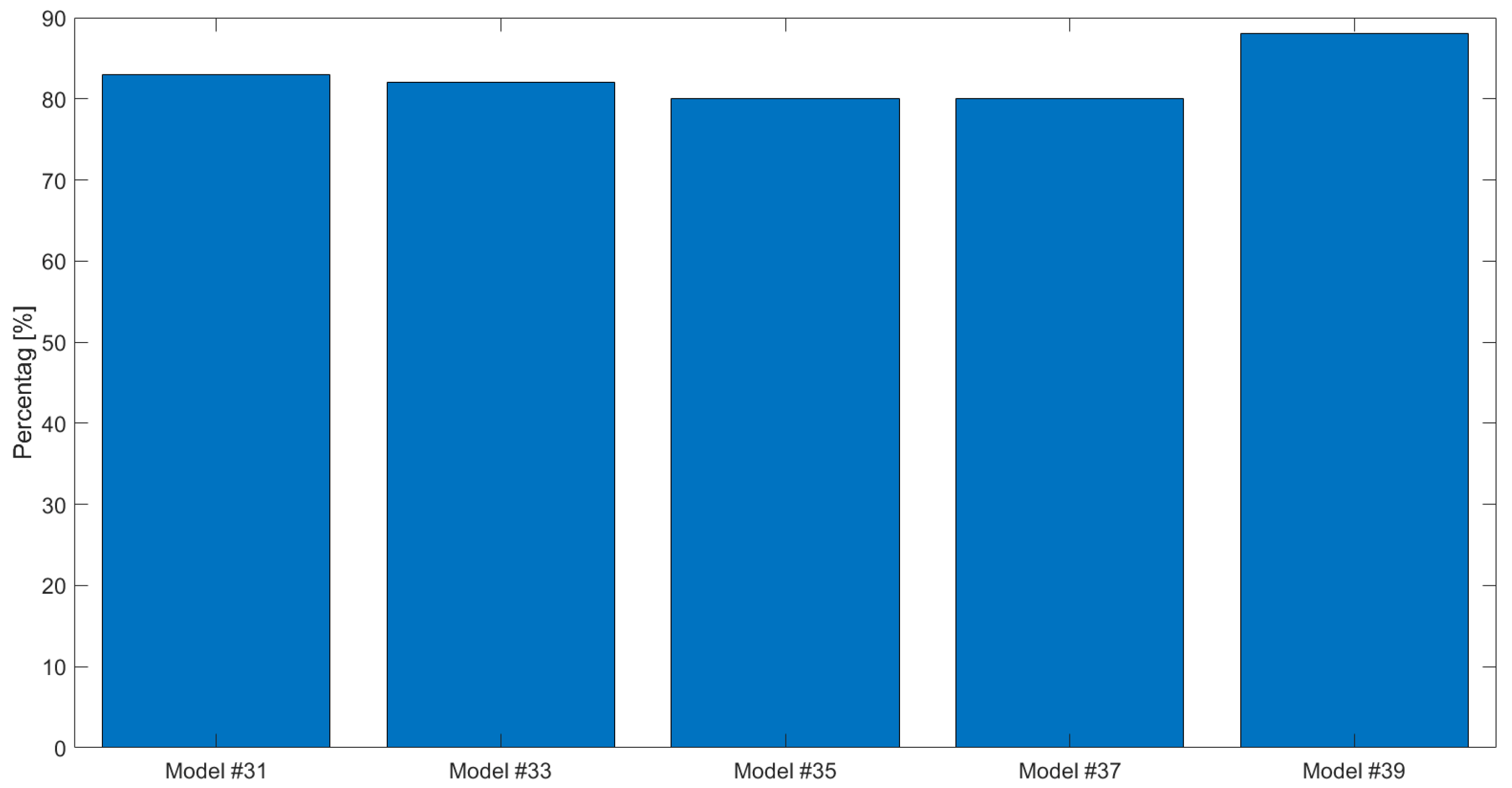
4. Results
4.1. Case Study #1—Random Boundary Condition
4.2. Case Study #2—Cyclic Boundary Condition
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Simunek, J.; Sejna, M.; Van Genuchten, M.T.; Šimůnek, J.; Šejna, M.; Jacques, D.; Sakai, M. HYDRUS-1D. Simulating the one-Dimensional Movement of Water, Heat, and Multiple Solutes in Variably-Saturated Media. 1998. Version 2. Available online: https://www.pc-progress.com/en/Default.aspx?hydrus-1d (accessed on 1 October 2022).
- Das, N.N.; Mohanty, B.P. Root zone soil moisture assessment using passive microwave remote sensing and vadose zonemodeling. Vadose Zone J. 2006, 5, 296–307. [Google Scholar] [CrossRef] [Green Version]
- Das, N.N.; Mohanty, B.P.; Cosh, M.H.; Jackson, T.J. Modeling and assimilation of root zone soil moisture using remote sensing observations in Walnut Gulch watershed during SMEX04. Remote Sens. Environ. 2008, 112, 415–429. [Google Scholar] [CrossRef]
- Brandhorst, N.; Erdal, D.; Neuweiler, I. Soil moisture prediction with the ensemble Kalman filter: Handling uncertainty of soil hydraulic parameters. Adv. Water Res. 2017, 110, 360–370. [Google Scholar] [CrossRef]
- Abbaszadeh, P.; Moradkhani, H.; Yan, H. Enhancing hydrologic data assimilation by evolutionary particle filter and Markov chain Monte Carlo. Adv. Water Res. 2018, 111, 192–204. [Google Scholar] [CrossRef]
- Bauser, H.H.; Berg, D.; Klein, O.; Roth, K. Inflation method for ensemble Kalman filter in soil hydrology. Hydrol. Earth Syst. Sci. 2018, 22, 4921–4934. [Google Scholar] [CrossRef] [Green Version]
- Berg, D.; Bauser, H.H.; Roth, K. Covariance resampling for particle filter–state and parameter estimation for soil hydrology. Hydrol. Earth Syst. Sci. 2019, 23, 1163–1178. [Google Scholar] [CrossRef] [Green Version]
- Jamal, A.; Linker, R. Inflation method based on confidence intervals for data assimilation in soil hydrology using ensemble Kalman filter. Vadose Zone J. 2020, 19, e20000. [Google Scholar] [CrossRef] [Green Version]
- Reichle, R.H.; McLaughlin, D.B.; Entekhabi, D. Hydrologic data assimilation with the ensemble Kalman filter. Mon. Weather Rev. 2002, 130, 103–114. [Google Scholar] [CrossRef]
- De Lannoy, G.J.; Reichle, R.H.; Houser, P.R.; Pauwels, V.R.; Verhoest, N.E. Correcting for forecast bias in soil moisture assimilation with the ensemble Kalman filter. Water Resour. Res. 2007, 43, 117. [Google Scholar] [CrossRef] [Green Version]
- DeChant, C.M.; Moradkhani, H. Examining the effectiveness and robustness of sequential data assimilation methods for quantification of uncertainty in hydrologic forecasting. Water Resour. Res. 2012, 48, 136. [Google Scholar] [CrossRef]
- Yin, S.; Zhu, X. Intelligent particle filter and its application to fault detection of nonlinear system. IEEE Trans. Ind. Electron. 2015, 62, 3852–3861. [Google Scholar] [CrossRef]
- Jamal, A.; Linker, R. Genetic Operator-Based Particle Filter Combined with Markov Chain Monte Carlo for Data Assimilation in a Crop Growth Model. Agriculture 2020, 10, 606. [Google Scholar] [CrossRef]
- Moradkhani, H.; Hsu, K.L.; Gupta, H.; Sorooshian, S. Uncertainty assessment of hydrologic model states and parameters: Sequential data assimilation using the particle filter. Water Resour. Res. 2005, 41, 480. [Google Scholar] [CrossRef] [Green Version]
- Moradkhani, H.; DeChant, C.M.; Sorooshian, S. Evolution of ensemble data assimilation for uncertainty quantification using the particle filter-Markov chain Monte Carlo method. Water Resour. Res. 2012, 48, 162. [Google Scholar] [CrossRef]
- Andrieu, C.; Doucet, A.; Holenstein, R. Particle markov chain monte carlo methods. J. R. Stat. Soc. Ser. B 2010, 72, 269–342. [Google Scholar] [CrossRef] [Green Version]
- Kroes, J.G.; Van Dam, J.C.; Bartholomeus, R.P.; Groenendijk, P.; Heinen, M.; Hendriks, R.F.A.; Van Walsum, P.E.V. SWAP Version 4 (No. 2780). Wageningen Environmental Research. 2017. Available online: https://research.wur.nl/en/publications/swap-version-4 (accessed on 1 October 2022).
- Hamby, D.M. A review of techniques for parameter sensitivity analysis of environmental models. Environ. Monit. Assess. 1994, 32, 135–154. [Google Scholar] [CrossRef]
- Della Peruta, R.; Keller, A.; Schulin, R. Sensitivity analysis, calibration and validation of EPIC for modelling soil phosphorus dynamics in Swiss agro-ecosystems. Environ. Model. Softw. 2014, 62, 97–111. [Google Scholar] [CrossRef]
- Wu, M.; Ran, Y.; Jansson, P.E.; Chen, P.; Tan, X.; Zhang, W. Global parameters sensitivity analysis of modeling water, energy and carbon exchange of an arid agricultural ecosystem. Agric. For. Meteorol. 2019, 271, 295–306. [Google Scholar]
- Xu, X.; Sun, C.; Huang, G.; Mohanty, B.P. Global sensitivity analysis and calibration of parameters for a physically-based agro-hydrological model. Environ. Model. Softw. 2016, 83, 88–102. [Google Scholar] [CrossRef] [Green Version]
- De Pue, J.; Rezaei, M.; Van Meirvenne, M.; Cornelis, W.M. The relevance of measuring saturated hydraulic conductivity: Sensitivity analysis and functional evaluation. J. Hydrol. 2019, 576, 628–638. [Google Scholar] [CrossRef]
- Claverie, M.; Demarez, V.; Duchemin, B.; Hagolle, O.; Ducrot, D.; Marais-Sicre, C.; Dedieu, G. Maize and sunflower biomass estimation in southwest France using high spatial and temporal resolution remote sensing data. Remote Sens. Environ. 2012, 124, 844–857. [Google Scholar] [CrossRef]
- Linker, R.; Kisekka, I. Concurrent data assimilation and model-based optimization of irrigation scheduling. Agric. Water Manag. 2022, 274, 107924. [Google Scholar] [CrossRef]
- Zhang, T.; Su, J.; Liu, C.; Chen, W.H. State and parameter estimation of the AquaCrop model for winter wheat using sensitivity informed particle filter. Comput. Electron. Agric. 2021, 180, 105909. [Google Scholar] [CrossRef]
- Manache, G.; Melching, C.S. Identification of reliable regression-and correlation-based sensitivity measures for importance ranking of water-quality model parameters. Environ. Model. Softw. 2008, 23, 549–562. [Google Scholar] [CrossRef]
- Shun, H.; Shi, L.; Huang, K.; Zha, Y.; Hu, X.; Ye, H.; Yang, Q. Improvement of sugarcane crop simulation by SWAP-WOFOST model via data assimilation. Field Crops Res. 2019, 232, 49–61. [Google Scholar]
- Gordon, N.J.; Salmond, D.J.; Smith, A.F. Novel approach to nonlinear/non-Gaussian Bayesian state estimation. IEE Proc. F (Radar Signal Process.) 1993, 140, 107–113. [Google Scholar] [CrossRef] [Green Version]
- Carpenter, J.; Clifford, P.; Fearnhead, P. Improved particle filter for nonlinear problems. IEE Proc. -Radar Sonar Navig. 1999, 146, 2–7. [Google Scholar] [CrossRef]
- Kitagawa, G. Monte Carlo filter and smoother for non-Gaussian nonlinear state space models. J. Comput. Graph. Stat. 1996, 5, 1–25. [Google Scholar]
- Asuero, A.G.; Sayago, A.; González, A.G. The correlation coefficient: An overview. Crit. Rev. Anal. Chem. 2006, 36, 41–59. [Google Scholar] [CrossRef]
- Rocha, D.; Abbasi, F.; Feyen, J. Sensitivity analysis of soil hydraulic properties on subsurface water flow in furrows. J. Irrig. Drain. Eng. 2006, 132, 418–424. [Google Scholar] [CrossRef]
- Schaap, M.G.; Leij, F.J.; Van Genuchten, M.T. Rosetta: A computer program for estimating soil hydraulic parameters with hierarchical pedotransfer functions. J. Hydrol. 2001, 251, 163–176. [Google Scholar] [CrossRef]
- Akoglu, H. User’s guide to correlation coefficients. Turk. J. Emerg. Med. 2018, 18, 91–93. [Google Scholar] [CrossRef] [PubMed]

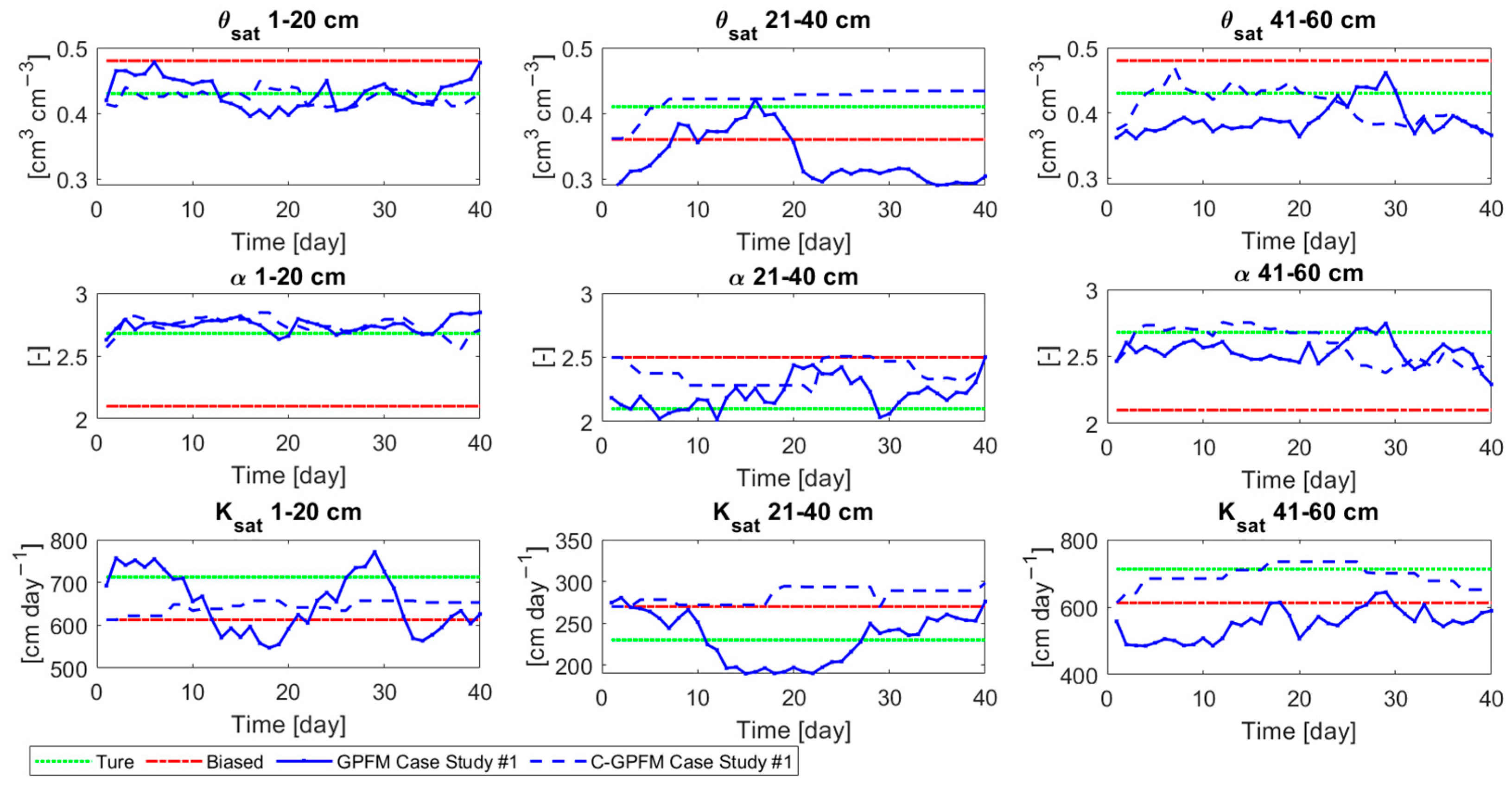






| Parameter | Description | Depth | ‘True’ | ‘Biased’ |
|---|---|---|---|---|
| Saturated water content | 0–20 cm 21–40 cm 41–60 cm | 0.43 0.41 0.43 | 0.48 0.36 0.48 | |
| Air entrance value parameters | 0–20 cm 21–40 cm 41–60 cm | 2.68 2.10 2.68 | 2.1 2.5 2.1 | |
| 0–20 cm 21–40 cm 41–60 cm | 713 230 713 | 613 270 613 | ||
| Residual water content | 0–20 cm 21–40 cm 41–60 cm | 0.045 0.061 0.045 | ||
| Shape parameter | 0–20 cm 21–40 cm 41–60 cm | 0.14 0.10 0.14 | ||
| Period | 0–20 cm Layer | 21–40 cm Layer | 41–60 cm Layer |
|---|---|---|---|
| Days 1–10 (wetting) | 2.63 | 1.42 | 0.71 |
| Days 11–20 (drying) | 0.36 | 0.24 | 0.77 |
| Days 21–30 (wetting) | 1.52 | 11.6 | 2.62 |
| Days 31–40 (drying) | 0.78 | 0.72 | 1.39 |
| Ratios Multiplication | 1.12 | 2.85 | 1.99 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jamal, A.; Linker, R. Covariance-Based Selection of Parameters for Particle Filter Data Assimilation in Soil Hydrology. Water 2022, 14, 3606. https://doi.org/10.3390/w14223606
Jamal A, Linker R. Covariance-Based Selection of Parameters for Particle Filter Data Assimilation in Soil Hydrology. Water. 2022; 14(22):3606. https://doi.org/10.3390/w14223606
Chicago/Turabian StyleJamal, Alaa, and Raphael Linker. 2022. "Covariance-Based Selection of Parameters for Particle Filter Data Assimilation in Soil Hydrology" Water 14, no. 22: 3606. https://doi.org/10.3390/w14223606




