Covariance-Based Selection of Parameters for Particle Filter Data Assimilation in Soil Hydrology
Abstract
1. Introduction
2. Methods
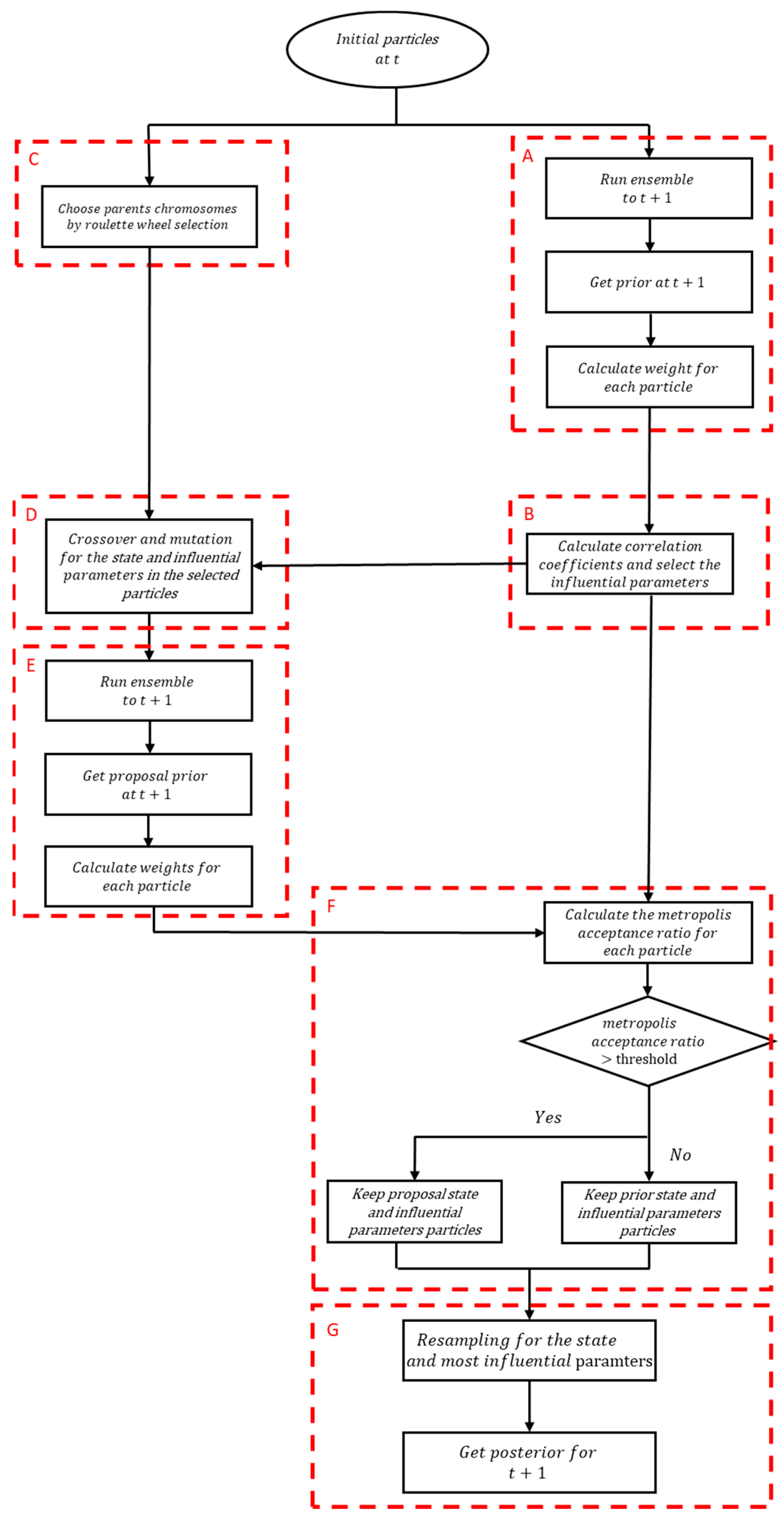
2.1. Particle Filtering
2.2. Correlation Analysis
3. Case Studies
4. Results
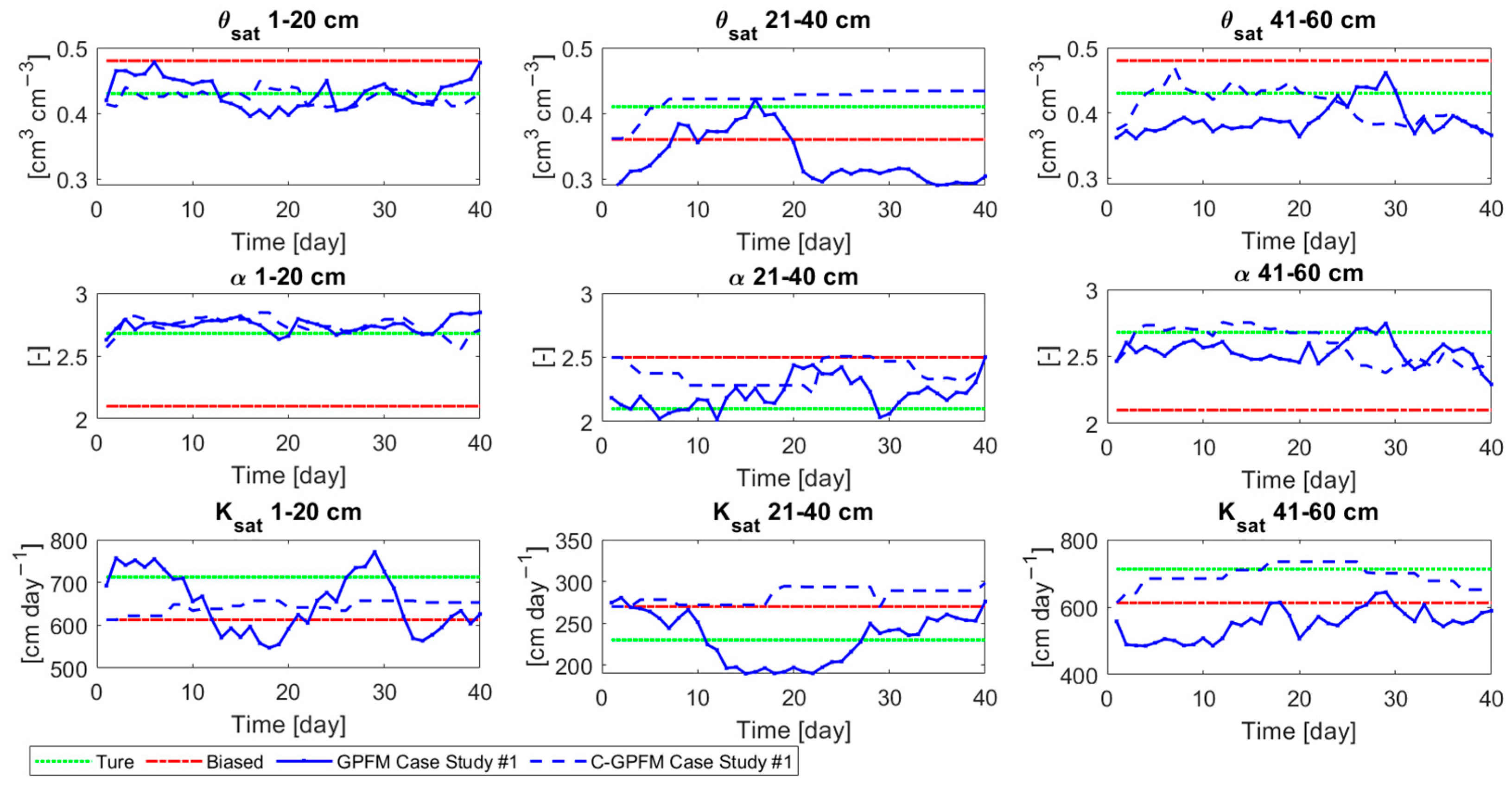
4.1. Case Study #1—Random Boundary Condition
4.2. Case Study #2—Cyclic Boundary Condition
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Simunek, J.; Sejna, M.; Van Genuchten, M.T.; Šimůnek, J.; Šejna, M.; Jacques, D.; Sakai, M. HYDRUS-1D. Simulating the one-Dimensional Movement of Water, Heat, and Multiple Solutes in Variably-Saturated Media. 1998. Version 2. Available online: https://www.pc-progress.com/en/Default.aspx?hydrus-1d (accessed on 1 October 2022).
- Das, N.N.; Mohanty, B.P. Root zone soil moisture assessment using passive microwave remote sensing and vadose zonemodeling. Vadose Zone J. 2006, 5, 296–307. [Google Scholar] [CrossRef]
- Das, N.N.; Mohanty, B.P.; Cosh, M.H.; Jackson, T.J. Modeling and assimilation of root zone soil moisture using remote sensing observations in Walnut Gulch watershed during SMEX04. Remote Sens. Environ. 2008, 112, 415–429. [Google Scholar] [CrossRef]
- Brandhorst, N.; Erdal, D.; Neuweiler, I. Soil moisture prediction with the ensemble Kalman filter: Handling uncertainty of soil hydraulic parameters. Adv. Water Res. 2017, 110, 360–370. [Google Scholar] [CrossRef]
- Abbaszadeh, P.; Moradkhani, H.; Yan, H. Enhancing hydrologic data assimilation by evolutionary particle filter and Markov chain Monte Carlo. Adv. Water Res. 2018, 111, 192–204. [Google Scholar] [CrossRef]
- Bauser, H.H.; Berg, D.; Klein, O.; Roth, K. Inflation method for ensemble Kalman filter in soil hydrology. Hydrol. Earth Syst. Sci. 2018, 22, 4921–4934. [Google Scholar] [CrossRef]
- Berg, D.; Bauser, H.H.; Roth, K. Covariance resampling for particle filter–state and parameter estimation for soil hydrology. Hydrol. Earth Syst. Sci. 2019, 23, 1163–1178. [Google Scholar] [CrossRef]
- Jamal, A.; Linker, R. Inflation method based on confidence intervals for data assimilation in soil hydrology using ensemble Kalman filter. Vadose Zone J. 2020, 19, e20000. [Google Scholar] [CrossRef]
- Reichle, R.H.; McLaughlin, D.B.; Entekhabi, D. Hydrologic data assimilation with the ensemble Kalman filter. Mon. Weather Rev. 2002, 130, 103–114. [Google Scholar] [CrossRef]
- De Lannoy, G.J.; Reichle, R.H.; Houser, P.R.; Pauwels, V.R.; Verhoest, N.E. Correcting for forecast bias in soil moisture assimilation with the ensemble Kalman filter. Water Resour. Res. 2007, 43, 117. [Google Scholar] [CrossRef]
- DeChant, C.M.; Moradkhani, H. Examining the effectiveness and robustness of sequential data assimilation methods for quantification of uncertainty in hydrologic forecasting. Water Resour. Res. 2012, 48, 136. [Google Scholar] [CrossRef]
- Yin, S.; Zhu, X. Intelligent particle filter and its application to fault detection of nonlinear system. IEEE Trans. Ind. Electron. 2015, 62, 3852–3861. [Google Scholar] [CrossRef]
- Jamal, A.; Linker, R. Genetic Operator-Based Particle Filter Combined with Markov Chain Monte Carlo for Data Assimilation in a Crop Growth Model. Agriculture 2020, 10, 606. [Google Scholar] [CrossRef]
- Moradkhani, H.; Hsu, K.L.; Gupta, H.; Sorooshian, S. Uncertainty assessment of hydrologic model states and parameters: Sequential data assimilation using the particle filter. Water Resour. Res. 2005, 41, 480. [Google Scholar] [CrossRef]
- Moradkhani, H.; DeChant, C.M.; Sorooshian, S. Evolution of ensemble data assimilation for uncertainty quantification using the particle filter-Markov chain Monte Carlo method. Water Resour. Res. 2012, 48, 162. [Google Scholar] [CrossRef]
- Andrieu, C.; Doucet, A.; Holenstein, R. Particle markov chain monte carlo methods. J. R. Stat. Soc. Ser. B 2010, 72, 269–342. [Google Scholar] [CrossRef]
- Kroes, J.G.; Van Dam, J.C.; Bartholomeus, R.P.; Groenendijk, P.; Heinen, M.; Hendriks, R.F.A.; Van Walsum, P.E.V. SWAP Version 4 (No. 2780). Wageningen Environmental Research. 2017. Available online: https://research.wur.nl/en/publications/swap-version-4 (accessed on 1 October 2022).
- Hamby, D.M. A review of techniques for parameter sensitivity analysis of environmental models. Environ. Monit. Assess. 1994, 32, 135–154. [Google Scholar] [CrossRef]
- Della Peruta, R.; Keller, A.; Schulin, R. Sensitivity analysis, calibration and validation of EPIC for modelling soil phosphorus dynamics in Swiss agro-ecosystems. Environ. Model. Softw. 2014, 62, 97–111. [Google Scholar] [CrossRef]
- Wu, M.; Ran, Y.; Jansson, P.E.; Chen, P.; Tan, X.; Zhang, W. Global parameters sensitivity analysis of modeling water, energy and carbon exchange of an arid agricultural ecosystem. Agric. For. Meteorol. 2019, 271, 295–306. [Google Scholar]
- Xu, X.; Sun, C.; Huang, G.; Mohanty, B.P. Global sensitivity analysis and calibration of parameters for a physically-based agro-hydrological model. Environ. Model. Softw. 2016, 83, 88–102. [Google Scholar] [CrossRef]
- De Pue, J.; Rezaei, M.; Van Meirvenne, M.; Cornelis, W.M. The relevance of measuring saturated hydraulic conductivity: Sensitivity analysis and functional evaluation. J. Hydrol. 2019, 576, 628–638. [Google Scholar] [CrossRef]
- Claverie, M.; Demarez, V.; Duchemin, B.; Hagolle, O.; Ducrot, D.; Marais-Sicre, C.; Dedieu, G. Maize and sunflower biomass estimation in southwest France using high spatial and temporal resolution remote sensing data. Remote Sens. Environ. 2012, 124, 844–857. [Google Scholar] [CrossRef]
- Linker, R.; Kisekka, I. Concurrent data assimilation and model-based optimization of irrigation scheduling. Agric. Water Manag. 2022, 274, 107924. [Google Scholar] [CrossRef]
- Zhang, T.; Su, J.; Liu, C.; Chen, W.H. State and parameter estimation of the AquaCrop model for winter wheat using sensitivity informed particle filter. Comput. Electron. Agric. 2021, 180, 105909. [Google Scholar] [CrossRef]
- Manache, G.; Melching, C.S. Identification of reliable regression-and correlation-based sensitivity measures for importance ranking of water-quality model parameters. Environ. Model. Softw. 2008, 23, 549–562. [Google Scholar] [CrossRef]
- Shun, H.; Shi, L.; Huang, K.; Zha, Y.; Hu, X.; Ye, H.; Yang, Q. Improvement of sugarcane crop simulation by SWAP-WOFOST model via data assimilation. Field Crops Res. 2019, 232, 49–61. [Google Scholar]
- Gordon, N.J.; Salmond, D.J.; Smith, A.F. Novel approach to nonlinear/non-Gaussian Bayesian state estimation. IEE Proc. F (Radar Signal Process.) 1993, 140, 107–113. [Google Scholar] [CrossRef]
- Carpenter, J.; Clifford, P.; Fearnhead, P. Improved particle filter for nonlinear problems. IEE Proc. -Radar Sonar Navig. 1999, 146, 2–7. [Google Scholar] [CrossRef]
- Kitagawa, G. Monte Carlo filter and smoother for non-Gaussian nonlinear state space models. J. Comput. Graph. Stat. 1996, 5, 1–25. [Google Scholar]
- Asuero, A.G.; Sayago, A.; González, A.G. The correlation coefficient: An overview. Crit. Rev. Anal. Chem. 2006, 36, 41–59. [Google Scholar] [CrossRef]
- Rocha, D.; Abbasi, F.; Feyen, J. Sensitivity analysis of soil hydraulic properties on subsurface water flow in furrows. J. Irrig. Drain. Eng. 2006, 132, 418–424. [Google Scholar] [CrossRef]
- Schaap, M.G.; Leij, F.J.; Van Genuchten, M.T. Rosetta: A computer program for estimating soil hydraulic parameters with hierarchical pedotransfer functions. J. Hydrol. 2001, 251, 163–176. [Google Scholar] [CrossRef]
- Akoglu, H. User’s guide to correlation coefficients. Turk. J. Emerg. Med. 2018, 18, 91–93. [Google Scholar] [CrossRef] [PubMed]







| Parameter | Description | Depth | ‘True’ | ‘Biased’ |
|---|---|---|---|---|
| Saturated water content | 0–20 cm 21–40 cm 41–60 cm | 0.43 0.41 0.43 | 0.48 0.36 0.48 | |
| Air entrance value parameters | 0–20 cm 21–40 cm 41–60 cm | 2.68 2.10 2.68 | 2.1 2.5 2.1 | |
| 0–20 cm 21–40 cm 41–60 cm | 713 230 713 | 613 270 613 | ||
| Residual water content | 0–20 cm 21–40 cm 41–60 cm | 0.045 0.061 0.045 | ||
| Shape parameter | 0–20 cm 21–40 cm 41–60 cm | 0.14 0.10 0.14 | ||
| Period | 0–20 cm Layer | 21–40 cm Layer | 41–60 cm Layer |
|---|---|---|---|
| Days 1–10 (wetting) | 2.63 | 1.42 | 0.71 |
| Days 11–20 (drying) | 0.36 | 0.24 | 0.77 |
| Days 21–30 (wetting) | 1.52 | 11.6 | 2.62 |
| Days 31–40 (drying) | 0.78 | 0.72 | 1.39 |
| Ratios Multiplication | 1.12 | 2.85 | 1.99 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jamal, A.; Linker, R. Covariance-Based Selection of Parameters for Particle Filter Data Assimilation in Soil Hydrology. Water 2022, 14, 3606. https://doi.org/10.3390/w14223606
Jamal A, Linker R. Covariance-Based Selection of Parameters for Particle Filter Data Assimilation in Soil Hydrology. Water. 2022; 14(22):3606. https://doi.org/10.3390/w14223606
Chicago/Turabian StyleJamal, Alaa, and Raphael Linker. 2022. "Covariance-Based Selection of Parameters for Particle Filter Data Assimilation in Soil Hydrology" Water 14, no. 22: 3606. https://doi.org/10.3390/w14223606
APA StyleJamal, A., & Linker, R. (2022). Covariance-Based Selection of Parameters for Particle Filter Data Assimilation in Soil Hydrology. Water, 14(22), 3606. https://doi.org/10.3390/w14223606





