Real-Time Data-Processing Framework with Model Updating for Digital Twins of Water Treatment Facilities
Abstract
:1. Introduction
2. Materials and Methods
2.1. Real-Time Data-Processing Framework
2.2. Coverage-Based Updating Algorithms
3. Datasets and Models
3.1. Testbed and Datasets
3.2. Models and Assessment of Accuracy
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| frequency of ith bin | |
| frequency of ith bin in max area | |
| frequency of ith bin in min area | |
| density of ith bin | |
| density of ith bin in max area | |
| density of ith bin in min area | |
| threshold of frequency density in histogram selection criteria | |
| number of bins | |
| number of useful samples in the insufficient bin | |
| maximum target value in the original training dataset | |
| minimum target value in the original training dataset | |
| bin width | |
| maximum target value in the previous training dataset | |
| minimum target value in the previous training dataset | |
| maximum target value in the new training dataset | |
| minimum target value in the new training dataset |
References
- Tao, F.; Zhang, H.; Liu, A.; Nee, A.Y. Digital twin in industry: State-of-the-art. IEEE Trans. Ind. Inform. 2018, 15, 2405–2415. [Google Scholar] [CrossRef]
- Kaur, M.J.; Mishra, V.P.; Maheshwari, P. The convergence of digital twin, IoT, and machine learning: Transforming data into action. In Digital Twin Technologies and Smart Cities; Springer: Berlin/Heidelberg, Germany, 2020; pp. 3–17. [Google Scholar]
- Silva, A.J.; Cortez, P.; Pereira, C.; Pilastri, A. Business analytics in industry 4.0: A systematic review. Expert Syst. 2021, 38, e12741. [Google Scholar] [CrossRef]
- Min, Q.; Lu, Y.; Liu, Z.; Su, C.; Wang, B. Machine learning based digital twin framework for production optimization in petrochemical industry. Int. J. Inf. Manag. 2019, 49, 502–519. [Google Scholar] [CrossRef]
- Snijders, R.; Pileggi, P.; Broekhuijsen, J.; Verriet, J.; Wiering, M.; Kok, K. Machine learning for digital twins to predict responsiveness of cyber-physical energy systems. In Proceedings of the 2020 8th Workshop on Modeling and Simulation of Cyber-Physical Energy Systems, online, 21 April 2020; pp. 1–6. [Google Scholar]
- Xu, Q.; Ali, S.; Yue, T. Digital twin-based anomaly detection in cyber-physical systems. In Proceedings of the 2021 14th IEEE Conference on Software Testing, Verification and Validation (ICST), Porto de Galinhas, Brazil, 12–16 April 2021; pp. 205–216. [Google Scholar]
- Wang, J.; Ye, L.; Gao, R.X.; Li, C.; Zhang, L. Digital Twin for rotating machinery fault diagnosis in smart manufacturing. Int. J. Prod. Res. 2019, 57, 3920–3934. [Google Scholar] [CrossRef]
- Wei, Y.; Hu, T.; Zhou, T.; Ye, Y.; Luo, W. Consistency retention method for CNC machine tool digital twin model. J. Manuf. Syst. 2021, 58, 313–322. [Google Scholar] [CrossRef]
- Farhat, M.H.; Chiementin, X.; Chaari, F.; Bolaers, F.; Haddar, M. Digital twin-driven machine learning: Ball bearings fault severity classification. Meas. Sci. Technol. 2021, 32, 044006. [Google Scholar] [CrossRef]
- Adam, G.A.; Chang, C.-H.K.; Haibe-Kains, B.; Goldenberg, A. Error Amplification When Updating Deployed Machine Learning Models. In Proceedings of the Machine Learning for Healthcare Conference, Durham, NC, USA, 5–6 August 2022. [Google Scholar]
- Li, D.-C.; Chang, C.-C.; Liu, C.-W.; Chen, W.-C. A new approach for manufacturing forecast problems with insufficient data: The case of TFT–LCDs. J. Intell. Manuf. 2013, 24, 225–233. [Google Scholar] [CrossRef]
- Li, D.-C.; Wu, C.-S.; Tsai, T.-I.; Lina, Y.-S. Using mega-trend-diffusion and artificial samples in small data set learning for early flexible manufacturing system scheduling knowledge. Comput. Oper. Res. 2007, 34, 966–982. [Google Scholar] [CrossRef]
- Wei, Y.; Law, A.W.-K.; Yang, C.; Tang, D. Combined Anomaly Detection Framework for Digital Twins of Water Treatment Facilities. Water 2022, 14, 1001. [Google Scholar] [CrossRef]
- Qi, D.; Majda, A.J. Using machine learning to predict extreme events in complex systems. Proc. Natl. Acad. Sci. USA 2020, 117, 52–59. [Google Scholar] [CrossRef]
- Gepperth, A.; Hammer, B. Incremental learning algorithms and applications. In Proceedings of the European Symposium on Artificial Neural Networks (ESANN), Bruges, Belgium, 27–29 April 2016. [Google Scholar]
- Castro, F.M.; Marín-Jiménez, M.J.; Guil, N.; Schmid, C.; Alahari, K. End-to-end incremental learning. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018. [Google Scholar]
- Rebuffi, S.-A.; Kolesnikov, A.; Sperl, G.; Lampert, C.H. icarl: Incremental classifier and representation learning. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017. [Google Scholar]
- Wu, Y.; Chen, Y.; Wang, L.; Ye, Y.; Liu, Z.; Guo, Y.; Fu, Y. Large scale incremental learning. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019. [Google Scholar]
- Chen, T.; Guestrin, C. Xgboost: A scalable tree boosting system. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016. [Google Scholar]
- Tarasenko, A. Is It Possible to Update a Model with New Data without Retraining the Model from Scratch? Available online: https://github.com/dmlc/xgboost/issues/3055#issuecomment-359648107 (accessed on 1 September 2022).
- Zhang, P.; Zhou, C.; Wang, P.; Gao, B.J.; Zhu, X.; Guo, L. E-Tree: An Efficient Indexing Structure for Ensemble Models on Data Streams. IEEE Trans. Knowl. Data Eng. 2015, 27, 461–474. [Google Scholar] [CrossRef]
- Guajardo, J.A.; Weber, R.; Miranda, J. A model updating strategy for predicting time series with seasonal patterns. Appl. Soft Comput. 2010, 10, 276–283. [Google Scholar] [CrossRef]
- Liu, Q.; Hu, X.; Ye, M.; Cheng, X.; Li, F. Gas recognition under sensor drift by using deep learning. Int. J. Intell. Syst. 2015, 30, 907–922. [Google Scholar] [CrossRef]
- Wang, X.; Fan, Y.; Huang, Y.; Ling, J.; Klimowicz, A.; Pagano, G.; Li, B. Solving Sensor Reading Drifting Using Denoising Data Processing Algorithm (DDPA) for Long-Term Continuous and Accurate Monitoring of Ammonium in Wastewater. ACS EST Water 2020, 1, 530–541. [Google Scholar] [CrossRef]
- Leigh, C.; Alsibai, O.; Hyndman, R.J.; Kandanaarachchi, S.; King, O.C.; McGree, J.M.; Neelamraju, C.; Strauss, J.; Talagala, P.D.; Turner, R.D. A framework for automated anomaly detection in high frequency water-quality data from in situ sensors. Sci. Total Environ. 2019, 664, 885–898. [Google Scholar] [CrossRef] [Green Version]
- Maag, B.; Zhou, Z.; Thiele, L. A survey on sensor calibration in air pollution monitoring deployments. IEEE Internet Things J. 2018, 5, 4857–4870. [Google Scholar] [CrossRef] [Green Version]
- Malinin, A.; Prokhorenkova, L.; Ustimenko, A. Uncertainty in Gradient Boosting via Ensembles. In Proceedings of the International Conference on Learning Representations, Online, 3–7 May 2021. [Google Scholar]
- Yang, Y.; Che, J.; Li, Y.; Zhao, Y.; Zhu, S. An incremental electric load forecasting model based on support vector regression. Energy 2016, 113, 796–808. [Google Scholar] [CrossRef]
- Mathur, A.P.; Tippenhauer, N.O. SWaT: A water treatment testbed for research and training on ICS security. In Proceedings of the 2016 International Workshop on Cyber-Physical Systems for Smart Water Networks (CySWater), Vienna, Austria, 11 April 2016. [Google Scholar]
- Raman, M.G.; Dong, W.; Mathur, A. Deep autoencoders as anomaly detectors: Method and case study in a distributed water treatment plant. Comput. Secur. 2020, 99, 102055. [Google Scholar] [CrossRef]
- Wang, D.; Thunéll, S.; Lindberg, U.; Jiang, L.; Trygg, J.; Tysklind, M.; Souihi, N. A machine learning framework to improve effluent quality control in wastewater treatment plants. Sci. Total Environ. 2021, 784, 147138. [Google Scholar] [CrossRef]
- Li, L.; Rong, S.; Wang, R.; Yu, S. Recent advances in artificial intelligence and machine learning for nonlinear relationship analysis and process control in drinking water treatment: A review. Chem. Eng. J. 2021, 405, 126673. [Google Scholar] [CrossRef]
- Al Aani, S.; Bonny, T.; Hasan, S.W.; Hilal, N. Can machine language and artificial intelligence revolutionize process automation for water treatment and desalination? Desalination 2019, 458, 84–96. [Google Scholar] [CrossRef]
- Newhart, K.B.; Goldman-Torres, J.E.; Freedman, D.E.; Wisdom, K.B.; Hering, A.S.; Cath, T.Y. Prediction of peracetic acid disinfection performance for secondary municipal wastewater treatment using artificial neural networks. ACS EST Water 2020, 1, 328–338. [Google Scholar] [CrossRef]
- Duan, T.; Anand, A.; Ding, D.Y.; Thai, K.K.; Basu, S.; Ng, A.; Schuler, A. Ngboost: Natural gradient boosting for probabilistic prediction. In Proceedings of the International Conference on Machine Learning, Online, 13–18 July 2020; pp. 2690–2700. [Google Scholar]
- Salcedo-Sanz, S.; Cornejo-Bueno, L.; Prieto, L.; Paredes, D.; García-Herrera, R. Feature selection in machine learning prediction systems for renewable energy applications. Renew. Sustain. Energy Rev. 2018, 90, 728–741. [Google Scholar] [CrossRef]
- Liashchynskyi, P.; Liashchynskyi, P. Grid search, random search, genetic algorithm: A big comparison for nas. arXiv 2019, arXiv:1912.06059. [Google Scholar]

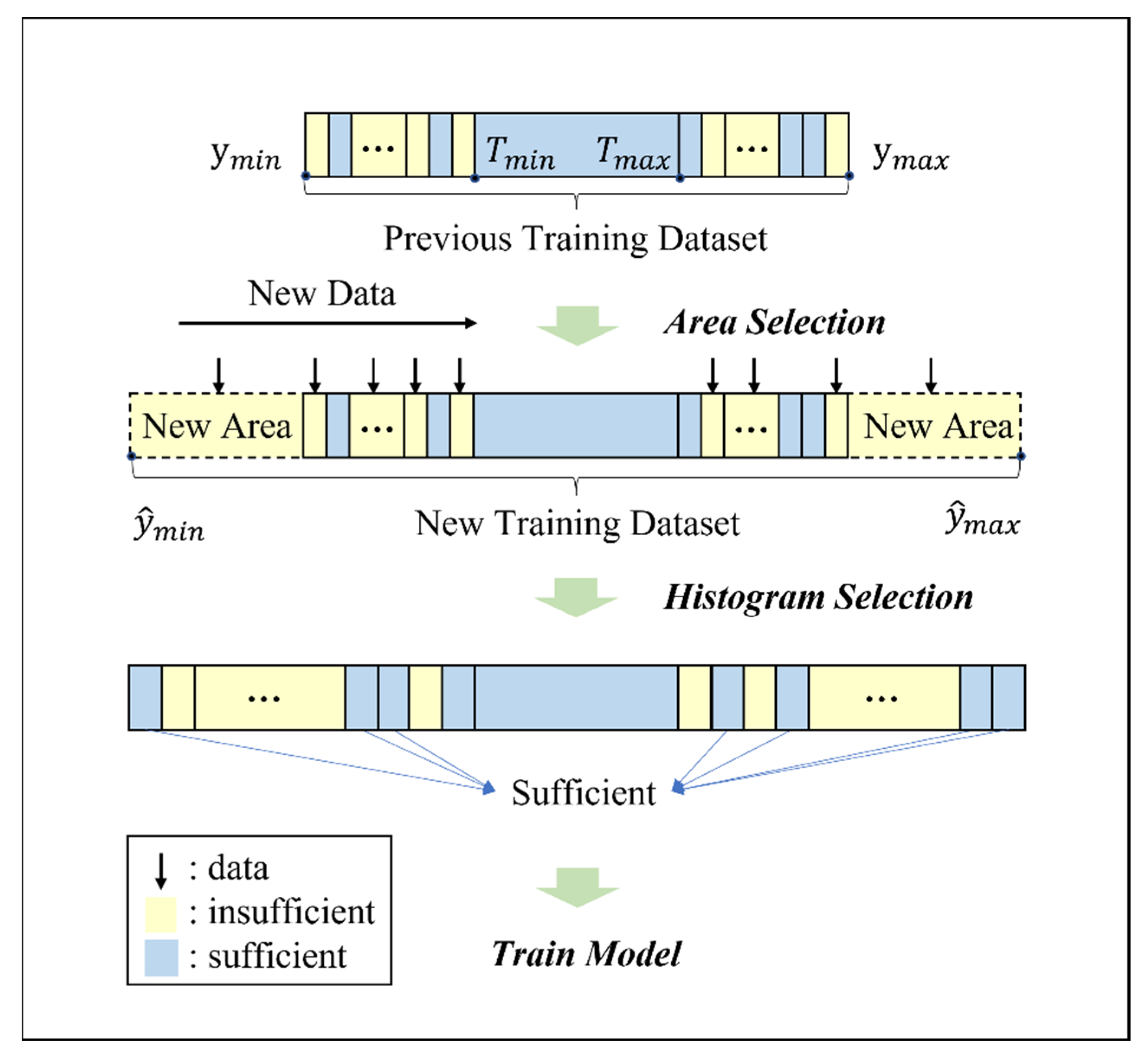




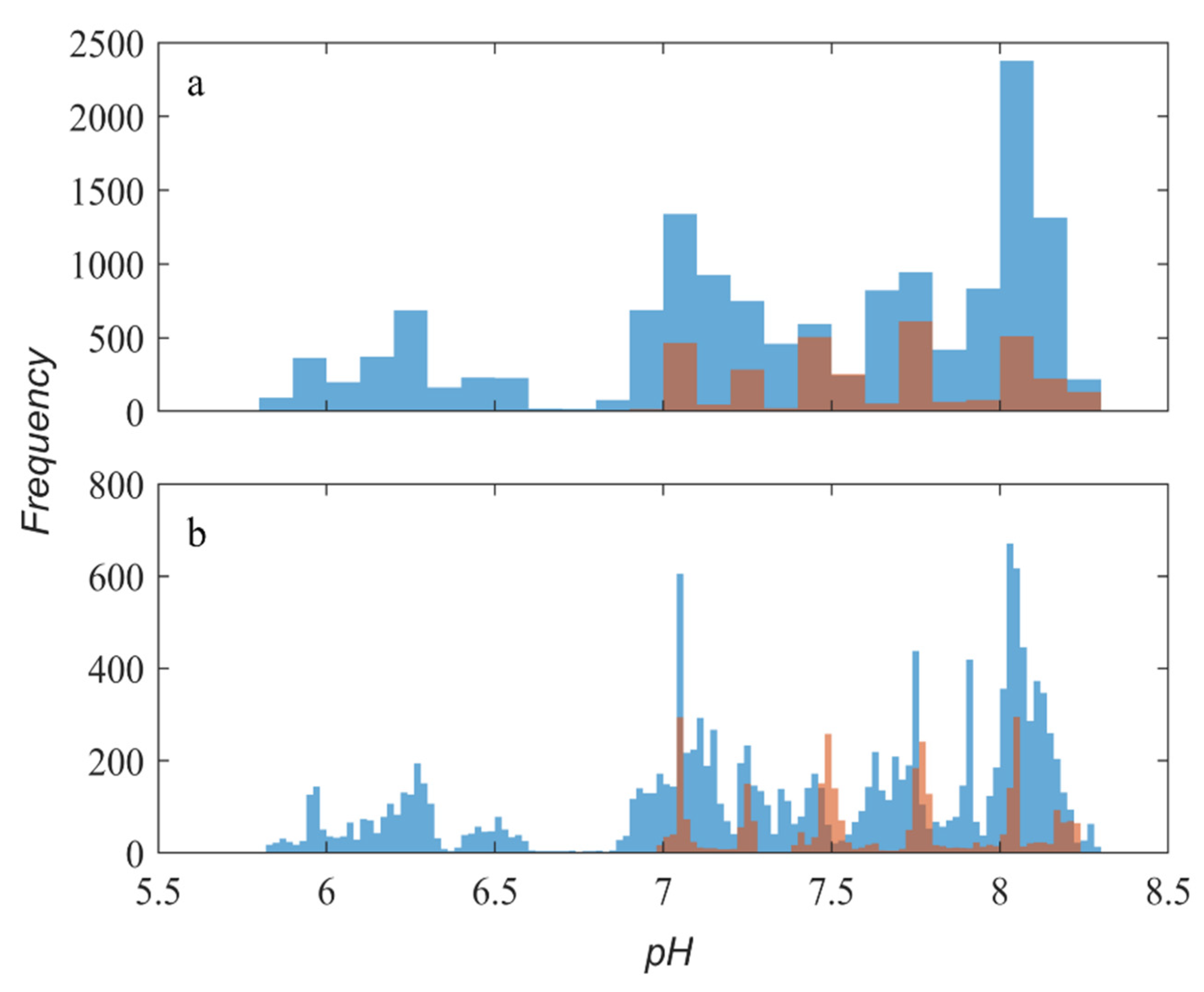

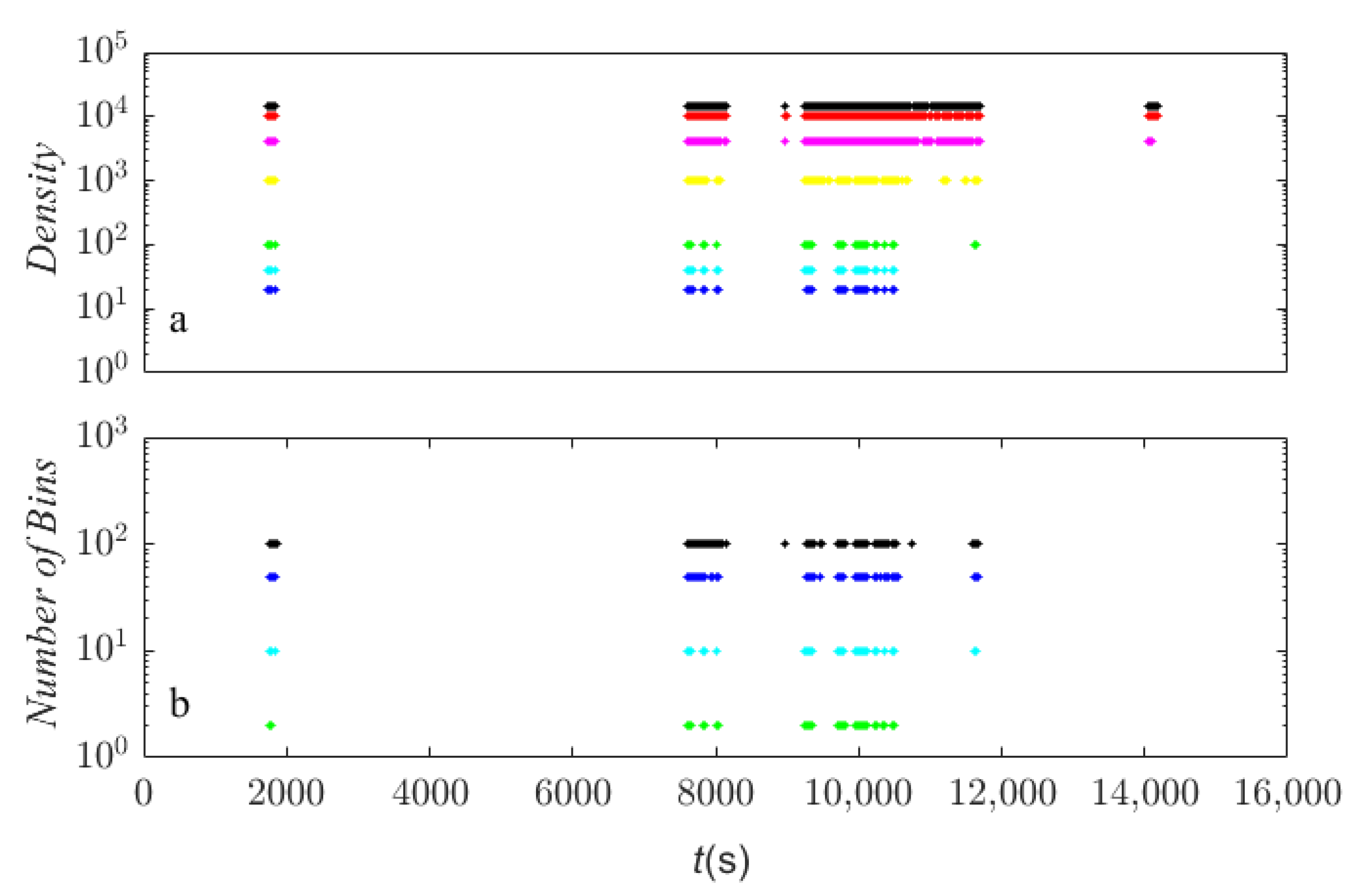
| Dataset | Size | Usage Purpose |
|---|---|---|
| Dataset 1 | 3282 samples | Original training dataset |
| Dataset 2 | 14,394 samples | Real-time data stream simulation |
| Dataset 3 | 218,952 samples | Model evaluation |
| Hyperparameter | Result |
|---|---|
| Base learner | DecisionTreeRegressor with max depth 4 |
| Distribution | Normal |
| Scoring rule | CRPScore |
| Minibatch fraction | 1 |
| Iterations | 500 |
| Subsample fraction | 1 |
| Learning rate | 0.1 |
| Extra Time (s) | 0 | 60 | 300 | 600 | 1800 |
| MAE | 0.01 | 0.04 | 0.12 | 0.22 | 0.53 |
| Density | 15,000 | 10,000 | 4000 | 1000 | 100 | 40 | 20 |
| MAE | 0.016 | 0.015 | 0.014 | 0.015 | 0.020 | 0.023 | 0.024 |
| Bins | 100 | 50 | 10 | 2 |
| Density = 4000 | 0.013 | 0.013 | 0.014 | 0.013 |
| Density = 100 | 0.017 | 0.019 | 0.020 | 0.021 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wei, Y.; Law, A.W.-K.; Yang, C. Real-Time Data-Processing Framework with Model Updating for Digital Twins of Water Treatment Facilities. Water 2022, 14, 3591. https://doi.org/10.3390/w14223591
Wei Y, Law AW-K, Yang C. Real-Time Data-Processing Framework with Model Updating for Digital Twins of Water Treatment Facilities. Water. 2022; 14(22):3591. https://doi.org/10.3390/w14223591
Chicago/Turabian StyleWei, Yuying, Adrian Wing-Keung Law, and Chun Yang. 2022. "Real-Time Data-Processing Framework with Model Updating for Digital Twins of Water Treatment Facilities" Water 14, no. 22: 3591. https://doi.org/10.3390/w14223591
APA StyleWei, Y., Law, A. W.-K., & Yang, C. (2022). Real-Time Data-Processing Framework with Model Updating for Digital Twins of Water Treatment Facilities. Water, 14(22), 3591. https://doi.org/10.3390/w14223591







