City Flood Disaster Scenario Simulation Based on 1D–2D Coupled Rain–Flood Model
Abstract
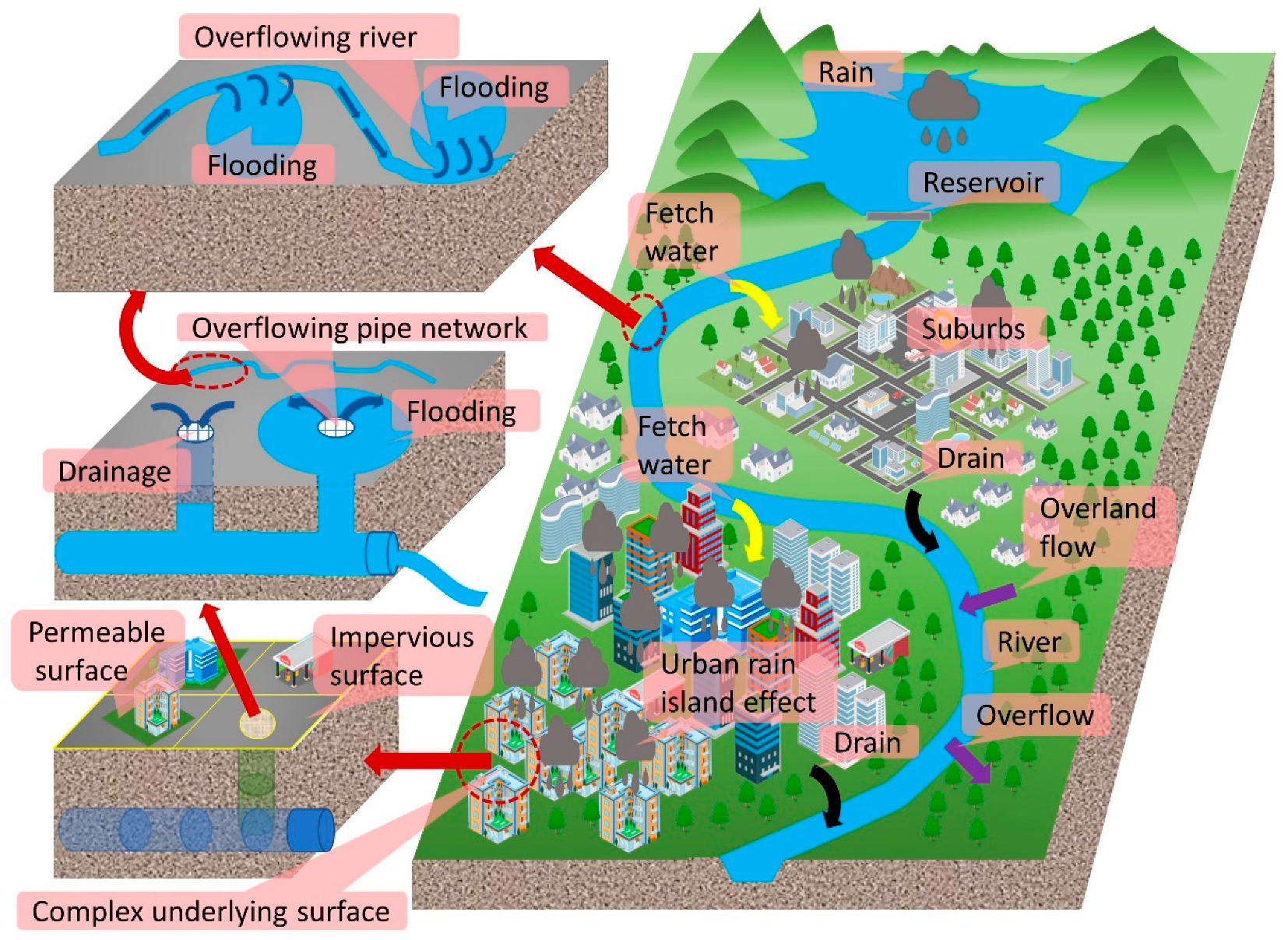
:1. Introduction
2. Materials and Methods
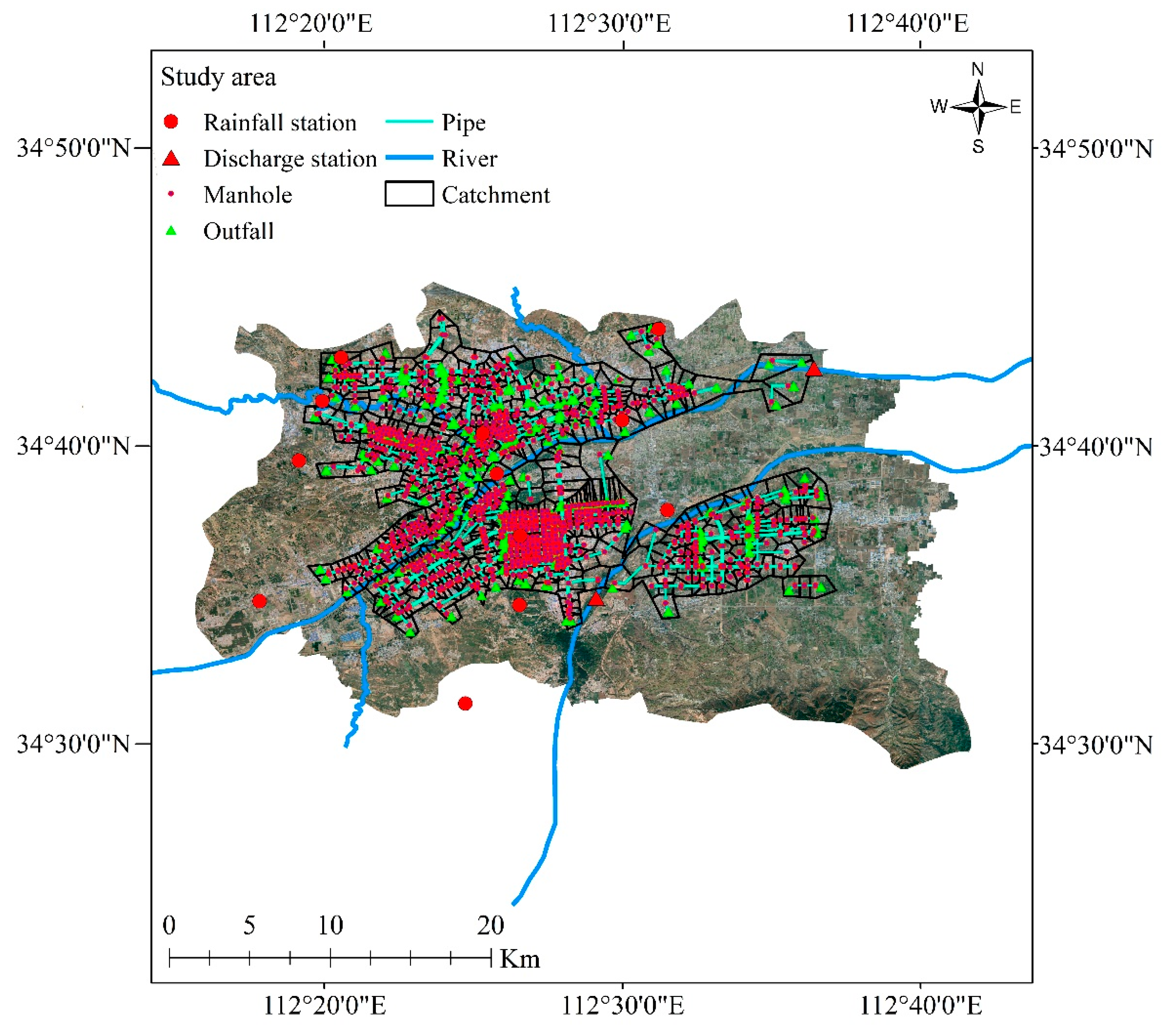
2.1. Study Site
2.2. Data Availability and Processing
2.2.1. Topographic Data
2.2.2. Drainage System Data
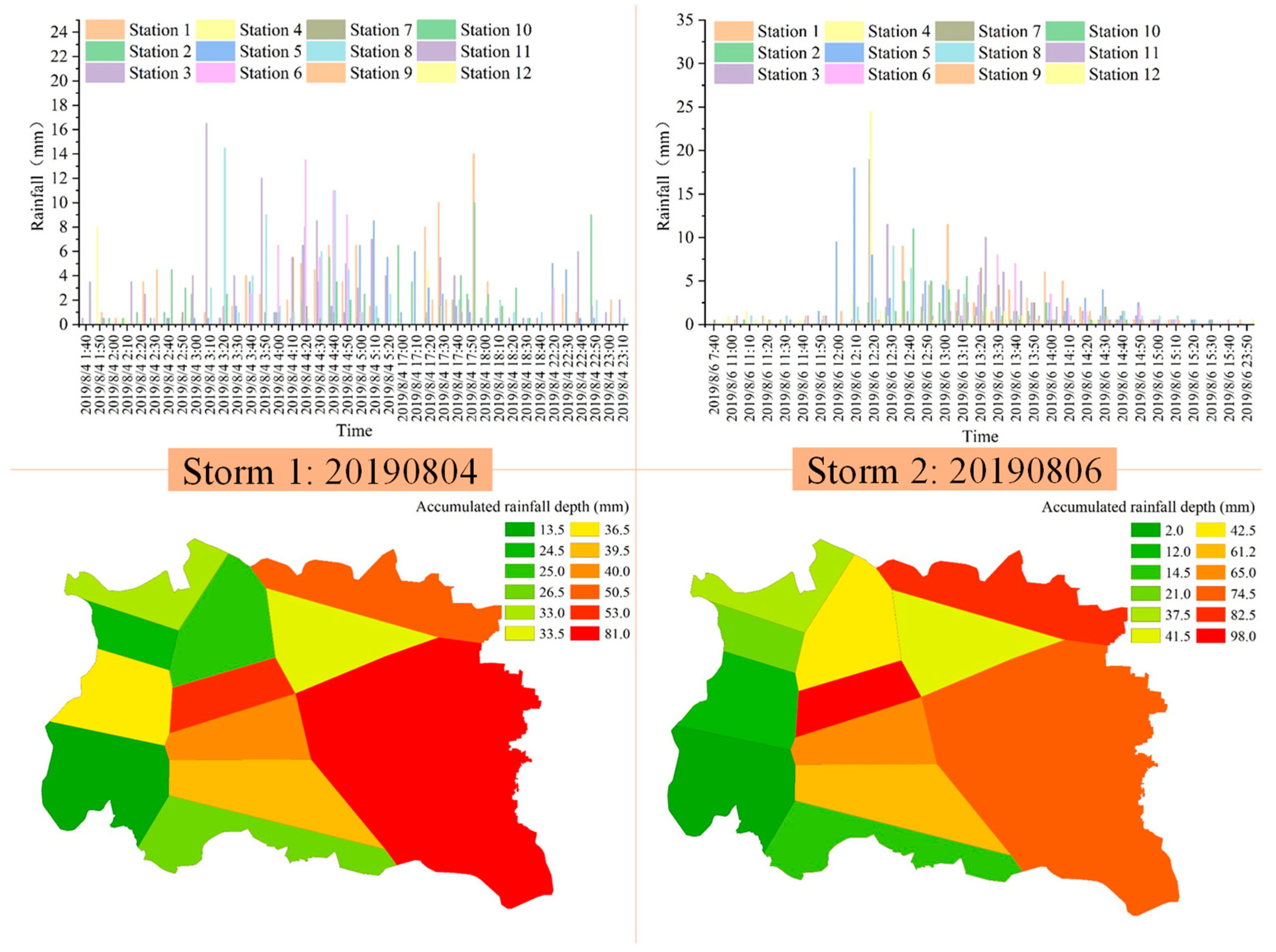
2.2.3. Rainstorm Data
2.3. 1D–2D Couples Model
2.3.1. Pipe and River Model
2.3.2. DSW Model
2.4. Model Evaluation Indicator Selection
2.4.1. Absolute Error
2.4.2. Relative Error
2.4.3. The Coefficient of Determination
2.4.4. Nash–Sutcliffe Efficiency
3. Result and Discussion
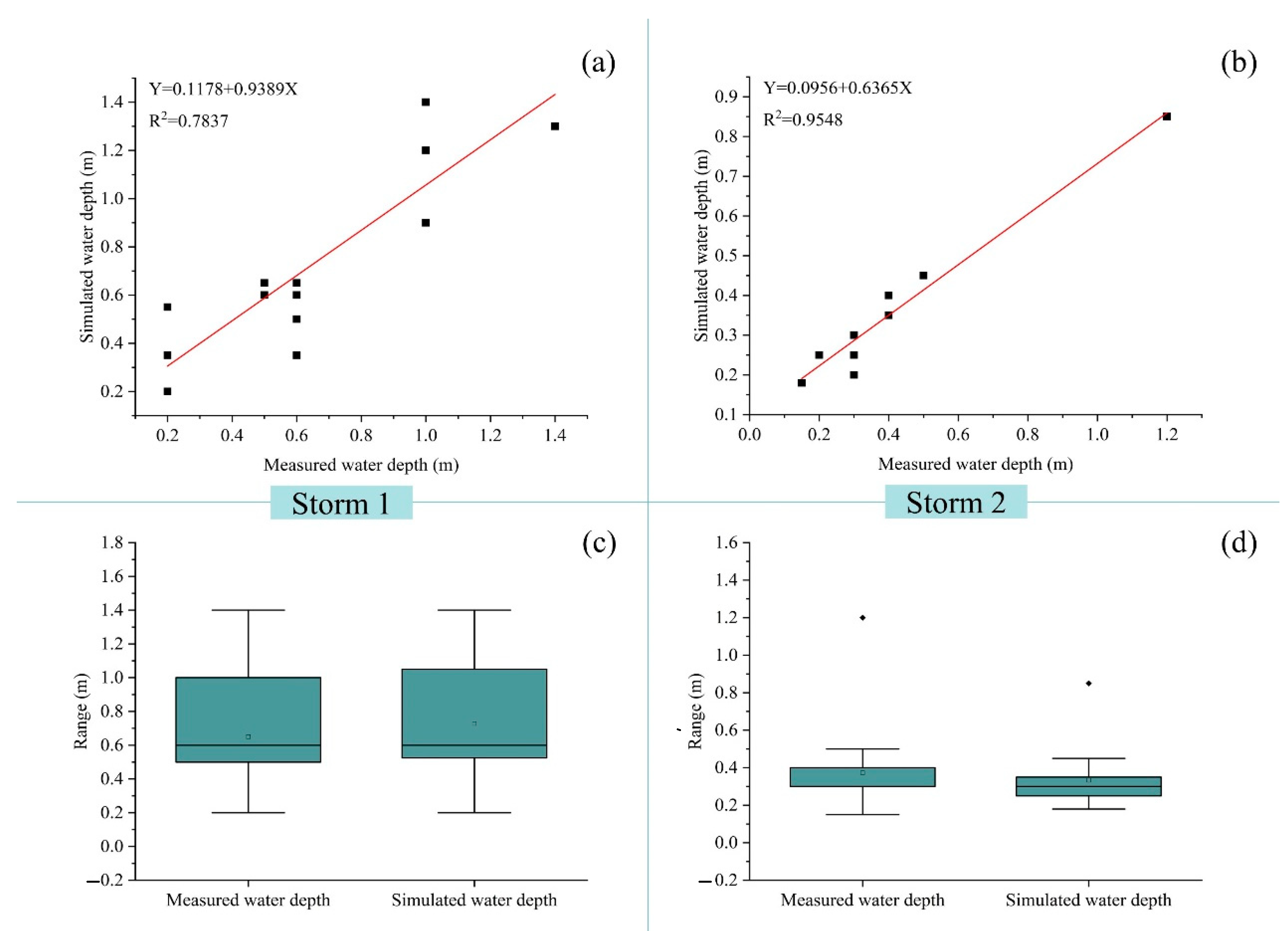
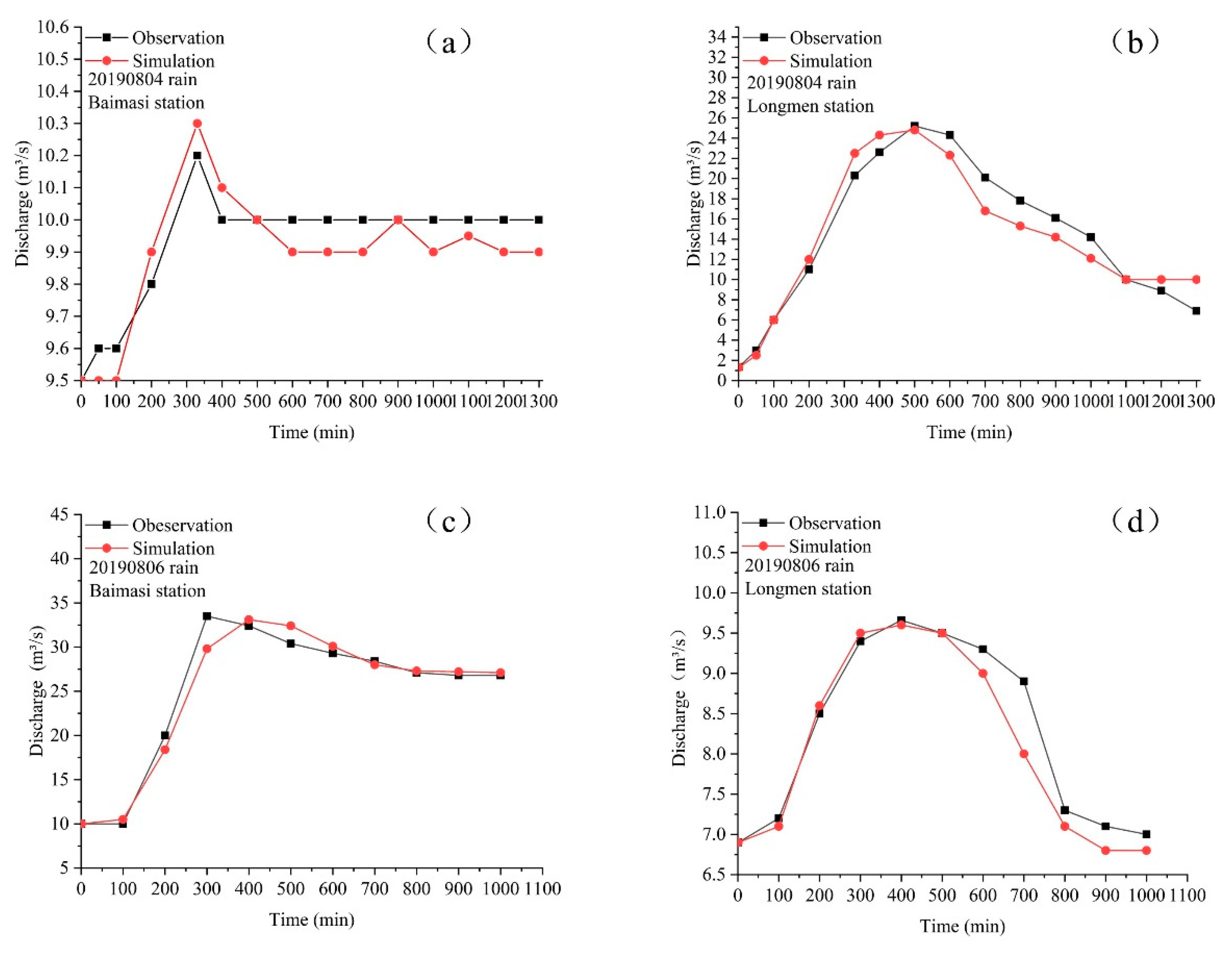
3.1. Coupled Model Calibration and Evaluation
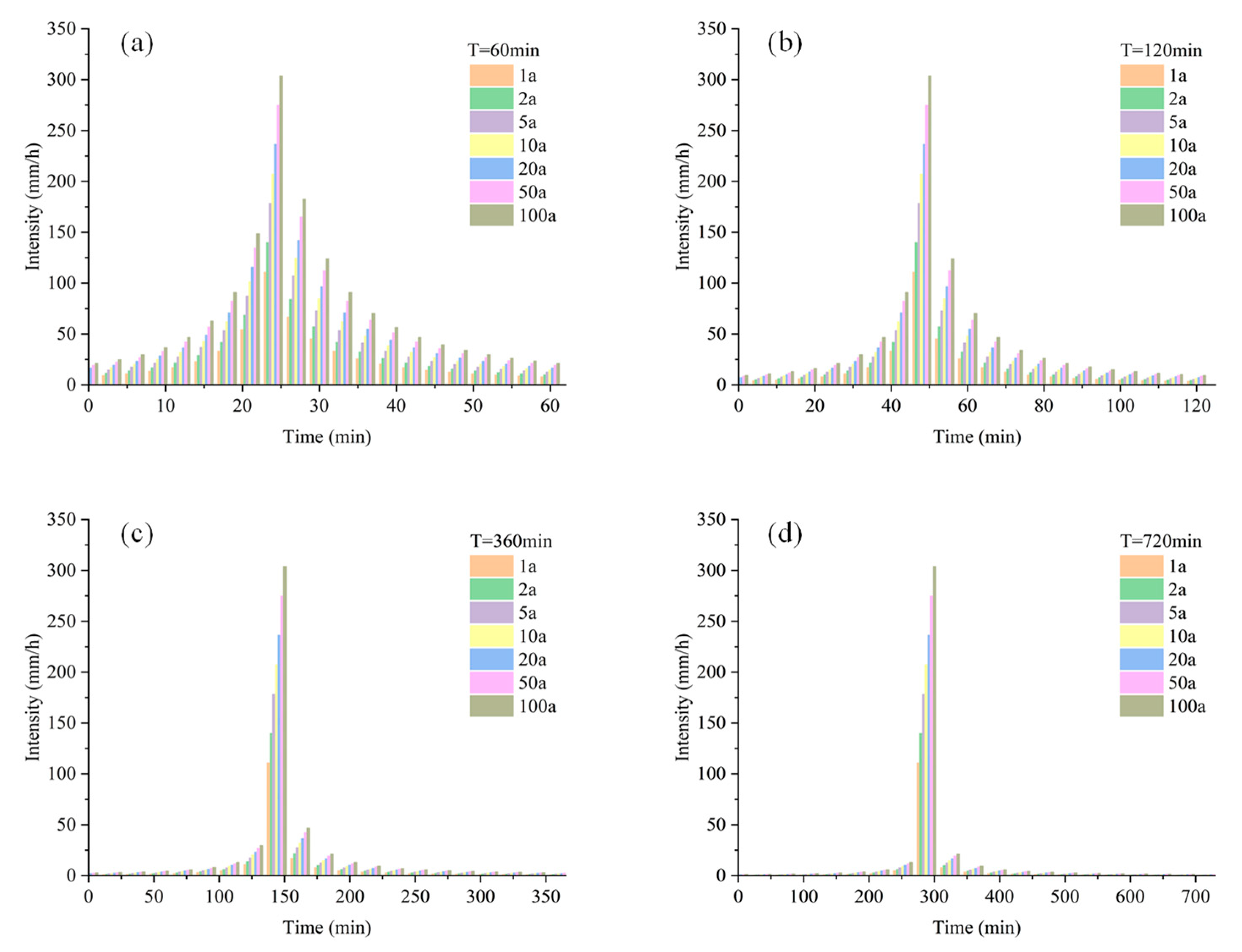
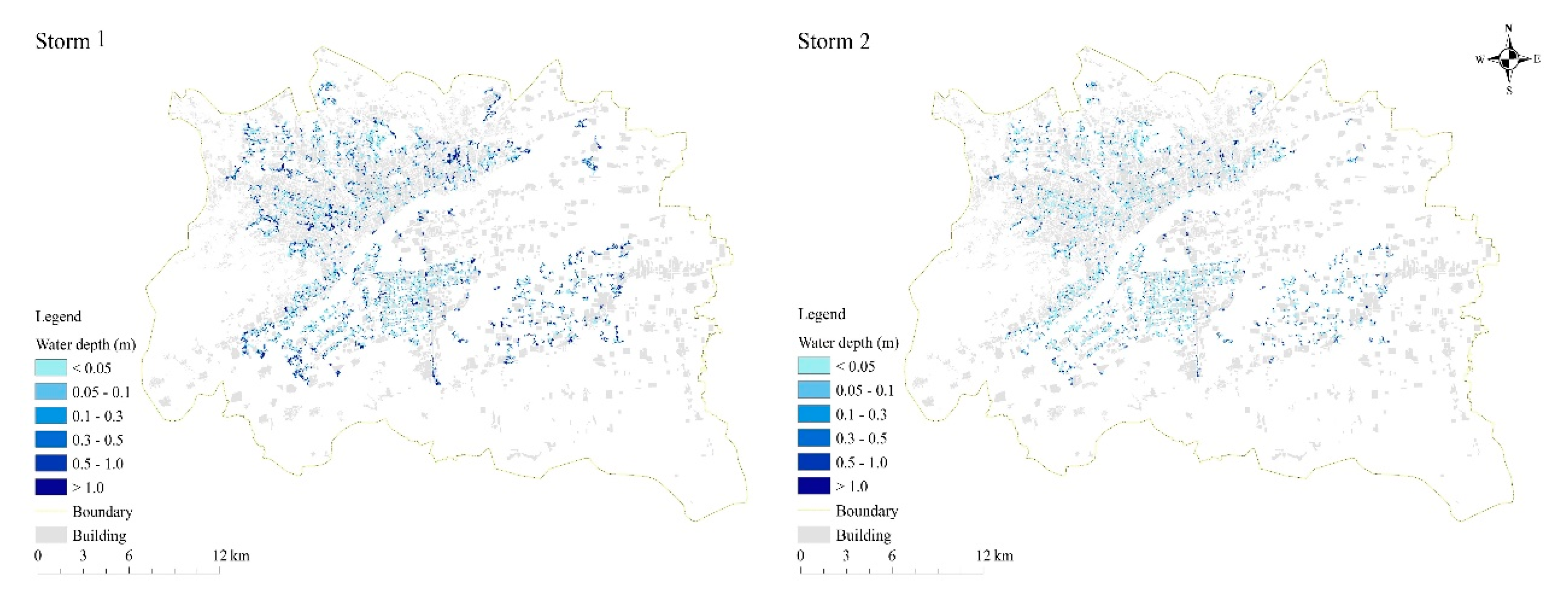
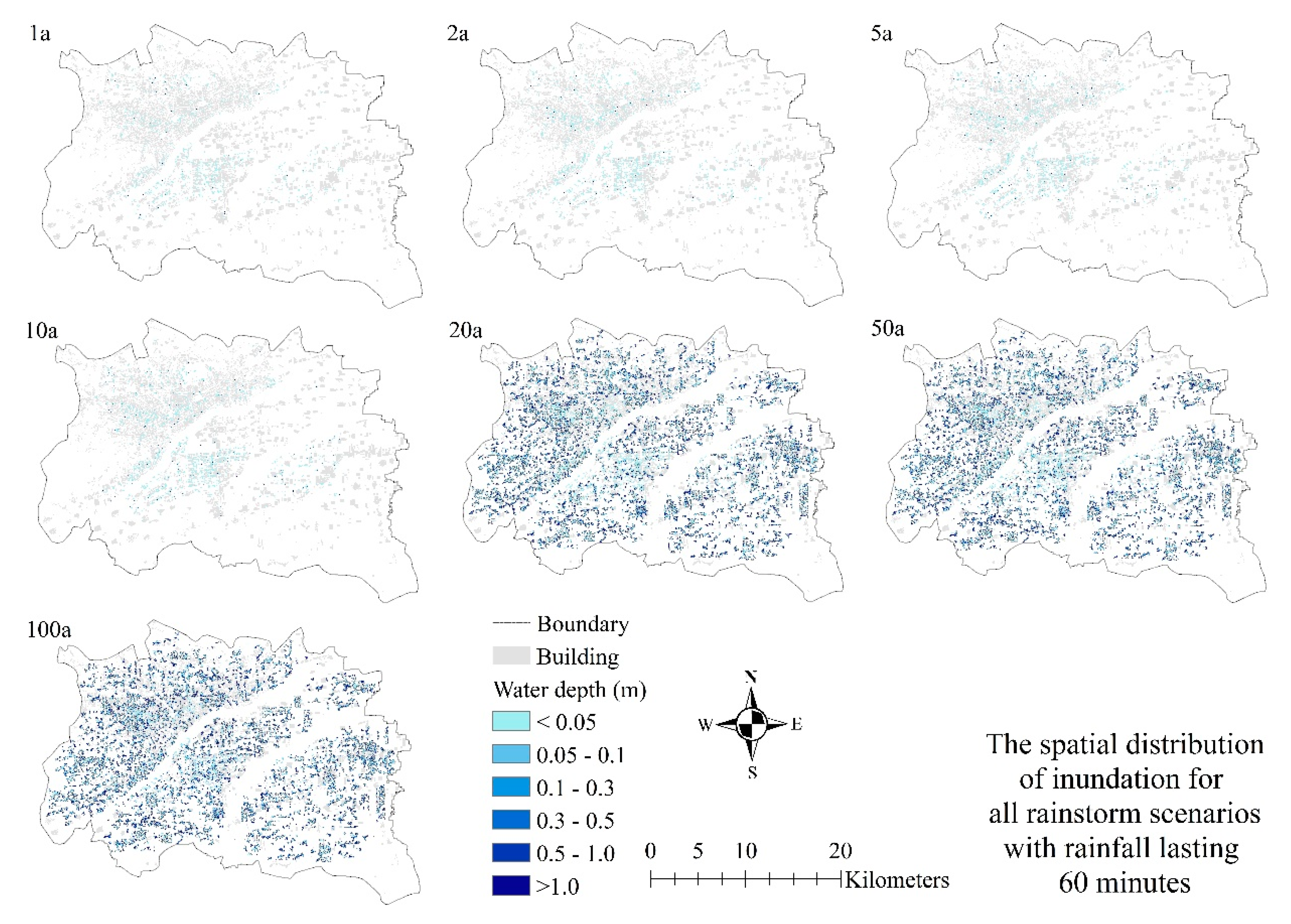
3.2. Inundation Result under Four Different Rainstorm Patterns
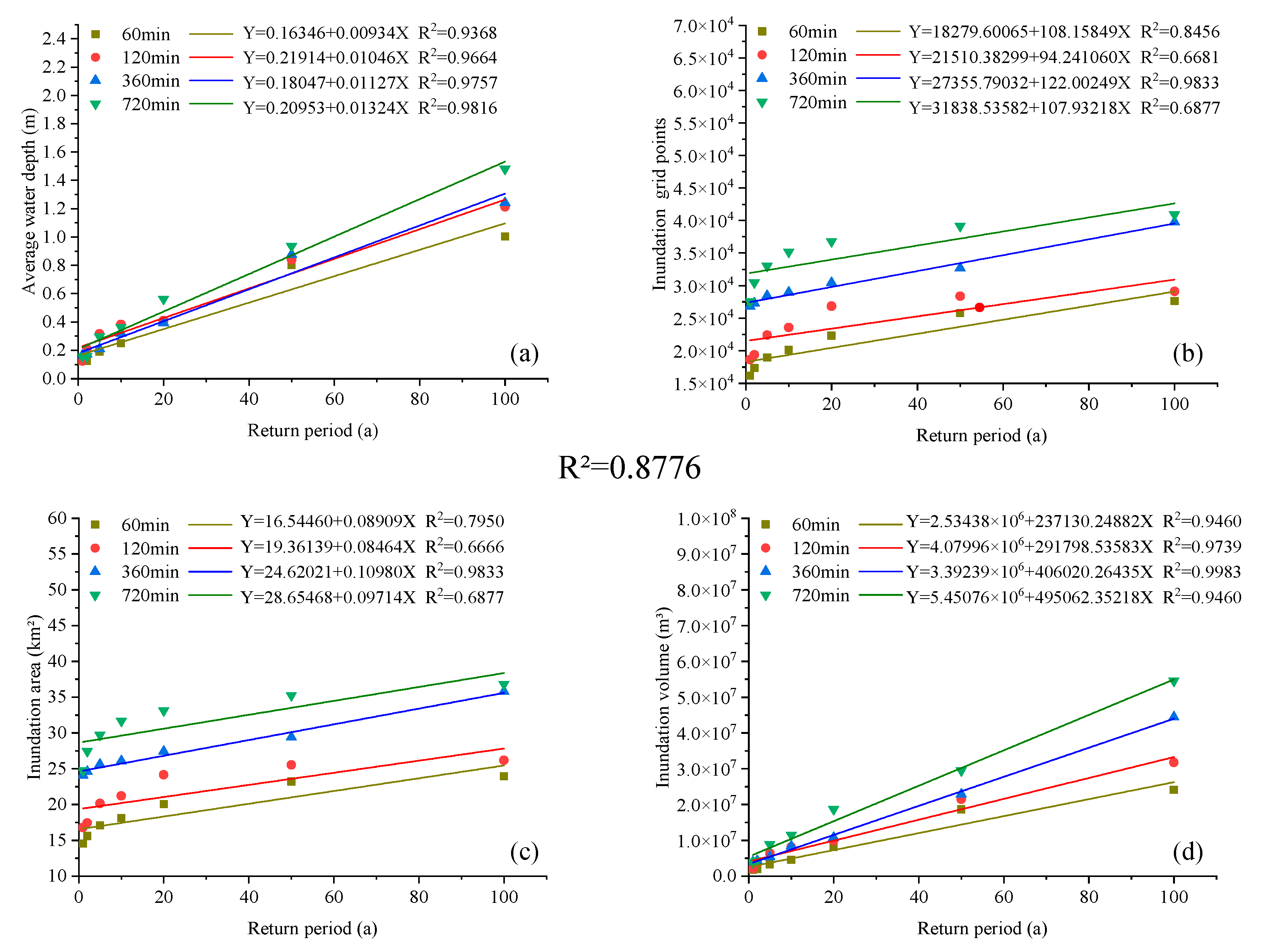
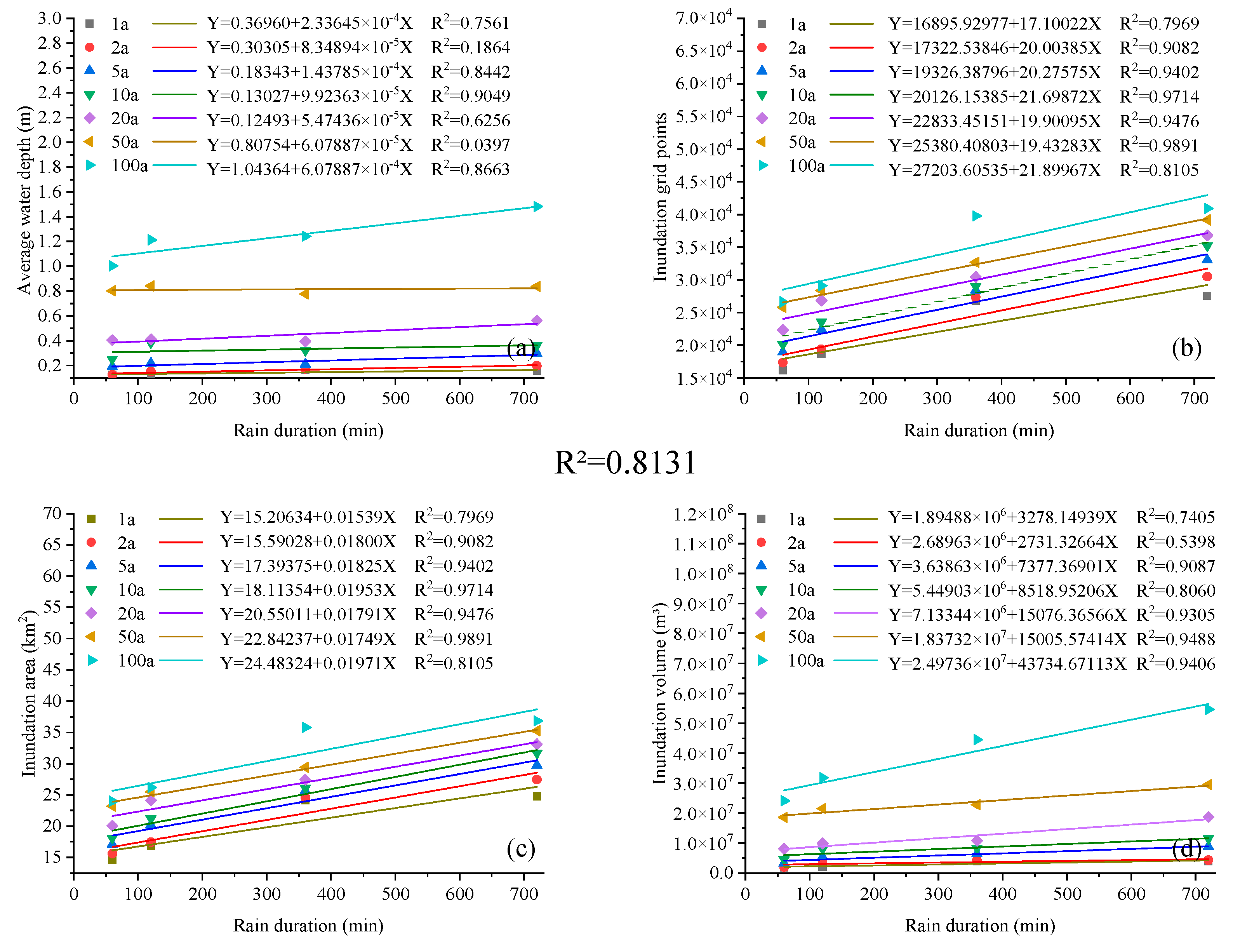
3.2.1. Total Inundation Volumes
3.2.2. Inundation Positions and Depths
3.2.3. Inundation Area
4. Discussion
4.1. The Rationality of Coupling Model Construction
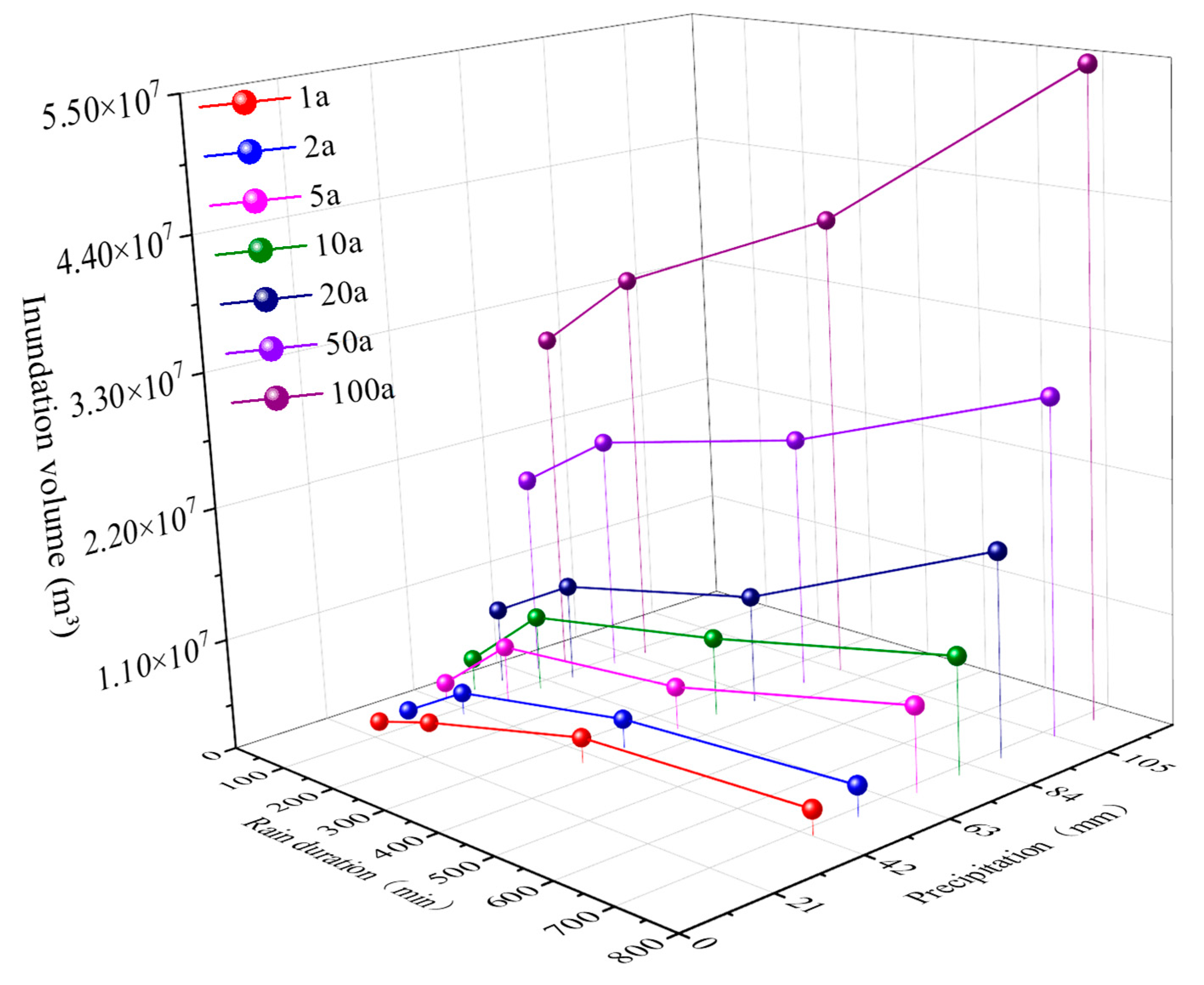
4.2. Relationship between Inundation Volume and Rainfall Duration
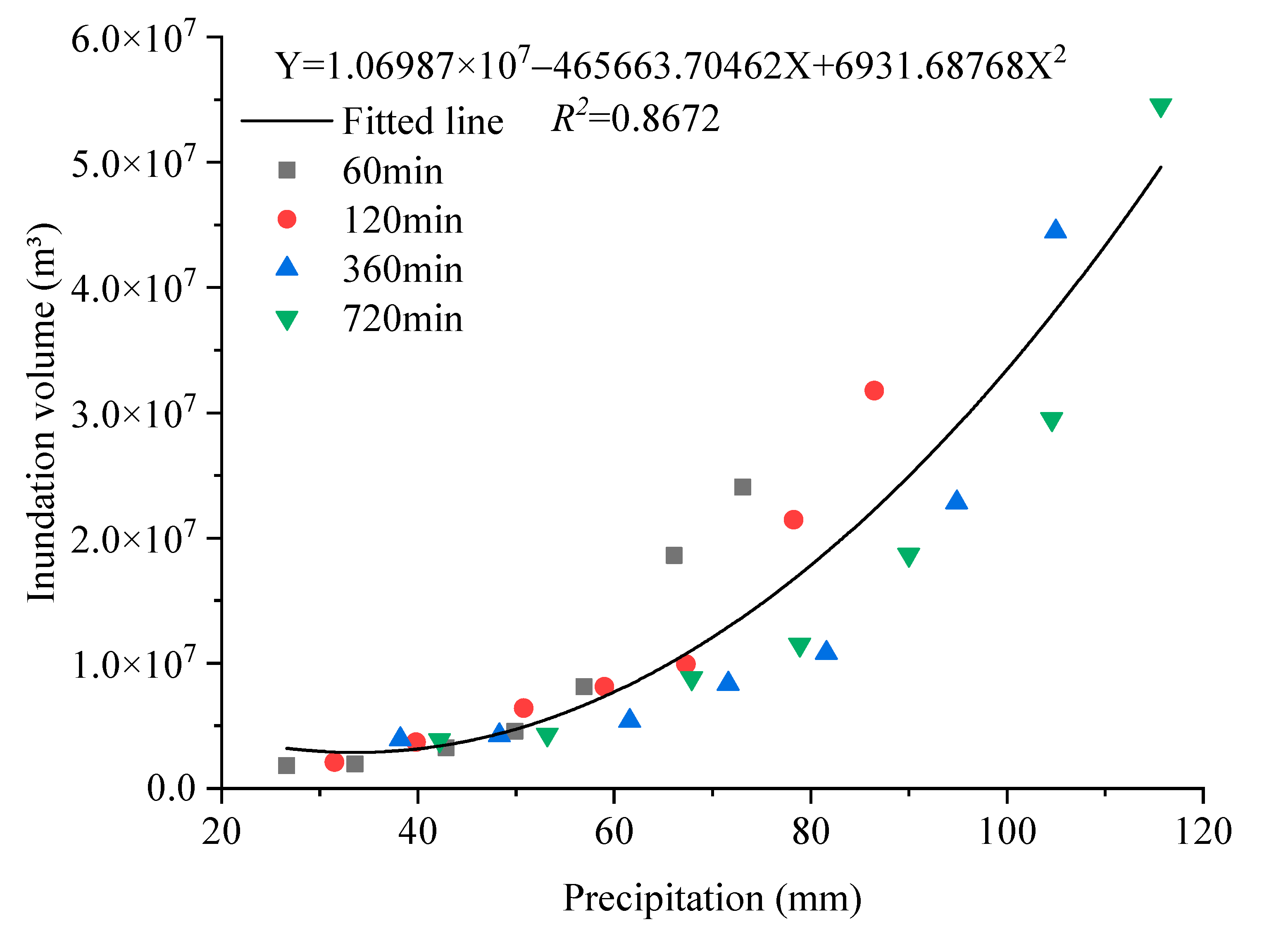
4.3. Relationship between Inundation Volume and Precipitation
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Grimm, N.B.; Faeth, S.H.; Golubiewski, N.E.; Redman, C.L.; Wu, J.; Bai, X.; Briggs, J.M. Global change and the ecology of cities. Science 2008, 319, 756–760. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, J.Y.; Hu, C.H.; Ma, B.Y.; Mu, X.L. Rapid Urbanization Impact on the Hydrological Processes in Zhengzhou, China. Water 2020, 12, 1870. [Google Scholar] [CrossRef]
- Dong, X.; Huang, S.; Zeng, S. Design and evaluation of control strategies in urban drainage systems in Kunming city. Front. Environ. Sci. Eng. 2017, 11, 13. [Google Scholar] [CrossRef]
- Xing, Y.; Liang, Q.H.; Wang, G.; Ming, X.D.; Xia, X.L. City-scale hydrodynamic modelling of urban flash floods: The issues of scale and resolution. Nat. Hazards 2019, 96, 473–496. [Google Scholar] [CrossRef] [Green Version]
- Turner, A.; Sahin, O.; Giurco, D.; Stewart, R.; Porter, M. The potential role of desalination in managing flood risks from dam overflows: The case of Sydney, Australia. J. Clean. Prod. 2016, 135, 342–355. [Google Scholar] [CrossRef] [Green Version]
- Pasquier, U.; He, Y.; Hooton, S.; Goulden, M.; Hiscock, K.M. An integrated 1D-2D hydraulic modelling approach to assess the sensitivity of a coastal region to compound flooding hazard under climate change. Nat. Hazards 2019, 98, 915–937. [Google Scholar] [CrossRef] [Green Version]
- Lyu, H.M.; Shen, S.L.; Zhou, A.N.; Yang, J. Perspectives for flood risk assessment and management for mega-city metro system. Tunn. Undergr. Space Technol. 2019, 84, 31–44. [Google Scholar] [CrossRef]
- Gao, Y.; Yuan, Y.; Wang, H.; Zhang, Z.; Ye, L. Analysis of impacts of polders on flood processes in Qinhuai River Basin, China, using the HEC-RAS model. Water Sci. Technol. Water Supply 2018, 18, 1852–1860. [Google Scholar] [CrossRef] [Green Version]
- Jiao, S.; Zhang, X.; Xu, Y. A review of Chinese land suitability assessment from the rainfall-waterlogging perspective: Evidence from the Su Yu Yuan area. J. Clean. Prod. 2017, 144, 100–106. [Google Scholar] [CrossRef]
- Mehta, D.J.; Ramani, M.M.; Joshi, M.M. Application of 1-D HEC-RAS model in design of channels. Methodology 2013, 1, 4–62. [Google Scholar]
- Bach, P.M.; Rauch, W.; Mikkelsen, P.S.; McCarthy, D.T.; Deletic, A. A critical review of integrated urban water modelling Urban drainage and beyond. Environ. Model. Softw. 2014, 54, 88–107. [Google Scholar] [CrossRef]
- Mei, C. Urban Hydrology and Hydrodynamic Coupling Model and Its Application Research. Ph.D. Thesis, China Institute of Water Resources and Hydropower Research, Beijing, China, 2019. [Google Scholar]
- Huang, G.-R.; Wang, X.; Huang, W. Simulation of Rainstorm Water Logging in Urban Area Based on InfoWorks ICM Model. Water Resour. Power 2017, 35, 66–70. [Google Scholar]
- Van Der Knijff, J.M.; Younis, J.; De Roo, A.P.J. LISFLOOD: 2010 a GIS-based distributed model for river basin scale water balance and flood simulation. Int. J. Geogr. Inf. Sci. 2010, 24, 189–212. [Google Scholar] [CrossRef]
- Liu, J.; Xia, L.; Mei, C.; Shao, W.; Yu, H.; Ma, J. Analysis of the role of deep tunnel drainage system in urban waterlogging prevention. J. Appl. Basic Sci. Eng. 2019, 27, 252–263. [Google Scholar]
- Lyu, H.M.; Shen, S.L.; Yang, J.; Yin, Z.Y. Inundation analysis of metro systems with the storm water management model incorporated into a geographical information system: A case study in Shanghai. Hydrol. Earth Syst. Sci. 2019, 23, 4293–4307. [Google Scholar] [CrossRef] [Green Version]
- Zischg, A.P.; Mosimann, M.; Bernet, D.B.; Rothlisberger, V. Validation of 2D flood models with insurance claims. J. Hydrol. 2018, 557, 350–361. [Google Scholar] [CrossRef] [Green Version]
- Martins, R.; Leandro, J.; Djordjevic, S. Influence of sewer network models on urban flood damage assessment based on coupled 1D/2D models. J. Flood Risk Manag. 2018, 11, S717–S728. [Google Scholar] [CrossRef]
- Fraga, I.; Cea, L.; Puertas, J. Validation of a 1D-2D dual drainage model under unsteady part-full and surcharged sewer conditions. Urban Water J. 2017, 14, 74–84. [Google Scholar] [CrossRef]
- Leandro, J.; Schumann, A.; Pfister, A. A step towards considering the spatial heterogeneity of urban key features in urban hydrology flood modelling. J. Hydrol. 2016, 535, 356–365. [Google Scholar] [CrossRef]
- van der Sterren, M.; Rahman, A.; Ryan, G. Modeling of a lot scale rainwater tank system in XP-SWMM: A case study in Western Sydney, Australia. J. Environ. Manag. 2014, 141, 177–189. [Google Scholar] [CrossRef]
- Gong, Y.; Li, X.; Zhai, D.; Yin, D.; Song, R.; Li, J.; Yuan, D. Influence of Rainfall, Model Parameters and Routing Methods on Stormwater Modelling. Water Resour. Manag. 2018, 32, 735–750. [Google Scholar] [CrossRef]
- Cheng, M.; Qin, H.; Fu, G.; He, K. Performance evaluation of time-sharing utilization of multi-function sponge space to reduce waterlogging in a highly urbanizing area. J. Environ. Manag. 2020, 269, 110760. [Google Scholar] [CrossRef] [PubMed]
- Bruni, G.; Reinoso, R.; van de Giesen, N.C.; Clemens, F.H.L.R.; ten Veldhuis, J.A.E. On the sensitivity of urban hydrodynamic modelling to rainfall spatial and temporal resolution. Hydrol. Earth Syst. Sci. 2015, 19, 691–709. [Google Scholar] [CrossRef]
- Bermudez, M.; Ntegeka, V.; Wolfs, V.; Willens, P. Development and Comparison of Two Fast Surrogate Models for Urban Pluvial Flood Simulations. Water Resour. Manag. 2018, 32, 2801–2815. [Google Scholar] [CrossRef]
- Yu, D.; Yin, J.; Liu, M. Validating city-scale surface water flood modelling using crowd-sourced data. Environ. Res. Lett. 2016, 11, 124011. [Google Scholar] [CrossRef]
- Chen, W.J.; Huang, G.R.; Zhang, H.; Wang, W.Q. Urban inundation response to rainstorm patterns with a coupled hydrodynamic model: A case study in Haidian Island, China. J. Hydrol. 2018, 564, 1022–1035. [Google Scholar] [CrossRef]
- Jang, J.-H. An Advanced Method to Apply Multiple Rainfall Thresholds for Urban Flood Warnings. Water 2015, 7, 6056–6078. [Google Scholar] [CrossRef] [Green Version]
- Hu, C.H.; Liu, C.S.; Yao, Y.C.; Wu, Q.; Ma, B.Y.; Jian, S.Q. Evaluation of the Impact of Rainfall Inputs on Urban Rainfall Models: A Systematic Review. Water 2020, 12, 2484. [Google Scholar] [CrossRef]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models part I—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Indrawati, D.; Yakti, B.; Purwanti, A.; Hadinagoro, R. Computing urban flooding of meandering river using 2D numerical model (case study: Kebon Jati-Kalibata segment, Ciliwung river basin). In Proceedings of the 2nd Conference for Civil Engineering Research Networks; Inst Teknologi Bandung, Fac Civil & Environm Engn: Bandung, Indonesia, 2019; Volume 270. [Google Scholar]
- Kim, S.E.; Lee, S.; Kim, D.; Song, C.G. Stormwater Inundation Analysis in Small and Medium Cities for the Climate Change Using EPA-SWMM and HDM-2D. J. Coast. Res. 2018, 991–995. [Google Scholar] [CrossRef]
- Djordjevic, S.; Prodanovic, D.; Maksimovic, C.; Ivetic, M.; Savic, D. SIPSON—Simulation of interaction between pipe flow and surface overland flow in networks. Water Sci. Technol. 2005, 52, 275–283. [Google Scholar] [CrossRef] [PubMed]
- Zheng, Q.; Shen, S.L.; Zhou, A.; Lyu, H.M. Inundation risk assessment based on G-DEMATEL-AHP and its application to Zhengzhou flooding disaster. Sustain. Cities Soc. 2022, 86, 104138. [Google Scholar] [CrossRef]
- Lowe, R.; Urich, C.; Domingo, N.S.; Mark, O.; Deletic, A.; Arnbjerg-Nielsen, K. Assessment of urban pluvial flood risk and efficiency of adaptation options through simulations—A new generation of urban planning tools. J. Hydrol. 2017, 550, 355–367. [Google Scholar] [CrossRef]





| River Name | Channel Length (km) | Number of River Sections | Average Distance of Section (m) |
|---|---|---|---|
| Yi river | 23.2 | 32 | 725.0 |
| Luo river | 44.5 | 84 | 529.7 |
| Chan river | 10.4 | 31 | 322.6 |
| Jian river | 19.2 | 32 | 600.0 |
| Ganshui river | 7.6 | 16 | 475.0 |
| Site Number | Road Section Name | Simulated Water Depth (m) | Measured Water Depth (m) | Absolute Error (m) | Relative Error (%) |
|---|---|---|---|---|---|
| 1 | Anju Road Railway Bridge Culvert | 0.60 | 0.50 | 0.10 | 20.0 |
| 2 | Luobai Road Anju Road Railway Bridge Culvert | 0.60 | 0.50 | 0.10 | 20.0 |
| 3 | Low-lying area of Taxi Village, Hanhe Hui District | 0.65 | 0.60 | 0.05 | 8.3 |
| 4 | Taikang Road Wangcheng Avenue Intersection to Xinyue Intersection | 0.65 | 0.50 | 0.05 | 10.0 |
| 5 | Niepan Road Jiaozhi Railway Bridge Culvert | 0.35 | 0.60 | 0.25 | 41.7 |
| 6 | Changchun Road, Jianxi District | 0.50 | 0.60 | 0.10 | 16.7 |
| 7 | Wanda Intersection | 0.60 | 0.60 | 0.05 | 8.3 |
| 8 | Sui-Tangcheng Road Longhai Railway Line Culvert | 0.20 | 0.20 | 0.01 | 5.0 |
| 9 | Guanlin Station Bridge, Erguang Expressway, Yibin District | 0.55 | 0.20 | 0.35 | 175.0 |
| 10 | Pingdeng Street Overpass, Chanhe District | 0.35 | 0.20 | 0.15 | 75.0 |
| 11 | Houzaimen Street, Yiren Road | 1.20 | 1.00 | 0.20 | 20.0 |
| 12 | Qiming East Road Jiaoliu Railway Bridge Culvert | 1.40 | 1.00 | 0.40 | 40.0 |
| 13 | Yiren Road, New District | 1.20 | 1.00 | 0.20 | 20.0 |
| 14 | East Huatan Overpass, Yanhe District | 0.90 | 1.00 | 0.10 | 10.0 |
| 15 | Longmen Avenue, Longmen North Bridge | 1.30 | 1.40 | 0.10 | 7.1 |
| 16 | Evergrande Oasis Section of East Zhongzhou Road | 0.60 | 0.50 | 0.10 | 20.0 |
| Site Number | Road Section Name | Simulated Water Depth (m) | Measured Water Depth (m) | Absolute Error (m) | Relative Error (%) |
|---|---|---|---|---|---|
| 1 | Anju Road Railway Bridge Culvert | 0.30 | 0.30 | 0.05 | 16.7 |
| 2 | Luobai Road Anju Road Railway Bridge Culvert | 0.30 | 0.30 | 0.05 | 16.7 |
| 3 | Low-lying area of Taxi Village, Chanhe District | 0.40 | 0.40 | 0.05 | 12.5 |
| 4 | Taikang Road Wangcheng Avenue Intersection to Xinyue Intersection | 0.25 | 0.30 | 0.05 | 16.7 |
| 5 | Niepan Road Jiaozhi Railway Bridge Culvert | 0.25 | 0.20 | 0.05 | 0.25 |
| 6 | Changchun Road, Jianxi District | 0.25 | 0.20 | 0.05 | 0.25 |
| 7 | Wanda Intersection | 0.35 | 0.40 | 0.05 | 12.5 |
| 8 | Sui-Tangcheng Road Longhai Railway Line Culvert | 0.25 | 0.30 | 0.05 | 16.7 |
| 9 | Guanlin Station Bridge, Erguang Expressway, Yibin District | 0.85 | 1.20 | 0.35 | 29.2 |
| 10 | Pingping Street Overpass, Yanhe District | 0.30 | 0.30 | 0.05 | 16.7 |
| 11 | Houzaimen Street, Yiren Road | 0.18 | 0.15 | 0.03 | 20.0 |
| 12 | Qiming East Road Jiaoliu Railway Bridge Culvert | 0.45 | 0.50 | 0.05 | 10.0 |
| 13 | Yiren Road, New District | 0.20 | 0.30 | 0.10 | 33.3 |
| 14 | East Huatan Overpass, Yanhe District | 0.90 | 1.00 | 0.10 | 10.0 |
| 15 | Longmen Avenue, Longmen North Bridge | 1.30 | 1.40 | 0.10 | 7.1 |
| 16 | Evergrande Oasis Section of East Zhongzhou Road | 0.60 | 0.50 | 0.10 | 20.0 |
| Return Period | 1a | 2a | 5a | 10a | 20a | 50a | 100a | |
|---|---|---|---|---|---|---|---|---|
| Rain Duration | ||||||||
| 60 min | 1,804,911.66 | 1,941,154.2 | 3,244,379.67 | 4,553,029.98 | 8,109,544.59 | 18,603,459.18 | 24,064,675.2 | |
| 120 min | 2,091,859.56 | 3,674,307.24 | 6,409,150.11 | 8,108,518.32 | 9,922,175.64 | 21,460,579.2 | 31,751,228.07 | |
| 360 min | 3,943,031.4 | 4,255,403.85 | 5,380,177.77 | 8,371,173.33 | 10,816,143.84 | 22,848,784.38 | 44,463,856.5 | |
| 720 min | 3,875,545.08 | 4,327,303.77 | 8,824,576.32 | 11,479,946.49 | 18,666,670.05 | 29,493,651.6 | 54,559,375.68 | |
| Return Period | 1a | 2a | 5a | 10a | 20a | 50a | 100a | |
|---|---|---|---|---|---|---|---|---|
| Rain Duration | ||||||||
| 60 min | 0.1242 | 0.1245 | 0.1901 | 0.2514 | 0.4039 | 0.8014 | 1.0040 | |
| 120 min | 0.1246 | 0.2108 | 0.3179 | 0.3826 | 0.4108 | 0.8408 | 1.2123 | |
| 360 min | 0.1635 | 0.1731 | 0.2101 | 0.3211 | 0.3946 | 0.7769 | 1.2425 | |
| 720 min | 0.1564 | 0.1577 | 0.2968 | 0.3623 | 0.5635 | 0.8365 | 1.4817 | |
| Return Period | 1a | 2a | 5a | 10a | 20a | 50a | 100a | |
|---|---|---|---|---|---|---|---|---|
| Rain Duration | ||||||||
| 60 min | 14.5323 | 15.5916 | 17.0667 | 18.1107 | 20.0781 | 23.2137 | 23.9688 | |
| 120 min | 16.7886 | 17.4303 | 20.1609 | 21.1932 | 24.1533 | 25.5240 | 26.1909 | |
| 360 min | 24.1164 | 24.5835 | 25.6077 | 26.0703 | 27.4104 | 29.4102 | 35.7858 | |
| 720 min | 24.7797 | 27.4401 | 29.7324 | 31.6863 | 33.1263 | 35.2584 | 36.8217 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, G.; Zhao, H.; Liu, C.; Wang, J.; Yang, F. City Flood Disaster Scenario Simulation Based on 1D–2D Coupled Rain–Flood Model. Water 2022, 14, 3548. https://doi.org/10.3390/w14213548
Li G, Zhao H, Liu C, Wang J, Yang F. City Flood Disaster Scenario Simulation Based on 1D–2D Coupled Rain–Flood Model. Water. 2022; 14(21):3548. https://doi.org/10.3390/w14213548
Chicago/Turabian StyleLi, Guo, Huadong Zhao, Chengshuai Liu, Jinfeng Wang, and Fan Yang. 2022. "City Flood Disaster Scenario Simulation Based on 1D–2D Coupled Rain–Flood Model" Water 14, no. 21: 3548. https://doi.org/10.3390/w14213548






