Statistical Model for the Sizing of a Prototype Solar Still Applicable to Remote Islands
Abstract
:1. Introduction
2. Solar Still Set-Up and Experimental Methods
2.1. Experimental Setup and Data Collection
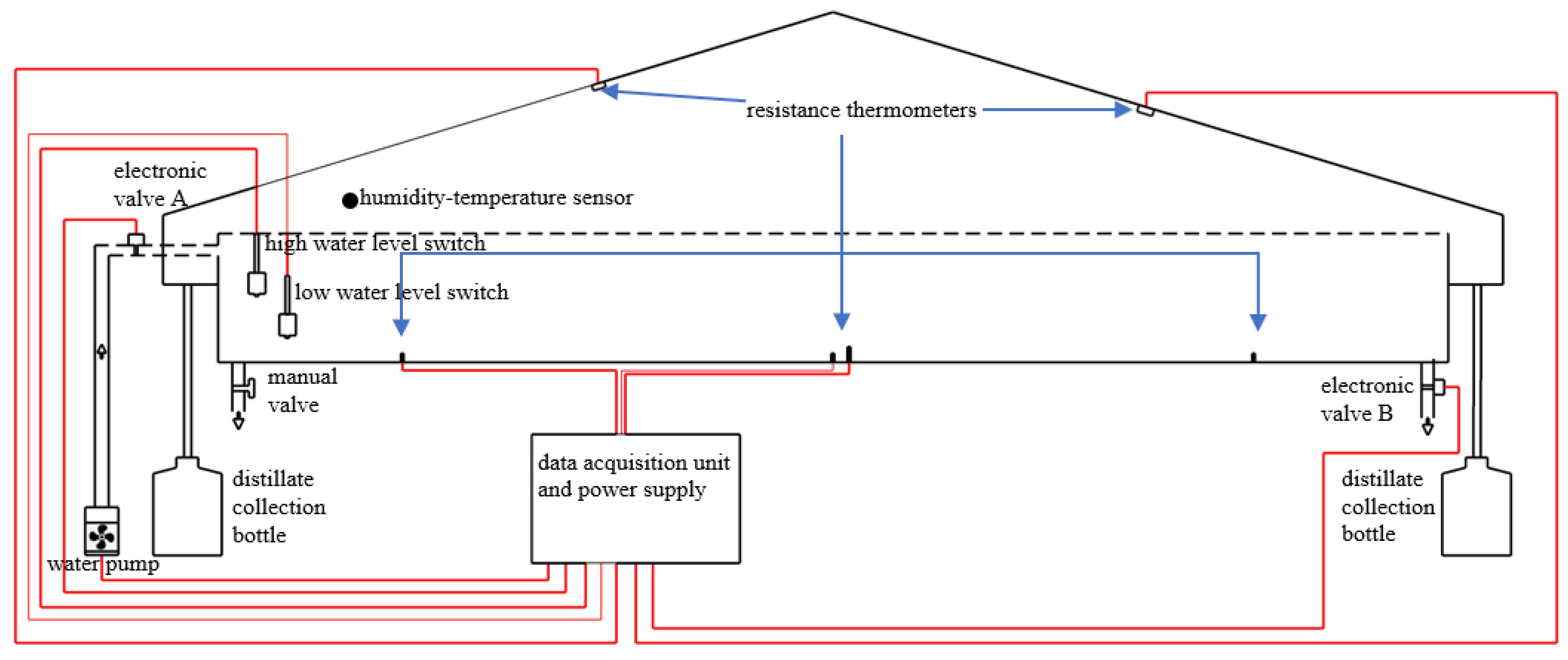
- The solar still was positioned in a north-south orientation such that the inclined glass covers were directed east and west while the heat pipe evacuated tube collectors (ETC) were inclined at 23° to the horizontal facing the south.
- The feedwater storage tub was filled with 120 L of water at least one day ahead of the experiment and the topside glass panes, side wall glass panes, fins, basin, and the solar water heater were also cleaned ahead of the experiment.
- Cotton wicks were prepared by cutting a roll of cotton yarn into 145 strands that were 0.002 m in diameter and 0.50 m long and were then placed in the feedwater to soak overnight.
- On the first day of the experiment at approximately 5:30 am, the glass cover was removed and two sets of fins were installed in the basin of the solar still, following which an electronic water pump was used to fill the basin with feedwater to the maximum water level (0.027 m for 60% recovery ratio, 0.040 m for 70% recovery, and 0.077 m for 80% recovery). The high-water level switch (Figure 2) controls the maximum water level by deactivating the water pump and electronic valve A simultaneously. The cotton wicks were then added to the larger rectangular fins (Figure 3).
- The glass cover was then repositioned on the basin and the gaps between the basin and the frame of the glass cover were sealed with foam material to prevent vapor from escaping.
- Hourly measurements of weather parameters such as total global solar radiation (Rad), ambient temperature (Ta), ambient relative humidity (RHa), and windspeed (Ws) were performed using equipment already installed at the test site such as the Eppley precision spectral pyranometers (Model PSP), Young Co. anemometer (Model 05103L), and Dwyer humidity-temperature transmitter (Model 657-1). Data for the fraction of cloud cover (CCr) for Tainan City was obtained from the Central Weather Bureau [33].
- The data acquisition modules along with the LabVIEW engineering software were used to make hourly measurements of the basin water temperature (TB), inner glass temperature, vapor temperature, and humidity of the solar still.
- The volume of distillate produced were measured at 8 am (overnight) and 5 pm (daytime) daily until the volume of the feedwater in the basin reaches the minimum level (approximately 1 cm above the absorber plate) which was controlled by the low water level switch (Figure 2).
- The low-level water switch activates electronic valve A which allows the residue water to flow into the brine residue storage tub. The volume of the residue water was then measured after which it was placed in an open area to evaporate (Figure 4a) and the mass of the crude salt that remained was measured by gravimetric analysis (drying and reweighing until two consecutive masses were within 1 g of each other and recorded).
- Following the collection of the residue water, the wicks and fins were then removed and cleaned.
- The procedure was then repeated for the next experiment.
2.2. Uncertainty Analysis
2.3. Data Analysis
3. Results and Discussion
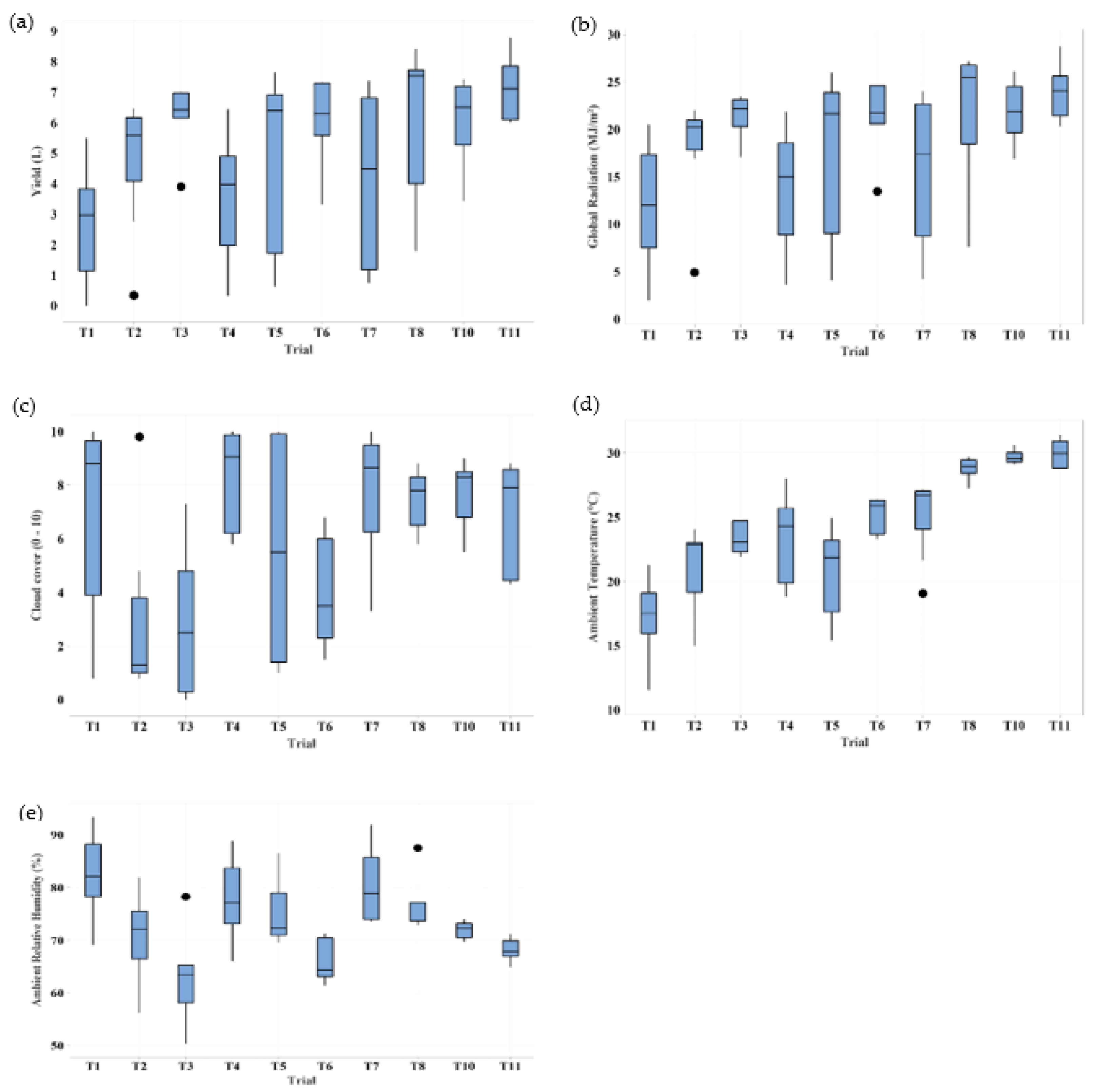
3.1. Summary of Data Collected from Experimental Trials at 70% Recovery Ratio
3.2. Effect of Recovery Ratio on the Performance of the Solar Still
3.3. Effect of Recovery Ratio on the Concentration of the Brine Residue
3.4. Modelling of the Daily Distillate Yield
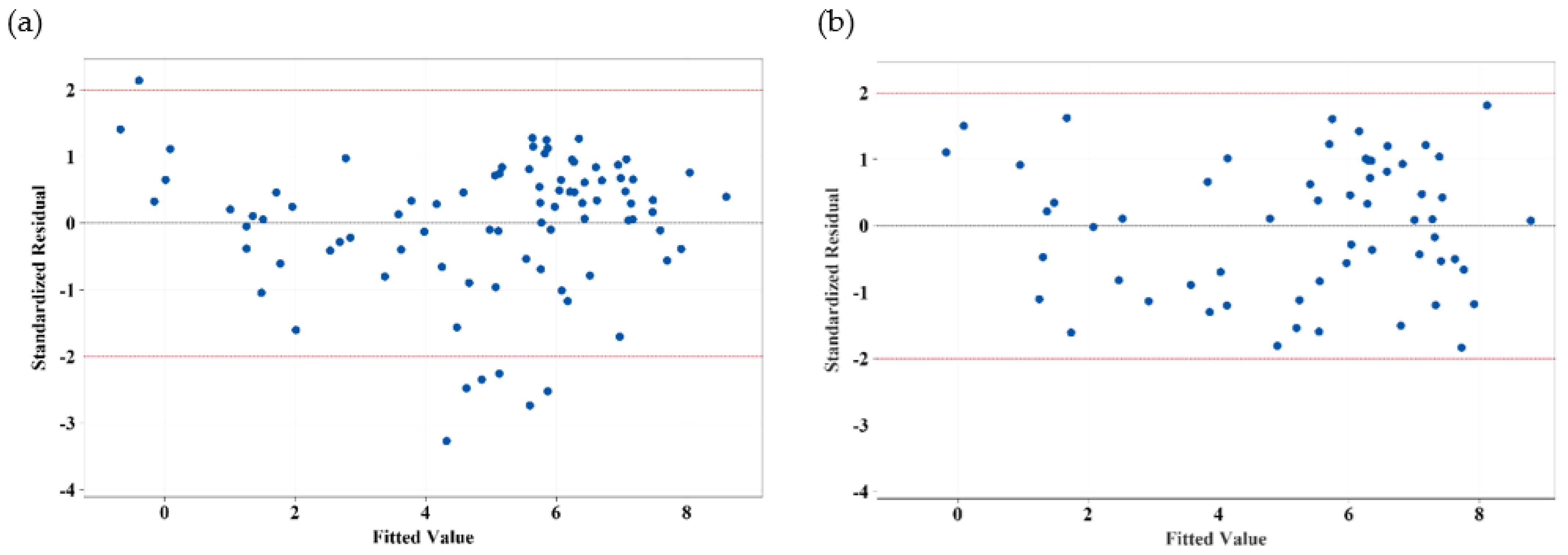
3.4.1. Identification of Outliers
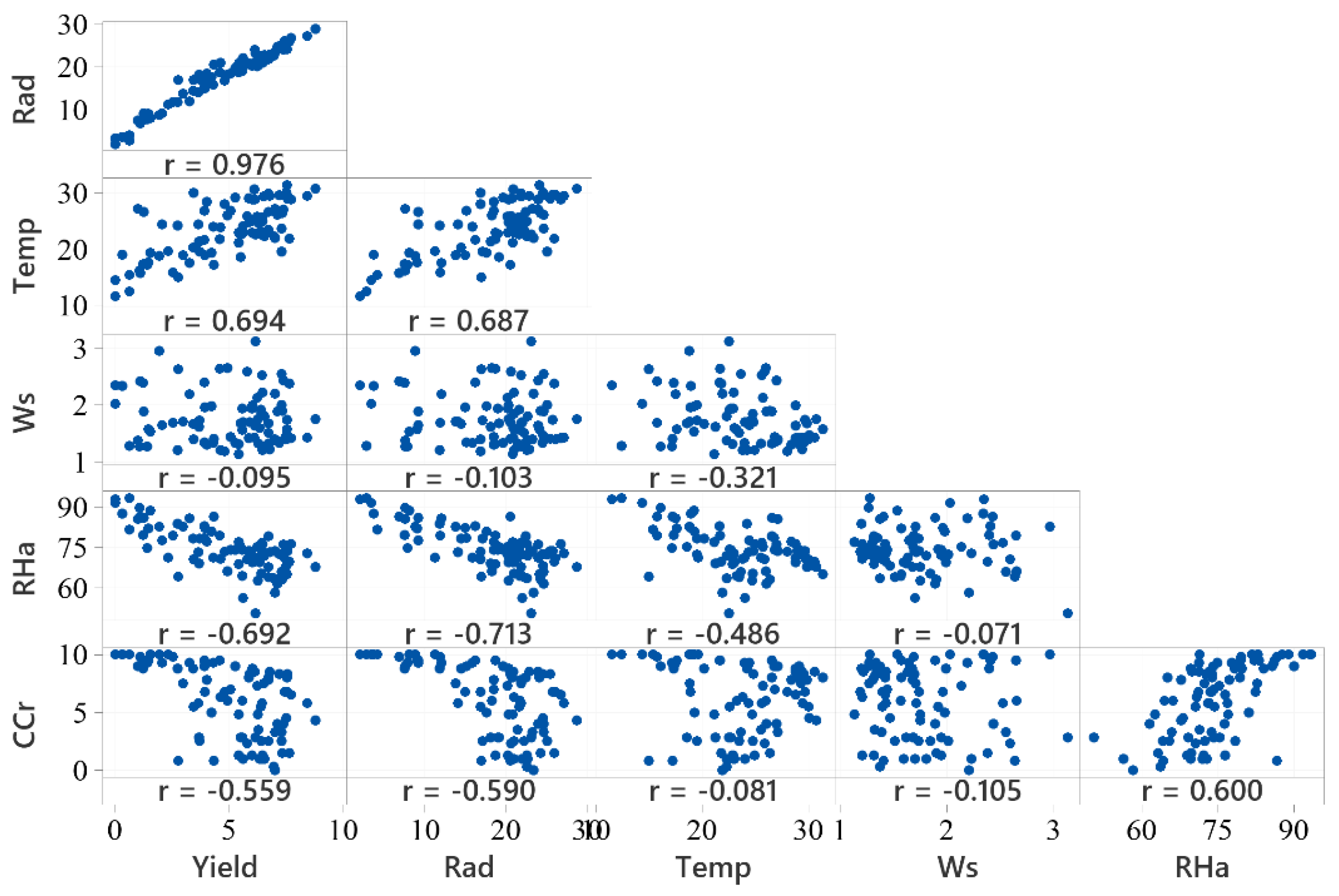
3.4.2. Predictor Variables and Pearson’s Correlation Matrix
3.4.3. Model Building
3.4.4. Model Evaluation
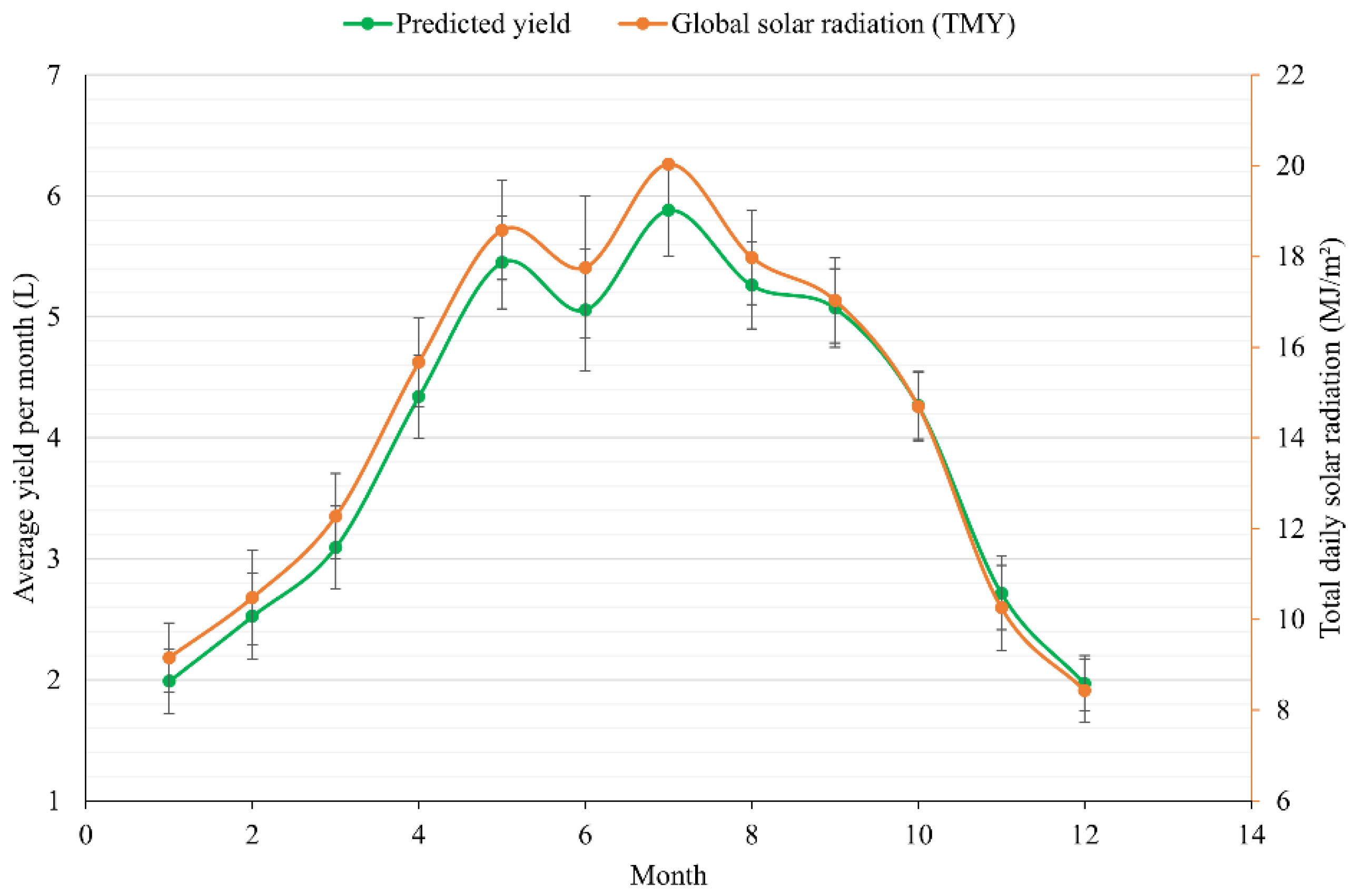
3.5. Application of Typical Meteorological Year (TMY) Data to the Model
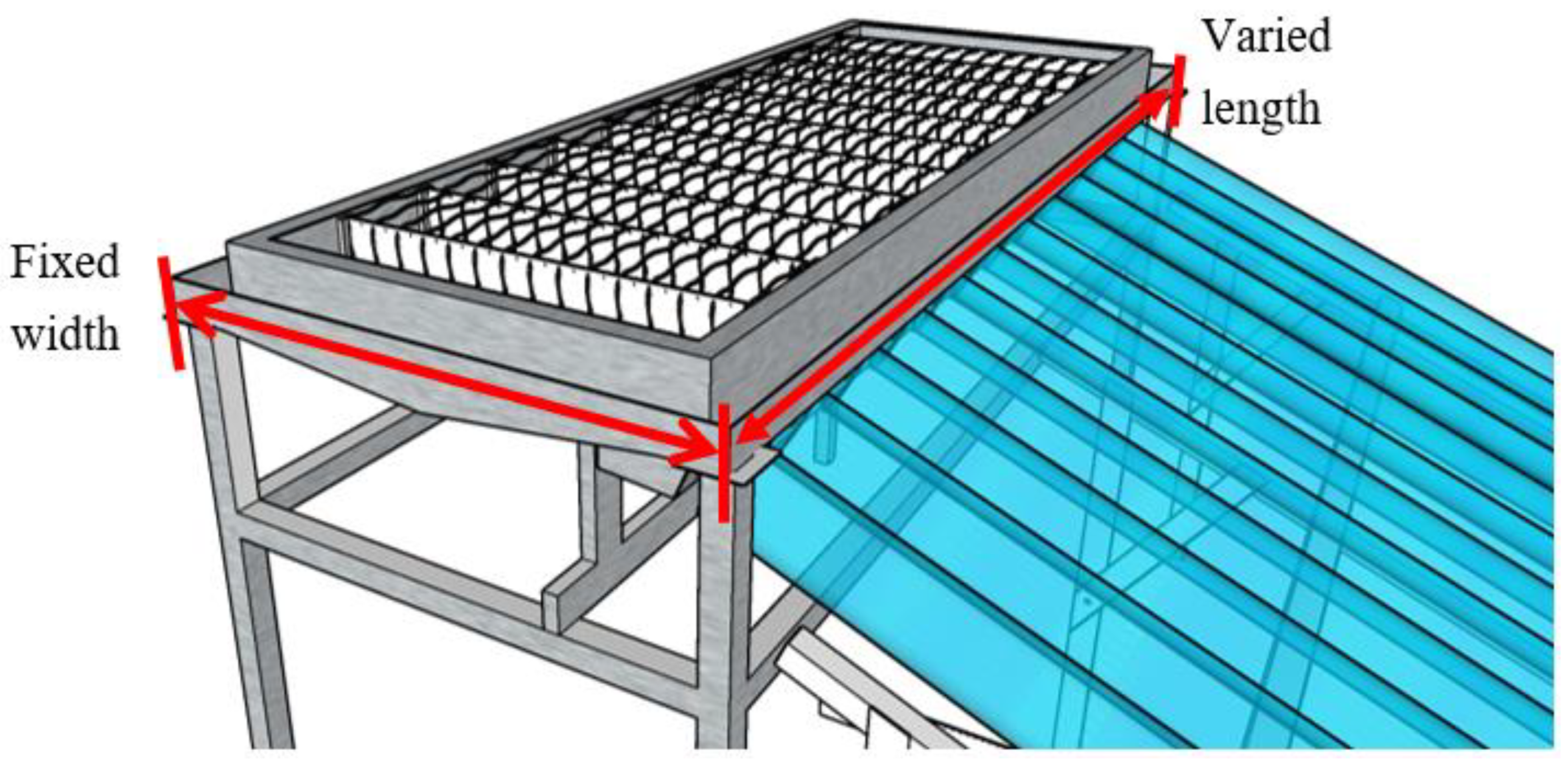
3.6. Sizing of the Solar Still Prototype
3.7. Payback Period
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Symbol | Description |
| Constant regression term | |
| Coefficient of the kth predictor variable | |
| Random error of regression model | |
| Standard deviation, Equation (2) | |
| ACF | Annual cash flow (NTD), Equation (21) |
| CCr | Cloud cover |
| Capital cost (NTD), Equation (21) | |
| Cost of fabrication (NTD) | |
| Cost of installation (NTD) | |
| Mallows test statistic, Equation (12) | |
| Durbin-Watson statistic, Equation (15) | |
| The ith error term, Equation (16) | |
| The ()th error term, Equation (17) | |
| ETC | Evacuated tube collector |
| i | ith observation |
| IQR | Interquartile range |
| jth predictor variable | |
| Number of variables | |
| M | Annual freshwater yield (L) |
| MAE | Mean absolute error, Equation (6) |
| MAPE | Mean absolute percentage error, Equation (9) |
| MPR | Market penetration rate (%) |
| Annual solar salt production (kg) | |
| MSE | Mean square error, Equation (7) |
| Number of observations | |
| NTD | New Taiwanese dollar |
| PP | Payback period, Equation (21) |
| p-value | Probability value |
| r | Correlation coefficient |
| R2 | Coefficient of determination, Equation (4) |
| Adjusted R-squared, Equation (6) | |
| Rad | Daily total global solar radiation |
| RHa | Ambient relative humidity |
| RMSE | Root mean square error, Equation (8) |
| RR | Recovery ratio (%), Equation (18) |
| S | Standard error of the regression, Equation (10) |
| SE | Standard error, Equation (11) |
| Selling price of crude solar sea salt (NTD) | |
| Selling price of distillate (NTD) | |
| SSE | Sum of squares error, Equation (13) |
| Ta | Ambient temperature (°C) |
| TB | Basin water temperature (°C) |
| Temp | Daily average ambient temperature (°C) |
| TDS | Total dissolved solids (mg/L) |
| TMM | Typical meteorological month |
| TMY | Typical meteorological year |
| T-value | Test statistic |
| Standard uncertainty, Equation (3) | |
| USD | United States dollar |
| VD | Volume of distillate (L) |
| VF | Volume of feedwater (L) |
| VIF | Variance inflation factor, Equation (11) |
| WHO | World Health Organization |
| Ws | Windspeed (m/s) |
| Predictor or independent variable | |
| Mean of measured values, Equation (1) | |
| ith measured value, Equation (1) | |
| Mean of the predictor variable | |
| The value of the ith predictor variable | |
| Response or dependent variable, Equation (19) | |
| Observed value | |
| Predicted value | |
| Mean value |
References
- Samuel, A.; Brizuela, J.; Chang, K.-C.; Lin, C.-T. Design and Investigation of an Effective Solar Still Applicable to Remote Islands. Water 2022, 14, 703. [Google Scholar] [CrossRef]
- WHO. Guidelines for Drinking Water Quality. In Guidelines for Drinking-Water Quality, 4th ed.; WHO: Geneva, Switzerland, 2017; Available online: https://www.who.int/publications/i/item/9789241549950 (accessed on 10 July 2022).
- Deveraux, T.; Freshwater, A. Desalination in Pacific Island Countries—A Preliminary Overview. SOPAC Water and Sanitation Programme. Available online: https://gsd.spc.int/sopac/docs/SOPAC%20Technical%20Report%20437%20Desalination%20for%20Pacific%20Island%20Countries.pdf (accessed on 9 July 2022).
- Muftah, A.F.; Alghoul, M.A.; Fudholi, A.; Abdul-Majeed, M.M.; Sopian, K. Factors affecting basin type solar still productivity: A detailed review. Renew. Sustain. Energy Rev. 2014, 32, 430–447. [Google Scholar] [CrossRef]
- Chamsa-Ard, W.; Fawcett, D.; Fung, C.C.; Poinern, G. Solar Thermal Energy Stills for Desalination: A Review of Designs, Operational Parameters and Material Advances. J. Energy Power Technol. 2020, 2, 1–48. [Google Scholar] [CrossRef]
- Manchanda, H.; Kumar, M. A comprehensive decade review and analysis on designs and performance parameters of passive solar still. Renew. Wind. Water Sol. 2015, 2, 17. [Google Scholar] [CrossRef]
- Hardik, K.; Jani, K.V.M. Techniques of Improving Rate of Heat Transfer in Solar Still as a Solar-Thermal Desalination Device—A Review. Int. J. Adv. Res. Innov. Ideas Educ. 2017, 3, 4081–4094. Available online: http://ijariie.com/AdminUploadPdf/Techniques_of_improving_rate_of_heat_transfer_in_Solar_Still_as_a_Solar_Thermal_Desalination_device_–_A_Review_ijariie4719.pdf (accessed on 2 July 2022).
- Sampathkumar, K.; Arjunan, T.V.; Pitchandi, P.; Senthilkumar, P. Active solar distillation—A detailed review. Renew. Sustain. Energy Rev. 2010, 14, 1503–1526. [Google Scholar] [CrossRef]
- Elango, C.; Gunasekaran, N.; Sampathkumar, K. Thermal models of solar still—A comprehensive review. Renew. Sustain. Energy Rev. 2015, 47, 856–911. [Google Scholar] [CrossRef]
- Pal, P.; Dev, R. Thermal Modeling, Experimental Validation, and Comparative Analysis of Modified Solar Stills. J. Sol. Energy Eng. 2019, 141, 061013. [Google Scholar] [CrossRef]
- Shukla, K.; Rai, A. Analytical thermal modeling of double slope solar still by using inner glass cover temperature. Therm. Sci. 2008, 12, 139–152. [Google Scholar] [CrossRef]
- Nayak, A.K.; Dev, R. Thermal Modelling and Performance Study of Modified Double Slope Solar Still. IJRET Int. J. Res. Eng. Technol. 2016, 5, 2321–7308. Available online: http://www.ijret.org (accessed on 16 June 2022).
- Dwivedi, V.; Tiwari, G. Experimental validation of thermal model of a double slope active solar still under natural circulation mode. Desalination 2010, 250, 49–55. [Google Scholar] [CrossRef]
- Tripathi, R.; Tiwari, G. Thermal modeling of passive and active solar stills for different depths of water by using the concept of solar fraction. Sol. Energy 2006, 80, 956–967. [Google Scholar] [CrossRef]
- Mashaly, A.F.; Alazba, A.; Al-Awaadh, A.; Mattar, M.A. Predictive model for assessing and optimizing solar still performance using artificial neural network under hyper arid environment. Sol. Energy 2015, 118, 41–58. [Google Scholar] [CrossRef]
- Santos, N.I.; Said, A.M.; James, D.E.; Venkatesh, N.H. Modeling solar still production using local weather data and artificial neural networks. Renew. Energy 2012, 40, 71–79. [Google Scholar] [CrossRef]
- Kandeal, A.W.; An, M.; Chen, X.; Algazzar, A.M.; Thakur, A.K.; Guan, X.; Wang, J.; Elkadeem, M.R.; Ma, W.; Sharshir, S.W. Productivity Modeling Enhancement of a Solar Desalination Unit with Nanofluids Using Machine Learning Algorithms Integrated with Bayesian Optimization. Energy Technol. 2021, 9, 2100189. [Google Scholar] [CrossRef]
- Nazari, M.A.; Salem, M.; Mahariq, I.; Younes, K.; Maqableh, B.B. Utilization of Data-Driven Methods in Solar Desalination Systems: A Comprehensive Review. Front. Energy Res. 2021, 9, 541. [Google Scholar] [CrossRef]
- Nomor, E.; Islam, R.; Alim, M.A.; Rahman, A. Production of Fresh Water by a Solar Still: An Experimental Case Study in Australia. Water 2021, 13, 3373. [Google Scholar] [CrossRef]
- Gnanaraj, S.J.P.; Ramachandran, S. Identification of operational parameter levels that optimize the production in solar stills with plain, corrugated, and compartmental basin. Environ. Sci. Pollut. Res. 2021, 29, 7096–7116. [Google Scholar] [CrossRef]
- Younis, S.M.; El-Shakweer, M.H.; El-Danasary, M.M.; Gharieb, A.A.; Mourad, R.I. Effect of Some Factors on Water Distillation by Solar Energy. Misr J. Agric. Eng. 2010, 27, 586–599. [Google Scholar] [CrossRef]
- Mashaly, A.F.; Alazba, A. Thermal performance analysis of an inclined passive solar still using agricultural drainage water and artificial neural network in arid climate. Sol. Energy 2017, 153, 383–395. [Google Scholar] [CrossRef]
- Gupta, P.; Singh, N. The Prediction of Productivity of Single Slope Solar Still: A Regression Approach. Int. J. Sci. Res. (IJSR) 2015, 4, 320–322. [Google Scholar]
- Dumka, P.; Mishra, D.R. An estimation of the distillate output from a CSS based on multivariable regression analysis. Int. J. Ambient Energy 2020, 43, 2417–2422. [Google Scholar] [CrossRef]
- Tsilingiris, P. Modeling heat and mass transport phenomena at higher temperatures in solar distillation systems—The Chilton–Colburn analogy. Sol. Energy 2010, 84, 308–317. [Google Scholar] [CrossRef]
- Singh, N.; Francis, V. Investigating the Effect of Water Temperature and Inclination Angle on the Performance of Single Slope Solar Still: A Taguchi Approach. Int. J. Eng. Res. Appl. (IJERA) 2013, 3, 404–407. [Google Scholar]
- Tarawneh, M.; Sethupathi, P.V.R.; Senthil, P. Parametric Optimization for Improving the Performance of Single Slope Solar Still Through Experimental Studies. Int. J. Eng. Sci. Res. Technol. 2016, 5, 291–299. [Google Scholar] [CrossRef]
- Mathioulakis, E.; Voropoulos, K.; Belessiotis, V. Modeling and prediction of long-term performance of solar stills. Desalination 1999, 122, 85–93. [Google Scholar] [CrossRef]
- Yadav, N.; Raich, V. An Implementation of Double Slope Basin Solar Still Plant Design to Predict the Distillate Yield and Instantaneous Efficiency. Int. J. Innov. Technol. Explor. Eng. 2020, 9, 2430–2433. [Google Scholar] [CrossRef]
- Renné, D.S. Resource assessment and site selection for solar heating and cooling systems. In Advances in Solar Heating and Cooling; Woodhead Publishing: Cambridge, UK, 2016; pp. 13–41. [Google Scholar] [CrossRef]
- Wilcox, S.; Marion, W. Users Manual for TMY3 Data Sets; National Renewable Energy Lab. (NREL): Golden, CO, USA, 2008. [Google Scholar] [CrossRef] [Green Version]
- China Post. Taiwan’s “Little Shanghai” Revives Thanks to Surging Tourists—SHINE News. Available online: https://www.shine.cn/feature/travel/2007202545/ (accessed on 20 July 2022).
- Central Weather Bureau. Available online: https://www.cwb.gov.tw/eng/ (accessed on 10 July 2022).
- Alwan, N.; Shcheklein, S.; Ali, O. Experimental Investigation of Modified Solar Still Productivity under Variable Climatic Conditions. Int. J. Des. Nat. Ecodyn. 2020, 19, 57–64. [Google Scholar] [CrossRef]
- Minitab Ltd. Data Analysis, Statistical & Process Improvement Tools|Minitab. Minitab. 2022. Available online: https://www.minitab.com/en-us/ (accessed on 5 June 2022).
- LeBlanc, D.C. Statistics: Concepts and Applications for Science; Jones and Bartlett: Sudbury, MA, USA, 2004. [Google Scholar]
- Mendenhall, W.M.; Sincich, T.L. Statistics for Engineering and the Sciences; CRC Press: Boca Raton, FL, USA, 2016; Available online: https://books.google.com.tw/books?id=x73RDwAAQBAJ (accessed on 15 March 2022).
- Larose, D.T. Data Mining Methods and Models; Wiley: Hoboken, NJ, USA, 2006; Available online: https://books.google.com.tw/books?id=xR_dHaEugEYC (accessed on 20 June 2022).
- 10.3—Regression with Autoregressive Errors|STAT 462. The Pennsylvania State University. 2018. Available online: https://online.stat.psu.edu/stat462/node/189/ (accessed on 20 March 2022).
- Karch, J. Improving on Adjusted R-Squared. Collabra Psychol. 2020, 6, 45. [Google Scholar] [CrossRef]
- Hsieh, T.E. Mapping the Global Solar Radiation and Diffuse Fraction Distributions in Taiwan Using Kriging Method; National Cheng Kung University: Tainan City, Taiwan, 2022. [Google Scholar]
- Furukawa, D.H. Desalination Processes and Technologies. 1996. Available online: http://inis.iaea.org/search/search.aspx?orig_q=RN:28008685 (accessed on 2 July 2022).
- Lachish, U. Optimizing the Efficiency of Reverse Osmosis Seawater Desalination. Available online: https://urila.tripod.com/Seawater.htm (accessed on 11 June 2022).
- Kamal, W.A. A theoretical and experimental study of the basin-type solar still under the Arabian gulf climatic conditions. Sol. Wind. Technol. 1988, 5, 147–157. [Google Scholar] [CrossRef]
- D’Cotha, J.S.; Sajeesh, P.; Suresh, P.R.; Jithu, J. Inherent configuration characteristics altering the distillate enhancement of passive stepped solar still: A review. J. King Saud Univ. Eng. Sci. 2021. [Google Scholar] [CrossRef]
- Jamil, B.; Akhtar, N. Effect of specific height on the performance of a single slope solar still: An experimental study. Desalination 2017, 414, 73–88. [Google Scholar] [CrossRef]
- Feilizadeh, M.; Estahbanati, M.K.; Ahsan, A.; Jafarpur, K.; Mersaghian, A. Effects of water and basin depths in single basin solar stills: An experimental and theoretical study. Energy Convers. Manag. 2016, 122, 174–181. [Google Scholar] [CrossRef]
- Ahdab, Y.D.; Thiel, G.P.; Böhlke, J.; Stanton, J.; Lienhard, J.H. Minimum energy requirements for desalination of brackish groundwater in the United States with comparison to international datasets. Water Res. 2018, 141, 387–404. [Google Scholar] [CrossRef] [Green Version]
- Montgomery, D.C.; Peck, E.A.; Vining, G.G. Introduction to Linear Regression Analysis; Wiley: Hoboken, NJ, USA, 2021; Available online: https://books.google.com.tw/books?id=Y2wYEAAAQBAJ (accessed on 20 March 2022).
- Omara, Z.; Abdullah, A.; Kabeel, A.; Essa, F. The cooling techniques of the solar stills’ glass covers—A review. Renew. Sustain. Energy Rev. 2017, 78, 176–193. [Google Scholar] [CrossRef]
- Bani-Hani, E.; Qassem, H.; Al Kandari, M.; Al Azmi, S.; Khalid, M.; Bu-Mijdad, H.; Khanafer, K.; Sedaghat, A. Experimental Analysis of an Improved Solar Still System with Cooling Fan and Preheating Oil. Energy Eng. 2017, 114, 55–71. [Google Scholar] [CrossRef]
- Al-Garni, A.Z. Productivity Enhancement of Solar Still Using Water Heater and Cooling Fan. J. Sol. Energy Eng. 2012, 134, 031006. [Google Scholar] [CrossRef]
- Berenson, M.; Levine, D.; Szabat, K.A.; Krehbiel, T.C. Basic Business Statistics: Concepts and Applications; Pearson Higher Education: Melbourne, Australia, 2012; Available online: https://books.google.com.tw/books?id=2TDiBAAAQBAJ (accessed on 21 March 2022).
- Bobbitt, Z. The Durbin-Watson Test: Definition & Example—Statology. Available online: https://www.statology.org/durbin-watson-test/ (accessed on 1 July 2022).
- Kenton, W. Durbin Watson Statistic Definition. Available online: https://www.investopedia.com/terms/d/durbin-watson-statistic.asp (accessed on 4 August 2021).
- Feria-Díaz, J.J.; López-Méndez, M.C.; Ortiz-Monterde, L.; Médina-Salgado, B.A.; Perez-Rosas, N.C. Performance Evaluation of Solar Still in Veracruz, Mexico Gulf Coastline. Water 2022, 14, 1567. [Google Scholar] [CrossRef]



| Meteorological Factors | Design Factors | Operational Factors | References |
|---|---|---|---|
| ambient temperature, sky temperature, global radiation, and wind velocity | - | - | [19] |
| daily solar radiation, average ambient air temperature | - | - | [28] |
| - | - | heat storage material, basin water depth, basin cover thickness and external mirrors | [20] |
| percentage of daylight, ambient temperature, solar radiation, windspeed | glass cover thickness | feedwater salinity, initial water depth | [21] |
| relative humidity, windspeed, solar radiation, ambient temperature | - | feedwater temperature, feedwater flow rate and feedwater TDS | [22] |
| - | inclination angle | feedwater temperature, salt concentration, depth | [23] |
| solar radiation intensity, ambient temperature | - | temperature difference between feedwater and inner condensing cover | [24] |
| - | inclination angle | feedwater temperature | [26] |
| - | quantity of stone used as energy storing medium, area of the double glazing used | feedwater level | [27] |
| solar radiation | - | feedwater temperature | [29] |
| Instrument | Make/Model | Range | Uncertainty (%) |
|---|---|---|---|
| Resistance thermocouple | Thermoway/PT100 | 0–100 °C | ±0.47% |
| Spectral pyranometers | Kipp & Zonen/CMP11 | 0–1400 W/ | ±1.41% |
| Anemometer | Vector Instruments/A100L2 | 0–77 m/s | ±1.16% |
| Humidity-temperature transmitter | Dwyer/657-1 | 0–100% 0–100 °C | ±1.73% ±0.58% |
| Beaker | Yeasten | 0–500 mL | ±2% |
| Top-pan balance | Shimadzu/EB-4300D | 0–4300 g | ±2.5% |
| Trial | Duration (Days) | Average Daily Yield (L/day) | Average Daily Rad (MJ/m2) | Average Daily Ta (°C) | Average Daily CCr | Average Daily Ws (m/s) | Average Daily RHa (%) |
|---|---|---|---|---|---|---|---|
| 1 | 17 | 2.552 | 11.73 | 17.28 | 7.22 | 1.75 | 82.57 |
| 2 | 9 | 4.879 | 18.27 | 21.33 | 2.64 | 2.10 | 70.73 |
| 3 | 7 | 6.205 | 21.37 | 23.27 | 2.89 | 1.92 | 63.16 |
| 4 | 12 | 3.631 | 13.93 | 23.43 | 8.22 | 1.99 | 77.98 |
| 5 | 9 | 4.778 | 17.90 | 20.64 | 5.32 | 2.21 | 74.97 |
| 6 | 7 | 6.101 | 21.52 | 25.32 | 3.91 | 1.91 | 65.76 |
| 7 | 10 | 4.291 | 16.10 | 25.36 | 7.76 | 1.81 | 80.21 |
| 8 | 7 | 6.126 | 21.70 | 28.80 | 7.43 | 1.49 | 76.44 |
| 9 | 10 | 4.270 | 15.45 | 28.00 | 8.36 | 1.59 | 79.62 |
| 10 | 7 | 6.100 | 21.81 | 29.69 | 7.73 | 1.34 | 71.94 |
| 11 | 6 | 7.117 | 23.92 | 29.96 | 6.98 | 1.68 | 68.19 |
| Parameters | Recovery Ratio (%) | |||
|---|---|---|---|---|
| 60 | 70 | 80 | ||
| Volume of feedwater (L) | 46 | 61 | 100 | |
| Total volume of distillate (L) | Overnight | 4.229 (15.3%) | 7.279 (16.9%) | 20.661 (25.8%) |
| Daytime | 23.436 (84.7%) | 35.690 (83.1%) | 59.534 (74.2%) | |
| Total | 27.665 (100%) | 43.001 (100%) | 80.195 (100%) | |
| Duration (days) | 6 | 9 | 16 | |
| Avg. productivity (L/day) | 4.61 | 4.78 | 5.01 | |
| Avg. rate of change of productivity (L/day2) | 0.768 | 0.531 (−30.9%) | 0.313 (−59.2%) | |
| Avg. daily total insolation (MJ/m2) | 17.1 | 17.9 | 18.6 | |
| Avg. daily Ta (°C) | 26.5 | 20.6 | 25.7 | |
| Avg. daily RHa (%) | 75.7 | 75.0 | 76.5 | |
| Avg. daily TB (°C) | 40.4 | 35.2 | 39.8 | |
| Recovery Ratio (%) | Mass of Salt (g) | Volume of Water Sample (L) | Concentration of Brine Residue (mg/L) | Change in Concentration (%) |
|---|---|---|---|---|
| 60 | 187.8 | 2.00 b | 93, 900 | - |
| 70 | 1, 700.0 a | 14.8 a | 114, 865 | 22.3 |
| 80 | 441.3 | 2.00 b | 220, 650 | 135.0 |
| Term | Coefficient | SE of Coefficient | p-Value | VIF | ||||
|---|---|---|---|---|---|---|---|---|
| Initial | Final | Initial | Final | Initial | Final | Initial | Final | |
| Constant | −1.786 | −1.073 | 0.926 | 0.14 | 0.057 | 0.00000 | - | - |
| Rad | 0.334 | 0.31015 | 0.0177 | 0.00775 | 0.000 | 0.00000 | 4.41 | 4.92 |
| Temp | 0.0207 | 0.04074 | 0.0195 | 0.00905 | 0.291 | 0.00004 | 2.86 | 3.13 |
| CCr | 0.0015 | −0.0741 | 0.0279 | 0.0109 | 0.958 | 0.00000 | 2.57 | 2.35 |
| RHa | 0.002 | 0.0028 | 0.0102 | 0.0055 | 0.844 | 0.61800 | 2.36 | 2.84 |
| Number of Variables (k) | R2 (%) | (%) | Mallows Cp | S | Rad | Temp | RHa | Ws | CCr |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 99.0 | 99.0 | 41.9 | 0.23036 | ✓ | ||||
| 1 | 59.3 | 58.5 | 3887.9 | 1.4768 | ✓ | ||||
| 2 | 99.3 | 99.2 | 19.2 | 0.20031 | ✓ | ✓ | |||
| 2 | 99.1 | 99.1 | 33.1 | 0.21900 | ✓ | ✓ | |||
| 3 | 99.5 | 99.4 | 2.5 | 0.17350 | ✓ | ✓ | ✓ | ||
| 3 | 99.3 | 99.2 | 19.9 | 0.20033 | ✓ | ✓ | ✓ | ||
| 4 | 99.5 | 99.4 | 4.1 | 0.17445 | ✓ | ✓ | ✓ | ✓ | |
| 4 | 99.5 | 99.4 | 4.4 | 0.17504 | ✓ | ✓ | ✓ | ✓ | |
| 5 | 99.5 | 99.4 | 6.0 | 0.17602 | ✓ | ✓ | ✓ | ✓ | ✓ |
| Data Set Used | MAE | RMSE | MAPE (%) | R2 (%) | (%) |
|---|---|---|---|---|---|
| Training | 0.144 | 0.167 | 9.709 | 99.47 | 99.44 |
| Testing | 0.178 | 0.246 | 4.591 | 98.39 | 97.58 |
| Month | TMY Year | Monthly Average TMM Values | Daily Average Predicted Yield (L) | ||
|---|---|---|---|---|---|
| Rad (MJ/m2) | Temp (°C) | CCr | |||
| January | 2013 | 9.16 | 17.05 | 7.02 | 1.99 |
| February | 2011 | 10.48 | 17.28 | 6.48 | 2.53 |
| March | 2015 | 12.27 | 20.75 | 6.55 | 3.10 |
| April | 2014 | 15.67 | 23.26 | 5.30 | 4.34 |
| May | 2007 | 18.58 | 25.97 | 4.05 | 5.45 |
| June | 2005 | 17.76 | 27.09 | 7.12 | 5.06 |
| July | 2015 | 20.03 | 28.28 | 5.54 | 5.88 |
| August | 2016 | 17.98 | 28.36 | 5.36 | 5.26 |
| September | 2013 | 17.03 | 27.35 | 3.49 | 5.07 |
| October | 2017 | 14.70 | 26.85 | 4.20 | 4.27 |
| November | 2009 | 10.25 | 23.08 | 6.08 | 2.72 |
| December | 2017 | 8.43 | 19.58 | 6.39 | 1.97 |
| Location | Avg. Yield | Avg. Days per Batch | Avg. Batches per Year | Annual Yield (L) | a Annual Mass of Crude Salt (kg) | |
|---|---|---|---|---|---|---|
| L/Day | L/M2 Day | |||||
| Dongji Island | 3.978 | 4.851 | 12.5 | 29.3 | 1456.9 | 49.8 |
| Location | a Basin Length Requirement | b Basin Size Requirement | c Evacuated Tube Requirement | |||
|---|---|---|---|---|---|---|
| Value (m) | % Increase | Value (m2) | % Increase | Amount | % Increase | |
| Dongji Islet | 3.30 | 88.6 | 1.95 | 88.5 | 23 | 91 |
| Location | (NTD) | ACF (NTD) | PP (Years) |
|---|---|---|---|
| Dongji Islet | 100, 567.5 (USD 3, 419.3) | 16, 421.76 (USD 558.3) | 6.1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Samuel, A.; Chang, K.-C. Statistical Model for the Sizing of a Prototype Solar Still Applicable to Remote Islands. Water 2022, 14, 3510. https://doi.org/10.3390/w14213510
Samuel A, Chang K-C. Statistical Model for the Sizing of a Prototype Solar Still Applicable to Remote Islands. Water. 2022; 14(21):3510. https://doi.org/10.3390/w14213510
Chicago/Turabian StyleSamuel, Alinford, and Keh-Chin Chang. 2022. "Statistical Model for the Sizing of a Prototype Solar Still Applicable to Remote Islands" Water 14, no. 21: 3510. https://doi.org/10.3390/w14213510






