Can Microplastic Pollution Change Soil-Water Dynamics? Results from Controlled Laboratory Experiments
Abstract
:1. Introduction
2. Materials and Methods
2.1. Soil and MP
2.2. Environmentally Relevant Levels of MP Pollution
2.3. Experimental Design
2.4. Soil-Water Measurements
- -
- Experiment 1: Water Holding Capacity (WHC)
- -
- Experiment 2: Bare Soil Evaporation (ER)
2.5. Statistical Tools: Linear Regression and Non-Parametric Analysis of Variance (Kruskal–Wallis ANOVA)
3. Results and Discussion
3.1. Linear Regression Analyses
3.1.1. Experiment 1: Water Holding Capacity (WHC)
3.1.2. Experiment 2: Bare Soil Evaporation (ER)
3.2. Kruskal–Wallis Statistical Analyses
4. Conclusions: Environmental Implications and Future Directions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Andrady, A.L. Microplastics in the marine environment. Mar. Pollut. Bull. 2011, 62, 1596–1605. [Google Scholar] [CrossRef] [PubMed]
- Available online: https://www.amazon.com/gp/product/B00CB39ICA (accessed on 2 May 2022).
- Banimahd, S.A.; Zand-Parsa, S.H. Simulation of evaporation, coupled liquid water, water vapor and heat transport through the soil medium. Agric. Water Manag. 2013, 130, 168–177. [Google Scholar] [CrossRef]
- Barnes, D.K.A.; Galgani, F.; Thompson, R.C.; Barlaz, M. Accumulation and fragmentation of plastic debris in global environments. Philos. Trans. R. Soc. B Biol. Sci. 2009, 364, 1985–1998. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- van den Berg, P.; Huerta-Lwanga, E.; Corradini, F.; Geissen, V. Sewage sludge application as a vehicle for microplastics in eastern Spanish agricultural soils. Environ. Pollut. 2020, 261, 114198. [Google Scholar] [CrossRef] [PubMed]
- Bigelow, D.; Borchers, A. Major Uses of Land in the United States, 2012; United States Department of Agriculture: Washington, DC, USA, 2017. [Google Scholar]
- Bittelli, M.; Ventura, F.; Campbell, G.S.; Snyder, R.L.; Gallegati, F.; Pisa, P.R. Coupling of heat, water vapor, and liquid water fluxes to compute evaporation in bare soils. J. Hydrol. 2008, 362, 191–205. [Google Scholar] [CrossRef]
- Bläsing, M.; Amelung, W. Plastics in soil: Analytical methods and possible sources. Sci. Total Environ. 2018, 612, 422–435. [Google Scholar] [CrossRef]
- Bonan, G. Ecological Climatology: Concepts and Applications; Cambridge University Press: Cambridge, UK, 2015. [Google Scholar]
- Browne, M.A.; Crump, P.; Niven, S.J.; Teuten, E.; Tonkin, A.; Galloway, T.; Thompson, R. Accumulation of microplastic on shorelines woldwide: Sources and sinks. Environ. Sci. Technol. 2011, 45, 9175–9179. [Google Scholar] [CrossRef] [PubMed]
- Brutsaert, W. Evaporation into the Atmosphere: Theory, History and Applications; Springer Science & Business Media: Berlin, Germany, 2013. [Google Scholar]
- Büks, F.; Kaupenjohann, M. Global concentrations of microplastics in soils—A review. Soil 2020, 6, 649–662. [Google Scholar] [CrossRef]
- Crawford, C.B.; Quinn, B. Microplastic Pollutants; Elsevier Limited: Amsterdam, The Netherlands, 2016. [Google Scholar]
- Crossman, J.; Hurley, R.R.; Futter, M.; Nizzetto, L. Transfer and transport of microplastics from biosolids to agricultural soils and the wider environment. Sci. Total Environ. 2020, 724, 138334. [Google Scholar] [CrossRef]
- Deb, S.K.; Shukla, M.K.; Sharma, P.; Mexal, J.G. Coupled liquid water, water vapor, and heat transport simulations in an unsaturated zone of a sandy loam field. Soil Sci. 2011, 176, 387–398. [Google Scholar] [CrossRef]
- Dong, Y.; Gao, M.; Qiu, W.; Song, Z. Effect of microplastics and arsenic on nutrients and microorganisms in rice rhizosphere soil. Ecotoxicol. Environ. Saf. 2021, 211, 111899. [Google Scholar] [CrossRef] [PubMed]
- Elliott, A.C.; Hynan, L.S. A SAS® macro implementation of a multiple comparison post hoc test for a Kruskal–Wallis analysis. Comput. Methods Programs Biomed. 2011, 102, 75–80. [Google Scholar] [CrossRef] [PubMed]
- Feng, X.; Wang, Q.; Sun, Y.; Zhang, S.; Wang, F. Microplastics change soil properties, heavy metal availability and bacterial community in a Pb-Zn-contaminated soil. J. Hazard. Mater. 2022, 424, 127364. [Google Scholar] [CrossRef] [PubMed]
- Forero-López, A.; Rimondino, G.; Truchet, D.; Colombo, C.; Buzzi, N.; Malanca, F.; Spetter, C.; Fernández-Severini, M. Occurrence, distribution, and characterization of suspended microplastics in a highly impacted estuarine wetland in Argentina. Sci. Total Environ. 2021, 785, 147141. [Google Scholar] [CrossRef]
- Fuller, S.; Gautam, A. A procedure for measuring microplastics using pressurized fluid extraction. Environ. Sci. Technol. 2016, 50, 5774–5780. [Google Scholar] [CrossRef] [Green Version]
- Geyer, R.; Jambeck, J.R.; Law, K.L. Production, use, and fate of all plastics ever made. Sci. Adv. 2017, 3, e1700782. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gregory, M.R. Plastic scrubbers’ in hand cleansers: A further (and minor) source for marine pollution identified. Mar. Pollut. Bull. 1996, 32, 867–871. [Google Scholar] [CrossRef]
- Han, J.; Zhou, Z. Dynamics of soil water evaporation during soil drying: Laboratory experiment and numerical analysis. Sci. World J. 2013, 2013, 240280. [Google Scholar] [CrossRef] [Green Version]
- Harley-Nyang, D.; Memon, F.; Jones, N.; Galloway, T. Investigation and analysis of microplastics in sewage sludge and biosolids: A case study from one wastewater treatment works in the UK. Sci. Total Environ. 2022, 823, 153735. [Google Scholar] [CrossRef] [PubMed]
- Hauer, F.R.; Lamberti, G.A. Methods in Stream Ecology; Academic Press: Cambridge, MA, USA, 2011. [Google Scholar]
- He, D.; Luo, Y.; Lu, S.; Liu, M.; Song, Y.; Lei, L. Microplastics in soils: Analytical methods, pollution characteristics and ecological risks. TrAC Trends Anal. Chem. 2018, 109, 163–172. [Google Scholar] [CrossRef]
- Hecke, T.V. Power study of anova versus Kruskal-Wallis test. J. Stat. Manag. Syst. 2012, 15, 241–247. [Google Scholar] [CrossRef]
- Helsel, D.R.; Hirsch, R.M. Statistical Methods in Water Resources; Elsevier: Amsterdam, The Netherlands, 1992. [Google Scholar]
- Hurley, R.R.; Nizzetto, L. Fate and occurrence of micro(nano)plastics in soils: Knowledge gaps and possible risks. Curr. Opin. Environ. Sci. Health 2018, 1, 6–11. [Google Scholar] [CrossRef]
- Iden, S.C.; Blöcher, J.R.; Diamantopoulos, E.; Durner, W. Capillary, film, and vapor flow in transient bare soil evaporation (1): Identifiability analysis of hydraulic conductivity in the medium to dry moisture range. Water Resour. Res. 2021, 57, e2020WR028513. [Google Scholar] [CrossRef]
- de Jesus Piñon-Colin, T.; Rodriguez-Jimenez, R.; Rogel-Hernandez, E.; Alvarez-Andrade, A.; Wakida, F.T. Microplastics in stormwater runoff in a semiarid region, Tijuana, Mexico. Sci. Total Environ. 2020, 704, 135411. [Google Scholar] [CrossRef]
- Jiang, X.J.; Liu, W.; Wang, E.; Zhou, T.; Xin, P. Residual plastic mulch fragments effects on soil physical properties and water flow behavior in the Minqin Oasis, northwestern China. Soil Tillage Res. 2017, 166, 100–107. [Google Scholar] [CrossRef]
- Kershaw, P. Sources, Fate and Effects of Microplastics in the Marine Environment: A Global Assessment; International Maritime Organization: London, UK, 2015. [Google Scholar]
- Kim, S.W.; An, Y.J. Soil microplastics inhibit the movement of springtail species. Environ. Int. 2019, 126, 699–706. [Google Scholar] [CrossRef] [PubMed]
- Kirkham, M.B. Principles of Soil and Plant Water Relations; Academic Press: Cambridge, MA, USA, 2014. [Google Scholar]
- Konert, M.; Vandenberghe, J.E.F. Comparison of laser grain size analysis with pipette and sieve analysis: A solution for the underestimation of the clay fraction. Sedimentology 1997, 44, 523–535. [Google Scholar] [CrossRef] [Green Version]
- Koutnik, V.; Alkidim, S.; Leonard, J.; DePrima, F.; Cao, S.; Hoek, E.; Mohanty, S. Unaccounted microplastics in wastewater sludge: Where do they go? ACS EST Water 2021, 1, 1086–1097. [Google Scholar] [CrossRef]
- Kumar, M.; Xiong, X.; He, M.; Tsang, D.C.W.; Gupta, J.; Khan, E.; Harrad, S.; Hou, D.; Ok, Y.S.; Bolan, N.S. Microplastics as pollutants in agricultural soils. Environ. Pollut. 2020, 265, 114980. [Google Scholar] [CrossRef]
- Kumar, R.; Sharma, P.; Bandyopadhyay, S. Evidence of microplastics in wetlands: Extraction and quantification in Freshwater and coastal ecosystems. J. Water Process Eng. 2021, 40, 101966. [Google Scholar] [CrossRef]
- Kumar, R.; Sharma, P.; Manna, C.; Jain, M. Abundance, interaction, ingestion, ecological concerns, and mitigation policies of microplastic pollution in riverine ecosystem: A review. Sci. Total Environ. 2021, 782, 146695. [Google Scholar]
- Lebreton, L.C.M.; Van Der Zwet, J.; Damsteeg, J.-W.; Slat, B.; Andrady, A.; Reisser, J. River plastic emissions to the world’s oceans. Nat. Commun. 2017, 8, 15611. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lehmann, A.; Fitschen, K.; Rillig, M.C. Abiotic and biotic factors influencing the effect of microplastic on soil aggregation. Soil Syst. 2019, 3, 21. [Google Scholar] [CrossRef] [Green Version]
- Li, J.; Ouyang, Z.; Liu, P.; Zhao, X.; Wu, R.; Zhang, C.; Lin, C.; Li, Y.; Guo, X. Distribution and characteristics of microplastics in the basin of Chishui River in Renhuai, China. Sci. Total Environ. 2021, 773, 145591. [Google Scholar] [CrossRef] [PubMed]
- Li, B.; Huang, S.; Wang, H.; Liu, M.; Xue, S.; Tang, D.; Cheng, W.; Fan, T.; Yang, X. Effects of plastic particles on germination and growth of soybean (Glycine max): A pot experiment under field condition. Environ. Pollut. 2021, 272, 116418. [Google Scholar] [CrossRef]
- Lian, J.; Liu, W.; Meng, L.; Wu, J.; Zeb, A.; Cheng, L.; Lian, Y.; Sun, H. Effects of microplastics derived from polymer-coated fertilizer on maize growth, rhizosphere, and soil properties. J. Clean. Prod. 2021, 318, 128571. [Google Scholar]
- Liang, Y.; Lehmann, A.; Ballhausen, M.-B.; Muller, L.; Rillig, M.C. Increasing temperature and microplastic fibers jointly influence soil aggregation by saprobic fungi. Front. Microbiol. 2019, 10, 2018. [Google Scholar] [CrossRef]
- Lindeque, P.K.; Cole, M.; Coppock, R.L.; Lewis, C.N.; Miller, R.Z.; Watts, A.J.R.; Wilson-McNeal, A.; Wright, S.L.; Galloway, T.S. Are we underestimating microplastic abundance in the marine environment? A comparison of microplastic capture with nets of different mesh-size. Environ. Pollut. 2020, 265, 114721. [Google Scholar] [CrossRef]
- Lozano, Y.M.; Lehnert, T.; Linck, L.T.; Lehmann, A.; Rillig, M.C. Microplastic shape, polymer type, and concentration affect soil properties and plant biomass. Front. Plant Sci. 2021, 12, 169. [Google Scholar]
- Maaß, S.; Daphi, D.; Lehmann, A.; Rillig, M.C. Transport of microplastics by two collembolan species. Environ. Pollut. 2017, 225, 456–459. [Google Scholar]
- MacArthur, E. The New Plastics Economy Rethinking the Future of Plastics. 2016. Available online: https://ellenmacarthurfoundation.org/the-new-plastics-economy-rethinking-the-future-of-plastics (accessed on 1 February 2022).
- Magnusson, K.; Norén, F. Screening of Microplastic Particles in and Down-Stream a Wastewater Treatment Plant, IVL Swedish Environmental Research Institute. 2014. Available online: http://urn.kb.se/resolve?urn=urn:nbn:se:naturvardsverket:diva-2226 (accessed on 10 February 2022).
- Meier, C.I.; Hauer, F.R. Strong effect of coarse surface layer on moisture within gravel bars: Results from an outdoor experiment. Water Resour. Res. 2010, 46, W05507. [Google Scholar] [CrossRef]
- Meixner, K.; Kubiczek, M.; Fritz, I. Microplastic in soil–current status in Europe with special focus on method tests with Austrian samples. AIMS Environ. Sci. 2020, 7, 174–191. [Google Scholar] [CrossRef]
- Montgomery, D.C.; Peck, E.A.; Vining, G.G. Introduction to Linear Regression Analysis; John Wiley & Sons: Hoboken, NJ, USA, 2021. [Google Scholar]
- Murphy, F.; Ewins, C.; Carbonnier, F.; Quinn, B. Wastewater treatment works (WwTW) as a source of microplastics in the aquatic environment. Environ. Sci. Technol. 2016, 50, 5800–5808. [Google Scholar] [CrossRef] [Green Version]
- Napper, I.E.; Thompson, R.C. Release of synthetic microplastic plastic fibres from domestic washing machines: Effects of fabric type and washing conditions. Mar. Pollut. Bull. 2016, 112, 39–45. [Google Scholar] [CrossRef] [PubMed]
- Ng, E.L.; Huerta Lwanga, E.; Eldridge, S.M.; Johnston, P.; Hu, H.W.; Geissen, V.; Chen, D. An overview of microplastic and nanoplastic pollution in agroecosystems. Sci. Total Environ. 2018, 627, 1377–1388. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, B.; Claveau-Mallet, D.; Hernandez, L.M.; Xu, E.G.; Farner, J.M.; Tufenkji, N. Separation and analysis of microplastics and nanoplastics in complex environmental samples. Acc. Chem. Res. 2019, 52, 858–866. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Nizzetto, L.; Bussi, G.; Futter, M.N.; Butterfield, D.; Whitehead, P.G. A theoretical assessment of microplastic transport in river catchments and their retention by soils and river sediments. Environ. Sci. Process. Impacts 2016, 18, 1050–1059. [Google Scholar] [CrossRef]
- Or, D.; Lehmann, P.; Shahraeeni, E.; Shokri, N. Advances in soil evaporation physics—A review. Vadose Zone J. 2013, 12, vzj2012-0163. [Google Scholar] [CrossRef]
- Padha, S.; Kumar, R.; Dhar, A.; Sharma, P. Microplastic pollution in mountain terrains and foothills: A review on source, extraction, and distribution of microplastics in remote areas. Environ. Res. 2022, 207, 112232. [Google Scholar] [CrossRef]
- Peters, A.; Iden, S.C.; Durner, W. Revisiting the simplified evaporation method: Identification of hydraulic functions considering vapor, film and corner flow. J. Hydrol. 2015, 527, 531–542. [Google Scholar] [CrossRef]
- Piehl, S.; Leibner, A.; Löder, M.G.J.; Dris, R.; Bogner, C.; Laforsch, C. Identification and quantification of macro-and microplastics on an agricultural farmland. Sci. Rep. 2018, 8, 17950. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Plastics—The Facts. 2018. Available online: https://plasticseurope.org/wp-content/uploads/2021/10/2018-Plastics-the-facts.pdf (accessed on 15 February 2022).
- Qi, R.; Jones, D.L.; Li, Z.; Liu, Q.; Yan, C. Behavior of microplastics and plastic film residues in the soil environment: A critical review. Sci. Total Environ. 2020, 703, 134722. [Google Scholar] [CrossRef] [PubMed]
- Qiu, G.Y.; Ben-Asher, J. Experimental determination of soil evaporation stages with soil surface temperature. Soil Sci. Soc. Am. J. 2010, 74, 13–22. [Google Scholar] [CrossRef]
- Rillig, M.C. Microplastic in terrestrial ecosystems and the soil? Environ. Sci. Technol. 2012, 46, 6453–6454. [Google Scholar] [CrossRef]
- Rochman, C.M.; Cook, A.M.; Koelmans, A.A. Plastic debris and policy: Using current scientific understanding to invoke positive change. Environ. Toxicol. Chem. 2016, 35, 1617–1626. [Google Scholar] [CrossRef] [Green Version]
- Rolsky, C.; Kelkar, V.; Driver, E.; Halden, R.U. Municipal sewage sludge as a source of microplastics in the environment. Curr. Opin. Environ. Sci. Health 2020, 14, 16–22. [Google Scholar] [CrossRef]
- Saito, H.; Šimunek, J.; Mohanty, B.P. Numerical analysis of coupled water, vapor, and heat transport in the vadose zone. Vadose Zone J. 2006, 5, 784–800. [Google Scholar] [CrossRef] [Green Version]
- Selonen, S.; Dolar, A.; Kokalj, A.J.; Skalar, T.; Dolcet, L.P.; Hurley, R.; van Gestel, C.A.M. Exploring the impacts of plastics in soil–The effects of polyester textile fibers on soil invertebrates. Sci. Total Environ. 2020, 700, 134451. [Google Scholar] [CrossRef]
- de Souza Machado, A.A.; Lau, C.W.; Till, J.; Kloas, W.; Lehmann, A.; Becker, R.; Rillig, M.C. Impacts of microplastics on the soil biophysical environment. Environ. Sci. Technol. 2018, 52, 9656–9665. [Google Scholar] [CrossRef] [Green Version]
- de Souza Machado, A.A.; Kloas, W.; Zarfl, C.; Hempel, S.; Rillig, M.C. Microplastics as an emerging threat to terrestrial ecosystems. Glob. Chang. Biol. 2018, 24, 1405–1416. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- de Souza Machado, A.A.; Lau, C.W.; Kloas, W.; Bergmann, J.; Bachelier, J.B.; Faltin, E.; Becker, R.; Görlich, A.S.; Rillig, M.C. Microplastics can change soil properties and affect plant performance. Environ. Sci. Technol. 2019, 53, 6044–6052. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sun, J.; Dai, X.; Wang, Q.; van Loosdrecht, M.C.M.; Ni, B.-J. Microplastics in wastewater treatment plants: Detection, occurrence and removal. Water Res. 2019, 152, 21–37. [Google Scholar] [CrossRef] [PubMed]
- Terzaghi, K.; Peck, R.B.; Mesri, G. Soil Mechanics in Engineering Practice; John Wiley & Sons: Hoboken, NJ, USA, 1996. [Google Scholar]
- Wagner III, W.E. Using IBM® SPSS® Statistics for Research Methods and Social Science Statistics; Sage Publications: Thousand Oaks, CA, USA, 2019. [Google Scholar]
- Wan, Y.; Wu, C.; Xue, Q.; Hui, X. Effects of plastic contamination on water evaporation and desiccation cracking in soil. Sci. Total Environ. 2019, 654, 576–582. [Google Scholar] [CrossRef] [PubMed]
- Weithmann, N.; Möller, J.N.; Löder, M.G.J.; Piehl, S.; Laforsch, C.; Freitag, R. Organic fertilizer as a vehicle for the entry of microplastic into the environment. Sci. Adv. 2018, 4, eaap8060. [Google Scholar] [CrossRef] [PubMed]
- Zhang, G.S.; Zhang, F.X.; Li, X.T. Effects of polyester microfibers on soil physical properties: Perception from a field and a pot experiment. Sci. Total Environ. 2019, 670, 1–7. [Google Scholar] [CrossRef] [PubMed]
- Zhang, S.; Yang, X.; Gertsen, H.; Peters, P.; Salánki, T.; Geissen, V. A simple method for the extraction and identification of light density microplastics from soil. Sci. Total Environ. 2018, 616–617, 1056–1065. [Google Scholar] [CrossRef] [Green Version]
- Zubris, K.A.V.; Richards, B.K. Synthetic fibers as an indicator of land application of sludge. Environ. Pollut. 2005, 138, 201–211. [Google Scholar] [CrossRef]

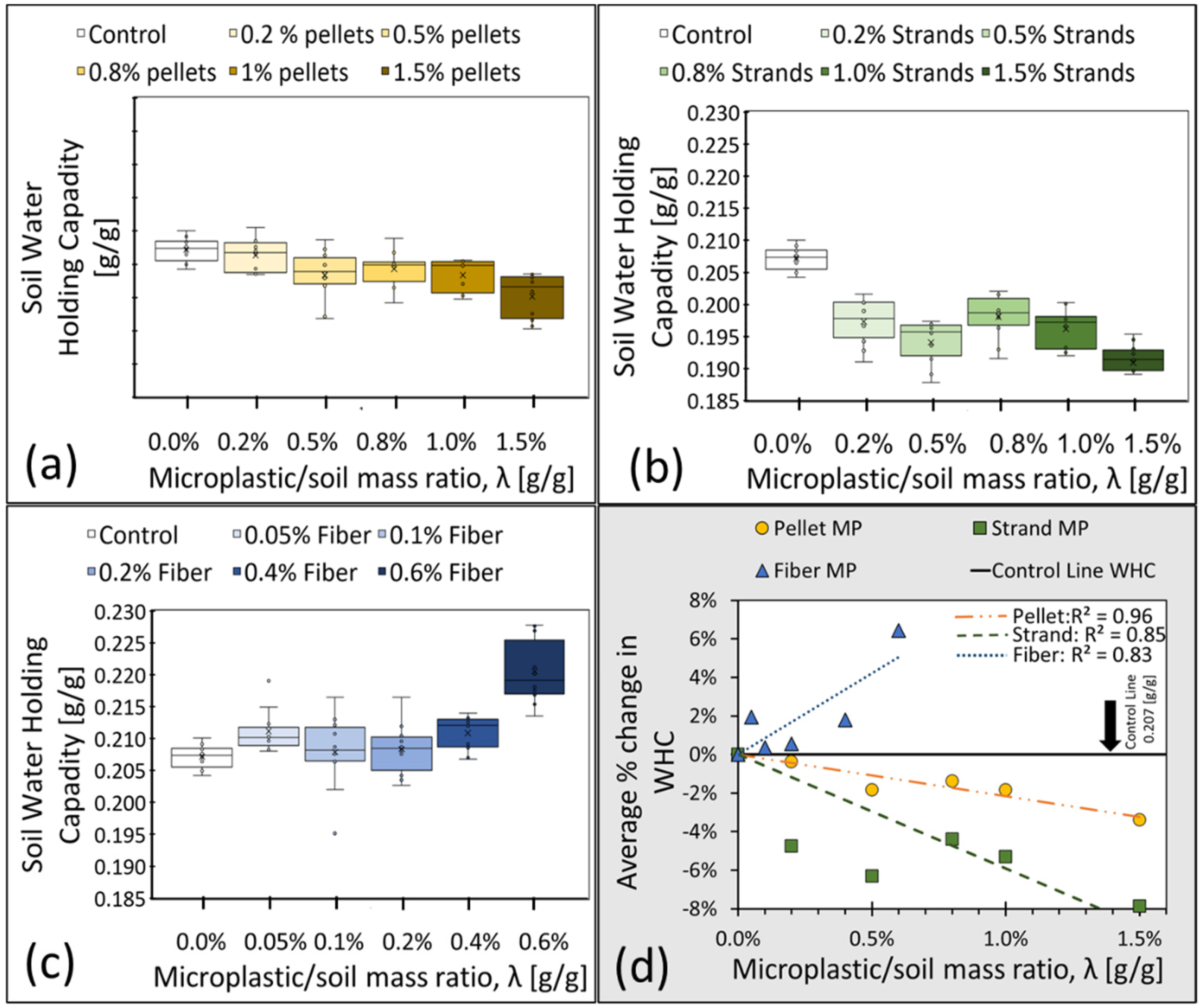
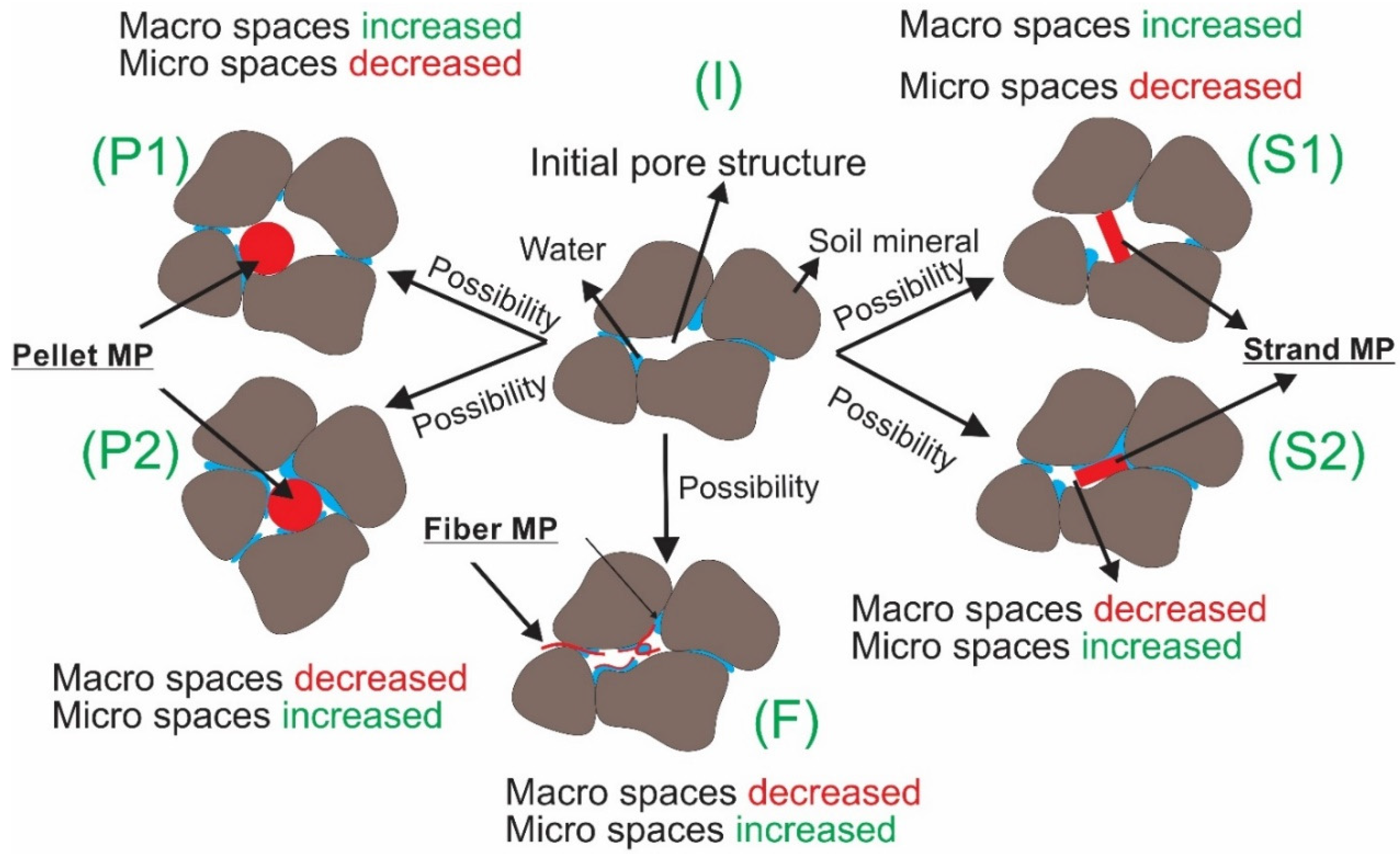
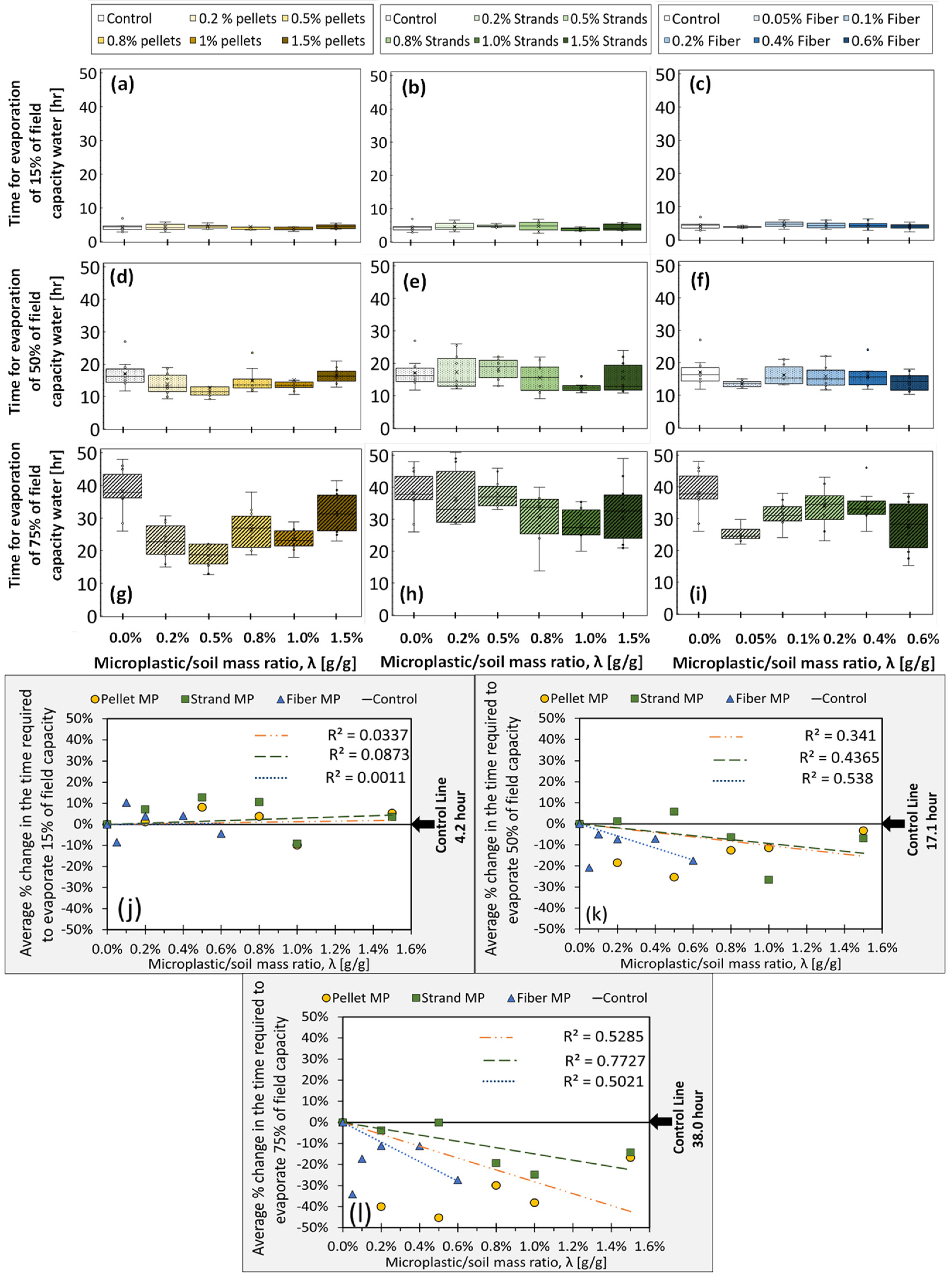
| Name of Experiment | Microplastic Type | Microplastic/Soil Mass Ratio, λ (g/g) | Dry Soil Mass (g) | Replicates (N) |
|---|---|---|---|---|
| 1. Soil water holding capacity (SWH) 2. Evaporation Rate (ER) | Clean soil (control) | 0.0% | 750 | 10 for each λ |
| Pellets | 0.2%, 0.5%, 0.8%, 1%, and 1.5% | |||
| Strands | 0.2%, 0.5%, 0.8%, 1%, and 1.5% | |||
| Fibers | 0.05%, 0.1%, 0.2%, 0.4%, and 0.6% |
| (a) | ||||||
| Pairwise Comparison based on shape | ||||||
| Dependent Variables | Significant Level | |||||
| WHC (g/g) | Pellet | Strand | <0.001 | |||
| ER15 (hr) | Pellet | Strand | 0.65 | |||
| ER50 (hr) | Pellet | Strand | 0.333 | |||
| ER75 (hr) | Pellet | Strand | <0.001 | |||
| (b) | ||||||
| Pairwise Comparison based on λ | ||||||
| Dependent Variables | (I) λ (g/g) | (J) λ (g/g) | Significant Level | |||
| WHC (g/g) | 0% | 0.2% | 0.001 | |||
| 0.5% | 0.002 | |||||
| 0.8% | <0.001 | |||||
| 1.0% | <0.001 | |||||
| 1.5% | 0.032 | |||||
| ER15 (hr) | 0% | 0.2% | Multiple comparisons are not performed because the overall test does not show significant differences across samples. | |||
| 0.5% | ||||||
| 0.8% | ||||||
| 1.0% | ||||||
| 1.5% | ||||||
| ER50 (hr) | 0% | 0.2% | ||||
| 0.5% | ||||||
| 0.8% | ||||||
| 1.0% | ||||||
| 1.5% | ||||||
| ER75 (hr) | 0% | 0.2% | 0.001 | |||
| 0.5% | 0.002 | |||||
| 0.8% | <0.001 | |||||
| 1.0% | <0.001 | |||||
| 1.5% | 0.032 | |||||
| Pairwise Comparison Based on λ | |||
|---|---|---|---|
| Dependent Variables | (I) λ (g/g) | (J) λ (g/g) | Significant Level |
| WHC (g/g) | 0% | 0.05% | 0.028 |
| 0.1% | 0.316 | ||
| 0.2% | 0.390 | ||
| 0.4% | 0.029 | ||
| 0.6% | <0.001 | ||
| ER15 (hr) | 0% | 0.05% | Multiple comparisons are not performed because the overall test does not show significant differences across samples. |
| 0.1% | |||
| 0.2% | |||
| 0.4% | |||
| 0.6% | |||
| ER50 (hr) | 0% | 0.05% | |
| 0.1% | |||
| 0.2% | |||
| 0.4% | |||
| 0.6% | |||
| ER75 (hr) | 0% | 0.05% | <0.001 |
| 0.1% | 0.041 | ||
| 0.2% | 0.212 | ||
| 0.4% | 0.017 | ||
| 0.6% | 0.004 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jazaei, F.; Chy, T.J.; Salehi, M. Can Microplastic Pollution Change Soil-Water Dynamics? Results from Controlled Laboratory Experiments. Water 2022, 14, 3430. https://doi.org/10.3390/w14213430
Jazaei F, Chy TJ, Salehi M. Can Microplastic Pollution Change Soil-Water Dynamics? Results from Controlled Laboratory Experiments. Water. 2022; 14(21):3430. https://doi.org/10.3390/w14213430
Chicago/Turabian StyleJazaei, Farhad, Tareq Jamal Chy, and Maryam Salehi. 2022. "Can Microplastic Pollution Change Soil-Water Dynamics? Results from Controlled Laboratory Experiments" Water 14, no. 21: 3430. https://doi.org/10.3390/w14213430




