Wheeled Capsule Threshold of Motion at Different Locations in a Horizontal Bend Pipeline Based on Hydraulic Capsule Pipeline Transportation
Abstract
1. Introduction
2. Physical Experiment
2.1. Wheeled Capsule
2.2. The Experiment System
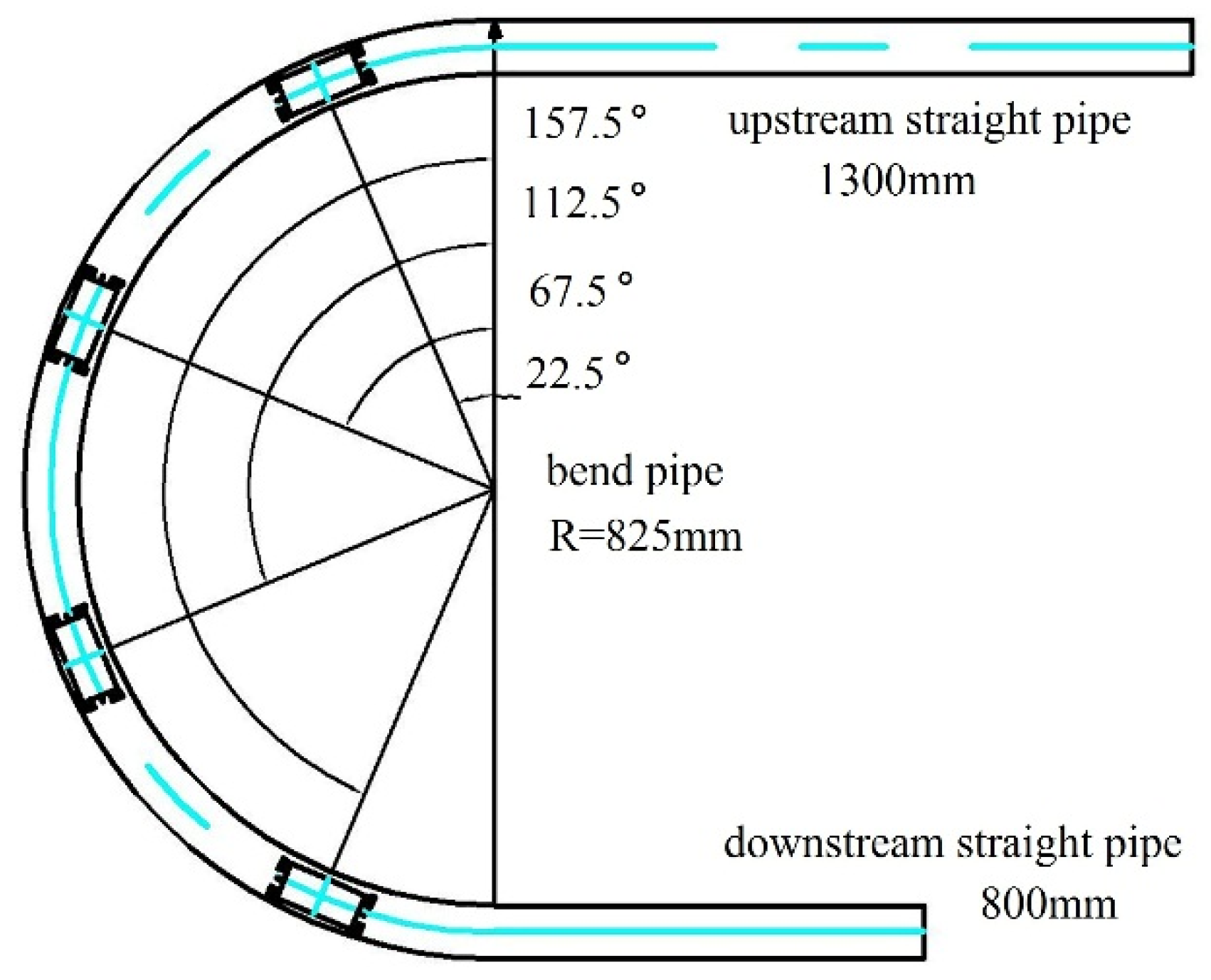
2.3. Analysis Condition Deployment
3. Numerical Simulation
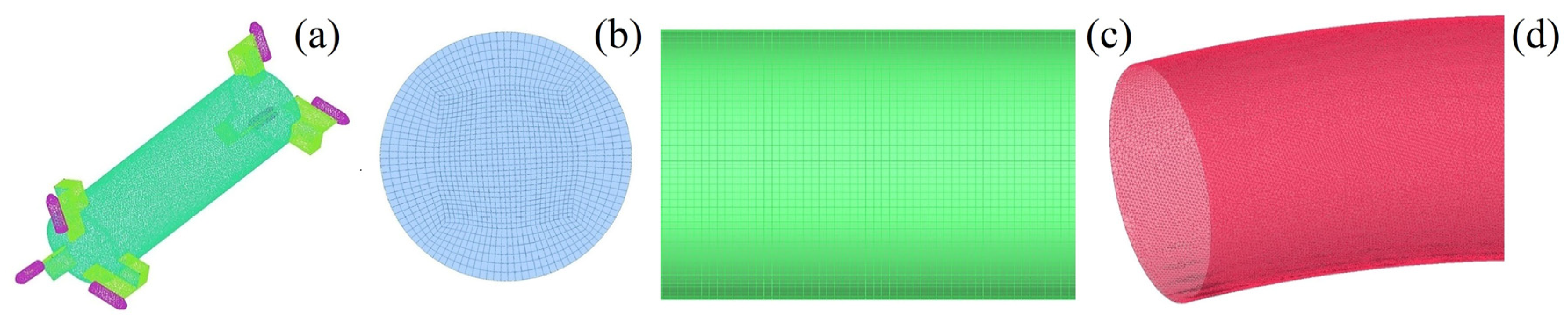
3.1. Simulation Domain Deployment and Mesh
3.2. Turbulence Model
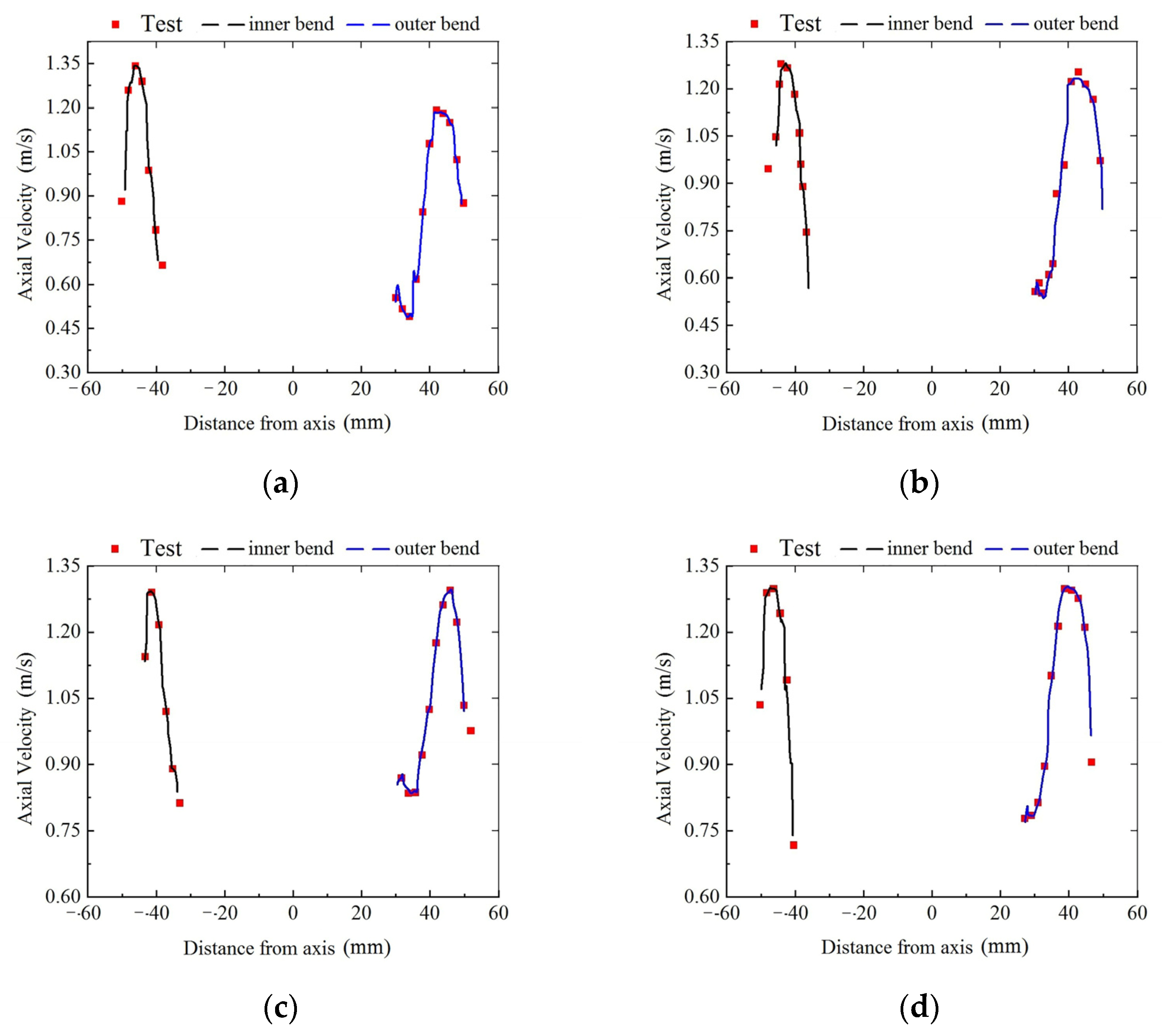
3.3. Verification of Simulation Result
4. Result and Discussion
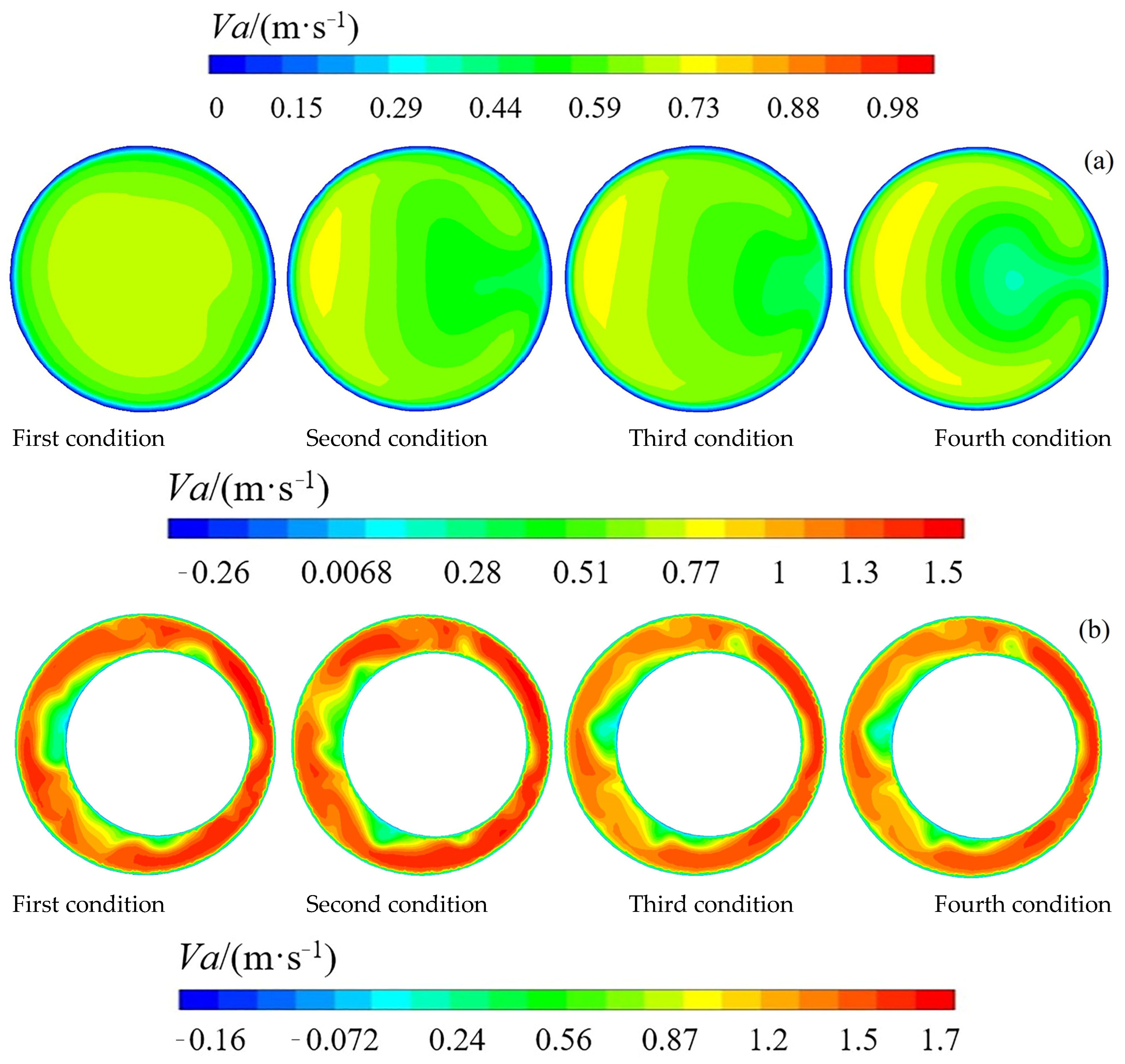
4.1. Total Flow Distribution during Capsule Threshold of Motion
4.2. Different Flow Distributions of the Four Threshold of Motion Conditions
4.2.1. The Axial Velocity Distribution
4.2.2. The Radial Velocity Distribution
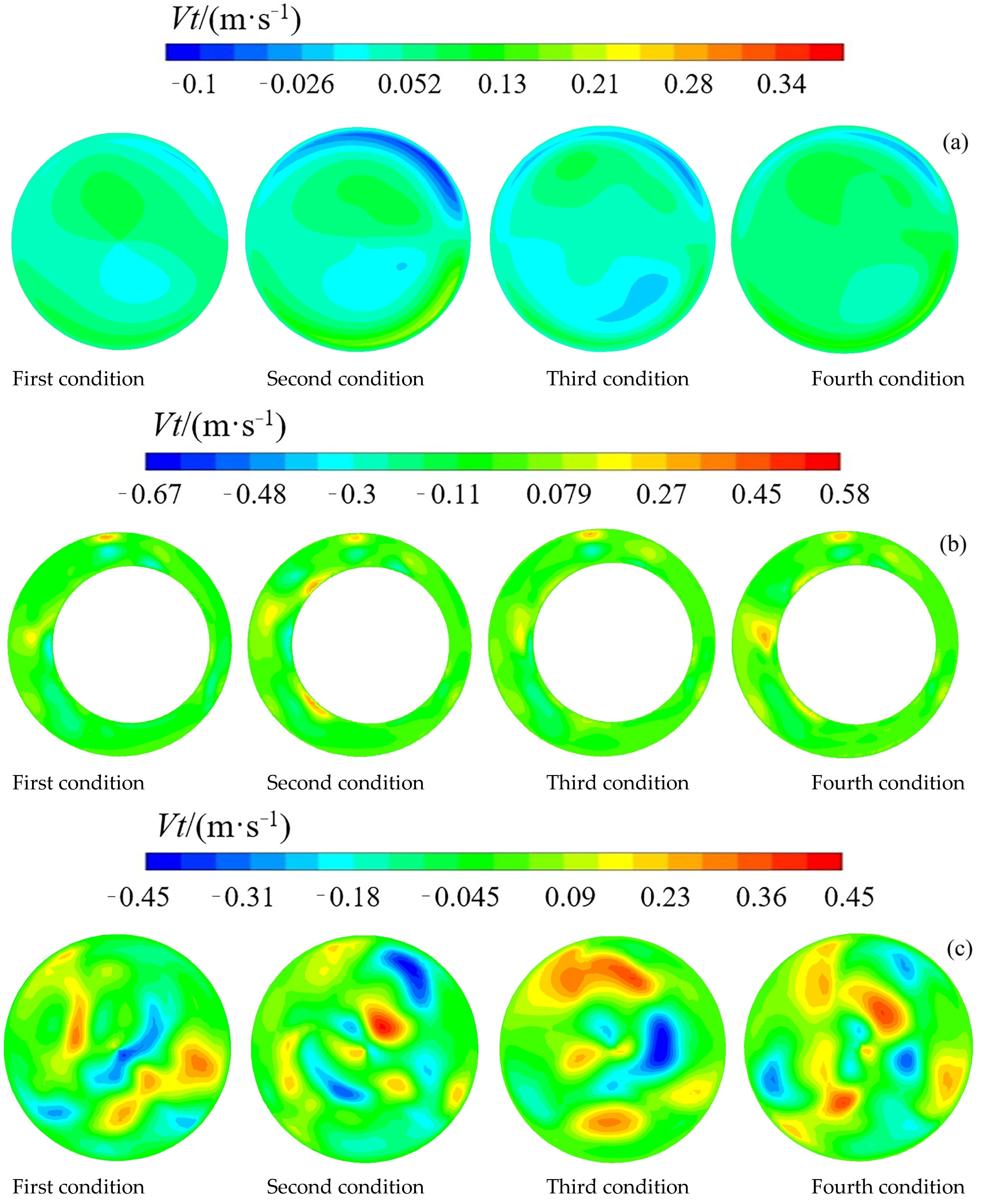
4.2.3. The Circular Velocity Distribution
4.3. Theory Analysis
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Minh, A.; Samudrala, S.; Bhattacharya, S. Valorisation of glycerol through catalytic hydrogenolysis routes for sustainable production of value-added C3 chemicals: Current and future trends. Sustain. Energ. Fules 2022, 6, 596–639. [Google Scholar] [CrossRef]
- Paul, A.; Bhattacharyya, S. Analysis and Design for Hydraulic Pipeline Carrying Capsule Train. J. Pipeline Syst. Eng. 2021, 2, 04021003. [Google Scholar] [CrossRef]
- Li, Y.; Sun, X.; Zhang, X. Study of the energy consumption of the piped vehicle hydraulic transportation. Adv. Mech. Eng. 2019, 11, 168781401988554. [Google Scholar] [CrossRef]
- Li, Y.; Gao, Y.; Sun, X.; Zhang, X. Study on Flow Velocity during Wheeled Capsule Hydraulic Transportation in a Horizontal Pipe. Water 2020, 12, 1181. [Google Scholar] [CrossRef]
- Jia, X.; Sun, X.; Song, J. Effect of Concentric Annular Gap Flow on Wall Shear Stress of Stationary Cylinder Pipe Vehicle under Different Reynolds Numbers. Math. Probl. Eng. 2020, 2020, 1253652. [Google Scholar] [CrossRef]
- Ulusarslan, D. Experimental investigation of the effect of diameter ratio on velocity ratio and pressure gradient for the spherical capsule train flow. Eur. J. Mech. B-Fluid 2013, 37, 42–47. [Google Scholar] [CrossRef]
- Teke, I.; Ulusarslan, D. Mathematical expression of pressure gradient in the flow of spherical capsules less dense than water. Int. J. Multiph. Flow 2007, 33, 658–674. [Google Scholar] [CrossRef]
- Asim, T.; Mishra, R. Computational fluid dynamics based optimal design of hydraulic capsule pipelines transporting cylindrical capsules. Power Technol. 2016, 295, 180–201. [Google Scholar] [CrossRef]
- Asim, T.; Mishra, R. Optimal design of hydraulic capsule pipelines transporting spherical capsules. Can. J. Chem. Eng. 2016, 94, 966–979. [Google Scholar] [CrossRef]
- Li, Y.; Sun, X. Mathematical Model of the Piped Vehicle Motion in Piped Hydraulic Transportation of Tube-Contained Raw Material. Math. Probl. Eng. 2019, 2019, 3930691. [Google Scholar] [CrossRef]
- Li, Y.; Sun, X.; Zhang, X. Experimental study of the wheeled capsule motion inside hydraulic pipeline. Adv. Mech. Eng. 2019, 11, 168781401984406. [Google Scholar] [CrossRef]
- Zhang, X.; Sun, X.; Li, Y.; Xi, X.; Guo, F.; Zheng, L. Numerical investigation of the concentric annulus flow around a cylindrical body with contrasted effecting factors. J. Hydrodyn. 2015, 27, 2273–2285. [Google Scholar] [CrossRef]
- Liu, H.; Graze, H.R. Lift and Drag on Stationary Capsule in Pipeline. J. Hydraul. Eng. 1983, 109, 28–47. [Google Scholar] [CrossRef]
- Yu, L. Incipient Motion of Static Material-logs in Slurry Pipeline. Mech. Eng. 2002, 24, 20–23. (In Chinese) [Google Scholar]
- Sun, X.; Li, Y.; Yan, Q. Experimental study on starting conditions of the hydraulic transportation on the piped carriage. In Proceedings of the 20th National Conference on Hydrodynamics, Beijing, China, 23–25 August 2007. [Google Scholar]
- Yang, X.; Ma, J.; Li, Y.; Sun, X.; Jia, X.; Li, Y. Wall Stresses in Cylinder of Stationary Piped Carriage Using COMSOL Multiphysics. Water 2019, 11, 1910. [Google Scholar] [CrossRef]
- Jia, X.; Sun, X.; Li, Y. Numerical Simulation of the Flow Field Characteristics of Stationary Two-Pipe Vehicles under Different Spacings. Water 2020, 12, 2158. [Google Scholar] [CrossRef]
- Zhang, C.; Sun, X.; Li, Y.; Zhang, X.; Zhang, X.; Yang, X.; Li, F. Effects of Guide Vane Placement Angle on Hydraulic Characteristics of Flow Field and Optimal Design of Hydraulic Capsule Pipelines. Water 2018, 10, 1378. [Google Scholar] [CrossRef]
- Zhao, Y.; Li, Y.; Song, X. PIV Measurement and Proper Orthogonal Decomposition Analysis of Annular Gap Flow of a Hydraulic Machine. Machines 2022, 10, 645. [Google Scholar] [CrossRef]
- Sigalotti, L.D.G.; Alvarado-Rodríguez, C.E.; Klapp, J.; Cela, J.M. Smoothed Particle Hydrodynamics Simulations of Water Flow in a 90° Pipe Bend. Water 2021, 13, 1081. [Google Scholar] [CrossRef]








| Experimental Setting | Main Parameter |
|---|---|
| Illumination | Dual Power Nd-YLF Laser (2 × 30 mJ) |
| Camera lens | 2 Imager pro HS cameras |
| Image dimension | 2016 × 2016 pixels |
| Interrogation area | 32 × 32 pixels |
| Time between pulses | 5 × 103 μs |
| Seeding material | Polystyrene particles diameter 55 μm |
| Resolution ratio | 39.68 μm/pixel |
| Condition | Reynolds Number |
|---|---|
| Straight pipe | 60,840 |
| Condition 1 (bend pipe) | 59,350 |
| Condition 2 (bend pipe) | 56,108 |
| Condition 3 (bend pipe) | 56,950 |
| Condition 4 (bend pipe) | 59,593 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, Y.; Zhao, Y.; Yuan, Y.; Tian, Y.; Sun, X. Wheeled Capsule Threshold of Motion at Different Locations in a Horizontal Bend Pipeline Based on Hydraulic Capsule Pipeline Transportation. Water 2022, 14, 3392. https://doi.org/10.3390/w14213392
Lu Y, Zhao Y, Yuan Y, Tian Y, Sun X. Wheeled Capsule Threshold of Motion at Different Locations in a Horizontal Bend Pipeline Based on Hydraulic Capsule Pipeline Transportation. Water. 2022; 14(21):3392. https://doi.org/10.3390/w14213392
Chicago/Turabian StyleLu, Yifan, Yiming Zhao, Yuan Yuan, Yu Tian, and Xihuan Sun. 2022. "Wheeled Capsule Threshold of Motion at Different Locations in a Horizontal Bend Pipeline Based on Hydraulic Capsule Pipeline Transportation" Water 14, no. 21: 3392. https://doi.org/10.3390/w14213392
APA StyleLu, Y., Zhao, Y., Yuan, Y., Tian, Y., & Sun, X. (2022). Wheeled Capsule Threshold of Motion at Different Locations in a Horizontal Bend Pipeline Based on Hydraulic Capsule Pipeline Transportation. Water, 14(21), 3392. https://doi.org/10.3390/w14213392






