Optimization Method to Determine the Kinetic Rate Constants for the Removal of Benzo[a]pyrene and Anthracene in Water through the Fenton Process
Abstract
:1. Introduction
2. Materials and Methods
2.1. Chemicals and Reagents
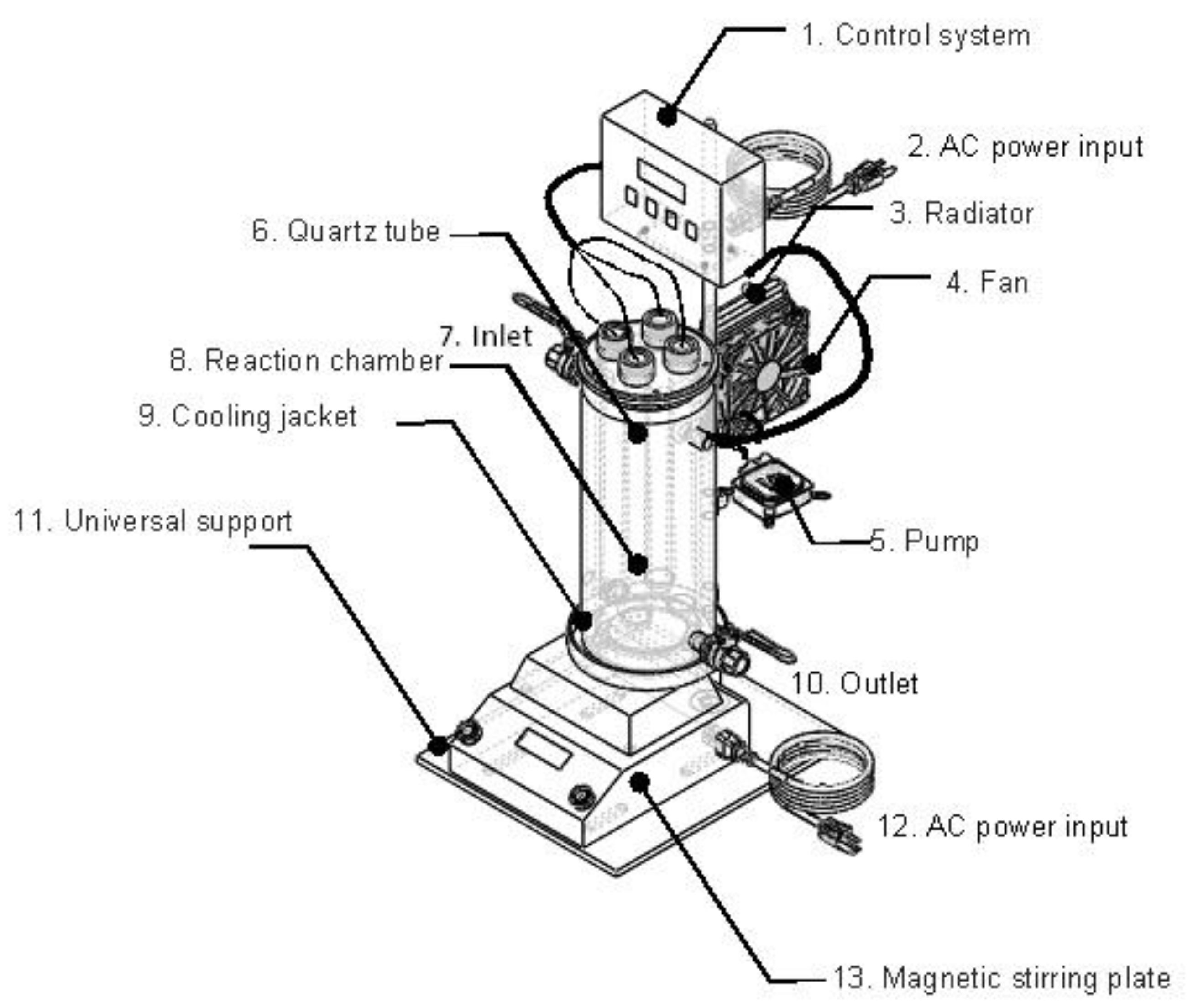
2.2. Experimental Setup
2.3. Analytical Methods
2.4. Kinetic Model Representing AN and BaP Removal
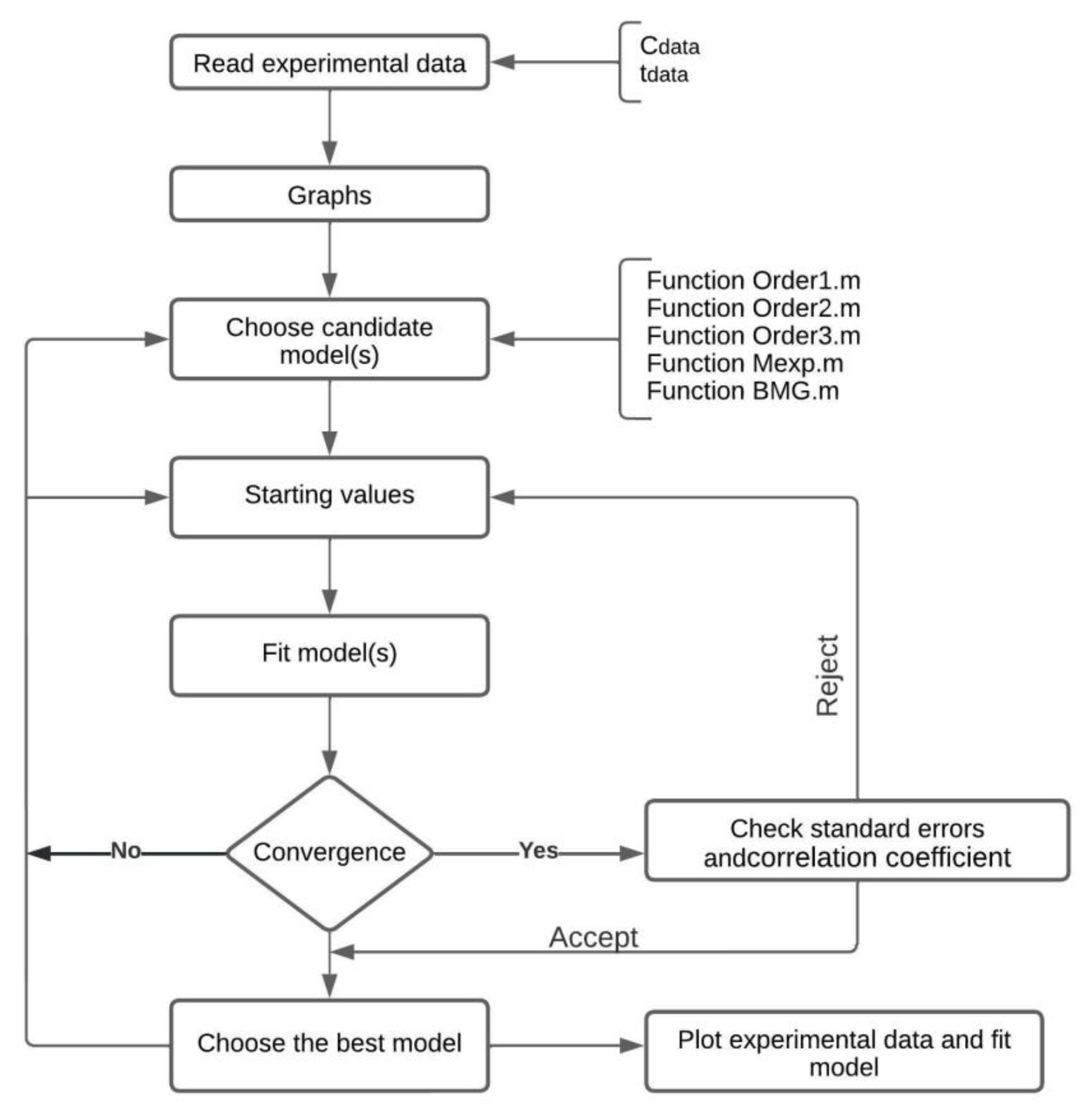
2.5. Optimization Method to Determine the Pollutant Removal Rate Constants
- The algorithm reads the vector of experimental data (Cdata) and the vector that records the time when the measurements of the species concentration were performed (tdata). The fitting function (g) should be defined. This function depends on one or several parameters to be fitted. Fitting the curve via optimization means finding these parameters that minimize the sum of squared errors.
- clear all
- close all
- clc
- fig = figure(3)
- ExpData = xlsread(‘Fenton’,’hoja1’, ’A1.B21’); % Read experimental data from an excel file
- tdata = ExpData(:,1);
- Cdata = ExpData(:,2);
- Then, the experimental data related to concentration vs. time are plotted using the function plot of MATLAB®.
- plot(tdata,Cdata,’ro’); % Plot the experimental data
- hold on;
- h = plot(tdata,Cdata,’b’);
- hold off;
- In the algorithm, it is necessary to define the objective function to be minimized that accepts the parameters to be optimized, in this particular case. When Cdatai (tdatai) represents the experimental AN or BaP concentration values measured throughout the time of treatment and are the simulated data, the function (F) can be rewritten as Equation (9).
- function E = Order1(x,tdata,Cdata)
- k1 = x(1);
- E = sum((Cdata - exp(-k1*tdata)).^2);
- fun = @(x)Order1(x,tdata,ydata);
- x0=rand(1,1);
- outputFcn = @(x,optimvalues,state) fitoutputfun(x,optimvalues,state,tdata,ydata,h);
- options = optimset(‘OutputFcn’,outputFcn,’TolX’,1e-80,’MaxFunEvals’, 10,000,000);
- bestx=fminsearch(fun,x0,options)
- For checking the quality of the fit, the resulting fitted response curve and the data are plotted. The response curve is created from the returned parameters of the model. Finally, the coefficient of determination (R2) was used to choose the best model that describes the removal of the compounds of interest.
- A = 1;
- k1 = bestx(1);
- yfit = A*exp(-k1 *tdata);
- FS=10;
- plot(tdata,ydata,’*’);
- hold on
- plot(tdata,yfit,’r’);
- hold on
- axis ([ 0 90 0 1.0 ])
- title(‘Experimental Data and Best Fitting Curve’)
- xlabel (‘Time (min)’)
- ylabel (‘[AN]/[AN]_o’)
- g=legend(‘Experimental data Fenton-NW’,’Fitting curve’,’location’,’best’);
- set(g,’Box’,’on’,’EdgeColor’,[1 1 1])
- set(gcf, ‘color’,’white’)
- set(gca,’FontSize’,FS,’yticklabel’,num2str(get(gca,’ytick’)’,’%.1f’));
- box off
- grid on
- a=corr(ydata,yfit)^2
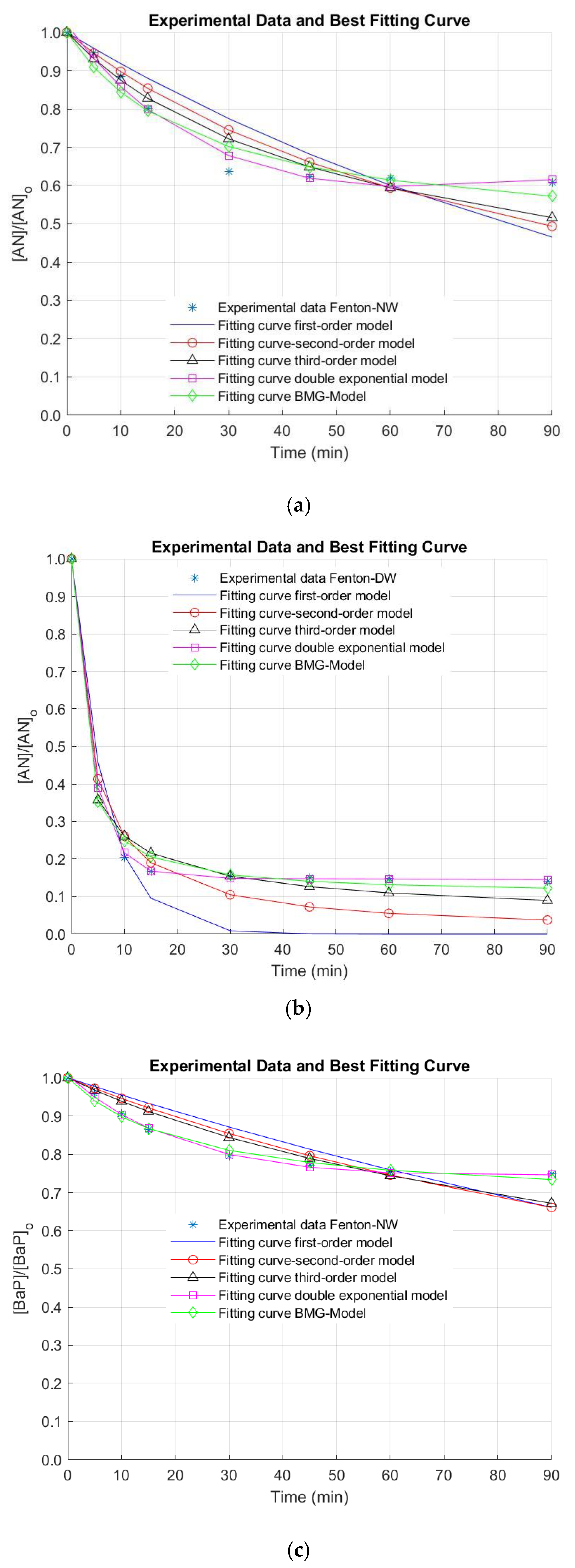
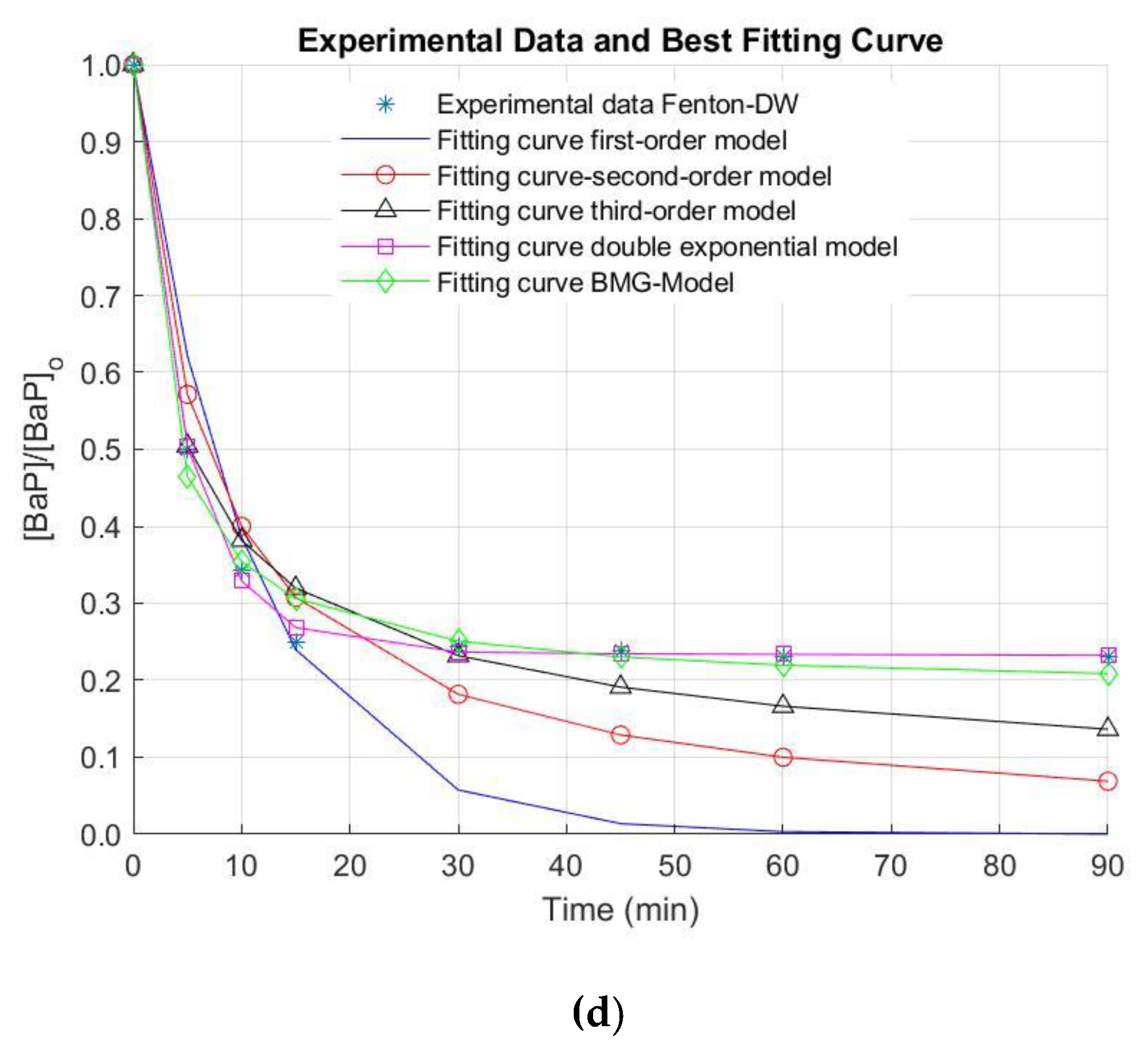
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chu, L.; Sun, Z.; Cang, L.; Fang, G.; Wang, X.; Zhou, D.; Gao, J. A novel sulfite coupling electro-fenton reactions with ferrous sulfide cathode for anthracene degradation. Chem. Eng. J. 2020, 400, 125945. [Google Scholar] [CrossRef]
- Fang, J.; Zhao, R.; Rao, B.; Rakowska, M.; Athanasiou, D.; Millerick, K.; Suying, W.; Xiangyan, L.; Helen, H.L.; Reible, D.D. Removal of polycyclic aromatic hydrocarbons from water using Mn (III)-based advanced oxidation process. J. Environ. Eng. 2021, 3, 04021002. [Google Scholar] [CrossRef]
- Zhang, M.H.; Dong, H.; Zhao, L.; Wang, D.X.; Meng, D. A review on Fenton process for organic wastewater treatment based on optimization perspective. Sci. Total Environ. 2019, 670, 110–121. [Google Scholar] [CrossRef] [PubMed]
- Jain, B.; Singh, A.K.; Kim, H.; Lichtfouse, E.; Sharma, V.K. Treatment of organic pollutants by homogeneous and heterogeneous Fenton reaction processes. Environ. Chem. Lett. 2018, 16, 947–967. [Google Scholar] [CrossRef] [Green Version]
- Öz, Ç.; Çetin, E. Treatment of bilge water by fenton oxidation followed by granular activated carbon adsorption. Water 2021, 13, 2792. [Google Scholar] [CrossRef]
- Rubio-Clemente, A.; Chica, E.; Peñuela, G.A. Petrochemical wastewater treatment by photo-Fenton process. Water Air Soil Pollut. 2015, 226, 62. [Google Scholar] [CrossRef]
- Gholami, M.; Shomali, A.; Abbasi Souraki, B.; Pendashteh, A. Advanced numerical kinetic model for predicting COD removal and optimisation of pulp and paper wastewater treatment by Fenton process. Int. J. Environ. Anal. Chem. 2022, 102, 2729–2752. [Google Scholar] [CrossRef]
- Sinha, S.; Roy, D.; Roy, O.; Neogi, S.; De, S. Removal of organic contaminants from flowback water using Fenton process. J. Water Process Eng. 2022, 47, 102680. [Google Scholar] [CrossRef]
- Li, Y.; Cheng, H. Chemical kinetic modeling of organic pollutant degradation in Fenton and solar photo-Fenton processes. J. Taiwan Inst. Chem. Eng. 2021, 123, 175–184. [Google Scholar] [CrossRef]
- Enesca, A.; Isac, L. Tandem structures semiconductors based on TiO2_SnO2 and ZnO_SnO2 for photocatalytic organic pollutant removal. Nanomaterials 2021, 11, 200. [Google Scholar] [CrossRef] [PubMed]
- Cüce, H.; Temel, F.A.; Yolcu, O.C. Modelling and optimization of Fenton processes through neural network and genetic algorithm. Korean J. Chem. Eng. 2021, 38, 2265–2278. [Google Scholar] [CrossRef]
- Rubio-Clemente, A.; Chica, E.; Peñuela, G.A. Benzo[a]pyrene emerging micropollutant oxidation under the action of Fenton reactants in real surface water: Process optimization and application. Polycycl. Aromat. Compd. 2021, 41, 95–108. [Google Scholar] [CrossRef]
- Rubio-Clemente, A.; Chica, E.L.; Peñuela, G.A. Direct large-volume injection analysis of polycyclic aromatic hydrocarbons in water. Univ. Sci. 2018, 23, 171–189. [Google Scholar] [CrossRef]
- Rubio-Clemente, A.; Chica, E.; Peñuela, G. Rapid determination of anthracene and benzo(a)pyrene by high-performance liquid chromatography with fluorescence detection. Anal. Lett. 2017, 50, 1229–1247. [Google Scholar] [CrossRef]
- Wu, Y.; Zhou, S.; Qin, F.; Zheng, K.; Ye, X. Modeling the oxidation kinetics of Fenton’s process on the degradation of humic acid. J. Hazard. Mater. 2010, 179, 533–539. [Google Scholar] [CrossRef]
- Aljuboury, D.A.D.; Palaniandy, P. Kinetic study of inorganic carbon (IC) removal and COD removal from refinery wastewater by solar Photo-Fenton. Glob. Nest J. 2017, 19, 641–649. [Google Scholar]
- Lopez-Lopez, C.; Martín-Pascual, J.; Martínez-Toledo, M.V.; Muñío, M.M.; Hontoria, E.; Poyatos, J.M. Kinetic modelling of TOC removal by H2O2/UV, photo-Fenton and heterogeneous photocatalysis processes to treat dye-containing wastewater. Int. J. Environ. Sci. Technol. 2015, 12, 3255–3262. [Google Scholar] [CrossRef] [Green Version]
- Chan, K.H.; Chu, W. Model applications and intermediates quantification of atrazine degradation by UV-enhanced Fenton process. J. Agric. Food Chem. 2006, 54, 1804–1813. [Google Scholar] [CrossRef]
- Bautista, P.; Mohedano, A.F.; Gilarranz, M.A.; Casas, J.A.; Rodriguez, J.J. Application of Fenton oxidation to cosmetic wastewaters treatment. J. Hazard. Mater. 2007, 143, 128–134. [Google Scholar] [CrossRef]
- Marcinowski, P.P.; Bogacki, J.P.; Naumczyk, J. Cosmetic wastewater treatment using the Fenton, Photo-Fenton and H2O2/UV processes. J. Environ. Sci. Health Part A 2014, 49, 1531–1541. [Google Scholar] [CrossRef]
- Li, C.; Mei, Y.; Qi, G.; Xu, W.; Zhou, Y.; Shen, Y. Degradation characteristics of four major pollutants in chemical pharmaceutical wastewater by Fenton process. J. Environ. Chem. Eng. 2021, 9, 104564. [Google Scholar] [CrossRef]
- Suna, S.P.; Li, C.J.; Sunb, J.H.; Shib, S.H.; Fand, M.H.; Zhoua, Q. Decolorization of an azo dye Orange G in aqueous solution by Fenton oxidation process: Effect of system parameters and kinetic study. J. Hazard. Mater. 2009, 161, 1052–1057. [Google Scholar] [CrossRef] [PubMed]
- Hu, K.; Zhou, P.; Yang, Y.; Hall, T.; Nie, G.; Yao, Y.; Wang, S. Degradation of microplastics by a thermal Fenton reaction. ACS ES&T Eng. 2021, 2, 110–120. [Google Scholar]
- Behnajady, M.A.; Modirshahla, N.; Ghanbary, F.A. kinetic model for the decolorization of C.I. Acid Yellow 23 by Fenton process. J. Hazard. Mater. 2007, 148, 98–102. [Google Scholar] [CrossRef]
- Saini, R.; Kumar Mondal, M.; Kumar, P. Fenton oxidation of pesticide methyl parathion in aqueous solution: Kinetic study of the degradation. Environ. Prog. Sustain. Energy 2017, 36, 420–427. [Google Scholar] [CrossRef]
- Ertugay, N.; Acar, F.N. Removal of COD and color from Direct Blue 71 azo dye wastewater by Fenton’s oxidation: Kinetic study. Arab. J. Chem. 2017, 10, S1158–S1163. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Q.; Wang, C.; Lei, Y. Fenton’s Oxidation Kinetics, Pathway, and Toxicity Evaluation of Diethyl Phthalate in Aqueous Solution. J. Adv. Oxid. Technol. 2016, 19, 125–133. [Google Scholar] [CrossRef]
- Gao, F.; Han, L. Implementing the Nelder-Mead simplex algorithm with adaptive parameters. Comput. Optim. Appl. 2012, 51, 259–277. [Google Scholar] [CrossRef]
- De la Cruz, D.R. Optimal Fit Non-linear Function for Allocating Emergency Goods during Initial Stage of Disaster Relief in Malolos City. Inst. Electron. Eng. Philipp. J. 2021, 4. Available online: http://www.iecepjournal.net/index.php/iecepjournal/article/view/8 (accessed on 31 August 2022).
- Nemet, A.; Bogataj, M.; Kravanja, Z. Optimization of the Sequence of Wastewater Treatment in the Cosmetic Industry. Chem. Eng. Trans. 2021, 88, 715–720. [Google Scholar]
- Mitsika, E.E.; Christophoridis, C.; Fytianos, K. Fenton and Fenton-like oxidation of pesticide acetamiprid in water samples: Kinetic study of the degradation and optimization using response surface methodology. Chemosphere 2013, 93, 1818–1825. [Google Scholar] [CrossRef] [PubMed]
- Ma, Y.; Chen, B.; Zhang, B.; Zheng, J.; Liu, B.; Zhang, H. Fenton oxidation process for remediation of produced water containing polycyclic aromatic hydrocarbons. In Proceedings of the CSE 2014 13th International Environmental Specialty Conferences, Halifax, NS, Canada, 28–31 May 2014; pp. 1–10. [Google Scholar]
- Homem, V.; Dias, Z.; Santos, L.; Alves, A. Preliminary feasibility study of benzo(a) pyrene oxidative degradation by Fenton treatment. J. Environ. Public Health 2009, 2009, 149034. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- De Souza e Silva, P.T.; Da Silva, V.L.; de Barros Neto, B.; Simonnot, M.O. Phenanthrene and pyrene oxidation in contaminated soils using Fenton’s reagent. J. Hazard. Mater. 2009, 161, 967–973. [Google Scholar] [CrossRef] [PubMed]
- Ribeiro, J.P.; Nunes, M.I. Recent trends and developments in Fenton processes for industrial wastewater treatment–A critical review. Environ. Res. 2021, 197, 110957. [Google Scholar] [CrossRef]
- Rodríguez, S.; Lorenzo, D.; Santos, A.; Romero, A. Comparison of real wastewater oxidation with Fenton/Fenton-like and persulfate activated by NaOH and Fe (II). J. Environ. Manag. 2020, 255, 109926. [Google Scholar] [CrossRef]
| Kinetic Model | Function |
|---|---|
| First-order model | function E = Order1(x,tdata,Cdata) k1 = x(1); E = sum((Cdata - exp(-k1*tdata)).^2); |
| Second-order model | function E = Order2(x,tdata,Cdata, A) C0 = A; k2 = x(1); E = sum((Cdata -1./(1+C0*k2*tdata)).^2); |
| Third-order model | function E = Order3(x,tdata,Cdata, A) C0 = A; k3 = x(1); E = sum((Cdata –sqrt(1./(1+C0^2*k3*tdata))).^2); |
| Behnajady-Modirshahla-Ghanbery (BMG) model | function E = Order3(x,tdata,Cdata) A1 = x(1); A2 = x(2); E = sum((Cdata -(1-tdata./(A1+A2*tdata))).^2); |
| Double exponential model | function E = Order3(x,tdata,Cdata) A3 = x(1); k6 = x(2); A4 = x(3); k7 = x(4); E = sum((Cdata - (A3*exp(-k6*tdata)+A4*exp(-k7*tdata))).^2); |
| Pollutant | Matrix | First-Order Model | Second-Order Model | Third-Order Model | BMG Model | Double Exponential Model | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| k1 (min−1) | R2 | k2 (µg−1 min−1) | R2 | k3 (µg−2 min−1) | R2 | A1 (min) | k3 (min−1) | A2 | k4 | R2 | A3 | k6 (min−1) | A4 | k7 (min−1) | R2 | ||
| AN | NW | 0.0085 | 0.8094 | 0.0038 | 0.8718 | 0.0034 | 0.9108 | 45.7838 | 0.0218 | 1.8278 | 0.5471 | 0.9526 | 0.6146 | 0.0344 | 0.4061 | −0.0041 | 0.9806 |
| DW | 0.1563 | 0.9607 | 0.0945 | 0.9691 | 0.1515 | 0.9819 | 2.1473 | 0.4657 | 1.1161 | 0.8960 | 0.9903 | 0.8515 | 0.2528 | 0.1495 | 0.0003 | 0.9996 | |
| BaP | NW | 0.0046 | 0.8148 | 0.0019 | 0.8549 | 0.0015 | 0.8885 | 67.9842 | 0.0147 | 2.9935 | 0.3341 | 0.9868 | 0.2984 | 0.0435 | 0.7074 | −0.0005 | 0.9970 |
| DW | 0.0952 | 0.8867 | 0.0500 | 0.9242 | 0.0651 | 0.9652 | 3.1959 | 0.3129 | 1.2282 | 0.8142 | 0.9893 | 0.7633 | 0.2104 | 0.2366 | 0.0002 | 0.9987 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rubio-Clemente, A.; Chica, E.; Peñuela, G.A. Optimization Method to Determine the Kinetic Rate Constants for the Removal of Benzo[a]pyrene and Anthracene in Water through the Fenton Process. Water 2022, 14, 3381. https://doi.org/10.3390/w14213381
Rubio-Clemente A, Chica E, Peñuela GA. Optimization Method to Determine the Kinetic Rate Constants for the Removal of Benzo[a]pyrene and Anthracene in Water through the Fenton Process. Water. 2022; 14(21):3381. https://doi.org/10.3390/w14213381
Chicago/Turabian StyleRubio-Clemente, Ainhoa, Edwin Chica, and Gustavo A. Peñuela. 2022. "Optimization Method to Determine the Kinetic Rate Constants for the Removal of Benzo[a]pyrene and Anthracene in Water through the Fenton Process" Water 14, no. 21: 3381. https://doi.org/10.3390/w14213381








