An Implicit Formulation for Calculating Final Conditions in Drainage Maneuvers in Pressurized Water Installations
Abstract
:1. Introduction
2. Numerical Approach
3. Analysis of Results
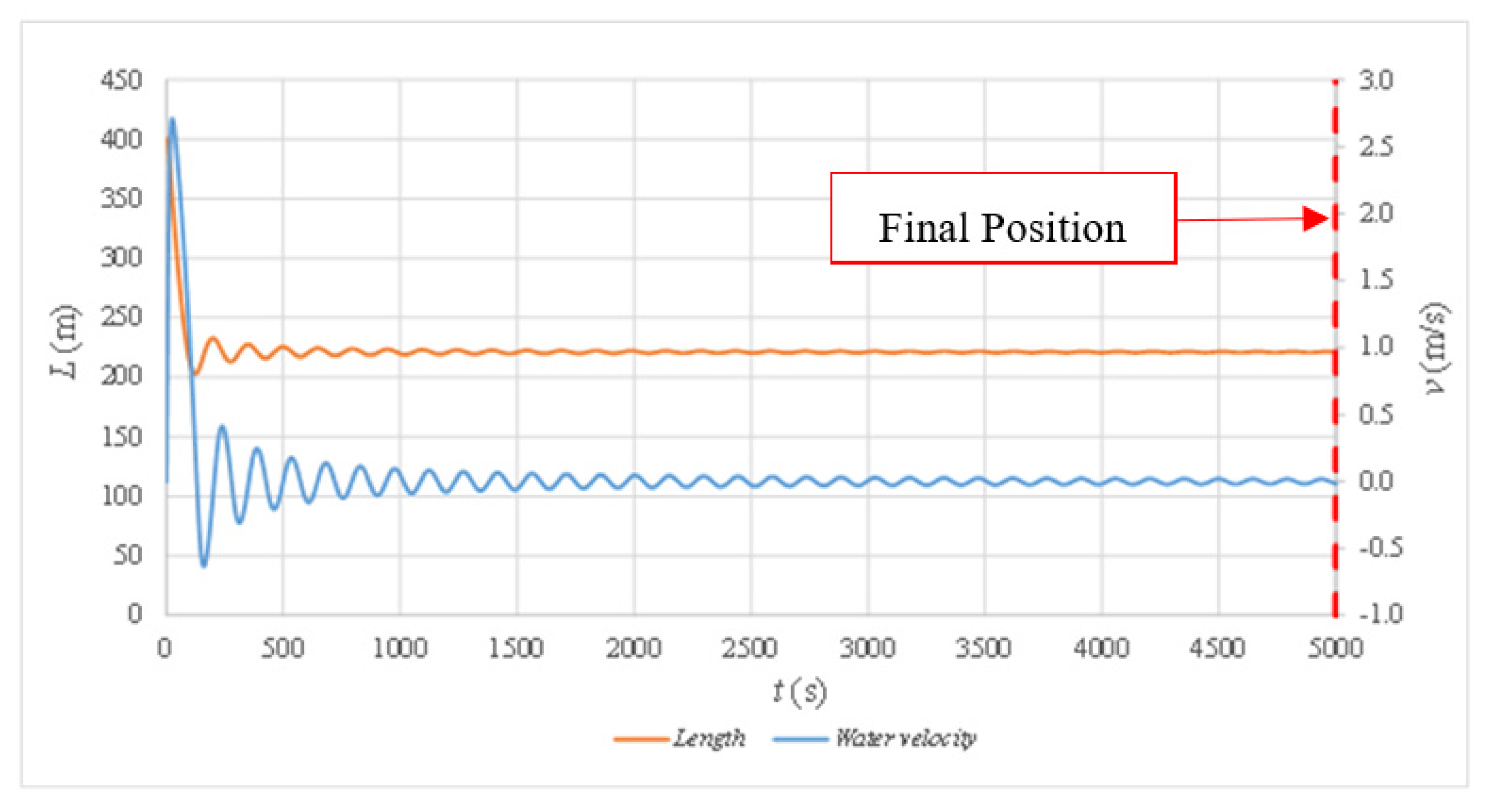
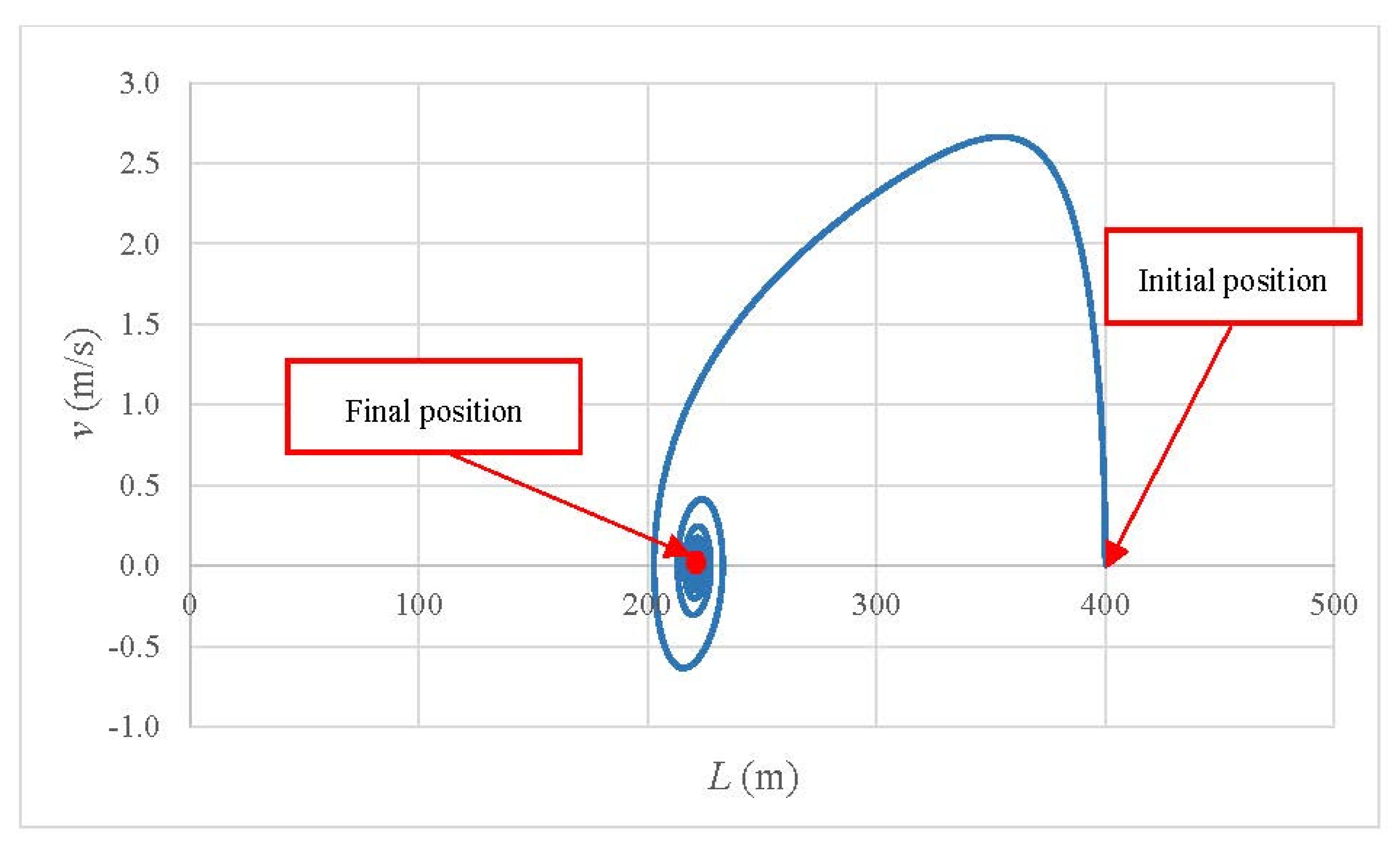
3.1. Practical Application
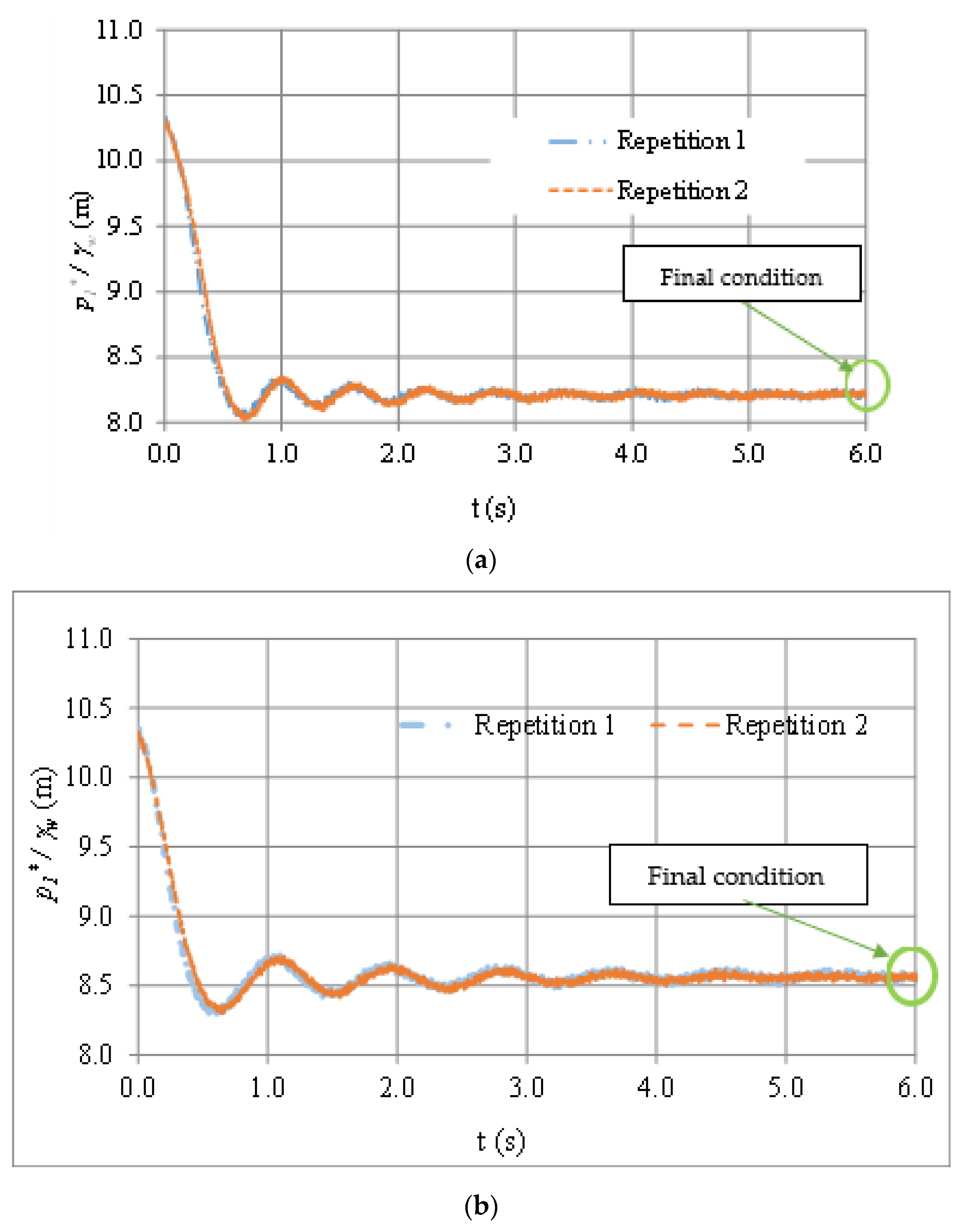
3.2. Validation
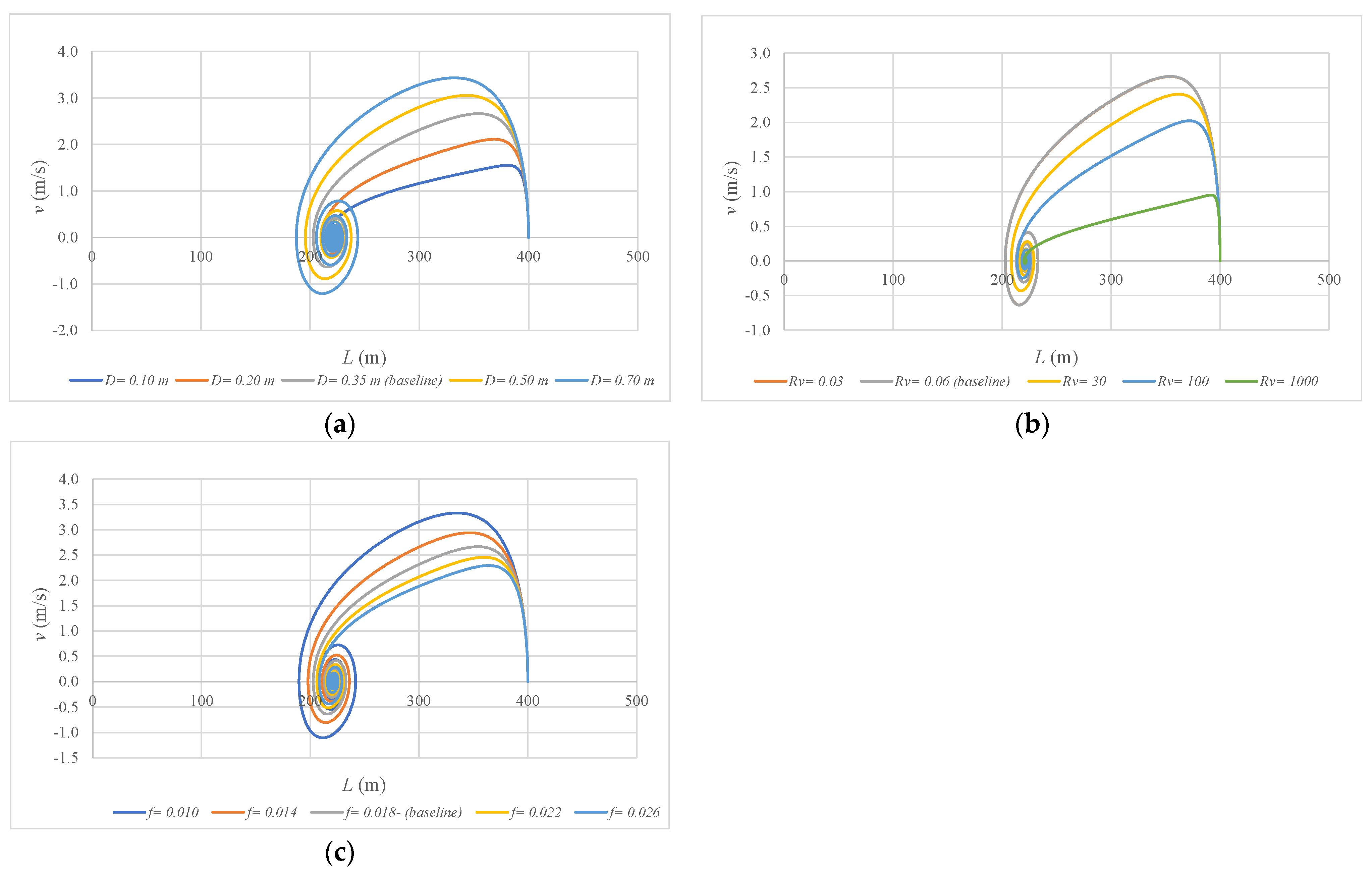
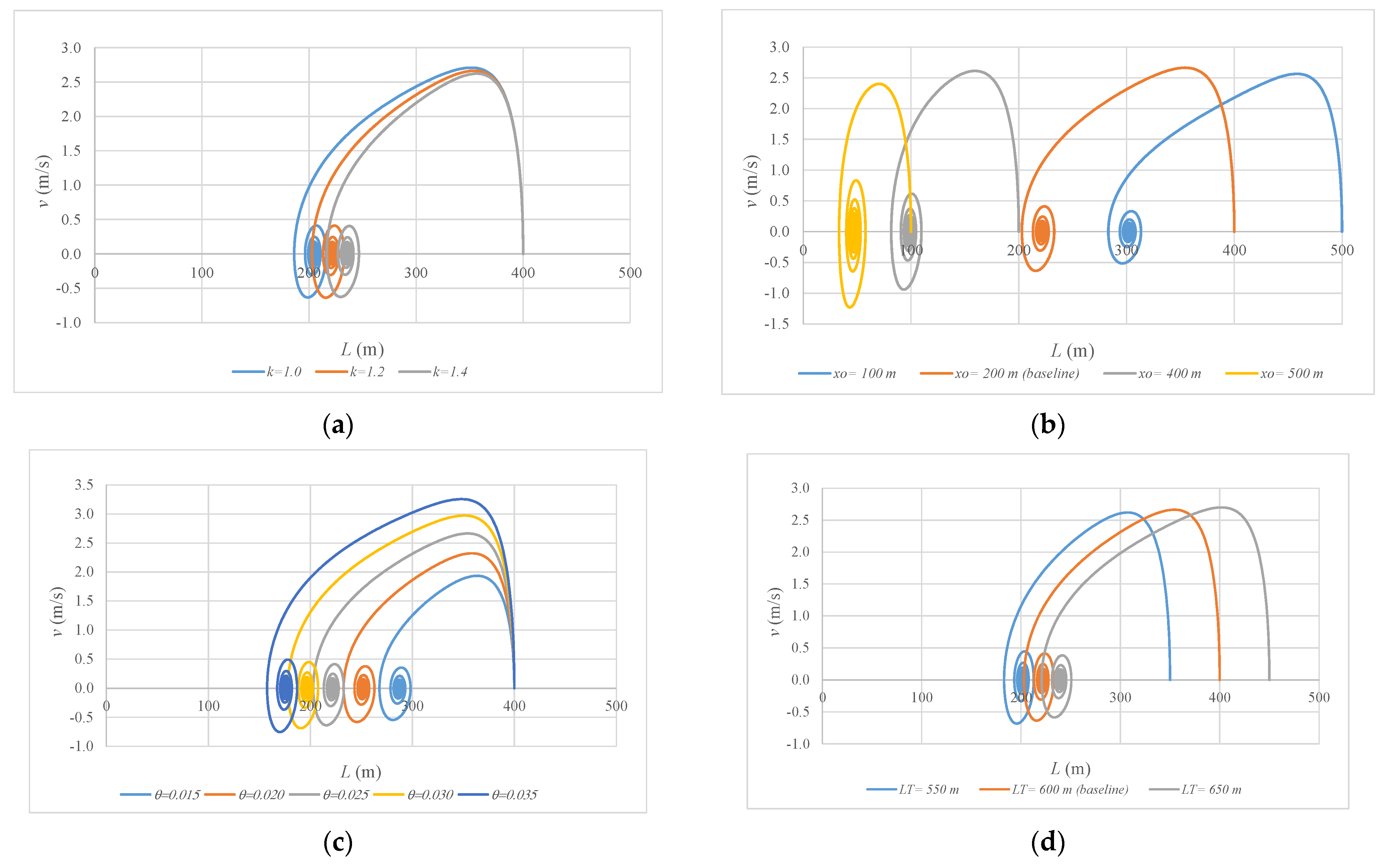
4. Sensitivity Analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| A | Cross-sectional area of pipe (m2) |
| D | Internal pipe diameter (m) |
| f | Friction factor (-) |
| g | Gravity acceleration (m s−2) |
| k | Polytropic coefficient (-) |
| j | Used function in the Newton–Raphson equation |
| L | Water column length (m) |
| LT | Pipe length (m) |
| P | Function based on piston flow model |
| patm* | Atmospheric pressure (101,325 Pa) |
| p*1 | Air pocket pressure (Pa) |
| Q | Function based on both mass oscillation equation and polytropic law |
| Rv | Resistance coefficient (ms2 m−6) |
| t | Time (s) |
| v | Water velocity (m s−1) |
| V | Vector field on a region in the plane (L, v) |
| x | Air pocket size (m) |
| X | Vector function of t |
| r | Water density (kg m−3) |
| θ | Pipe slope (rad) |
| γw | Water unit weight (N m−3) |
| Subscripts | |
| 0 | Refers to an initial condition |
| f | Refers to a final condition |
| i | Iteration number |
| Superscripts | |
| ′ | Derivative |
References
- Ramezani, L.; Karney, B.; Malekpour, A. The Challenge of Air Valves: A Selective Critical Literature Review. J. Water Resour. Plan. Manag. 2016, 141, 04015017. [Google Scholar] [CrossRef]
- Fuertes-Miquel, V.S.; Coronado-Hernández, Ó.E.; Mora-Melia, D.; Iglesias-Rey, P.L. Hydraulic Modeling during Filling and Emptying Processes in Pressurized Pipelines: A Literature Review. Urban Water J. 2019, 16, 299–311. [Google Scholar] [CrossRef]
- AWWA (American Water Works Association). Manual of Water Supply Practices M51—Air Valves: Air Release, Air/Vacuum and Combination; AWWA: Denver, CO, USA, 2016. [Google Scholar]
- Coronado-Hernández, O.E.; Fuertes-Miquel, V.S.; Besharat, M.; Ramos, H.M. Subatmospheric Pressure in a Water Draining Pipeline with an Air Pocket. Urban Water J. 2018, 15, 346–352. [Google Scholar] [CrossRef]
- Coronado-Hernández, O.E.; Fuertes-Miquel, V.S.; Iglesias-Rey, P.L.; Martínez-Solano, F.J. Rigid Water Column Model for Simulating the Emptying Process in a Pipeline Using Pressurized Air. J. Hydraul. Eng. 2018, 144, 06018004. [Google Scholar] [CrossRef]
- Coronado-Hernández, Ó.E.; Fuertes-Miquel, V.S.; Quiñones-Bolaños, E.E.; Gatica, G.; Coronado-Hernández, J.R. Simplified Mathematical Model for Computing Draining Operations in Pipelines of Undulating Profiles with Vacuum Air Valves. Water 2020, 12, 2544. [Google Scholar] [CrossRef]
- Laanearu, J.; Annus, I.; Koppel, T.; Bergant, A.; Vučkovič, S.; Hou, Q.; van’t Westende, J.M.C. Emptying of Large-Scale Pipeline by Pressurized Air. J. Hydraul. Eng. 2012, 138, 1090–1100. [Google Scholar] [CrossRef] [Green Version]
- Tijsseling, A.; Hou, Q.; Bozku¸s, Z.; Laanearu, J. Improved One-Dimensional Models for Rapid Emptying and Filling of Pipelines. J. Press. Vessel Technol. 2016, 138, 031301. [Google Scholar] [CrossRef] [Green Version]
- Besharat, M.; Coronado-Hernández, O.E.; Fuertes-Miquel, V.S.; Viseu, M.T.; Ramos, H.M. Backflow Air and Pressure Analysis in Emptying Pipeline Containing Entrapped Air Pocket. Urban Water J. 2018, 15, 769–779. [Google Scholar] [CrossRef]
- Hurtado-Misal, A.D.; Hernández-Sanjuan, D.; Coronado-Hernández, O.E.; Espinoza-Román, H.; Fuertes-Miquel, V.S. Analysis of Sub-Atmospheric Pressures during Emptying of an Irregular Pipeline without an Air Valve Using a 2D CFD Model. Water 2021, 13, 2526. [Google Scholar] [CrossRef]
- Besharat, M.; Coronado-Hernández, O.E.; Fuertes-Miquel, V.S.; Viseu, M.T.; Ramos, H.M. Computational fluid dynamics for sub-atmospheric pressure analysis in pipe drainage. J. Hydraul. Res. 2020, 58, 553–565. [Google Scholar] [CrossRef]
- Liou, C.P.; Hunt, W.A. Filling of pipelines with undulating elevation profiles. J. Hydraul. Eng. 1996, 122, 534–539. [Google Scholar] [CrossRef]
- Izquierdo, J.; Fuertes, V.; Cabrera, E.; Iglesias, P.; Garcia-Serra, J. Pipeline start-up with entrapped air. J. Hydraul. Res. 1999, 37, 579–590. [Google Scholar] [CrossRef]
- Martins, N.M.; Delgado, J.N.; Ramos, H.M.; Covas, D.I. Maximum transient pressures in a rapidly filling pipeline with entrapped air using a CFD model. J. Hydraul. Res. 2017, 55, 506–519. [Google Scholar] [CrossRef]
- Zhou, L.; Liu, D. Experimental Investigation of Entrapped Air Pocket in a Partially Full Water Pipe. J. Hydraul. Res. 2013, 51, 469–474. [Google Scholar] [CrossRef]
- Zhou, L.; Liu, D.; Karney, B. Investigation of hydraulic transients of two entrapped air pockets in a water pipeline. J. Hydraul. Eng. 2013, 139, 949–959. [Google Scholar] [CrossRef]
- Fuertes-Miquel, V.S.; López-Jiménez, P.A.; Martínez-Solano, F.J.; López-Patiño, G. Numerical modelling of pipelines with air pockets and air valves. Can. J. Civ. Eng. 2016, 43, 1052–1061. [Google Scholar] [CrossRef] [Green Version]
- Chapra, S.; Canale, R. Numerical Methods for Engineers, 7th ed.; Mcgraw-Hill Education, Cop: New York, NY, USA, 2015. [Google Scholar]
- Stoer, J.; Bulirsch, R. Introduction to Numerical Analysis; Springer: New York, NY, USA; London, UK, 2011. [Google Scholar]
- Zill, D. Differential Equations with Boundary-Value Problems; Cengage Learning: Melbourne, Australia, 2016. [Google Scholar]
- Suribabu, C.R. Location and Sizing of Scour Valves in Water Distribution Network. J. Hydraul. Eng. 2009, 15, 118–130. [Google Scholar] [CrossRef]
- Suribabu, C.R. Optimal locations and sizing of scour valves in water distribution networks. J. Pipeline Syst. Eng. 2020, 11, 04019056. [Google Scholar] [CrossRef]
- Fuertes-Miquel, V.S.; Coronado-Hernández, Ó.E.; Mora-Melia, D.; Iglesias-Rey, P.L. Transient phenomena during the emptying process of a single pipe with water–air interaction. J. Hydraul. Res. 2018, 57, 3. [Google Scholar] [CrossRef]





| i | Lf,i (m) | J (Lf,i) | j′ (Lf,i) | Lf,i+1 (m) | Lf,i+1 − Lf,i (m) |
|---|---|---|---|---|---|
| 0 | 204.33 | −0.03197 | 0.00202 | 220.16 | 15.83 |
| 1 | 220.16 | −0.00185 | 0.00180 | 221.19 | 1.03 |
| 2 | 221.19 | −0.00001 | 0.00178 | 221.20 | 0.00 |
| 3 | 221.20 | 0.00000 | 0.00178 | 221.20 | 0.00 |
| … | … | … | … | … | … |
| 18 | 221.20 | 0.00000 | 0.00178 | 221.20 | 0.00 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Coronado-Hernández, O.E.; Bonilla-Correa, D.M.; Lovo, A.; Fuertes-Miquel, V.S.; Gatica, G.; Linfati, R.; Coronado-Hernández, J.R. An Implicit Formulation for Calculating Final Conditions in Drainage Maneuvers in Pressurized Water Installations. Water 2022, 14, 3364. https://doi.org/10.3390/w14213364
Coronado-Hernández OE, Bonilla-Correa DM, Lovo A, Fuertes-Miquel VS, Gatica G, Linfati R, Coronado-Hernández JR. An Implicit Formulation for Calculating Final Conditions in Drainage Maneuvers in Pressurized Water Installations. Water. 2022; 14(21):3364. https://doi.org/10.3390/w14213364
Chicago/Turabian StyleCoronado-Hernández, Oscar E., Dalia M. Bonilla-Correa, Aldo Lovo, Vicente S. Fuertes-Miquel, Gustavo Gatica, Rodrigo Linfati, and Jairo R. Coronado-Hernández. 2022. "An Implicit Formulation for Calculating Final Conditions in Drainage Maneuvers in Pressurized Water Installations" Water 14, no. 21: 3364. https://doi.org/10.3390/w14213364
APA StyleCoronado-Hernández, O. E., Bonilla-Correa, D. M., Lovo, A., Fuertes-Miquel, V. S., Gatica, G., Linfati, R., & Coronado-Hernández, J. R. (2022). An Implicit Formulation for Calculating Final Conditions in Drainage Maneuvers in Pressurized Water Installations. Water, 14(21), 3364. https://doi.org/10.3390/w14213364








