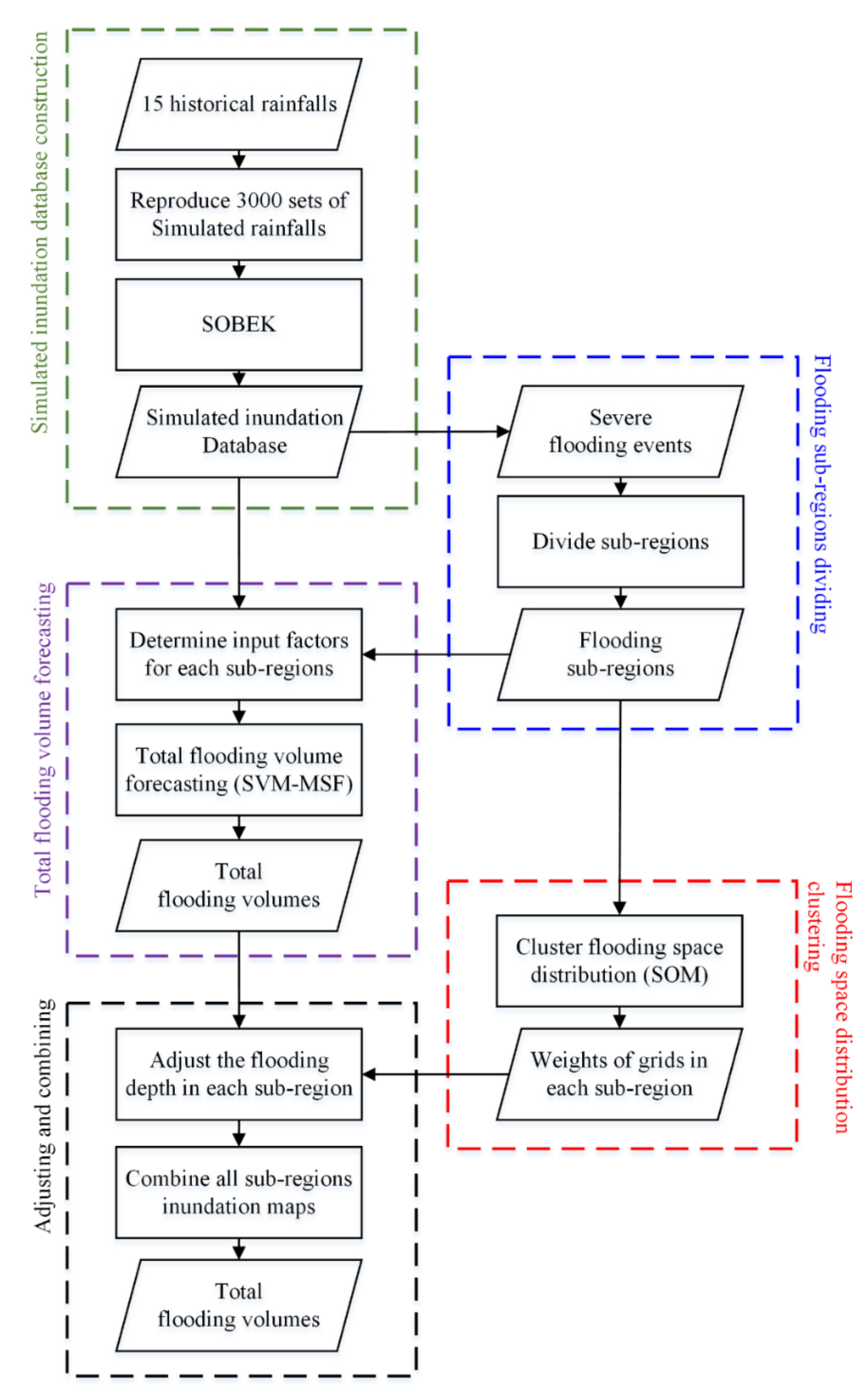
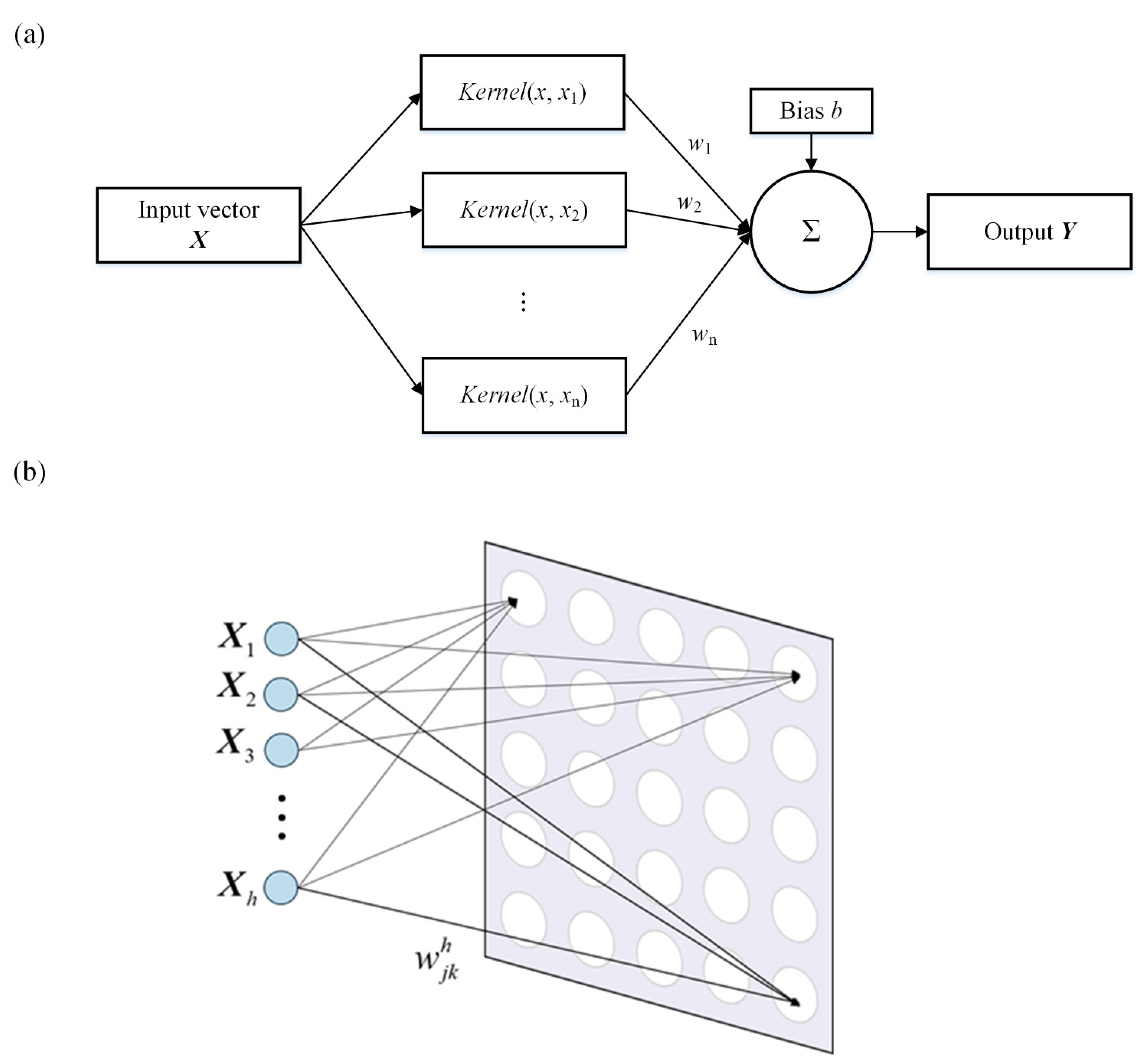
The results of the five steps mentioned in
Section 3.1 are presented in this section. In
Section 4.1, the flooding and virtual rainfall station sub-regions, which were divided by previous simulated flooding events, are shown. In
Section 4.2, the results of the total flooding volume forecasted by SVM-MSF are illustrated. How SOM was used to classify the 3000 simulated flooding events into several categories results are shown in
Section 4.3. Finally, the SVM-MSF and SOM merger results are presented in
Section 4.4.
4.1. Sub-Region and Virtual Rainfall Station
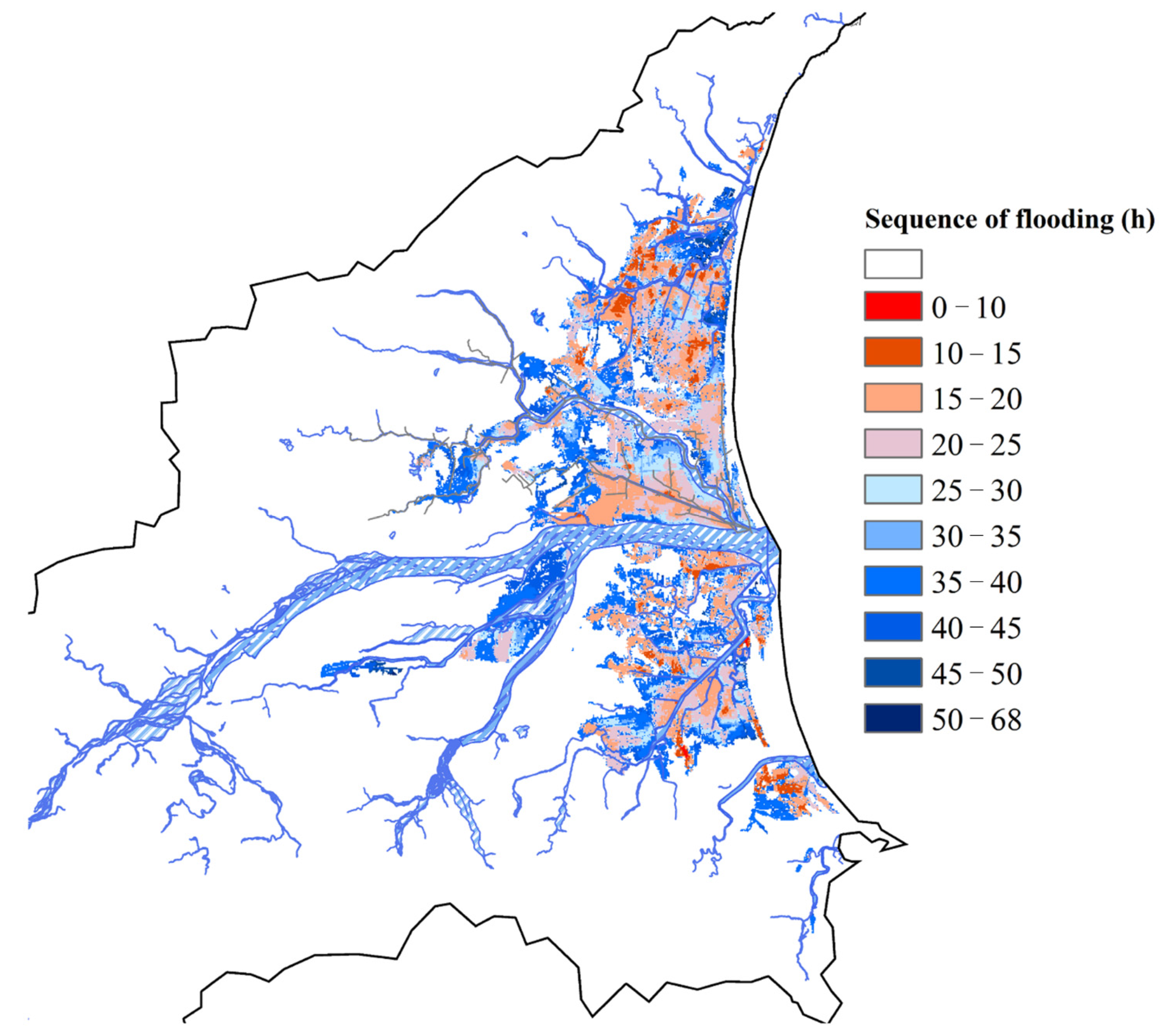
The most severe flooding event among the 3000 simulated flooding events was selected as the standard for dividing the flooding sub-regions in order to contain severe flooding characteristics.
Figure 4 shows the order of the flood sequence; the colored labels in the figure represent the time when the grid began to flood. The grids closer to the dark red indicate earlier flooding and are regarded as the starting position for the flooding. Otherwise, the areas closer to the blue indicate the later flooding region. The interconnected red areas will be considered as the same starting position. By examining flooding sequences and watershed features, we judged which areas had the same flooding characteristics and divided them into nine sub-regions, as
Figure 5 shows. From south to north, we named these sub-regions S1 to S9, respectively.
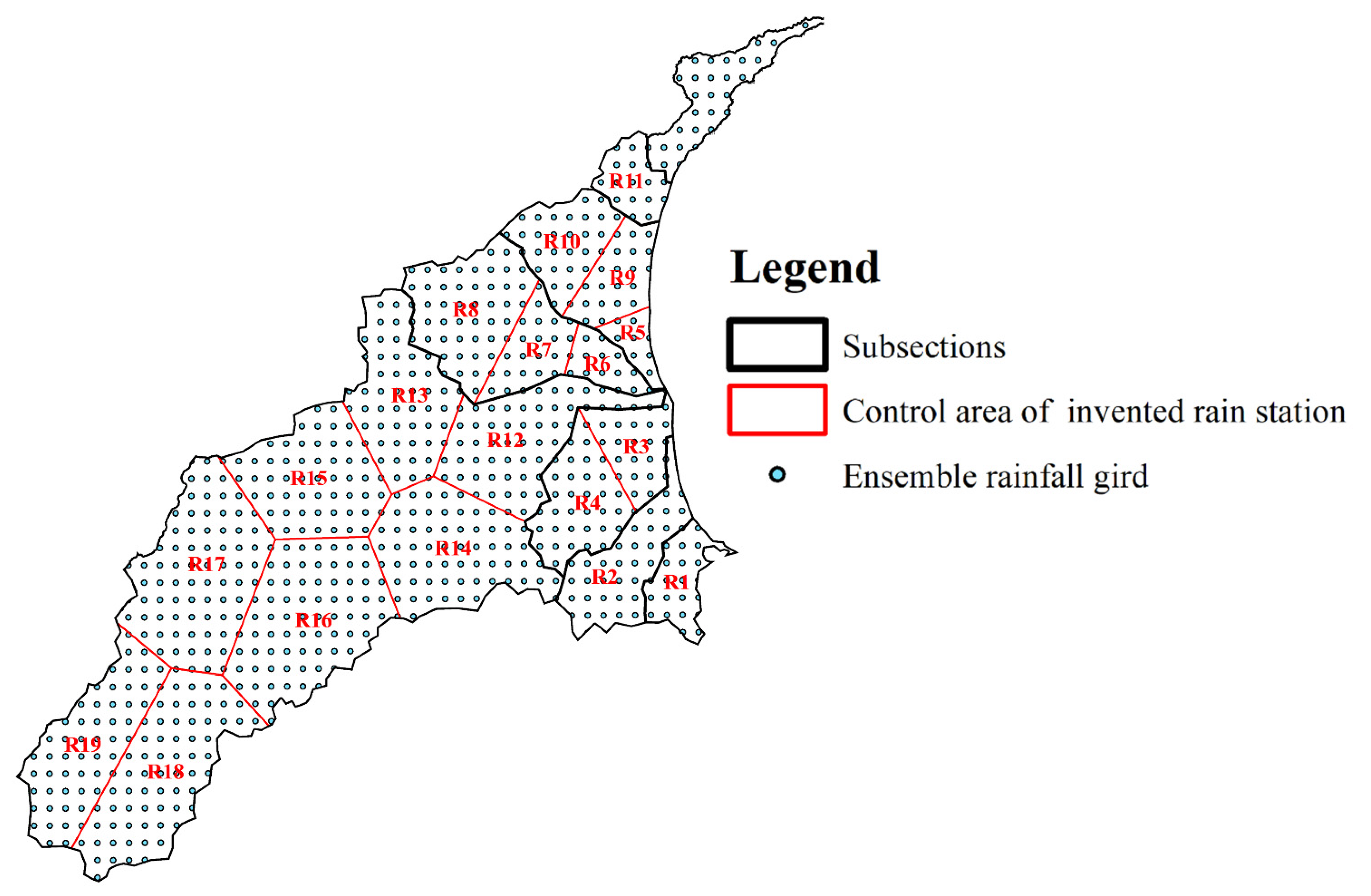
The ensemble gridded rainfall data used to construct the total flooding volume forecasting models in this study and the control area of each rainfall station are shown in
Figure 6. Each spot on the figure represents the cumulative rainfall for an hour on the
grid. However, even though we had such detailed rainfall information, there were still two predicaments to be overcome. Too many adjacent rainfall inputs caused a high dependency and led the model to overfit. In addition, the huge number of inputs might lead to determination difficulties and long computational times, which cannot be applied in real time. For the above reasons, we simplified the rainfall inputs from original grids scaling to 19 virtual rainfall station data according to the catchments, control areas, and Thiessens’s polygon method. Given that mountainous rainfall cannot cause an immediate threat to urban flooding, a virtual rainfall station located in a mountainous area could cover a larger control area, such as virtual rainfall stations 15 to 19 on the left-hand side of the figure. On the contrary, the heavy rainfall in the urban area might lead to flood inundation caused by inner water rapidly rising. Hence, the control area of the virtual rainfall station, which was located in the metropolis, was smaller than those in the mountainous area.
4.2. Performance of SVM
As mentioned in
Section 3.2, different parameter combinations for SVM would greatly affect model performance. The optimal parameters (kernel function, cost,
ε, and
γ) and input combinations determined by the grid search method are listed in
Table 2. We could summarize from the table that rainfall information upstream would take longer than rainfall information downstream. This pattern can be found most clearly in S6. For the downstream data (R5), there is only one hour of data required, and as the data areas move upstream, two hours (R6) and three hours (R7) of data are required. The pattern was in line with our assumptions on time of flow concentration that the early rainfall in mountainous areas would cause urban external water flooding. On the other hand, urban rainfall might directly cause accumulated flooding, so only short-term rainfall information was required. It is worth noting that rainfall data in mountainous areas (R15–R19) were not needed by the model for flood forecasting in urban areas. The determined results showed that rainfall in the mountainous areas of the study did not significantly flood the urban area, and the water source was mainly handled by the existing drainage system. For heavy rainfall events, urban floods were still dominated by local rainfall and near-regional rainfall.
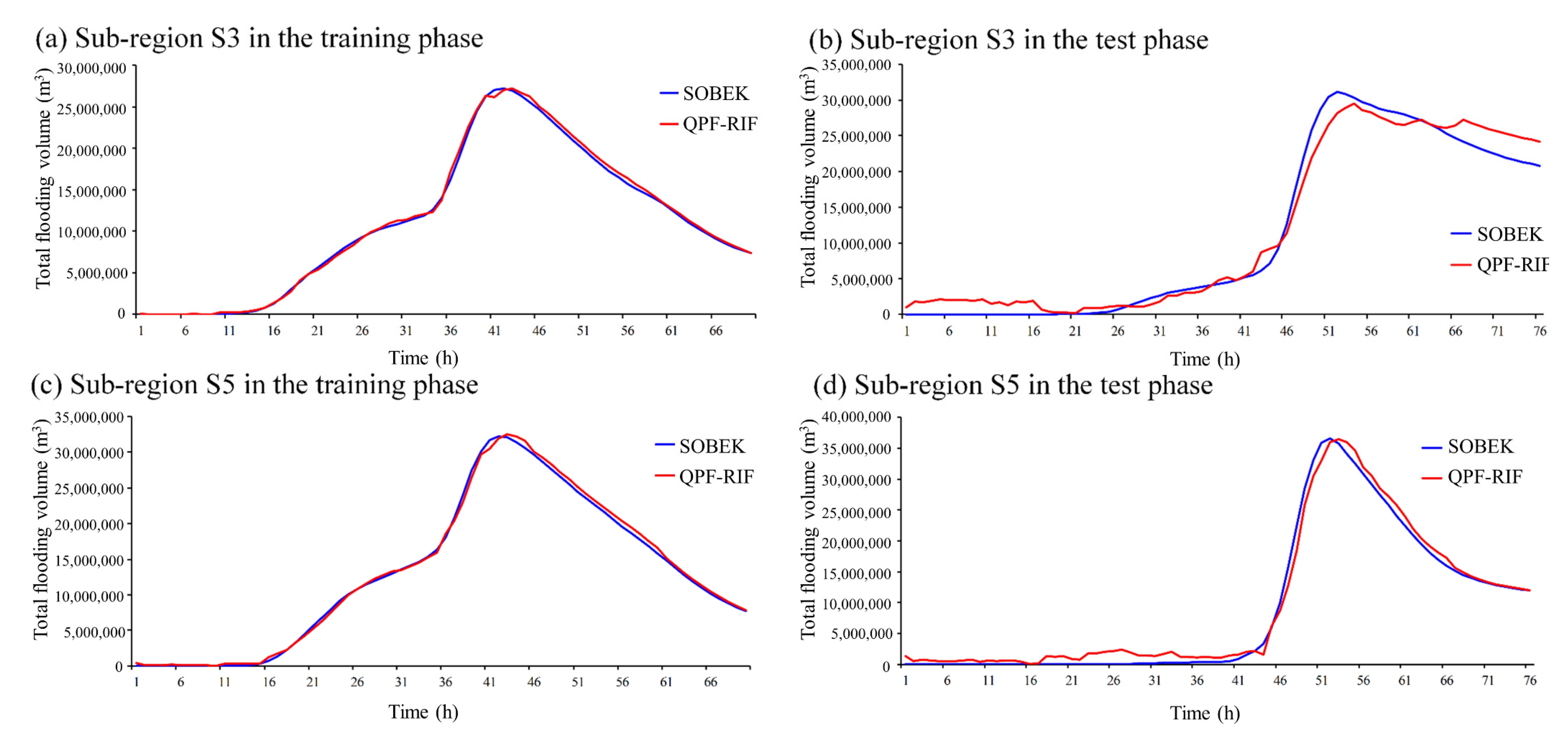
Due to the limited contexts, the performances of the model were presented with the most severe flooding events in training and testing events. That is, the following discussions focus on sub-region S3 (Donshan river) which had the maximum area, and sub-region S5 (Meifu drainage) which was the most prone to flooding and tended to flood most severely. The total flooding volume hydrographs were presented under two different conditions, short-term (
t + 1) and long-term (
t + 72) forecasting results. The results of the short-term forecast are shown in
Figure 7.
Figure 7a,c present the 1 h ahead forecasting results with the most severe flooding event in the training stage in the S3 and S5 sub-regions. The red curve represents the forecasting total flooding volume from the SVM-MSF model, and the blue curve was simulated by SOBEK. Each point of data in the red curve is the flooded volume predicted by the SVM-MSF using the input data available one hour before. As the figure shows, the results forecasted by SVM-MSF almost ideally fitted the SOBEK results, which were considered target values no matter the rising limb, falling limb, and even peak value. For the peak value timing forecasting, the lag time of the peak value was less than 0.5 h in the training phase. That is, there was no hysteresis effect when showing the training phase. In addition, according to the distance between the red and blue lines, the forecasting performance of sub-region S5 was slightly worse than that of S3. Nonetheless, the SVM-MSF forecasts are fairly close to the flooding simulations by SOBEK. The forecasting results in the testing phase, as
Figure 7b,d shows, were slightly overestimated in the foremost flat period and falling limbs. For the rising limbs, it was slightly underestimated. These over- and underestimates were mainly caused by slight hysteresis forecasts, with the curve moving overall to the right. The lag time was also a trifle longer than the results in the training phases but could still last than an hour for the peak value forecasting. In sub-region S3, the model tended to underestimate the peak value. On the contrary, it accurately forecasted the peak value in sub-region S5 in spite of being overestimated in other segments. It was speculated that sub-region S3 faced more uncertainty due to the larger control area, which led to worse performance on peak value forecasting.
The performance measures of all sub-regions are listed in
Table 3. The RMSE and MAE listed in the table have been averaged by the gridded number of each sub-region and presented the mean of all grids. We derived from the performance measures that the RMSEs were less than 7.72 m
3 and the MAEs were less than 6.03 m
3 in all sub-regions except S5. Namely, the error of peak value and average flooding depth forecasting were both less than 5 mm. Even though the RMSE and MAE in sub-region S5 were higher than in other sub-regions, the average error of forecasting flood depth was still less than 1 cm. The rationale that the error of forecasting the flooding depth in sub-region S5 was higher than in the other sub-regions was that the uncertainty and scope of S5 were larger than the remaining eight sub-regions. In terms of CC, except for sub-region S1, the other eight sub-regions achieved excellent performance with a CC value higher than 0.9, no matter the training or testing scenarios. The CC value of sub-region S1 was 0.7. The reason that S1 had a worse performance was that fewer flooding events could be referred to, and the circumstances of each flood that could have occurred in S1 were very different, further increasing the difficulty of forecasting.
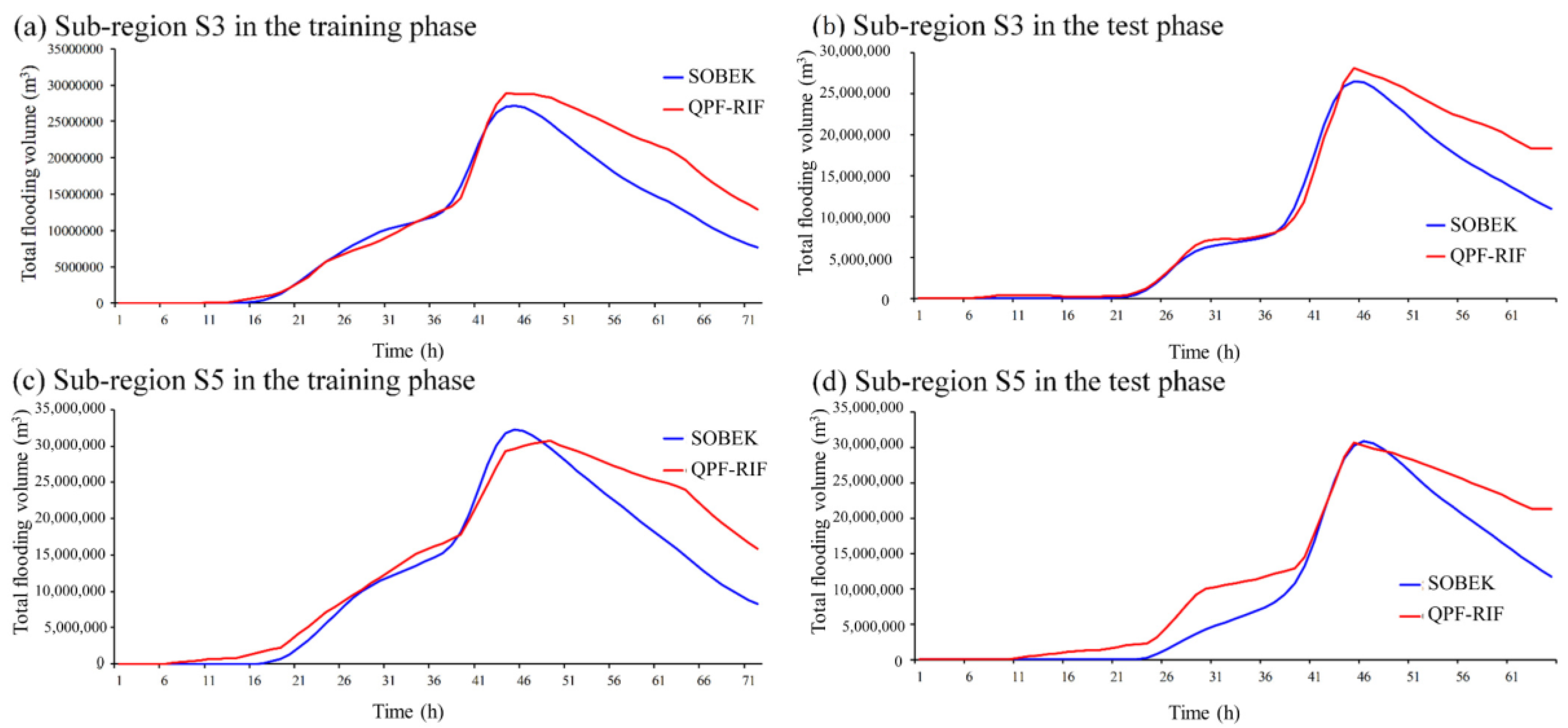
Figure 8 shows the long-term forecasting flooding volume hydrographs. The MSF results from forecasting 1 to 72 h ahead (
t + 1 to
t + 72) were shown in these figures. We also chose sub-regions S3 and S5 as representative analyses due to the space limitation. In sub-region S3, the SVM-MSF can accurately forecast the rising limbs and the timing of flooding peak (about 46 h lead time) both in the training and testing phases. Regarding the peak value and value of falling limbs, the model tended to slightly overestimate. On the other hand, in sub-region S5, no matter what phases tended to overestimate rising limbs and falling limbs. However, for peak value forecasting, the model effectively forecasted timing and value. It is worth noting that in the two sub-regions, there was no serious lag time hysteresis in the training or testing phases, mainly because our rainfall data contained more upstream rainfall data, which can contain future information. The existing lag time may come from the uncertainty of future on-site rainfall.
In summary, the SVM-MSF caught the trend of the total flooding volume no matter short-, mid-, or long-term forecasting, especially for characteristics of the peak value. The possible sources for errors in mid- and long-term forecasting were mainly the accumulative errors generated by recursive forecasting and the uncertainties from the numerical weather prediction system.
4.3. Performance of SOM
In this section, we are going to discuss the parameters used by the SOM and the topologies clustered by the SOM. First of all, the optimal parameters (determined by the grid search method) used in the SOM to classify several different types of inundation distribution are listed. In addition, the classified results are presented as average flooding depth maps. As in the previous sections, due to the space limitation of the article, in this section, we used sub-region S3 to discuss the determination process and the final training results of topology.
According to the principle of SOM, a reasonable topology size would highly affect the representativeness of the groups. Thus, we focused on the determination of topology size in this section.
Table 4 shows the classified results in sub-region S3 with different topology sizes. To quantify the model performance, RMSE and MAE were also employed as a benchmark for the forecasting error of the maximum flooding and average depths. As the table shows, the model had the best RMSE and second place MAE, while the topology size was settled as
. When using the topology size
, the RMSE improved by 5% compared with the suboptimal solution of
, while the MAE part only increased by 3% compared with the suboptimal solution of
. Given that disaster researchers often concentrate more on situations with severe disasters, RMSE optimized by 5% should be considered a critical factor. In view of this, the optimal topology size for sub-region S3 was
. Other sub-regions were determined by the topology size with the same standards. The other optimal sizes of topologies are listed in
Table 5. As shown in the table, the RMSEs and MAEs of sub-regions S3, S5, and S8 were higher than those of the others. The reason was that these three sub-regions were the areas with the most severe flooding conditions (located downstream of major rivers), which was consistent with the actual situation of flooding.
According to the determination previously mentioned, 3000 sets of simulated flooding events in sub-region S3 were divided into 25 categories with SOM. The clustering results by SOM, without artificial ranking, are shown in
Figure 9. The values in the lower left corner of sub-figures indicate the proportion of this category in all training data, and the lower right corner shows the average flooding depth of all the grids in each category. With these values, we analyzed the probability of floods in this category and how severe the flooding was. As shown in the lower-left corner of the graph, although in the flooding database, there were still 73.4% flooding maps, the average flooding depth was less than 1 cm. As the average flooding depth of the grid increased, the probability of its occurrence significantly decreased. However, when the average depth of flooding was higher than 0.1 m, the odds for all groups were fairly close. This phenomenon reflected the climate characteristics in the study area. When moderate rainfall or long-term weak rainfall occurred, there were very few floods in the area, and most floods were caused by extreme weather events. From flood depth and distribution analysis, each adjacent flooding map had high correlations, and the average flood depth gradually increased from the bottom right category to the top left category. To be more specific, each category had its own unique characteristics; from the right category to the left, it was found that the categories tended to gradually increase the flooding range. On the other hand, from the bottom category to the top, it tended to deepen the flooded area.
4.4. Adjusted and Combined Results
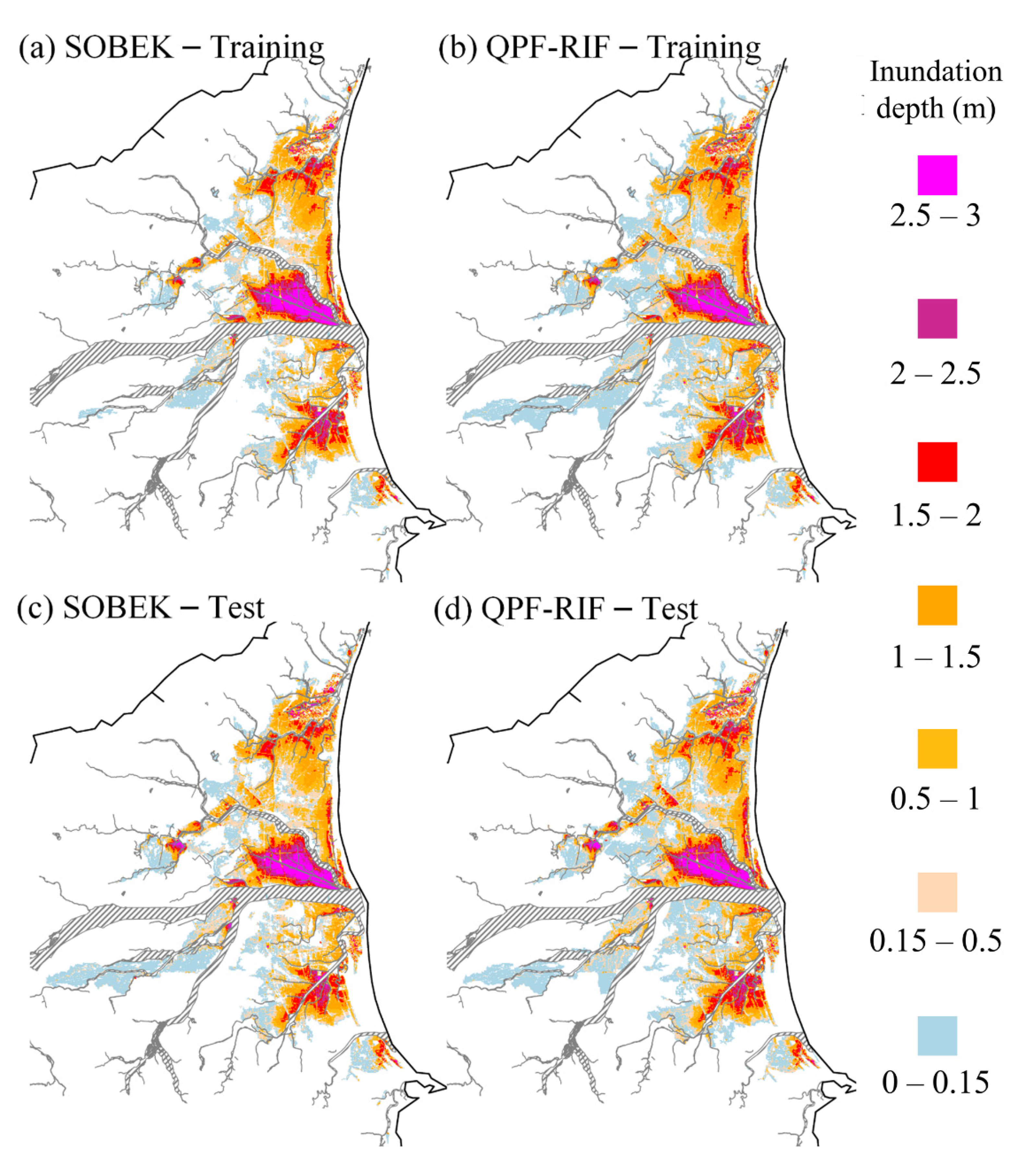
The Yilan County-wide flooding depth forecasting maps were generated by combining the results of SVM-MSF and SOM clustering and were named QPF-RIF. For the demonstration event, the most severe training and testing events in the database were selected, and the timing was the time when the flooding depth was the deepest (approximately 51 h). The results of flooding depth forecasting maps are shown in
Figure 10. On the left-hand side,
Figure 10a shows the flooding depth map simulated by SOBEK,
Figure 10b is the forecasting result from QPF-RIF in the most severe training event, and
Figure 10c,d is from the testing event. As mentioned in the previous section, the most severely flooded sub-regions during historical events were S3, S5, and S8, which is in line with the situation in this event. As the figure shows, the flooding depth map can accurately be forecasted by the QPF-RIF proposed in this study. A flooding area shallower than 0.15 m is shown as light blue in this figure. The range of the inundation zone exceeding 0.15 to 3 m is marked in sequence from light blue to purple, as the labels show. From
Figure 10, regardless of the events of the training or testing groups, the results of the SOBEK simulated severe flooding area (deeper than 0.15 m) are quite close to that of the long-term QPF-RIF forecasts, both in terms of inundation range and depth indication. The obvious disadvantage of QPF-RIF was that the forecast in the light blue area was larger than that simulated by the SOBEK model. The main reason was that the group average mentioned in
Section 4.3 contained information from multiple events. The shallow flooding areas may have occurred at some points in the remaining events, which were taken into account by the model. Although shallow flooding areas may be overestimated, it is enough to confirm that QPF-RIF proposed in this study is able to effectively simulate the flooding depths close to those resulting from SOBEK, which are considered actual values in this study.
Besides the simulated events, the model was also calibrated by recent heavy rainfall and typhoon events. There must be sufficient rainfall intensity and flooding-related data collected for the selected events. Thus, during the heavy rainfall event on 11 October 2017, Typhoons Saola, Megi, and Migta were adopted.
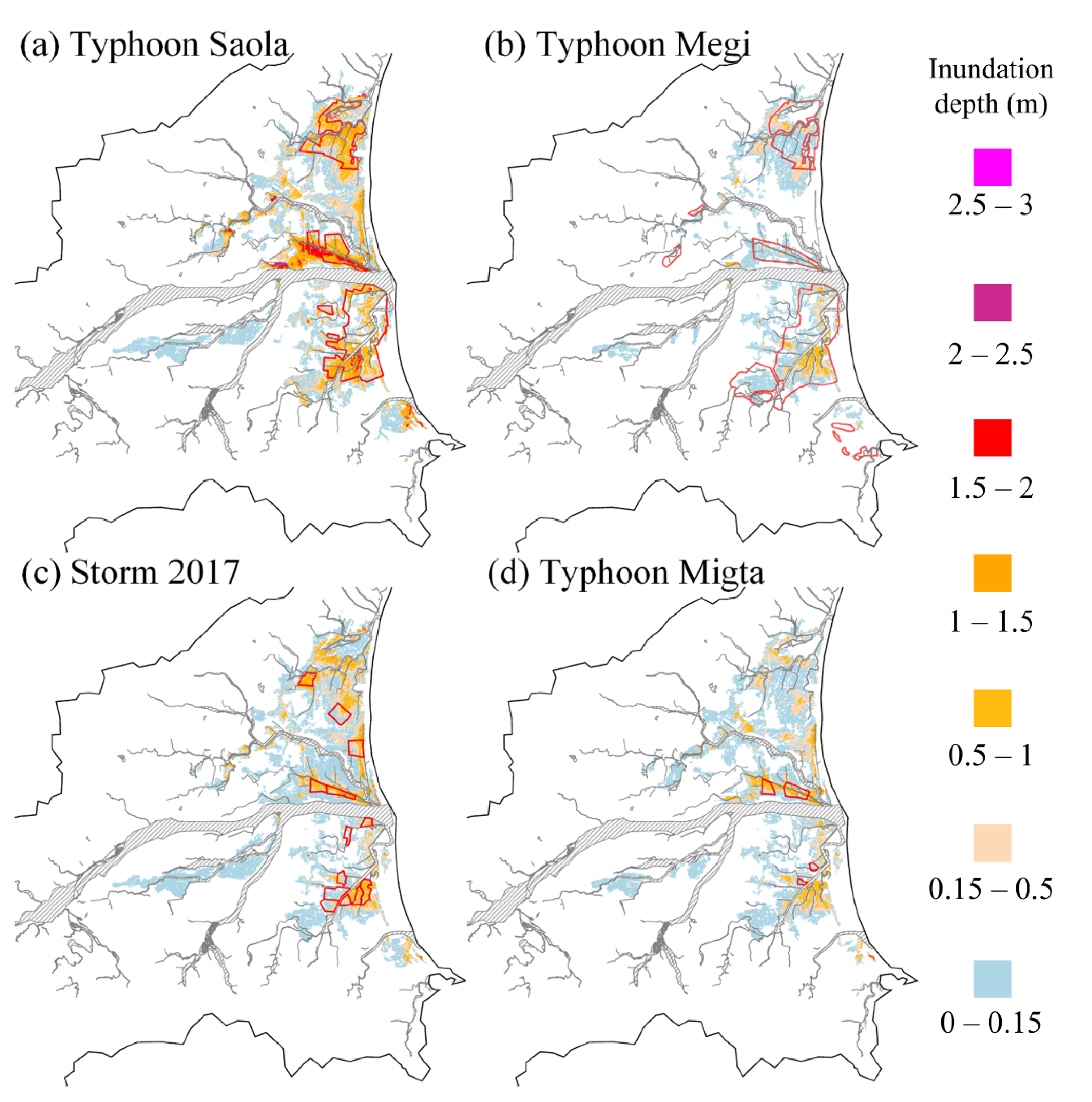
Figure 11 shows the comparisons between the flooding depth forecasted by QPF-RIF and the EMIC report information mentioned in
Section 2. In
Figure 11a, the forecasted flooding depth and EMIC of Typhoon Saola are shown. The color of each grid represents the depth of flooding forecasted by QPF-RIF, and the area marked by the red line is the actual flooding area framed according to the EMIC. Compared with EMIC data, in the S3, S5, and S8 sub-regions, models accurately forecasted the flooding area, especially in areas with severe inundation (both sides of the riverbanks and low-lying urban areas). As forecasts from the model, the local flooding depth in these three areas was deeper than 0.5 m, which was also close to the actual flooding depth of the most serious flooding position in the reported data.
The forecasting result of Typhoon Megi is plotted in
Figure 11b. As shown in the figure, the floods in this event were milder than those in Typhoon Saola, and the flooding areas of Typhoon Megi were more dispersed, such as in sub-region S1 and the upper reaches of the Yilan River. In general, except for some underestimations downstream of sub-regions S3 and S8, other flooding areas and levels were effectively forecasted.
Figure 11c shows the comparison between the flooding depth forecasted by the QPF-RIF and the EMIC using the heavy rainfall event data on 11 October 2017. According to the EMIC report, flooding occurred in sub-region S3 with a depth ranging from 0 to 90 cm. The model forecasted flooding area was indeed highly similar to the grids from EMIC. The partial grids forecasted flooding depths greater than 15 cm and, even rarer, deeper than 1 m, which was similar to the reported information. There were also some small flooding areas reported in sub-regions S6, S9, and the right bank of S5. The depths forecasted in these areas were also similar to the EMIC data. In general, most areas with severe flooding can be pre-warned by QPF-RIF forecasting in this heavy rainfall case. Finally, the comparison between the forecasted results and the range of EMIC in Typhoon Migta is shown in
Figure 11d. According to the EMIC report, flooding that occurred in sub-regions S3 and S5 was lesser than that in Typhoon Megi. Only small-scale shallow water was reported in sub-region S3. In the sub-region S5, the flooding depth of the EMIC report was about 0.5 to 1 m, which was similar to the forecasting value.
The EMIC-reported information did not perfectly represent all the flooded locations in the study area during the historical events and was based on the results of surveys from residents and public officials. The full confusion matrix cannot be used in this study due to data limitations. Hence, in the following, the TPR (used in the confusion matrix) will be adopted to calculate the forecast accuracy in the EMIC flooding range to quantify the model performance. The TPRs of five historical storm events are listed below in
Table 6 under three different flooding standards (0, 0.15, and 0.30 m). Standard 0 represents the area where the water level was over 0 cm, as seen as a flooding area, the standard 15 and standard 30 represent the same. As
Table 6 shows, QPF-RIF forecasted about 83% of the flooding area of the EMIC reports in Typhoons Saola, Migta, and the storm in 2017 under standard 0. That is, the model forecasted over 80% of the inundation area no matter how shallow the water or severe the inundation. Limited by the contents of EMIC reports, the information cannot correctly reflect the real depth of floods. However, we still can use standards 15 and 30 to evaluate the proportion of the area suffering from the disaster in this event. As standard 15 shows, in the last three events, the ratio of the flooding area over 15 cm to the total EMIC-reported area was about 60%. For standard 30, the proportions of each event were quite different. In Typhoons Saola and Migta, the area that flooded deeper than 30 cm was over half of the total EMIC-reported area. On the other hand, in other events, the flooding area over 30 cm was less than 30%. We can use these thresholds to determine whether the flooding in this rainfall event was a shallow and harmless event or a situation that will actually cause economic losses.
In addition, the TPRs in Typhoons Parma and Megi were obviously smaller than the other three events. The rationale was that large-scale hydraulic structures were built in the study area in 2012, which led to quite different flooding characteristics after 2012. As mentioned in
Section 2, the study area and data used to construct the SOBEK model were updated in 2019. Thus, the model was reasonable to underestimate the inundation severity for typhoon events that happened before 2012. The TPRs of standard 0 showed the accuracy of events after 2012 at an average of 24% higher than those before 2012. Also, the TPRs of standards 15 and 30 have substantial differences. The proof model does have the ability to catch flood protection by hydraulic structures.
In sum, the results of this research proved that QPF-RIF has sufficient ability to forecast the medium- and long-term flooding range and depth, especially in severely flooded areas. It can effectively assist in policy formulation, pump scheduling, and disaster prevention operations.