Assessing the Performance of SHETRAN Simulating a Geologically Complex Catchment
Abstract
:1. Introduction
2. Materials and Methods
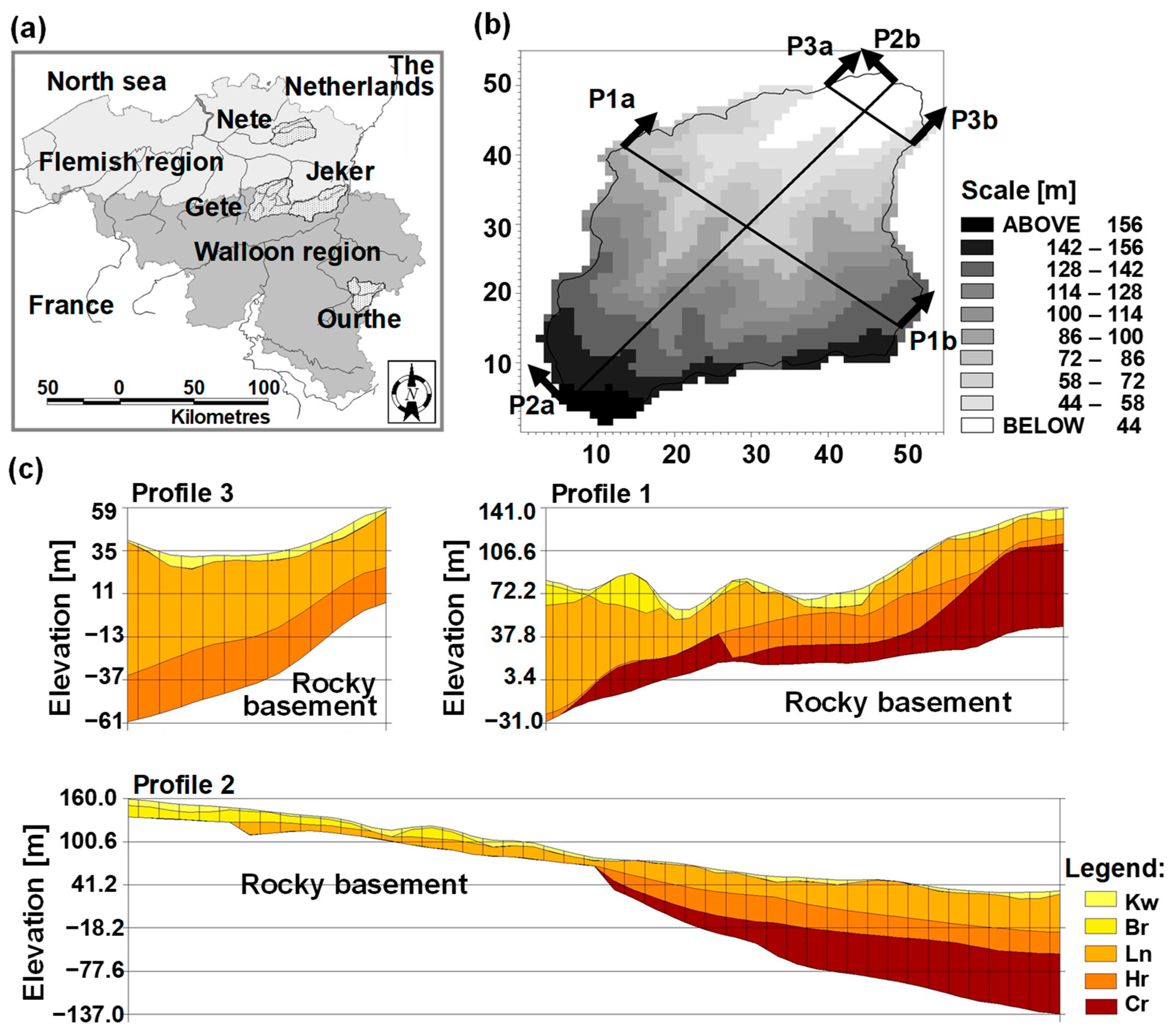
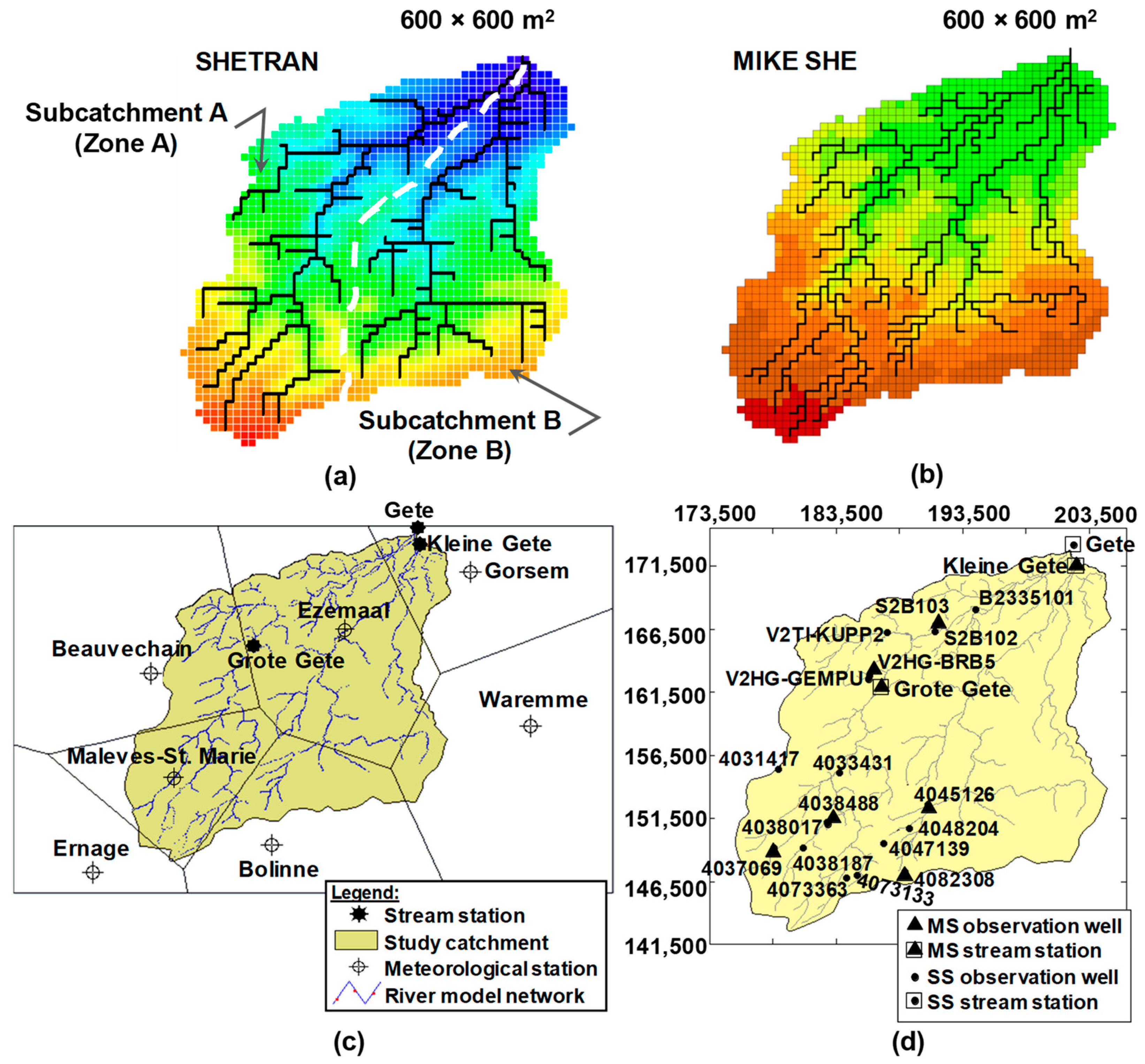
2.1. The Study Site
2.2. Hydrological Codes
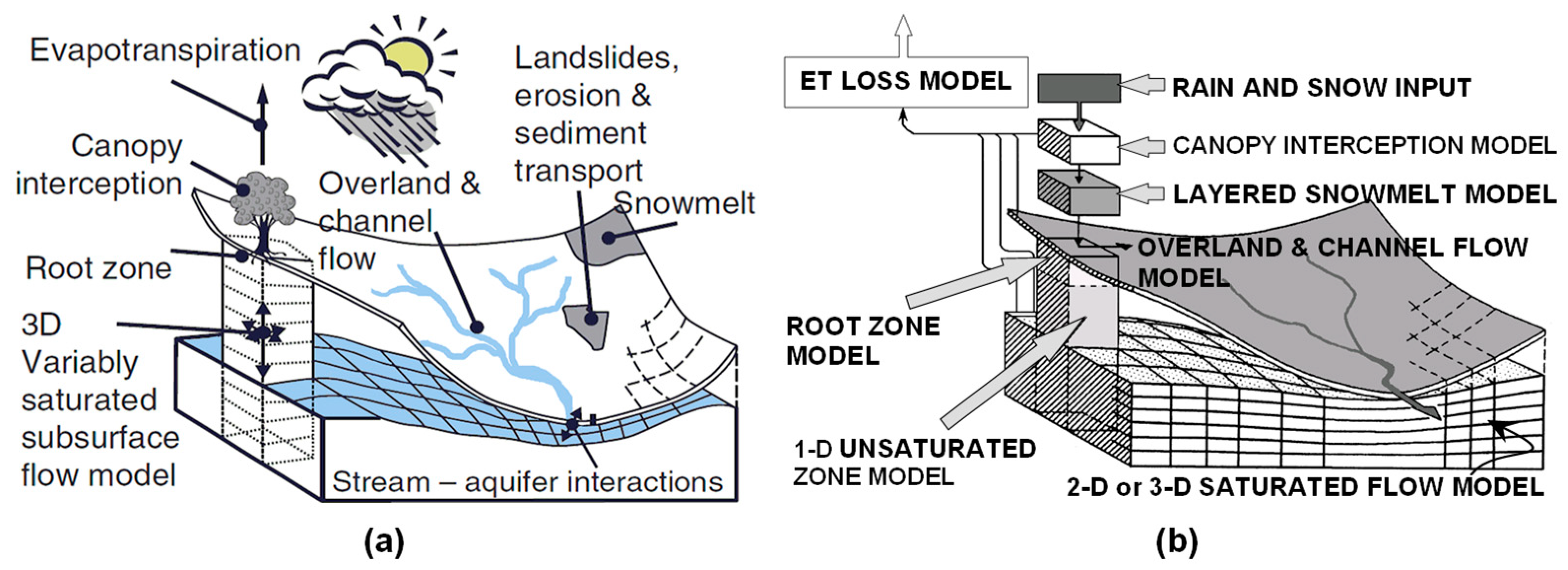
2.2.1. SHETRAN Hydrological Code
2.2.2. MIKE SHE Hydrological Code
2.2.3. Comparison between SHETRAN and MIKE SHE
2.3. Data Availability and Code Parameterisation
2.4. Model Performance
2.4.1. Multi-Objective Model Performance Statistics
2.4.2. Analysis of Simulated Time Series
3. Results
3.1. Values of the Effective Model Parameters
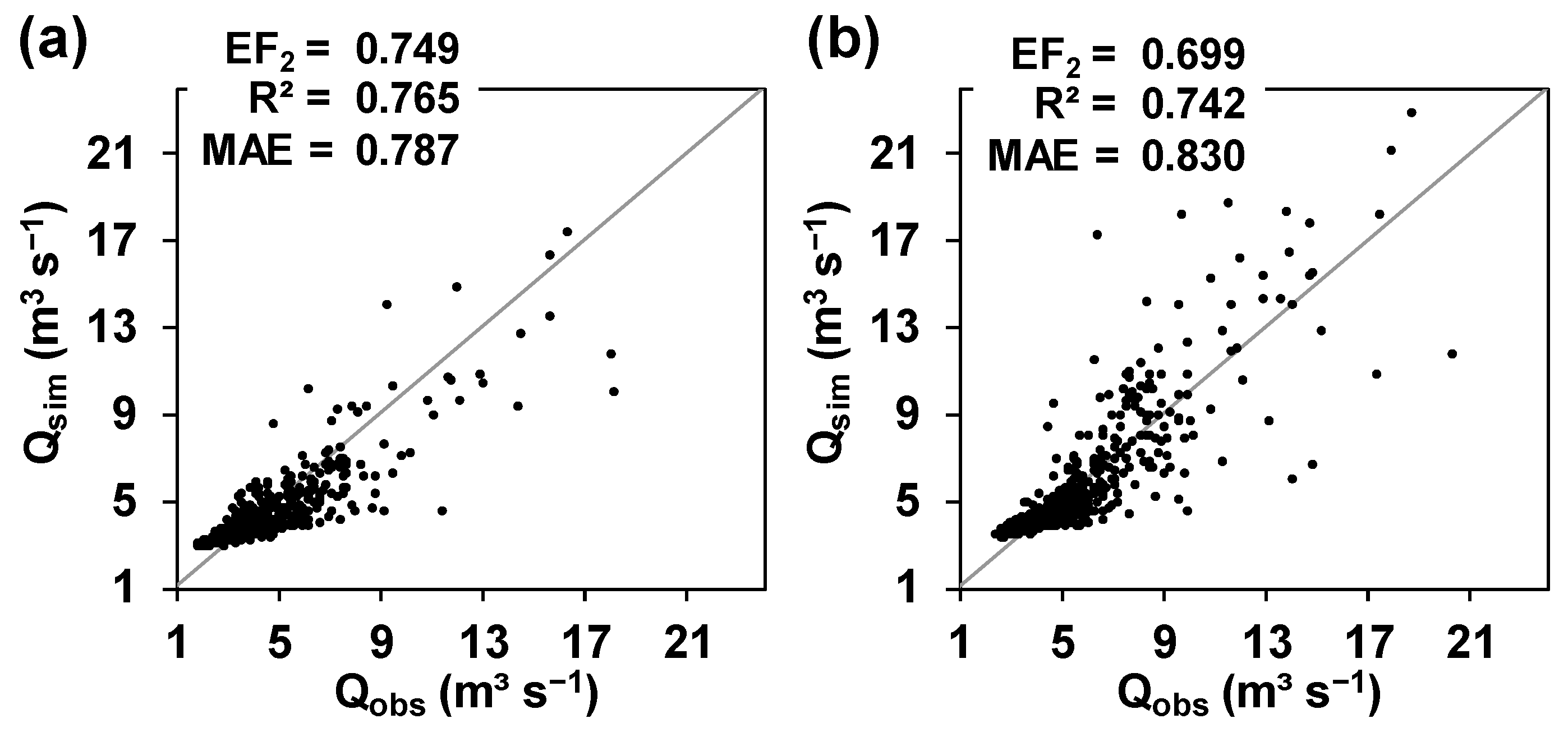
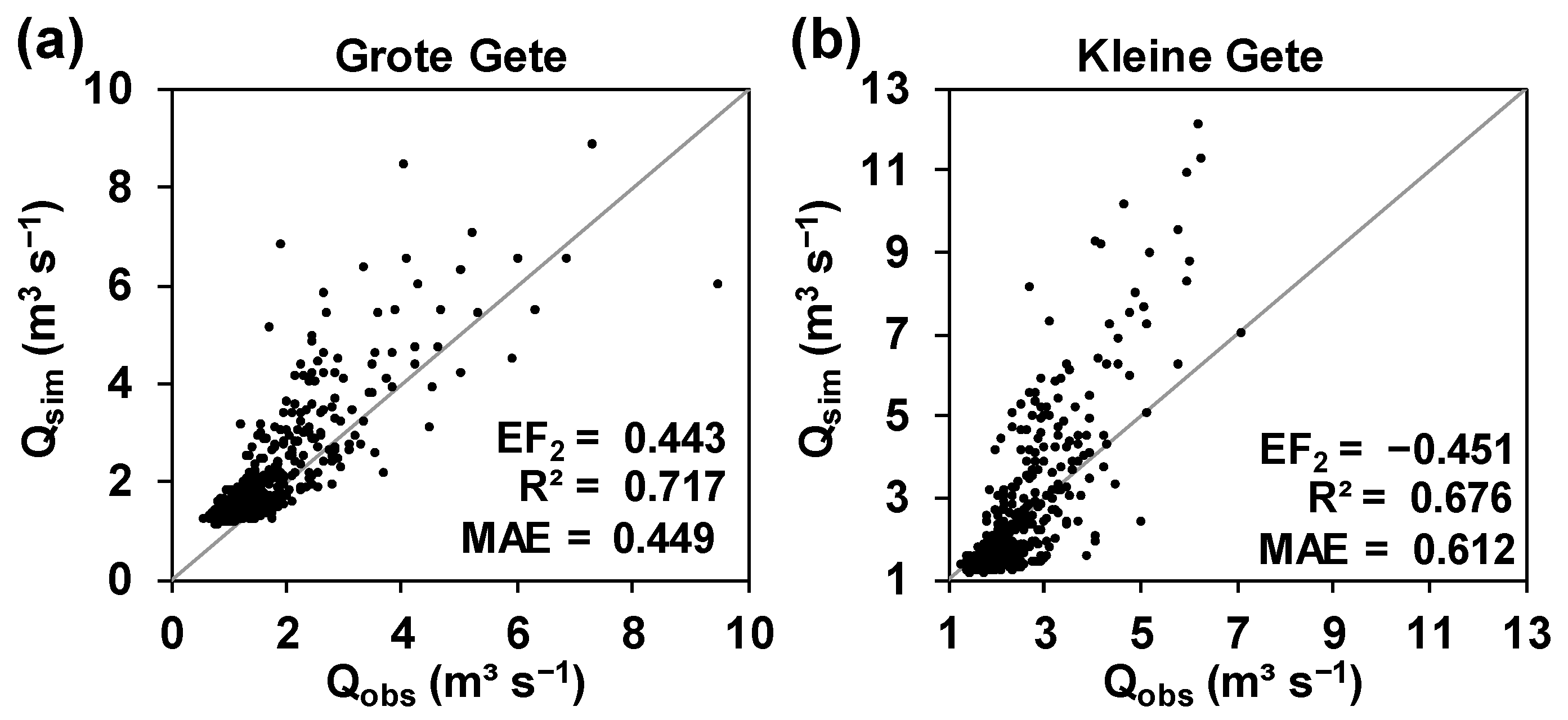
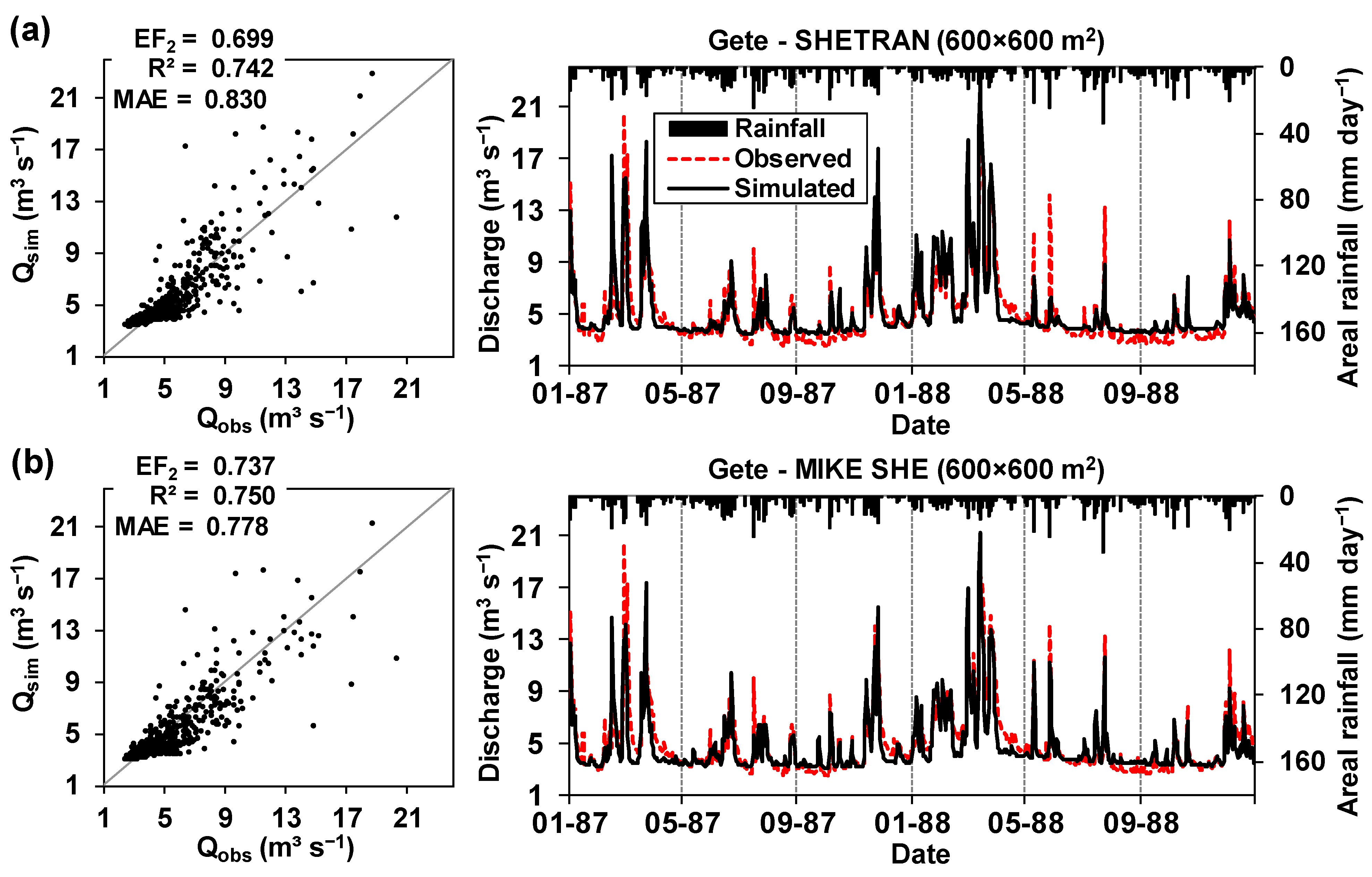
3.2. Multi-Objective Model Performance Statistics
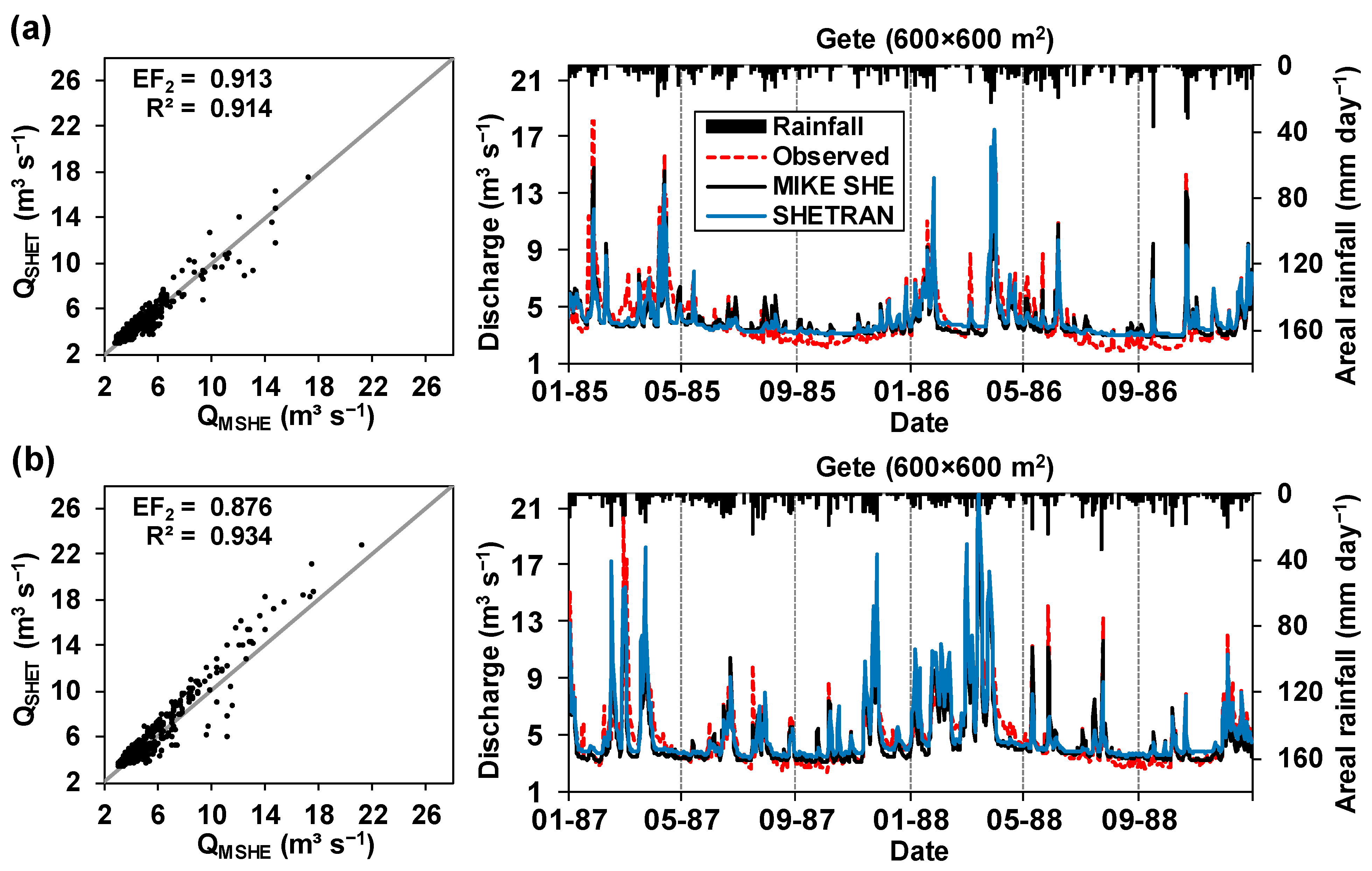
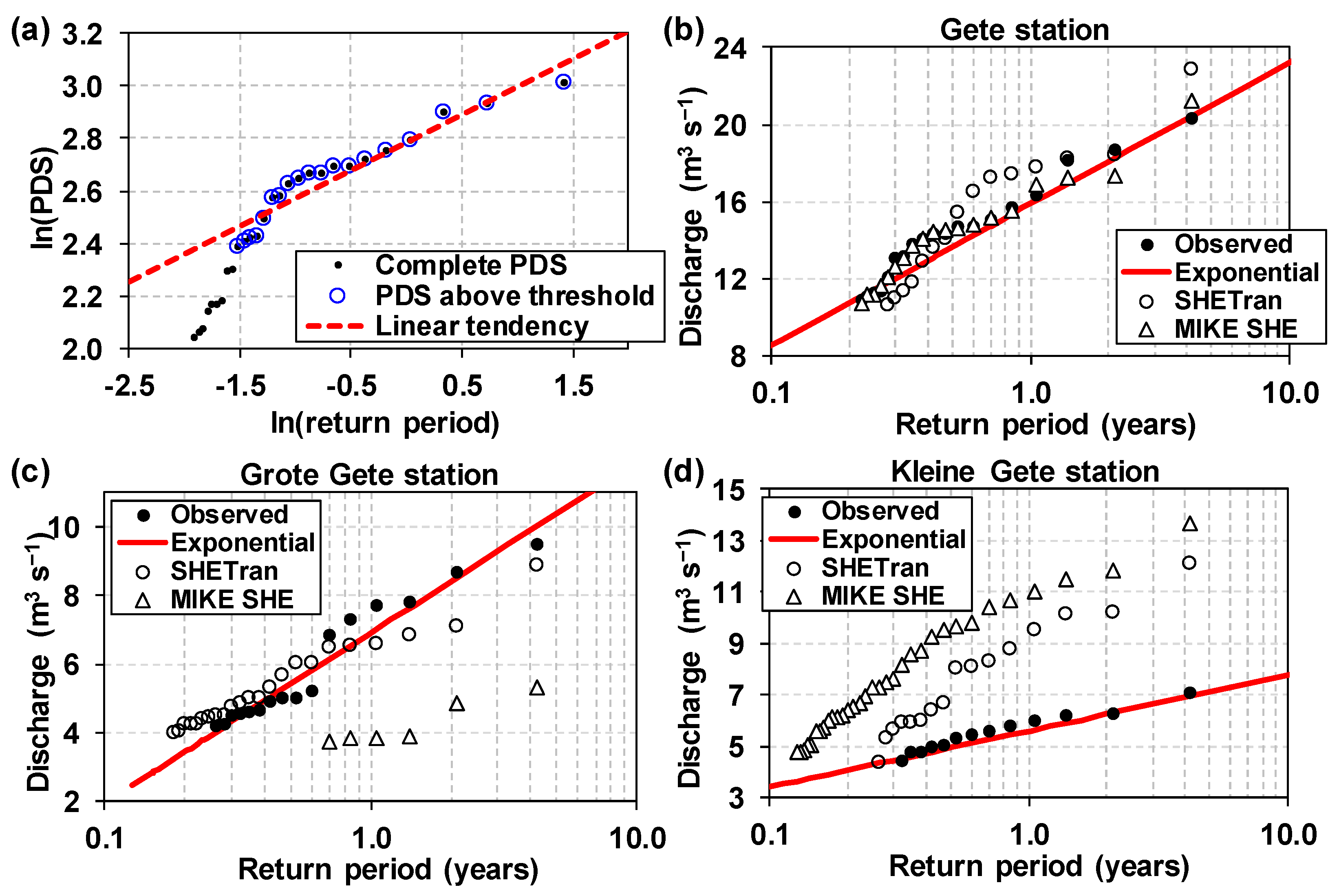
3.3. Comparison of the SHETRAN and MIKE SHE Predictions
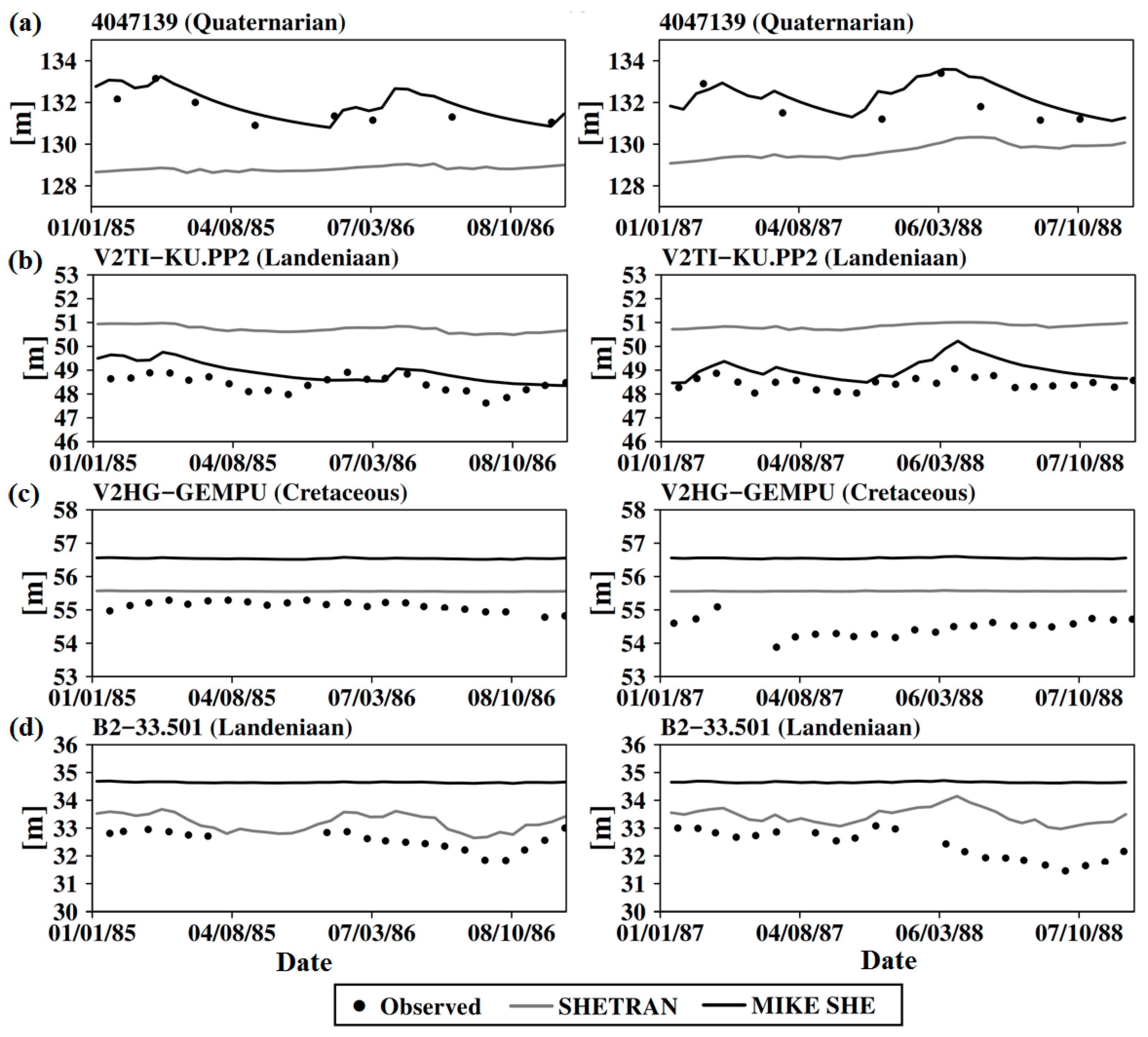
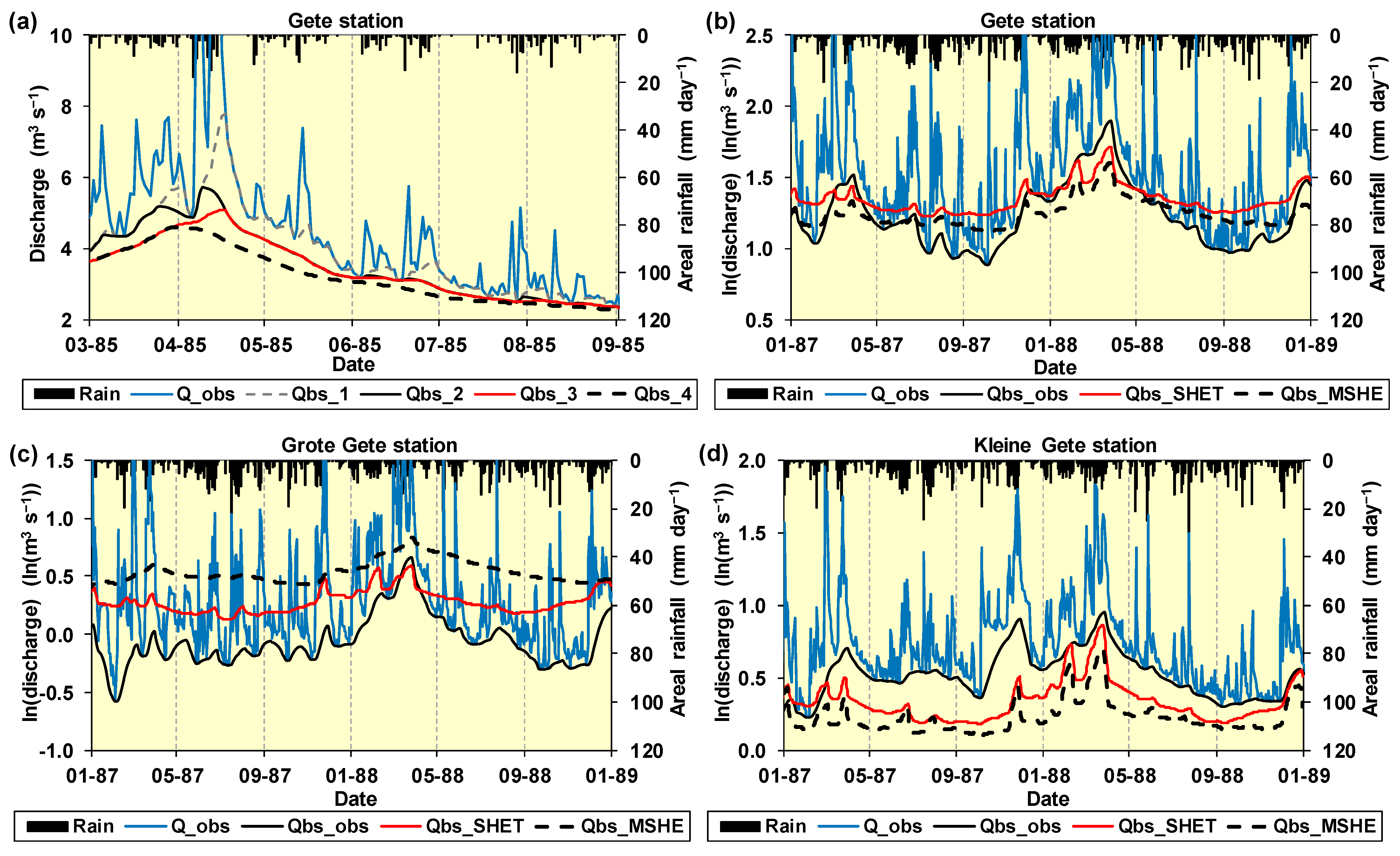
3.4. Analysis of Simulated Time Series
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Feyen, J.; Vázquez, R.F. Modeling hydrological consequences of climate and land use change—Progress and Challenges. MASKANA 2011, 2, 83–100. [Google Scholar] [CrossRef]
- Refsgaard, J.C. Parameterisation, calibration and validation of distributed hydrological models. J. Hydrol. 1997, 198, 69–97. [Google Scholar] [CrossRef]
- Vázquez, R.F.; Feyen, L.; Feyen, J.; Refsgaard, J.C. Effect of grid-size on effective parameters and model performance of the MIKE SHE code applied to a medium sized catchment. Hydrol. Process. 2002, 16, 355–372. [Google Scholar] [CrossRef]
- Beven, K.J. Rainfall-Runoff Modelling: The Primer, 2nd ed.; John Wiley and Sons: Chichester, UK, 2012; p. 457. [Google Scholar]
- Zhang, R.; Santos, C.A.G.; Moreira, M.; Freire, P.K.M.M.; Corte-Real, J. Automatic Calibration of the SHETRAN Hydrological Modelling System Using MSCE. Water Resour. Manag. 2013, 27, 4053–4068. [Google Scholar] [CrossRef] [Green Version]
- Zhang, R.; Moreira, M.; Corte-Real, J. Multi-objective calibration of the physically based, spatially distributed SHETRAN hydrological model. J. Hydroinformatics 2016, 18, 428–445. [Google Scholar] [CrossRef] [Green Version]
- Zhang, J.; Zhang, M.; Song, Y.; Lai, Y. Hydrological simulation of the Jialing River Basin using the MIKE SHE model in changing climate. J. Water Clim. Change 2021, 12, 2495–2514. [Google Scholar] [CrossRef]
- Madsen, H. Parameter estimation in distributed hydrological catchment modelling using automatic calibration with multiple objectives. Adv. Water Resour. 2003, 26, 205–216. [Google Scholar] [CrossRef]
- Vázquez, R.F. Assessment of the performance of physically based distributed codes simulating medium size hydrological systems. Doctoral Dissertation, Katholieke Universiteit Leuven (K.U. Leuven), Leuven, Belgium, 2003. [Google Scholar]
- McMichael, C.E.; Hope, A.S.; Loaiciga, H.A. Distributed hydrological modelling in California semi-arid shrublands: MIKE SHE model calibration and uncertainty estimation. J. Hydrol. 2006, 317, 307–324. [Google Scholar] [CrossRef]
- Vázquez, R.F.; Beven, K.; Feyen, J. GLUE based assessment on the overall predictions of a MIKE SHE application. Water Resour. Manag. 2009, 23, 1325–1349. [Google Scholar] [CrossRef]
- Vázquez, R.F.; Hampel, H. Prediction limits of a catchment hydrological model using different estimates of ETp. J. Hydrol. 2014, 513, 216–228. [Google Scholar] [CrossRef]
- Vázquez, R.F.; Hampel, H. A Simple Approach to Account for Stage-Discharge Uncertainty in Hydrological Modelling. Water 2022, 14, 1045. [Google Scholar] [CrossRef]
- Guerreiro, S.B.; Birkinshaw, S.; Kilsby, C.; Fowler, H.J.; Lewis, E. Dry getting drier—The future of transnational river basins in Iberia. J. Hydrol. Reg. Stud. 2017, 12, 238–252. [Google Scholar] [CrossRef]
- Op de Hipt, F.; Diekkrüger, B.; Steup, G.; Yira, Y.; Hoffmann, T.; Rode, M.; Näschen, K. Modeling the effect of land use and climate change on water resources and soil erosion in a tropical West African catch-ment (Dano, Burkina Faso) using SHETRAN. Sci. Total Environ. 2019, 653, 431–445. [Google Scholar] [CrossRef] [PubMed]
- Cieśliński, R. Determination of retention value using Mike She model in the area of young glacial catchments. Appl. Water Sci. 2020, 11, 5. [Google Scholar] [CrossRef]
- Ewen, J.; Parkin, G.; O’Connell Patrick, E. SHETRAN: Distributed River Basin Flow and Transport Modeling System. J. Hydrol. Eng. 2000, 5, 250–258. [Google Scholar] [CrossRef] [Green Version]
- Mourato, S.; Moreira, M.; Corte-Real, J. Water Resources Impact Assessment under Climate Change Scenarios in Mediterranean Watersheds. Water Resour. Manag. 2015, 29, 2377–2391. [Google Scholar] [CrossRef]
- Đukić, V.; Radić, Z. Sensitivity Analysis of a Physically based Distributed Model. Water Resour. Manag. 2016, 30, 1669–1684. [Google Scholar] [CrossRef]
- Shrestha, P.K.; Shakya, N.M.; Pandey, V.P.; Birkinshaw, S.J.; Shrestha, S. Model-based estimation of land subsidence in Kathmandu Valley, Nepal. Geomat. Nat. Hazards Risk 2017, 8, 974–996. [Google Scholar] [CrossRef] [Green Version]
- Sreedevi, S.; Eldho, T.I.; Madhusoodhanan, C.G.; Jayasankar, T. Multiobjective sensitivity analysis and model parameterization approach for coupled streamflow and groundwater table depth simulations using SHETRAN in a wet humid tropical catchment. J. Hydrol. 2019, 579, 124217. [Google Scholar] [CrossRef]
- Suroso; Wahyuni, A.D.; Santoso, P.B. Prediction of Streamflow at the Pemali catchment area using Shetran model. IOP Conf. Ser. Earth Environ. Sci. 2021, 698, 012009. [Google Scholar] [CrossRef]
- Birkinshaw, S.J.; O’Donnell, G.; Glenis, V.; Kilsby, C. Improved hydrological modelling of urban catchments using runoff coefficients. J. Hydrol. 2021, 594, 125884. [Google Scholar] [CrossRef]
- Escobar-Ruiz, V.; Smith, H.G.; Blake, W.H.; Macdonald, N. Assessing the performance of a physically based hydrological model using a proxy-catchment approach in an agricultural environment. Hydrol. Processes 2019, 33, 3119–3137. [Google Scholar] [CrossRef] [Green Version]
- Op de Hipt, F.; Diekkrüger, B.; Steup, G.; Yira, Y.; Hoffmann, T.; Rode, M. Applying SHETRAN in a Tropical West African Catchment (Dano, Burkina Faso)—Calibration, Validation, Uncertainty Assessment. Water 2017, 9, 101. [Google Scholar] [CrossRef] [Green Version]
- Op de Hipt, F.; Diekkrüger, B.; Steup, G.; Yira, Y.; Hoffmann, T.; Rode, M. Modeling the impact of climate change on water resources and soil erosion in a tropical catchment in Burkina Faso, West Africa. CATENA 2018, 163, 63–77. [Google Scholar] [CrossRef]
- Thiemann, M.; Trosser, M.; Gupta, H.; Sorooshian, S. Bayesian recursive parameter estimation for hydrologic models. Water Resour. Res. 2001, 37, 2521–2536. [Google Scholar] [CrossRef]
- Vázquez, R.F.; Willems, P.; Feyen, J. Improving the predictions of a MIKE SHE catchment-scale application by using a multi-criteria approach. Hydrol. Process. 2008, 22, 2159–2179. [Google Scholar] [CrossRef]
- Feyen, L.; Vazquez, R.F.; Christiaens, K.; Sels, O.; Feyen, J. Application of a distributed physically-based hydrological model to a medium size catchment. Hydrol. Earth Syst. Sci. 2000, 4, 47–63. [Google Scholar] [CrossRef]
- Birkinshaw, S.J. Technical note: Automatic river network generation for a physically-based river catchment model. Hydrol. Earth Syst. Sci. 2010, 14, 1767–1771. [Google Scholar] [CrossRef] [Green Version]
- Refsgaard, J.C.; Storm, B. MIKE SHE. In Computer Models of Watershed Hydrology; Singh, V.P., Ed.; Water Resources Publications: Littleton, CO, USA, 1995; pp. 809–846. [Google Scholar]
- Ma, L.; He, C.; Bian, H.; Sheng, L. MIKE SHE modeling of ecohydrological processes: Merits, applications, and challenges. Ecol. Eng. 2016, 96, 137–149. [Google Scholar] [CrossRef]
- Abbott, M.B.; Bathurst, J.C.; Conge, P.E.; O’Connell, P.E.; Rasmussen, J. An introduction to the European Hydrological System Système Hydrologique Européen, ‘SHE’, 1. History and philosophy of a physically based distributed modeling system. J. Hydrol. 1986, 87, 45–59. [Google Scholar] [CrossRef]
- Abbott, M.B.; Bathurst, J.C.; Cunge, P.E.; O’Connell, P.E.; Rasmussen, J. An introduction to the European Hydrological System Systéme Hydrologique Européen, ‘SHE’, 2. Structure of a Physically-based, Distributed Modelling System. J. Hydrol. 1986, 87, 61–77. [Google Scholar] [CrossRef]
- Bathurst, J.C.; Birkinshaw, S.J.; Cisneros, F.; Fallas, J.; Iroumé, A.; Iturraspe, R.; Novillo, M.G.; Urciuolo, A.; Alvarado, A.; Coello, C.; et al. Forest impact on floods due to extreme rainfall and snowmelt in four Latin American environments 2: Model analysis. J. Hydrol. 2011, 400, 292–304. [Google Scholar] [CrossRef]
- Vázquez, R.F.; Feyen, J. Assessment of the performance of a distributed code in relation to the ETp estimates. Water Resour. Manag. 2002, 16, 329–350. [Google Scholar] [CrossRef]
- Vázquez, R.F.; Feyen, J. Assessment of the effects of DEM gridding on the predictions of basin runoff using MIKE SHE and a modelling resolution of 600 m. J. Hydrol. 2007, 334, 73–87. [Google Scholar] [CrossRef]
- Vereecken, H. Pedotransferfunctions for the generation of hydraulic properties for Belgian soils. Doctoral Dissertation, Katholieke Universiteit Leuven (K.U.Leuven), Leuven, Belgium, 1988. [Google Scholar]
- Allen, G.R.; Pereira, L.S.; Raes, D.; Martin, S. Crop Evapotranspiration-Guidelines for Computing Crop Water Requirements; FAO: Rome, Italy, 1998; p. 300. [Google Scholar]
- Vázquez, R.F.; Feyen, J. Potential Evapotranspiration for the distributed modelling of Belgian basins. J. Irrig. Drain. Eng. 2004, 130, 1–8. [Google Scholar] [CrossRef]
- Feddes, R.A.; Kowalik, P.; Neuman, S.P.; Bresler, E. Finite difference and finite element simulation of field water uptake by plants/Simulation de la différence finie et de l’élément fini de l’humidité du sol utilisée par les plantes. Hydrol. Sci. Bull. 1976, 21, 81–98. [Google Scholar] [CrossRef]
- Shuttleworth, W.J. Evaporation. In Handbook of Hydrology; Maidment, D.R., Ed.; McGRaw Hill: New York, NY, USA, 1993; Volume 1, pp. 4.1–4.47. [Google Scholar]
- NU. SHETRAN Water Flow Component, Equations and Algorithms; Newcastle University: Newcastle, UK, 2001; p. 55. [Google Scholar]
- Rutter, A.J.; Kershaw, K.A.; Robins, P.C.; Morton, A.J. A predictive model of rainfall interception in forests, 1. Derivation of the model from observations in a plantation of Corsican pine. Agric. Meteorol. 1971, 9, 367–384. [Google Scholar] [CrossRef]
- Boons-Prins, E.R.; Koning, G.H.J.D.; Diepen, C.A.V.; Penning, F.W.T.D. Crop-Specific Simulation Parameters for Yield Forecasting across the European Community; Centre for Agrobiological Research: Wageningen, The Netherlands, 1993; p. 200. [Google Scholar]
- Breuer, L.; Eckhardt, K.; Frede, H.-G. Plant parameter values for models in temperate climates. Ecol. Model. 2003, 169, 237–293. [Google Scholar] [CrossRef]
- Kristensen, K.J.; Jensen, S.E. A model for estimating actual evapotranspiration from potential evapotranspiration. Nord. Hydrol. 1975, 6, 170–188. [Google Scholar] [CrossRef] [Green Version]
- Engman, E.T. Roughness coefficients for routing surface runoff. J. Irrig. Drain. Eng. 1986, 112, 39–53. [Google Scholar] [CrossRef]
- Chow, V.T.; Maidment, D.R.; Mays, L.W. Applied Hydrology; McGraw-Hill International Editions: Singapore, 1988; p. 572. [Google Scholar]
- Anderson, M.P.; Woessner, W.W.; Hunt, R. Applied Groundwater Modelling Simulation of Flow and Advective Transport, 2nd ed.; Academic Press: Cambridge, MA, USA, 2015; p. 630. [Google Scholar]
- Dehotin, J.; Vázquez, R.F.; Braud, I.; Debionne, S.; Viallet, P. Hydrological modelling using unstructured and irregular grids: Example of 2D groundwater modelling. J. Hydrol. Eng. 2011, 16, 108–125. [Google Scholar] [CrossRef] [Green Version]
- Biondi, D.; Freni, G.; Iacobellis, V.; Mascaro, G.; Montanari, A. Validation of hydrological models: Conceptual basis, methodological approaches and a proposal for a code of practice. Phys. Chem. Earth Parts A/B/C 2012, 42–44, 70–76. [Google Scholar] [CrossRef]
- Li, D.; Liang, Z.; Zhou, Y.; Li, B.; Fu, Y. Multicriteria assessment framework of flood events simulated with vertically mixed runoff model in semiarid catchments in the middle Yellow River. Nat. Hazards Earth Syst. Sci. 2019, 19, 2027–2037. [Google Scholar] [CrossRef] [Green Version]
- Bizhanimanzar, M.; Leconte, R.; Nuth, M. Modelling of shallow water table dynamics using conceptual and physically based integrated surface-water–groundwater hydrologic models. Hydrol. Earth Syst. Sci. 2019, 23, 2245–2260. [Google Scholar] [CrossRef] [Green Version]
- Legates, D.R.; McCabe, G.J. Evaluating the use of ‘goodness-of-fit’ measures in hydrological and hydroclimatic model validation. Water Resour. Res. 1999, 35, 233–241. [Google Scholar] [CrossRef]
- Nash, J.E.; Sutcliffe, J. River flow forecasting through conceptual models, I, A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Willems, P. Compound intensity/duration/frequency-relationships of extreme precipitation for two seasons and two storm types. J. Hydrol. 2000, 233, 189–205. [Google Scholar] [CrossRef]
- Pandey, M.D.; van Gelder, P.H.A.J.M.; Vrijling, J.K. Bootstrap simulations for evaluating the uncertainty associated with peaks-over-threshold estimates of extreme wind velocity. Environmetrics 2003, 14, 27–43. [Google Scholar] [CrossRef]
- Pickands, J. Statistical Inference using extreme order statistics. Annals Stat. 1975, 3, 119–131. [Google Scholar]
- Hong, H.P.; Li, S.H. Plotting positions and approximating first two moments of order statistics for Gumbel distribution: Estimating quantiles of wind speed. Wind. Struct. 2014, 19, 371–387. [Google Scholar] [CrossRef]
- Stedinger, J.R.; Vogel, R.M.; Foufoula-Georgiou, E.F. Frequency Analysis of extreme events. In Handbook of Hydrology; Maidment, D.R., Ed.; McGraw-Hill Inc.: New York, NY, USA, 1993; pp. 18.11–18.66. [Google Scholar]
- Vimos-Lojano, D.J.; Martínez-Capel, F.; Hampel, H.; Vázquez, R.F. Hydrological influences on aquatic communities at the mesohabitat scale in high Andean streams of southern Ecuador. Ecohydrology 2019, 12, e2033. [Google Scholar] [CrossRef]
- Nathan, R.J.; McMahon, T.A. Evaluation of automated techniques for baseflow and recession analysis. Water Resour. Res. 1990, 26, 1465–1473. [Google Scholar] [CrossRef]
- Arnold, J.G.; Allen, P.M.; Muttiah, R.; Bernhardt, G. Automated Base Flow Separation and Recession Analysis Techniques. Groundwater 1995, 33, 1010–1018. [Google Scholar] [CrossRef]
- Ahiablame, L.; Chaubey, I.; Engel, B.; Cherkauer, K.; Merwade, V. Estimation of annual baseflow at ungauged sites in Indiana USA. J. Hydrol. 2013, 476, 13–27. [Google Scholar] [CrossRef]
- Chapman, T. Comment on “Evaluation of automated techniques for base flow and recession analyses” by R. J. Nathan and T. A. McMahon. Water Resour. Res. 1991, 27, 1783–1784. [Google Scholar] [CrossRef]
- Willems, P. A time series tool to support the multi-criteria performance evaluation of rainfall-runoff models. Environ. Model. Softw. 2009, 24, 311–321. [Google Scholar] [CrossRef]
- Houthuys, R. A sedimentary model of the Brussels Sands, Eocene, Belgium. Geol. Belg. 2011, 14, 55–74. [Google Scholar]
- DHI. MIKE-SHE v 2001 User Guide and Technical Reference Manual; Danish Hydraulic Institute: Horsolm, Denmark, 2001. [Google Scholar]
- DHI. MIKE SHE User Guide and Reference Manual; Danish Hydraulic Institute: Horsolm, Denmark, 2022; p. 820. [Google Scholar]
| Model Parameter | Geological Unit | Bound of Interval | |
|---|---|---|---|
| Lower | Upper | ||
| nov (s m−1/3) | Not applicable | 0.025 | 0.070 |
| nriv (s m−1/3) | Not applicable | 0.10 | 6.25 |
| Kx (m s−1) | Quaternarian Brusselian Landeniaan Heers Cretaceous | 1.0 × 10−7 7.0 × 10−5 5.0 × 10−6 5.0 × 10−7 1.0 × 10−6 | 4.0 × 10−5 2.0 × 10−3 5.0 × 10−4 5.0 × 10−5 1.0 × 10−5 |
| Kz (m s−1) | Quaternarian Brusselian Landeniaan Heers Cretaceous | 1.0 × 10−8 7.0 × 10−6 5.0 × 10−7 1.0 × 10−8 1.0 × 10−8 | 1.0 × 10−6 7.0 × 10−5 5.0 × 10−5 5.0 × 10−6 1.0 × 10−7 |
| Parameter | (Spatial) Zone | Geological Unit | SHETRAN | MIKE SHE |
|---|---|---|---|---|
| nov (s m−1/3) | Maize crop fields | Not applicable | 0.44 | 0.29 |
| nriv (s m−1/3) | Average (river network) | Not applicable | 0.065 | 0.065 |
| Kx (m s−1) | A (Figure 3a) | Quaternarian | 1.00 × 10−7 | 1.0 × 10−7 |
| Landeniaan | 8.80 × 10−5 | 7.87 × 10−5 | ||
| Kz (m s−1) | Quaternarian | 1.00 × 10−8 | 9.10 × 10−7 | |
| Landeniaan | 5.00 × 10−5 | 2.75 × 10−6 | ||
| Kx (m s−1) | B (Figure 3a) | Quaternarian | 1.00 × 10−7 | 1.00 × 10−7 |
| Landeniaan | 8.28 × 10−5 | 7.87 × 10−5 | ||
| Kz (m s−1) | Quaternarian | 1.00 × 10−8 | 1.90 × 10−7 | |
| Landeniaan | 5.00 × 10−5 | 2.98 × 10−5 | ||
| Kx (m s−1) | Average (whole catchment) | Brusselian | 6.43 × 10−4 | 1.65 × 10−3 |
| Heers | 2.84 × 10−5 | 4.55 × 10−5 | ||
| Cretaceous | 4.27 × 10−6 | 1.00 × 10−6 | ||
| Kz (m s−1) | Brusselian | 7.00 × 10−5 | 7.00 × 10−6 | |
| Heers | 5.00 × 10−6 | 2.28 × 10−6 | ||
| Cretaceous | 1.00 × 10−7 | 7.54 × 10−8 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vázquez, R.F.; Brito, J.E.; Hampel, H.; Birkinshaw, S. Assessing the Performance of SHETRAN Simulating a Geologically Complex Catchment. Water 2022, 14, 3334. https://doi.org/10.3390/w14203334
Vázquez RF, Brito JE, Hampel H, Birkinshaw S. Assessing the Performance of SHETRAN Simulating a Geologically Complex Catchment. Water. 2022; 14(20):3334. https://doi.org/10.3390/w14203334
Chicago/Turabian StyleVázquez, Raúl F., Josué E. Brito, Henrietta Hampel, and Stephen Birkinshaw. 2022. "Assessing the Performance of SHETRAN Simulating a Geologically Complex Catchment" Water 14, no. 20: 3334. https://doi.org/10.3390/w14203334