Coupled Hydro-Climatic Signals in the Radial Growth of Oaks Benefitting from Groundwater Availability
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area
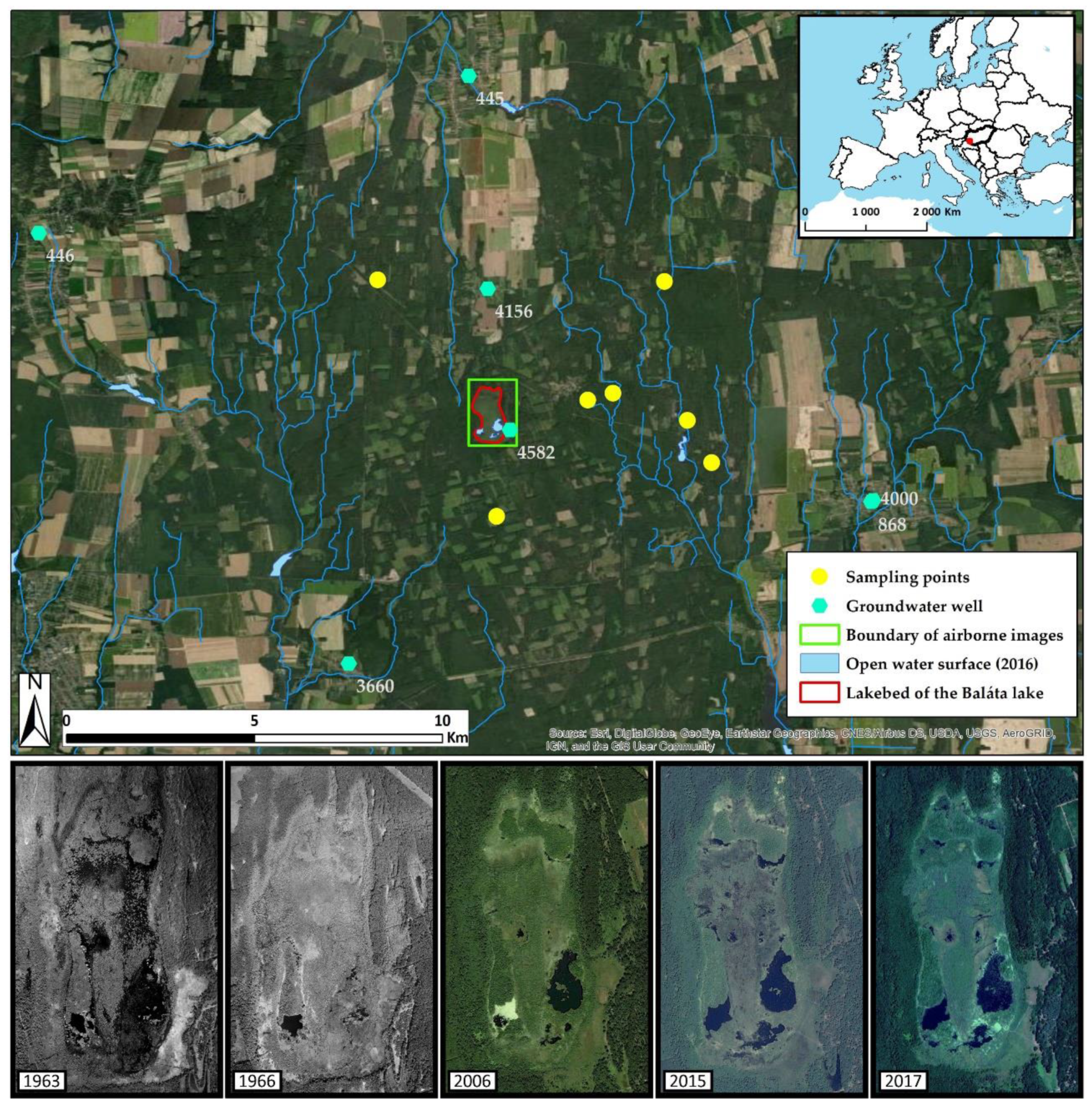
2.2. Tree-Ring Sampling and Measurement
2.3. Groundwater and Climate Data
2.4. Statistical Analysis
3. Results
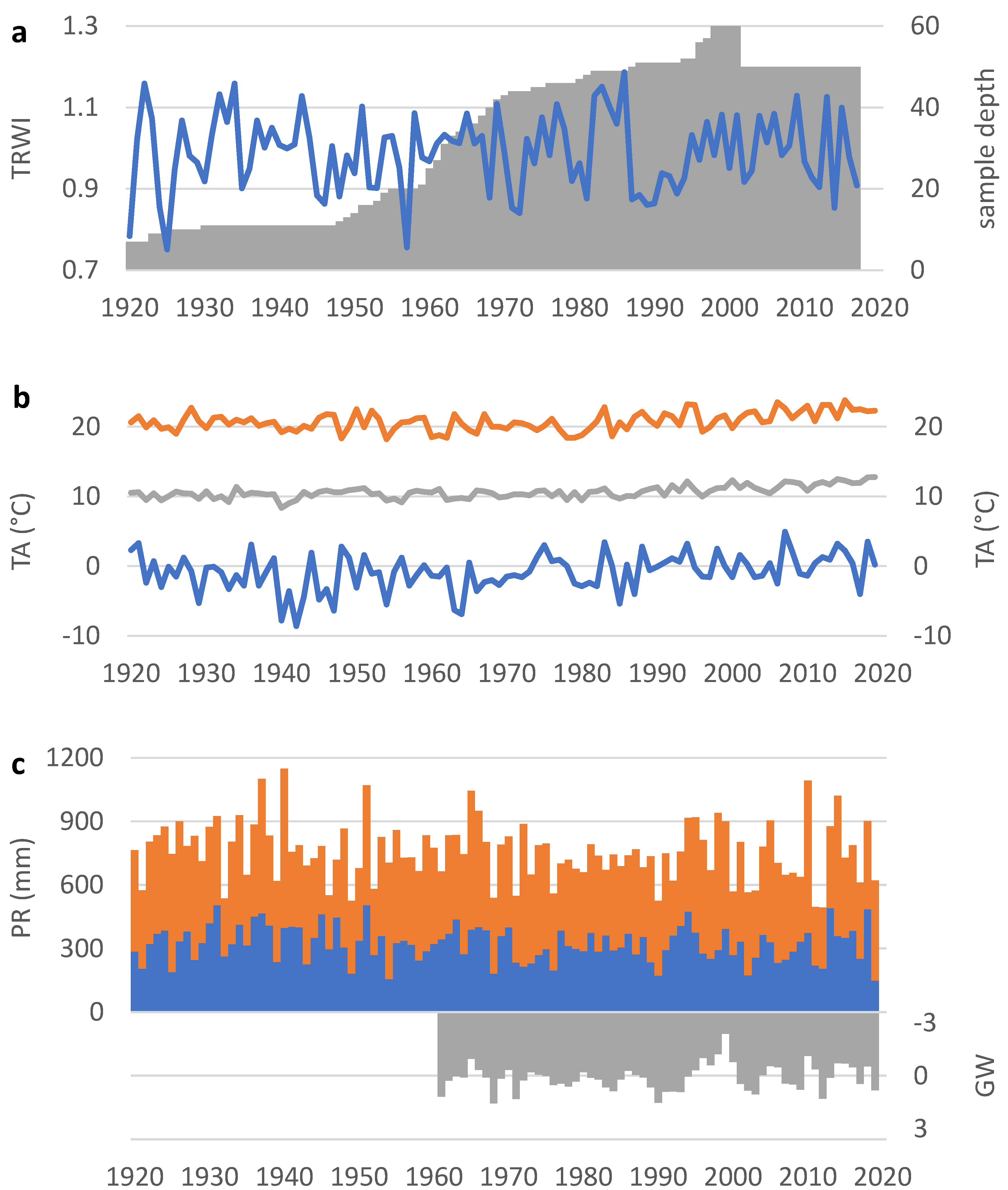
3.1. General Hydro-Climatic Signals in Radial Growth
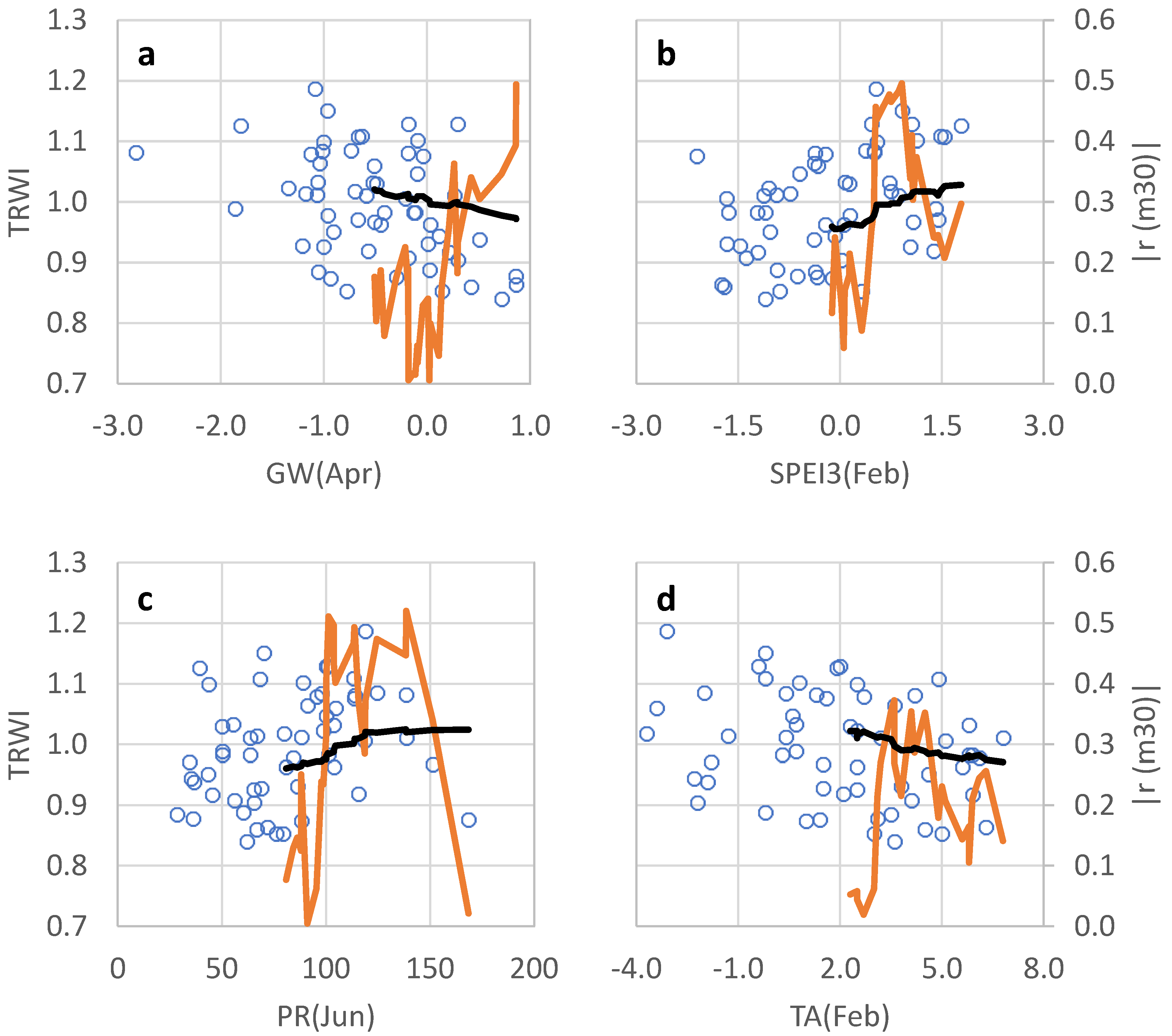
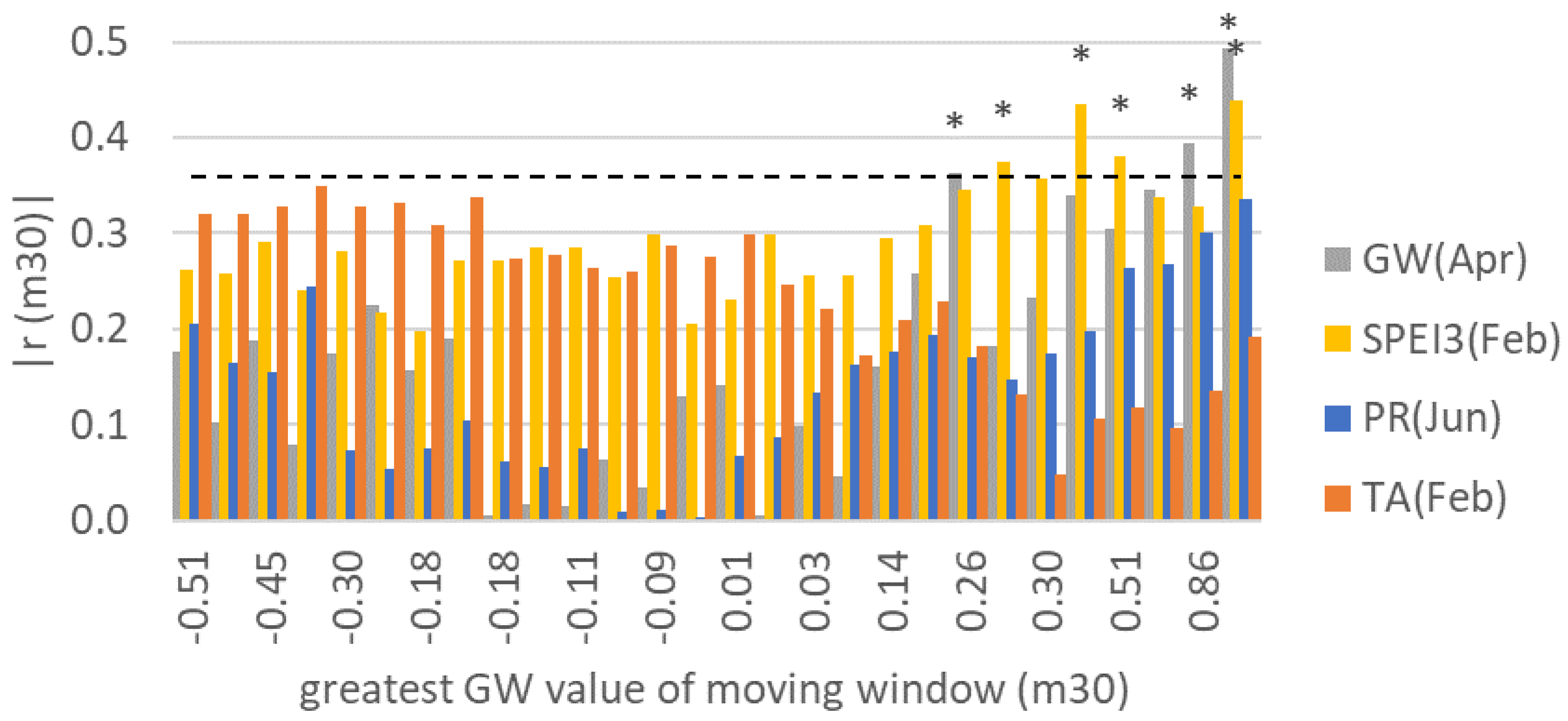
3.2. Detailed Relationships between Radial Growth, Climate, and Groundwater
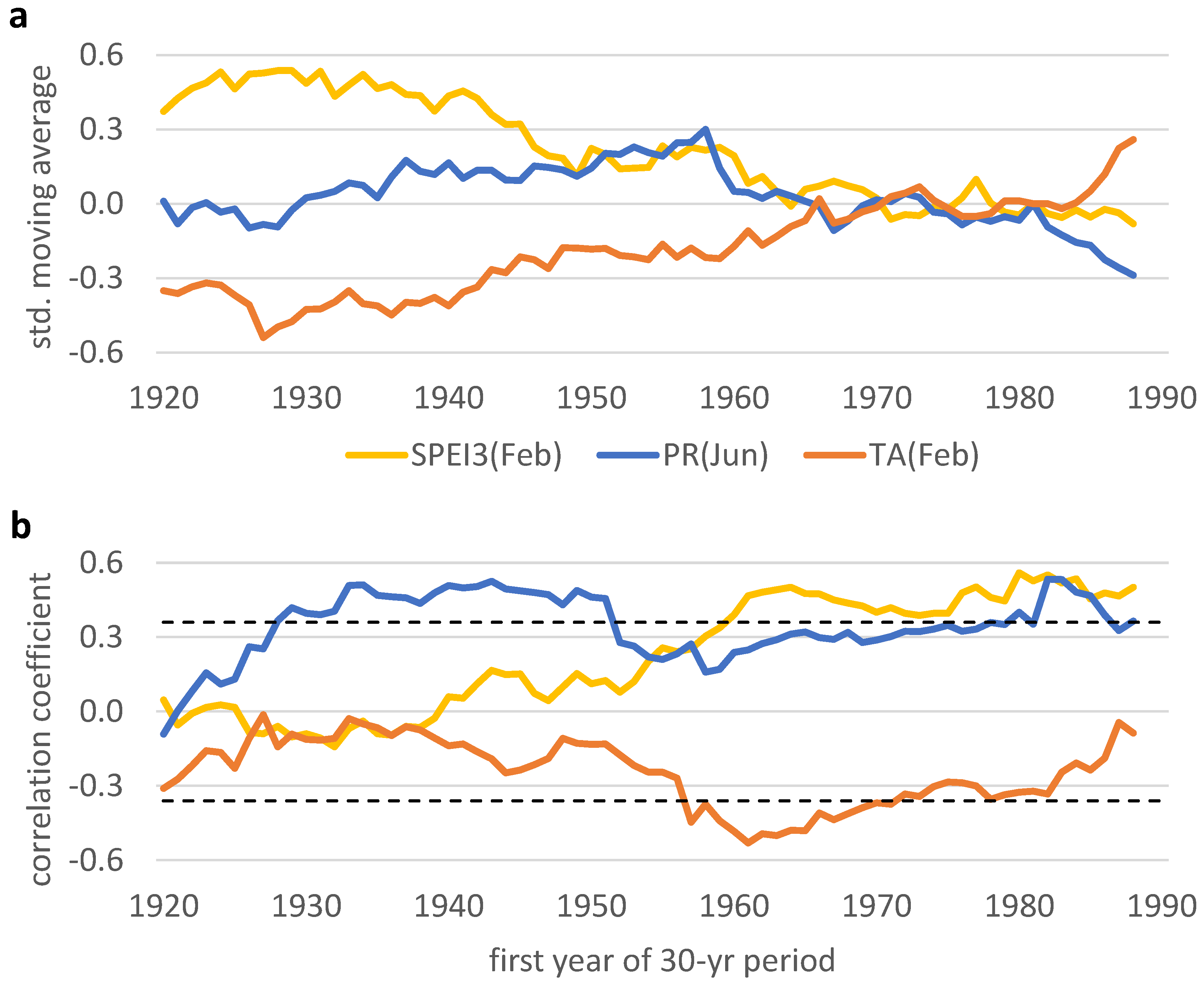
3.3. Climatic Trends and Changing Correlation with Radial Growth
4. Discussion
4.1. Coupled Hydro-Climatic Signals in the Radial Growth
4.2. Observed Trends and Their Implications on Tree Growth
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- Leuschner, C.; Ellenberg, H. Ecology of Central European Forests; Springer International Publishing: Cham, Switzerland, 2017. [Google Scholar]
- Skiadaresis, G.; Schwarz, J.A.; Bauhus, J. Groundwater extraction in floodplain forests reduces radial growth and increases summer drought sensitivity of pedunculate oak trees (Quercus robur L.). Front. Glob. Chang. 2019, 2, 5. [Google Scholar] [CrossRef]
- Skiadaresis, G.; Schwarz, J.; Stahl, K.; Bauhus, J. Groundwater extraction reduces tree vitality, growth and xylem hydraulic capacity in Quercus robur during and after drought events. Sci. Rep. 2021, 11, 5149. [Google Scholar] [CrossRef] [PubMed]
- Schweingruber, F.H. Tree Rings and Environment: Dendroecology; Paul Haupt: Bern, Switzerland, 1996. [Google Scholar]
- Perez-Valdivia, C.; Sauchyn, D. Tree-ring reconstruction of groundwater levels in Alberta, Canada: Long term hydroclimatic variability. Dendrochronologia 2011, 29, 41–47. [Google Scholar] [CrossRef]
- Hunter, S.C.; Allen, D.M.; Kohfeld, K.E. Comparing Approaches for Reconstructing Groundwater Levels in the Mountainous Regions of Interior British Columbia, Canada, Using Tree Ring Widths. Atmosphere 2020, 11, 1374. [Google Scholar] [CrossRef]
- Gričar, J.; De Luis, M.; Hafner, P.; Levanič, T. Anatomical characteristics and hydrologic signals in tree-rings of oaks (Quercus robur L.). Trees 2013, 27, 1669–1680. [Google Scholar] [CrossRef]
- Stojanović, D.B.; Levanič, T.; Matović, B.; Orlović, S. Growth decrease and mortality of oak floodplain forests as a response to change of water regime and climate. Eur. J. Res. 2015, 134, 555–567. [Google Scholar] [CrossRef]
- Tumajer, J.; Treml, V. Response of floodplain pedunculate oak (Quercus robur L.) tree-ring width and vessel anatomy to climatic trends and extreme hydroclimatic events. For. Ecol. Manage. 2016, 379, 185–194. [Google Scholar] [CrossRef]
- Tulik, M.; Grochowina, A.; Jura-Morawiec, J.; Bijak, S. Groundwater Level Fluctuations Affect the Mortality of Black Alder (Alnus glutinosa Gaertn.). Forests 2020, 11, 134. [Google Scholar] [CrossRef]
- Tumajer, J.; Treml, V. Influence of artificial alteration of groundwater level on vessel lumen area and tree-ring width of Quercus robur. Trees 2017, 31, 1945–1957. [Google Scholar] [CrossRef]
- OVF. A Duna-vízgyűjtő magyarországi része. In Vízgyűjtő-Gazdálkodási Terv—2015; General Directorate of Water Management: Budapest, Hungary, 2015. [Google Scholar]
- Murray, B.R.; Zeppel, M.; Hose, G.; Eamus, D. Groundwater-dependent ecosystems in Australia: Its more than just water for rivers. Ecol. Manag. Restor. 2003, 4, 109–113. [Google Scholar] [CrossRef]
- Clifton, C.A.; Evans, R. Environmental water requirements of groundwater dependent ecosystems. In Environmental Flows Initiative Technical Report No. 2; Sinclair Knight Merz Pty Ltd.: Canberra, Australia, 2001. [Google Scholar]
- Eötvös, C.B.; Horváth, L. Changes of groundwater levels in Szenta-Forest as a result of Kaszó-LIFE project. Erdtud. Közl. 2018, 8, 17–23. [Google Scholar] [CrossRef]
- Čufar, K.; Grabner, M.; Morgós, A.; Martínez del Castillo, E.; Merela, M.; De Luis, M. Common climatic signals affecting oak tree-ring growth in SE Central Europe. Trees 2014, 28, 1267–1277. [Google Scholar] [CrossRef]
- Garamszegi, B.; Nagy-Khell, M.; Farkas, M.; Nagy, L. Impact of weather conditions on the interannual growth characteristics of alder and oak stand with improved groundwater-management. Erdtud. Közl. 2018, 8, 9–16. [Google Scholar] [CrossRef]
- Csillag, G.; Fodor, L.; Sebe, K.; Müller, P.; Ruszkiczay-Rüdiger, Z.; Thamóné, B.E.; Bada, G. A szélerózió szerepe a Dunántúl negyedidőszaki felszínfejlődésében [The role of wind erosion in the surface development of Transdanubia during the Quarternary]. Földt. Közlöny 2010, 140, 463–482. [Google Scholar]
- Kovács, A.; Szőcs, T.; Tóth, G.; Marton, A.; Kun, É.; Kerékgyártó, T. A talajvíz klímaérzékenységének modellezése a NATéR projekt keretei között; Research Report; MFGI: Budapest, Hungary, 2015. [Google Scholar]
- Gondár, K.; Király, Z.; Könczöl, N.; Molnár, M.; Tóth, G.; Ács, T.; Kozma, Z.; Muzelák, B.; Simonffy, Z.; Szalay, M. A felszín alatti víztől függő ökoszisztémák ökológiai vízigényének meghatározása. In Background material no. 6-4-4, Second River Basin Management Plan of Hungary; General Directorate of Water Management: Budapest, Hungary, 2015. [Google Scholar]
- Szalai, S.; Auer, I.; Hiebl, J.; Milkovich, J.; Radim, T.; Stepanek, P.; Zahradnicek, P.; Bihari, Z.; Lakatos, M.; Szentimrey, T.; et al. Climate of the Greater Carpathian Region. Final. Tech. Rep. 2013. Available online: www.carpatclim-eu.org (accessed on 9 September 2022).
- Borhidi, A. Dynamical changes of free floating water-plant communities of different N sources in the Nature Reservation Area of Baláta-Pond. Acta Biol. 1968, 19, 523. [Google Scholar]
- Borhidi, A.; Komlódi, M. Zusammenhang der Niederschlags- und Wasserstandsfluktuation auf dem Naturschutzgebiet des Baláta-Teiches. Időjárás 1995, 63, 225–229. [Google Scholar]
- Sümegi, P.; Náfrádi, K.; Jakab, G.; Persaits, G.; Törőcsik, T. The environmental history of Lake Baláta. A Kaposvári Rippl-Rónai Múzeum Közleményei 2014, 3, 5–28. [Google Scholar] [CrossRef]
- Decree No. 19/2008 a Baláta-Tó Természetvédelmi Terület Bővítéséről és Erdőrezervátummá Nyilvánításáról; Ministry of Environment and Water: KvVM, Hungary, 2008.
- Gribovszki, Z.; Cseke, C.; Csáki, P.; Horváth, L.; Kalicz, P.; Nagy, L.; Szőke, E.; Zagyvai-Kiss, K.A. Evaluation of riparian forest water supply with groundwater monitoring and numerical modelling. In Proceedings of the EGU General Assembly 2020, Online, 4–8 May 2020. EGU2020–13934. [Google Scholar]
- ESRI. ArcMap 10.8 Basemap Layer. Available online: https://desktop.arcgis.com/en/arcmap/latest/get-started/introduction/whats-new-in-arcgis.htm (accessed on 9 September 2022).
- Lechner Nonprofit Kft. Digitális légifelvétel archívum. 2022. Available online: https://www.fentrol.hu (accessed on 9 September 2022).
- Stokes, M.A.; Smiley, T.L. An Introduction to Tree-Ring Dating; The University of Chicago Press: Chicago, IL, USA, 1968. [Google Scholar]
- Orvis, K.H.; Grissino-Mayer, H.D. Standardizing the reporting of abrasive papers used to surface tree-ring samples. Tree-Ring Res. 2002, 58, 47–50. [Google Scholar]
- Rinn, F. TSAP Reference Manual; Rinntech: Heidelberg, Germany, 2005. [Google Scholar]
- Regent Instruments. WinDENDRO for Tree-ring Analysis; Regent Instruments: Quebec, QC, Canada, 2017. [Google Scholar]
- Holmes, R.L. Computer-assisted quality control in tree-ring dating and measurement. Tree Ring Bull. 1983, 43, 69–75. [Google Scholar]
- Grissino-Mayer, H.D. Evaluating crossdating accuracy: A manual and tutorial for the computer program COFECHA. Tree-Ring Res. 2001, 57, 205–221. [Google Scholar]
- Cook, E.R. A Time Series Analysis Approach to Tree-ring Standardization. Ph.D. Thesis, The University of Arizona, Tucson, AZ, USA, 1985. [Google Scholar]
- Cook, E.R.; Krusic, P.J. ARSTAN4.1b_XP. 2006. Available online: http://www.ldeo.columbia.edu (accessed on 9 September 2022).
- van der Werf, G.W.; Sass-Klaassen, U.G.; Mohren, G.M.J. The impact of the 2003 summer drought on the intra-annual growth pattern of beech (Fagus sylvatica L.) and oak (Quercus robur L.) on a dry site in the Netherlands. Dendrochronologia 2007, 25, 103–112. [Google Scholar] [CrossRef]
- Kern, Z.; Patkó, M.; Kázmér, M.; Fekete, J.; Kele, S.; Pályi, Z. Multiple tree-ring proxies (earlywood width, latewood width and δ13C) from pedunculate oak (Quercus robur L.) in Hungary. Quat. Int. 2013, 239, 257–267. [Google Scholar] [CrossRef]
- Mosteller, F.; Tukey, J.W. Data Analysis and Regression; Addison-Wesley: Reading, MA, USA, 1977. [Google Scholar]
- Wigley, T.M.L.; Briffa, K.R.; Jones, P.D. On the average value of correlated time series, with applications in dendroclimatology and hydrometeorology. J. Clim. Appl. Meteorol. 1984, 23, 201–213. [Google Scholar] [CrossRef]
- Buras, A. A comment on the expressed population signal. Dendrochronologia 2017, 44, 130–132. [Google Scholar] [CrossRef]
- Harris, I.; Jones, P.D.; Osborn, T.J.; Lister, D.H. Updated high-resolution grids of monthly climatic observations—the CRU TS3. 10 Dataset. Int. J. Climatol. 2014, 34, 623–642. [Google Scholar] [CrossRef]
- Schneider, U.; Becker, A.; Finger, P.; Meyer-Christoffer, A.; Ziese, M. GPCC Full Data Monthly Product Version 2018 at 0.5°: Monthly Land-Surface Precipitation from Rain-Gauges Built on GTS-Based and Historical Data. Global Precipitation Climatology Centre. 2018. Available online: http://gpcc.dwd.de/ (accessed on 9 September 2022).
- Vicente-Serrano, S.M.; Beguería, S.; López-Moreno, J.I. A multiscalar drought index sensitive to global warming: The standardized precipitation evapotranspiration index. J. Clim. 2010, 23, 1696–1718. [Google Scholar] [CrossRef]
- Beguería, S.; Vicente-Serrano, S.M.; Reig, F.; Latorre, B. Standardized precipitation evapotranspiration index (SPEI) revisited: Parameter fitting, evapotranspiration models, tools, datasets and drought monitoring. Int. J. Climatol. 2014, 34, 3001–3023. [Google Scholar] [CrossRef]
- R Development Core Team. A Language and Environment for Statistical Computing, R Foundation for Statistical Computing; R Development Core Team: Vienna, Austria, 2017. [Google Scholar]
- Thornthwaite, C.W. An approach toward a rational classification of climate. Geogr. Rev. 1948, 38, 55–94. [Google Scholar] [CrossRef]
- Garamszegi, B.; Kázmér, M.; Kolozs, L.; Kern, Z. Changing climatic sensitivity and effects of drought frequency on the radial growth of Fagus sylvatica at the xeric frontiers of Central Europe. Idojaras 2020, 124, 227–251. [Google Scholar] [CrossRef]
- Fritts, H.C. Tree Rings and Climate; Academic Press: London, UK, 1976. [Google Scholar]
- Móricz, N.; Illés, G.; Mészáros, I.; Garamszegi, B.; Berki, I.; Bakacsi, Z.; Kámpel, J.; Szabó, O.; Rasztovits, E.; Cseke, K.; et al. Different drought sensitivity traits of young sessile oak (Quercus petraea (Matt.) Liebl.) and Turkey oak (Quercus cerris L.) stands along a precipitation gradient in Hungary. For. Ecol. Manage. 2021, 492, 119165. [Google Scholar] [CrossRef]
- Welch, B.L. The generalization of ‘Student’s’ problem when several different population variances are involved. Biometrika 1947, 34, 28–35. [Google Scholar] [CrossRef] [PubMed]
- Matyasovszky, I. Statisztikus Klimatológia: Idősorok Elemzése; ELTE Eötvös Kiadó: Budapest, Hungary, 2002. [Google Scholar]
- Shapiro, S.S.; Wilk, M.B. An analysis of variance test for normality (complete samples). Biometrika 1965, 52, 591–611. [Google Scholar] [CrossRef]
- Árvai, M.; Morgós, A.; Kern, Z. Growth-climate relations and the enhancement of drought signals in pedunculate oak (Quercus robur L.) tree-ring chronology in Eastern Hungary. iForest 2018, 11, 267. [Google Scholar] [CrossRef]
- Čater, M.; Levanič, T. Physiological and growth response of Quercus robur in Slovenia. Dendrobiology 2015, 74, 3–12. [Google Scholar] [CrossRef]
- Fischer, E.M.; Seneviratne, S.I.; Vidale, P.L.; Lüthi, D.; Schär, C. Soil moisture–atmosphere interactions during the 2003 European summer heat wave. J. Clim. 2007, 20, 5081–5099. [Google Scholar] [CrossRef]
- Gutiérrez, J.M.; Jones, R.G.; Narisma, G.T.; Alves, L.M.; Amjad, M.; Gorodetskaya, I.V.; Grose, M.; Klutse, N.A.B.; Krakovska, S.; Li, J.; et al. Atlas. In Climate Change 2021: The Physical Science Basis. Contribution of Working Group I to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change; Masson-Delmotte, V., Zhai, P., Pirani, A., Connors, S.L., Péan, C., Berger, S., Caud, N., Chen, Y., Goldfarb, L., Gomis, M.I., et al., Eds.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2021; pp. 1927–2058. [Google Scholar]
- Pongrácz, R.; Bartholy, J.; Kis, A. Estimation of future precipitation conditions for Hungary with special focus on dry periods. Időjárás 2014, 118, 305–321. [Google Scholar]
- Topál, D.; Hatvani, I.G.; Kern, Z. Refining projected multidecadal hydroclimate uncertainty in East-Central Europe using CMIP5 and single-model large ensemble simulations. Theor. Appl. Clim. 2020, 142, 1147–1167. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Garamszegi, B.; Nagy, L.; Ács, T.; Morgós, A.; Árvai, M.; Pinke, Z.; Kern, Z. Coupled Hydro-Climatic Signals in the Radial Growth of Oaks Benefitting from Groundwater Availability. Water 2022, 14, 3328. https://doi.org/10.3390/w14203328
Garamszegi B, Nagy L, Ács T, Morgós A, Árvai M, Pinke Z, Kern Z. Coupled Hydro-Climatic Signals in the Radial Growth of Oaks Benefitting from Groundwater Availability. Water. 2022; 14(20):3328. https://doi.org/10.3390/w14203328
Chicago/Turabian StyleGaramszegi, Balázs, László Nagy, Tamás Ács, András Morgós, Mátyás Árvai, Zsolt Pinke, and Zoltán Kern. 2022. "Coupled Hydro-Climatic Signals in the Radial Growth of Oaks Benefitting from Groundwater Availability" Water 14, no. 20: 3328. https://doi.org/10.3390/w14203328
APA StyleGaramszegi, B., Nagy, L., Ács, T., Morgós, A., Árvai, M., Pinke, Z., & Kern, Z. (2022). Coupled Hydro-Climatic Signals in the Radial Growth of Oaks Benefitting from Groundwater Availability. Water, 14(20), 3328. https://doi.org/10.3390/w14203328






