Real-Time Leak Diagnosis in Water Distribution Systems Based on a Bank of Observers and a Genetic Algorithm
Abstract
:1. Introduction
2. Preliminaries
2.1. Pipeline Dynamical Model
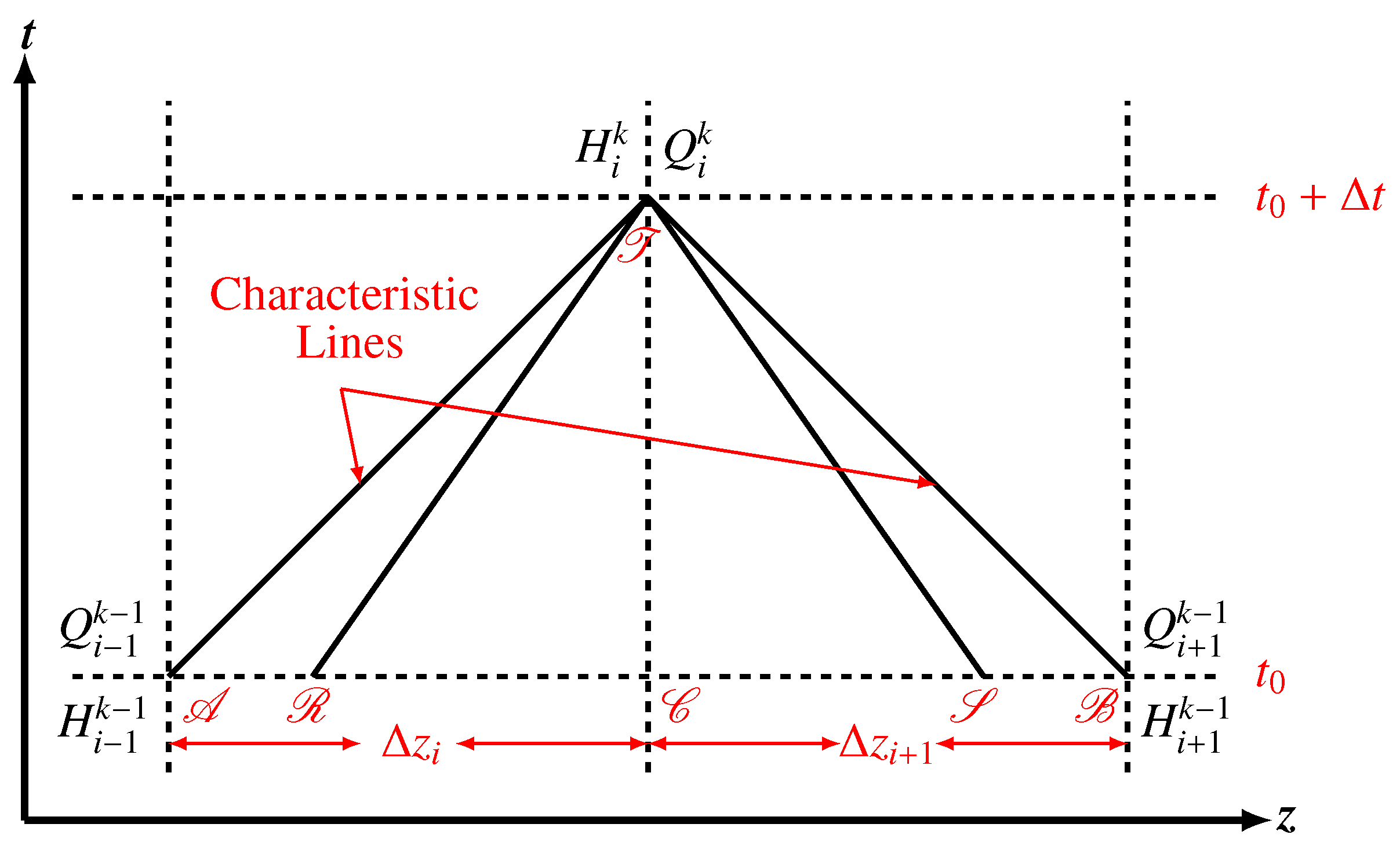
2.2. Solution of Governing Equations through the Method of Characteristics (MOC)
2.2.1. Convergence and Stability Conditions
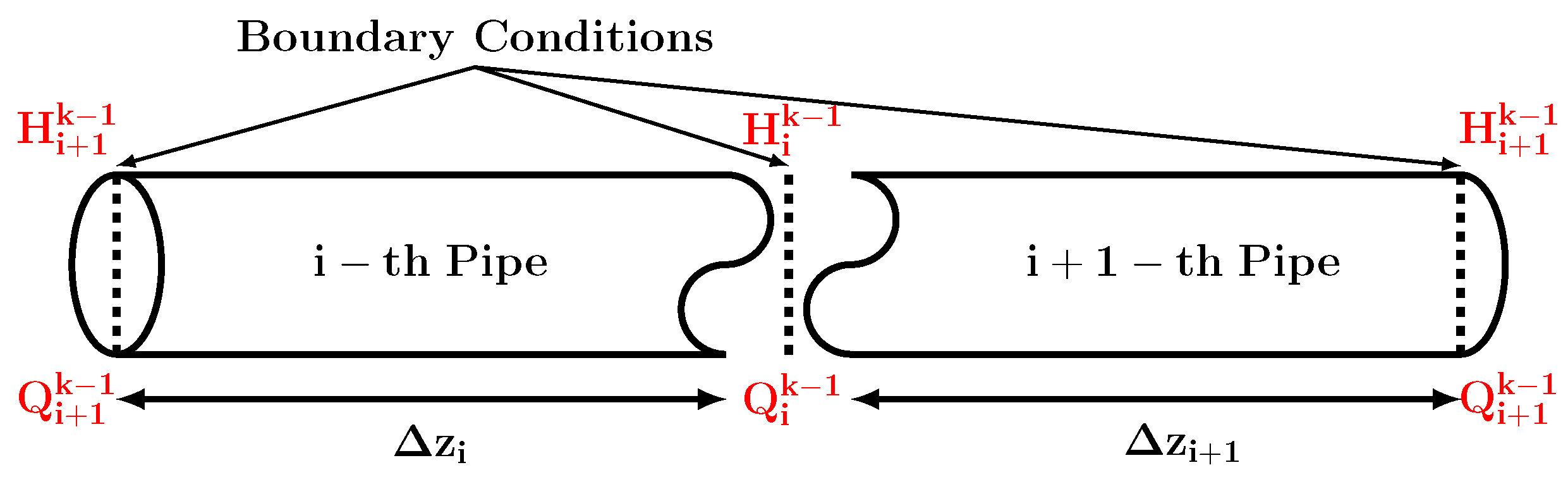
2.2.2. Special Boundary Conditions
2.3. Discrete Time Extended Kalman Filter
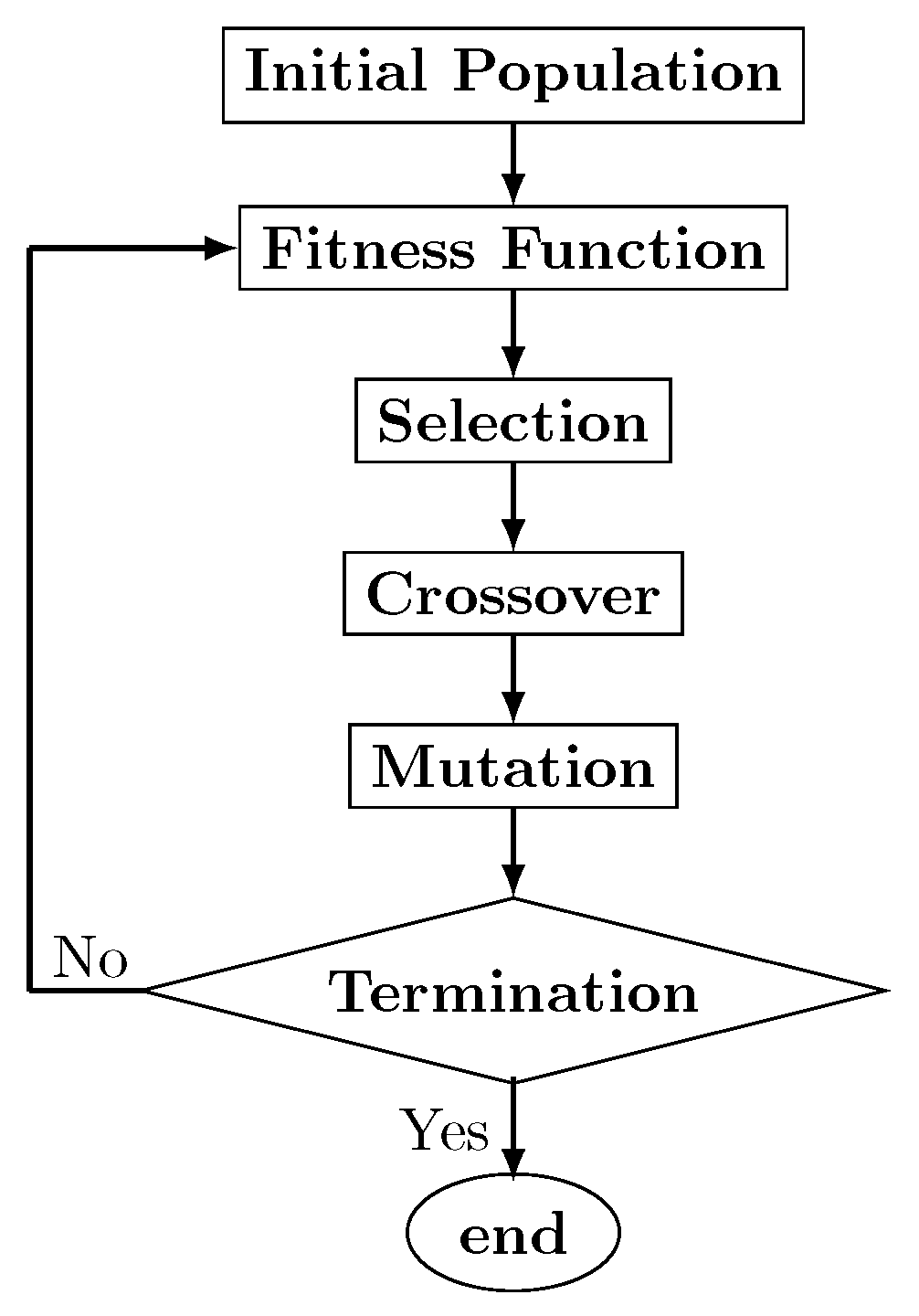
2.4. Genetic Algorithms
3. LDI Scheme in a Branched Pipeline WDN
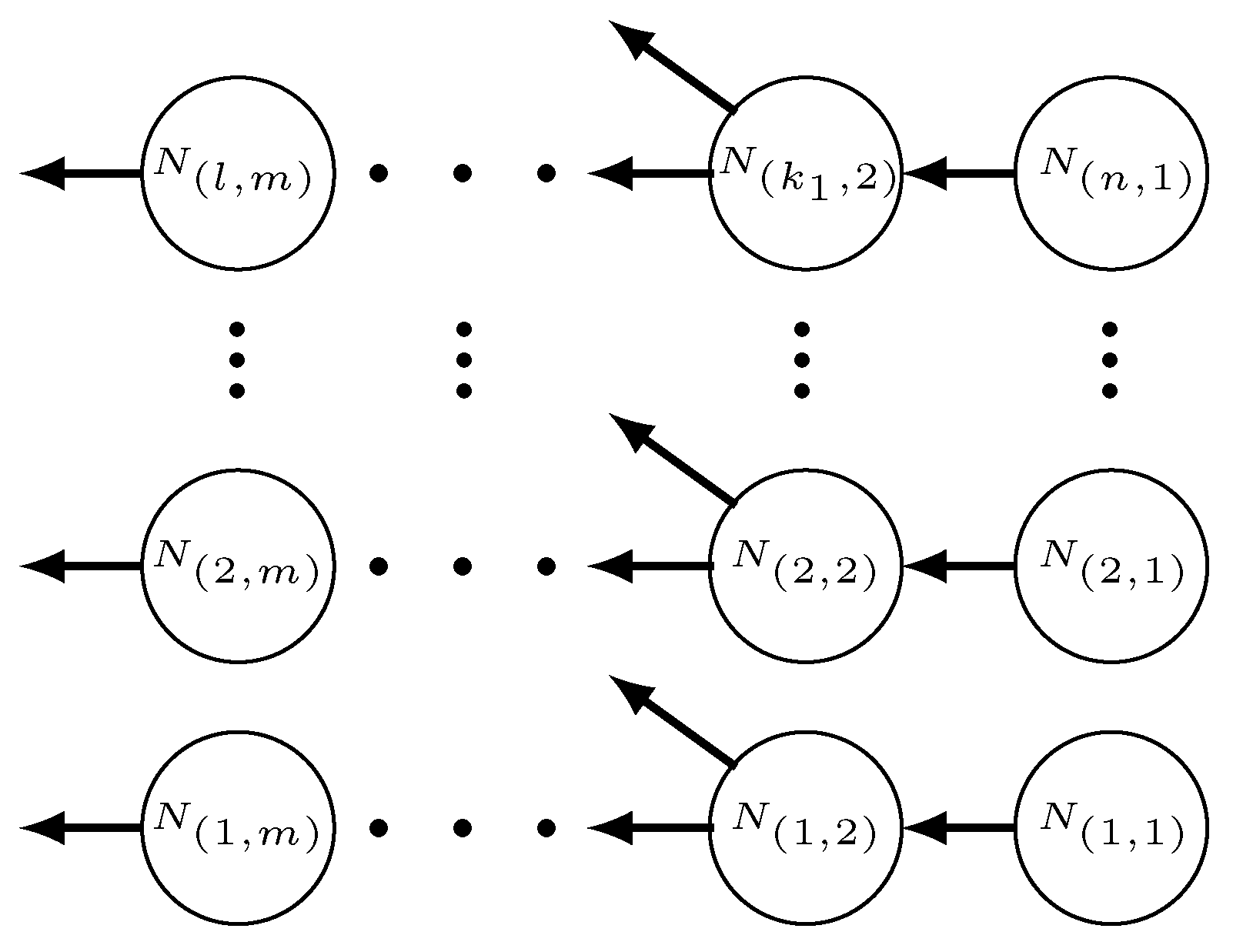
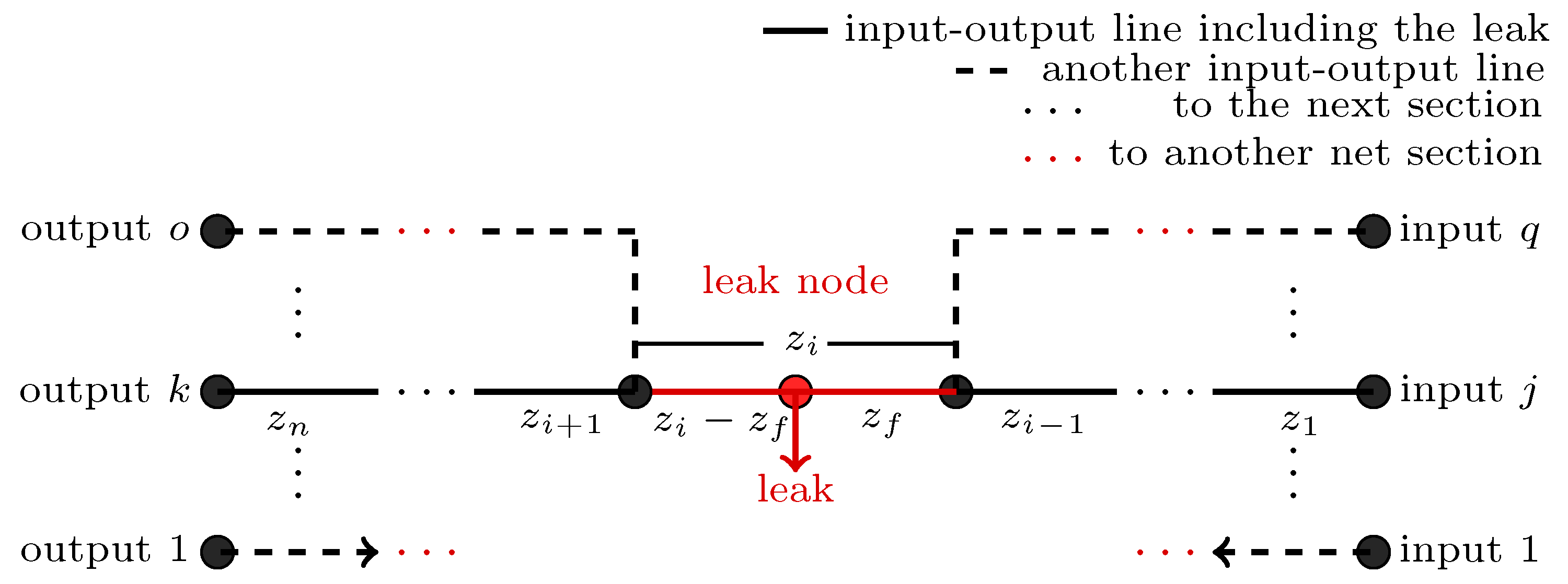
3.1. General Branched Pipeline LDI System Design Principles
3.2. Leak Detection and Isolation Process
3.2.1. Leak Detection
3.2.2. Branch Identification
3.2.3. Leak Isolation
3.2.4. LDI Pseudo Code
| Algorithm 1 LDI Scheme |
|
4. Tuxtla Gutiérrez Pilot Plant: A Case Study
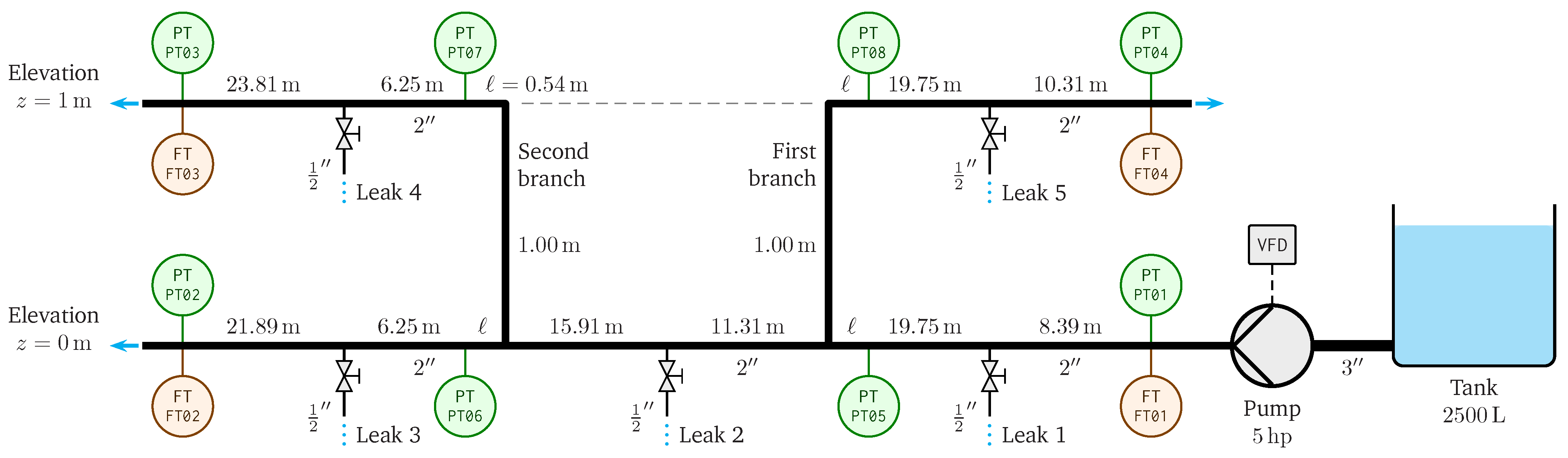
4.1. Pilot Pipeline Description
4.2. Pilot Plant Modeling
4.3. Experimental Results
4.4. Some Final Remarks
- (1)
- The algorithm can hardly identify the parameters of a leak with a rate greater than 10 % of the nominal flow since this event can be considered as a catastrophic failure instead of a simple fault, this is because the assumptions to obtain a modeling of the system could not be fulfilled correctly. Moreover the smallest leak that can be detected depends directly on the accuracy of the flow rate sensors (noise variance).
- (2)
- To obtain moving average values of the input and output measurements, they are filtered with the equation [31]:where is the smoothed value for the signal at time k, N is the number of neighboring data taken on either side of , and is the span dimension.
- (3)
- The initial conditions of the observer, are fixed as follows: , , , , and are equal to the mean values of the measured outputs in a steady-state leak-free condition.
- (4)
- (5)
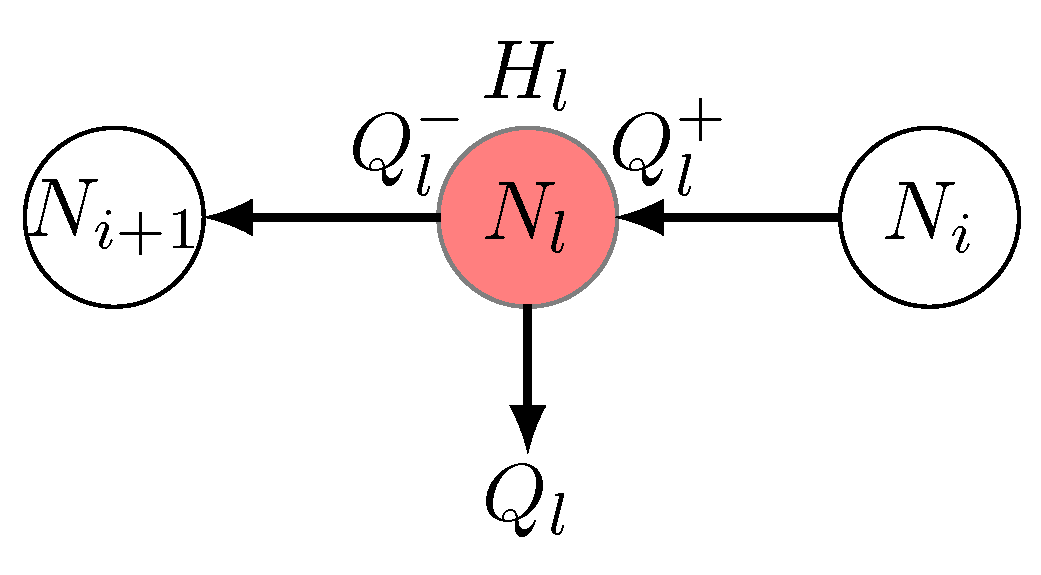
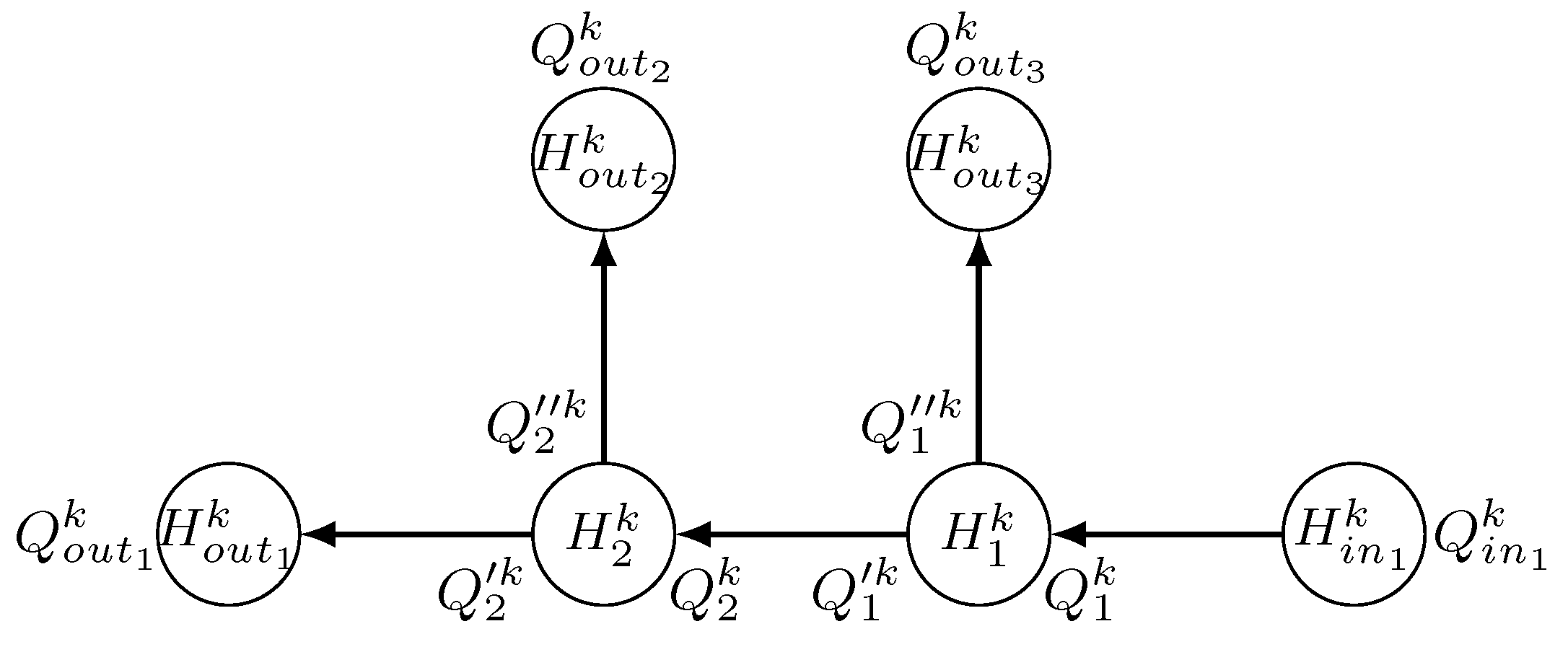
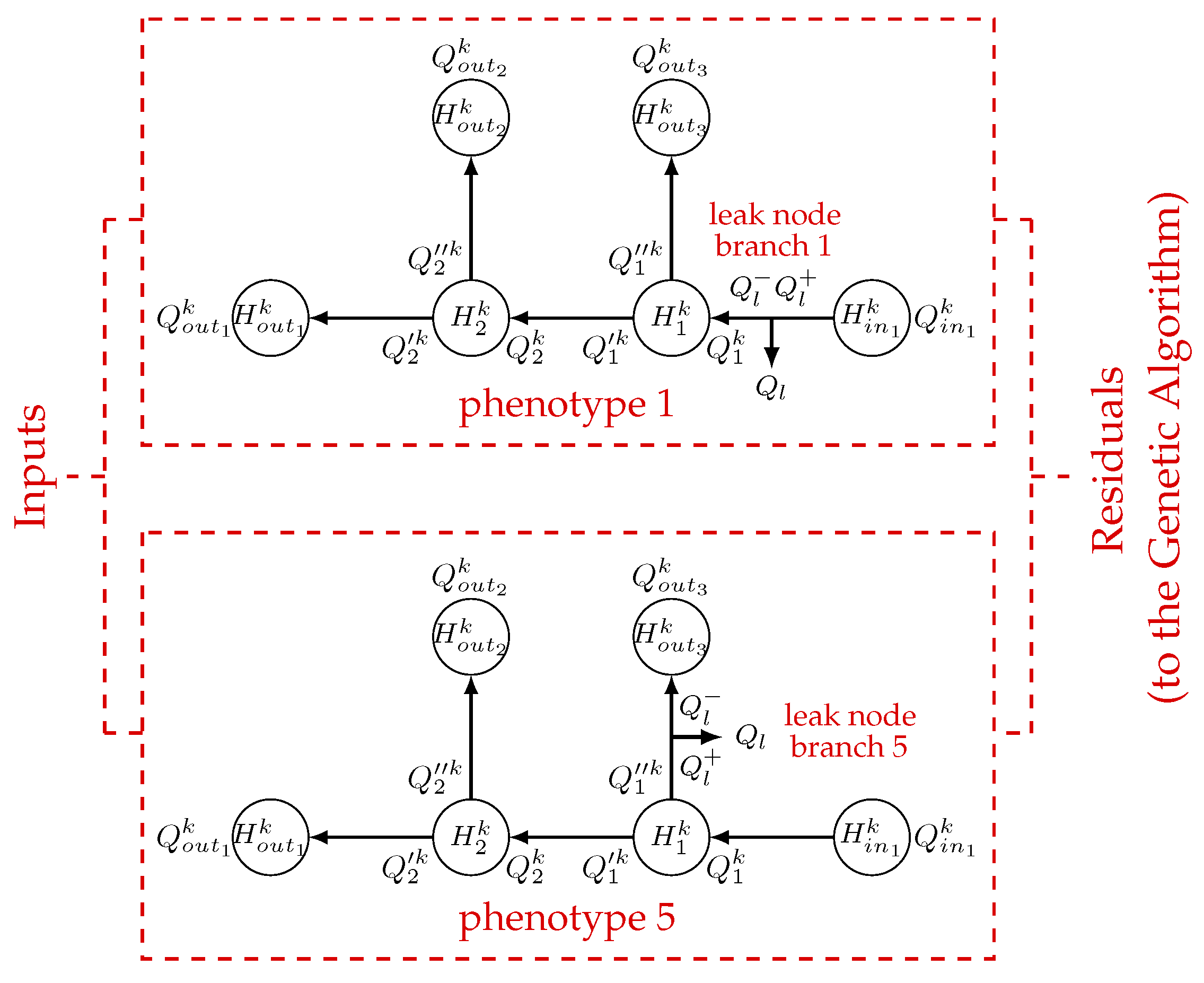
- On the other hand, the inner flow-rate initial conditions. , , , , , , are computed using the law of conservation of mass:where, as before, . Moreover, due to the same law and in steady-state conditions, the next relationships must be satisfied: , , and (see Figure 10).
- (6)
5. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- OECD. Water Governance in Cities; OECD Studies on Water; OECD Publishing: Paris, France, 2016; p. 140. [Google Scholar] [CrossRef]
- Santos-Ruiz, I.; López-Estrada, F.R.; Puig, V.; Valencia-Palomo, G.; Hernández, H.R. Pressure Sensor Placement for Leak Localization in Water Distribution Networks Using Information Theory. Sensors 2022, 22, 443. [Google Scholar] [CrossRef] [PubMed]
- Morales-González, I.O.; Santos-Ruiz, I.; López-Estrada, F.R.; Puig, V. Pressure Sensor Placement for Leak Localization Using Simulated Annealing with Hyperparameter Optimization. In Proceedings of the 2021 5th International Conference on Control and Fault-Tolerant Systems (SysTol), Saint-Raphaël, France, 29–30 September 2021; pp. 205–210. [Google Scholar] [CrossRef]
- Perez, R.; Sanz, G.; Puig, V.; Quevedo, J.; Cuguero Escofet, M.A.; Nejjari, F.; Meseguer, J.; Cembrano, G.; Mirats Tur, J.M.; Sarrate, R. Leak Localization in Water Networks: A Model-Based Methodology Using Pressure Sensors Applied to a Real Network in Barcelona [Applications of Control]. IEEE Control Syst. Mag. 2014, 34, 24–36. [Google Scholar] [CrossRef] [Green Version]
- Levinas, D.; Perelman, G.; Ostfeld, A. Water Leak Localization Using High-Resolution Pressure Sensors. Water 2021, 13, 591. [Google Scholar] [CrossRef]
- Sun, C.; Parellada, B.; Puig, V.; Cembrano, G. Leak Localization in Water Distribution Networks Using Pressure and Data-Driven Classifier Approach. Water 2020, 12, 54. [Google Scholar] [CrossRef] [Green Version]
- Delgado-Aguiñaga, J.; Besançon, G. EKF-based leak diagnosis schemes for pipeline networks. IFAC-PapersOnLine 2018, 51, 723–729. [Google Scholar] [CrossRef]
- Torres, L.; Verde, C.; Molina, L. Leak diagnosis for pipelines with multiple branches based on model similarity. J. Process Control 2021, 99, 41–53. [Google Scholar] [CrossRef]
- Delgado-Aguiñaga, J.; Santos-Ruiz, I.; Besançon, G.; López-Estrada, F.; Puig, V. EKF-based observers for multi-leak diagnosis in branched pipeline systems. Mech. Syst. Signal Process. 2022, 178, 109198. [Google Scholar] [CrossRef]
- Pan, B.; Capponi, C.; Meniconi, S.; Brunone, B.; Duan, H.F. Efficient leak detection in single and branched polymeric pipeline systems by transient wave analysis. Mech. Syst. Signal Process. 2022, 162, 108084. [Google Scholar] [CrossRef]
- Liao, Z.; Yan, H.; Tang, Z.; Chu, X.; Tao, T. Deep learning identifies leak in water pipeline system using transient frequency response. Process Saf. Environ. Prot. 2021, 155, 355–365. [Google Scholar] [CrossRef]
- Chaudhry, M.H. Transient-flow equations. In Applied Hydraulic Transients; Springer: Berlin/Heidelberg, Germany, 2014; pp. 35–64. [Google Scholar]
- Streeter, V.L.; Lai, C. Water-hammer analysis including fluid friction. Trans. Am. Soc. Civ. Eng. 1963, 128, 1491–1524. [Google Scholar] [CrossRef]
- Srbislava, G.; Ivana, A.; Petara, K.; Markob, J.; Nikolab, B.; Vojislavc, G. A review of explicit approximations of Colebrook’s equation. FME Trans. 2011, 39, 67–71. [Google Scholar]
- Abdulameer, L.S.; Dzhumagulova, N.; Algretawee, H.; Zhuravleva, L.; Alshammari, M.H. Comparison between Hazen-Williams and Darcy-Weisbach Equations to Calculate Head Loss through Conveyancing Treated Wastewater in Kerbala City, Iraq. East.-Eur. J. Enterp. Technol. 2022, 1, 115. [Google Scholar] [CrossRef]
- Dulhoste, J.F.; Besançon, G.; Ortiz, F.L.T.; Begovich, O.; Navarro, A. About friction modeling for observer-based leak estimation in pipelines. In Proceedings of the 2011 50th IEEE Conference on Decision and Control and European Control Conference, Orlando, FL, USA, 12–15 December 2011; pp. 4413–4418. [Google Scholar]
- Carlsson, J. Water Hammer Phenomenon Analysis Using the Method of Characteristics and Direct Measurements Using a “Stripped” Electromagnetic Flow Meter. Master’s Thesis, Royal Institute of Technology, Stockholm, Sweden, 2016. [Google Scholar]
- O’Brien, G.G.; Hyman, M.A.; Kaplan, S. A Study of the Numerical Solution of Partial Differential Equations. J. Math. Phys. 1950, 29, 223–251. [Google Scholar] [CrossRef]
- Simon, D. Optimal State Estimation: Kalman, H Infinity, and Nonlinear Approaches; John Wiley & Sons: Hoboken, NJ, USA, 2006. [Google Scholar]
- Fujii, K.; The ACDA-Sim-J Group. Extended Kalman Filter. Reference Manual. 2013, pp. 14–22. Available online: https://www-jlc.kek.jp/2004sep/subg/offl/kaltest/doc/ReferenceManual.pdf (accessed on 3 May 2022).
- Katoch, S.; Chauhan, S.S.; Kumar, V. A review on genetic algorithm: Past, present, and future. Multimed. Tools Appl. 2021, 80, 8091–8126. [Google Scholar] [CrossRef] [PubMed]
- Kumar, M.; Husain, M.; Upreti, N.; Gupta, D. Genetic Algorithm: Review and Application (1 December 2010). Available online: https://ssrn.com/abstract=3529843 (accessed on 16 April 2022).
- Mathew, T.V. Genetic Algorithm. Report Submitted at IIT Bombay 2012. Indian Institute of Technology, Bombay, Mumbai. Available online: http://datajobstest.com/data-science-repo/Genetic-Algorithm-Guide-[Tom-Mathew].pdf (accessed on 16 April 2022).
- Isermann, R. Fault-Diagnosis Systems: An Introduction from Fault Detection to Fault Tolerance; Springer: Berlin/Heidelberg, Germany, 2005. [Google Scholar]
- Gertler, J.J. Fault Detection and Diagnosis in Engineering Systems; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]
- Boaz, L.; Kaijage, S.; Sinde, R. An overview of pipeline leak detection and location systems. In Proceedings of the 2nd Pan African International Conference on Science, Computing and Telecommunications (PACT 2014), Arusha, Tanzania, 14–18 July 2014; pp. 133–137. [Google Scholar]
- Soldevila, A.; Boracchi, G.; Roveri, M.; Tornil-Sin, S.; Puig, V. Leak detection and localization in water distribution networks by combining expert knowledge and data-driven models. Neural Comput. Appl. 2022, 34, 4759–4779. [Google Scholar] [CrossRef]
- Navarro, A.; Delgado-Aguiñaga, J.A.; Sánchez-Torres, J.D.; Begovich, O.; Besançon, G. Evolutionary Observer Ensemble for Leak Diagnosis in Water Pipelines. Processes 2019, 7, 913. [Google Scholar] [CrossRef] [Green Version]
- Lindstrom, L.; Gracy, S.; Magnusson, S.; Sandberg, H. Leakage Localization in Water Distribution Networks: A Model-Based Approach. arXiv 2022, arXiv:2204.00050. [Google Scholar]
- Santos-Ruiz, I.; Bermúdez, J.; López-Estrada, F.; Puig, V.; Torres, L.; Delgado-Aguiñaga, J. Online leak diagnosis in pipelines using an EKF-based and steady-state mixed approach. Control Eng. Pract. 2018, 81, 55–64. [Google Scholar] [CrossRef]
- Delgado-Aguiñaga, J.; Begovich, O. Water leak diagnosis in pressurized pipelines: A real case study. In Modeling and Monitoring of Pipelines and Networks; Verde, C., Torres, L., Eds.; Springer International Publishing: Berlin/Heidelberg, Germany, 2017; pp. 235–262. [Google Scholar]





| Parameter | Symbol | Value | Dimension |
|---|---|---|---|
| Inner diameter | |||
| Wave speed | b | ||
| Relative roughness | − | ||
| Fluid kinematic viscosity | |||
| Fluid density | |||
| Acceleration due to gravity | g |
| Case | GA [m] | EKF [m] |
|---|---|---|
| Experiment 1 | ||
| Experiment 2 | ||
| Experiment 3 |
| Branch Number | Symbol | Value |
|---|---|---|
| 1 | ||
| 2 | ||
| 3 | ||
| 4 | ||
| 5 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Navarro-Díaz, A.; Delgado-Aguiñaga, J.A.; Santos-Ruiz, I.; Puig, V. Real-Time Leak Diagnosis in Water Distribution Systems Based on a Bank of Observers and a Genetic Algorithm. Water 2022, 14, 3289. https://doi.org/10.3390/w14203289
Navarro-Díaz A, Delgado-Aguiñaga JA, Santos-Ruiz I, Puig V. Real-Time Leak Diagnosis in Water Distribution Systems Based on a Bank of Observers and a Genetic Algorithm. Water. 2022; 14(20):3289. https://doi.org/10.3390/w14203289
Chicago/Turabian StyleNavarro-Díaz, Adrián, Jorge Alejandro Delgado-Aguiñaga, Ildeberto Santos-Ruiz, and Vicenç Puig. 2022. "Real-Time Leak Diagnosis in Water Distribution Systems Based on a Bank of Observers and a Genetic Algorithm" Water 14, no. 20: 3289. https://doi.org/10.3390/w14203289






