Development of a Runoff Pollution Empirical Model and Pollution Machine Learning Models of the Paddy Field in the Taihu Lake Basin Based on the Paddy In Situ Observation Method
Abstract
:1. Introduction
2. Calculation of Runoff Pollution Loads of Paddy Fields Based on PIOM
2.1. Materials and Data
2.1.1. Experimental Site
2.1.2. Data Collection
2.2. Paddy In Situ Observation Method
2.2.1. Runoff Calculation of the Paddy Field
2.2.2. Evapotranspiration and Infiltration Estimation in Steadily Declining Water Level Period
2.2.3. Evapotranspiration Calculation
2.2.4. Infiltration Estimation and (ET + F) Estimation within the Rice Growing Period
2.2.5. Runoff Pollution Calculation
2.2.6. Statistical Analysis
2.3. Results and Discussion
2.3.1. Runoff Calculation of Paddy Fields
2.3.2. Runoff Pollution Loads of the Paddy Field
3. Development of a Runoff Pollution Empirical Model of the Paddy Field
3.1. Runoff Model of the Paddy Field
3.1.1. Infiltration
3.1.2. The Lowest Ridge Height of the Paddy Field
- (1)
- After sowing, the field should be kept moist in the bud stage without ponding and irrigation. Therefore, the ridge height in the bud stage was set to 50 mm. If the amount of rainfall was large, rainfall runoff occurred.
- (2)
- Irrigation overflow and rainfall runoff might occur during normal irrigation and rainfall in the seedling stage, tillering stage, jointing–booting stage and milk-ripening stage. The ridge height of the paddy field showed dynamic changes, especially before and after irrigation and rainfall. The ridge height of paddy fields decreased due to frequent irrigation and rainfall erosion. The irrigation amount was typically large. Due to extensive water management, irrigation overflow often occurred after irrigation [19]. Based on the analysis of paddy field experiments, the ridge height for irrigation overflow and rainfall runoff was set to 75 and 70 mm, respectively.
- (3)
- The lowest ridge height of the paddy field during artificial drainage in the jointing–booting stage was set to 0 mm.
- (4)
- The ridge height in the mature stage and yellow ripe stage was set to 0 mm.
3.1.3. Irrigation and Irrigation Overflow
- (1)
- IrrigationThe basic irrigation principles of direct seeding paddy fields are as follows: moist in the bud stage, thin water in the seedling stage, intermittent irrigation in the early tillering stage, enough seedlings to dry the field in the middle and late tillering stages, irrigation with little water in the jointing–booting stage and wet–dry alternation in the strong seed stage. The basic irrigation strategy obtained by statistical analysis is as follows.
- (i)
- The plow sole of the paddy field was formed by early muddy irrigation at 50 mm. There was no other irrigation in the bud stage.
- (ii)
- The irrigation volume was determined to be 80 mm according to the upper limit of 95% confidence of the average irrigation amount of paddy fields during the growth period.
- (iii)
- Irrigation was carried out when there was no water in the paddy field in the seedling stage and one day after no water in the paddy field in the jointing–booting stage. Artificial drainage and drying of fields was carried out in the tillering stage. Generally, the last irrigation was performed when entering the milk-ripening stage. If there was no water and no rain for consecutive days in a paddy field, appropriate supplementary irrigation was carried out. There was no irrigation during the yellow ripe stage.
- (iv)
- The irrigation period was generally 5 to 8 days and adjusted according to the variation in the surface water depth of the paddy field.
- (2)
- Irrigation overflow
3.1.4. Artificial Drainage
- (1)
- In the tillering stage of the drying field
- (2)
- With excess rainfall
3.1.5. Rainfall Runoff
3.2. Surface Water Concentration Model of the Paddy Field
3.3. Validation of RPEM
3.3.1. Runoff Verification of Paddy Fields
3.3.2. Runoff Pollution Load Verification of Paddy Fields
4. Development of Runoff Pollution Machine Learning Models of Paddy Fields
4.1. Machine Learning Algorithm
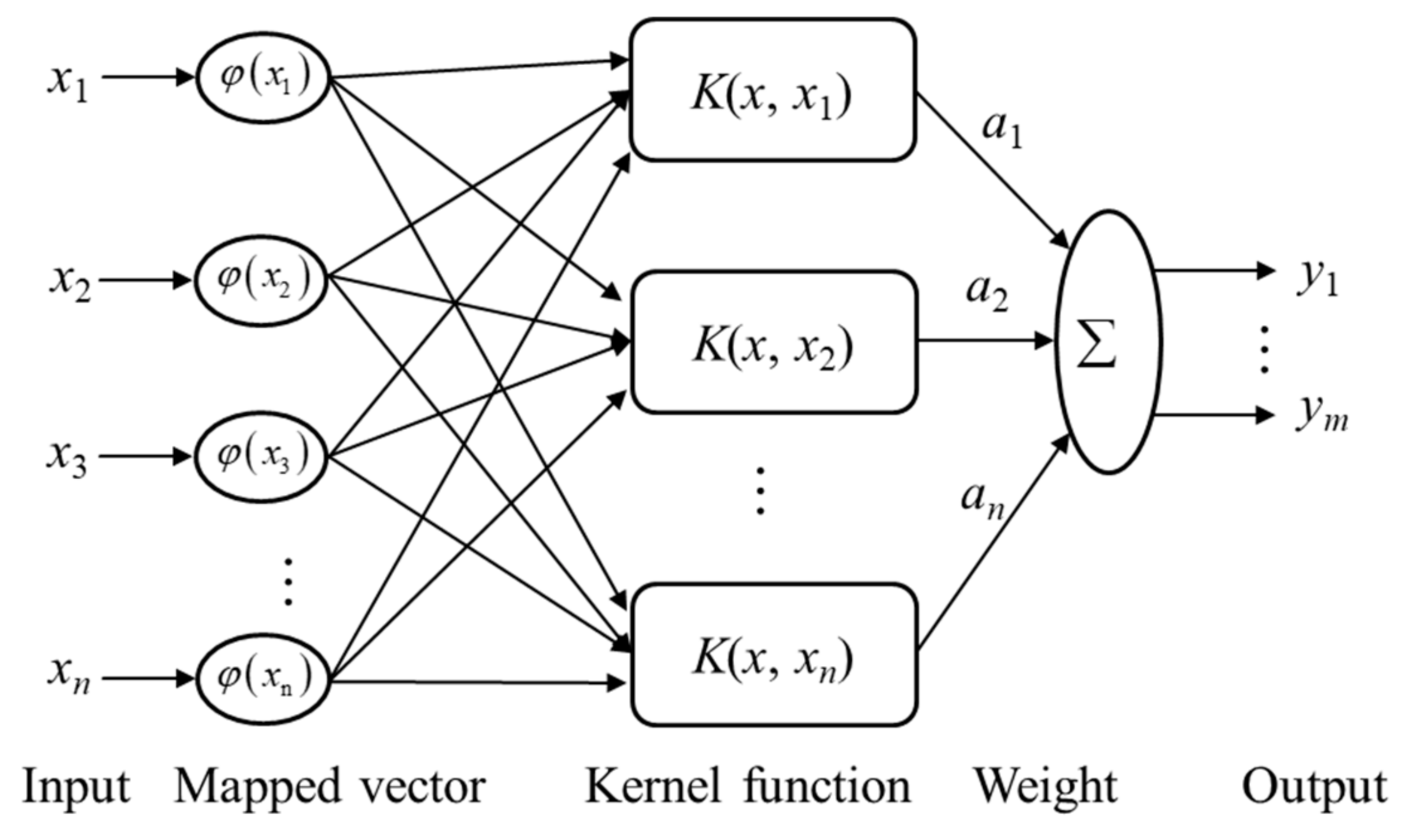
4.1.1. SVM
4.1.2. ANN
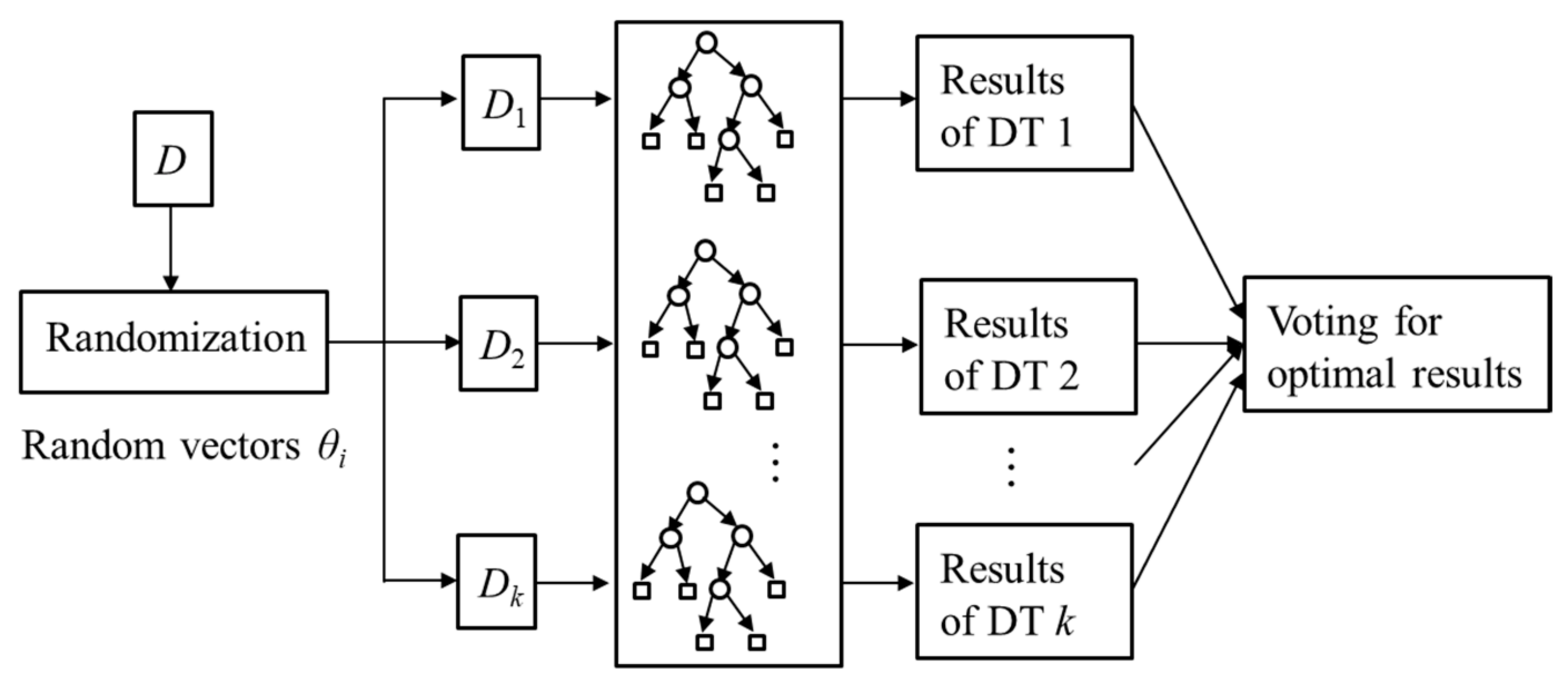
4.1.3. RF
4.2. Model Construction and Simulation
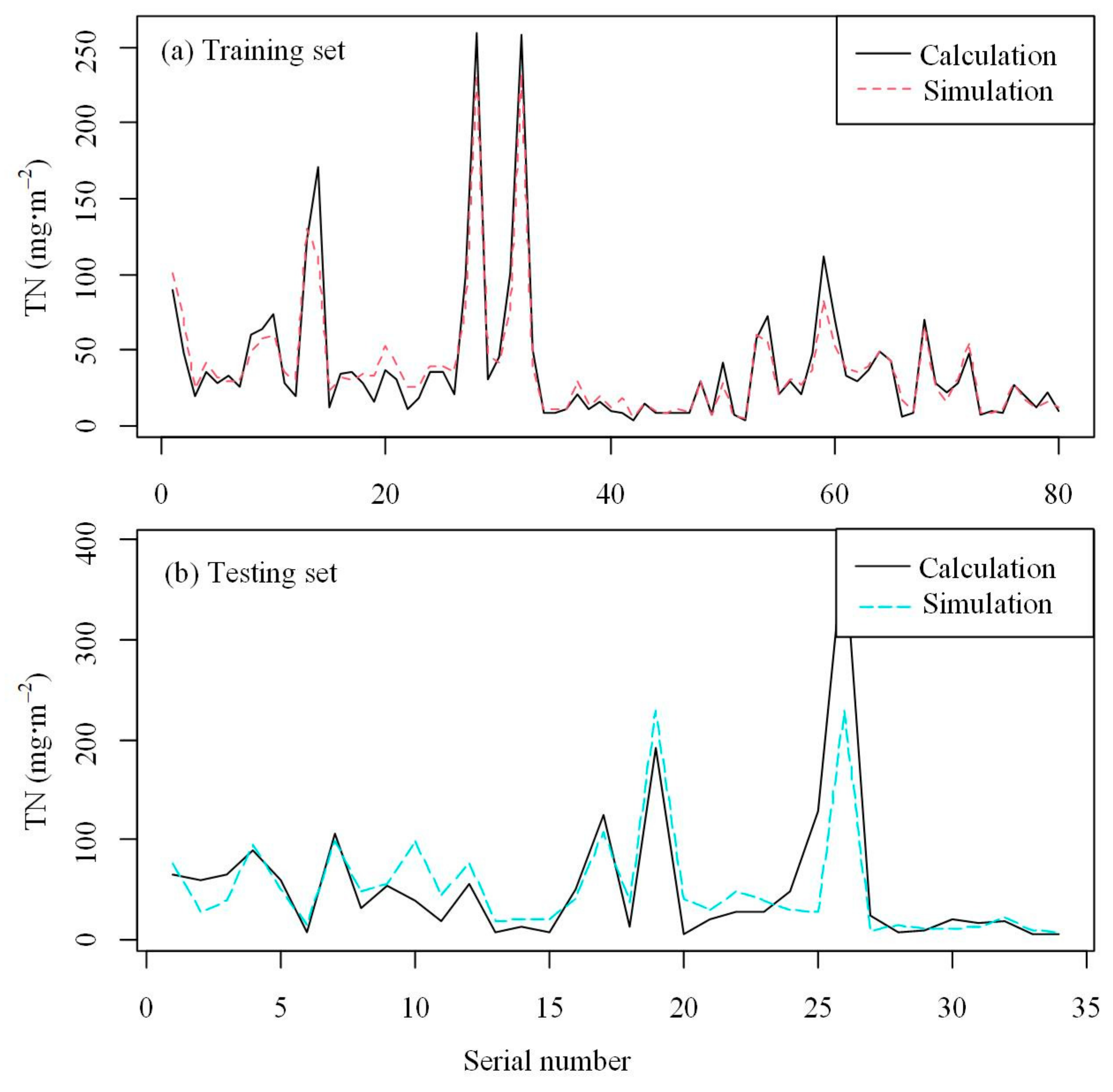
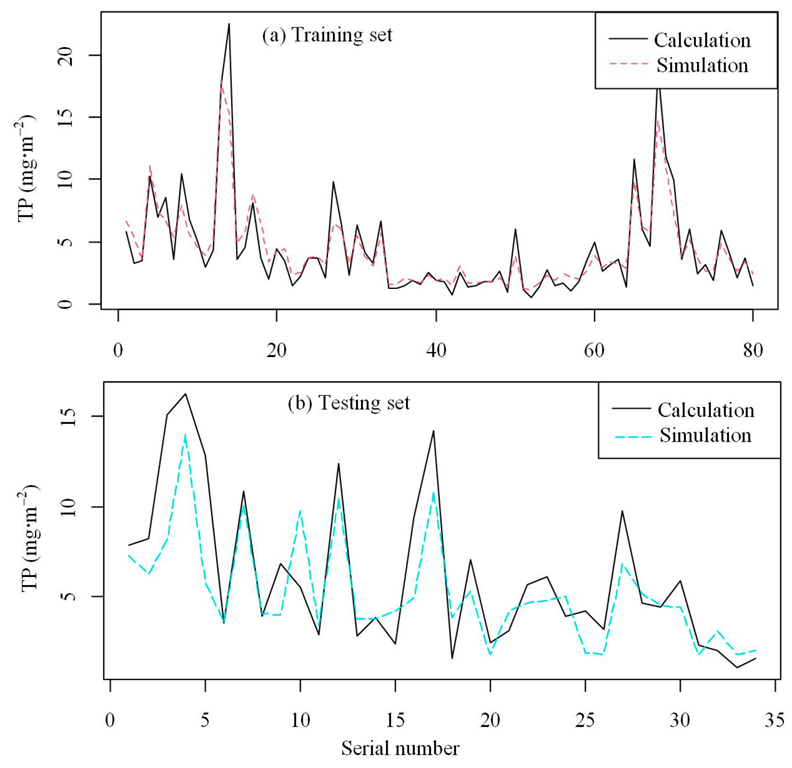
4.3. Results and Optimal Model Selection
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Vitousek, P.M.; Naylor, R.; Crews, T.; David, M.B.; Drinkwater, L.E.; Holland, E.; Johnes, P.J.; Katzenberger, J.; Martinelli, L.A.; Matson, P.A. Nutrient imbalances in agricultural development. Science 2009, 324, 1519–1520. [Google Scholar] [CrossRef] [PubMed]
- Ongley, E.D.; Xiaolan, Z.; Tao, Y. Current status of agricultural and rural non-point source Pollution assessment in China. Environ. Pollut. 2010, 158, 1159–1168. [Google Scholar] [CrossRef] [PubMed]
- Jiang, S.; Qiu, S.; Zhou, H.; Chen, M. Can FinTech development curb agricultural nonpoint source pollution? Int. J. Environ. Res. Public Health 2019, 16, 4340. [Google Scholar] [CrossRef] [Green Version]
- Xu, B.; Niu, Y.; Zhang, Y.; Chen, Z.; Zhang, L. China’s agricultural non-point source pollution and green growth: Interaction and spatial spillover. Environ. Sci. Pollut. Res. 2022, 29, 60278–60288. [Google Scholar] [CrossRef] [PubMed]
- Geng, R.; Sharpley, A.N. A novel spatial optimization model for achieve the trad-offs placement of best management practices for agricultural non-point source pollution control at multi-spatial scales. J. Clean Prod. 2019, 234, 1023–1032. [Google Scholar] [CrossRef]
- Peng, S.; He, Y.; Yang, S.; Xu, J. Effect of controlled irrigation and drainage on nitrogen leaching losses from paddy fields. Paddy Water Environ. 2015, 13, 1–10. [Google Scholar] [CrossRef]
- Liu, W.; Yang, H.; Ciais, P.; Stamm, C.; Schulin, R. Integrative crop-soil-management modeling to assess global phosphorus losses from major crop cultivations. Glob. Biogeochem. Cycles 2018, 32, 1074–1086. [Google Scholar] [CrossRef] [Green Version]
- Fu, J.; Jian, Y.; Wu, Y.; Chen, D.; Zhao, X.; Ma, Y.; Niu, S.; Wang, Y.; Zhang, F.; Xu, C.; et al. Nationwide estimates of nitrogen and phosphorus losses via runoff from rice paddies using data-constrained model simulations. J. Clean Prod. 2021, 279, 123642. [Google Scholar] [CrossRef]
- Qiao, J.; Yang, L.; Yan, T.; Xue, F.; Zhao, D. Nitrogen fertilizer reduction in rice production for two consecutive years in the Taihu Lake area. Agric. Ecosyst. Environ. 2012, 146, 103–112. [Google Scholar] [CrossRef]
- Reidsma, P.; Feng, S.; Loon, M.V.; Luo, X.; Kang, C.; Lubbers, M.; Kanellopoulos, A.; Wolf, J.; Ittersum, M.K.V.; Qu, F. Integrated assessment of agricultural land use policies on nutrient pollution and sustainable development in Taihu Basin, China. Environ. Sci. Policy 2012, 18, 66–76. [Google Scholar] [CrossRef]
- Chen, X.; He, G.; Liu, X.; Li, B.; Peng, W.; Dong, F.; Huang, A.; Wang, W.; Lian, Q. Sub-Watershed Parameter Transplantation Method for Non-Point Source Pollution Estimation in Complex Underlying Surface Environment. Land 2021, 10, 1387. [Google Scholar] [CrossRef]
- Cui, N.; Cai, M.; Zhang, X.; Abdelhafez, A.A.; Zhou, L.; Sun, H.; Chen, G.; Zou, G.; Zhou, S. Runoff loss of nitrogen and phosphorus from a rice paddy field in the east of China: Effects of long-term chemical N fertilizer and organic manure applications. Glob. Ecol. Conserv. 2020, 22, e01011. [Google Scholar] [CrossRef]
- Ruan, S.; Zhuang, Y.; Zhang, L.; Li, S.; Chen, J.; Wen, W.; Zhai, L.; Liu, H.; Du, Y. Improved estimation of nitrogen dynamics in paddy surface water in China. J. Environ. Manag. 2022, 312, 114932. [Google Scholar] [CrossRef]
- Liao, Y.; He, J.; Su, B.; Dou, J.; Xu, Y.; Li, L. Validation of an in-situ observation method for nonpoint source pollution in paddy fields: A case study of a Beijing paddy field. Water 2021, 13, 3235. [Google Scholar] [CrossRef]
- Xin, Y.; Liu, G.; Xie, Y.; Gao, Y.; Liu, B.; Shen, B. Effects of soil conservation practices on soil losses from slope farmland in northeastern China using runoff plot data. Catena 2019, 174, 417–424. [Google Scholar] [CrossRef]
- Cherobim, V.F.; Huang, C.-H.; Favaretto, N. Tillage system and time post-liquid dairy manure: Effects on runoff, sediment and nutrients losses. Agric. Water Manag. 2017, 184, 96–103. [Google Scholar] [CrossRef] [Green Version]
- Choi, J.D.; Park, W.J.; Park, K.W.; Lim, K.J. Feasibility of SRI methods for reduction of irrigation and NPS pollution in Korea. Paddy Water Environ. 2013, 11, 241–248. [Google Scholar] [CrossRef]
- Huang, N.B.; Su, B.L.; Li, R.R.; Yang, W.Z.; Shen, M.M. A field-scale observation method for non-point source pollution of paddy fields. Agric. Water Manag. 2014, 146, 305–313. [Google Scholar] [CrossRef]
- Xu, Y.; Su, B.; Wang, H.; He, J.; Yang, Y. Analysis of the water balance and the nitrogen and phosphorus runoff pollution of a paddy field in situ in the Taihu Lake basin. Paddy Water Environ. 2020, 18, 385–398. [Google Scholar] [CrossRef]
- Phong, T.K.; Nguyen, M.H.T.; Komany, S.; Vu, S.H.; Watanabe, H. Alternative water management for controlling simetryn and thiobencarb runoff from paddy fields. Bull. Environ. Contam. Toxicol. 2006, 77, 375–382. [Google Scholar] [CrossRef]
- Liu, B.; Ding, M.; Shaham, S.; Rahayu, W.; Farokhi, F.; Lin, Z. When machine learning meets privacy: A survey and outlook. ACM Comput. Surv. 2021, 54, 1–36. [Google Scholar] [CrossRef]
- Sun, S.; Cao, Z.; Zhu, H.; Zhao, J. A survey of optimization methods from a machine learning perspective. IEEE Trans. Cybern. 2020, 50, 3668–3681. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Khepar, S.D.; Yadav, A.K.; Sondhi, S.K.; Siag, M. Water balance model for paddy fields under intermittent irrigation practices. Irrig. Sci. 2000, 19, 199–208. [Google Scholar] [CrossRef]
- Tsubo, M.; Shu, F.; Basnayake, J.; Tuong, T.P.; Bouman, B.; Harnpichitvitaya, D. Estimating percolation and lateral water flow on sloping land in rainfed lowland rice ecosystem. Plant. Prod. Sci. 2005, 8, 354–357. [Google Scholar] [CrossRef]
- Zhao, X.; Zhou, Y.; Wang, S.; Xing, G.; Shi, W.; Xu, R.; Zhu, Z. Nitrogen balance in a highly fertilized rice–wheat double-cropping system in southern China. Soil Sci. Soc. Am. J. 2012, 76, 1068. [Google Scholar] [CrossRef]
- Wang, W.; Liang, T.; Wang, L.; Liu, Y.; Wang, Y. The effects of fertilizer applications on runoff loss of phosphorus. Environ. Earth Sci. 2013, 68, 1313–1319. [Google Scholar] [CrossRef]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop evapotranspiration: Guidelines for computing crop water requirements. Fao Irrig. Drain. Pap. 1998, 56, 300. [Google Scholar]
- Xu, Y.; Su, B.; Wang, H.; He, J. A new method for indirectly estimating infiltration of paddy fields in situ. Proc. Int. Assoc. Hydrol. Sci. 2018, 379, 205–210. [Google Scholar] [CrossRef] [Green Version]
- Li, S.; Liu, H.; Zhang, L.; Li, X.; Wang, H.; Zhuang, Y.; Zhang, F.; Zhai, L.; Fan, X.; Hu, W.; et al. Potential nutrient removal function of naturally existed ditches and ponds in paddy regions: Prospect of enhancing water quality by irrigation and drainage management. Sci. Total Environ. 2020, 718, 137418. [Google Scholar] [CrossRef]
- Zhao, X.; Zhou, Y.; Min, J.; Wang, S.; Shi, W.; Xing, G. Nitrogen runoff dominates water nitrogen pollution from rice-wheat rotation in the Taihu Lake region of China. Agric. Ecosyst. Environ. 2012, 156, 1–11. [Google Scholar] [CrossRef]
- Liu, L.; Ouyang, W.; Liu, H.; Zhu, J.; Ma, Y.; Wu, Q.; Chen, J.; Zhang, D. Potential of paddy drainage optimization to water and food security in China. Resour. Conserv. Recycl. 2021, 171, 105624. [Google Scholar] [CrossRef]
- Liu, J.; Ouyang, X.; Shen, J.; Li, Y.; Sun, W.; Jiang, W.; Wu, J. Nitrogen and phosphorus runoff losses were influenced by chemical fertilization but not by pesticide application in a double rice-cropping system in the subtropical hilly region of China. Sci. Total Environ. 2020, 715, 136852. [Google Scholar] [CrossRef] [PubMed]
- Chen, Q.; Xi, Y.; Wang, L.; Li, Y.; Zhang, C.; Tian, W.; Tian, R.; Xiao, X.; Zhao, K. Characteristics of nitrogen and phosphorus runoff losses in organic and conventional rice-wheat rotation farmland in Taihu Lake Region. J. Ago-Enironment Sci. 2016, 35, 1550–1558, (In Chinese with English Abstract). [Google Scholar]
- Tian, Y.H.; Yin, B.; Yang, L.Z.; Yin, S.X.; Zhu, Z.L. Nitrogen runoff and leaching losses during rice-wheat rotations in Taihu Lake region, China. Pedosphere 2007, 17, 445–456. [Google Scholar] [CrossRef]
- Zhan, X.; Zhang, Q.; Zhang, H.; Hussain, H.A.; Yang, Z. Pathways of nitrogen loss and optimized nitrogen management for a rice cropping system in arid irrigation region, northwest China. J. Environ. Manag. 2020, 268, 110702. [Google Scholar]
- Chen, D.; Dahlgren, R.A.; Shen, Y.; Lu, J. A Bayesian approach for calculating variable total maximum daily loads and uncertainty assessment. Sci. Total Environ. 2012, 430, 59–67. [Google Scholar] [CrossRef]
- Zhang, Y.; Wu, H.; Yao, M.; Zhou, J.; Wu, K.; Hu, M.; Shen, H.; Chen, D. Estimation of nitrogen runoff loss from croplands in the Yangtze River Basin: A meta-analysis. Environ. Pollut. 2021, 272, 116001. [Google Scholar] [CrossRef]
- Liu, L.; Ouyang, W.; Liu, H.; Zhu, J.; Fan, X.; Zhang, F.; Ma, Y.; Chen, J.; Hao, F.; Lian, Z. Drainage optimization of paddy field watershed for diffuse phosphorus pollution control and sustainable agricultural development. Agric. Ecosyst. Environ. 2021, 308, 107238. [Google Scholar] [CrossRef]
- Wang, J.; Wang, D.; Zhang, G.; Wang, Y.; Wang, C.; Teng, Y.; Christie, P. Nitrogen and phosphorus leaching losses from intensively managed paddy fields with straw retention. Agric. Water Manag. 2014, 141, 66–73. [Google Scholar] [CrossRef]
- Ouyang, W.; Wu, Y.; Hao, Z.; Zhang, Q.; Bu, Q.; Gao, X. Combined impacts of land use and soil property changes on soil erosion in a mollisol area under long-term agricultural development. Sci. Total Environ. 2018, 613, 798–809. [Google Scholar] [CrossRef]
- Zhao, X.; Xie, Y.X.; Xiong, Z.Q.; Yan, X.Y.; Xing, G.X.; Zhu, Z.L. Nitrogen fate and environmental consequence in paddy soil under rice-wheat rotation in the Taihu lake region, China. Plant Soil 2009, 319, 225–234. [Google Scholar] [CrossRef]
- Yang, W. Modeling Of Hydrological and Nitrogen Processes for Paddy Field; Beijing Normal University: Beijing, China, 2013; (In Chinese with English Abstract). [Google Scholar]
- Ouyang, W.; Wei, P.; Gao, X.; Srinivasan, R.; Yen, H.; Xie, X.; Liu, L.; Liu, H. Optimization of SWAT-Paddy for modeling hydrology and diffuse pollution of large rice paddy fields. Environ. Model. Softw. 2020, 130, 104736. [Google Scholar] [CrossRef]
- Tan, X.; Shao, D.; Liu, H.; Yang, F.; Xiao, C.; Yang, H. Effects of alternate wetting and drying irrigation on percolation and nitrogen leaching in paddy fields. Paddy Water Environ. 2013, 11, 381–395. [Google Scholar] [CrossRef]
- Ye, Y.; Liang, X.; Chen, Y.; Liu, J.; Gu, J.; Guo, R.; Li, L. Alternate wetting and drying irrigation and controlled-release nitrogen fertilizer in late-season rice. Effects on dry matter accumulation, yield, water and nitrogen use. Field Crops Res. 2013, 144, 212–224. [Google Scholar] [CrossRef]
- Zhang, S.; Zhang, G.; Wang, D.; Liu, Q. Long-term straw return with N addition alters reactive nitrogen runoff loss and the bacterial community during rice growth stages. J. Environ. Manag. 2021, 292, 112772. [Google Scholar] [CrossRef] [PubMed]
- Karandish, F.; Darzi-Naftchali, A.; Asgari, A. Application of machine-learning models for diagnosing health hazard of nitrate toxicity in shallow aquifers. Paddy Water Environ. 2017, 15, 201–215. [Google Scholar] [CrossRef]
- Azimi, S.; Azhdary, M.M.; Hashemi, M. Prediction of annual drinking water quality reduction based on Groundwater Resource Index using the artificial neural network and fuzzy clustering. J. Contam. Hydrol. 2019, 220, 6–17. [Google Scholar] [CrossRef]
- Shan, W.; Cai, S.; Liu, C. A new comprehensive evaluation method for water quality: Improved fuzzy support vector machine. Water 2018, 10, 1303. [Google Scholar] [CrossRef] [Green Version]
- Xu, J.; Xu, Z.; Kuang, J.; Lin, C.; Xiao, L.; Huang, X.; Zhang, Y. An alternative to laboratory testing: Random forest-based water quality prediction framework for inland and nearshore water bodies. Water 2021, 13, 3262. [Google Scholar] [CrossRef]
- Tiyasha; Tung, T.M.; Yaseen, Z.M. A survey on river water quality modelling using artificial intelligence models: 2000–2020. J. Hydrol. 2020, 585, 124670. [Google Scholar] [CrossRef]
- Modaresi, F.; Araghinejad, S. A comparative assessment of support vector machines, probabilistic neural networks, and k-nearest neighbor algorithms for water quality classification. Water Resour. Manag. 2014, 28, 4095–4111. [Google Scholar] [CrossRef]
- Chen, Y.; Song, L.; Liu, Y.; Yang, L.; Li, D. A review of the artificial neural network models for water quality prediction. Appl. Sci. 2020, 10, 5776. [Google Scholar] [CrossRef]
- Rumelhart, D.; Hinton, G.E.; Williams, R.J. Learning representations by back propagating errors. Nature 1986, 323, 533–536. [Google Scholar] [CrossRef]
- Nour, M.H.; Smith, D.W.; El-Din, M.G.; Prepas, E.E. The application of artificial neural networks to flow and phosphorus dynamics in small streams on the Boreal Plain, with emphasis on the role of wetlands. Ecol. Model. 2006, 191, 19–32. [Google Scholar] [CrossRef]
- Tyralis, H.; Papacharalampous, G.; Langousis, A. A brief review of random forests for water scientists and practitioners and their recent history in water resources. Water 2019, 11, 910. [Google Scholar] [CrossRef] [Green Version]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
- Wu, G.; Li, L.; Ahmad, S.; Chen, X. A dynamic model for vulnerability assessment of regional water resources in arid areas: A case study of Bayingolin, China. Water Resour. Manag. 2013, 27, 3085–3101. [Google Scholar] [CrossRef]
- Zhang, L.; Wang, L.; Zhang, X.; Liu, S.; Sun, P.; Wang, T. The basic principle of random forest and its applications in ecology: A case study of Pinus yunnanensis. Acta Ecol. Sin. 2014, 34, 650–659, (In Chinese with English Abstract). [Google Scholar]

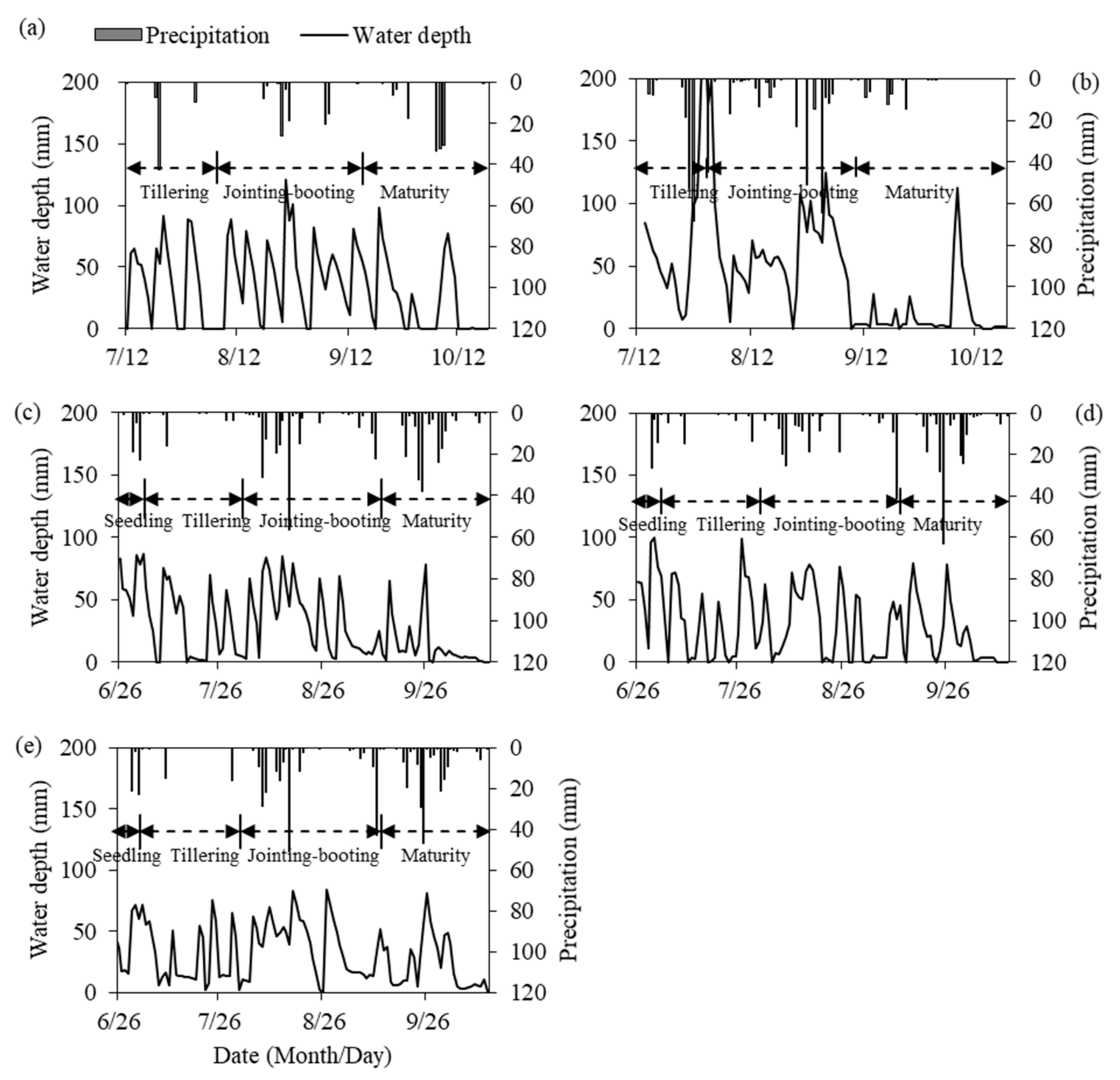
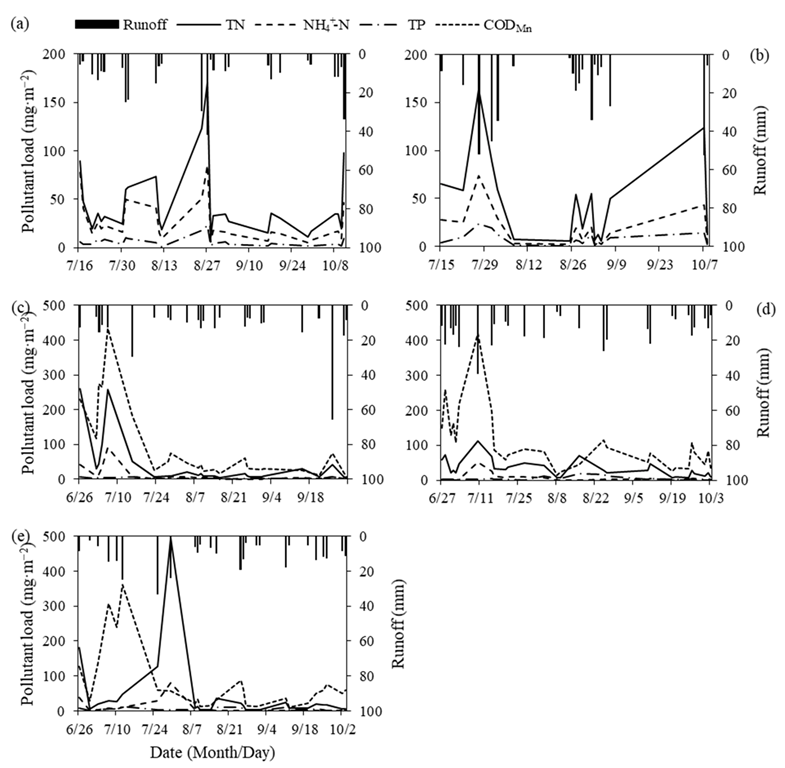



| Paddy Field | Precipitation | Irrigation | Runoff | Rainfall Runoff | Drainage Runoff | Irrigation Overflow |
|---|---|---|---|---|---|---|
| LC13 | 279.0 | 879.9 | 330.3 | 124.8 | 125.9 | 79.6 |
| LC14 | 494.7 | 451.5 | 355.4 | 201.8 | 76.6 | 77.1 |
| ZT | 463.7 | 809.7 | 327.6 | 167.0 | 41.7 | 118.9 |
| HQ | 471.9 | 825.5 | 405.0 | 179.7 | 74.2 | 151.0 |
| WS | 482.5 | 786.3 | 292.5 | 151.6 | 72.3 | 68.5 |
| Paddy Field | Pollution Loads (kg·ha−1) | Fertilizer Loss Rates (%) | ||||
|---|---|---|---|---|---|---|
| TN | NH4+-N | TP | CODMn | N | P | |
| LC13 | 12.18 | 7.13 | 1.55 | / | 4.73 | 3.33 |
| LC14 | 8.59 | 3.50 | 1.36 | / | 3.91 | 2.34 |
| Mean of Liyang Paddy fields | 10.39 | 5.31 | 1.46 | / | 4.32 | 2.83 |
| ZT | 9.73 | 2.55 | 0.62 | 21.61 | 3.75 | 0.86 |
| HQ | 9.42 | 1.56 | 1.29 | 28.93 | 3.63 | 1.78 |
| WS | 11.49 | 2.00 | 1.02 | 19.92 | 4.43 | 1.41 |
| Mean of Yixing Paddy fields | 10.21 | 2.04 | 0.97 | 23.49 | 3.93 | 1.35 |
| ID | Stage | S | C | F |
|---|---|---|---|---|
| 1 | seedling | 5.85 | 2.60 | 8.45 |
| 2 | tillering | 4.11 | 6.71 | |
| 3 | jointing–booting | 4.85 | 7.45 | |
| 4 | maturity | 6.14 | 8.74 | |
| 5 | growth period | 4.62 | 7.22 |
| Drainage Time | Stage | Duration (d) | Water Discharge (mm) |
|---|---|---|---|
| 1 | early tillering | 2 | water depth of the previous day |
| 2 | middle tillering | approximately 5 | water depth of the previous two days |
| 3 | late tillering | 2 | naturally dried without artificial drainage |
| Method | Field | Irrigation | Runoff | Rainfall Runoff | Drainage Runoff | Irrigation Overflow |
|---|---|---|---|---|---|---|
| RPEM | ZT | 800.0 | 336.3 | 172.5 | 53.8 | 110.0 |
| PIOM | 809.7 | 327.6 | 167.0 | 41.7 | 118.9 | |
| Difference (%) | −1.2 | 2.7 | 3.3 | 29.0 | −7.5 | |
| RPEM | HQ | 800.0 | 417.6 | 202.1 | 67.6 | 147.9 |
| PIOM | 825.5 | 405.0 | 179.7 | 74.2 | 151.0 | |
| Difference (%) | −3.1 | 3.1 | 12.5 | −8.9 | −2.1 |
| Methods | Paddy Fields | TN | NH4+-N | TP | CODMn |
|---|---|---|---|---|---|
| RPEM | ZT | 9.77 | 2.30 | 0.63 | 26.42 |
| PIOM | 9.73 | 2.55 | 0.62 | 21.61 | |
| Difference (%) | 0.5 | −10.0 | 2.2 | 22.3 | |
| RPEM | HQ | 10.61 | 1.85 | 1.08 | 32.13 |
| PIOM | 9.42 | 1.56 | 1.29 | 28.93 | |
| Difference (%) | 12.7 | 18.9 | −15.7 | 11.1 |
| Pollution | Machine | Training Set | Testing Set | Best Model Selection | ||
|---|---|---|---|---|---|---|
| RMSE (mg·m−2) | R2 | RMSE (mg·m−2) | R2 | |||
| TN | SVM | 29.20 | 0.59 | 55.97 | 0.60 | |
| BPNN | 59.03 | 0.49 | 104.22 | 0.38 | ||
| RF | 21.55 | 0.85 | 38.14 | 0.73 | √ | |
| NH4+-N | SVM | 10.17 | 0.75 | 11.02 | 0.52 | |
| BPNN | 21.70 | 0.60 | 20.34 | 0.64 | ||
| RF | 9.07 | 0.84 | 9.44 | 0.75 | √ | |
| TP | SVM | 2.86 | 0.61 | 3.77 | 0.42 | |
| BPNN | 5.20 | 0.44 | 6.57 | 0.32 | ||
| RF | 2.19 | 0.79 | 2.47 | 0.68 | √ | |
| CODMn | SVM | 31.93 | 0.82 | 40.22 | 0.84 | √ |
| BPNN | 114.16 | 0.62 | 153.22 | 0.58 | ||
| RF | 46.12 | 0.67 | 44.94 | 0.81 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, Y.; Su, B.; Wang, H. Development of a Runoff Pollution Empirical Model and Pollution Machine Learning Models of the Paddy Field in the Taihu Lake Basin Based on the Paddy In Situ Observation Method. Water 2022, 14, 3277. https://doi.org/10.3390/w14203277
Xu Y, Su B, Wang H. Development of a Runoff Pollution Empirical Model and Pollution Machine Learning Models of the Paddy Field in the Taihu Lake Basin Based on the Paddy In Situ Observation Method. Water. 2022; 14(20):3277. https://doi.org/10.3390/w14203277
Chicago/Turabian StyleXu, Yunqiang, Baolin Su, and Hongqi Wang. 2022. "Development of a Runoff Pollution Empirical Model and Pollution Machine Learning Models of the Paddy Field in the Taihu Lake Basin Based on the Paddy In Situ Observation Method" Water 14, no. 20: 3277. https://doi.org/10.3390/w14203277
APA StyleXu, Y., Su, B., & Wang, H. (2022). Development of a Runoff Pollution Empirical Model and Pollution Machine Learning Models of the Paddy Field in the Taihu Lake Basin Based on the Paddy In Situ Observation Method. Water, 14(20), 3277. https://doi.org/10.3390/w14203277






