Energy Analysis of a Quasi-Two-Dimensional Friction Model for Simulation of Transient Flows in Viscoelastic Pipes
Abstract
:1. Introduction
2. Materials and Methods
2.1. Governing Equations
2.2. Kelvin-Voigt Model
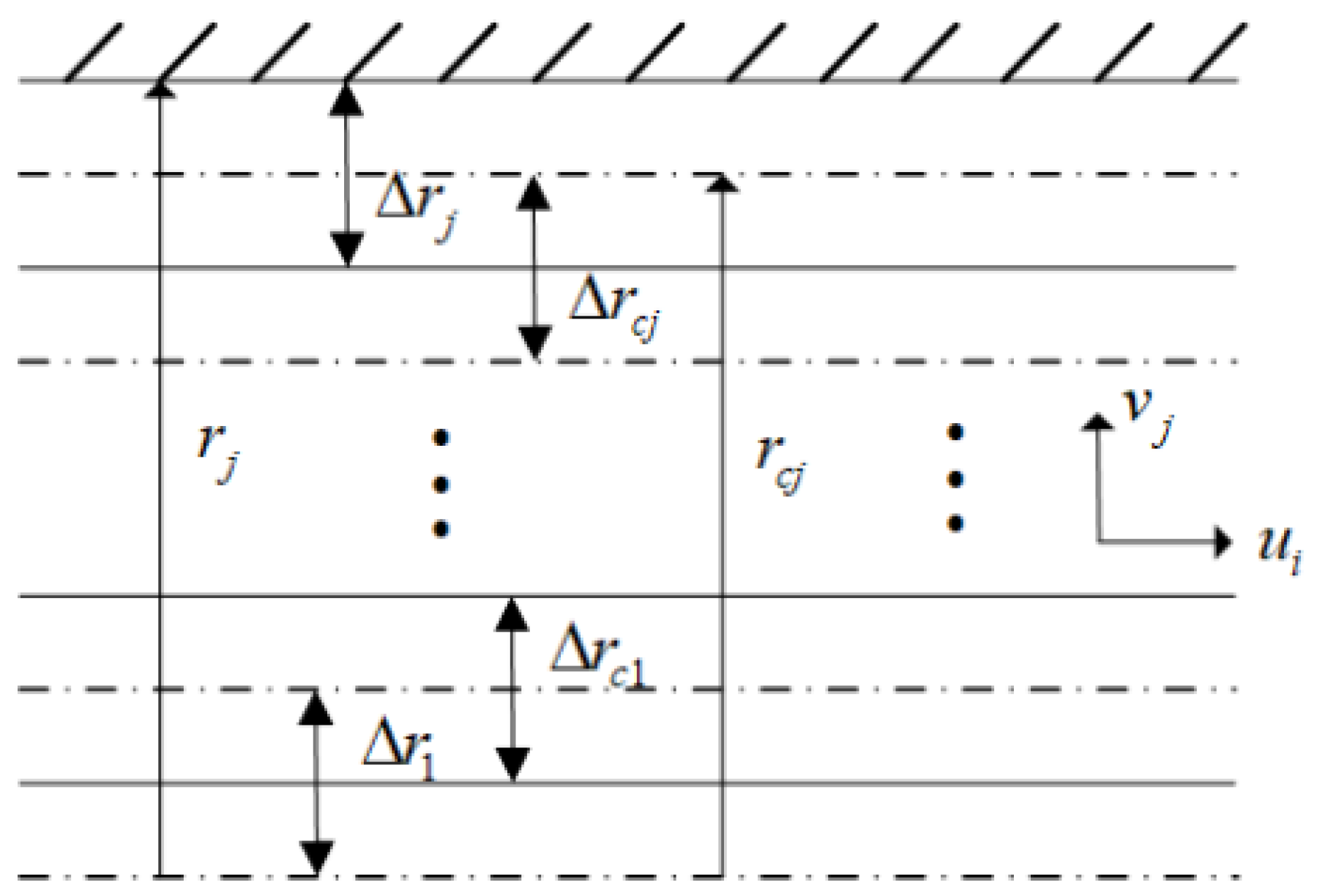
2.3. Numerical Scheme of 1D and Quasi-2D Models
2.4. ITE Method Based on Quasi-2D Friction Model
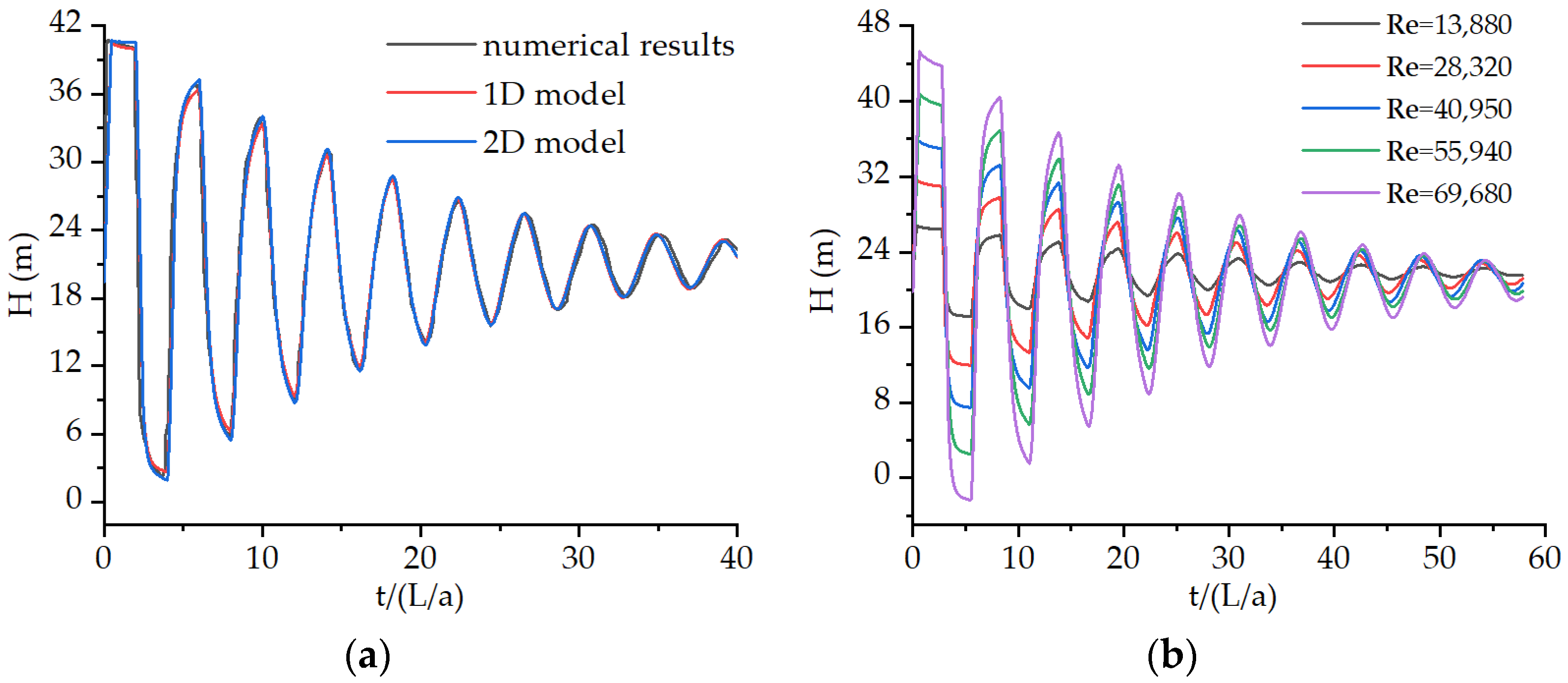
3. Results: Experimental Setup and Validation
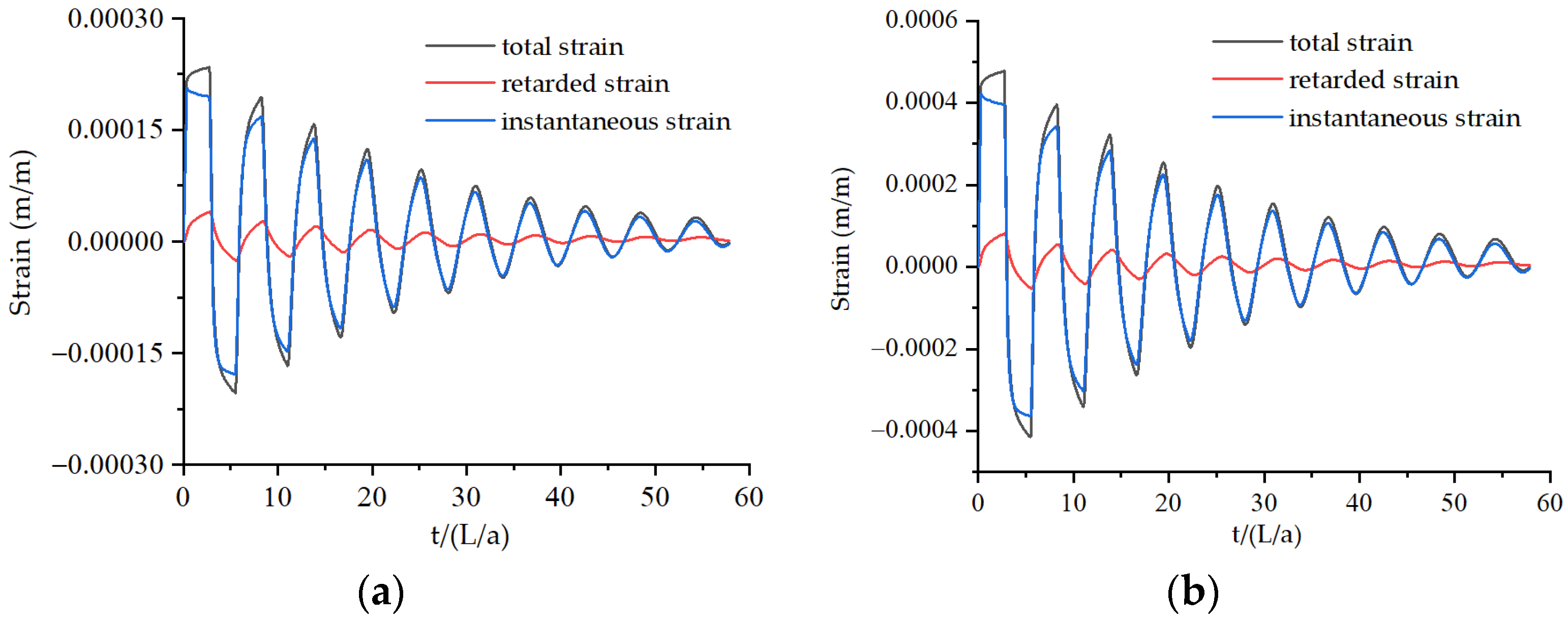
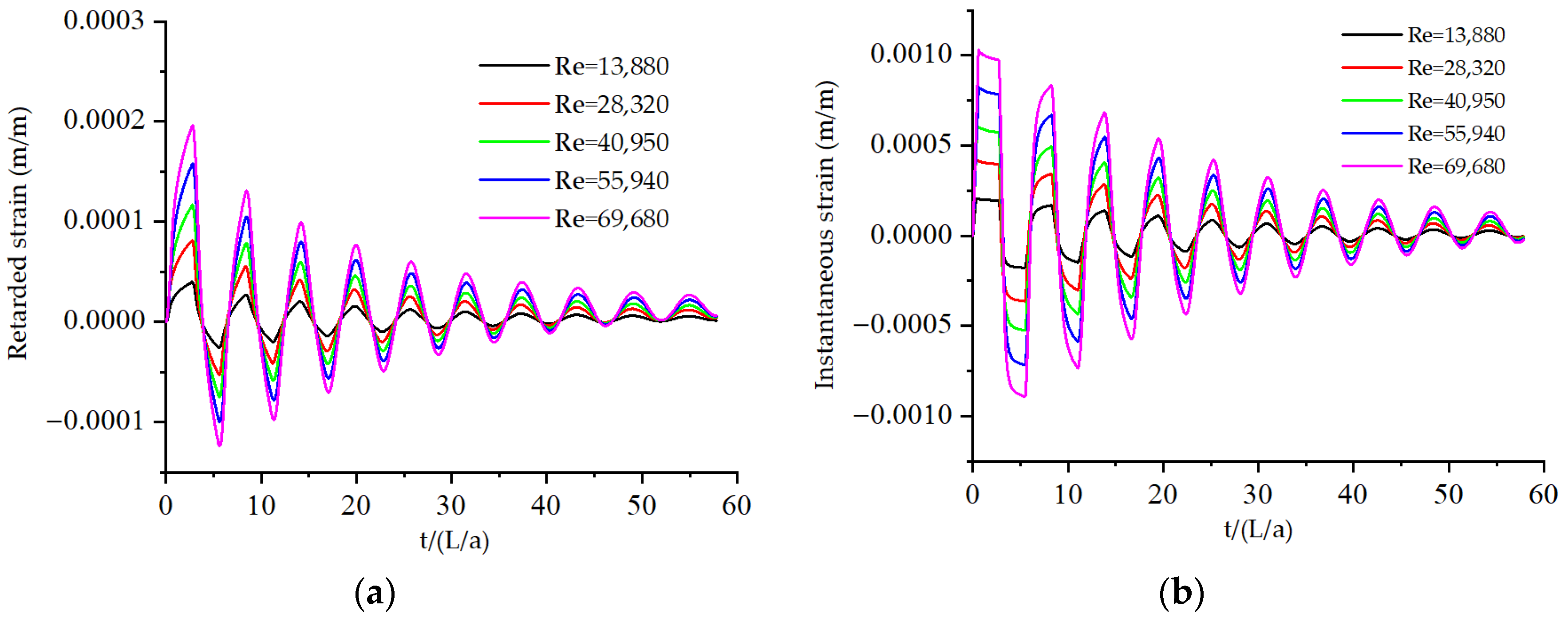
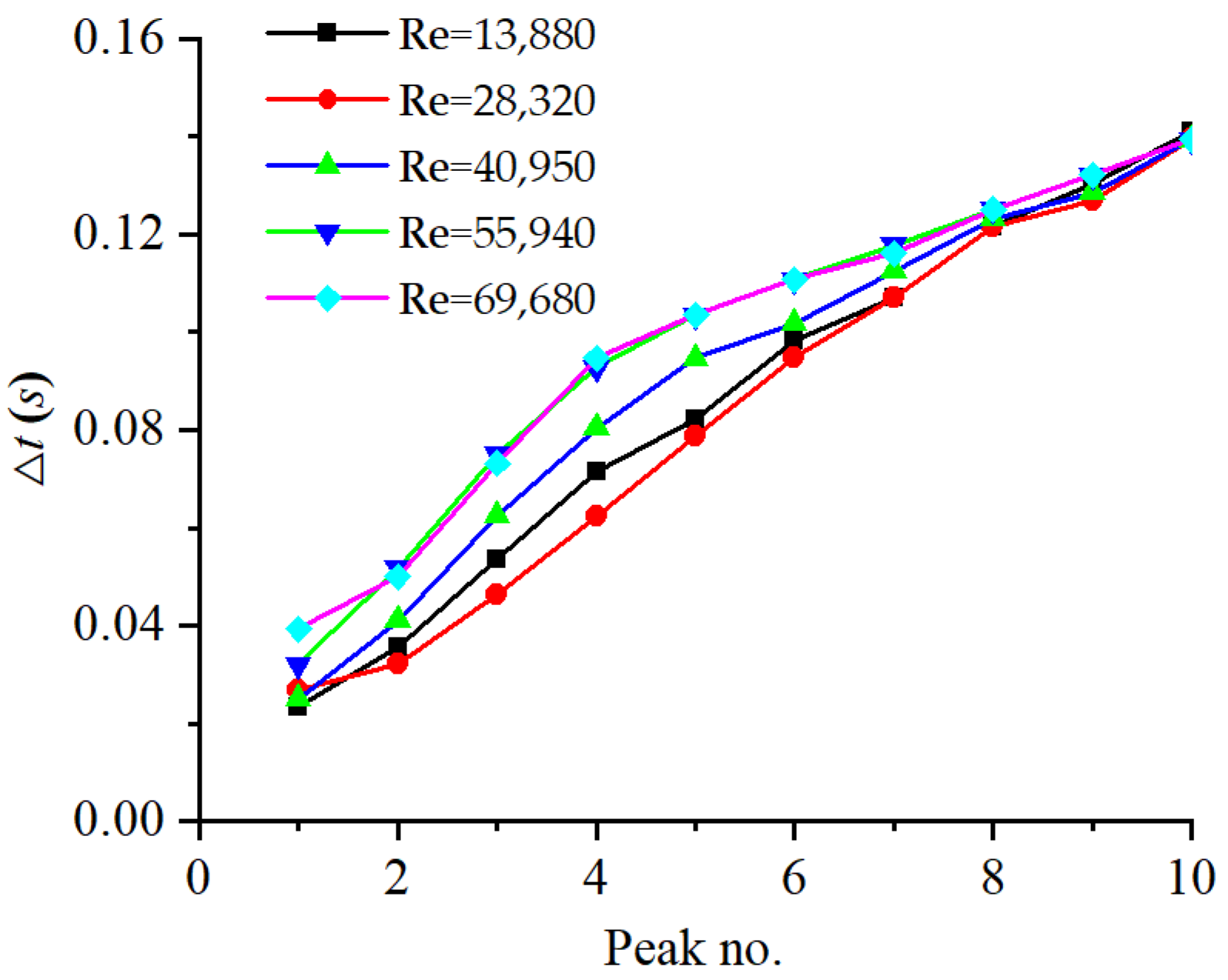
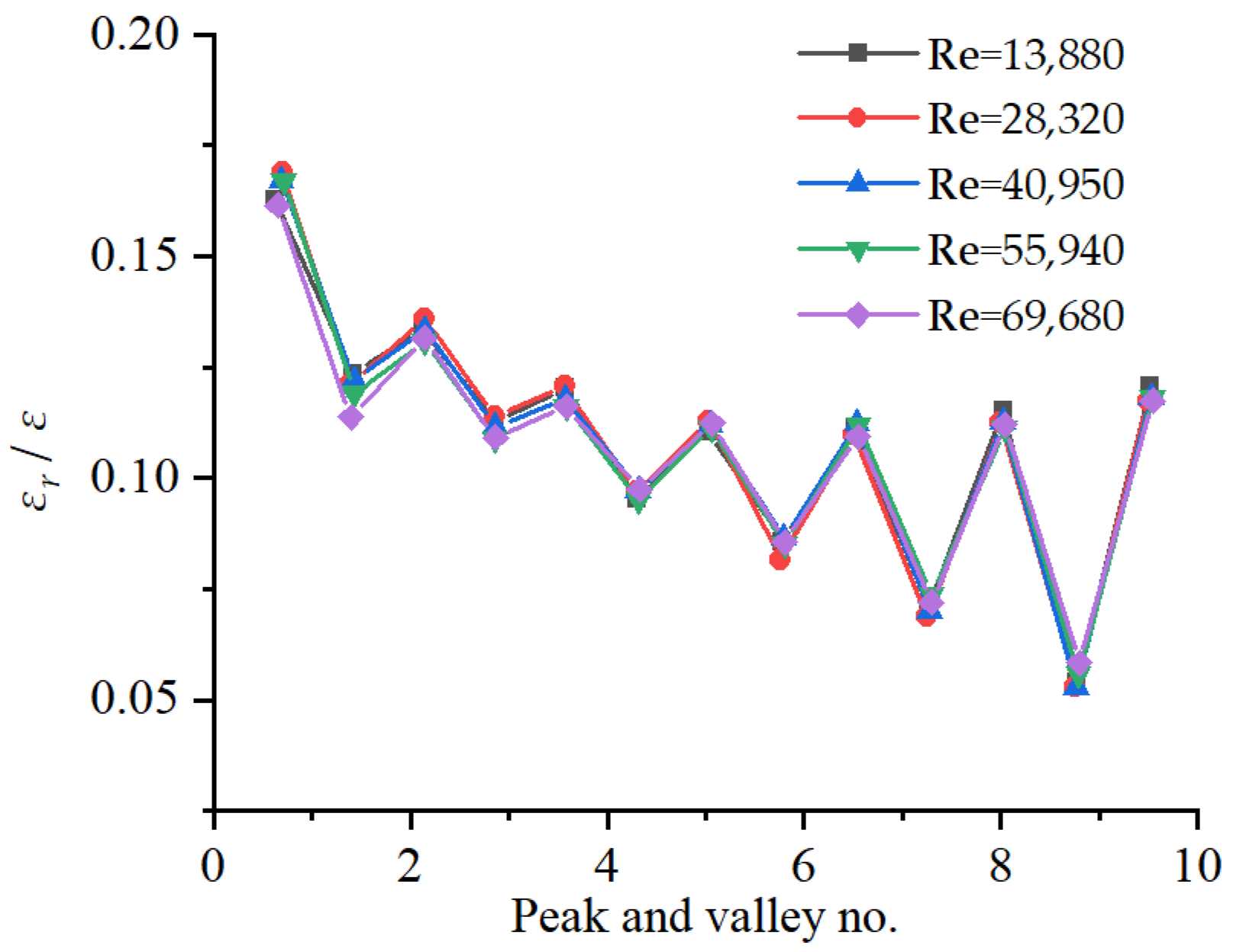
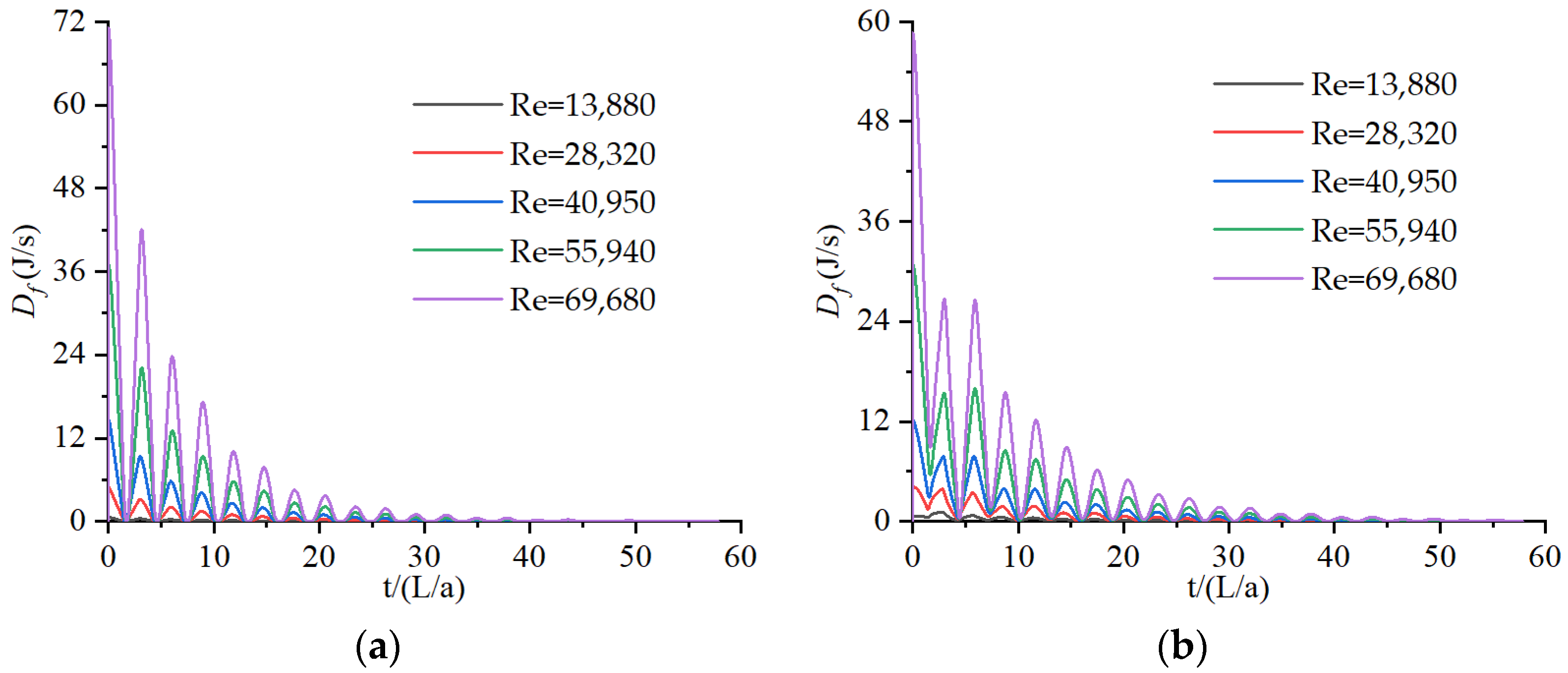
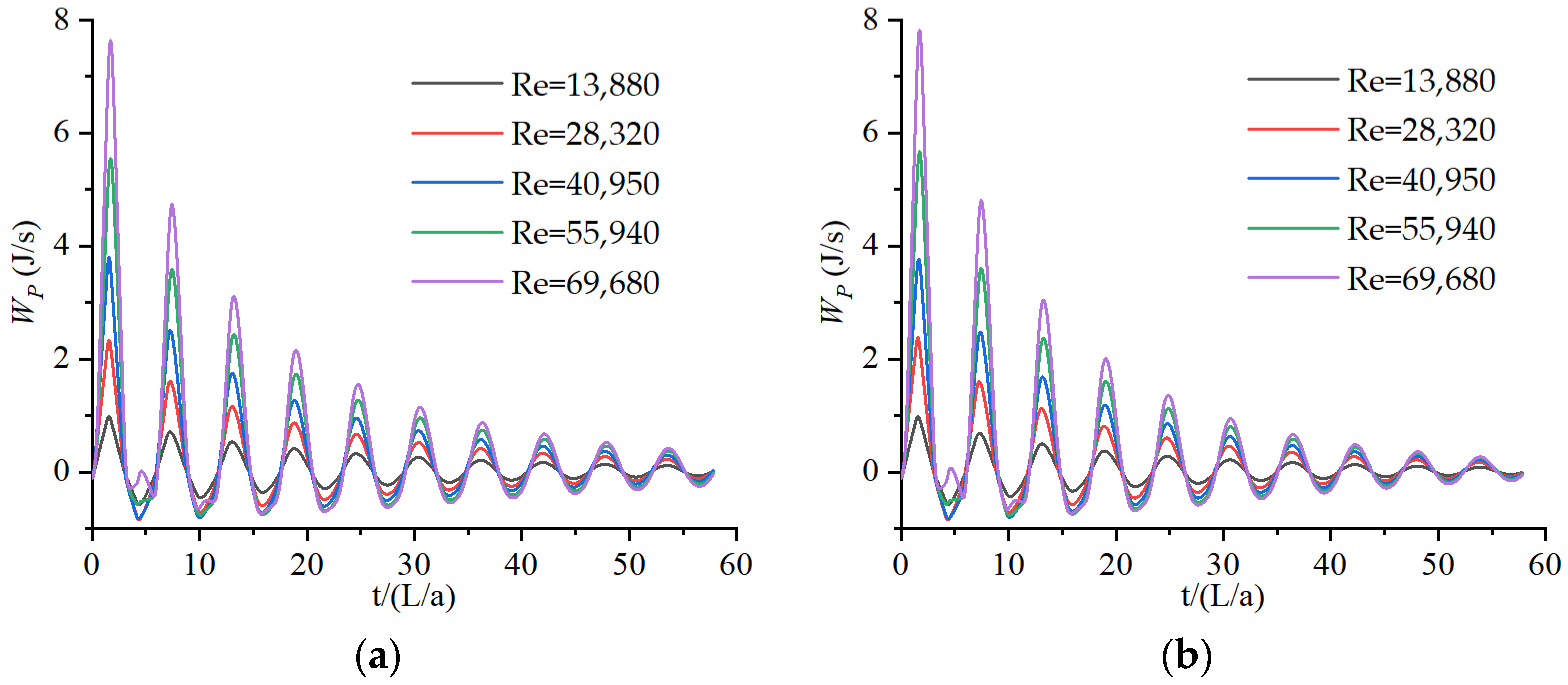
4. Discussion: Energy Analysis at Different Reynolds Numbers
4.1. Df in 1D and 2D Models
4.2. WP in 1D and 2D Models
4.3. Energy integral in 2D Models
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| A | cross-sectional area of the pipeline |
| a | wave speed |
| D | pipe diameter |
| Df | total rate of frictional dissipation |
| elasticity modulus of the k-th element | |
| e | wall thickness |
| g | gravitational acceleration |
| H | pressure head |
| J | creep compliance of the k-th element |
| j | subscript representing the radial grid number |
| Nr | number of segments along the radius |
| Nr0 | number of cylinders along the radius |
| Q | discharge |
| q | radial flux |
| r | radial distance from the pipe centre |
| rcj | radial distance between the centre of the cylinder j cross-section and the pipe centre |
| rj | radial distance between the outer surface of the cylinder j cross-section and the pipe centre |
| T | total kinetic energy of the system |
| t | time |
| U | total internal energy of the system |
| u | longitudinal velocity |
| v | radial velocity |
| WE | total rate of work from the ends of the pipe |
| WP | total rate of work from the pipe wall |
| x | axial coordinate along the pipe |
| Greek Symbols | |
| constraint coefficient | |
| ε, θ | weighting coefficients |
| retarded strain | |
| density | |
| shear stress | |
| retarded time of the k-th element | |
| pipe-wall shear stress | |
| bulk weight | |
| Abbreviations | |
| quasi-2D | quasi-two-dimensional |
| 1D | one-dimensional |
| Re | Reynolds number |
| K-V | Kelvin-Voight |
| HDPE | high-density polyethylene pipe |
| MOC | method of characteristics |
Appendix A. Derivation of Equation (29)
References
- Duan, H.F.; Pan, B.; Wang, M.L.; Chen, L.; Zheng, F.; Zhang, Y. State-of-the-art review on the transient flow modeling and utilization for urban water supply system (UWSS) management. J. Water Supply Res. Technol. 2020, 69, 858–893. [Google Scholar] [CrossRef]
- Rieutord, E.; Blanchard, A. Pulsating viscoelastic pipe flow–water-hammer. J. Hydraul. Res. 1979, 17, 217–229. [Google Scholar] [CrossRef]
- Covas, D.; Stoianov, I.; Mano, J.F.; Ramos, H.; Graham, N.; Maksimovic, C. The dynamic effect of pipe-wall visco-elasticity in hydraulic transients. Part I: Experimental analysis and creep characterization. J. Hydraul. Res. 2004, 42, 516–530. [Google Scholar] [CrossRef]
- Covas, D.; Stoianov, I.; Mano, J.F.; Ramos, H.; Graham, N.; Maksimovic, C. The dynamic effect of pipe-wall viscoelasticity in hydraulic transients. Part II: Model development, calibration and verification. J. Hydraul. Res. 2005, 43, 56–70. [Google Scholar] [CrossRef]
- Urbanowicz, K. Analytical expressions for effective weighting functions used during simulations of water hammer. J. Theor. Appl. Mech. 2017, 55, 1029–1040. [Google Scholar] [CrossRef] [Green Version]
- Pezzinga, G. Quasi-2D model for unsteady flow in pipe networks. J. Hydraul. Eng. 1999, 125, 676–685. [Google Scholar] [CrossRef]
- Firkowski, M.; Urbanowicz, K.; Duan, H.F. Simulation of unsteady flow in viscoelastic pipes. SN Appl. Sci. 2019, 1, 519. [Google Scholar] [CrossRef] [Green Version]
- Urbanowicz, K.; Duan, H.F.; Bergant, A. Transient liquid flow in plastic pipes. J. Mech. Eng. 2020, 66, 77–90. [Google Scholar] [CrossRef]
- Sun, Q.; Zhang, Z.; Wu, Y.; Xu, Y.; Liang, H. Numerical analysis of transient pressure damping in viscoelastic pipes at different water temperatures. Materials 2022, 15, 4904. [Google Scholar] [CrossRef]
- Duan, H.F.; Ghidaoui, M.S.; Lee, P.J.; Tung, Y.-K. Energy analysis of viscoelasticity effects in pipe fluid transients. J. Appl. Mech. 2010, 77, 044503.1–044503.5. [Google Scholar] [CrossRef]
- Karney, B.W. Energy relations in transient closed-conduit flow. J. Hydraul. Eng. 1990, 116, 1180–1196. [Google Scholar] [CrossRef]
- Duan, H.F.; Meniconi, S.; Lee, P.J.; Brunone, B.; Ghidaoui, M.S. Local and integral energy-based evaluation for the unsteady friction relevance in transient pipe flows. J. Hydraul. Eng. 2017, 143, 04017015. [Google Scholar] [CrossRef] [Green Version]
- Meniconi, S.; Brunone, B.; Ferrante, M.; Massari, C. Energy dissipation and pressure decay during transients in viscoelastic pipes with an in-line valve. J. Fluids Struct. 2014, 45, 235–249. [Google Scholar] [CrossRef]
- Meniconi, S.; Duan, H.F.; Brunone, B.; Ghidaoui, M.S.; Lee, P.J.; Ferrante, M. Further developments in rapidly decelerating turbulent pipe flow modeling. J. Hydraul. Eng. 2014, 140, 04014028. [Google Scholar] [CrossRef] [Green Version]
- Riasi, A.; Nourbakhsh, A.; Raisee, M. Energy dissipation in unsteady turbulent pipe flows caused by water hammer. Comput. Fluids 2013, 73, 124–133. [Google Scholar] [CrossRef]
- Keramat, A.; Haghighi, A. Straightforward transient-based approach for the creep function determination in viscoelastic pipes. J. Hydraul. Eng. 2014, 140, 04014058. [Google Scholar] [CrossRef]
- Gong, J.; Zecchin, A.C.; Lambert, M.F.; Simpson, A.R. Determination of the creep function of viscoelastic pipelines using system resonant frequencies with hydraulic transient analysis. J. Hydraul. Eng. 2016, 142, 04016023. [Google Scholar] [CrossRef] [Green Version]
- Urbanowicz, K.; Firkowski, M.; Zarzycki, Z. Modelling water hammer in viscoelastic pipelines: Short brief. J. Phys. Conf. Ser. 2016, 760, 012037. [Google Scholar] [CrossRef]
- Pezzinga, G.; Brunone, B.; Meniconi, S. Relevance of pipe period on Kelvin-Voigt viscoelastic parameters: 1D and 2-D inverse transient analysis. J. Hydraul. Eng. 2016, 142, 04016063. [Google Scholar] [CrossRef]
- Pan, B.; Duan, H.F.; Meniconi, S.; Urbanowicz, K.; Che, T.C.; Brunone, B. Multistage Frequency-Domain Transient-Based Method for the Analysis of Viscoelastic Parameters of Plastic Pipes. J. Hydraul. Eng. 2020, 146, 04019068. [Google Scholar] [CrossRef]
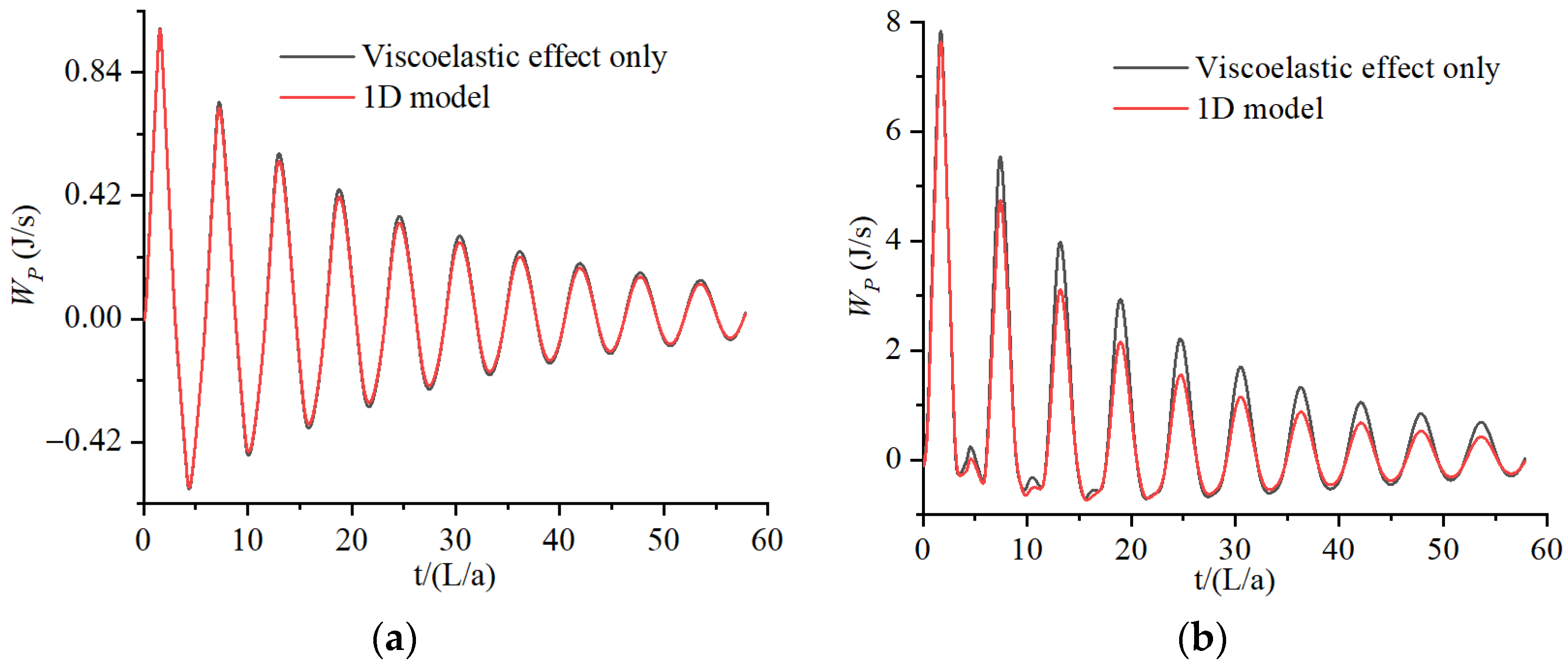
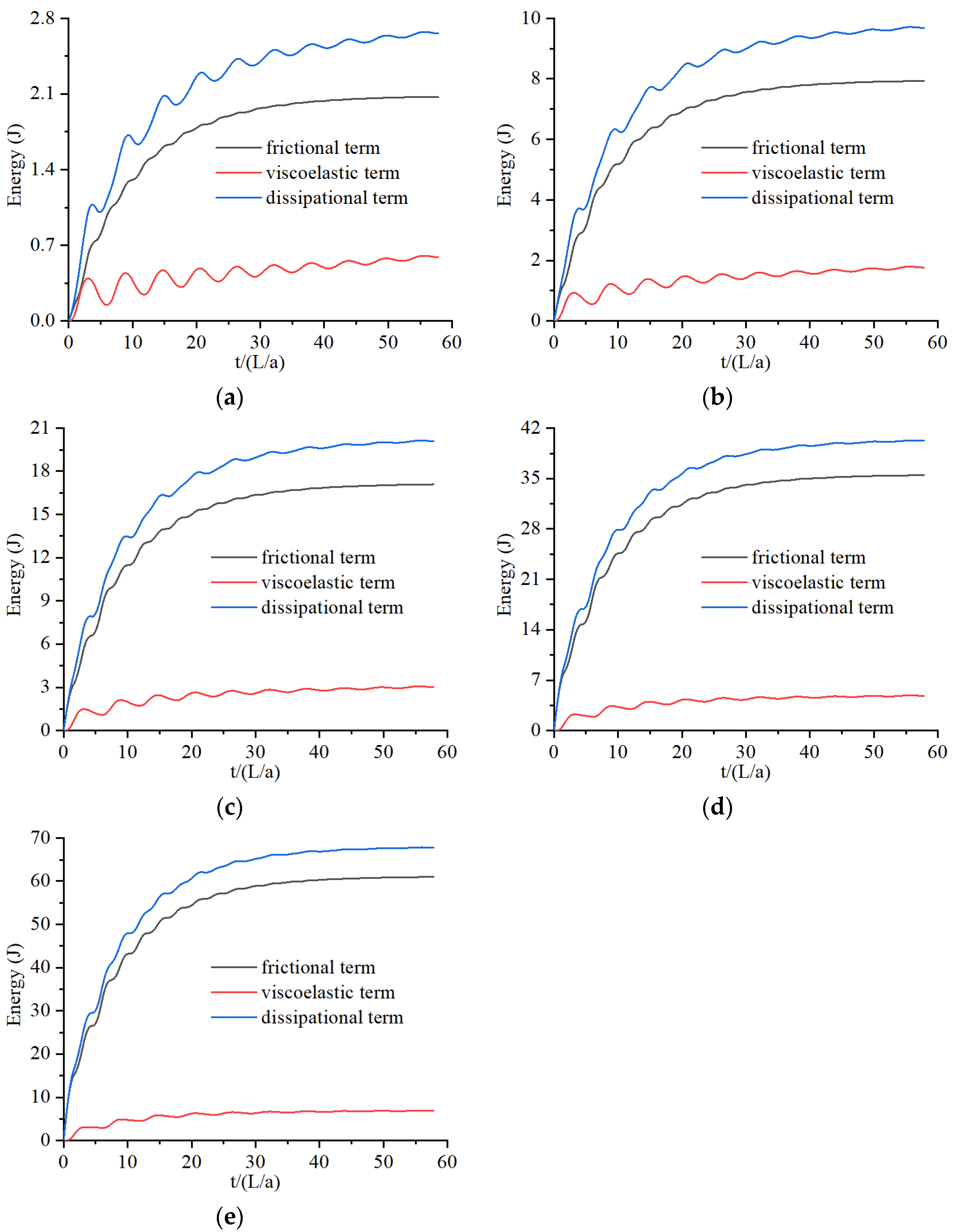
| Case | Q (L/s) | Re | H0 (m) | Tc (s) |
|---|---|---|---|---|
| 1 | 1 | 13,380 | 21.63 | 0.0875 |
| 2 | 2.04 | 28,320 | 21.13 | 0.0752 |
| 3 | 2.95 | 40,950 | 20.74 | 0.1188 |
| 4 | 4.03 | 55,940 | 20.34 | 0.1575 |
| 5 | 5.02 | 69,680 | 19.82 | 0.1533 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, K.; Feng, Y.; Xu, Y.; Liang, H.; Liu, G. Energy Analysis of a Quasi-Two-Dimensional Friction Model for Simulation of Transient Flows in Viscoelastic Pipes. Water 2022, 14, 3258. https://doi.org/10.3390/w14203258
Wu K, Feng Y, Xu Y, Liang H, Liu G. Energy Analysis of a Quasi-Two-Dimensional Friction Model for Simulation of Transient Flows in Viscoelastic Pipes. Water. 2022; 14(20):3258. https://doi.org/10.3390/w14203258
Chicago/Turabian StyleWu, Kai, Yujie Feng, Ying Xu, Huan Liang, and Guohong Liu. 2022. "Energy Analysis of a Quasi-Two-Dimensional Friction Model for Simulation of Transient Flows in Viscoelastic Pipes" Water 14, no. 20: 3258. https://doi.org/10.3390/w14203258






