Study of a Control Algorithm with the Disturbance of Massive Discharge on an Open Channel
Abstract
:1. Introduction
2. Construction of Hydraulic Simulation Model
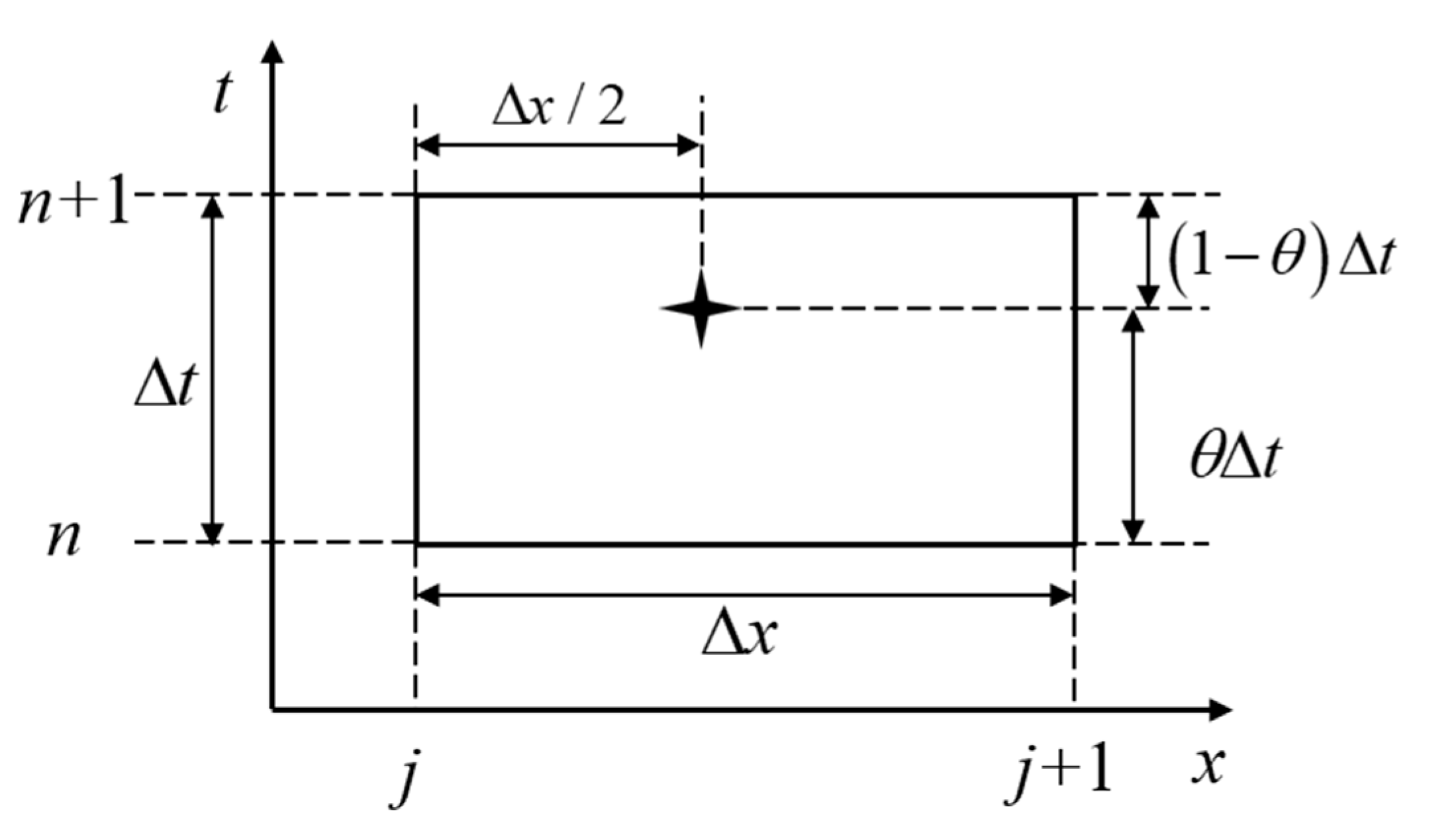
2.1. Governing Equation
2.2. Inner Boundary Handling
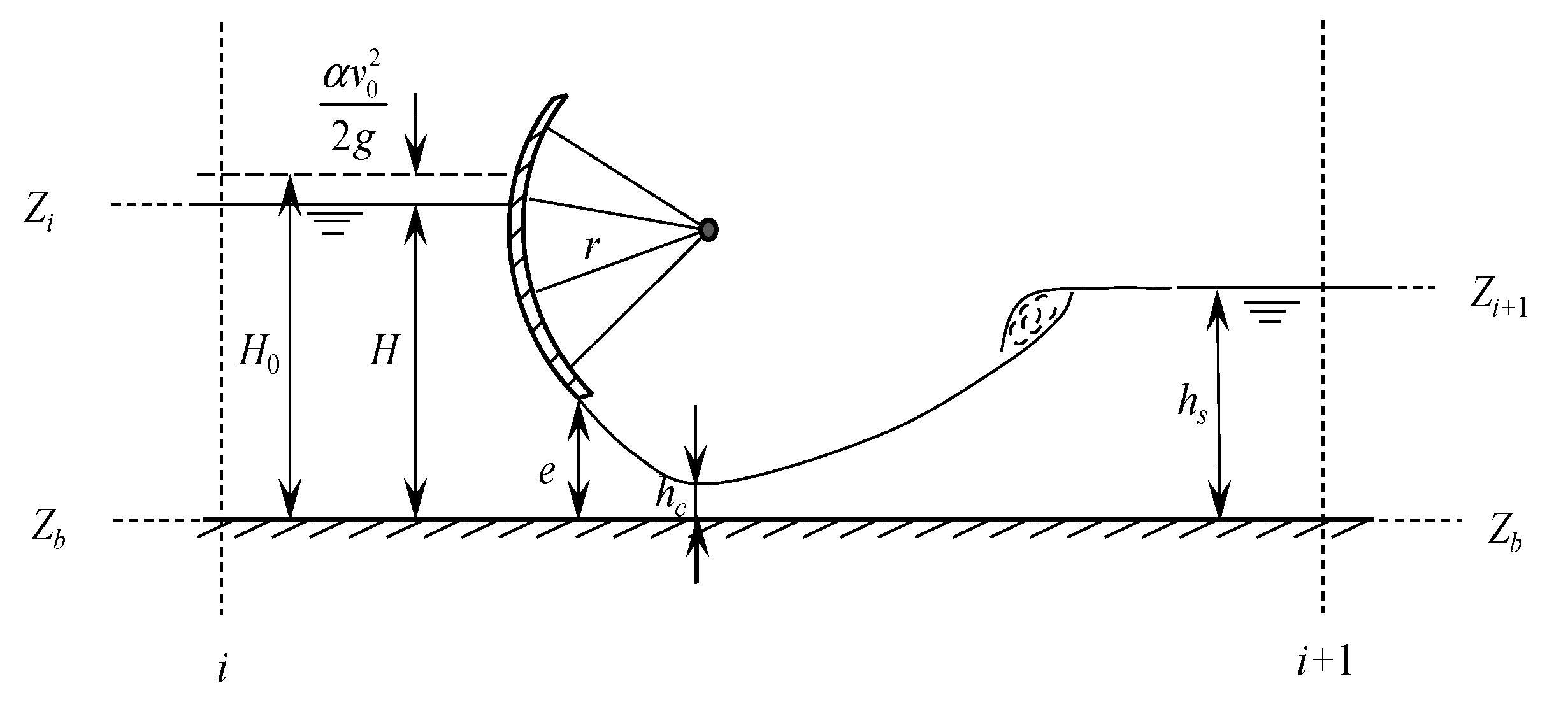
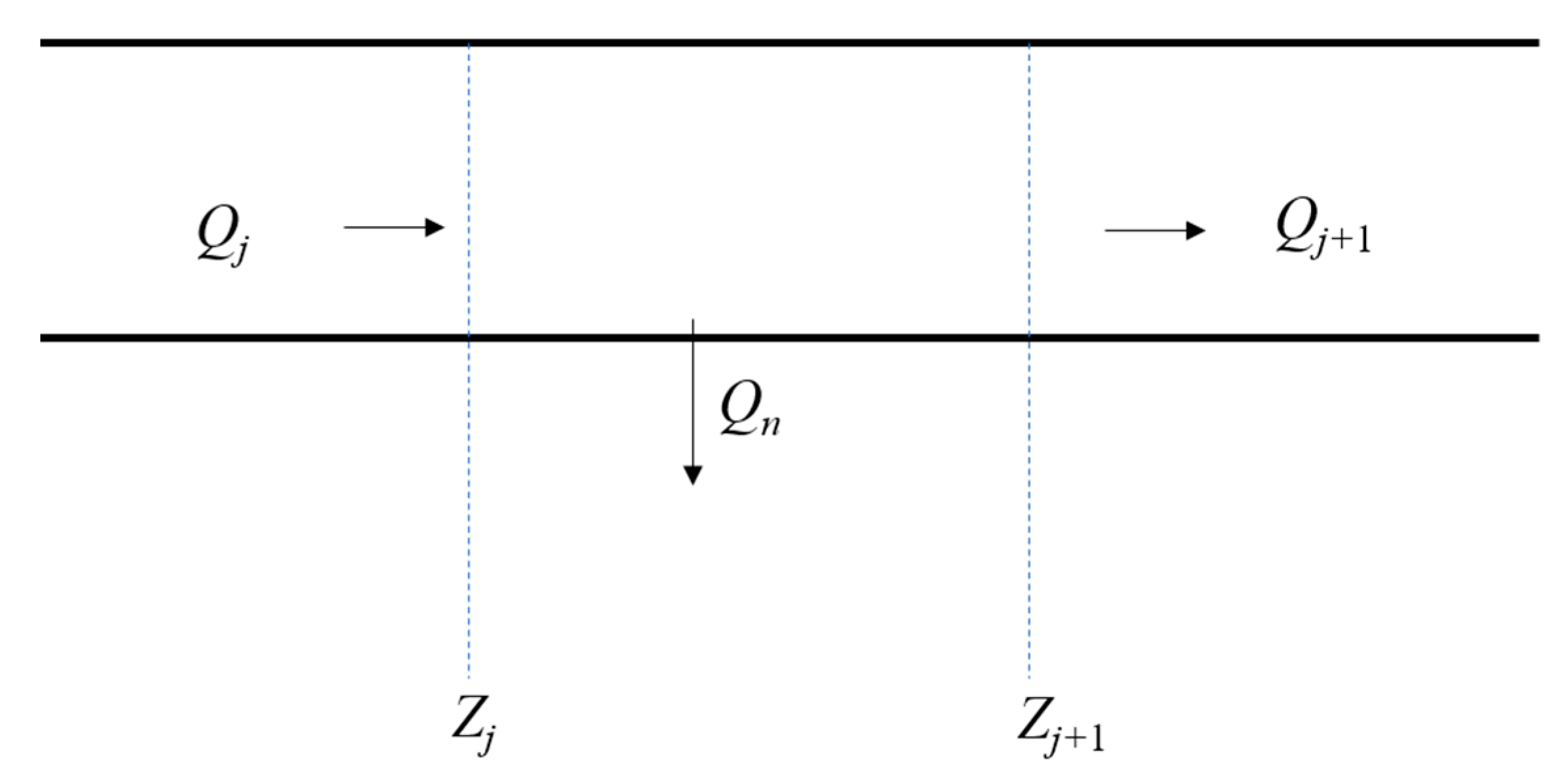
2.3. Water Divider Generalization
3. Control Algorithm in the Case of Large Flow Diversion Disturbance
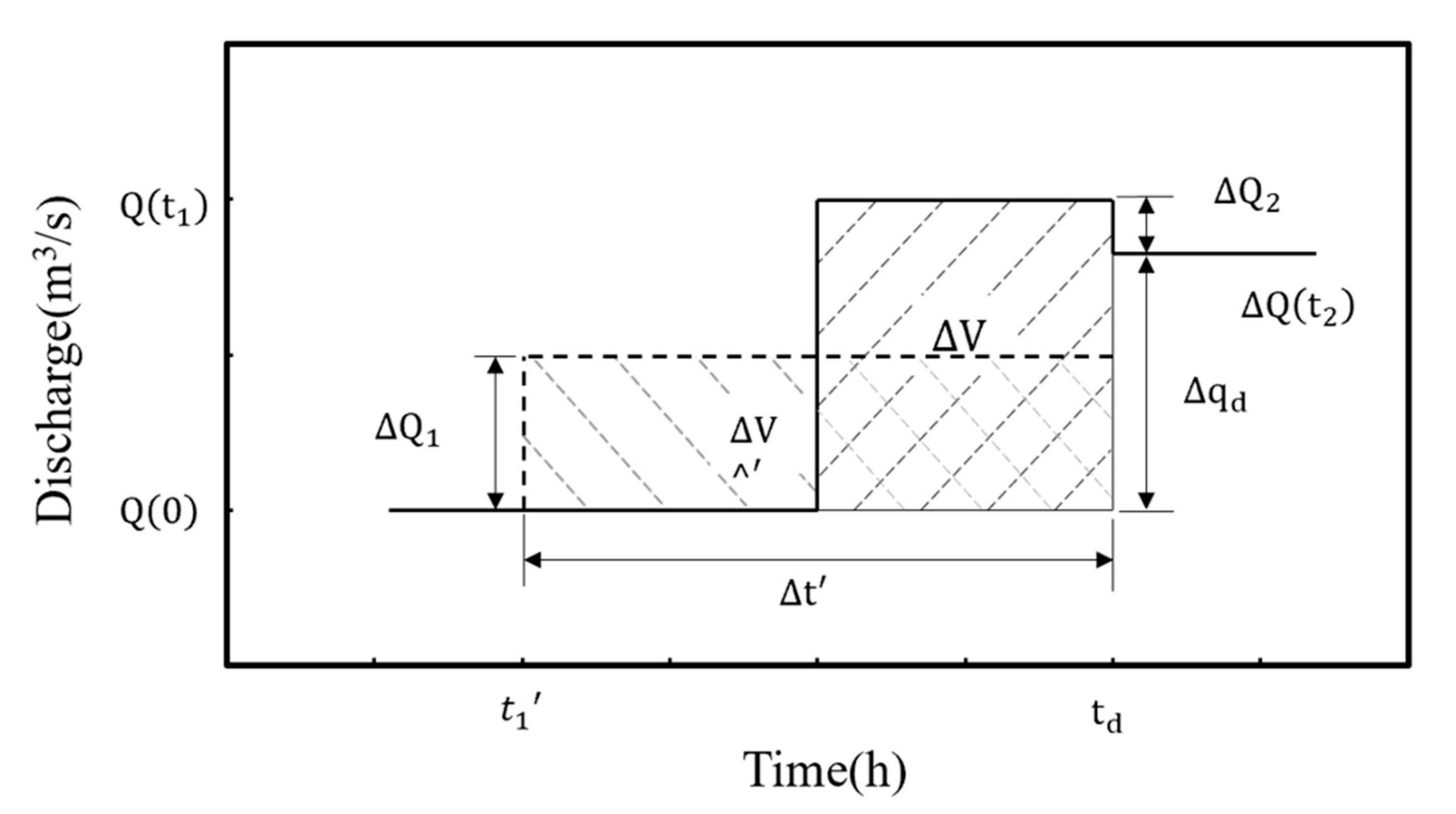
3.1. Stepwise Storage Compensation Algorithm
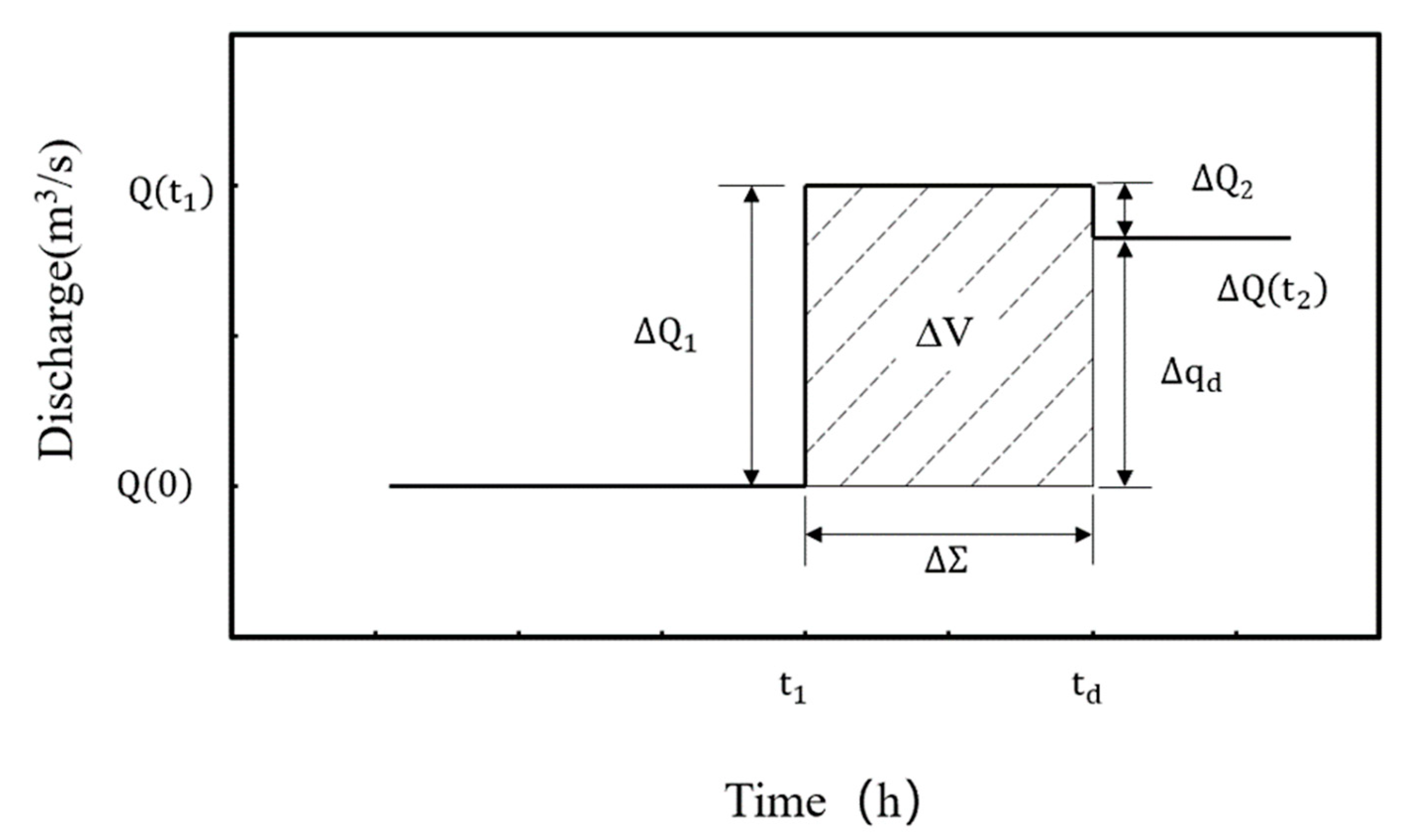
Traditional Storage Compensation Algorithm
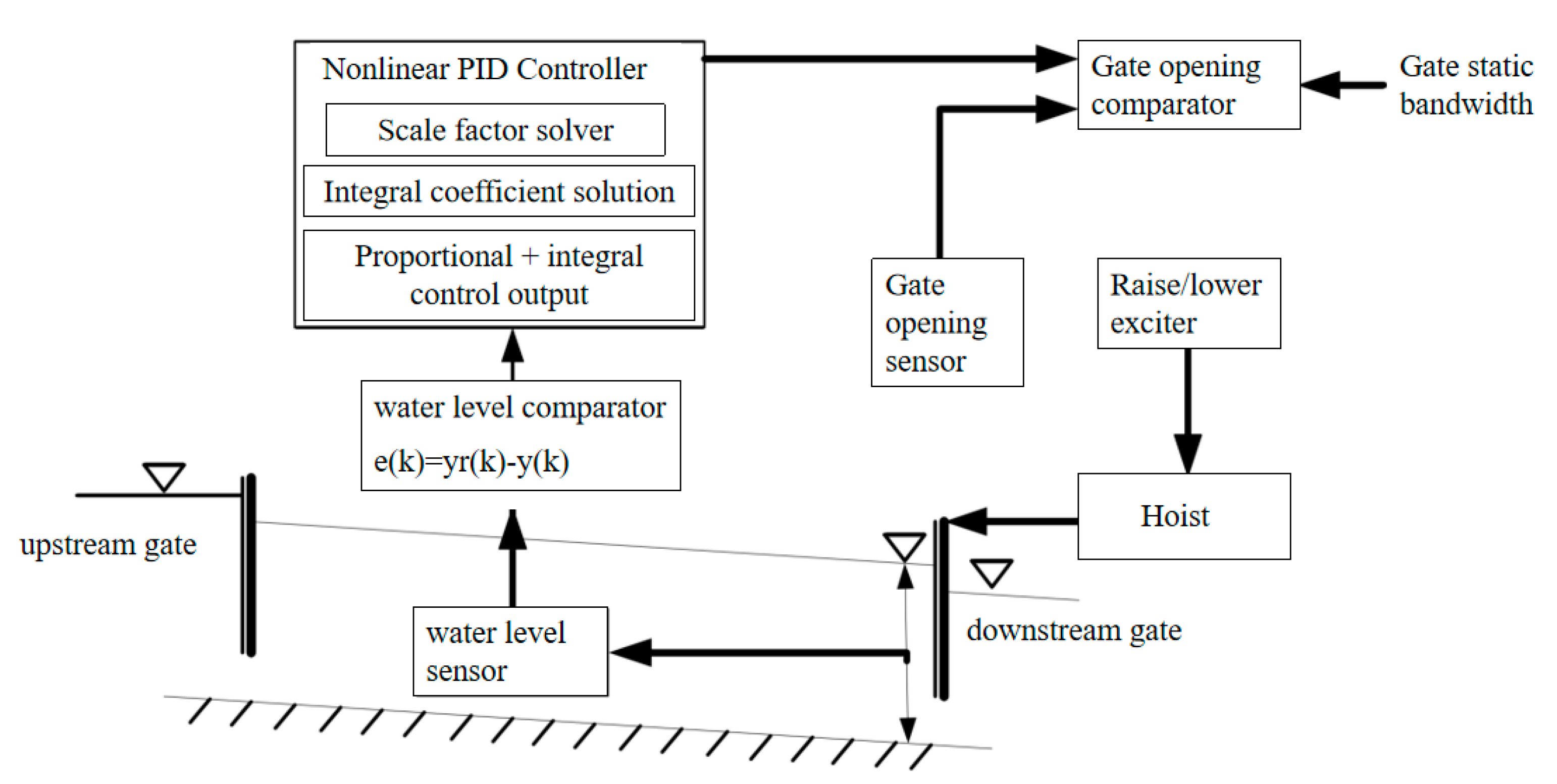
3.2. Improved PID Control Algorithm
3.2.1. Traditional PID Control Algorithm
3.2.2. Improved PID Control Algorithm
3.3. Storage Compensation Algorithm and Non-Linear PID Control Algorithm
4. Conclusions
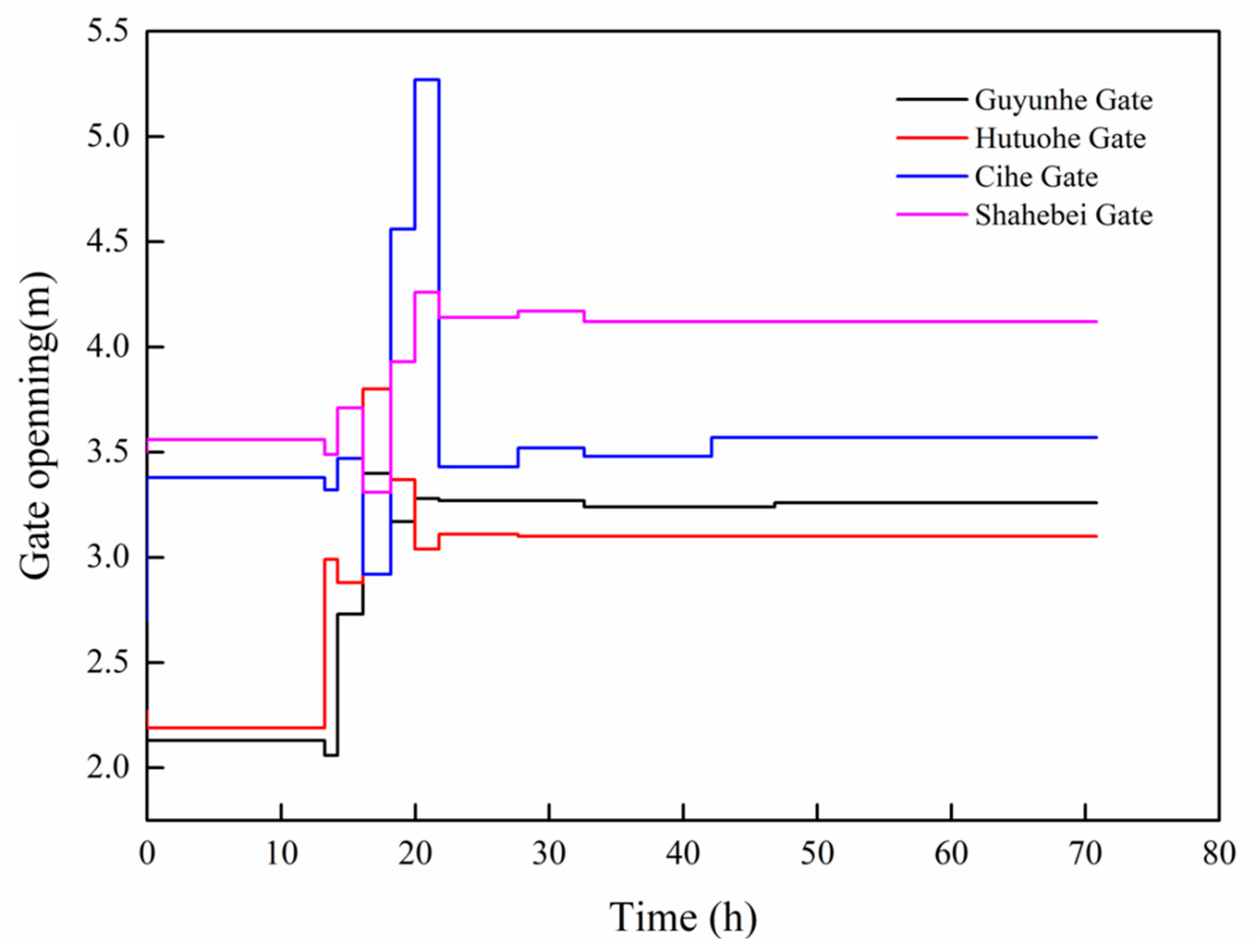
4.1. Analysis of Control Results of Traditional Storage Compensation Algorithm
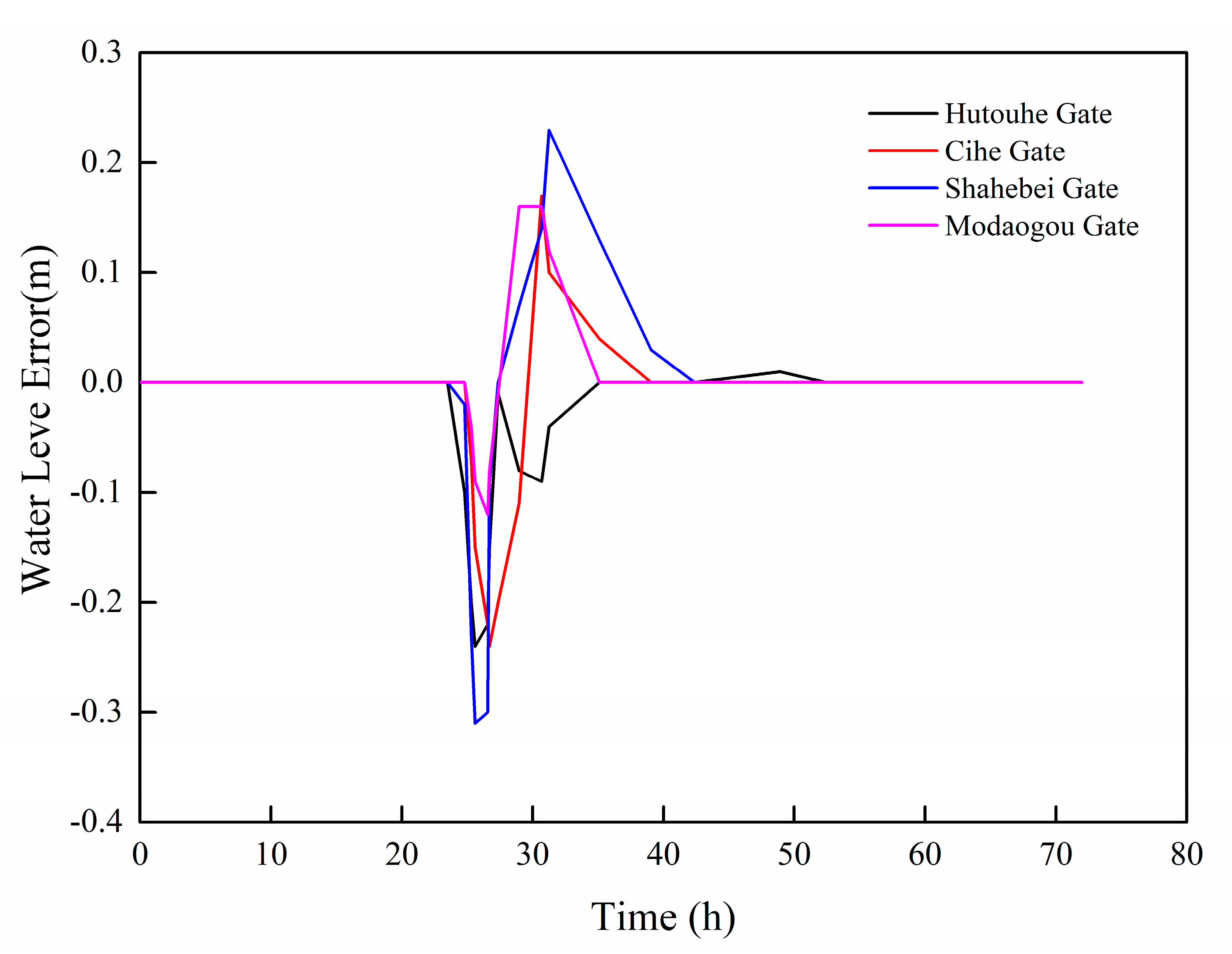
4.2. Analysis of the Results of the Storage Compensation and Improved PID Coupling Control Algorithm
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Li, S.; Yuan, F.; Mao, Z. Design and Simulation Verification of Water Dispatching System for Yintao Water Supply Phase I Project. China Rural. Water Conserv. Hydropower 2020, 9, 122–126. [Google Scholar]
- Guan, G.; Liao, W.; Mao, Z. Non-superimposed and insufficient compensation optimization algorithm for large-scale aqueduct systems. Huazhong Univ. Sci. Technol. 2019, 9, 60–66. [Google Scholar]
- Guan, G.; Liao, W.; Mao, Z. Comparison and Improvement of Time Delay Parameter Algorithm for Feedforward Storage Compensation Control of Canal System. Chin. J. Agric. Eng. 2018, 34, 72–80. [Google Scholar]
- Chen, L.; Sun, Y.; Huang, Y. Optimal scheduling model and application of reservoir flood control and other storage capacity. Prog. Water Sci. 2018, 29, 374–382. [Google Scholar]
- Lama, G.F.C.; Errico, A.; Pasquino, V.; Mrzaer, S.; Preti, F.; Chirico, G.B. Velocity uncertainty quantification based on Riparian vegetation indices in open channels colonized by Phragmites australis. Ecohydraulics 2022, 7, 71–76. [Google Scholar] [CrossRef]
- Khan, M.A.; Sharma, N.; Lama, G.F.C.; Hasan, M.; Garg, R.; Busico, G.; Alharbi, R.S. Three-Dimensional Hole Size (3DHS) Approach for Water Flow Turbulence Analysis over Emerging Sand Bars: Flume-Scale Experiments. Water 2022, 14, 1889. [Google Scholar] [CrossRef]
- Yang, K. Research progress and frontier scientific issues of hydraulic control of long-distance water delivery. J. Hydraul. Eng. 2016, 47, 424–435. [Google Scholar]
- Fang, S.; Li, Y.; Wu, B. Study on constant water level in front of sluice of large water transfer channel. Adv. Water Sci. 2008, 1, 68–71. [Google Scholar]
- Cui, W.; Chen, W.; Mu, X. Research on improved storage compensation algorithm for open channel feedforward control. Irri. Drai 2011, 30, 12–17. [Google Scholar]
- Wu, H.; Lei, X.; Qin, T.; Xu, H. Operation and Control Mode of Canal System Storage Compensation in the Middle Route of South-to-North Water Diversion. South-North Water Divers. Water Conserv. Sci. Technol. 2015, 13, 788–792+802. [Google Scholar]
- Yan, P.; Zhang, Z.; Lei, X. A Simple Method for the Control Time of a Pumping Station to Ensure a Stable Water Level Immediately Upstream of the Pumping Station under a Change of the Discharge in an Open Channel. Water 2021, 13, 355. [Google Scholar] [CrossRef]
- Gu, W.; Yao, J.; Yao, Z. Output feedback model predictive control of hydraulic systems with disturbances compensation. ISA Trans. 2018, 88, 216–224. [Google Scholar] [CrossRef] [PubMed]
- Maryam, J.; Mojtaba, S. Comparative Application of Model Predictive Control and Particle Swarm Optimization in Optimum Operation of a Large-Scale Water Transfer System. Water Resour. Manag. 2021, 35, 707–727. [Google Scholar]
- Ding, Z.; Wang, C.; Tan, G. Research on the operation mode of the downstream constant water level of canal storage compensation. Appl. Basic Eng. Sci. 2011, 19, 700–711. [Google Scholar]
- Shang, Y.; Wu, B.; Li, T. Design and Simulation of Predictable Algorithm for Channel Water Diversion Disturbance. Adv. Water Sci. 2011, 22, 242–248. [Google Scholar]
- Cui, W.; Chen, W.; Mu, X.; Guo, X. Study on feedforward control time of long water conveyance channel. Hydraul. Conserv. 2009, 40, 1345–1350. [Google Scholar]
- Robert, S.G.; Eduardo, B.; Robert, J.S. Automated scheduling of open-channel deliveries: Potential and limiations. In SCADA and Related Technologiesfor Irrigation District Modernization, 2nd ed.; USCID: Phoenix, AZ, USA, 2007; pp. 23–32. [Google Scholar]
- Schuurmans, J.; Clemmens, A.J.; Dijkstra, S.; Hof, A.; Brouwer, R. Modeling of Irrigation and Drainage Canals for Controller Design. J. Irrig. Drain. Eng. 1999, 125, 338–344. [Google Scholar] [CrossRef] [Green Version]
- Bautista, E.; Clemmens, A. Volume Compensation Method for Routing Irrigation Canal Demand Changes. J. Irrig. Drain. Eng. 2005, 131, 494–503. [Google Scholar] [CrossRef] [Green Version]
- Parrish, J. A Methodologyfor Automated Control of Sloping Canals; University of Iowa: Lowa City, IA, USA, 1997. [Google Scholar]
- Kong, L.; Wang, H.; Lei, X.; Quan, J.; Yang, Q. Research on real-time control of open canal based on linear predictive control method. J. Hydraul. Eng. 2020, 51, 326–334. [Google Scholar]
- Srinivas, N.; Deb, K. Muiltiobj ective Optimization Using Nondominated Sorting in Genetic Algorithms. Evol. Comput. 1994, 2, 221–248. [Google Scholar] [CrossRef]
- Buyalski, C.P.; Ehler, D.G.; Falvey, H.T.; Rogers, D.C.; Serfozo, E.A. Canal Systems Automation Manual: Volume 1; US Bureau of Reclamation: Denver, CO, USA, 1991.
- Cui, W.; Chen, W.; Mu, X. Dynamic regulation algorithm of volumes for long distance water division canal. J. China Inst. Water Resour. Hydropower Res. 2015, 13, 421–427. [Google Scholar]
- Wang, H.; Wang, X.; Lei, X.; Liao, W.; Wang, C.; Wang, J. The development and prospect of key techniques in the cascade reservoir operation. J. Hydraul. Eng. 2019, 50, 25–37. [Google Scholar]
- Wang, Y.; Li, W.; Fang, W. Optimized dispatch of flood control of cascade gate group on river channel in irrigation area. J. Nat. Disasters 2011, 20, 51–56. [Google Scholar]
- Clemmens, A.J.; Kacerek, T.F.; Grawitz, B.E.A. Test Cases for Canal Control Algorithms. J. Irrig. Drain. Eng. 1998, 124, 23–30. [Google Scholar] [CrossRef]
- Cui, W.; Chen, W.; Mu, X.; Bai, Y. Canal controller for the largest water transfer project in China. Irrig. Drain 2014, 63, 501–511. [Google Scholar] [CrossRef]
- Cui, W.; Chen, W.; Mu, X.; Guo, X. Anticipation time estimation for feedforward control of long canal. J. Hydraul. Eng. 2009, 40, 1345–1350. [Google Scholar]
- Fan, Y.; Gao, Z.; Chen, H.; Wang, S.; Chang, H. Analysis of canal feedforward control time based on constant water volume. Drain. Irrig. Mach. Eng. 2018, 36, 1131–1136. [Google Scholar]
- Yao, X.; Wang, C.; Li, C. Operation mode of serial canal system based on water volume control method. J. Hydraul. Eng. 2008, 39, 733–738. [Google Scholar]


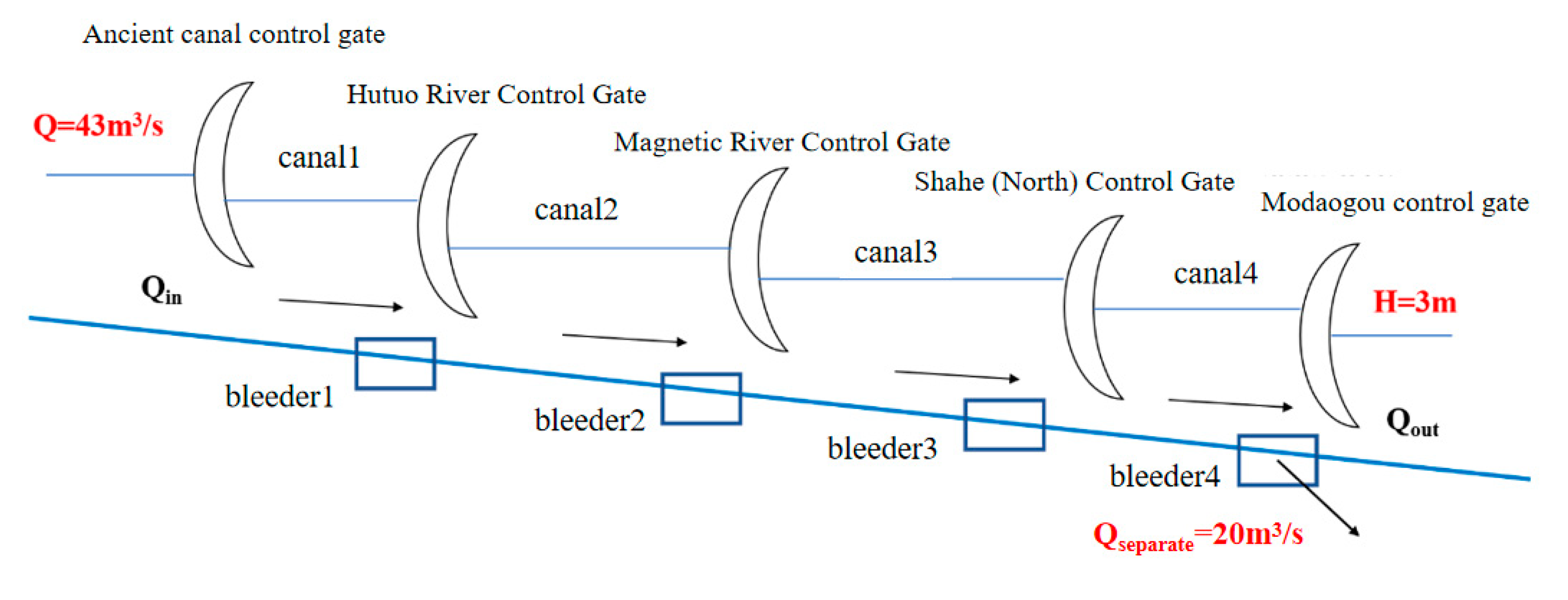


| Channel Number | Gate | Length (km) | Discharge (m3/s) | Water Depth (m) | Outflow (m3/s) | Roughness | Canal Bottom Elevation | ||
|---|---|---|---|---|---|---|---|---|---|
| Up | Down | Up (m) | Down (m) | ||||||
| 1 | Guyunhe gate | Hutuohe Gate | 9.87 | 43 | 3.3 | 0 | 0.023 | 70.40 | 69.86 |
| 2 | Hutuohe Gate | Cihe Gate | 22.03 | 43 | 3.21 | 0 | 0.023 | 69.86 | 69.13 |
| 3 | Cihe Gate | Shahebei Gate | 15.21 | 43 | 3.03 | 0 | 0.023 | 69.13 | 68.36 |
| 4 | Shahebei Gate | Modaogou Gate | 19.73 | 13 | 3 | 20 | 0.023 | 68.36 | 66.70 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shen, J.; Kang, B.; Tao, Y.; Lin, F.; Song, X. Study of a Control Algorithm with the Disturbance of Massive Discharge on an Open Channel. Water 2022, 14, 3252. https://doi.org/10.3390/w14203252
Shen J, Kang B, Tao Y, Lin F, Song X. Study of a Control Algorithm with the Disturbance of Massive Discharge on an Open Channel. Water. 2022; 14(20):3252. https://doi.org/10.3390/w14203252
Chicago/Turabian StyleShen, Jian, Bo Kang, Yuezan Tao, Fei Lin, and Xuegong Song. 2022. "Study of a Control Algorithm with the Disturbance of Massive Discharge on an Open Channel" Water 14, no. 20: 3252. https://doi.org/10.3390/w14203252






