Influence of the Gyeongju Earthquake on Observed Groundwater Levels at a Power Plant
Abstract
:1. Introduction
2. Materials and Methods
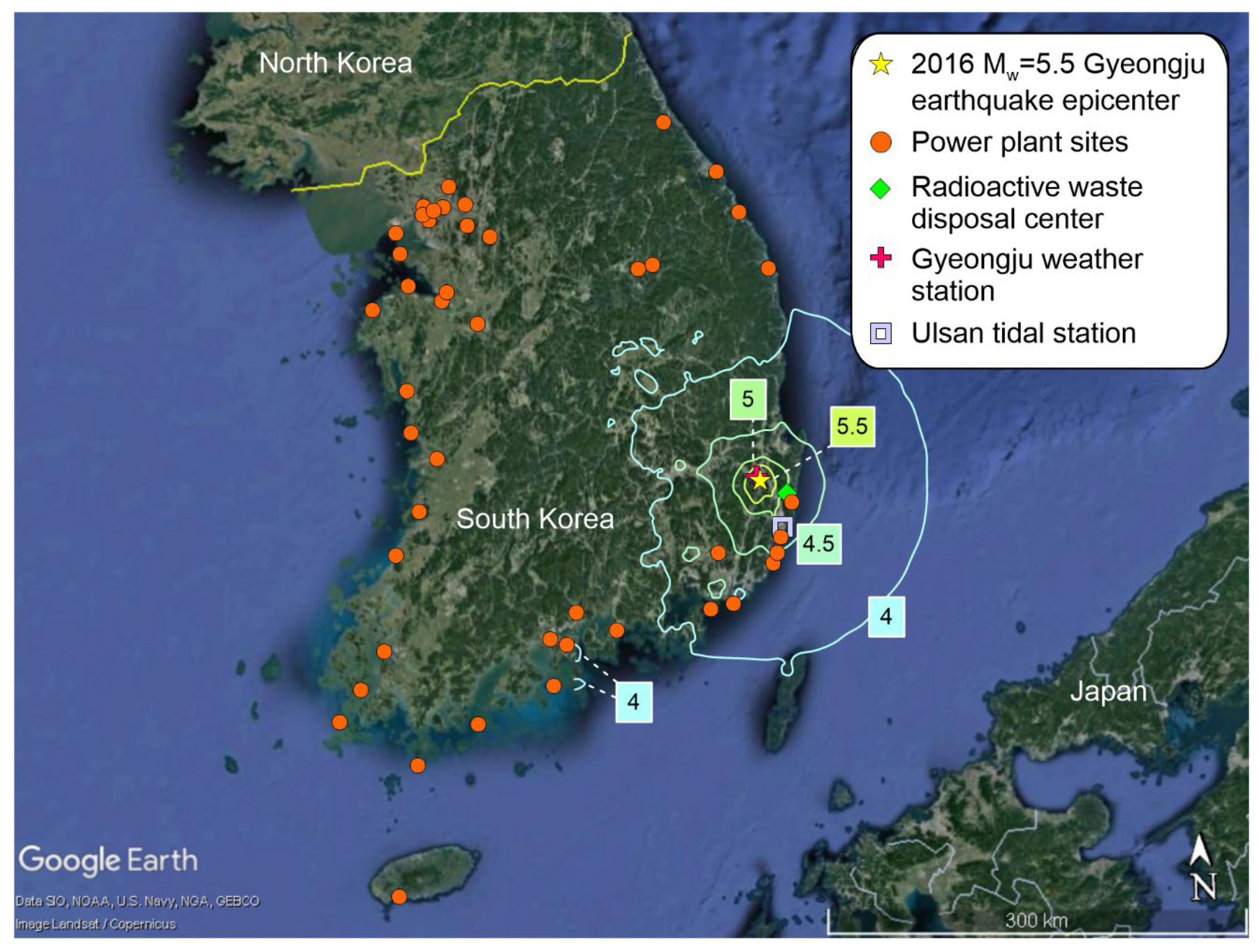
2.1. Study Site
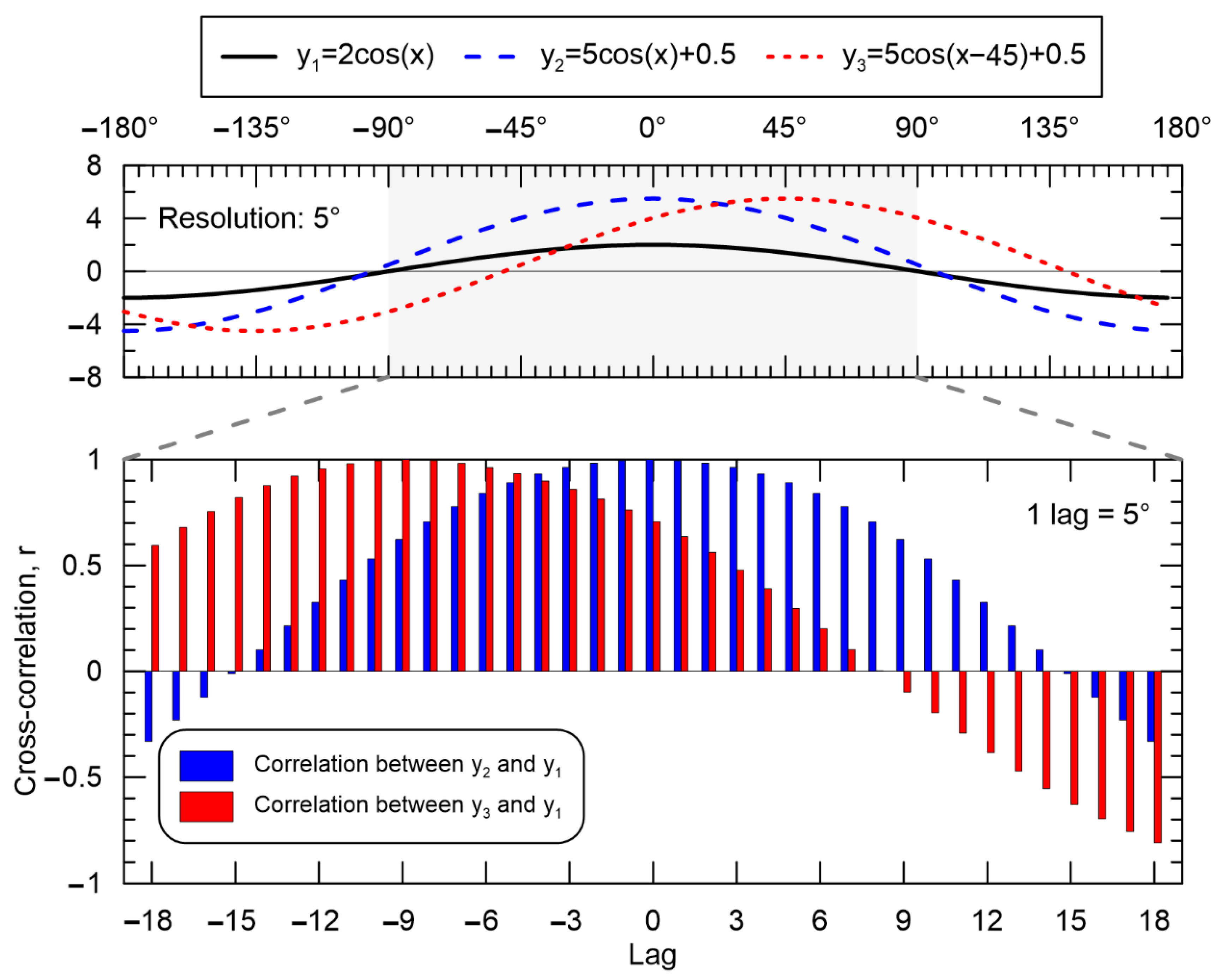
2.2. Cross-Correlation Analysis
2.3. Granger Causality Test
3. Results
3.1. Power Plant Environment
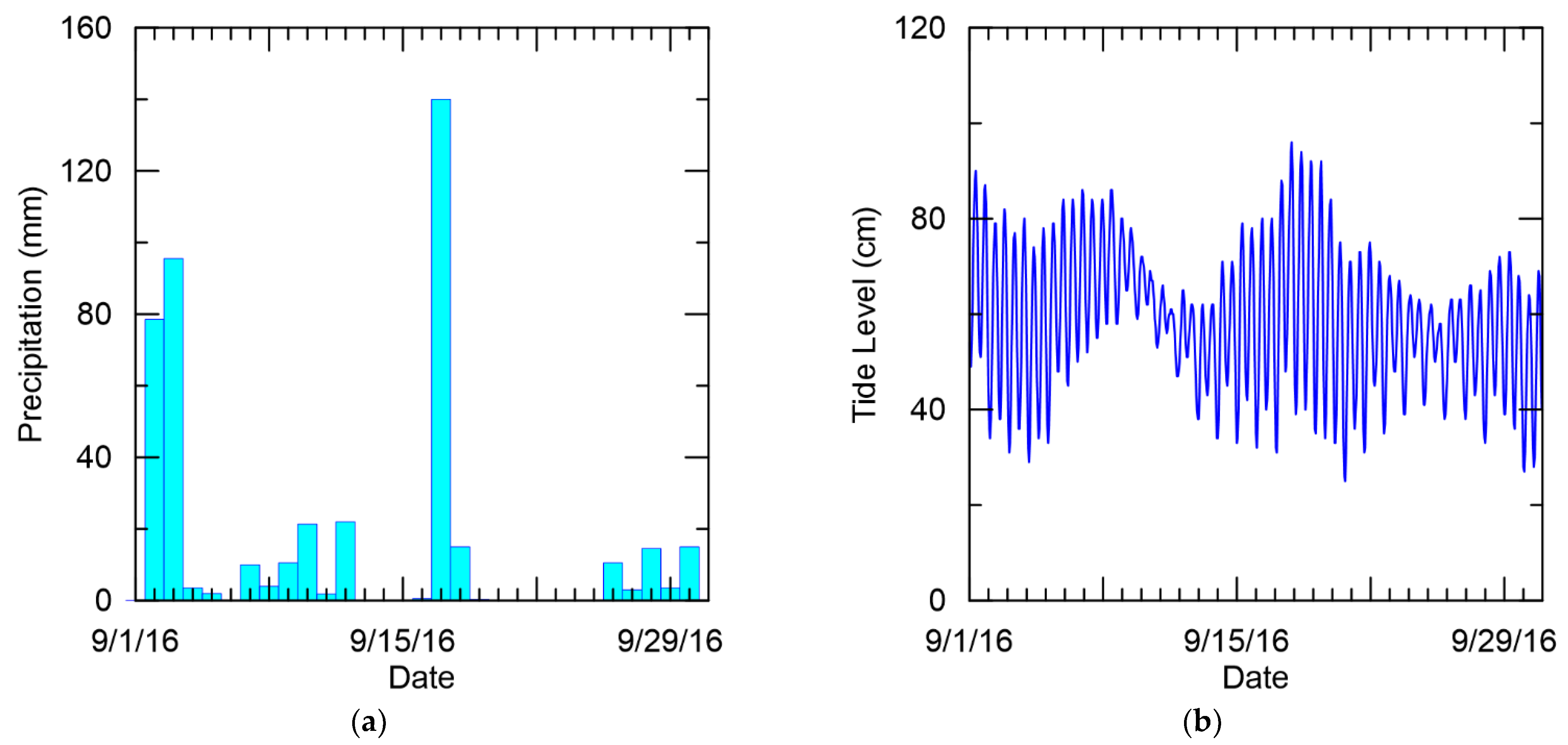
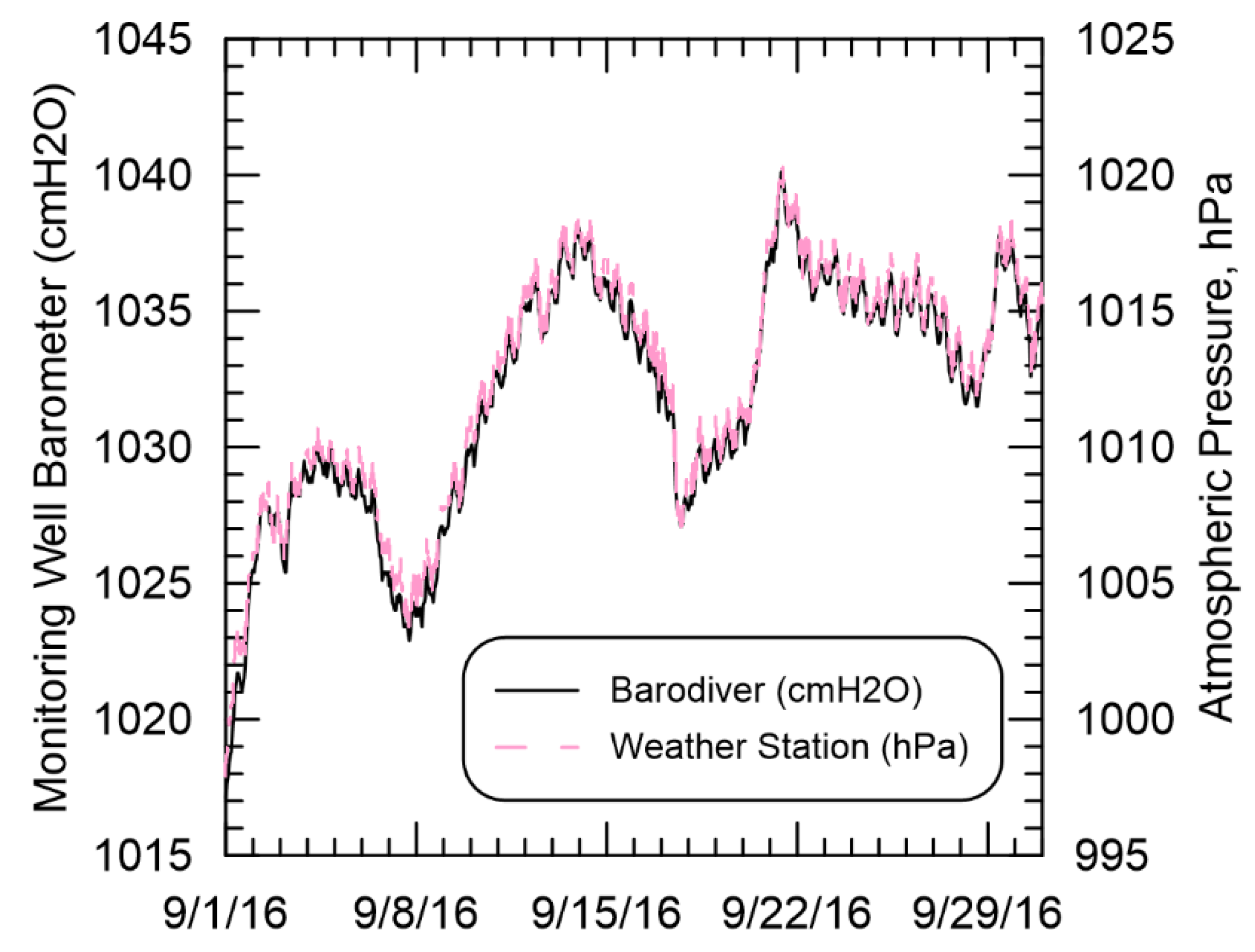
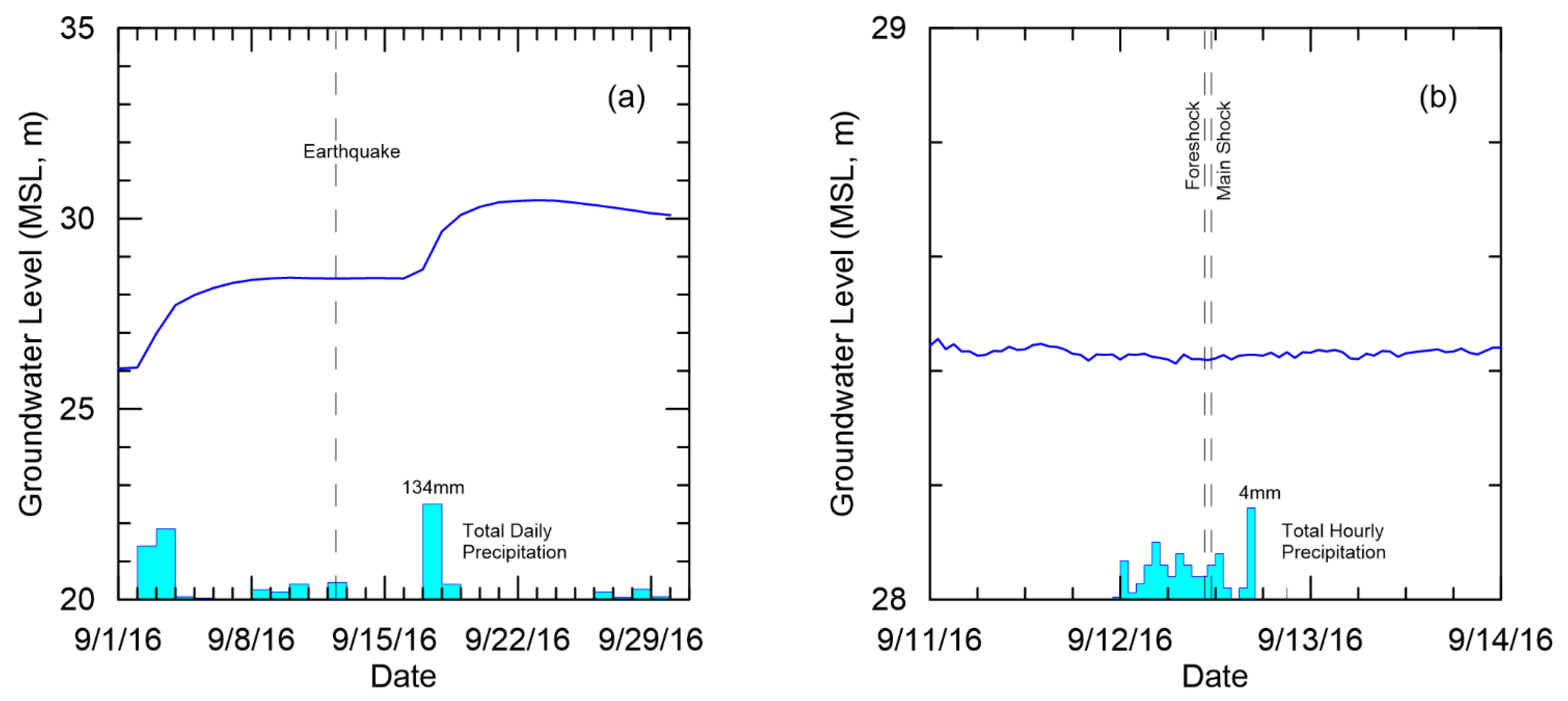
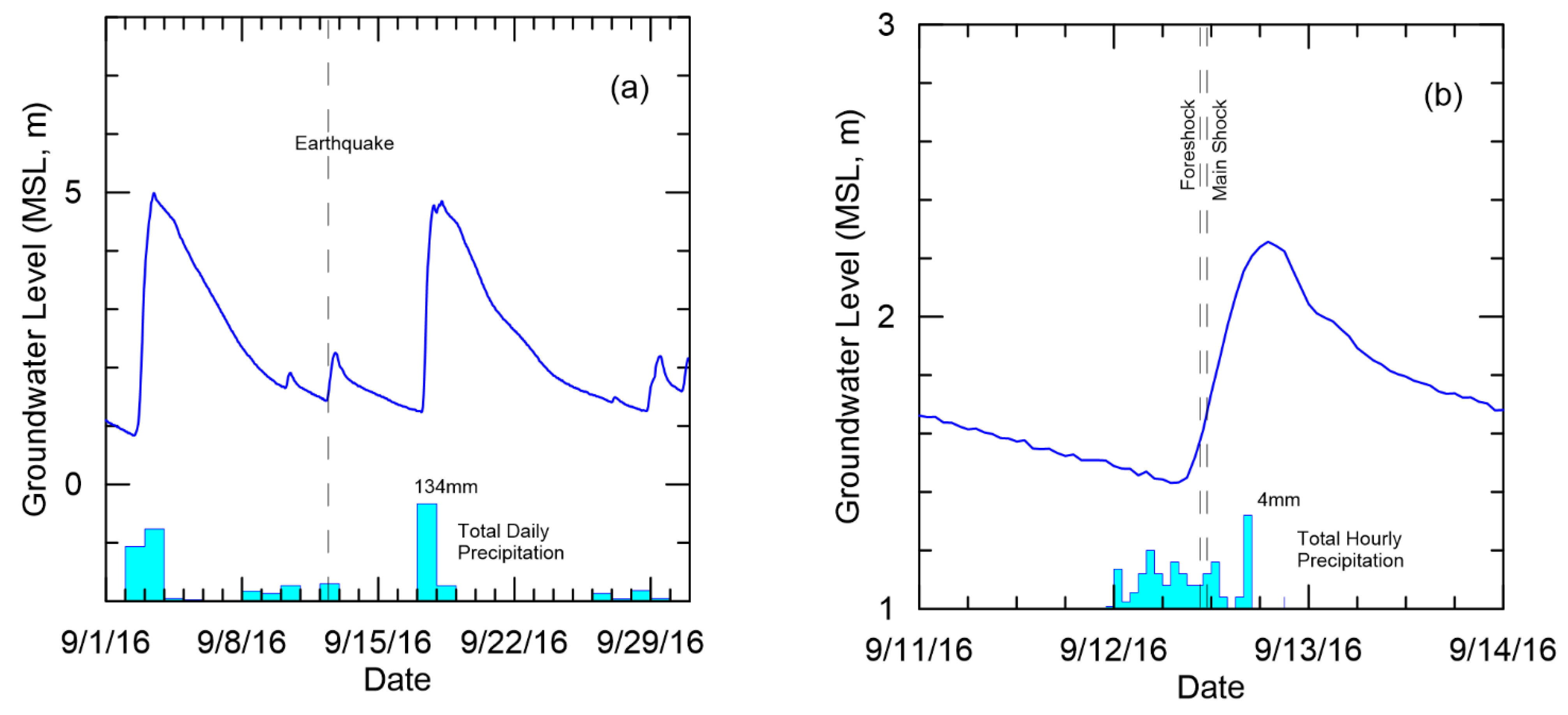
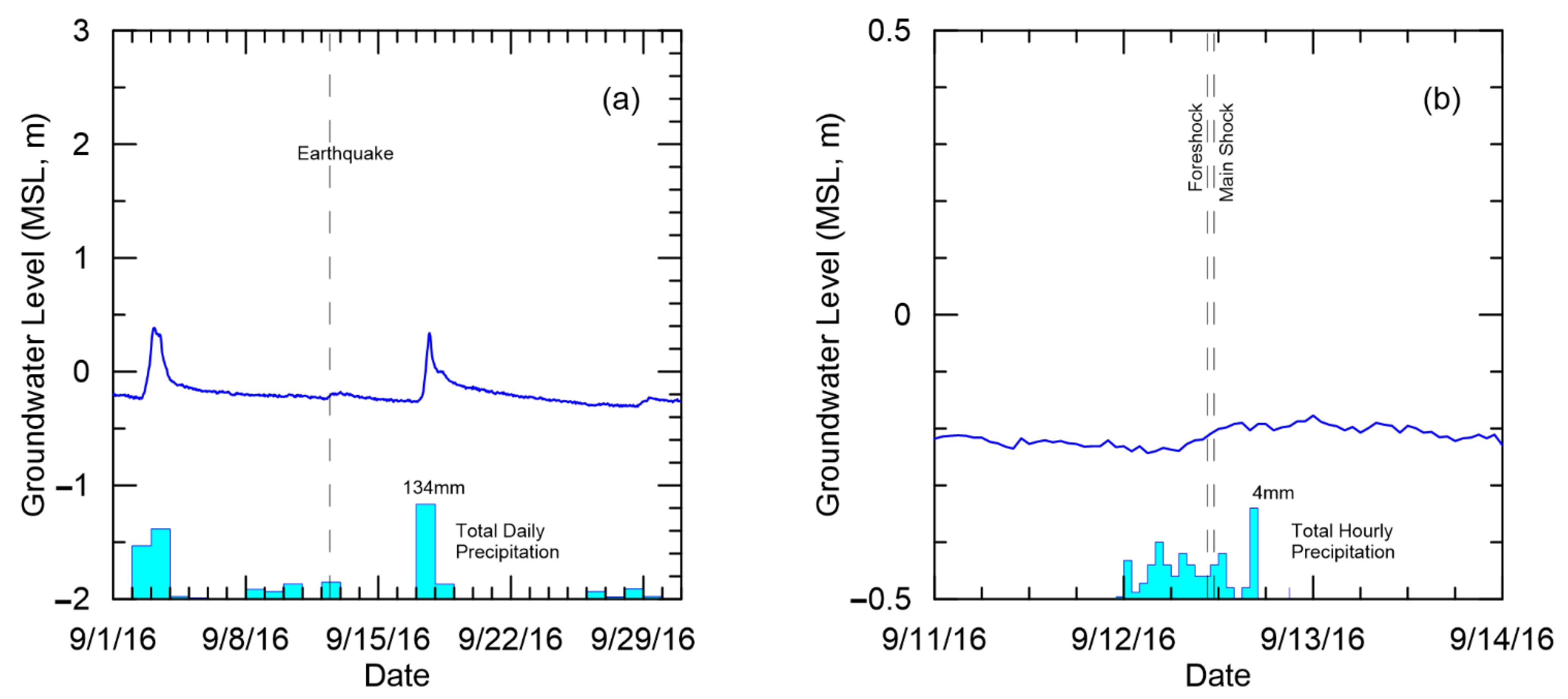
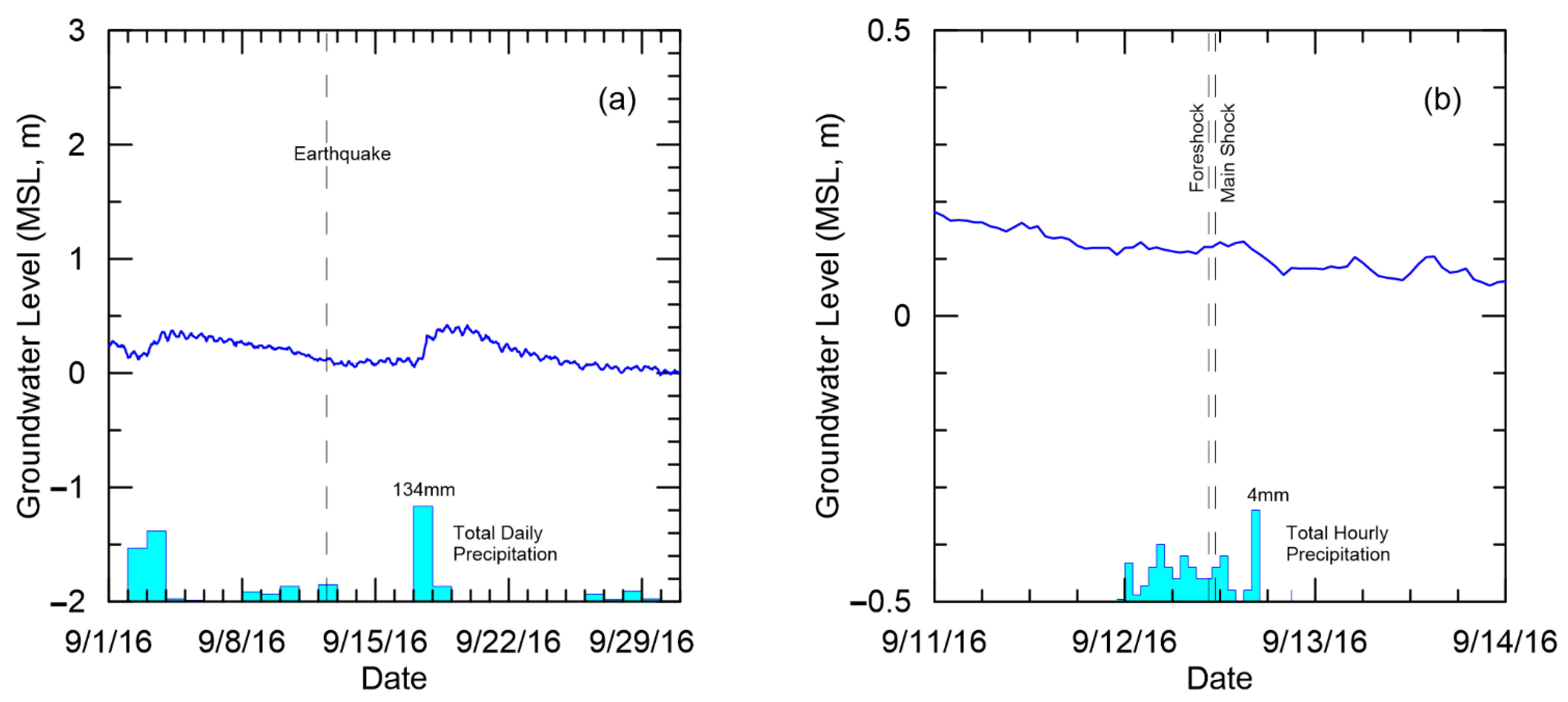
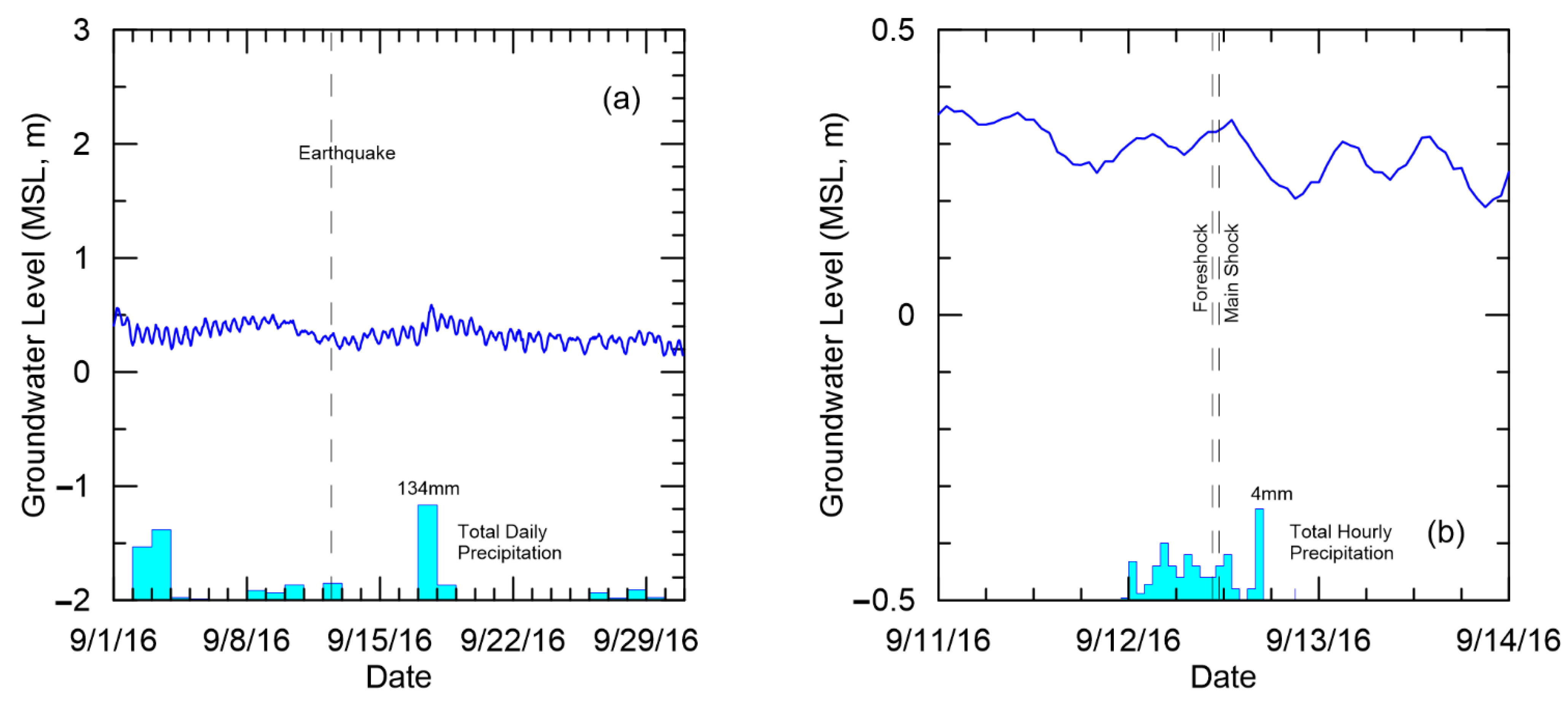
3.2. Groundwater Monitoring Wells
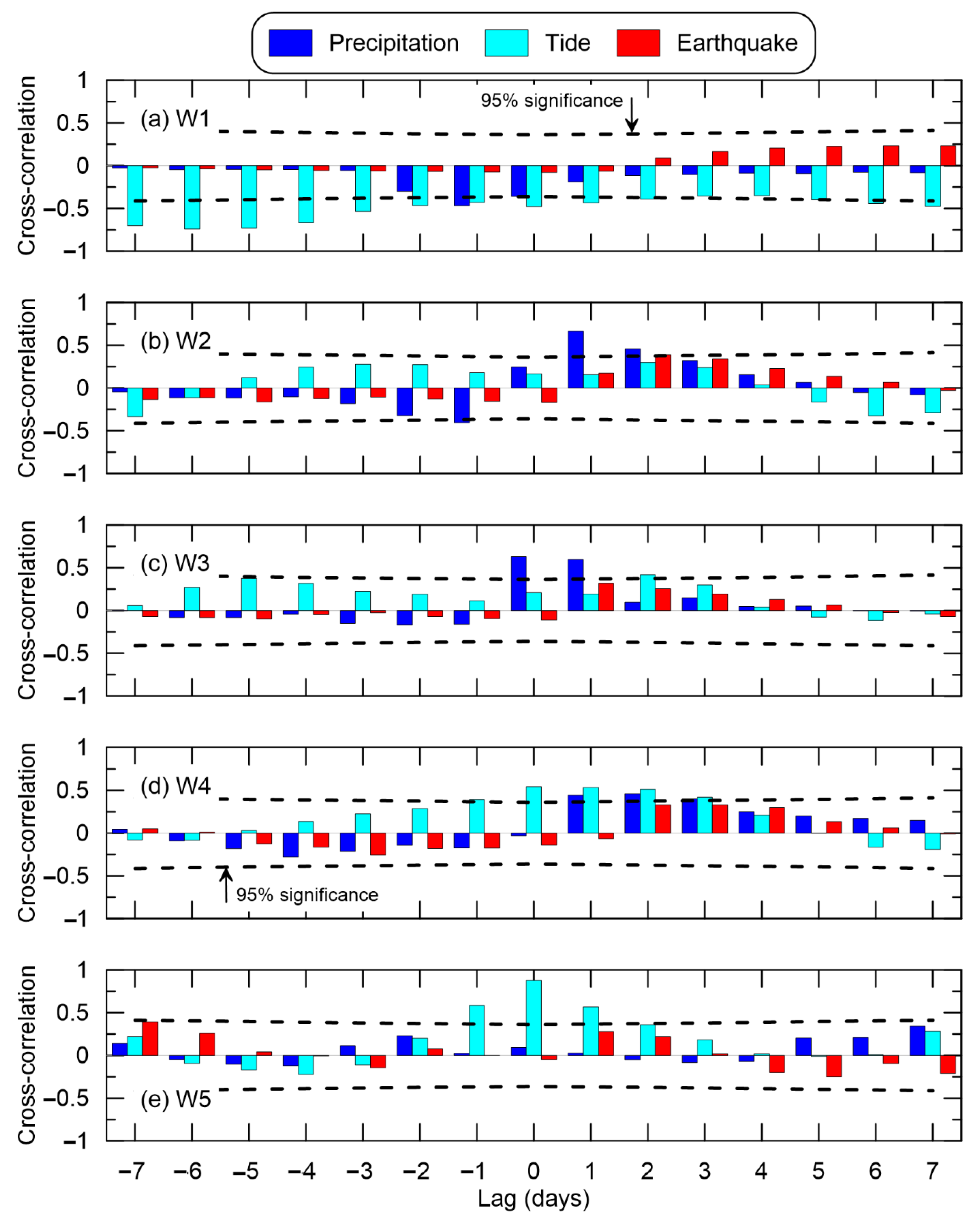
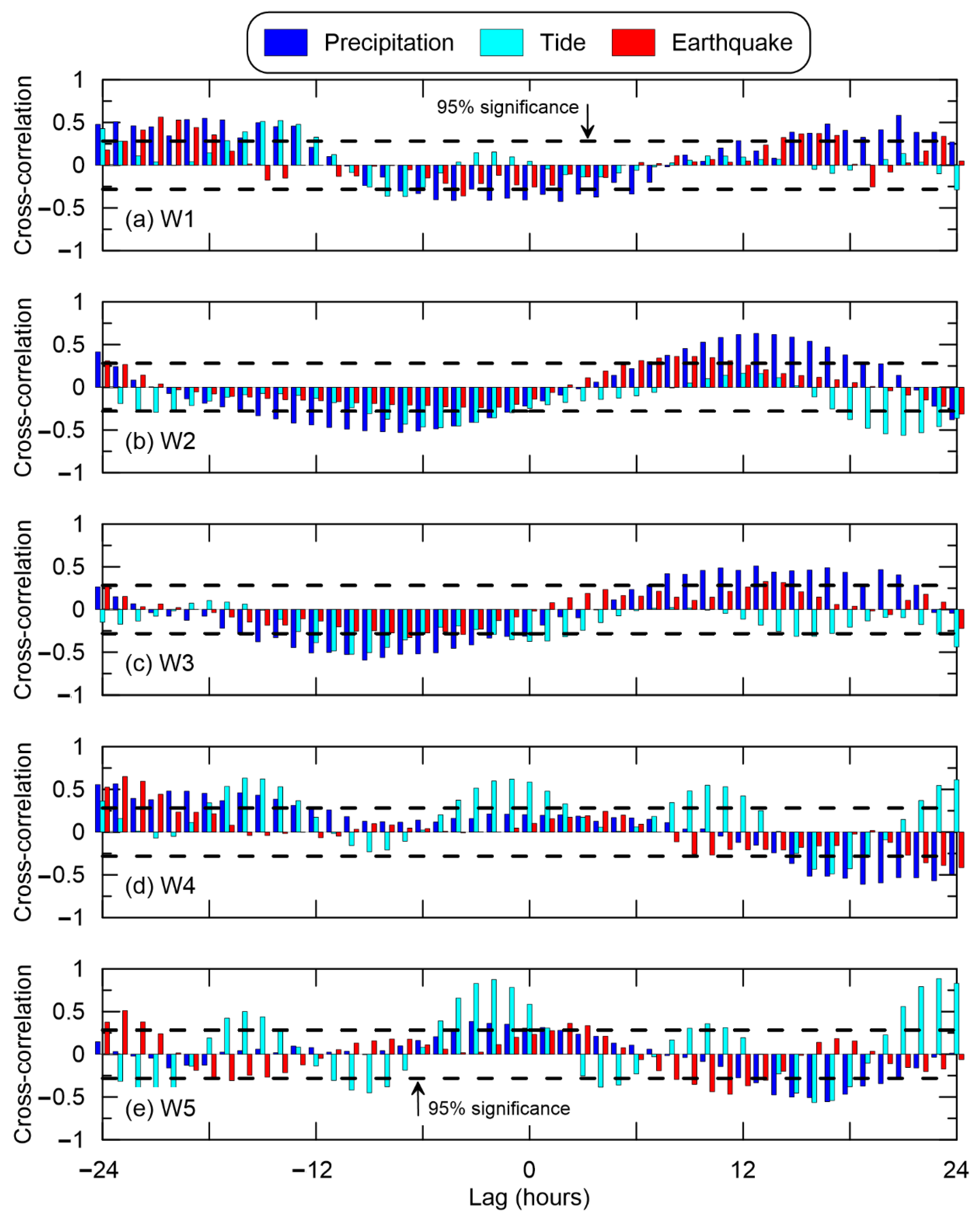
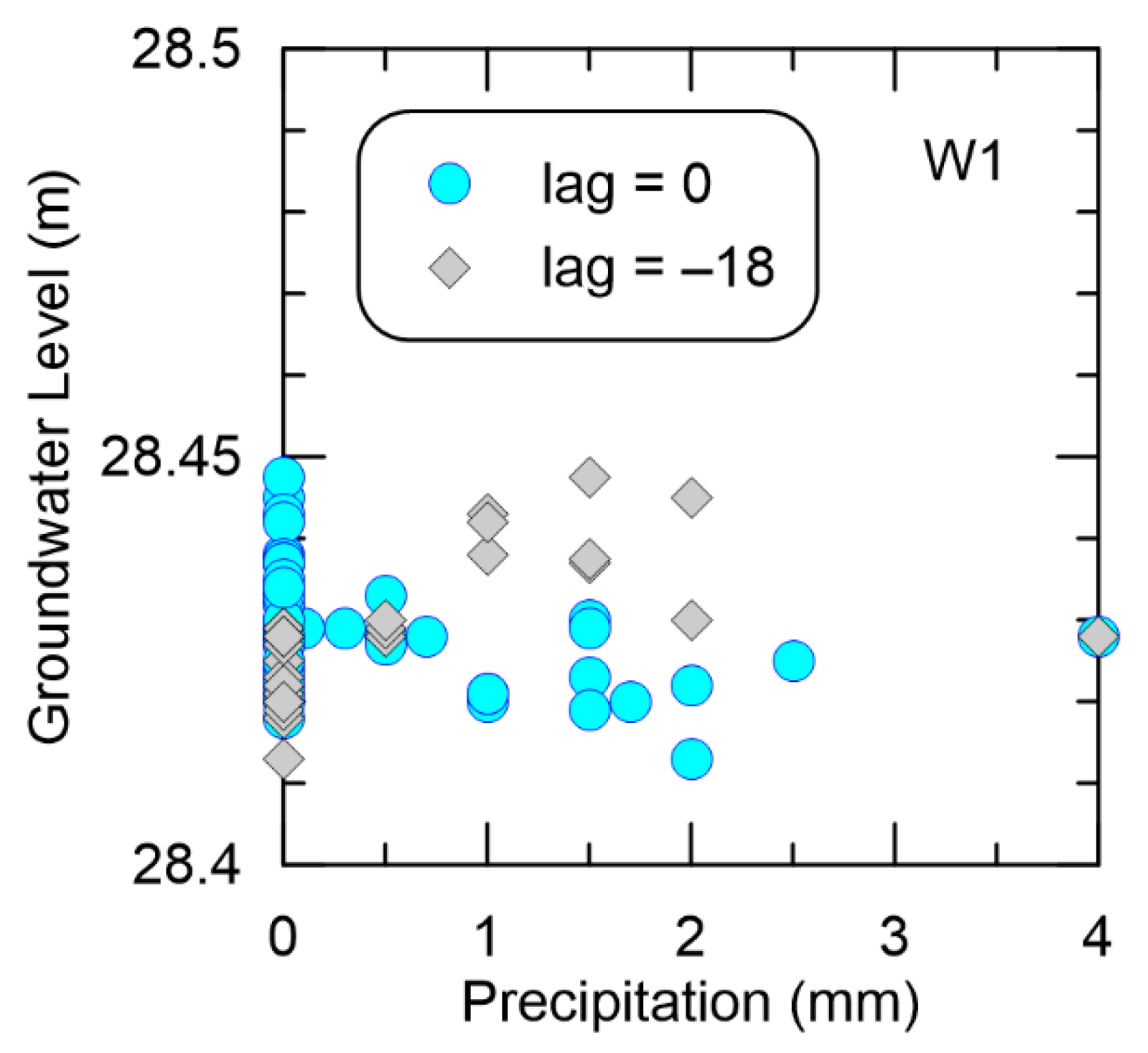
3.3. Cross-Correlation Analysis
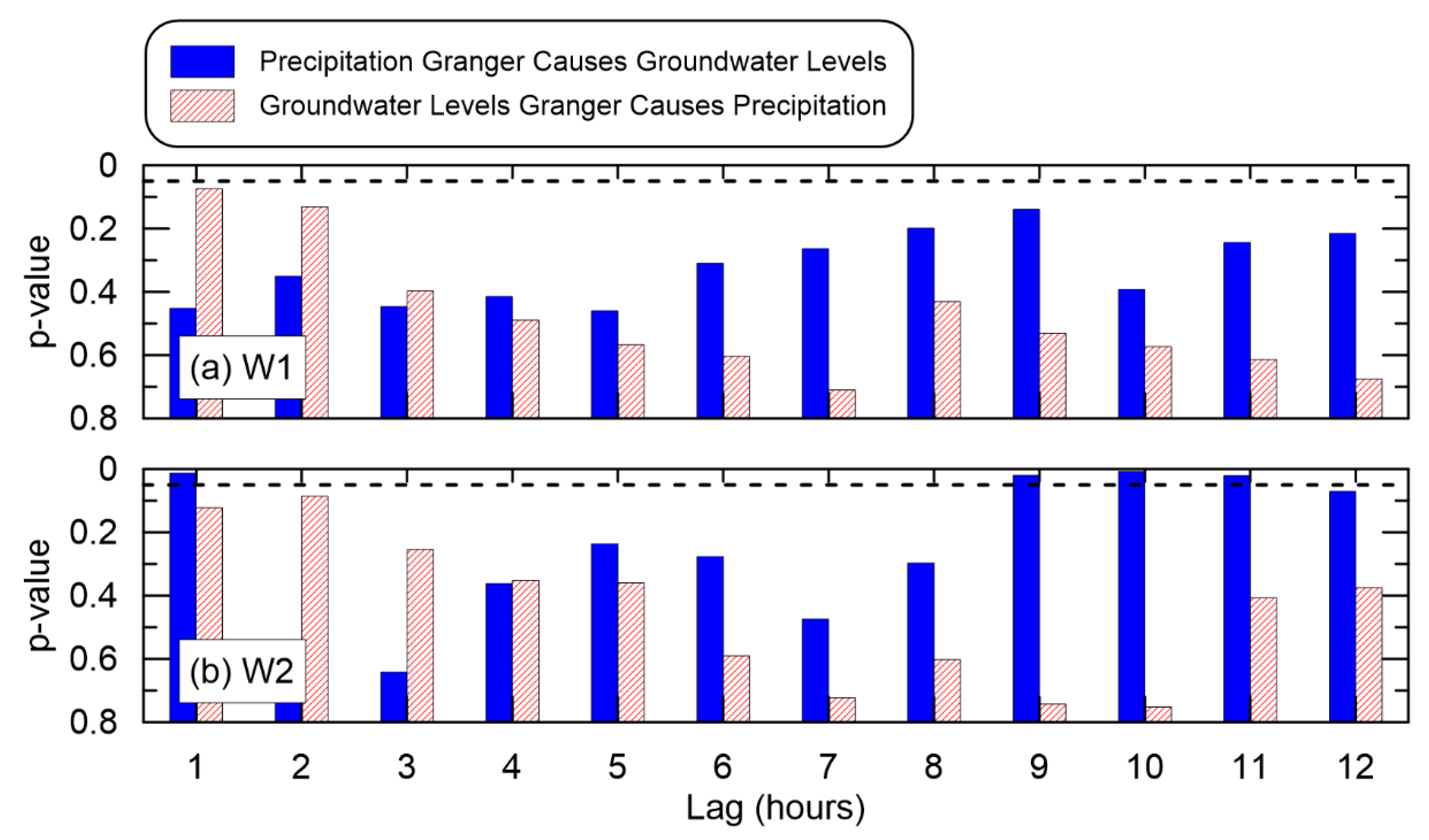
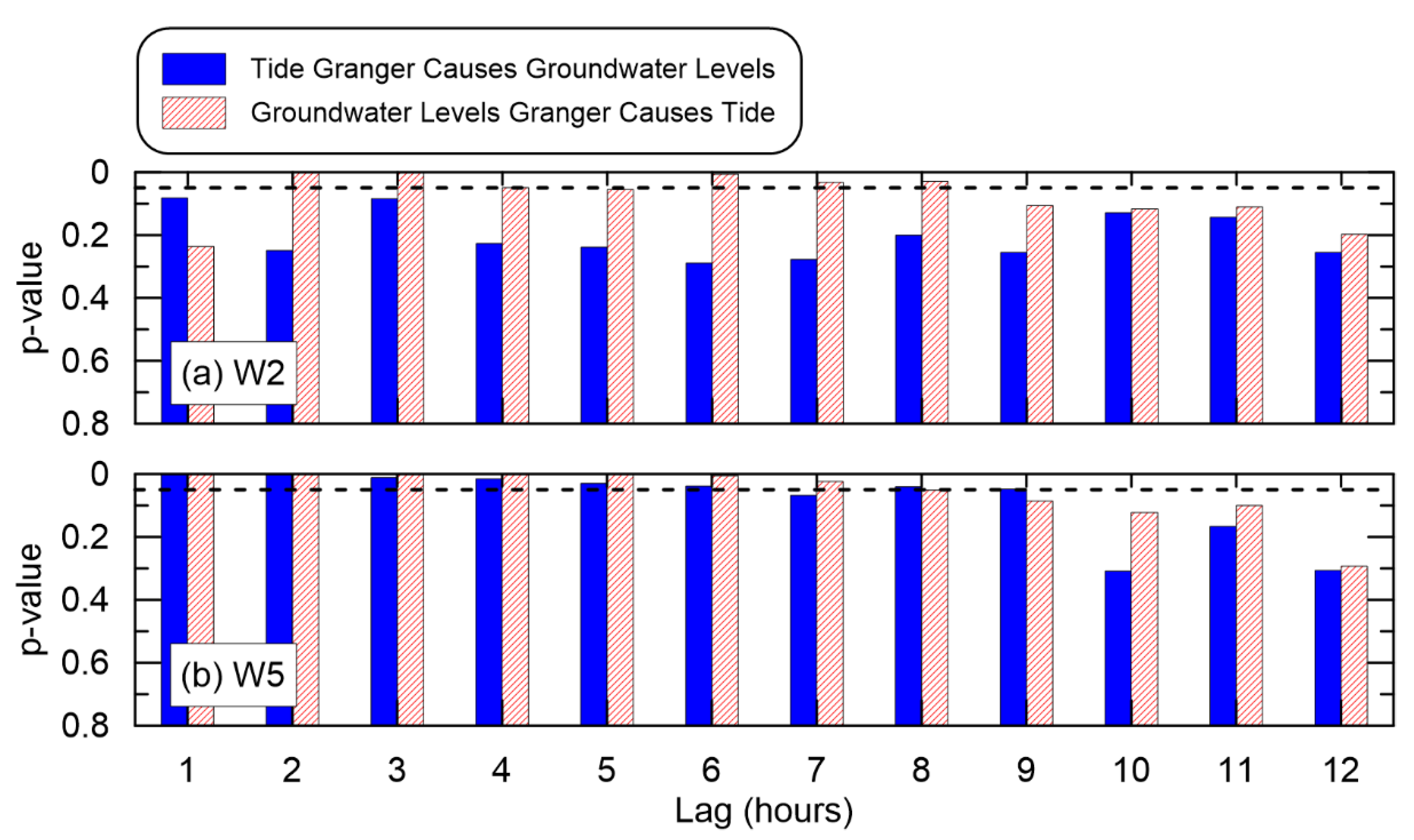
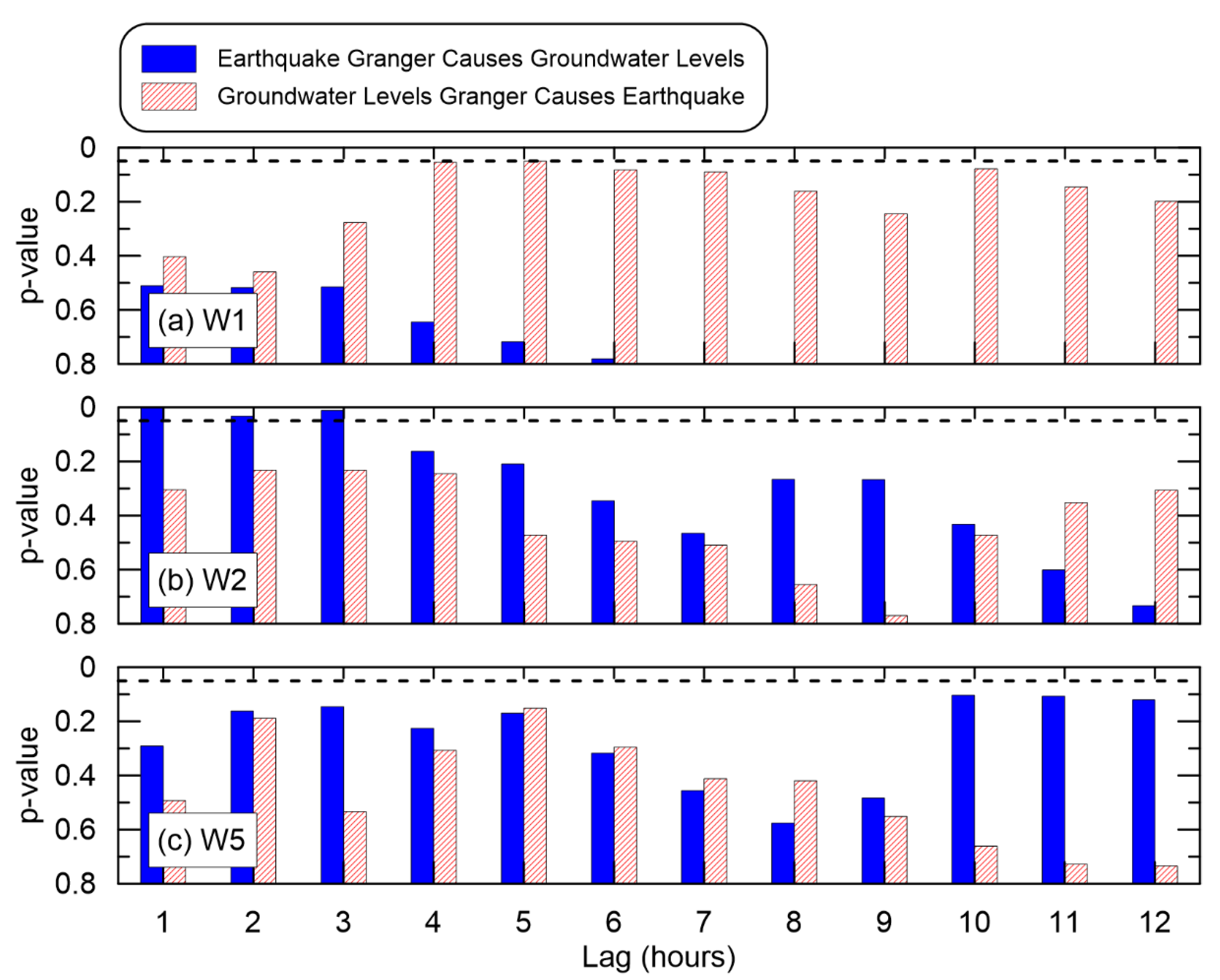
3.4. Granger Causality Tests
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Baba, A.; Kaya, A.; Birsoy, Y. The effect of yatagan thermal power plant (mugla, turkey) on the quality of surface and ground waters. Water Air Soil Pollut. 2003, 149, 93–111. [Google Scholar] [CrossRef]
- Pandey, V.; Ray, M.; Kumar, V. Assessment of water-quality parameters of groundwater contaminated by fly ash leachate near Koradi Thermal Power Plant, Nagpur. Environ. Sci. Pollut. Res. 2020, 27, 27422–27434. [Google Scholar] [CrossRef]
- Zhao, Y.Y.; Zhang, Y.; Liu, X.C.; Wang, J. Prediction of groundwater environmental impact on a power plant under accident conditions. Environ. Earth Sci. 2018, 77, 522. [Google Scholar] [CrossRef]
- Eldardiry, H.; Habib, E. Carbon capture and sequestration in power generation: Review of impacts and opportunities for water sustainability. Energy Sustain. Soc. 2018, 8, 6. [Google Scholar] [CrossRef] [Green Version]
- Park, J.B.; Jung, H.R.; Lee, E.Y.; Kim, C.L.; Kim, G.Y.; Kim, K.S.; Koh, Y.K.; Park, K.W.; Cheong, J.H.; Jeong, C.W.; et al. Wolsong low- and intermediate-level radioactive waste disposal center: Progress and challenges. Nucl. Eng. Technol. 2009, 41, 477–492. [Google Scholar] [CrossRef] [Green Version]
- Liu, L.-B.; Roeloffs, E.; Zheng, X.-Y. Seismically induced water level fluctuations in the Wali well, Beijing, China. J. Geophys. Res. 1989, 94, 9453–9462. [Google Scholar] [CrossRef]
- Ohno, M.; Wakita, H.; Kanjo, K. A water well sensitive to seismic waves. Geophys. Res. Lett. 1997, 24, 691–694. [Google Scholar] [CrossRef]
- Muir-Wood, R.; King, G.C.P. Hydrological signatures of earthquake strain. J. Geophys. Res. Solid Earth 1993, 98, 22035–22068. [Google Scholar] [CrossRef]
- Roeloffs, E. Poroelastic techniques in the study of earthquake-related hydrologic phenomena. Adv. Geophys. 1996, 37, 135–195. [Google Scholar] [CrossRef]
- Wang, H.F. Effects of deviatoric stress on undrained pore pressure response to fault slip. J. Geophys. Res. Solid Earth 1997, 102, 17943–17950. [Google Scholar] [CrossRef]
- Domenico, P.A.; Schwartz, F.W. Physical and Chemical Hydrogeology, 2nd ed.; Wiley and Sons: New York, NY, USA, 1998; pp. 1–528. [Google Scholar]
- Cooper, H.H., Jr.; Bredehoeft, J.D.; Papadopulos, I.S.; Bennett, R.R. The response of well-aquifer systems to seismic waves. J. Geophys. Res. 1965, 70, 3915–3926. [Google Scholar] [CrossRef]
- Brodsky, E.E.; Roeloffs, E.; Woodcock, D.; Gall, I.; Manga, M. A mechanism for sustained groundwater pressure changes induced by distant earthquakes. J. Geophys. Res. 2003, 108, 1–10. [Google Scholar] [CrossRef] [Green Version]
- Cleasson, L.; Skelton, A.; Graham, C.; Morth, C.M. The timescale and mechanisms of fault sealing and water–rock interaction after an earthquake. Geofluids 2007, 7, 427–440. [Google Scholar] [CrossRef]
- Jang, C.S.; Liu, C.W.; Chia, Y.; Cheng, L.H.; Chen, Y.C. Changes in hydrogeological properties of the River Choushui alluvial fan aquifer due to the 1999 Chi-Chi earthquake, Taiwan. Hydrogeol. J. 2008, 16, 389–397. [Google Scholar] [CrossRef]
- M 5.4–6 km S of Gyeongju, South Korea. Available online: https://earthquake.usgs.gov/earthquakes/eventpage/us10006p1f/executive (accessed on 6 May 2022).
- Uchide, T.H.; Song, S.G. Fault rupture model of the 2016 gyeongju, south korea, earthquake and its implication for the underground fault system. Geophys. Res. Lett. 2018, 45, 2257–2264. [Google Scholar] [CrossRef]
- Woo, J.U.; Rhie, J.K.; Kim, S.R.; Kang, T.S.; Kim, K.H.; Kim, Y.H. The 2016 gyeongju earthquake sequence revisited: Aftershock interactions within a complex fault system. Geophys. J. Int. 2019, 217, 58–74. [Google Scholar] [CrossRef] [Green Version]
- M 4.9–14 km SW of Gyeongju, South Korea. Available online: https://earthquake.usgs.gov/earthquakes/eventpage/us10006p12/executive (accessed on 6 May 2022).
- Davison, C. On scales of seismic intensity and on the construction and use of isoseismal lines. Bull. Seismol. Soc. Am. 1921, 11, 95–129. [Google Scholar] [CrossRef]
- Wood, H.O.; Neumann, F. Modified Mercalli Intensity Scale of 1931. Bull. Seismol. Soc. Am. 1931, 21, 277–283. [Google Scholar] [CrossRef]
- The National Atlas of Korea. Available online: http://nationalatlas.ngii.go.kr/pages/page_1288.php (accessed on 6 May 2022).
- Kim, G.B.; Choi, M.R.; Lee, C.J.; Shin, S.H.; Kim, H.J. Characteristics of spatio-temporal distribution of groundwater level’s change after 2016 gyeongju earthquake. J. Geol. Soc. Korea 2018, 54, 93–105. [Google Scholar] [CrossRef]
- Lee, J.Y. Gyeongju earthquakes recorded in daily groundwater data at national groundwater monitoring stations in gyeongju. J. Soil Groundw. Environ. 2016, 21, 80–86. [Google Scholar] [CrossRef]
- Lee, J.W.; Woo, N.C.; Koh, D.-C.; Kim, K.-Y.; Ko, K.-S. Assessing aquifer responses to earthquakes using temporal variations in groundwater monitoring data in alluvial and sedimentary bedrock aquifers. Geomat. Nat. Hazards Risk 2020, 11, 742–765. [Google Scholar] [CrossRef]
- Lee, H.A.; Hamm, S.Y.; Woo, N.C. The abnormal groundwater changes as potential precursors of 2016 ml 5.8 gyeongju earthquake in korea. Econ. Environ. Geol. 2018, 51, 393–400. [Google Scholar] [CrossRef]
- Lee, H.A.; Hamm, S.Y.; Woo, N.C. Pilot-scale groundwater monitoring network for earthquake surveillance and forecasting research in korea. Water 2021, 13, 2448. [Google Scholar] [CrossRef]
- Wallace, R.E.; Teng, T.-L. Prediction of the Sungpan-Pingwu earthquakes, August 1976. Bull. Seismol. Soc. Am. 1980, 70, 1199–1223. [Google Scholar] [CrossRef]
- Merifield, P.; Lamar, D. Possible strain events reflected in water levels in wells along San Jacinto fault zone, southern California. Pure Appl. Geophys. 1984, 122, 245–254. [Google Scholar] [CrossRef]
- Martinelli, G. Contributions to a history of earthquake prediction research. Seismol. Res. Lett. 2000, 71, 583–588. [Google Scholar] [CrossRef]
- Song, S.-R.; Ku, W.-Y.; Chen, Y.-L.; Lin, Y.-C.; Liu, C.-M.; Kuo, L.-W.; Yang, T.F.; Lo, H.-J. Groundwater chemical anomaly before and after the Chi-Chi earthquake in Taiwan. Terr. Atmos. Ocean. Sci. 2003, 14, 311–320. [Google Scholar] [CrossRef] [Green Version]
- Huang, F.; Li, M.; Ma, Y.; Han, Y.; Tian, L.; Yan, W.; Li, X. Studies on earthquake precursors in China: A review for recent 50 years. Geod. Geodyn. 2017, 8, 1–12. [Google Scholar] [CrossRef]
- Senthilkumar, M.; Gnanasundar, D.; Mohapatra, B.; Jain, A.K.; Nagar, A.; Parchure, P.K. Earthquake prediction from high frequency groundwater level data: A case study from Gujarat, India. HydroResearch 2020, 3, 118–123. [Google Scholar] [CrossRef]
- Rikitake, T. Earthquake precursors. Bull. Seismol. Soc. Am. 1975, 65, 1133–1162. [Google Scholar] [CrossRef]
- Cicerone, R.D.; Ebel, J.E.; Britton, J. A systematic compilation of earthquake precursors. Tectonophysics 2009, 476, 371–396. [Google Scholar] [CrossRef]
- Korea Meteorological Administration. Available online: http://www.kma.go.kr (accessed on 6 May 2022).
- Korea Hydrographic and Oceanographic Agency. Available online: http://www.khoa.go.kr/ (accessed on 6 May 2022).
- Granger, C.W.J. Investigating causal relations by econometric models and cross-spectral methods. Econometrica 1969, 37, 424–438. [Google Scholar] [CrossRef]
- Granger, C.W.J. Testing for causality: A personal viewpoint. J. Econ. Dyn. Control 1980, 2, 329–352. [Google Scholar] [CrossRef]
- Stokes, P.A.; Purdon, P.L. A study of problems encountered in granger causality analysis from a neuroscience perspective. Proc. Natl. Acad. Sci. USA 2017, 114, E7063–E7072. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Dickey, D.A.; Fuller, W.A. Distribution of the estimators for autoregressive time series with a unit root. J. Am. Stat. Assoc. 1979, 74, 427–431. [Google Scholar] [CrossRef]
- Fuller, W.A. Introduction to Statistical Time Series; John Wiley and Sons: New York, NY, USA, 1976. [Google Scholar]
- Dobrovolsky, I.P.; Zubkov, S.I.; Miachkin, V.I. Estimation of the size of earthquake preparation zones. Pure Appl. Geophys. 1979, 117, 1025–1044. [Google Scholar] [CrossRef]

| Well | I(0) | I(1) |
|---|---|---|
| W1 | No | Yes |
| W2 | No | Yes |
| W3 | Yes | Yes |
| W4 | No | Yes |
| W5 | Yes | Yes |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yee, E.; Choi, M. Influence of the Gyeongju Earthquake on Observed Groundwater Levels at a Power Plant. Water 2022, 14, 3229. https://doi.org/10.3390/w14203229
Yee E, Choi M. Influence of the Gyeongju Earthquake on Observed Groundwater Levels at a Power Plant. Water. 2022; 14(20):3229. https://doi.org/10.3390/w14203229
Chicago/Turabian StyleYee, Eric, and Minjune Choi. 2022. "Influence of the Gyeongju Earthquake on Observed Groundwater Levels at a Power Plant" Water 14, no. 20: 3229. https://doi.org/10.3390/w14203229
APA StyleYee, E., & Choi, M. (2022). Influence of the Gyeongju Earthquake on Observed Groundwater Levels at a Power Plant. Water, 14(20), 3229. https://doi.org/10.3390/w14203229






