Residual-Oriented Optimization of Antecedent Precipitation Index and Its Impact on Flood Prediction Uncertainty
Abstract
:1. Introduction
2. Materials and Methods
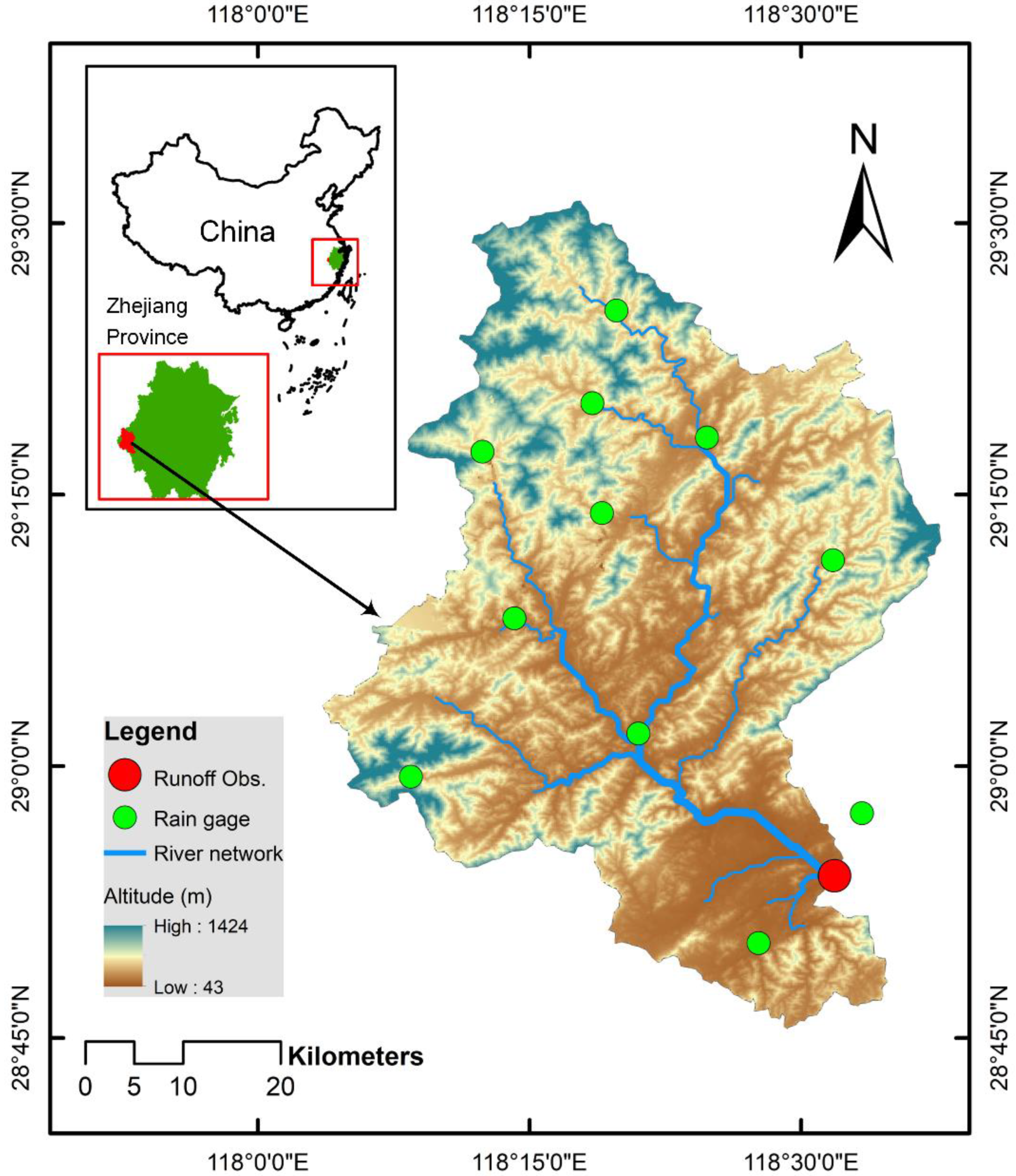
2.1. Study Area and Data
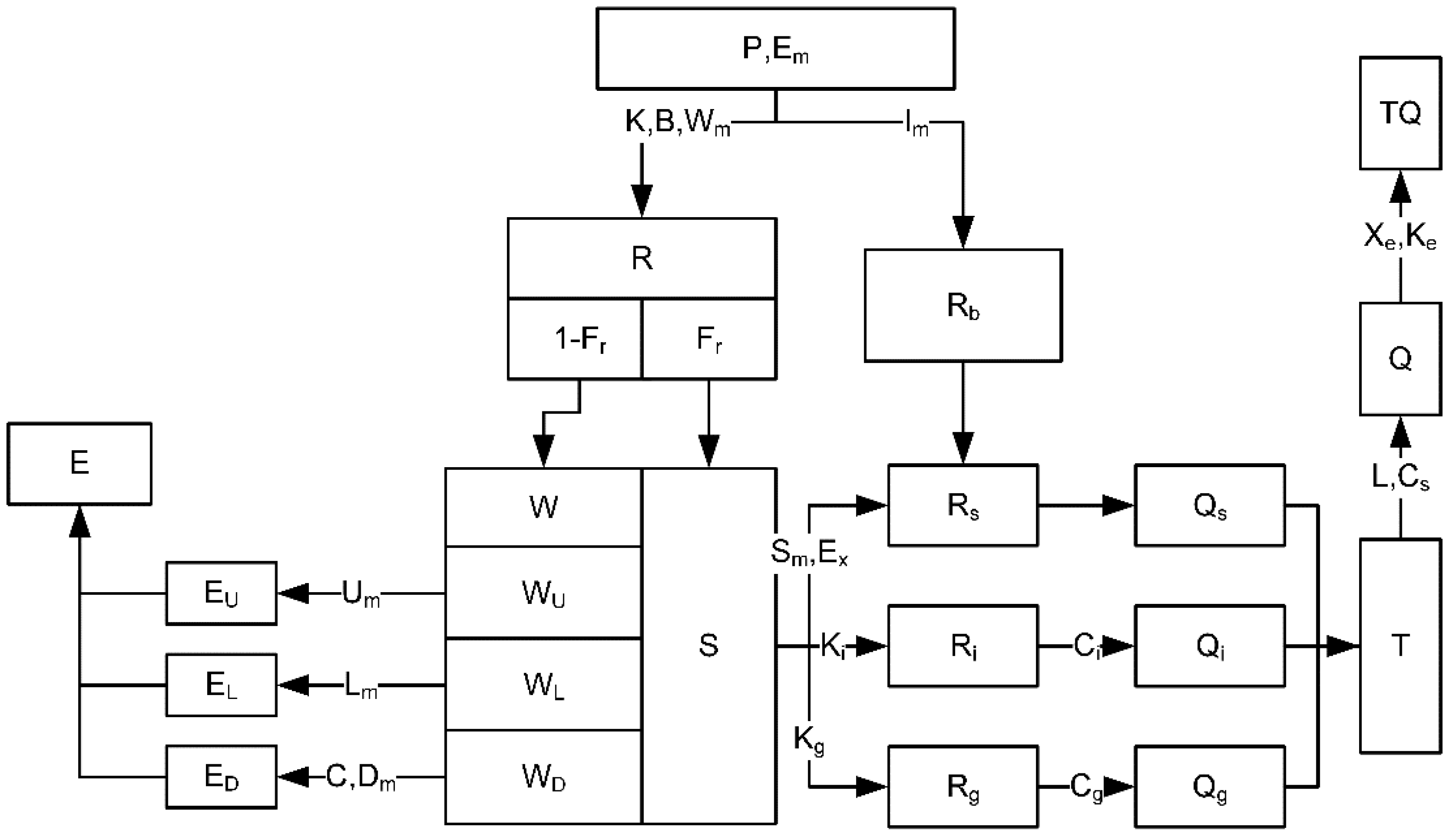
2.2. The Xinanjiang Model
2.3. Kernel-Based Residual Error (KRE) Model
2.4. Residual-Oriented Antecedent Precipitation Index (RAPI)
2.5. Calibration Method
2.5.1. The MI-LXPM Algorithm
2.5.2. Two-Stage Calibration Procedure
2.6. Probabilistic Predictions
- (1)
- Sample innovations from the inverse of the estimated innovation distribution in Equation (8):
- (2)
- Model temporal structure with Equation (7):Note that we set the raw residual replicates at the first time step as .
- (3)
- Calculate the value of regression function and CV function by substituting the corresponding regressor into Equations (4) and (6) sequentially.
- (4)
- Generate samples of using Equation (3):
- (5)
- Combine with the deterministic model output
2.7. Probabilistic Prediction Performance Metrics
2.7.1. Reliability Metric
2.7.2. Precision Metric
3. Results and Discussion
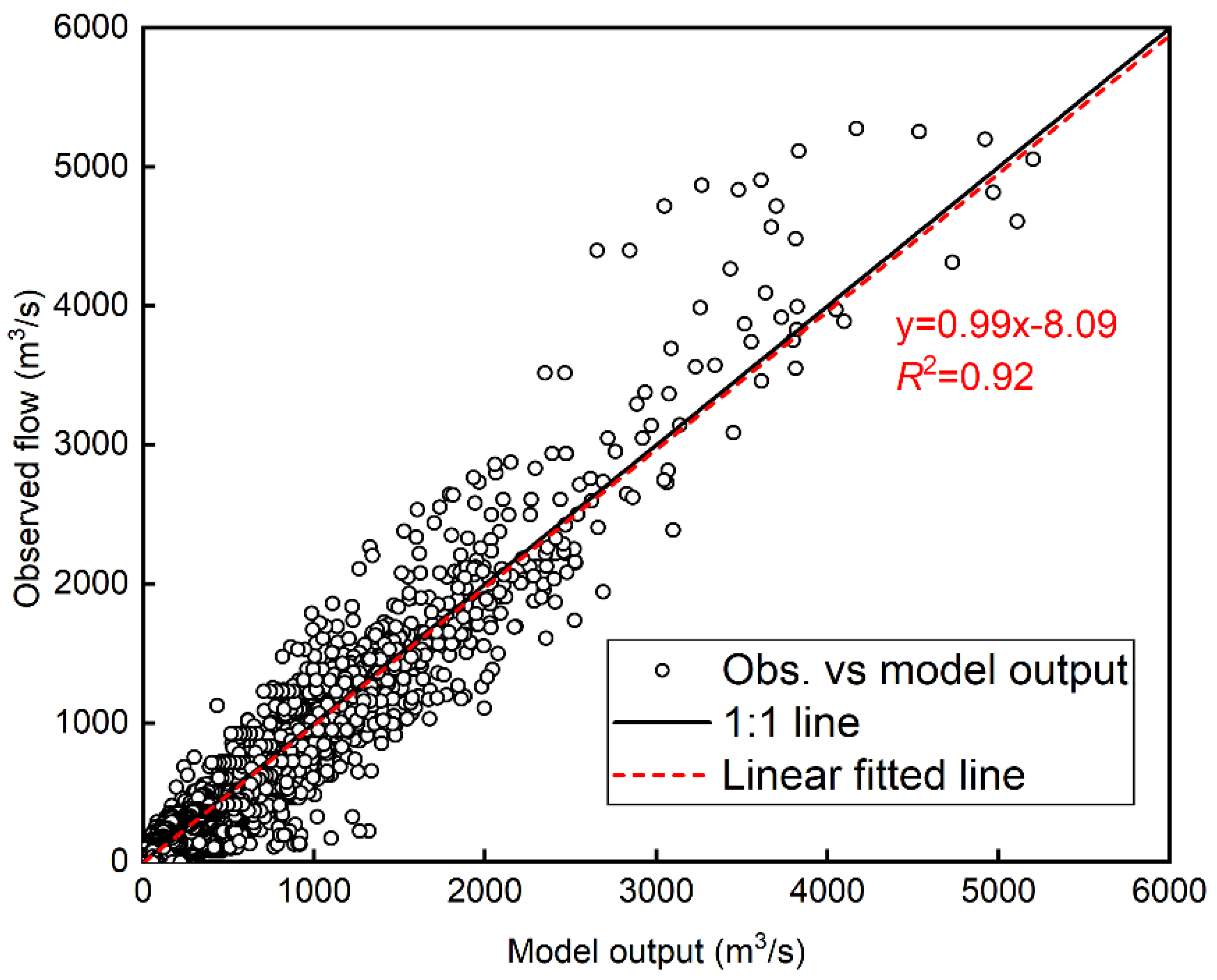
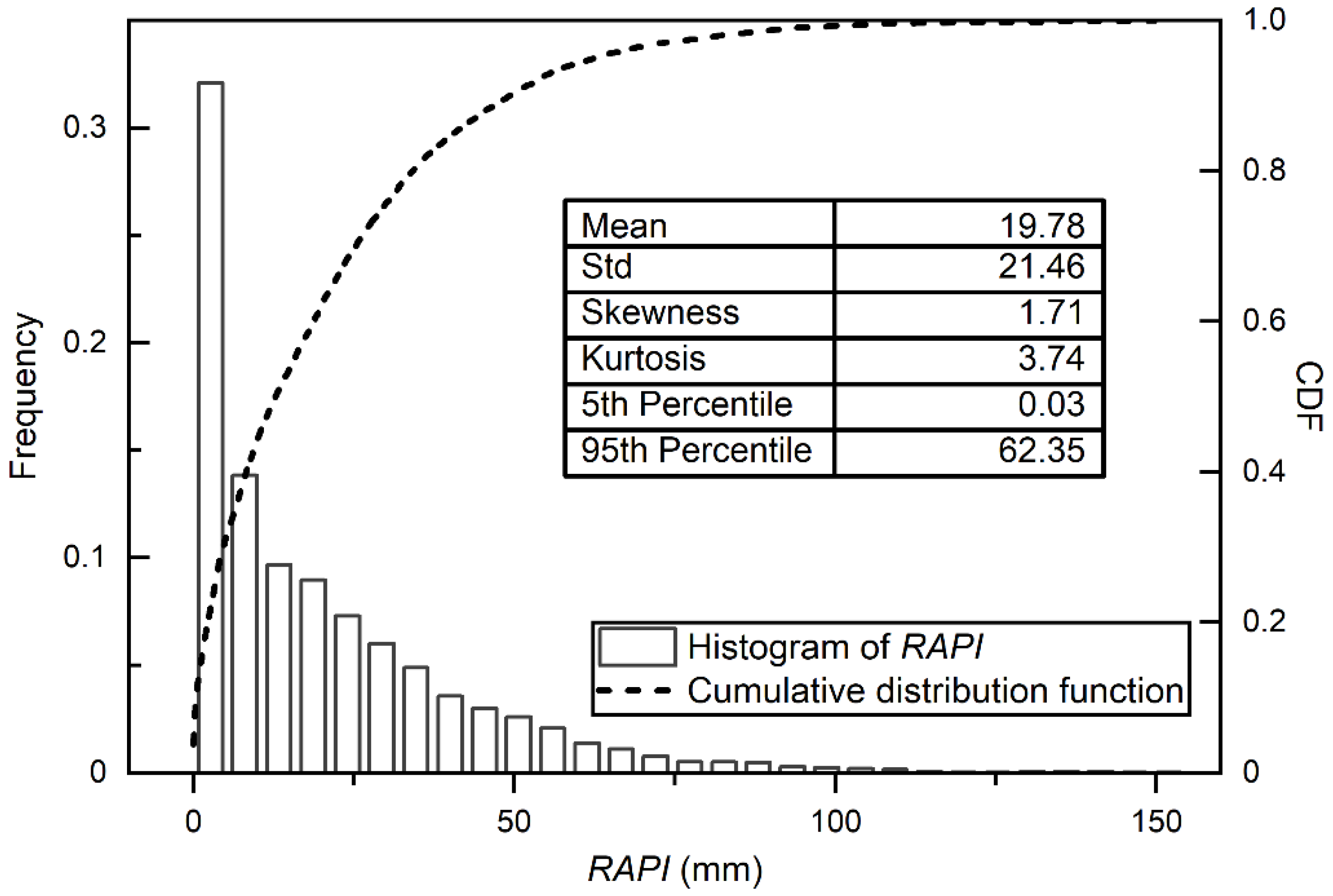
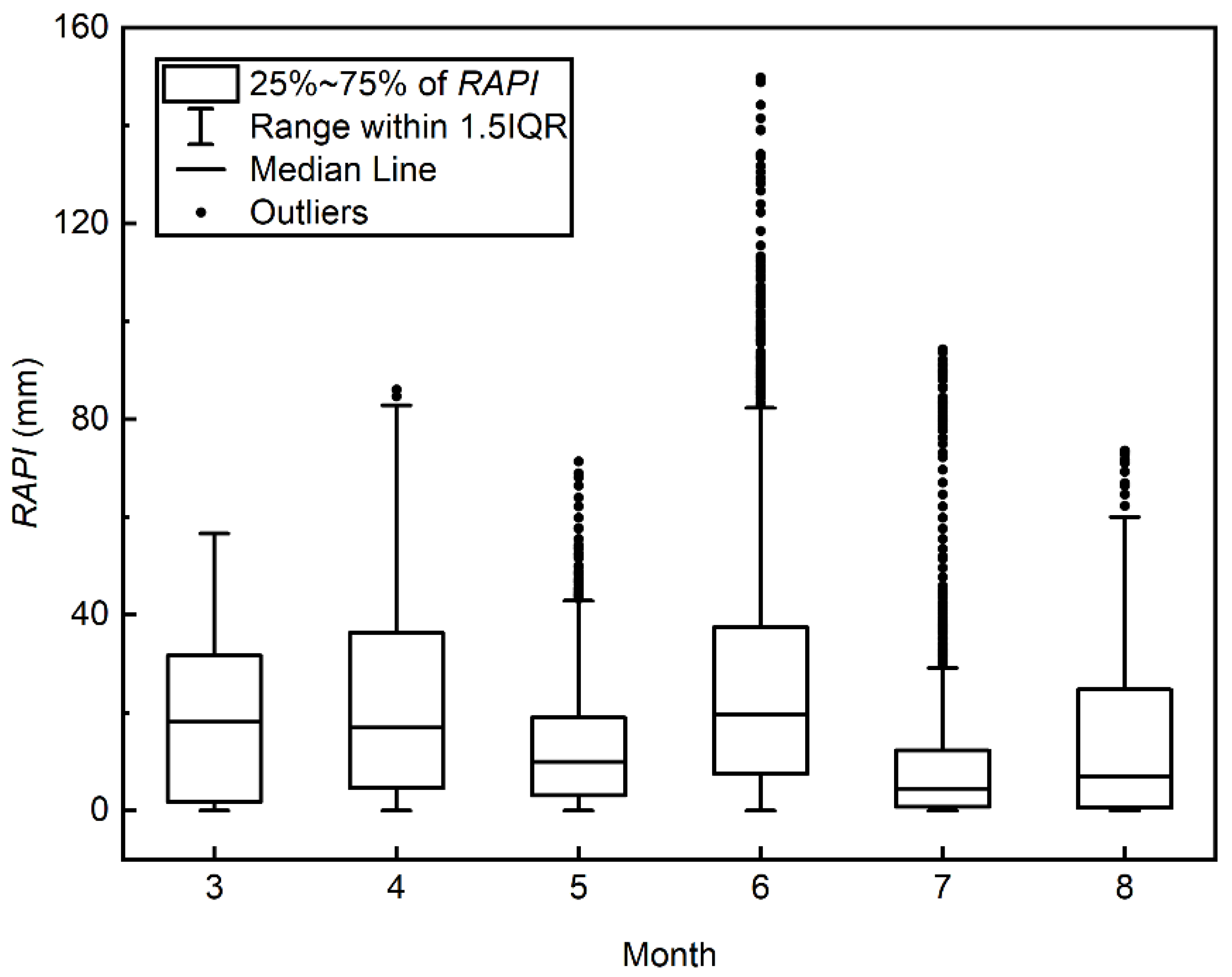
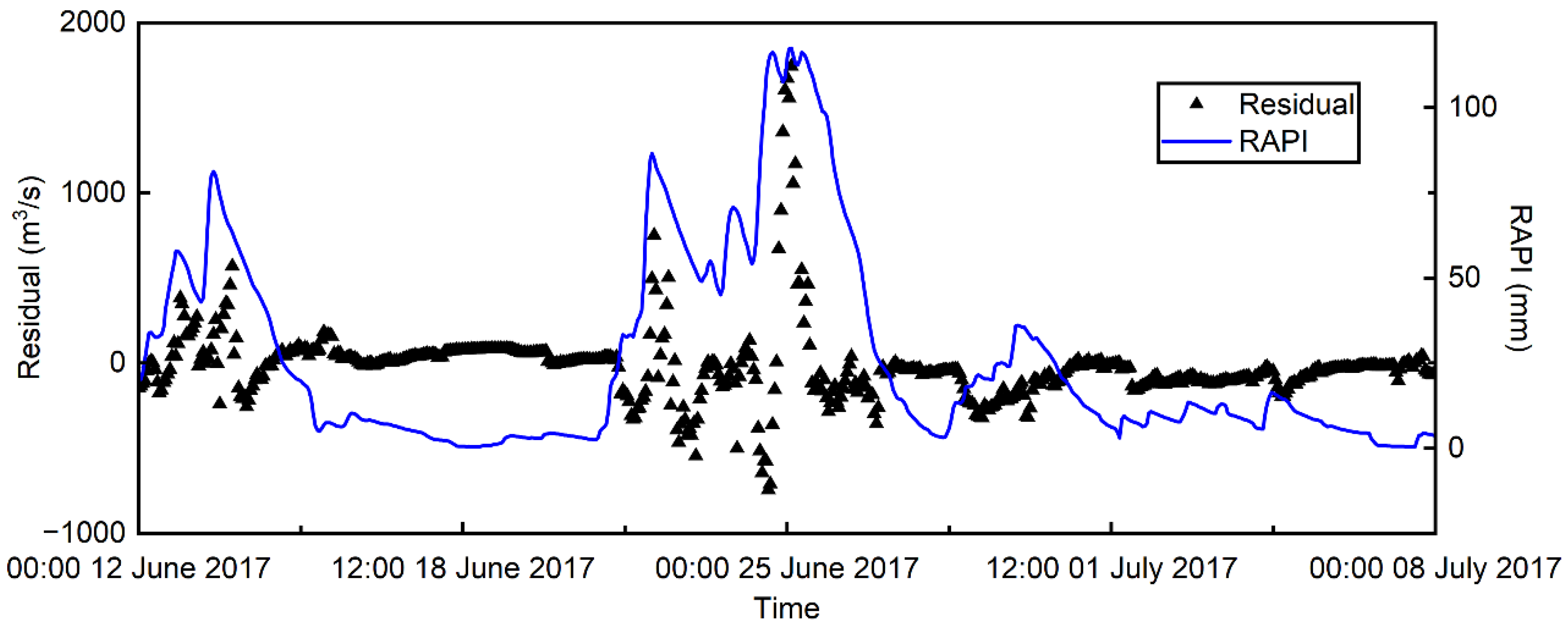
3.1. Flood Prediciton Residuals and RAPI Estimates
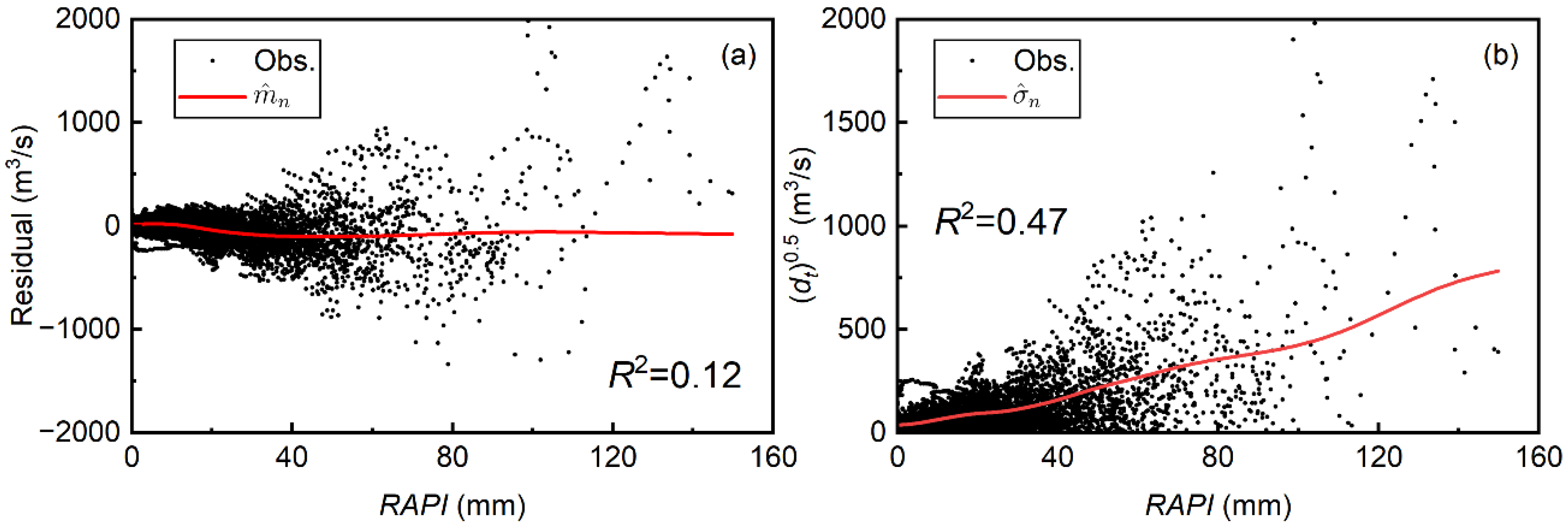
3.2. Impact of the Optimal RAPI on Flood Residual
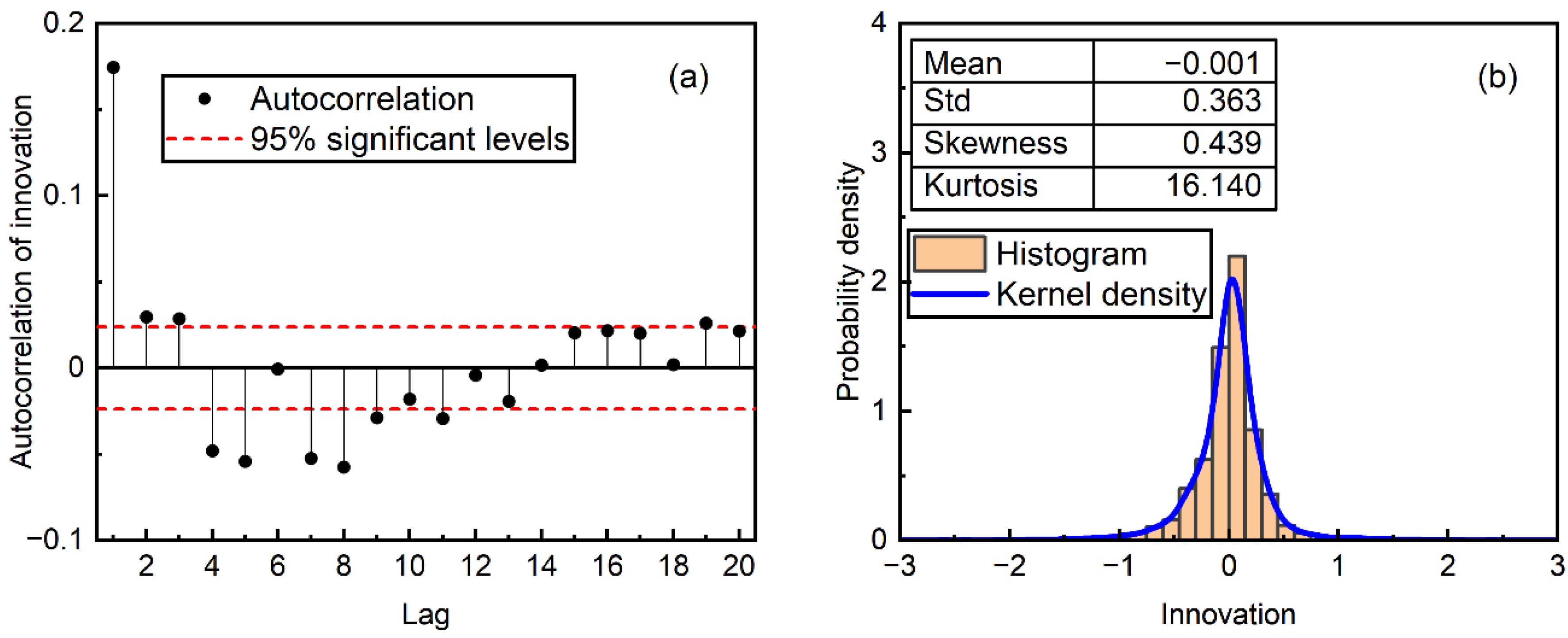
3.3. Stochastic Predictive Performance
3.4. Impact of Soil Moisture on Predictive Performance of Flood
3.5. Comparison of the Regressor
3.6. Limitations and Future Work
4. Conclusions
- For hourly flood predictions, the optimal RAPI can be the weighted average of hourly precipitation falls in the antecedent days with a mild decay. The distribution of the optimal RAPI is found to be highly peaked with positive skewness.
- The optimal RAPI influences the residual conditional volatility more than the conditional mean. As a result, a poor bias-correction ability can be found when making probabilistic flood predictions with RAPI.
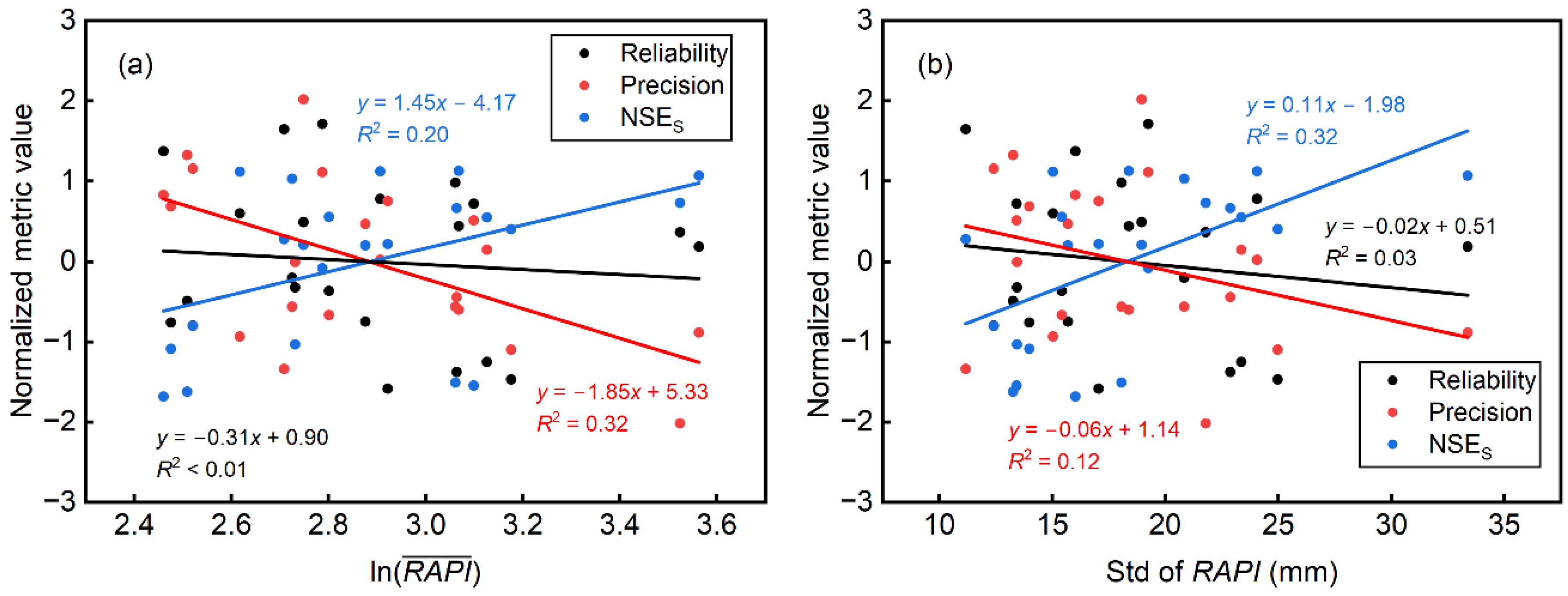
- The reliability of probabilistic flood prediction is almost independent of the RAPI value. On the contrary, prediction precision and unbiasedness are found to improve with increasing value and variability of the RAPI.
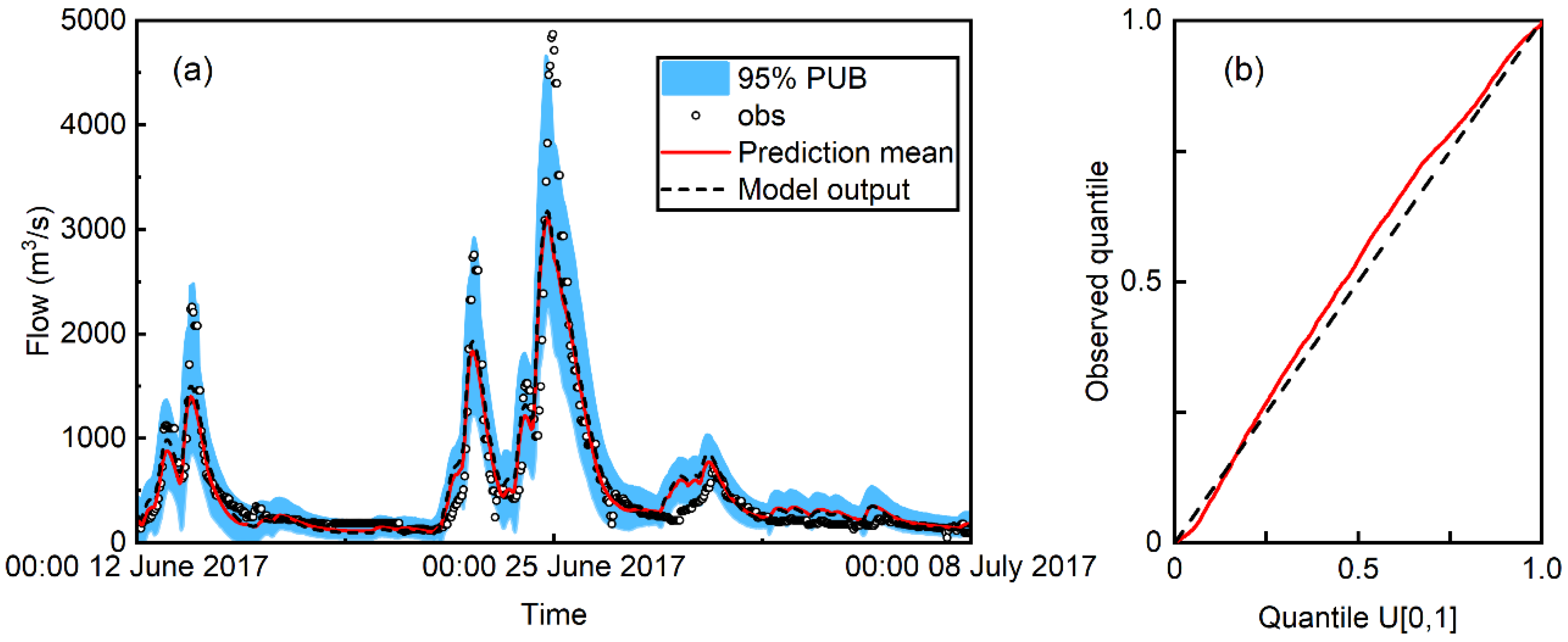
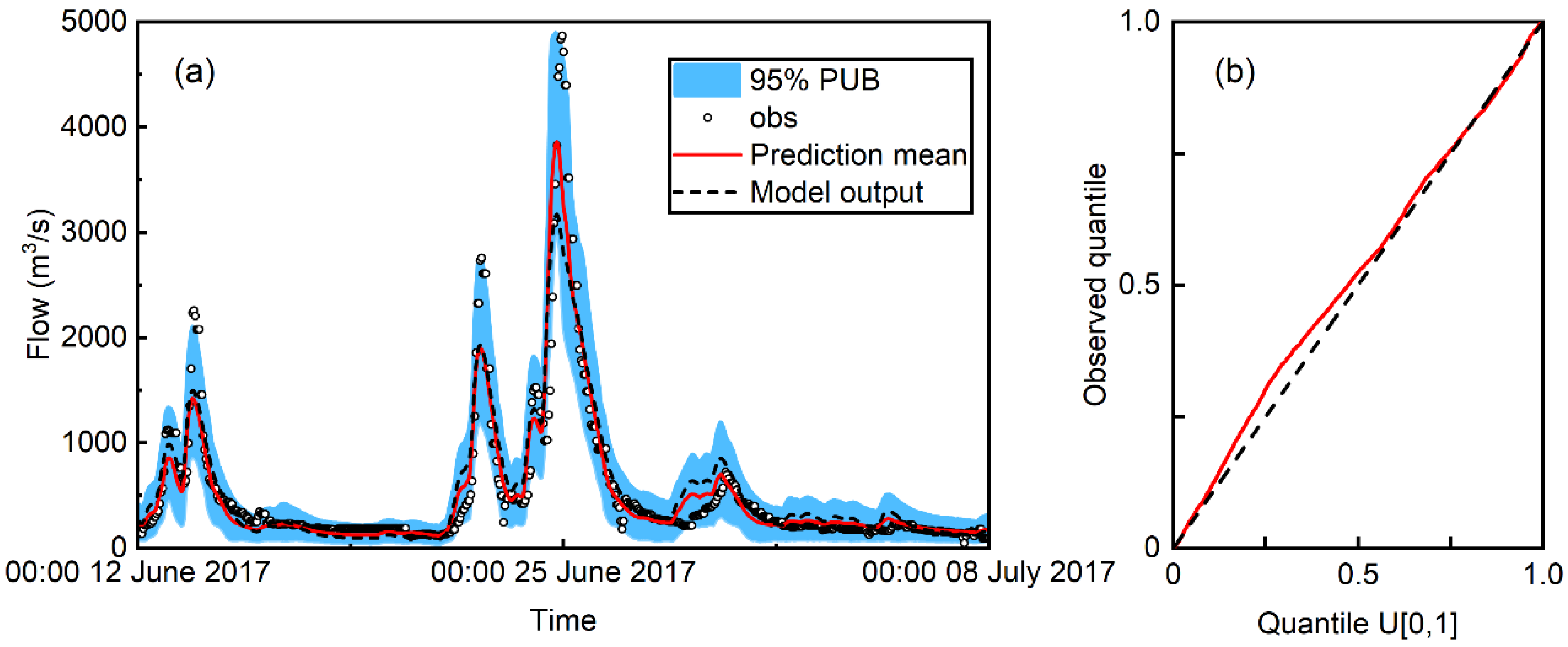
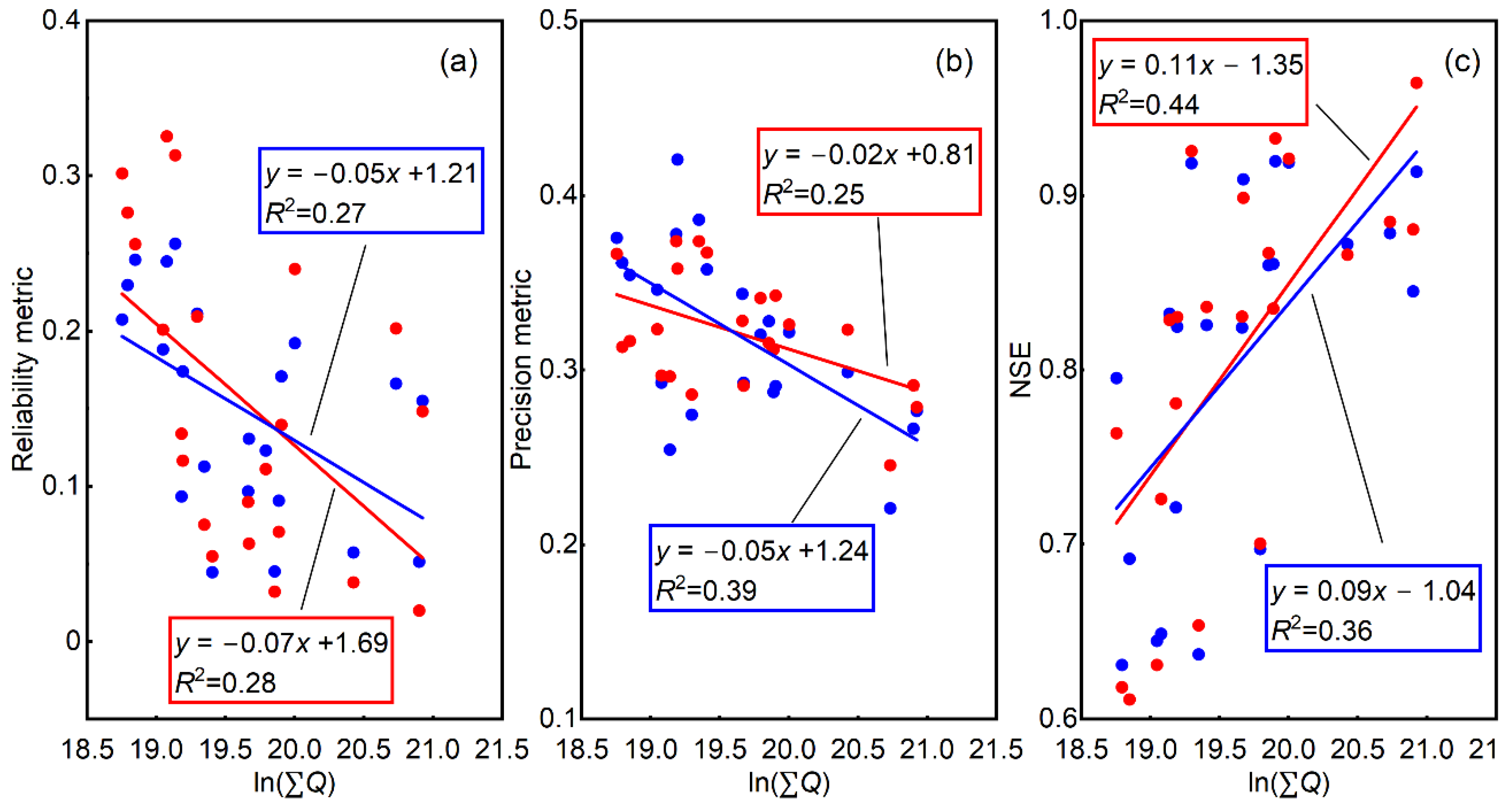
- As a regressor, the RAPI produces better probabilistic flood predictions for small to median flood events than the deterministic model output . On the contrary, provides better predictions of extreme flood events.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Beven, K.; Binley, A. The future of distributed models: Model calibration and uncertainty prediction. Hydrol. Process. 1992, 6, 279–298. [Google Scholar] [CrossRef]
- Del Giudice, D.; Honti, M.; Scheidegger, A.; Albert, C.; Reichert, P.; Rieckermann, J. Improving uncertainty estimation in urban hydrological modeling by statistically describing bias. Hydrol. Earth Syst. Sci. 2013, 17, 4209–4225. [Google Scholar] [CrossRef] [Green Version]
- Reichert, P.; Ammann, L.; Fenicia, F. Potential and Challenges of Investigating Intrinsic Uncertainty of Hydrological Models with Stochastic, Time-Dependent Parameters. Water Resour. Res. 2021, 57, e2020W–e28400W. [Google Scholar] [CrossRef]
- Renard, B.; Kavetski, D.; Kuczera, G.; Thyer, M.; Franks, S.W. Understanding predictive uncertainty in hydrologic modeling: The challenge of identifying input and structural errors. Water Resour. Res. 2010, 46, 1–22. [Google Scholar] [CrossRef]
- Schoups, G.; Vrugt, J.A. A formal likelihood function for parameter and predictive inference of hydrologic models with correlated, heteroscedastic, and non-Gaussian errors. Water Resour. Res. 2010, 46, w10531. [Google Scholar] [CrossRef] [Green Version]
- McInerney, D.; Thyer, M.; Kavetski, D.; Lerat, J.; Kuczera, G. Improving probabilistic prediction of daily streamflow by identifying P areto optimal approaches for modeling heteroscedastic residual errors. Water Resour. Res. 2017, 53, 2199–2239. [Google Scholar] [CrossRef]
- Sun, R.; Yuan, H.; Liu, X. Effect of heteroscedasticity treatment in residual error models on model calibration and prediction uncertainty estimation. J. Hydrol. 2017, 554, 680–692. [Google Scholar] [CrossRef]
- Evin, G.; Thyer, M.; Kavetski, D.; McInerney, D.; Kuczera, G. Comparison of joint versus postprocessor approaches for hydrological uncertainty estimation accounting for error autocorrelation and heteroscedasticity. Water Resour. Res. 2014, 50, 2350–2375. [Google Scholar] [CrossRef]
- Hunter, J.; Thyer, M.; McInerney, D.; Kavetski, D. Achieving high-quality probabilistic predictions from hydrological models calibrated with a wide range of objective functions. J. Hydrol. 2021, 603, 126578. [Google Scholar] [CrossRef]
- Li, M.; Wang, Q.J.; Bennett, J.C.; Robertson, D.E. Error reduction and representation in stages (ERRIS) in hydrological modelling for ensemble streamflow forecasting. Hydrol. Earth Syst. Sci. 2016, 20, 3561–3579. [Google Scholar] [CrossRef]
- Jiang, X.; Gupta, H.V.; Liang, Z.; Li, B. Toward Improved Probabilistic Predictions for Flood Forecasts Generated Using Deterministic Models. Water Resour. Res. 2019, 55, 9519–9543. [Google Scholar] [CrossRef]
- Pianosi, F.; Raso, L. Dynamic modeling of predictive uncertainty by regression on absolute errors. Water Resour. Res. 2012, 48, W03516. [Google Scholar] [CrossRef]
- Bennett, B.; Leonard, M.; Deng, Y.; Westra, S. An empirical investigation into the effect of antecedent precipitation on flood volume. J. Hydrol. 2018, 567, 435–445. [Google Scholar] [CrossRef]
- Song, S.; Wang, W. Impacts of Antecedent Soil Moisture on the Rainfall-Runoff Transformation Process Based on High-Resolution Observations in Soil Tank Experiments. Water 2019, 11, 296. [Google Scholar] [CrossRef] [Green Version]
- Chen, X.; Parajka, J.; Széles, B.; Valent, P.; Viglione, A.; Blöschl, G. Impact of Climate and Geology on Event Runoff Characteristics at the Regional Scale. Water 2020, 12, 3457. [Google Scholar] [CrossRef]
- Khatun, A.; Ganguli, P.; Bisht, D.S.; Chatterjee, C.; Sahoo, B. Understanding the impacts of predecessor rain events on flood hazard in a changing climate. Hydrol. Process. 2022, 36, e14500. [Google Scholar] [CrossRef]
- Zscheischler, J.; Westra, S.; van den Hurk, B.J.J.M.; Seneviratne, S.I.; Ward, P.J.; Pitman, A.; AghaKouchak, A.; Bresch, D.N.; Leonard, M.; Wahl, T.; et al. Future climate risk from compound events. Nat. Clim. Chang. 2018, 8, 469–477. [Google Scholar] [CrossRef]
- Kohler, M.A.; Linsley, R.K. Predicting the Runoff from Storm Rainfall; US Department of Commerce, Weather Bureau: Washington, DC, USA, 1951.
- Heggen, R.J. Normalized Antecedent Precipitation Index. J. Hydrol. Eng. 2001, 6, 377–381. [Google Scholar] [CrossRef]
- Ren-Jun, Z. The Xinanjiang model applied in China. J. Hydrol. 1992, 135, 371–381. [Google Scholar] [CrossRef]
- Kuczera, G.; Kavetski, D.; Franks, S.; Thyer, M. Towards a Bayesian total error analysis of conceptual rainfall-runoff models: Characterising model error using storm-dependent parameters. J. Hydrol. 2006, 331, 161–177. [Google Scholar] [CrossRef]
- Yang, J.; Reichert, P.; Abbaspour, K.C.; Yang, H. Hydrological modelling of the Chaohe Basin in China: Statistical model formulation and Bayesian inference. J. Hydrol. 2007, 340, 167–182. [Google Scholar] [CrossRef]
- Fan, J.; Yao, Q. Efficient Estimation of Conditional Variance Functions in Stochastic Regression. Biometrika 1998, 85, 645–660. [Google Scholar] [CrossRef] [Green Version]
- Ahmed, H.I.E.S.; Salha, R.B.; El-Sayed, H.O. Adaptive weighted Nadaraya–Watson estimation of the conditional quantiles by varying bandwidth. Commun. Stat. Simul. Comput. 2020, 49, 1105–1117. [Google Scholar] [CrossRef]
- Wand, M.P.; Marron, J.S.; Ruppert, D. Transformations in Density Estimation. J. Am. Stat. Assoc. 1991, 86, 343–353. [Google Scholar] [CrossRef]
- Abramson, I.S. On Bandwidth Variation in Kernel Estimates-A Square Root Law. Ann. Stat. 1982, 10, 1217–1223. [Google Scholar] [CrossRef]
- Silverman, B.W. Density Estimation for Statistics and Data Analysis; Chapman & Hall: London, UK, 1986. [Google Scholar]
- Evin, G.; Kavetski, D.; Thyer, M.; Kuczera, G. Pitfalls and improvements in the joint inference of heteroscedasticity and autocorrelation in hydrological model calibration. Water Resour. Res. 2013, 49, 4518–4524. [Google Scholar] [CrossRef] [Green Version]
- Deep, K.; Singh, K.P.; Kansal, M.; Mohan, C. A real coded genetic algorithm for solving integer and mixed integer optimization problems. Appl. Math. Comput. 2009, 212, 505–518. [Google Scholar] [CrossRef]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models part I—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Shang, H.L. Estimation of a functional single index model with dependent errors and unknown error density. Commun. Stat. Simul. Comput. 2020, 49, 3111–3133. [Google Scholar] [CrossRef]
- Thyer, M.; Renard, B.; Kavetski, D.; Kuczera, G.; Franks, S.; Srikanthan, S. Critical evaluation of parameter consistency and predictive uncertainty in hydrological modeling: A case study using Bayesian total error analysis. Water Resour. Res. 2009, 45, W00B14. [Google Scholar] [CrossRef]
- Ammann, L.; Fenicia, F.; Reichert, P. A likelihood framework for deterministic hydrological models and the importance of non-stationary autocorrelation. Hydrol. Earth Syst. Sci. 2019, 23, 2147–2172. [Google Scholar] [CrossRef] [Green Version]
- McInerney, D.; Thyer, M.; Kavetski, D.; Bennett, B.; Lerat, J.; Gibbs, M.; Kuczera, G. A simplified approach to produce probabilistic hydrological model predictions. Environ. Model. Softw. 2018, 109, 306–314. [Google Scholar] [CrossRef]
- Romero-Cuellar, J.; Gastulo-Tapia, C.J.; Hernández-López, M.R.; Prieto Sierra, C.; Francés, F. Towards an Extension of the Model Conditional Processor: Predictive Uncertainty Quantification of Monthly Streamflow via Gaussian Mixture Models and Clusters. Water 2022, 14, 1261. [Google Scholar] [CrossRef]
- Del Giudice, D.; Albert, C.; Rieckermann, J.; Reichert, P. Describing the catchment-averaged precipitation as a stochastic process improves parameter and input estimation. Water Resour. Res. 2016, 52, 3162–3186. [Google Scholar] [CrossRef] [Green Version]
- Nanding, N.; Wu, H.; Tao, J.; Maggioni, V.; Beck, H.E.; Zhou, N.; Huang, M.; Huang, Z. Assessment of Precipitation Error Propagation in Discharge Simulations over the Contiguous United States. J. Hydrometeorol. 2021, 22, 1987–2008. [Google Scholar] [CrossRef]
- Gao, Y.; Sarker, S.; Sarker, T.; Leta, O.T. Analyzing the critical locations in response of constructed and planned dams on the Mekong River Basin for environmental integrity. Environ. Res. Commun. 2022, 4, 101001. [Google Scholar] [CrossRef]
- Sarker, S.; Veremyev, A.; Boginski, V.; Singh, A. Critical Nodes in River Networks. Sci. Rep. 2019, 9, 11178. [Google Scholar] [CrossRef] [Green Version]
- Wu, X.; Marshall, L.; Sharma, A. Quantifying input error in hydrologic modeling using the Bayesian error analysis with reordering (BEAR) approach. J. Hydrol. 2021, 598, 126202. [Google Scholar] [CrossRef]
- Shimizu, K.; Yamada, T.; Yamada, T.J. Uncertainty Evaluation in Hydrological Frequency Analysis Based on Confidence Interval and Prediction Interval. Water 2020, 12, 2554. [Google Scholar] [CrossRef]
- Kavetski, D.; Kuczera, G.; Franks, S. Bayesian analysis of input uncertainty in hydrological modeling: 1. Theory. Water Resour. Res. 2006, 42, W03407. [Google Scholar] [CrossRef]
| Parameter | K * | B * | Wm * | Im | Fr | Um | Lm | C | Dm | Sm * |
|---|---|---|---|---|---|---|---|---|---|---|
| Upper limit | 0.7 | 0.1 | 100 | - | - | - | - | - | - | 5 |
| Estimate | 1.190 | 0.662 | 136.483 | 0.010 | 0 | 20.000 | 60.000 | 0.180 | 56.483 | 10.453 |
| Lower limit | 1.3 | 0.8 | 150 | - | - | - | - | - | - | 50 |
| Parameter | Ex | Ki | Kg * | Ci * | Cg * | Cs * | L * | Xe * | Ke * | |
| Upper limit | - | - | 0.01 | 0.8 | 0.93 | 0 | 0 | −0.5 | 1 | |
| Estimate | 1.500 | 0.359 | 0.341 | 0.892 | 0.995 | 0.865 | 6 | −0.195 | 1.500 | |
| Lower limit | - | - | 0.69 | 0.95 | 0.995 | 1 | 20 | 0.5 | 2.5 |
| Parameter | ||||||
|---|---|---|---|---|---|---|
| Upper limit | 0.01 | 0.01 | 0.01 | 0.10 | 0.10 | 1 |
| Estimates for KA | 0.92 | 0.10 | 0.07 | 0.93 | 0.97 | 51 |
| Estimates for KF | 0.59 | 0.22 | 0.12 | 0.95 | - | - |
| Lower limit | 1.00 | 1.00 | 10.00 | 0.99 | 0.99 | 240 |
| Scenario | Reliability Metric | Precision Metric | 1 | −log(Lk) |
|---|---|---|---|---|
| KA | 0.04 | 0.33 | 0.82 | 30077 |
| KF | 0.04 | 0.35 | 0.84 | 30221 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liang, J.; Hu, Z.; Liu, S.; Zhong, G.; Zhen, Y.; Makhinov, A.N.; Araruna, J.T. Residual-Oriented Optimization of Antecedent Precipitation Index and Its Impact on Flood Prediction Uncertainty. Water 2022, 14, 3222. https://doi.org/10.3390/w14203222
Liang J, Hu Z, Liu S, Zhong G, Zhen Y, Makhinov AN, Araruna JT. Residual-Oriented Optimization of Antecedent Precipitation Index and Its Impact on Flood Prediction Uncertainty. Water. 2022; 14(20):3222. https://doi.org/10.3390/w14203222
Chicago/Turabian StyleLiang, Jiyu, Zichen Hu, Shuguang Liu, Guihui Zhong, Yiwei Zhen, Aleksei Nikolavich Makhinov, and José Tavares Araruna. 2022. "Residual-Oriented Optimization of Antecedent Precipitation Index and Its Impact on Flood Prediction Uncertainty" Water 14, no. 20: 3222. https://doi.org/10.3390/w14203222






