Application of Rainfall Threshold for Sediment-Related Disasters in Malaysia: Status, Issues and Challenges

Abstract

Sediment-related disaster is one of the most significant natural disasters, from the perspective of magnitude, damage and loss to human life and infrastructure, and disruption to socio-economic activities. Debris, mud flood, landslide and cliff failure are the major catastrophic problems commonly experienced in most developing countries, including Malaysia. As rainfall is the main culprit to sediment-related disaster occurrences, rainfall data are crucial in the correlation of the occurred events. Several studies have been undertaken worldwide to estimate the critical rainfall conditions and draw the benchmark to predict landslide occurrences, specifically for debris and mudflows (DMF), and shallow landslides. Therefore, this paper presents an up-to-date picture on the development of the rainfall threshold from Malaysia’s perspective. Additionally, the open issues and challenges of deriving the rain threshold are also discussed in three aspects: collection of the dataset features, identification of the threshold and validation of the threshold. The outcomes of this review could serve as references for future studies in Malaysia and other developing countries in managing sediment-related disasters.

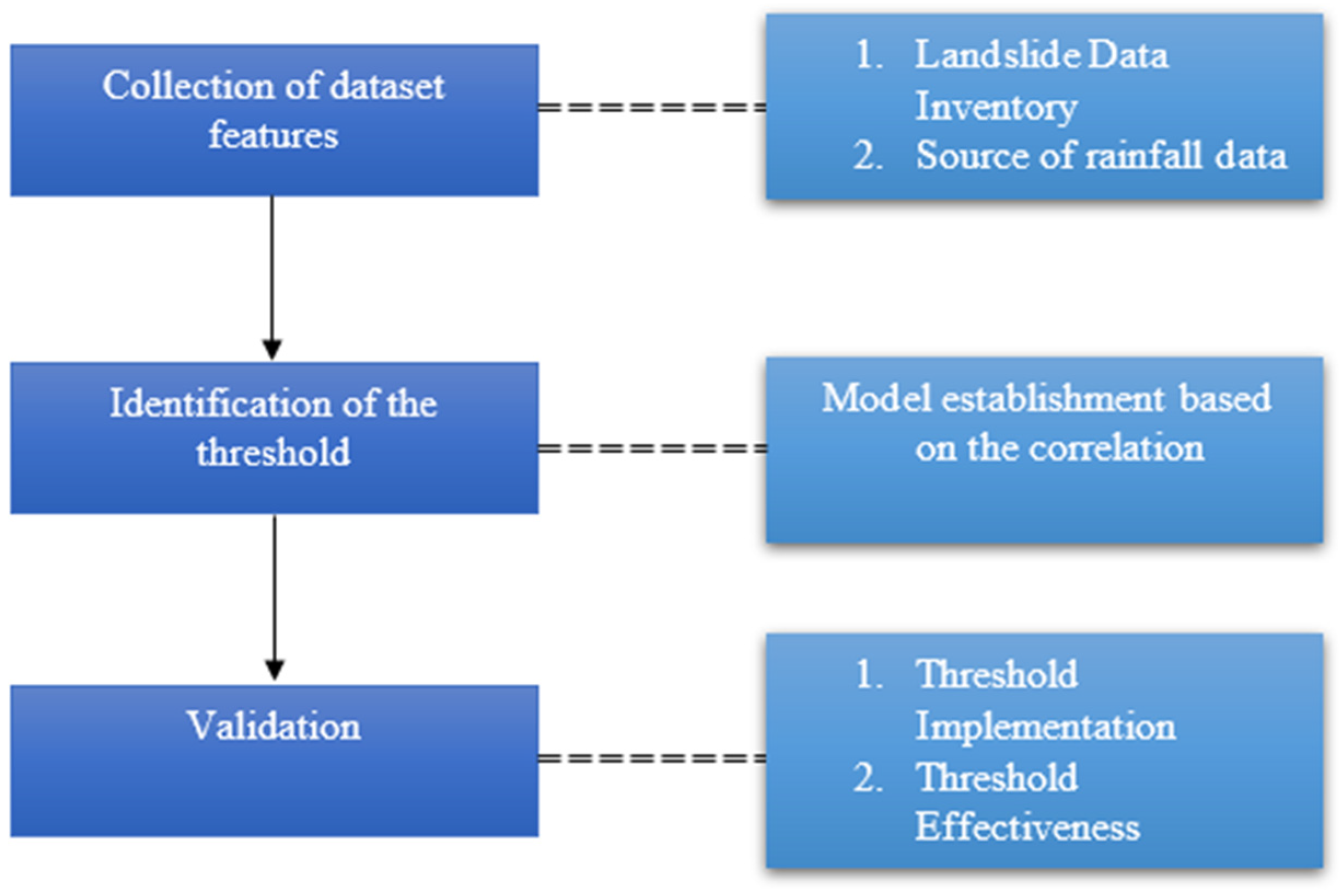
1. Introduction

Landslides, debris and mudflows (DMF), and rockfalls are types of sediment-related disasters whereby rainfall is the main triggering factor [1] The debris flow slide downslope under the influence of gravity consists of a mixture of coarse material, air and water to create a slurry and its ability to wash away anything along its path in high velocity depends on the slope gradient. Mudflow, also known as earth flow, contains at least 50% sand, silt and clay particles and the materials flow downslope rapidly. It is often referred to as a mud flood when the mixture reaches the equilibrium state, as well as when the landslide dam collapses. These sediment-related disasters occur in a sporadic and unpredictable manner. However, based on the extent, regularity and consequences of historical events, forecasting these phenomena has become a global subject of considerable interest. As Guzzetti et al. [2] defined, the rainfall threshold is the condition or amount of rainfall that is likely to initiate sediment-related disasters. Therefore, it is agreed that the rainfall threshold is the most significant tool to predict impending occurrences, and this has been enhanced to facilitate an adaptable and reliable prediction [3].

Referring to the work of Piciullo et al. [4], the rainfall threshold can be implemented as a warning model for landslide early warning systems (LEWS). LEWS are one of the passive countermeasures in the framework of landslide risk management at both local and regional scales [5]. Local LEWS (Lo-LEWS) are more specific in the monitoring of a single landslide at the slope scale, while territorial LEWS (Te-LEWS) monitor multiple sites at a regional scale.

The issues with and challenges of assessing the rain threshold for the alert, the forecast and the warning rain greatly concern the development of the landslide model. The effectiveness of the warning model also depends on the false alert rate and time for evacuation. Therefore, this kind of effective evaluation would only be possible once the warning model is well established with the specified or identified threshold. However, the hydrological threshold does not provide the spatial information and impact of the upcoming event.

In Malaysia, sediment-related disasters are associated with hilly and mountainous landscapes, coupled with intense or prolonged rainfall [6,7,8,9,10,11,12,13]. Figure 1 graphically summarizes the major disaster events recorded in Malaysian history. The first-ever massive landslip took place in 1961, which injured 35 people and claimed another 16 lives in Ringlet, Cameron Highlands. The 1996 debris flow incident in Keningau, Sabah, was perhaps the deadliest disaster with 302 recorded deaths and 4925 houses destroyed. The threat of landslides was further witnessed as recently as 2020, when three people were killed. Over the past decades, DMF and landslide disasters have occurred on a frequent basis with a total loss of more than 600 lives (Figure 1 and

Table 1. Details of the historical summary of sediment-related disaster events in Malaysia.

ID No.	Date	Disaster Type	Location	Death	Injury	Cost (Million RM)	Consequence
1	October 2017	Landslide	Tanjung Bungah, Penang Island	11	NA	NA	NA
2	October 2018	Landslide	Bukit Kukus Road, Georgetown, Penang Island	9	NA	NA	NA
3	31 December 1993	Landslide	KM 59.5, East-West Highway	1	3	NA	Damaged one car
4	October 1973	Landslide	Kampung Kacang Putih, Ipoh	42	NA	64.78	NA
5	June 2020	Landslide	Taman Silibin Indah, Ipoh	1	NA	NA	NA
6	December 2004	Rock fall	Limestone hill in Bercham, Ipoh	2	NA	NA	Buried back portion of illegal factory at the foot of a limestone hill
7	November 2020	Landslide	The Banjaran Hotspring Retreat, Tambun	2	NA	NA	NA
8	24 October 1993	Landslide	KM 58, Kuala Lipis-Gua Musang Road	1	15	NA	NA
9	6 January 1996	Landslide	North-South Expressway (NSE) near Tempurung Cave, Gopeng	1	NA	6.7	NA
10	29 August 1996	Mud slide	Pos Dipang Kg. Sahom, Kampar	44	NA	69	NA
11	28 November 1993	Landslide	Kuala Lumpur-Karak Expressway	2	NA	NA	NA
11	30 June 1995	Landslide	Kuala Lumpur-Karak Expressway	20	22	48.3	Damaged 10 cars
12	December 2001	Debris flow	Pulai Mount, Johor	5	NA	NA	Washed away settlements along the river bank
13	18 October 1996	Landslide	Gelang Patah, Johor	1	NA	NA	Six people evacuated
14	28 January 2002	Shallow rotational slide	Simunjan, Sarawak	16	NA	28	Buried a number of houses
15	26 December 2000	Landslide	Kampung Baru Cina, Kapit, Sarawak	2	NA	NA	Buried two villagers, destroyed nine wooden houses
16	26 December 1996	Debris flow	Keningau, Sabah	302	NA	NA	Wiped out several villages, destroyed 4925 houses
17	January 1999	Shallow rotational slide	Squatters settlement, Sandakan, Sabah	13	NA	NA	Buried a number of house/huts
18	8 February 1999	Landslide	Kampung Gelam, Sandakan, Sabah	17	2	NA	Destroyed four houses
19	1 May 1961	Massive landslip	Ringlet, Cameron Highlands	16	35	3.48
19	4–7 December 1994	Landslide	Cameron Highlands	7	NA	NA
19	24 October 1995	Landslide	Tringkap, Cameron Highlands	1	NA	NA	Damaged one house
19	December 1995	Landslide	Cameron Highlands	7	NA	NA	Damaged a few houses
19	9 October 1996	Landslide	Terla, Cameron Highlands	3	2	NA	Damaged a few houses
19	9 January 2000	Debris flow	KM 81.6, Tanah Rata—Brinchang Road	6	NA	NA	Washed away worker squatters
19	April 2006	Landslide	KM 33, Simpang Pulai Road	35	NA	4.6
19	23 October 2013	Mud flood	Bertam Valley, Cameron Highlands	3			Damaged 80 houses
20	December 2008	Landslide	Bukit Antarabangsa, Hulu Kelang	4	15	NA	NA
20	6 December 2008	Landslide	Taman Bukit Mewah, Ampang	5	7	7.6	Damaged 14 bungalows
20	22 May 2011	Landslide	FELCRA Semungkis, Hulu Langat	16	NA	NA	NA
20	11 December 1993	Landslide	Highland Tower, Taman Hillview, Hulu Kelang	2	184	NA	Collapse of one block of a 12-storey high apartment
	2 May 1994	Landslide	Puchong Perdana	3	NA	NA	10 families evacuated
20	11 May 1997	Landslide	Pantai Dalam, Kuala Lumpur	2	4	NA	19 families evacuated
20	15 May 1999	Landslide	Bukit Antarabangsa, Hulu Kelang	NA	NA	5.4	1000 people evacuated
20	22 September 2001	Landslide	Sg. Chinchin, Gombak	1	NA	NA	Partly destroyed one house
20	20 November 2002	Landslide	Taman Hillview, Ampang	8	5	17.4	Damaged one bungalow
20	November 2003	Rock debris	New Klang Valley Expressway (NKVE)	8	NA	36	Expressway closed for more than 6 months
20	November 2004	Debris flow	Taman Harmonis, Gombak	1	NA	NA	NA
20	31 May 2006	Landslide	Kampung Pasir, Hulu Kelang	4	NA	21	Damaged three blocks of longhouses

), and several research efforts have been carried out, focusing on the high-risk areas. Therefore, this paper aims to address Malaysia’s efforts by reviewing the relevant literature on the rainfall threshold development framework and its employment for sediment-related disaster occurrence in the country. The status, issues and challenges discussed in this review are believed to be useful references for the application of sediment-related disaster management worldwide, especially for developing countries.

2. Rainfall Threshold

A warning model for LEWS can be based on physical or empirical models. The empirical model is mainly based on the correlations between rainfall events that have caused landslides [14], whereas the physical method involves physically computing the force balance between shear-force and shear-force resistance at each slope. Papa et al. [15] highlighted that the established physical model requires instrumentation to compute certain inputs such matric suction within the soil layers, hydraulic conductivity, soil moisture and pore water pressure. It also includes the infinite slope stability analysis, of which the main parameter is the groundwater table that, when fully saturated, leads to failure. Therefore, the physical-based model is highly suitable for a site-specific slope, but it is very costly if one has to apply it to the regional threshold. The conceptual model is also considered as a process-based model that represent the physical analogy, representing the quantitative understanding between rainfall and landslides. It is more widespread than the instrumentation installation requirement. The example of the conceptual model is the leaky barrel model [16] and the soil water index (SWI) [17,18]. On the other hand, the work of Yamazaki et al. [19] has successfully identified the critical rainfall condition to simulate the disaster temporally and spatially. The advantage of this method is that it takes into account that the event may occur during the observation with no rain forecast. The rainfall condition curve is segregated according to their slope classification or spatial condition when the current rainfall condition breaches the curve, hence indicating when the disaster is likely to occur.

While the empirical model is more widespread, the application of empirical rainfall thresholds has been in place since 1987, with many studies conducted in many countries, especially in Italy, and central and southern Europe [20]. There are several types and characteristics of rainfall thresholds, namely the intensity–duration (I-D), accumulated rainfall–duration (E-D), intensity–accumulated rainfall (I-E), accumulated rainfall–accumulated rainfall (E-E) and antecedent or working rainfall or rainfall index. The most common and pioneering is the I-D threshold established by Caine [21] Most of the threshold correlating the rainfall characteristic to landslide events is presented in terms of the power law relationship [22]. The main goal in the empirical model development is to identify the rain that has triggered the disaster despite other additional factors, if present. Therefore, the definition of rainfall intensity plays the most crucial part in this manner [23]. Rainfall intensity refers to the rainfall depth over a certain duration, depending on the observation period. The timescale is normally in an hourly format [3]. For a short period, it may represent the current intensity of the rainfall during the occurrence of the disaster. Likewise, for a long period, it may represent the average value of the rainfall over hours, i.e., 2, 3 or 24 h. The definition should be consistent during the construction of the numerical rainfall characteristic of the historical events, and the forecasting rainfall (forecasting events) and the observed rainfall (monitoring events). Due to the diversity of the definition, one should state clearly the definition of rainfall intensity in their work for others to compare and adopt the method accordingly. The disaster is likely to occur when the current rainfall characteristic based on the observed rainfall data (or real-time data) are beyond the rainfall characteristic that resulted in the disaster in the past, referred to as the rainfall threshold. The framework is adopted in the early warning system as a warning model that the impending disaster can be forecasted, in order to alert the respective stakeholder (authority or community). Figure 2 illustrates the conceptual description of the I-D threshold under ideal conditions, where there is a clear separation between the sediment-related disaster-triggering and non-triggering rainfall conditions [24].

Both the physical and empirical model are significant and can be used as warning models employed in any early warning system in order to reduce the disaster risk. However, the chosen model should be tailored according to the local environment, climate and geological condition of the area under surveillance. Since sediment-related disaster is caused by many factors—either spatial or climatic factors and types of behavior—it is pertinent to compile all of the important information related to the possible causes [25]. In general, the process or step of the threshold development is illustrated in the figure below.

Based on Figure 3, the general steps of rainfall threshold development are as follows: firstly, the collection of the dataset features. This process includes the landslide data inventory and the determination of the rainfall data source. The catalogue of the data should be accurate or almost accurate, including items such as the date, time, type of landslide, the location and the data source. Other information such as the slope gradient, topography and lithology and details of the landslide are essential for analysis and comparison. The selection of rainfall data is very crucial as it is correlated with the risk of landslide. Therefore, details on the criteria of the rainfall data to be used in the analysis are very important. The method of criteria selection of rainfall data such as a single reference, manual/expert judgement, the reference rain gauge, the nearest rainfall station and the Theisen polygon method should be specified clearly in the study [3]. The rainfall parameter that governs the relationship of the landslide is determined, whereby the governing parameter is considered to be the causal rain. Next is the identification of the threshold. The outcome of this step is the established relationship between the causal rain and the disaster with the threshold line. This process requires the modeler to draw the separation line and once it is breached, the disaster is likely to occur. Therefore, the drawn line is very subjective; if it is too conservative then the warning could be missed; on the contrary, if it is too low then it could end up resulting in a false alarm. The practical method, as suggested by Nikolopoulos et al. [24], is based upon visual observation of the modeler to separate the safe zone and unsafe zone at the heuristic lower boundary of the empirical data. Another method is based on the frequentist method [26]. Lastly, is the validation of the model. This step is categorized into two parts. Firstly, is the model validation and secondly, is the model performance. In order to reach the second category, the model should be implemented or applied in the early warning system. As per the first category, there is no standard method in place worldwide as yet, but Segoni et al. [3] suggested that the validation can be made using the same dataset or independent datasets. The warning model is not static but has a dynamic manner. Having said that, it should be reviewed within a certain period and the threshold line should be updated to incorporate the latest event. Abraham et al. [27] used physical instrumentation, namely tilting sensors, to enhance the established empirical model. Bezak et al. [28] re-evaluated the soil moisture content in their case study in order for the established warning model to stay relevant and more reliable.

The review of the threshold development in Malaysia is based on the steps and the process shown in Figure 3 above. Firstly, the threshold is compiled; then, the process conducted is compared with the steps and the process mentioned. Next, the missing steps or unclear specific steps are highlighted in the development of the threshold. The status and the issues are compiled as the benchmark or reference for future study.

3. Rainfall Threshold Development in Malaysia

Table 2. Studies on rainfall thresholds in Malaysia for landslides (2006–2020).

References	Extent	Area	Landslide Type	Parameter	No of Events	Equation and Range	Remarks
Dom et al. [29]	Local	Cameron Highlands	DMF	Rainfall index	2	-	Pre-acquisition of the snake curve line/graph.
Jamaludin and Ali [14]	Local	Ampang/ Hulu Kelang	Shallow Landslide	I-D	16	I = 11D–0.5317	Very rough estimation.
		Penang	Shallow Landslide	I-D	15	I = 15.64D–0.81
Lee et al. [30]	Local	Hulu Kelang	Major landslide	E3-API30	6	E3 = −0.762API30 + 295	Reliability 97%.
			Medium landslide	E3-API30	15	E3 = −0.762API30 + 194.3
Jamaludin et al. [31]	Regional	Peninsular Malaysia	Shallow landslide and DMF	Ip-D	4	Ip = 121.4D−0.602	Investigated the ID threshold and compared it to the selected worldwide threshold.
Mukhilisin et al. [32]	Local	Hulu Kelang	Landslide	SWI	15	-	Confirmed that the SWI method is significant to identify the rainfall critical threshold.
Abidin and Dom [33]	Local	Cameron Highlands	-	Rainfall index	4	-	Improved the critical line of the snake curve graph.
Matlan et al. [34]	Local	Ranau	-	SWI	10	-	The SWI method can be used to predict the impending landslide.
Kasim et al. [35]	Regional	Peninsular Malaysia	DMF	I-D	8	I = 42.30D−0.392	Peninsular Malaysia threshold is higher than that used by Caine [21], Cancelli and Nova [36] Wieczorek [37], Ceriani et al. [38] Aleotti [39], and Pereira and Zezere [40]
Maturidi et al. [41]	Local	Cameron Highlands	Shallow landside	I-D	12	I = 29.09D−0.075	Rainfall intensity (25 mm/h) for a duration less than 10 h can trigger a shallow landslide.

Note: DMF = debris and mudflows; I-D = rainfall intensity–duration threshold; E3-API30 = cumulative 3-day rainfall–30-day antecedent precipitation index threshold; Ip-D = highest rainfall intensity–duration threshold; SWI = soil water index; I = rainfall intensity; D = rainfall duration; Ip = highest rainfall intensity; E3 = cumulative 3-day rainfall amount; API30 = 30-day antecedent precipitation index.

summarizes the studies on rainfall thresholds in Malaysia. Malaysian researchers typically investigate the initial rainfall condition that is likely to trigger the landslide disasters, including the DMF, for shallow, medium and major landslides. Low and Dom [18], undertook perhaps the first study that exalted the benefits of flood hazard maps as a useful tool in predicting the onset of potential debris flow events. Their studies introduced a chart of hourly and warranted rain that juxtaposes a snake line, critical line, warning line and evacuation line. This concept was introduced as a future enhancement to be taken up for further research and development in terms of a debris-flow warning.

The first attempt at the mudflow model was made by Dom et al. [29], guided by the Typhoon Committee Hydrology Component Workshop in 2004. The threshold was drawn based on two major DMF events in the Cameron Highlands, and the method was developed in 2005 using the rainfall data at the nearest station from 1994 to 2002. The threshold parameter is the rainfall index expressed by a combination of rainfall intensity and total rainfall. A rainfall intensity–total rainfall graph was plotted to delineate the safe and unsafe zones that cause DMF. However, there has been no significant incidence of mudflow that can be directly predicted by the threshold model since.

Of particular interest, Jamaludin and Ali [14] re-evaluated the mudflow model (as mentioned above) and suggested that any landslide early warning systems to be developed in Malaysia should be implemented based on the empirical correlation of precipitation and landslide events. Their work emphasized the advantage of an empirical approach over a physical-based approach, especially at a regional level. It is worth noting that the pilot project was selected by the Public Works Department (PWD) for the National Slope Master Plan Study (NSMP) [42]. By adopting the methodology by Caine [21], with some enhancement work by Crozier [43], the rainfall thresholds are expressed as:

For Ampang/Hulu Kelang,

I = 11D^−0.5317

(1)

For Penang,

I = 15.64D^–0.81

(2)

where I and D are the rainfall intensity and duration of rainfall, respectively. Both datasets for Ampang and Penang used the landslide events recorded from 1984 to 2010. As for the Cameron Highlands, with a focus on DMF, it was recommended to use the work of Dom et al. [29]. In their investigation, both correlations were claimed to be a very rough estimation. Due to the limitation of the rainfall data to the specific locations, the rainfall used in the analysis was the single source of the nearest rain gauge to the event. Furthermore, this analysis did not elaborate further on the threshold parameter, which seems important as part of the model fitting. On the other hand, the landslide record did not include the sources, which leads to unspecified information other than limitation cases of landslide data.

Next, Lee et al. [30] drew the threshold for the Hulu Kelang area based on the cumulative rainfall intensity for 3 days against the 30-day antecedent precipitation index (E3-API30) and tested the threshold with 97.6% reliability. The rainfall thresholds were proposed for major and medium landslides, as expressed in Equations (3) and (4), respectively. However, there is a lack of information on the rainfall data used in their study. The study did not discuss the rain gauge selection criteria and the data treatment of the observed data. As for the validation, the study claimed that some datasets might be used to test the threshold’s accuracy if there were more landslide inventory data of the said study area.

E₃ = −0.762API₃₀ + 295

(3)

E₃ = −0.762API₃₀ + 194.3

(4)

In the same year, Jamaludin et al. [31] investigated the correlation of DMF and rainfall intensity and duration for Peninsular Malaysia. In their analysis, there were eight cases of recorded DMF. Unfortunately, the study selected only four events for the analysis as the hourly rainfall data of the events were readily achievable. Among the four events: three located at the east highway of Peninsular Malaysia and one situated at Gunung Pulai, Johor, the southern part of Peninsular Malaysia, were used to correlate the maximum hourly rainfall and its duration. The study then compared those four DMF events with the worldwide threshold data reported by Caine [21], Cancelli and Nova [36], Wieczorek [37], Ceriani et al. [38] Innes [44], Cannon and Ellen [45], Wilson et al. [46], Larsen and Simon [47], Wilson and Wieczoreck [16], and Montgomery et al. [48]. It was concluded that the said events were close to those described by Wilson et al. [46], as shown in Equation (5). Note that I_p is the highest rainfall intensity during the rainfall event.

I_p = 121.4D^−0.602

(5)

In the study of Mukhilisin et al. [32], the effect of rainfall on slope stability was investigated, selecting the location of Ulu Klang, Malaysia, as a case study. This study adopted the effective working rainfall and SWI as the rainfall threshold. The landslide dataset from 15 cases recorded from 1993 to 2012 was obtained from the nearest rainfall station to the event. The study had successfully drawn the correlative relationship between the landslide and rainfall. It is concluded that this method can be applied to identify the threshold and be the tool for an alert system, though there is no information on the threshold value and the validation of the model.

In the same year, Abidin and Dom [33] further evaluated the work of Dom et al. [29]. The study established the methodology for developing the debris and mudflow warning system (DMFWS) for the Cameron Highlands, which was urgently required by the Department of Irrigation and Drainage Malaysia (DID). The model’s setup was based on rainfall intensity and working rainfall. Compared to the previous model in 2006, the model in 2015 was improved with more rainfall data and more events, including the two major DMF events that occurred in October 2012 and November 2013. Both disasters significantly impacted the Bertam River in the agricultural town of Bertam Valley. These disasters were eye-opening to the relevant authorities due to the loss of millions of Malaysian Ringgit, the psychological effect on the community and several casualties. Another positive outcome following the DMF occurrence was the opportunity to further upgrade the established model into the new mathematical computer-based model and have the framework of the early warning system. Nonetheless, the concept of the said threshold was successfully developed into a prototypal system of the debris and mudflow warning system [49].

Next, Matlan et al. [34] extended the work of Mukhlisin et al. [32] by further exploring the SWI method. The mountainous area in Ranau, located on the western coast of Sabah, was selected as the study area. It was based on the ten recorded events of landslides. In their study, the effect of working rainfall (14 days) and major rainfall (1.5 h) were found to be substantial to initiate a landslide. The SWI method was concluded to be used as one of the rainfall threshold parameters other than the rainfall index. The results support that the initial soil moisture is also significant in triggering landslides. In the study, there is some missing information such as the time of the event, the criterion in selecting the rainfall data and the threshold of the SWI. Nonetheless, the study should be able to assess the impact of SWI on a landslide event, whereby the rain infiltration will increase the water content and pore water pressure.

Recently, Khalid [50] studied the effect of slope displacement on the stability of transmission tower structures located on hilly topography and areas prone to landslides. The study looked into the rainfall threshold value that could initiate the slope displacement at the border of the Cameron Highlands and Kelantan, on the east coast of Malaysia. This study confirmed that the antecedent rainfall (5 days) and prolonged rainfall (cumulative rainfall) are the parameters to predict landslide occurrence. Based on the findings, 91% of the predictive rainfall is in good response to the displacement data through statistical analysis. The findings agree with other studies of Naidu et al. [51] and Rahardjo et al. [52], whereby the antecedent 5-day rainfall is an essential parameter for landslide occurrence. Rahimi et al. [53] also stated that the soil properties play an important role in slope stability, affecting the infiltration of rainwater. This study is not meant to be used to implement the threshold on a local scale but rather to understand the response of the rainfall on slope displacement, and consequently, on the stability of the transmission tower.

Meanwhile, Kasim et al. [36] studied the I-D threshold for Peninsular Malaysia based on eight events. The threshold was mainly developed for debris flows, as shown in Equation (6). The rainfall data were adopted from the nearest rain gauge, varying from 2.2 km to 20.2 km from the event. However, the study did not discuss the source of the rainfall data and the validation of the threshold in detail.

I = 42.30D^−0.392

(6)

On the other hand, Maturidi et al. [42] established the I-D threshold for shallow landslides in the Cameron Highlands (as shown in Equation (7)) based on the 12 landslide events using the rain gauge within 5 km to 15 km from the landslide location. In their study, there was no elaboration on the treatment of the rainfall data source, which is the main setting of the model. However, in terms of the landslide’s catalogue, the details are considered to be complete and were improved from the previous study. It was found that the rainfall threshold established in this study (Equation (7)) was higher than those established by Kasim et al. [36] for Peninsular Malaysia, Pereira and Zezere [41] for Douro Valley Portugis, Dahal and Hasegawa [54] for Nepal Himalaya, Guzetti et al. [23] for the Central European Adriatic Danubian South-Eastern Space (CADSES) area, Aleotti [40] for the Piedmont region, Italy, and Caine [21] worldwide.

I = 29.09D^−0.075

(7)

4. Discussion

The status and the issues of the rainfall threshold in Malaysia based on the general steps and process are summarized in the table below;

As noted in

Table 3. Status and issues of the rainfall threshold in Malaysia.

No	Rainfall Threshold	Modelling	Status	Issues
1	Dom et al. [29]	Mathematical model	Preliminary assessment	No validation on the model itself
2	Jamaludin and Ali [14]	Mathematical model	Preliminary assessment	No information on the landslide source and no validation on the model itself
3	Lee et al. [30]	Mathematical model	Preliminary assessment with validation of the model	Did not discuss the rain gauge selection criteria and the data treatment of the observed data.
4	Jamaludin et al. [31]	Mathematical model	Preliminary assessment	No validation on the model itself
5	Mukhilisin et al. [32]	Conceptual model	Initial compilation	No threshold was established, but it was confirmed that the model was significant tools to predict sediment-related disaster
6	Abidin and Dom [33]	Mathematical model	Protype	No performance on the model to determine its effectiveness
7	Matlan, et al. [34])	Conceptual model	Initial compilation	No threshold was established Missing information such as the time of the event and the criterion in selecting the rainfall data
8	Kasim et al. [35]	Mathematical model	Preliminary assessment	Did not discuss the source of rainfall data and no validation of the model
9	Maturidi et al. [41]	Mathematical model	Preliminary assessment	No validation of the model

, there are two types of rainfall threshold: conceptual (physical) and empirical-based models. In Malaysia, most of the developed rainfall thresholds are empirically based, as compiled in Table 3. Most relationships are plotted in Cartesian, semi-logarithmic, or logarithmic coordinates. As the empirical model is a derivation from the numerical criteria of the correlation between past event and rainfall past characteristics, it is also known as a mathematical model. As such, certain numerical characteristics of the rainfall that has caused the disaster becomes the benchmark for the upcoming event. The disaster is likely to occur again when this benchmark, which is considered as the threshold, is breached. Hence, the mathematical model can be employed as a warning model in the early warning system. As is cognized from the development of the threshold rainfall worldwide, as reviewed by Guzzetti et al. [2] and Segoni et al. [3], there are generally few steps involved in the procedure, namely the collection of dataset features, the identification of the threshold, and finally, the validation of the threshold, as illustrated in the Figure 3.

The dataset features are the landslide information (location, date and time of the occurrences and types of landslides) and the information on the rainfall associated with the event. According to Piciullo et al. [55], the source of the landslide event can be obtained from reports, newspapers, the internet and official databases. However, there is no proper landslide catalog in Malaysia, as there are pieces here and there. It is necessary to improve the catalog that contains complete and reliable data. Besides, there is lack of information on most historical events, such as the source and occurrence time. These data are crucial as they are being correlated with the causal rainfall. Furthermore, this can lead to differences in the threshold estimation. Another issue arising from the data collection is the incompleteness of the recorded events. In other words, the threshold analysis was limited to the events involving damaged properties and casualties, which neglected those occurring in the forest. Therefore, a comparison could be made between the threshold at a disturbed slope (manmade) and a natural slope in the near future.

Moreover, the source of the rainfall is another crucial piece of information in terms of the rainfall threshold determination. The development of thresholds in Malaysia is based on hourly rainfall data measured by rain gauges. This method is in line with most thresholds analyzed by other researchers globally, whereby more than half are using the hourly rainfall data to define the threshold [3]. However, most of the thresholds that have been developed in Malaysia did not specifically mention the selection criteria of the rainfall gauge/sources that were being used in their analysis. Furthermore, they did not explain the details relating to the treatment of the rainfall data input that was being used in the analysis. This includes rainfall data quality control that involves filtering and infilling missing data.

In some cases, the researchers relied on the existing rainfall network due to the limitation of the rain gauges installed in the study area. Nonetheless, this information should be mentioned in the criteria for rainfall gauge selection as to whether the analysis used manual judgment, the nearest rainfall station, sole reference or automatic selection. As determined by Winter et al. [56], the closest rainfall gauge should be considered within the 20 km range from the event; otherwise, radar data should be used instead. On the other hand, Althuwaynee et al. [57] suggested the analysis of events should be within a 6 km range of the nearest rainfall gauge and exclude those that are not in this range. As defined by Martelloni et al. [58], another criterion to select the station should be based on the geographical and technical setting of the site. This led to the analysis by Rosi et al. [59] and Berti et al. [60], which used the Thiessen Polygon method for all the available rain gauges in the study area.

The last step in the rainfall threshold development is the validation process. As Segoni et al. [3] classified, the validation can be made using the same dataset or independent dataset, while the standard method of validation is not in place worldwide as yet. However, there is no validation analysis of developed thresholds in Malaysia, as the preliminary assessment is more likely to confirm thresholds as the event’s prediction tool. In summary, all of the developed rainfall thresholds have not been implemented into the operational early warning system, except for those established by DID, which can be considered as implemented into the prototypal early warning system. Therefore, the effectiveness of the threshold cannot be carried out accordingly.

As rainfall is the main triggering factor that finally leads to the failure of a slope, the rainfall threshold is highly significant as a predictor for an impending disaster. The adaptation of this governing parameter depends on the extent of the area under surveillance, but it determines the characteristics of rainfall that causes a landslide. The rainfall threshold can be used as one of the counter measures in disaster risk management, alongside strengthening policy implementation. The variation in rainfall threshold compromises the landslides data compilation and analysis, real-time monitoring, disaster preparedness and emergency response, and susceptibility maps. The rainfall data are readily available, despite the fact that disaster events are limited and there is an inconsistency of events during certain periods. However, further evaluation should be carried out accordingly as the model is dynamic from time to time.

5. Conclusions and Future Perspectives

The rainfall threshold is critical in predicting the occurrences of landslides, particularly DMF and shallow landslides. The procedures along the development process are equally necessary. The landslide information recorded on databases should include a record of occurrences in lower-impact areas and should not be limited to information such as date, time, location, and type of landslide. The record should be centralized and archived among government agencies involved in assessing landslides.

The best rainfall threshold value will be determined by assessing rainfall quantity and quality. Furthermore, the assessment should include details such as the source of the recorded event and the rain gauge selection. Inadequate assessment results from a lack of information because the threshold is not solely dependent on the method used.

Above all, the validation process is key to the application of the rainfall threshold in Malaysia. While drawing a critical line and separation line between occurrence and non-occurrence is very subjective, it requires engineering or modeler judgment; thus, this process is crucial to enhancing the warning of landslides. It comprehends model judgment to suit the area conditions or situation when rain varies with time and space. As such, more data should be measured other than solely the rain threshold. These include the soil water content, hydrometric threshold and local observations of rivers and slopes. Future work should involve reviewing the accuracy of the prediction once the threshold had established.

Therefore, the preliminary assessment (50%) of the rainfall threshold is very worthy as a starting points for sediment-related disaster management globally. As Malaysia needs to move quickly towards embracing the whole aspects of determining the threshold and implementing it into operational thresholds, it is essential to initiate the momentum. At the same time, collaboration or networking among government agencies should be enhanced and strengthened.