A Literature Review and Result Interpretation of the System Identification of Arch Dams Using Seismic Monitoring Data
Abstract
:1. Introduction
2. Review of the Modal Identification Methods
2.1. ARX
2.2. FDD
2.3. ERA and SSI
2.4. Time-Varying Modal Identification Using RSSI
3. Pacoima Arch Dam and Its Earthquake Observation
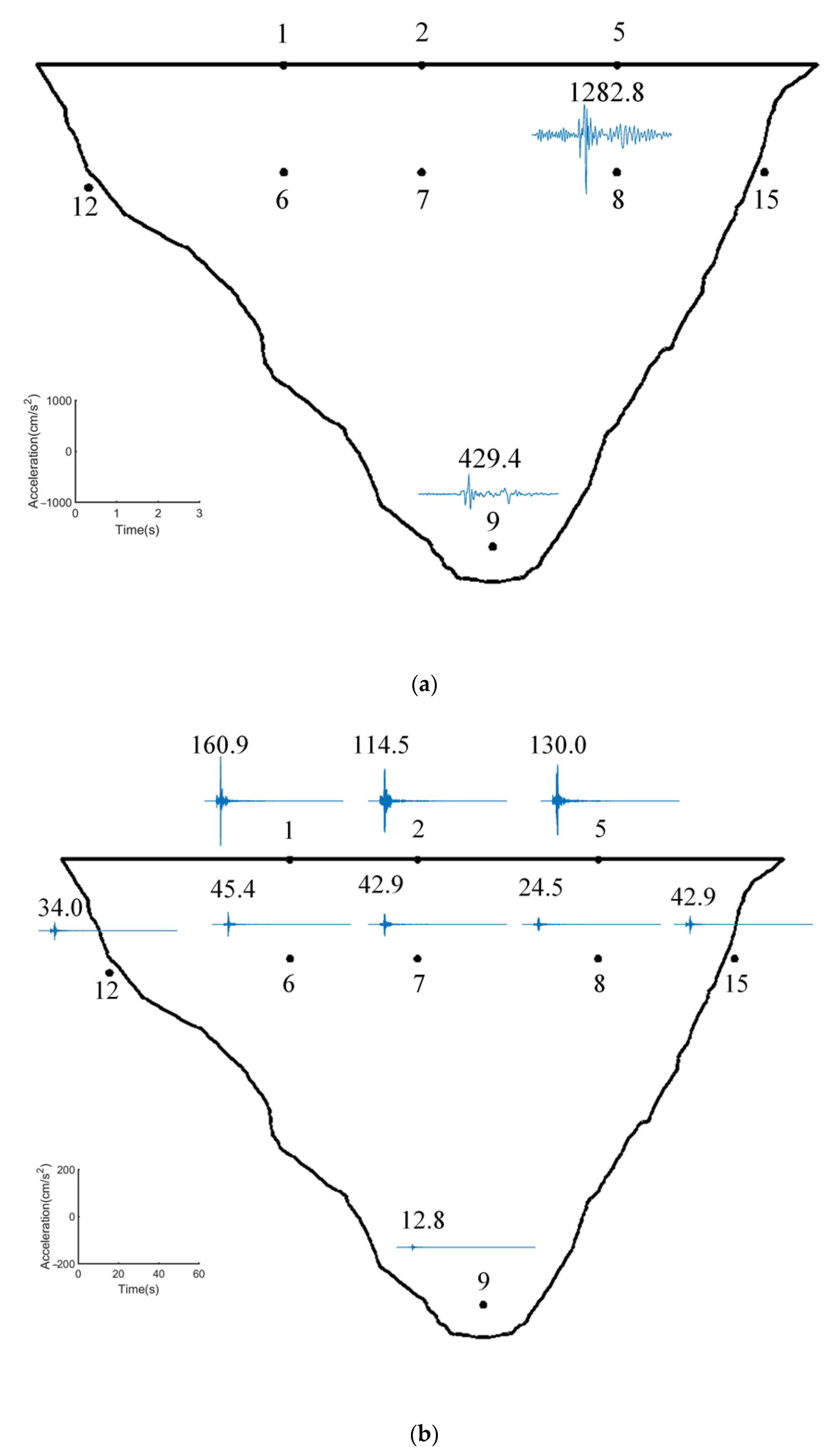
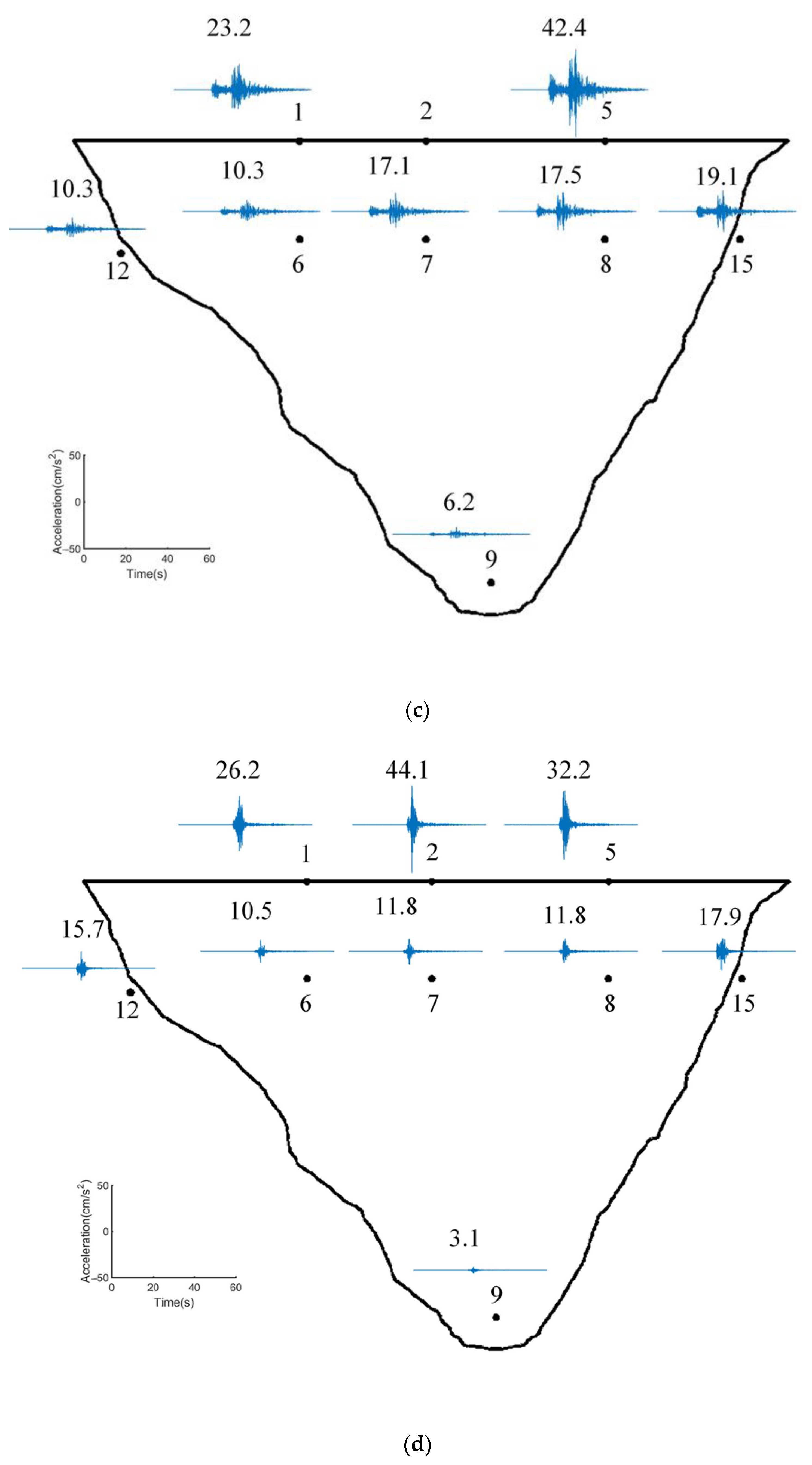
4. Modal Identification Results Using LTI Methods
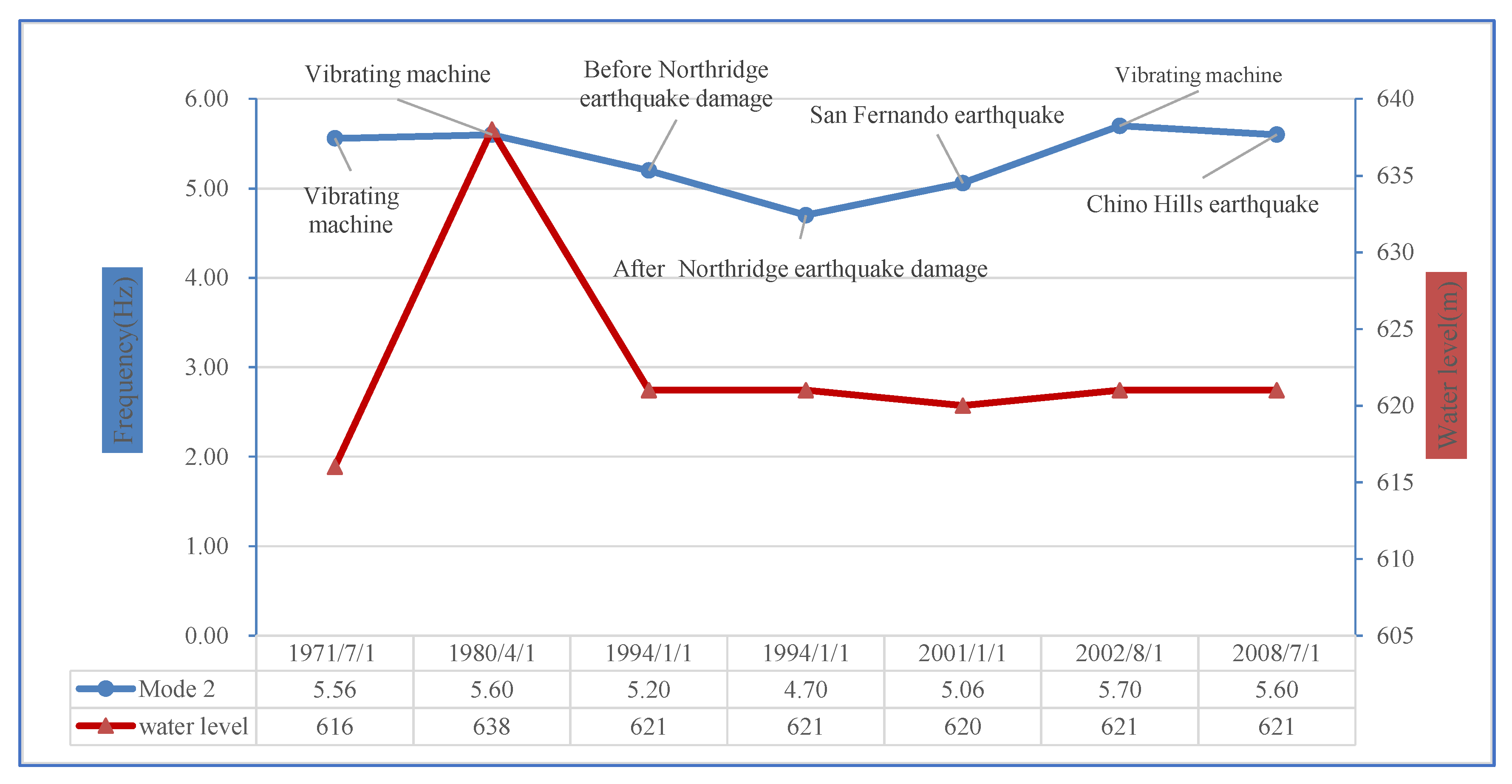
4.1. Identification Results for Frequency and Damping Ratio Based on a Literature Review
4.2. Identification Results Comparison for the Frequency and Damping Ratio Using Different Methods
4.2.1. Identification Results Using OO-Type Method
4.2.2. Identification Results for IO-Type Method
4.3. Identification Results Comparison for Modal Shapes
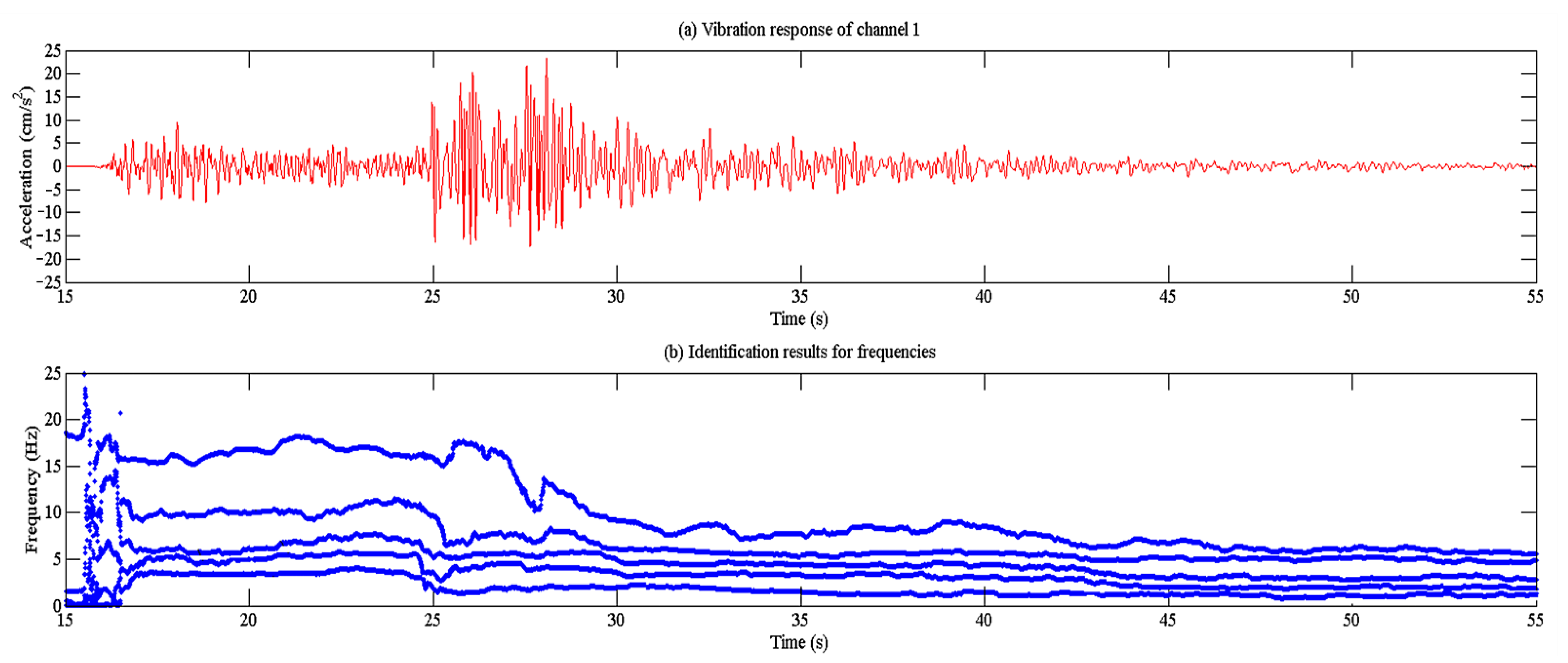
5. Modal Identification Using LTV Methods
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Hansen, K.D.; Nuss, L.K. Lessons learned from the earthquake performance of concrete dams. Int. Water Power Dam Constr. 2011, 63, 32–34, 36–37. [Google Scholar] [CrossRef]
- Hall, J.F. The dynamic and earthquake behaviour of concrete dams: Review of experimental behaviour and observational evidence. Soil Dyn. Earthq. 1988, 7, 58–121. [Google Scholar] [CrossRef]
- Chopra, A.K. Earthquake analysis of arch dams: Factors to be considered. J. Struct. Eng. 2012, 138, 205–214. [Google Scholar] [CrossRef] [Green Version]
- Tarinejad, R.; Ahmadi, M.T.; Harichandran, R.S. Full-scale experimental modal analysis of an arch dam: The first experience in Iran. Soil Dyn. Earthq. Eng. 2014, 61–62, 188–196. [Google Scholar] [CrossRef] [Green Version]
- Birtharia, A.; Jain, S.K. Applications of ambient vibration testing: An overview. Int. Res. J. Eng. Technol. 2015, 02, 845–852. [Google Scholar]
- Bukenya, P. Ambient Vibration Testing of Concrete Dams. Master’s Dissertation, University of Cape Town, Cape Town, South Africa, 2011. [Google Scholar]
- Cheng, L.; Yang, J.; Zheng, D.J. The Health Monitoring Method of Concrete Dams Based on Ambient Vibration Testing and Kernel Principle Analysis. Shock Vib. 2015, 2015, 342358. [Google Scholar] [CrossRef] [Green Version]
- Cheng, L.; Yang, J.; Zheng, D.J.; Tong, F.; Zheng, S.Y. The dynamic finite element model calibration method of concrete dams based on strong-motion records and multivariate relevant vector machines. J. Vibroengineering 2016, 18, 3811–3828. [Google Scholar] [CrossRef] [Green Version]
- Darbre, G.R. Strong-motion instrumentation of dams. Earthq. Eng. Struct. Dyn. 1995, 24, 1101–1111. [Google Scholar] [CrossRef]
- Chen, H.Q. Important Strong Earthquake Data and Analysis of China’s Hydraulic Structure; Seismological Press: Beijing, China, 2000. (In Chinese) [Google Scholar]
- Fry, J.J.; Matsumoto, N. Validation of dynamic analyses of dams and their equipment. In Edited Contributions to the International Symposium on the Qualification of Dynamic Analyses of Dams and their Equipments; CRC Press: Saint-Malo, France, 2018. [Google Scholar]
- Darbre, G.R.; De Smet, C.A.M.; Kraemer, C. Natural frequencies measured from ambient vibration response of the arch dam of Mauvoisin. Earthq. Eng. Struct. Dyn. 2000, 29, 577–586. [Google Scholar] [CrossRef]
- Morrison, P.; Maley, R.; Brady, G.; Porcella, R. Earthquake Recordings on or Near Dams; USCOLD Committee on Earthquakes: Pasadena, CA, USA, 1977. [Google Scholar]
- Oliveira, S.; Alegre, A. Seismic and structural health monitoring of dams in Portugal. In Seismic Structural Health Monitoring; Springer: Cham, Switzerland, 2019; pp. 87–113. [Google Scholar] [CrossRef]
- Cheng, L.; Tong, F.; Li, Y.L.; Yang, J.; Zheng, D.J. Comparative Study of the Dynamic Back-Analysis Methods of Concrete Gravity Dams Based on Multivariate Machine Learning Models. J. Earthq. Eng. 2018, 2018, 1–22. [Google Scholar] [CrossRef]
- Cheng, L.; Tong, F. Application of Blind Source Separation Algorithms and Ambient Vibration Testing to the Health Monitoring of Concrete Dams. Math. Probl. Eng. 2016, 2016, 4280704. [Google Scholar] [CrossRef] [Green Version]
- Moyo, P.; Bukenya, P. Experiences with continuous monitoring of deformation and modal properties of an arch dam. In Proceedings of the 8th Structural Health Monitoring of Intelligent Infrastructure Conference, Brisbane, Australia, 5 December 2017. [Google Scholar]
- Yang, J.; Jin, F.; Wang, J.T.; Kou, L.H. System identification and modal analysis of an arch dam based on earthquake response records. Soil Dyn. Earthq. Eng. 2017, 92, 109–121. [Google Scholar] [CrossRef]
- Cheng, L.; Zheng, D.J. The identification of a dam’s modal parameters under random support excitation based on the Hankel matrix joint approximate diagonalization technique. Mech. Syst. Signal Process. 2014, 42, 42–57. [Google Scholar] [CrossRef]
- Zhang, L.F.; Xing, G.L.; Zhang, M. Analysis of strong earthquake of gravity arch dam in Longyang gorge. J. Hroelectric Eng. 1998, 1998, 14–17. [Google Scholar] [CrossRef]
- Li, S.; Wang, J.T.; Jin, A.Y. Parametric analysis of SSI algorithm in modal identification of high arch dams. Soil Dyn. Earthq. Eng. 2020, 129, 105929. [Google Scholar] [CrossRef]
- Loh, C.H.; Wu, T.S. Identification of Fei-Tsui arch dam from both ambient and seismic response data. Soil Dyn. Earthq. Eng. 1996, 15, 465–483. [Google Scholar] [CrossRef]
- Proulx, J.; Darbre, G.R.; Kamileris, N. Analytical and experimental investigation of damping in arch dams based on recorded earthquakes. In Proceedings of the 13th WCEE, Vancouver, BC, Canada, 1–6 August 2004. [Google Scholar]
- Chopra, A.K. Comparison of recorded and computed responses of arch dams. In Proceedings of the International Symposium on Dams, Kyoto, Japan, 23 July 2012. [Google Scholar]
- Okuma, N.; Etou, Y.; Kanazawa, K.; Hirata, K. Dynamic property of a large arch dam after forty-four years of completion. In Proceedings of the 14th World Conference on Earthquake Engineering, Beijing, China, 12–17 October 2008. [Google Scholar]
- Tarinejad, R.; Falsafian, K.; Aalami, M.T. Modal identification of Karun IV arch dam based on ambient vibration tests and seismic responses. J. Vibroengineering 2016, 18, 3869–3880. [Google Scholar] [CrossRef] [Green Version]
- Alves, S.W. Nonlinear Analysis of Pacoima Dam with Spatially Non-Uniform Ground Motion. Ph.D. Dissertation, Rep. EERL 2004-11 Earthquake Engineering Research Lab., CA. Inst. of Tech., Pasadena, CA, USA, 2005. [Google Scholar]
- Bukenya, P.; Moyo, P.; Beushausen, H.; Oosthuizen, C. Health monitoring of concrete dams: A literature review. J. Civ. Struct. Health Monit. 2014, 4, 235–244. [Google Scholar] [CrossRef]
- Ghalishooyan, M.; Shooshtari, A.; Abdelghani, M. Output-only modal identification by in-operation modal appropriation for use with enhanced frequency domain decomposition method. J. Mech. Sci. Technol. 2019, 33, 3055–3067. [Google Scholar] [CrossRef]
- Chang, M.; Pakzad, S.N.; Leonard, R. Modal identification using SMIT. In Topics on the Dynamics of Civil Structures; Springer: New York, NY, USA, 2012. [Google Scholar] [CrossRef]
- Chang, M.; Pakzad, S.N. Modified natural excitation technique for stochastic modal identification. J. Struct. Eng. 2013, 139, 1753–1762. [Google Scholar] [CrossRef]
- Lus, H.; Betti, R.; Longman, R.W. Identification of linear structural systems using earthquake induced vibration data. Earthq. Eng. Struct. Dyn. 1999, 28, 1449–1467. [Google Scholar] [CrossRef]
- Juang, J.N. System realization using information matrix. J. Guid. Control. Dyn. 2012, 20, 492–500. [Google Scholar] [CrossRef] [Green Version]
- Kim, J.; Lynch, J.P. Subspace system identification of support-excited structures-part I: Theory and black-box system identification. Earthq. Eng. Struct. Dyn. 2012, 41, 2235–2251. [Google Scholar] [CrossRef] [Green Version]
- Van Overschee, P.; De Moor, B. Subspace algorithms for the stochastic identification problem. Automatica 1993, 29, 649–660. [Google Scholar] [CrossRef]
- Ruben, L.B.; Joaquin, A.B. Interpretation of stabilization diagrams using density-based clustering algorithm. Eng. Struct. 2019, 178, 245–257. [Google Scholar] [CrossRef]
- Gong, M.S. Structural modal parameters identification and application based on earthquake response data. Ph.D. Dissertation, Institute of Engineering Mechanics of China Earthquake Administration, Harbin, China, 2005. [Google Scholar]
- Liu, Y.C.; Loh, C.H.; Ni, Y.Q. Stochastic subspace identification for output-only modal analysis: Application to super high-rise tower under abnormal loading condition. Earthq. Eng. Struct. Dyn. 2013, 42, 477–498. [Google Scholar] [CrossRef]
- Cheng, L.; Tong, F.; Yang, J.; Zheng, D.J. Online modal identification of concrete dams using the subspace tracking-based method. Shock Vib. 2019, 2019, 7513261. [Google Scholar] [CrossRef] [Green Version]
- Processed data for Pacoima Dam—Channels 8 through 11 from the Northridge Earthquake of 17 January 1994; Report OSMS 94-15 A; California Strong Motion Instrumentation Prg: Sacramento, CA, USA, 1994.
- Phase 1 data for Pacoima Dam—Channels 1-6, 12, 13 and 15-17 from the Northridge Earthquake of 17 January 1994; Report OSMS 95-05; California Strong Motion Instrumentation Prg: Sacramento, CA, USA, 1995.
- Alves, S.W.; Hall, J.F. System identification of a concrete arch dam and calibration of its finite element model. Earthq. Eng. Struct. Dyn. 2006, 35, 1321–1337. [Google Scholar] [CrossRef]
- Tarinejad, R.; Damadipour, M. Extended FDD-WT method based on correcting the errors due to non-synchronous sensing of sensor. Mech. Syst. Signal Process. 2016, 72–73, 547–566. [Google Scholar] [CrossRef]
- Someh, R.F. Modal identification of an arch dam during various earthquakes. In Proceedings of the 1st International Conference on Dams & Hydropower, Tehran, Iran, 1 January 2012. [Google Scholar]
- Wang, J.T.; Chopra, A.K. Linear analysis of concrete arch dams including dam-water-foundation rock interaction considering spatially varying ground motions. Earthq. Eng. Struct. Dyn. 2010, 39, 731–750. [Google Scholar] [CrossRef]
- Alves, S.W.; Hall, J.F. Generation of spatially nonuniform ground motion for nonlinear analysis of a concrete arch dam. Earthq. Eng. Struct. Dyn. 2006, 35, 1339–1357. [Google Scholar] [CrossRef]
- Tarinejad, R.; Fatehi, R.; Harichandran, R.S. Response of an arch dam to non-uniform excitation generated by a seismic wave scattering model. Soil Dyn. Earthq. Eng. 2013, 52, 40–54. [Google Scholar] [CrossRef] [Green Version]
- Okamoto, S. Introduction to Earthquake Engineering, 2nd ed.; University of Tokyo Press: Tokyo, Japan, 1984. [Google Scholar]
- Kou, L.H.; Jin, F.; Chi, F.D.; Wang, L. Analysis of prototype dynamic test of concrete arch dams at home and abroad. J. Hydroelectr. Eng. 2007, 26, 31–37. [Google Scholar] [CrossRef]
- Liu, N.F.; Li, N.; Li, G.F.; Song, Z.P.; Wang, S.J. Method for Evaluating the Equivalent Thermal Conductivity of a Freezing Rock Mass Containing Systematic Fractures. Rock Mech. Rock Eng. 2022. [Google Scholar] [CrossRef]


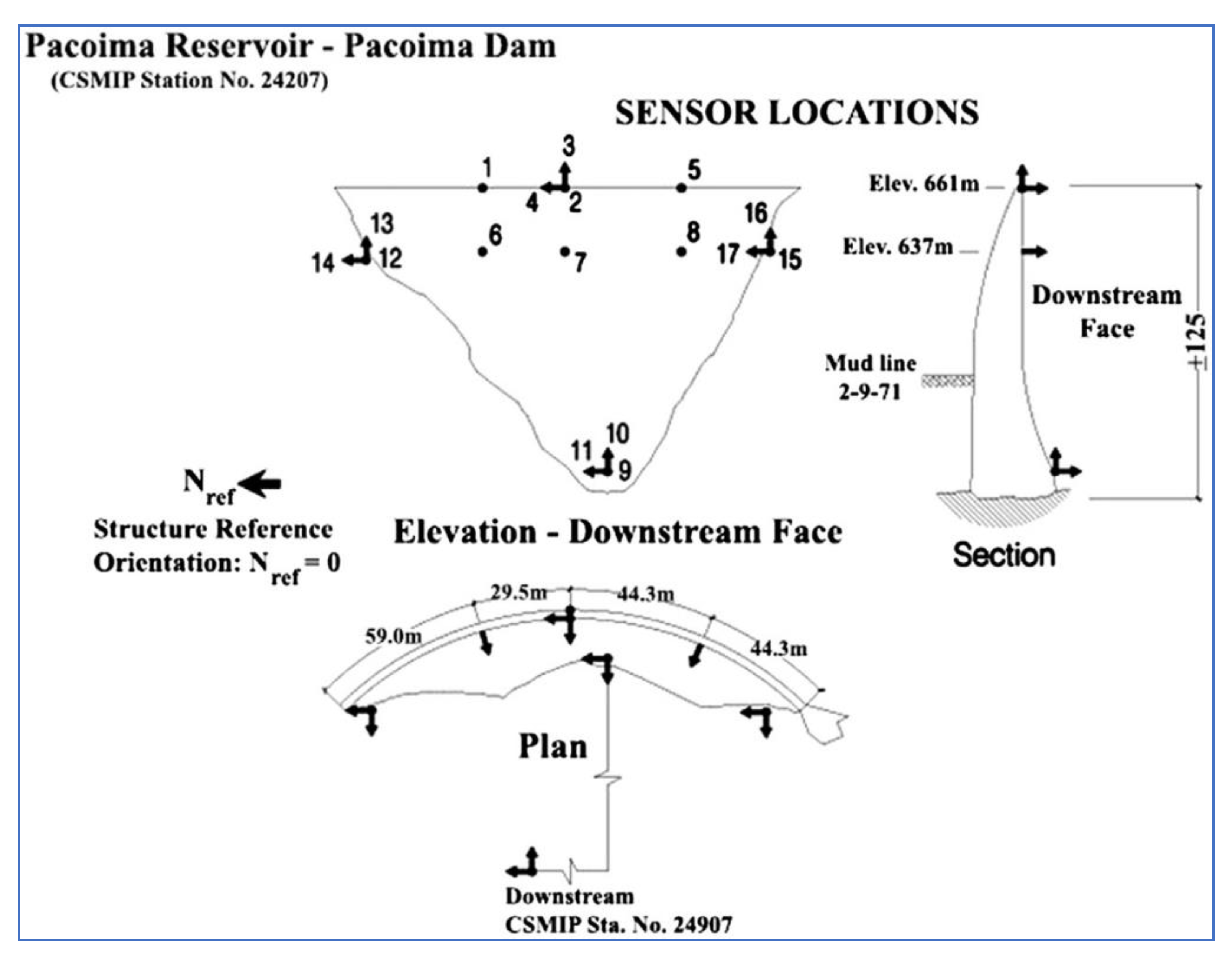
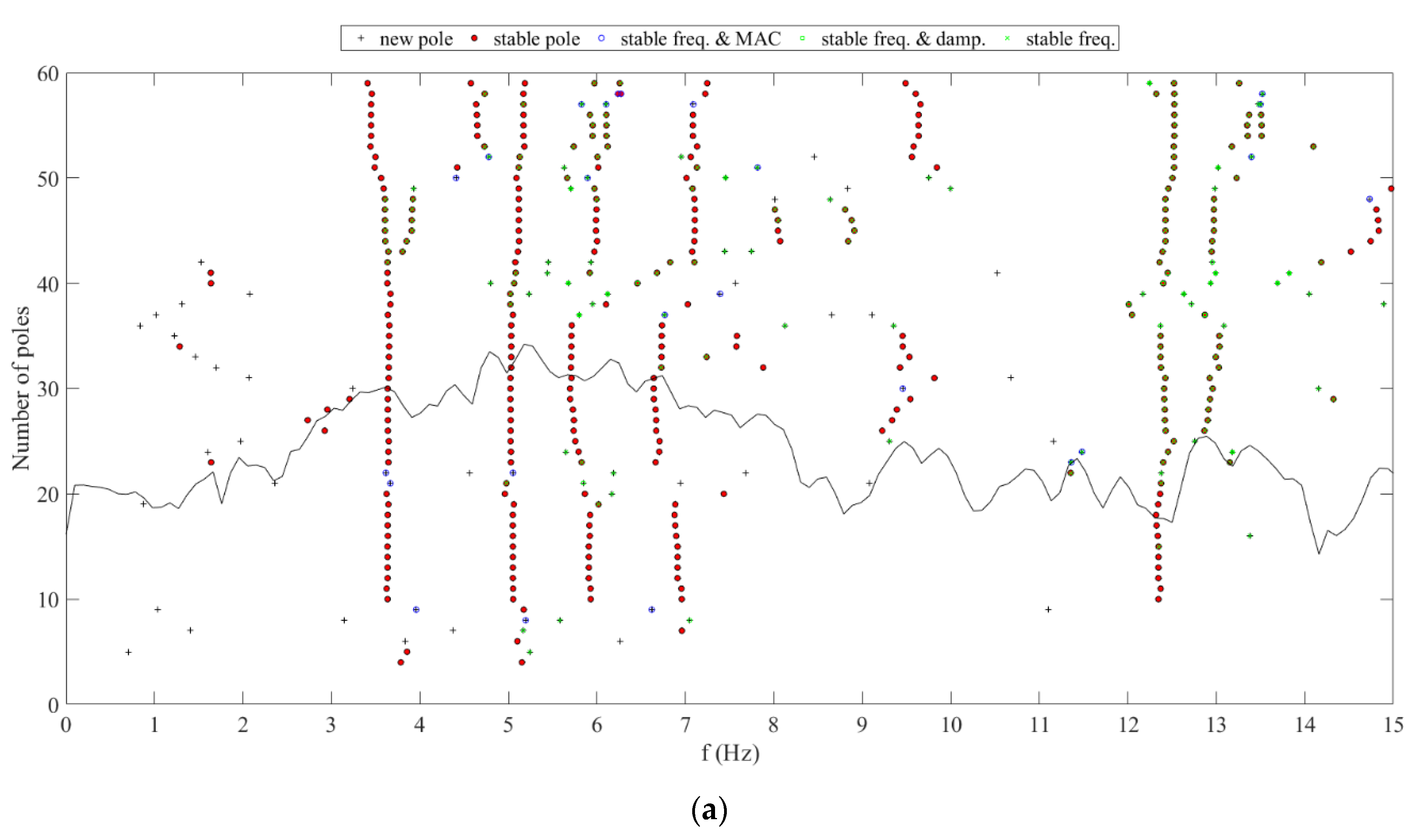
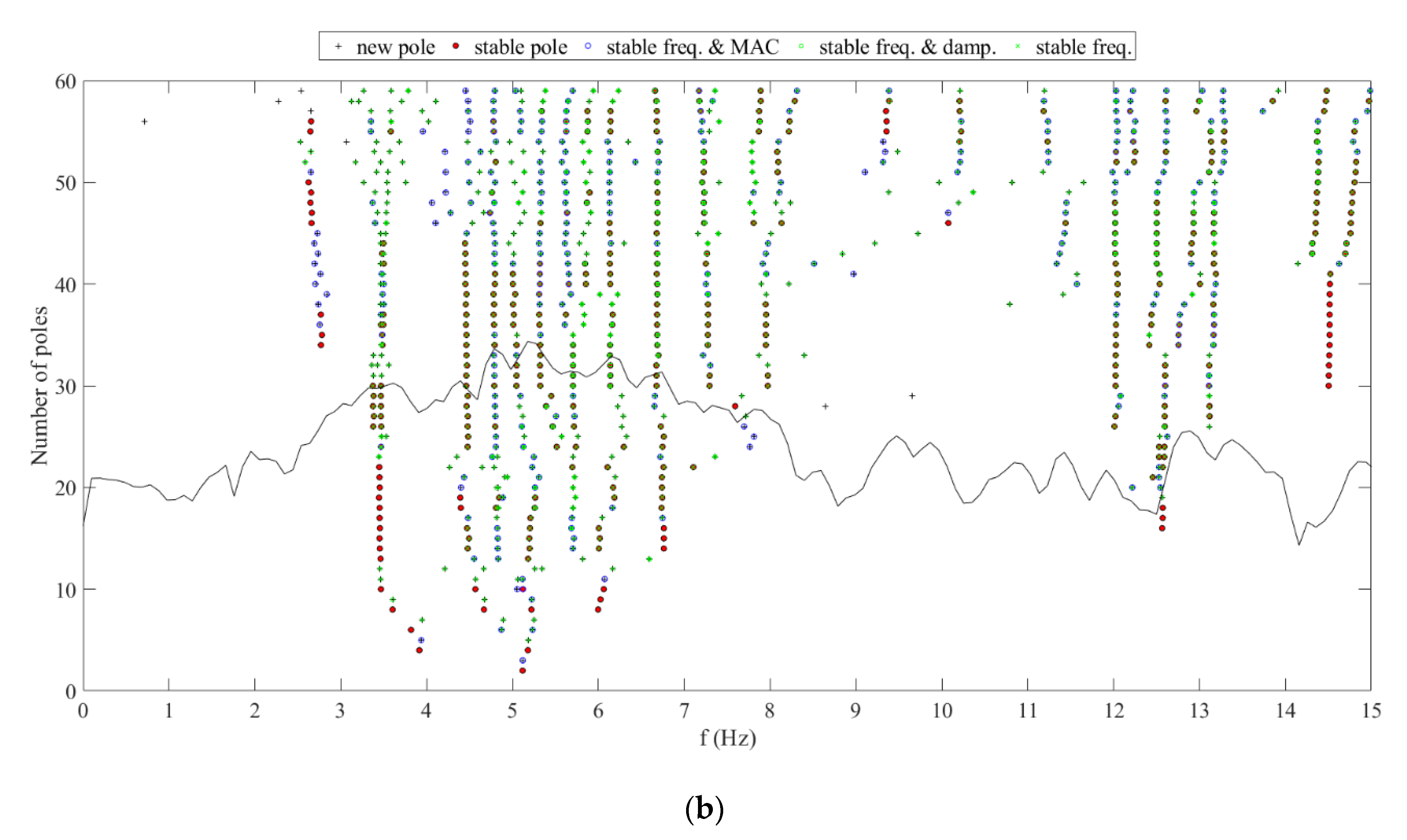
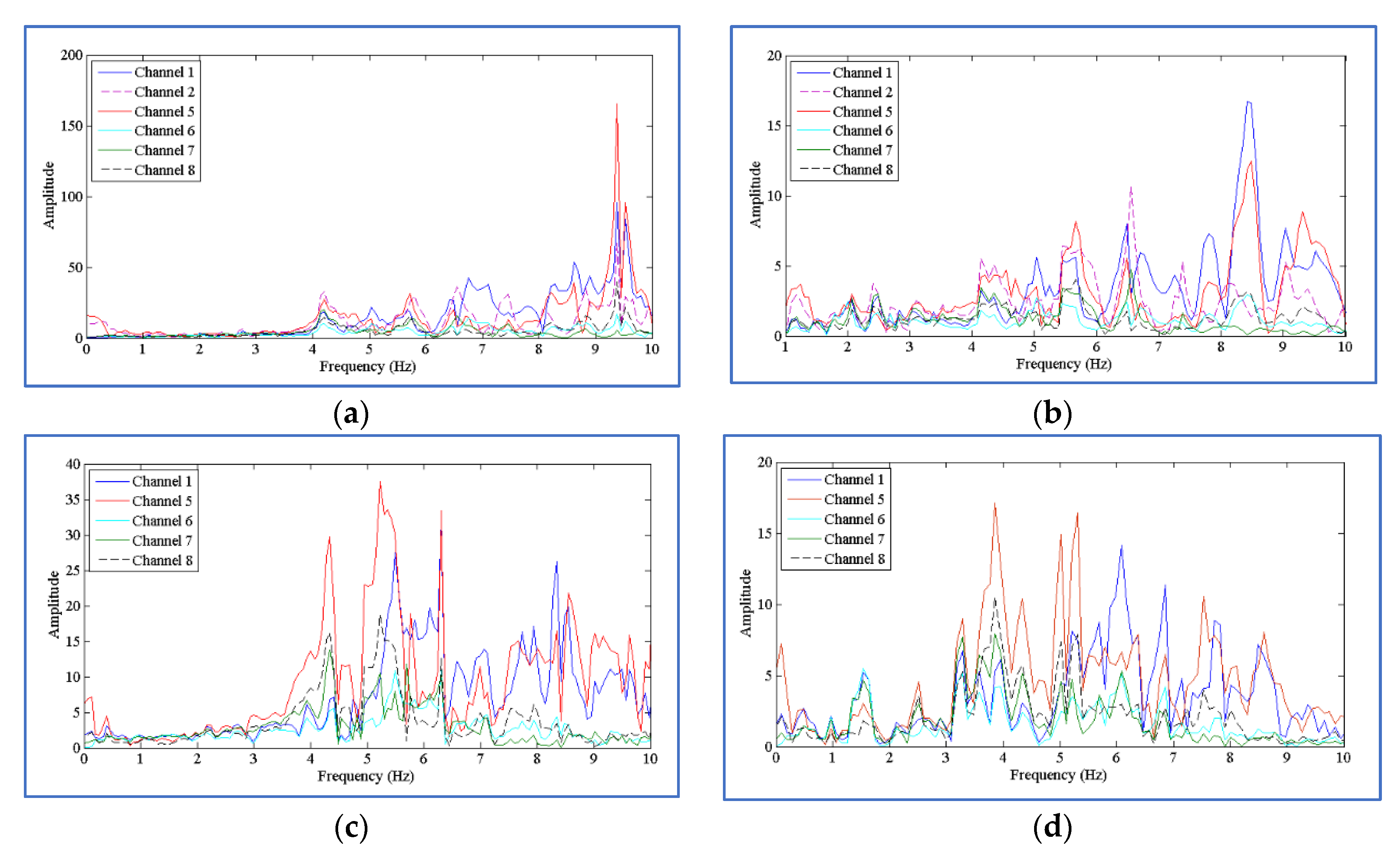
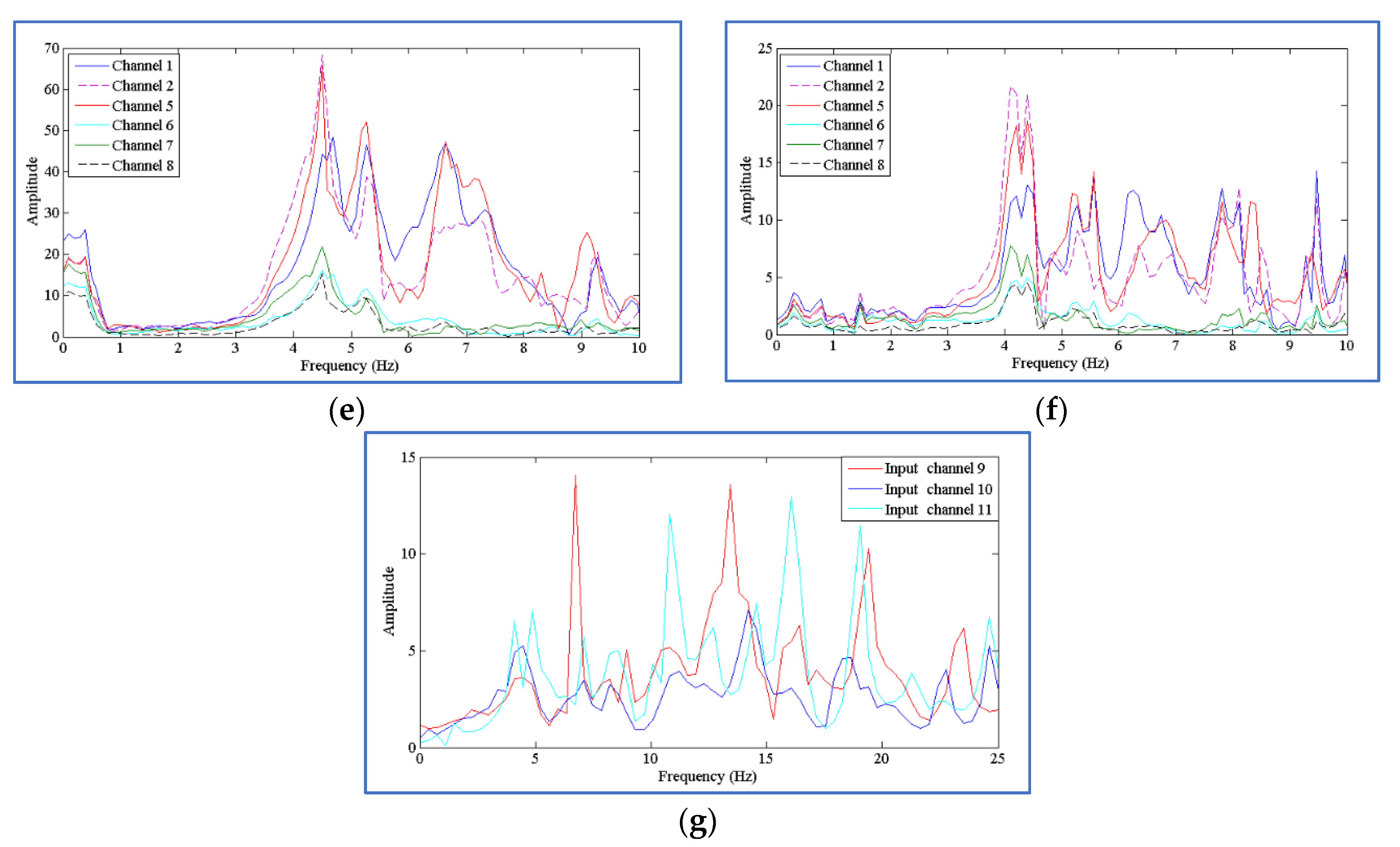

| Country /Region | Project Name | Height (m) | Modal Id. Method | Application of System Identification Results | FVT | AVT | ||
|---|---|---|---|---|---|---|---|---|
| Seismic Parameter Extraction | Model Calibration | Damage Diagnosis | ||||||
| China | Ertan arch dam [18] | 240 | ARX | ✔ | ✔ | ✔ | ||
| Shuikou gravity dam [19] | 101 | BSS | ✔ | ✔ | ✔ | ✔ | ||
| Longyangxia arch dam [20] | 178 | PP | ✔ | ✔ | ✔ | |||
| Xiluodu arch dam [21] | 2855 | SSI | ✔ | |||||
| Taiwan, China | Fei-Tsui arch dam [22] | 122.5 | ARX | ✔ | ✔ | ✔ | ✔ | |
| Switzerland | Emosson arch dam [23] | 180 | PP | ✔ | ✔ | ✔ | ✔ | |
| Mauvoisin arch dam [24] | 250 | PP | ✔ | ✔ | ✔ | |||
| Punt-dal-Gall arch dam [24] | 130 | PP | ✔ | ✔ | ✔ | |||
| Japan | Kurobe arch dam [11] | 186 | FDD | ✔ | ||||
| Tagokura gravity dam [11] | 145 | FDD | ✔ | |||||
| Hitotsuse arch dam [25] | 130 | PP | ✔ | |||||
| Portugal | Cabril arch dam [14] | 132 | FDD | ✔ | ✔ | ✔ | ||
| Cahora Bassa arch dam [14] | 170 | FDD | ✔ | ✔ | ✔ | |||
| Baixo Sabor arch dam [14] | 123 | FDD | ✔ | ✔ | ✔ | |||
| Iran | Karun IV arch dam [26] | 230 | FDD | ✔ | ✔ | ✔ | ||
| Earthquake Name | Date | Water Level below Crest (m) | Earthquake Magnitude (Richter Scale) | Epicentral Distance from the Dam (km) | Depth of Hypocenter (km) | Horizontal Peak Acceleration (g) | |
|---|---|---|---|---|---|---|---|
| Ground | Structure | ||||||
| San Fernando | 9 February 1971 | 45 | 6.6 | 8.0 | 9.0 | 1.250 | - |
| Northridge | 17 January 1994 | 40 | 6.7 | 18.0 | 19.0 | 1.530 | 2.010 |
| San Fernando | 13 January 2001 | 41 | 4.3 | 6.1 | 9.0 | 0.021 | 0.164 |
| Chino Hills | 29 July 2008 | 40 | 5.5 | 71.9 | 13.7 | 0.006 | 0.0043 |
| Newhall | 1 September 2011 | - | 4.2 | 7.8 | - | 0.003 | 0.045 |
| Num. | System Ident. by | Date | Water Level below Crest (m) | Excitation Input | Id. Method | Frequency (Hz) | Damping (%) | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 1 | 2 | |||||||
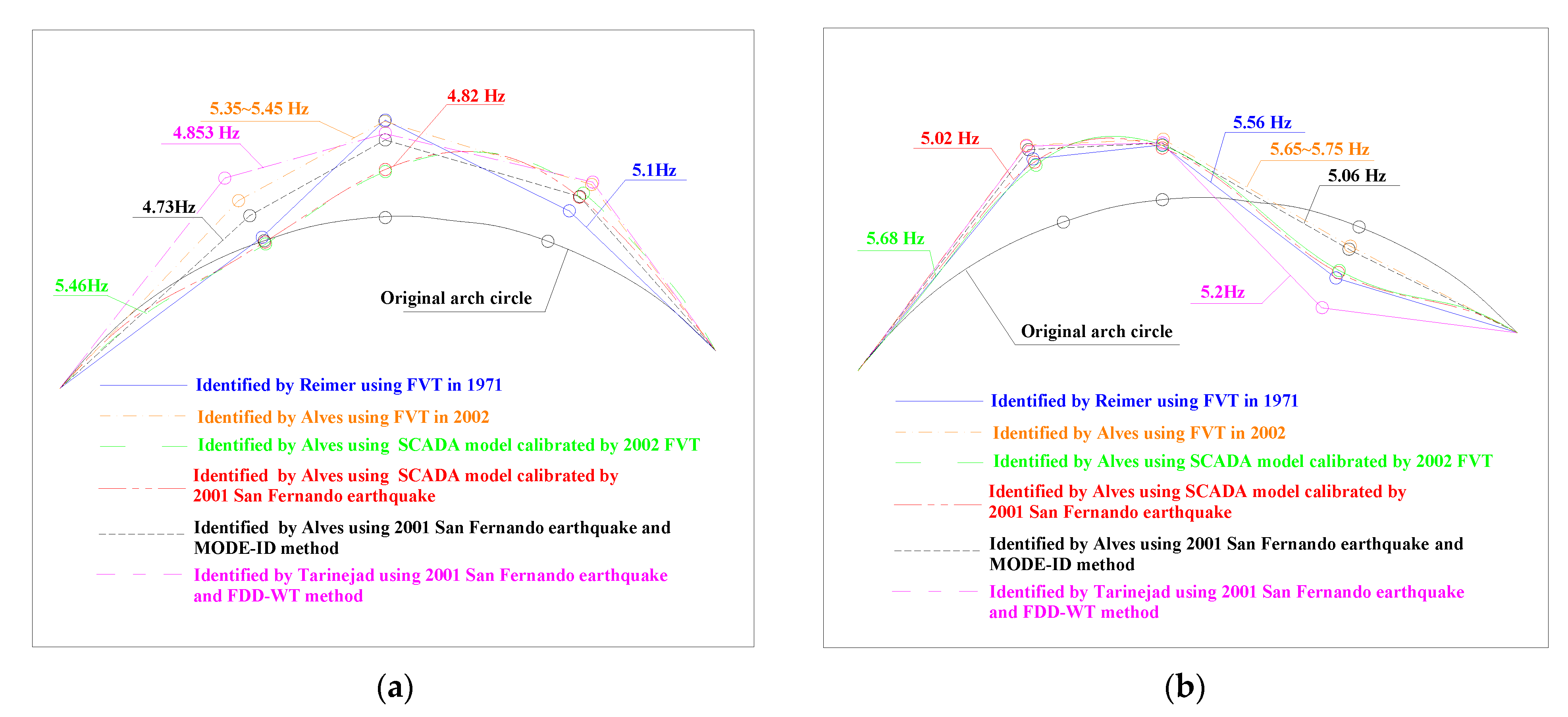
| 1 | Reimer [27] | July 1971 | empty | Vibrator | curve fitting of FRF | 5.10 | 5.56 | - | - | - | |
| 2 | ANCO Engineers [27] | April 1980 | 23 | Vibrator | curve fitting of FRF | 5.45 | 5.60 | - | 7.3 | 9.8 | |
| 3 | Alves [27] | July/August, 2002 | 36 | Vibrator | curve fitting of FRF | 5.35~5.45 | 5.65~5.75 | - | 4.0~7.0 | 4.5~5.5 | |
| 4 | Alves [27] | 17 January 1994 | 40 | Northridge earthquake | MODE-ID | undamaged | 4.80 | 5.20 | - | 10.0 | 8.0 |
| damaged | 3.80 | 4.70 | - | 6.0~9.0 | - | ||||||
| 5 | Jalali [27] | 17 January 1994 | 40 | Northridge earthquake | ARX | undamaged | 4.90 | - | - | - | - |
| damaged | 3.90 | - | - | - | - | ||||||
| 6 | Alves [42] | 13 January 2001 | 41 | San Fernando earthquake | MODE-ID | 4.73~4.83 | 5.06 | - | 6.2 | 6.6~7.3 | |
| 7 | Tarinejad [43] | 13 January 2001 | 41 | San Fernando earthquake | FDD-WT | 3.67 | 4.85 | 5.20 | - | - | |
| 8 | Tarinejad [43] | 13 January 2001 | 41 | San Fernando earthquake | 4-spectral | 3.60~3.70 | 4.80–5.00 | 5.10~5.30 | - | - | |
| 9 | Fatehi [44] | 13 January 2001 | 41 | San Fernando earthquake | ARX | 4.68 | 5.07 | - | - | - | |
| 10 | Wang [45] | 13 January 2001 | 41 | San Fernando earthquake | Half-power bandwidth | - | - | - | 7.0 | 6.7 | |
| 11 | Someh [44] | 29 July 2008 | 40 | Chino Hills earthquake | ARX | 5.40 | 5.75 | - | - | - | |
| 12 | Alves [46] | 13 January 2001 | 38 | - | SCADA (calibrated using 2001 San Fernando earthquake) | 4.82 | 5.02 | - | - | - | |
| 13 | Tarinejad [47] | 29 July 2008 | 40 | - | EACD-3D2008 (calibrated using 2008 Chino Hills earthquake) | 5.43 | 5.60 | - | - | - | |
| Earthquake | ID. Method | Frequency (Hz) | Damping (%) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 1 | 2 | 3 | 4 | ||
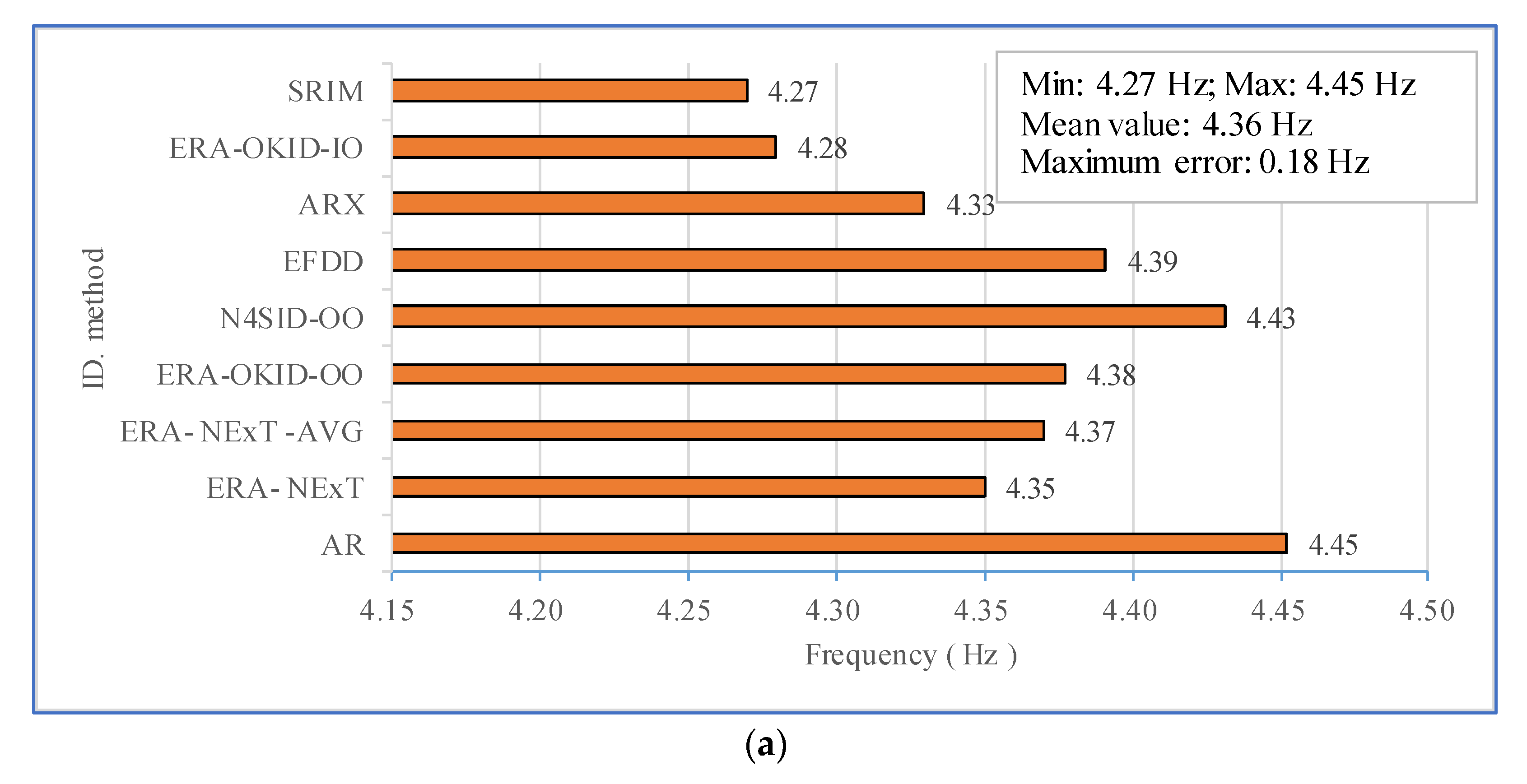
| 2001 San Fernando | AR | 3.52 | 4.45 | 5.25 | 6.14 | 2.88 | 0.98 | 2.78 | 5.69 |
| ERA-NExT | 3.55 | 4.35 | 5.17 | 6.23 | 1.71 | 2.44 | 1.81 | 1.03 | |
| ERA-NExT-AVG | - | 4.37 | 5.23 | 6.24 | - | 7.74 | 2.30 | 2.48 | |
| ERA-OKID-OO | 3.52 | 4.38 | 5.16 | 6.15 | 9.44 | 2.46 | 1.98 | 5.41 | |
| N4SID-OO | 3.47 | 4.43 | 5.17 | 6.23 | 6.75 | 1.38 | 1.57 | 1.28 | |
| EFDD | 3.42 | 4.39 | 5.19 | 6.15 | 4.55 | 5.03 | 4.39 | 4.78 | |
| 2008 Chino Hills | AR | 3.91 | 4.34 | 5.31 | - | 9.38 | 8.37 | 5.88 | - |
| ERA-NExT | 3.73 | 4.26 | 5.29 | - | 5.91 | 5.33 | 4.96 | - | |
| ERA-NExT-AVG | 3.88 | 4.26 | 5.41 | - | 4.40 | 3.45 | 1.13 | - | |
| ERA-OKID-OO | 3.85 | 4.23 | 5.31 | - | 9.66 | 5.46 | 5.88 | - | |
| N4SID-OO | 3.73 | 4.20 | 5.22 | - | 6.06 | 8.80 | 6.83 | - | |
| EFDD | 3.71 | 4.29 | 5.37 | 6.05 | 4.15 | 3.66 | 5.76 | 1.55 | |
| 2011 Newhall | AR | - | 4.20 | 5.65 | 6.79 | - | 1.52 | 1.96 | 3.16 |
| ERA-NExT | - | 4.26 | 5.66 | 6.87 | - | 2.89 | 1.18 | 0.67 | |
| ERA-NExT-AVG | - | 4.27 | 5.70 | 6.82 | - | 4.75 | 1.38 | 1.66 | |
| ERA-OKID-OO | - | 4.27 | 5.59 | 6.79 | - | 7.58 | 3.22 | 3.90 | |
| N4SID-OO | - | 4.28 | 5.70 | 6.92 | - | 6.03 | 4.13 | 5.98 | |
| EFDD | - | 4.20 | 5.66 | 6.83 | - | 0.16 | 3.11 | 3.72 | |
| Earthquake | ID. Method | Frequency (Hz) | Damping (%) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 1 | 2 | 3 | 4 | ||
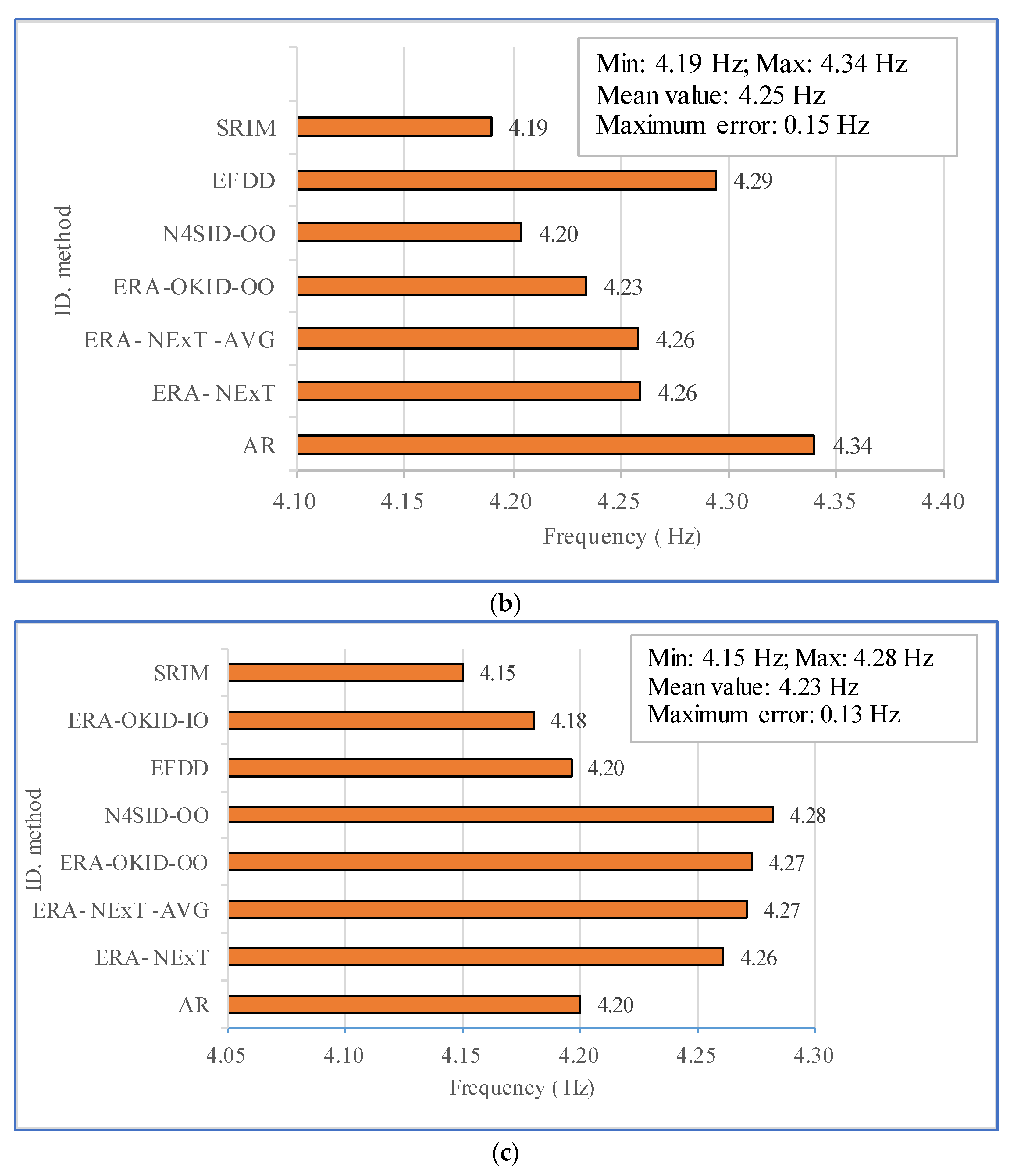
| 2001 San Fernando | AR | 3.58 | 4.34 | 5.13 | 6.25 | 9.20 | 8.00 | 2.59 | 3.83 |
| ERA-NExT | 3.59 | - | 5.21 | 6.27 | 2.73 | - | 1.59 | 2.54 | |
| ERA-NExT-AVG | 3.66 | 4.30 | 5.32 | 6.14 | 4.88 | 6.71 | 3.98 | 2.93 | |
| ERA-OKID-OO | 3.58 | 4.33 | 5.15 | 6.30 | 9.20 | 7.52 | 2.87 | 2.88 | |
| N4SID-OO | 3.56 | 4.41 | 5.24 | 6.18 | 9.50 | 8.85 | 3.47 | 2.42 | |
| EFDD | 3.42 | 4.39 | 5.19 | 6.15 | 4.29 | 4.15 | 4.61 | 4.91 | |
| 2008 Chino Hills | AR | 3.88 | 4.16 | 5.30 | - | 3.88 | 7.19 | 6.40 | - |
| ERA-NExT | 3.78 | - | 5.33 | - | 5.69 | - | 9.79 | - | |
| ERA-NExT-AVG | 3.79 | 4.23 | 5.26 | - | 8.66 | 7.13 | 4.80 | - | |
| ERA-OKID-OO | 3.83 | 4.17 | 5.30 | - | 8.93 | 7.33 | 6.41 | - | |
| N4SID-OO | 3.97 | 4.36 | 5.37 | - | 6.65 | 6.87 | 5.95 | - | |
| EFDD | 3.71 | 4.29 | 5.37 | 6.05 | 1.28 | 3.41 | 3.88 | 2.00 | |
| 2011 Newhall | AR | - | 4.27 | 5.64 | 6.79 | - | 4.02 | 3.14 | 2.82 |
| ERA-NExT | - | 4.24 | 5.65 | 6.83 | - | 2.34 | 2.05 | 0.77 | |
| ERA-NExT-AVG | - | 4.22 | 5.71 | 6.84 | - | 4.38 | 1.70 | 3.31 | |
| ERA-OKID-OO | - | 4.27 | 5.72 | 6.84 | - | 2.71 | 9.66 | 2.99 | |
| N4SID-OO | - | 4.23 | 5.71 | 6.85 | - | 4.98 | 2.66 | 1.96 | |
| EFDD | - | 4.20 | 5.66 | 6.83 | - | 4.42 | 3.22 | 3.22 | |
| Earthquake | ID. Method | Frequency (Hz) | Damping (%) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 1 | 2 | 3 | 4 | ||
| 2001 San Fernando | ARX | - | 4.32 | 5.15 | 6.17 | - | 4.59 | 4.06 | 5.49 |
| ERA-OKID-IO | - | - | - | - | - | - | - | ||
| SRIM | 3.50 | 4.27 | 5.28 | 6.19 | 3.39 | 8.87 | 1.33 | 0.71 | |
| N4SID-IO | - | 4.28 | 5.22 | - | - | 5.50 | 3.47 | - | |
| 2008 Chino Hills | ARX | - | 4.16 | 5.29 | - | - | 7.39 | 6.09 | - |
| ERA-OKID-IO | - | 4.15 | 5.26 | - | - | 7.09 | 6.50 | - | |
| SRIM | - | 4.17 | 5.29 | - | - | 7.72 | 1.46 | - | |
| N4SID-IO | - | 5.32 | 5.91 | - | - | 8.19 | 5.30 | ||
| 2011 Newhall | ARX | - | 4.20 | - | 5.80 | - | 6.10 | - | 6.89 |
| ERA-OKID-IO | - | - | - | - | - | - | - | - | |
| SRIM | 3.18 | 4.25 | - | 5.61 | 3.25 | 1.77 | - | 7.27 | |
| N4SID-IO | - | - | - | 5.67 | - | - | - | 3.34 | |
| Earthquake | ID. Method | Frequency (Hz) | Damping (%) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 1 | 2 | 3 | 4 | ||
| 2001 San Fernando | ARX | - | 4.33 | 5.08 | 6.16 | - | 2.18 | 3.79 | 2.31 |
| ERA-OKID-IO | - | 4.28 | 5.04 | - | - | 6.18 | 3.01 | 5.01 | |
| SRIM | 3.47 | 4.27 | 5.15 | 6.19 | 1.90 | 1.61 | 0.89 | 2.07 | |
| N4SID-IO | 3.59 | - | 5.27 | - | 2.98 | 8.78 | 4.17 | 3.77 | |
| 2008 Chino Hills | ARX | 3.35 | - | 5.14 | 5.87 | 9.75 | - | 8.11 | 1.22 |
| ERA-OKID-IO | - | - | 5.14 | 5.70 | - | - | 4.63 | 4.40 | |
| SRIM | 3.23 | 4.19 | 5.14 | - | 0.56 | 1.42 | 1.64 | - | |
| N4SID-IO | - | - | 5.17 | 5.80 | - | - | 6.30 | 3.99 | |
| 2011 Newhall | ARX | - | - | - | 5.80 | - | - | 2.94 | - |
| ERA-OKID-IO | - | 4.18 | - | 5.63 | - | 9.74 | 3.97 | - | |
| SRIM | 3.21 | 4.15 | - | 5.74 | 3.10 | 2.20 | 0.66 | 1.61 | |
| N4SID-IO | - | - | - | 5.73 | - | - | 3.96 | 4.71 | |
| ID. Method | FEM | 2002 FVT |
|---|---|---|
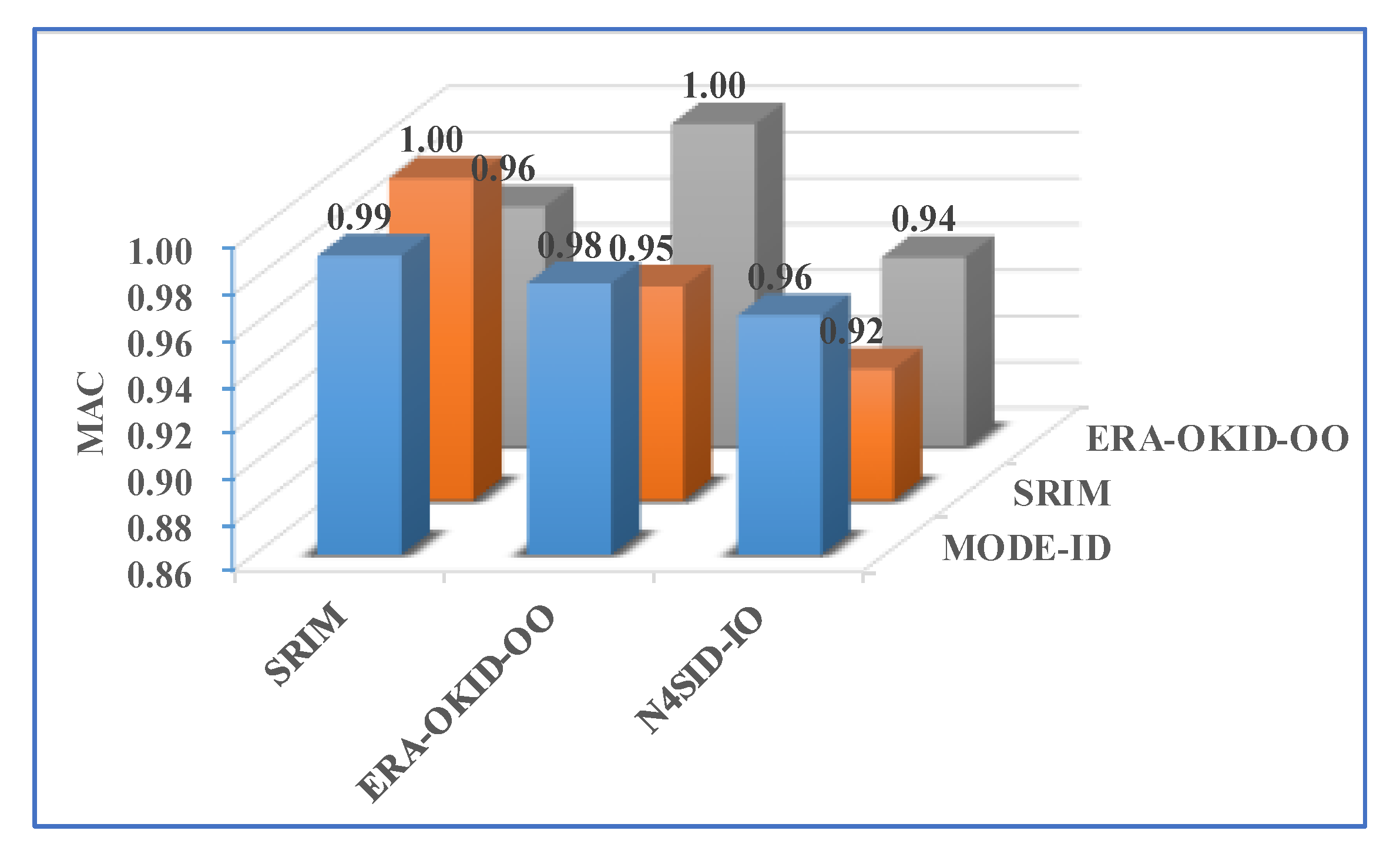
| MODE-ID |  MAC = 0.708 | 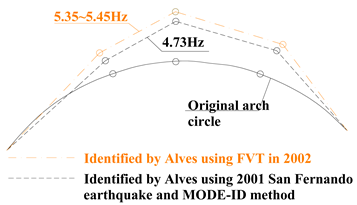 MAC = 0.900 |
| SRIM |  MAC = 0.876 |  MAC = 0.950 |
| ERA-OKID-OO |  MAC = 0.818 | 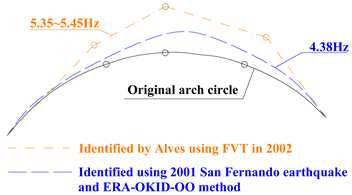 MAC = 0.849 |
| N4SID-IO |  MAC = 0.872 | 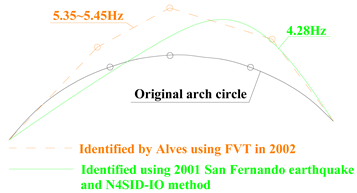 MAC = 0.912 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cheng, L.; Ma, C.; Yuan, X.; Yang, J.; Hu, L.; Zheng, D. A Literature Review and Result Interpretation of the System Identification of Arch Dams Using Seismic Monitoring Data. Water 2022, 14, 3207. https://doi.org/10.3390/w14203207
Cheng L, Ma C, Yuan X, Yang J, Hu L, Zheng D. A Literature Review and Result Interpretation of the System Identification of Arch Dams Using Seismic Monitoring Data. Water. 2022; 14(20):3207. https://doi.org/10.3390/w14203207
Chicago/Turabian StyleCheng, Lin, Chunhui Ma, Xina Yuan, Jie Yang, Liangcai Hu, and Dongjian Zheng. 2022. "A Literature Review and Result Interpretation of the System Identification of Arch Dams Using Seismic Monitoring Data" Water 14, no. 20: 3207. https://doi.org/10.3390/w14203207
APA StyleCheng, L., Ma, C., Yuan, X., Yang, J., Hu, L., & Zheng, D. (2022). A Literature Review and Result Interpretation of the System Identification of Arch Dams Using Seismic Monitoring Data. Water, 14(20), 3207. https://doi.org/10.3390/w14203207









