Experimental Investigation on Water Seepage through Transparent Synthetic Rough-Walled Fractures
Abstract
:1. Introduction
2. Materials and Methods
2.1. Parameters Affecting Fracture Flow
2.2. Synthetic Fracture Designing
2.3. Experimental Setup
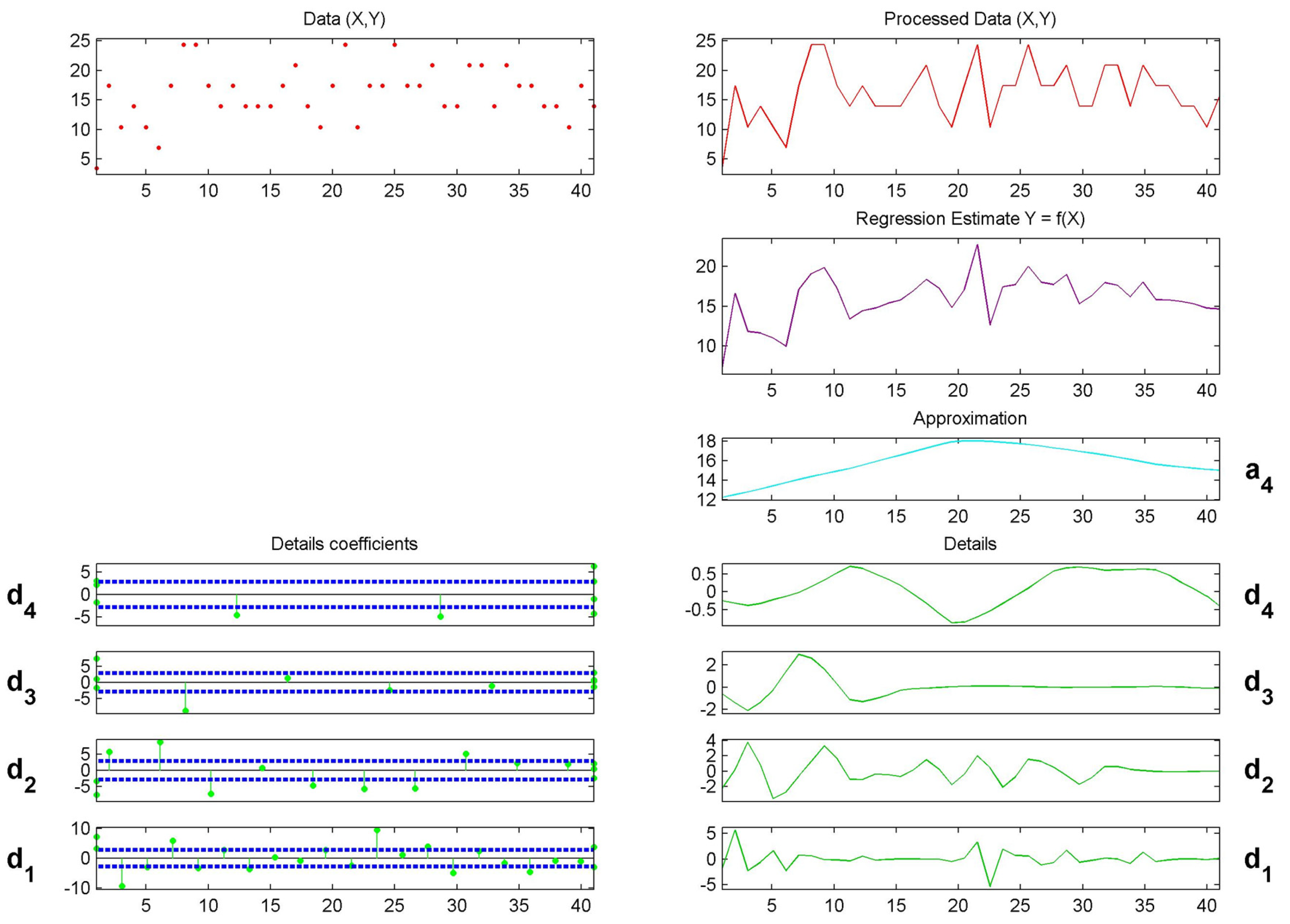
2.4. Flow Rate Prediction
3. Results and Discussion
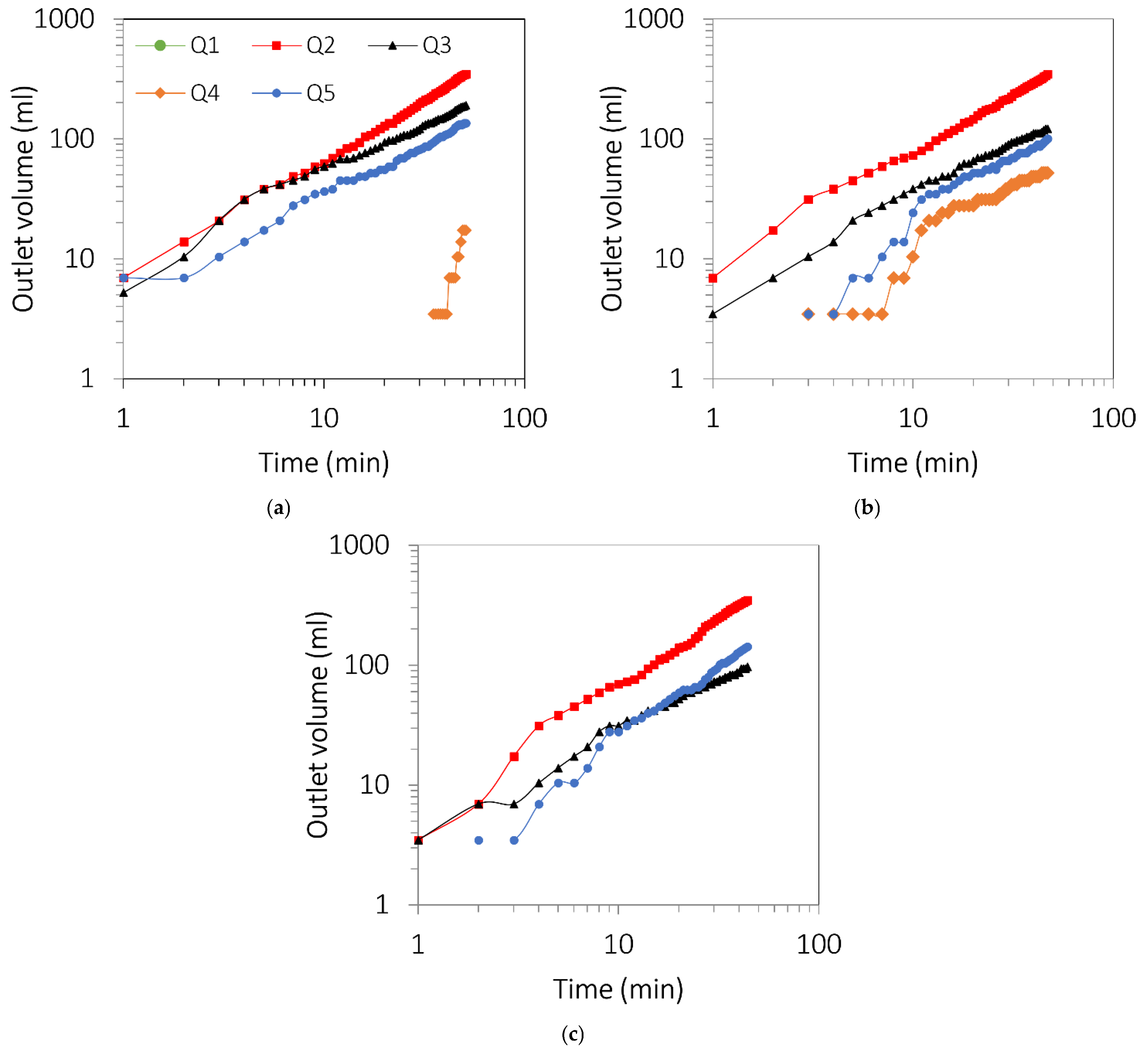
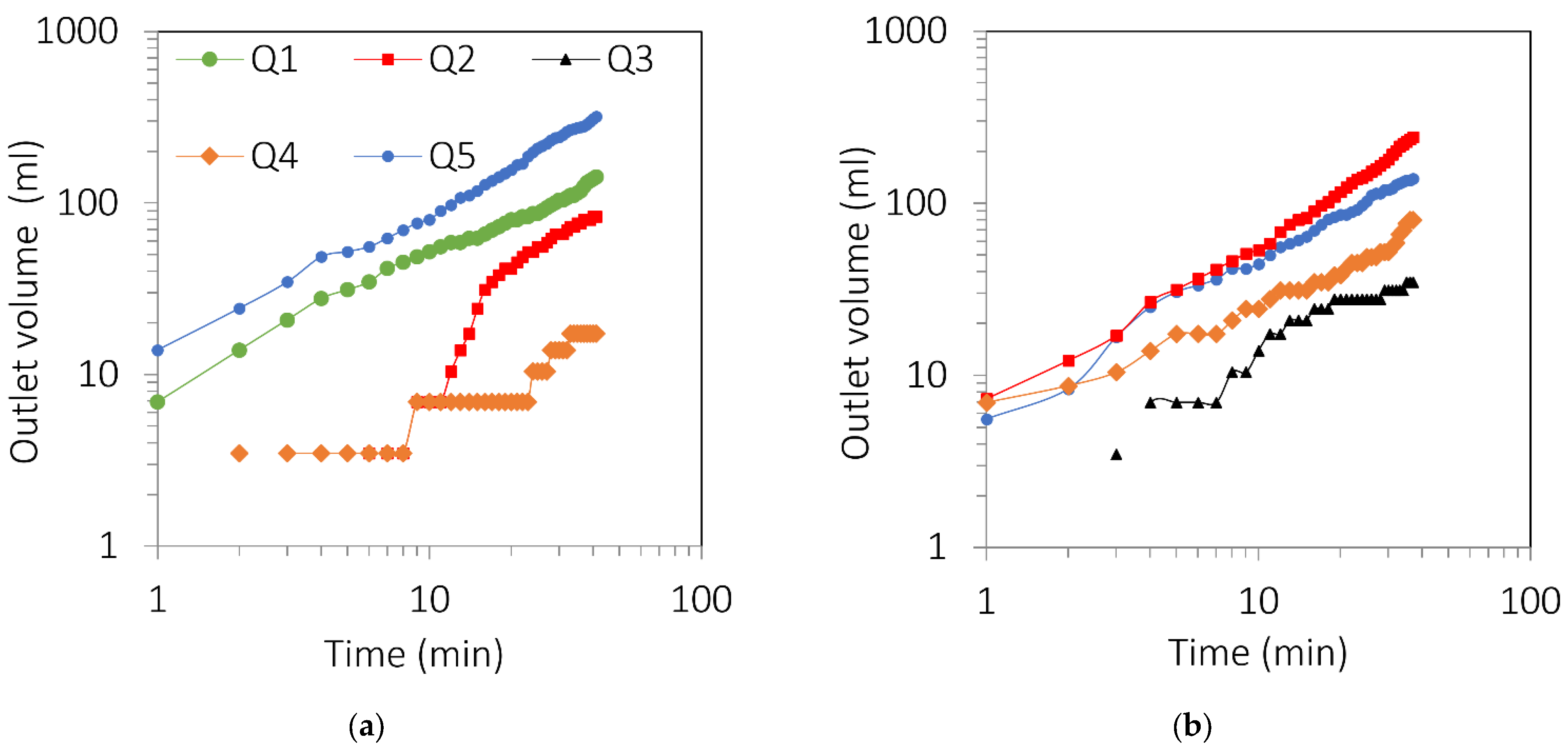
3.1. Flow Rate along the Fracture Outlets
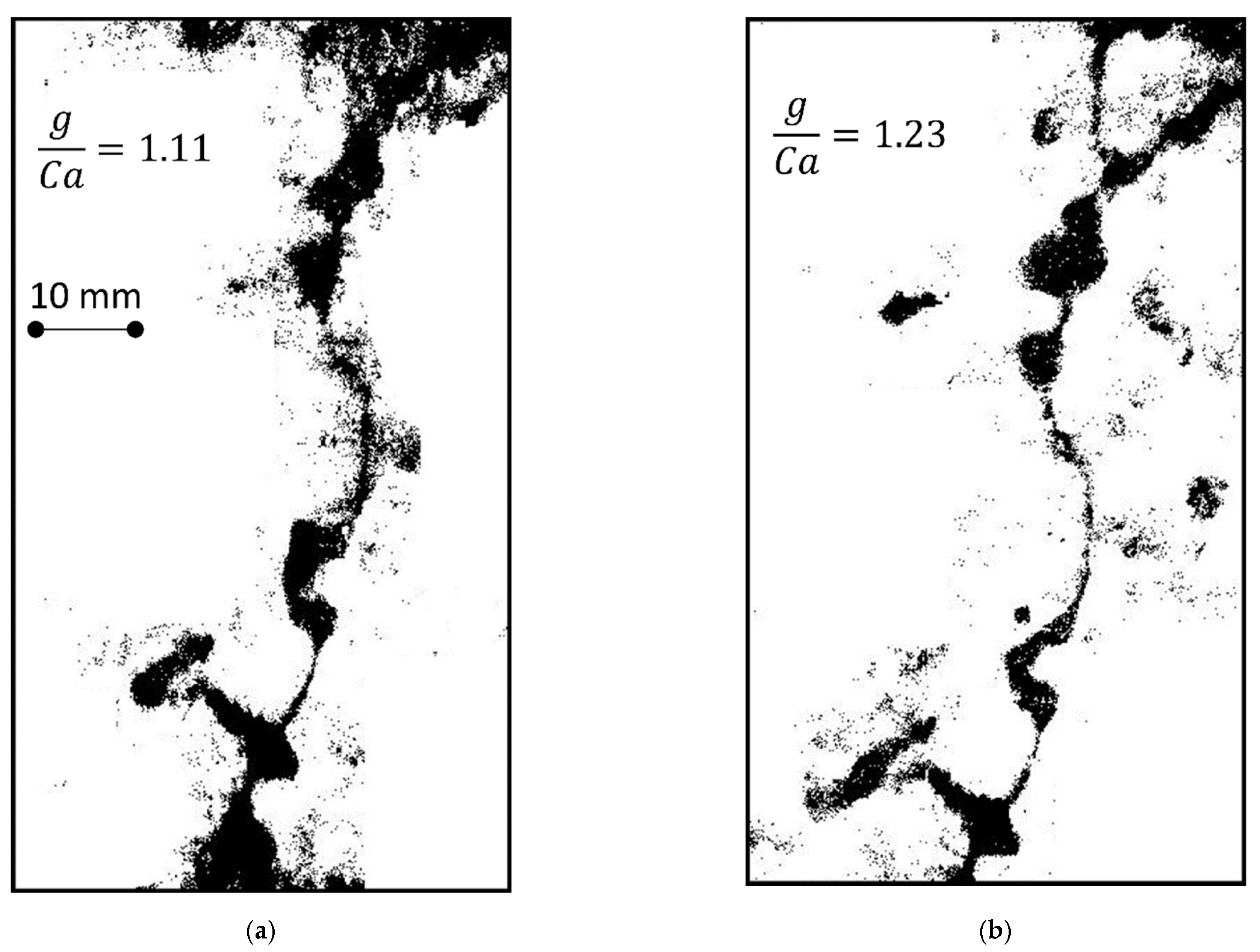
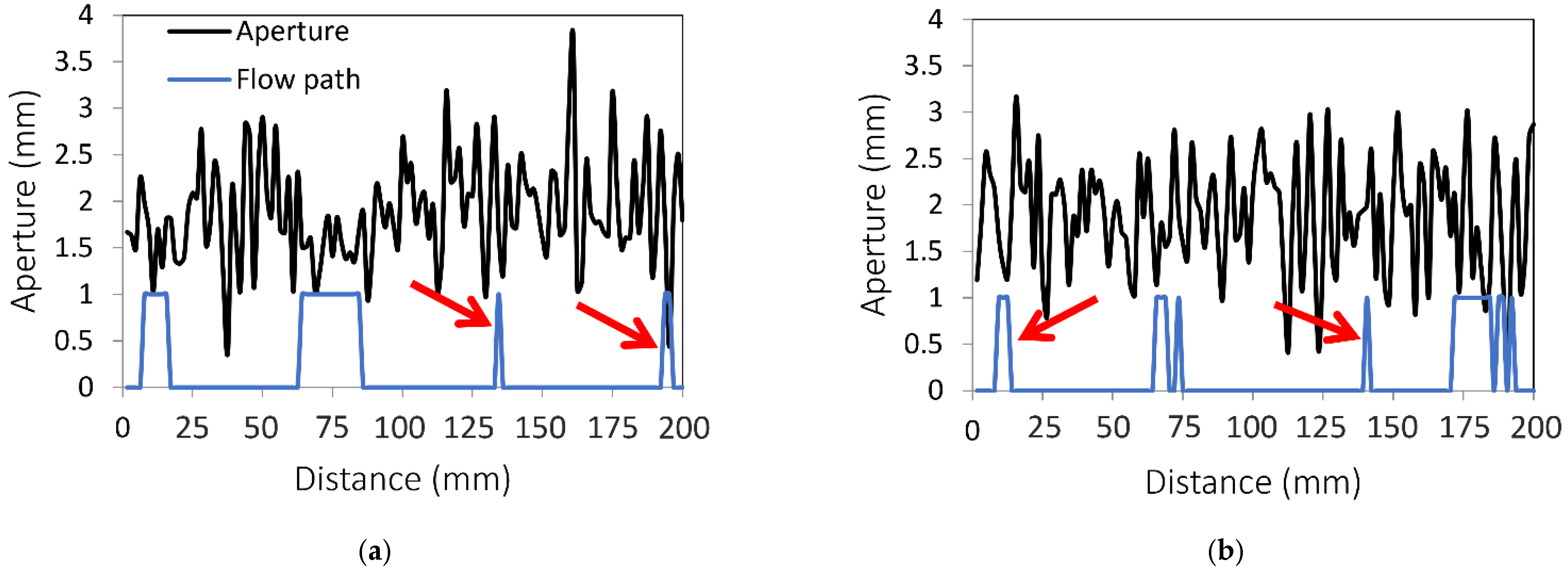
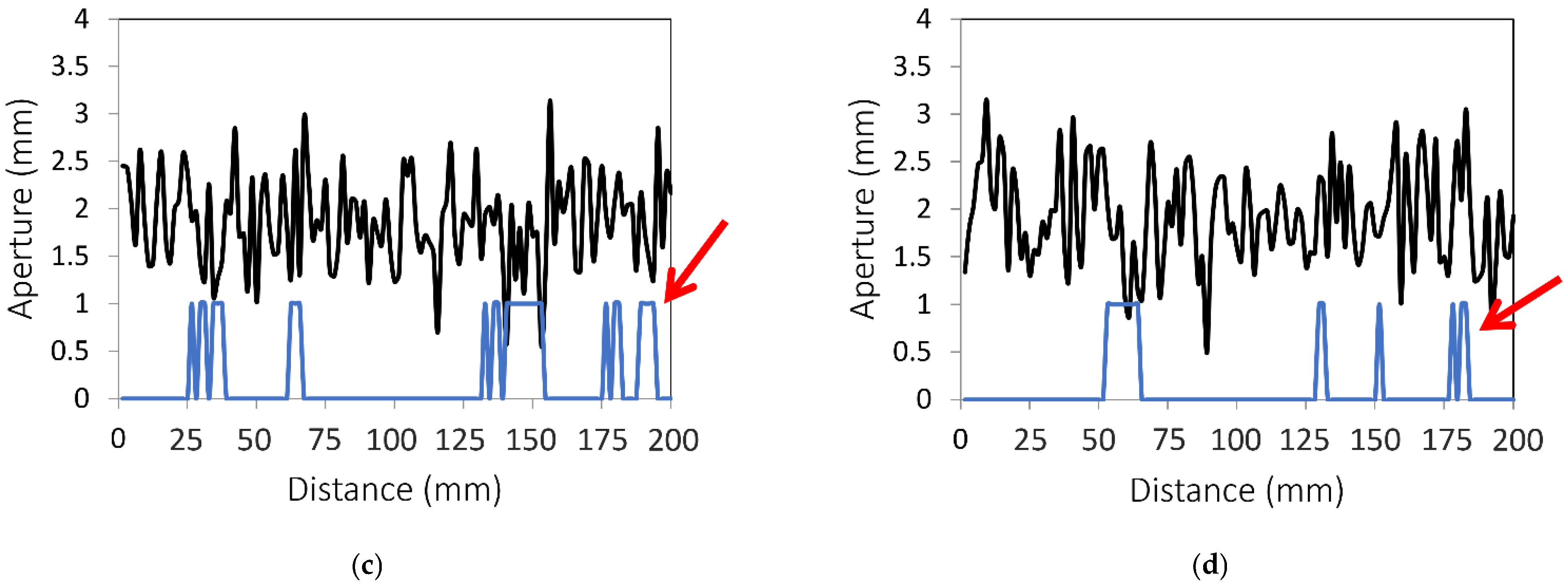
3.2. Preferential Flow Paths in Dry Fractures
3.3. Effect of Fractal Dimension and Mismatch Length on Preferential Flow Path
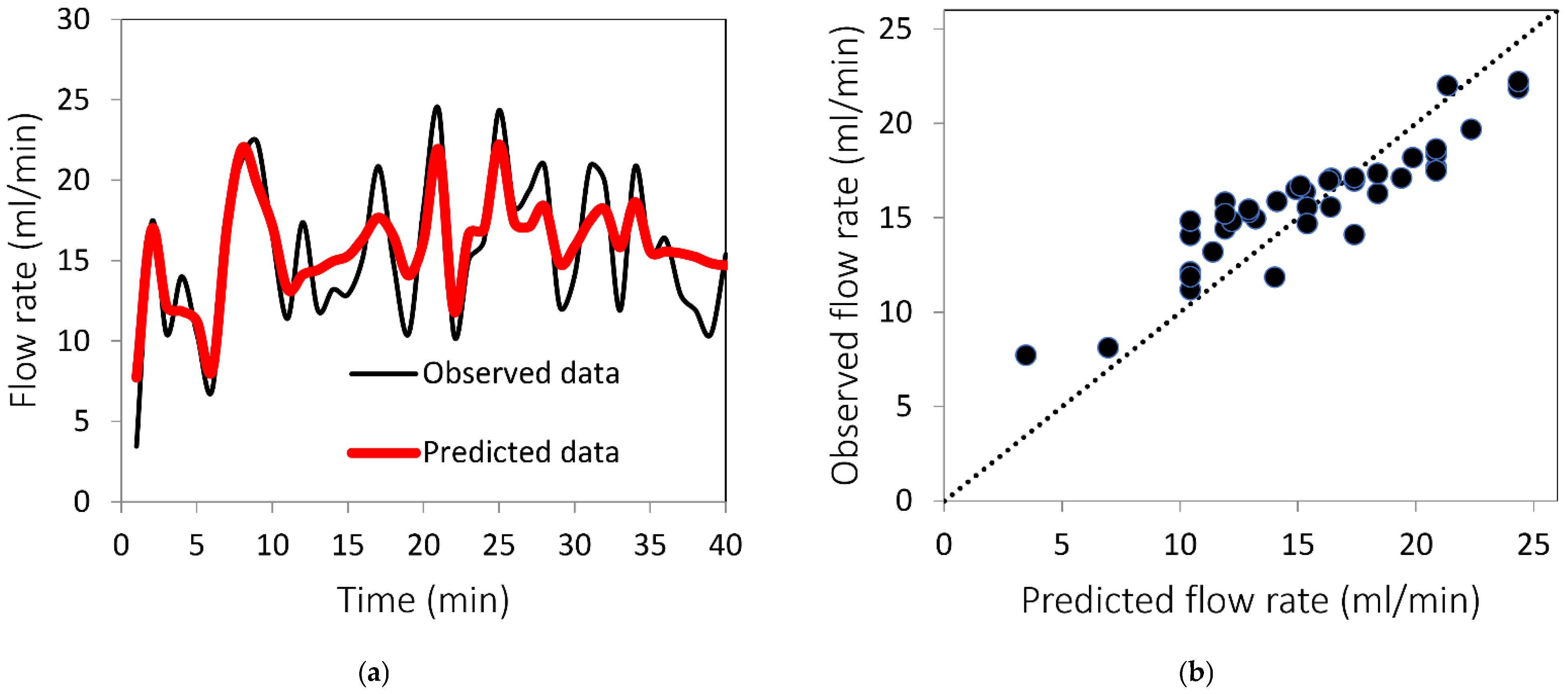
3.4. Prediction of Total Flow Rate
3.5. Prediction of Flow Rate Time Series
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Caplan, J.S.; Giménez, D.; Hirmas, D.R.; Brunsell, N.A.; Blair, J.M.; Knapp, A.K. Decadal-scale shifts in soil hydraulic properties as induced by altered precipitation. Sci. Adv. 2019, 5, eaau6635. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hirmas, D.R.; Giménez, D.; Nemes, A.; Kerry, R.; Brunsell, N.; Wilson, C.J. Climate-induced changes in continental-scale soil macroporosity may intensify water cycle. Nature 2018, 561, 100–103. [Google Scholar] [CrossRef] [PubMed]
- Salve, R.; Ghezzehei, T.A.; Jones, R. Infiltration into fractured bedrock. Water Resour. Res. 2008, 44, W01434. [Google Scholar] [CrossRef] [Green Version]
- Faybishenko, B.; Bodvarsson, G.S.; Salve, R. On the physics of unstable infiltration, seepage, and gravity drainage in partially saturated tuffs. J. Contam. Hydrol. 2003, 62–63, 63–87. [Google Scholar] [CrossRef] [Green Version]
- Cherubini, C.; Giasi, C.I.; Pastore, N. Bench scale laboratory tests to analyze non-linear flow in fractured media. Hydrol. Earth Syst. Sci. 2012, 16, 2511–2522. [Google Scholar] [CrossRef] [Green Version]
- Ishibashi, T.; Watanabe, N.; Hirano, N.; Okamoto, A.; Tsuchiya, N. GeoFlow: A novel model simulator for prediction of the 3-D channeling flow in a rock fracture network. Water Resour. Res. 2012, 48, W07601. [Google Scholar] [CrossRef]
- Snow, D.T. A Parallel Plate Model of Fractured Permeable Media. Ph.D. Thesis, University of California, Berkeley, CA, USA, 1965. [Google Scholar]
- Huitt, J.L. Fluid Flow in Simulated Fractures. Am. Inst. Chem. Eng. J. 1955, 2, 259–264. [Google Scholar] [CrossRef]
- Noiriel, C.; Gouze, P.; Madé, B. 3D analysis of geometry and flow changes in a limestone fracture during dissolution. J. Hydrol. 2013, 486, 211–223. [Google Scholar] [CrossRef]
- Ge, S. A governing equation for fluid flow in rough fractures. Water Resour. Res. 1997, 33, 53–61. [Google Scholar] [CrossRef]
- Zimmerman, R.W.; Yeo, I.-W. Fluid flow in rock fractures: From the Navier-Stokes equations to the cubic law. Geophys. Monogr.-Am. Geophys. Union 2000, 122, 213–224. [Google Scholar]
- Kishida, K.; Sawada, A.; Yasuhara, H.; Hosoda, T. Estimation of fracture flow considering the inhomogeneous structure of single rock fractures. Soils Found. 2013, 53, 105–116. [Google Scholar] [CrossRef]
- Crandall, D.; Bromhal, G.; Karpyn, Z.T. Numerical simulations examining the relationship between wall-roughness and fluid flow in rock fractures. Int. J. Rock Mech. Min. Sci. 2010, 47, 784–796. [Google Scholar] [CrossRef]
- Liu, R.; Jiang, Y.; Li, B.; Wang, X. A fractal model for characterizing fluid flow in fractured rock masses based on randomly distributed rock fracture networks. Comput. Geotech. 2015, 65, 45–55. [Google Scholar] [CrossRef] [Green Version]
- Li, J.; Cherubini, C.; Torres, S.A.G.; Li, Z.; Pastore, N.; Li, L. Laboratory Investigation of Flow Paths in 3D Self-Affine Fractures with Lattice Boltzmann Simulations. Energies 2018, 11, 168. [Google Scholar] [CrossRef] [Green Version]
- Javadi, M.; Sharifzadeh, M.; Shahriar, K.; Mitani, Y. Critical Reynolds number for nonlinear flow through rough-walled fractures: The role of shear processes. Water Resour. Res. 2014, 50, 1789–1804. [Google Scholar] [CrossRef] [Green Version]
- Zou, L.; Jing, L.; Cvetkovic, V. Shear-enhanced nonlinear flow in rough-walled rock fractures. Int. J. Rock Mech. Min. Sci. 2017, 97, 33–45. [Google Scholar] [CrossRef] [Green Version]
- Zhang, W.; Dai, B.; Liu, Z.; Zhou, C. A pore-scale numerical model for non-Darcy fluid flow through rough-walled fractures. Comput. Geotech. 2017, 87, 139–148. [Google Scholar] [CrossRef]
- Wang, L.; Cardenas, M.B. Non-Fickian transport through two-dimensional rough fractures: Assessment and prediction. Water Resour. Res. 2014, 50, 871–884. [Google Scholar] [CrossRef]
- Chen, Y.-F.; Guo, N.; Wu, D.-S.; Hu, R. Numerical investigation on immiscible displacement in 3D rough fracture: Comparison with experiments and the role of viscous and capillary forces. Adv. Water Resour. 2018, 118, 39–48. [Google Scholar] [CrossRef]
- Su, G.W.; Geller, J.T.; Pruess, K.; Wen, F. Experimental studies of water seepage and intermittent flow in unsaturated, rough-walled fractures. Water Resour. Res. 1999, 35, 1019–1037. [Google Scholar] [CrossRef]
- Watanabe, N.; Hirano, N.; Tsuchiya, N. Determination of aperture structure and fluid flow in a rock fracture by high-resolution numerical modeling on the basis of a flow-through experiment under confining pressure. Water Resour. Res. 2008, 44, W06412. [Google Scholar] [CrossRef]
- Khan, F.; Enzmann, F.; Kersten, M. Beam-hardening correction by a surface fitting and phase classification by a least square support vector machine approach for tomography images of geological samples. Solid Earth Discuss. 2015, 7, 3383–3408. [Google Scholar]
- Schill, E.; Genter, A.; Cuenot, N.; Kohl, T. Hydraulic performance history at the Soultz EGS reservoirs from stimulation and long-term circulation tests. Geothermics 2017, 70, 110–124. [Google Scholar] [CrossRef]
- Stoll, M.; Huber, F.; Trumm, M.; Enzmann, F.; Meinel, D.; Wenka, A.; Schill, E.; Schäfer, T. Experimental and numerical investigations on the effect of fracture geometry and fracture aperture distribution on flow and solute transport in natural fractures. J. Contam. Hydrol. 2018, 221, 82–97. [Google Scholar] [CrossRef]
- Ghezzehei, T.A.; Or, D. Liquid fragmentation and intermittent flow regimes in unsaturated fractured media. Water Resour. Res. 2005, 41, W12406. [Google Scholar] [CrossRef] [Green Version]
- Phillips, T.; Bultreys, T.; Bisdom, K.; Kampman, N.; Van Offenwert, S.; Mascini, A.; Cnudde, V.; Busch, A. A Systematic Investigation Into the Control of Roughness on the Flow Properties of 3D-Printed Fractures. Water Resour. Res. 2021, 57, ewrcr-25233. [Google Scholar] [CrossRef]
- Suzuki, A.; Minto, J.M.; Watanabe, N.; Li, K.; Horne, R.N. Contributions of 3D Printed Fracture Networks to Development of Flow and Transport Models. Transp. Porous Media 2018, 129, 485–500. [Google Scholar] [CrossRef] [Green Version]
- Suzuki, A.; Bjarkason, E.K.; Yamaguchi, A.; Hawkins, A.J.; Hashida, T. Estimation of flow-channel structures with uncertainty quantification: Validation by 3D-printed fractures and field application. Geothermics 2022, 105, 102480. [Google Scholar] [CrossRef]
- Yang, W.; Zhang, D.; Lei, G. Experimental study on multiphase flow in fracture-vug medium using 3D printing technology and visualization techniques. J. Pet. Sci. Eng. 2020, 193, 107394. [Google Scholar] [CrossRef]
- Yin, P.; Zhao, C.; Ma, J.; Yan, C.; Huang, L. Experimental study of non-linear fluid flow though rough fracture based on fractal theory and 3D printing technique. Int. J. Rock Mech. Min. Sci. 2020, 129, 104293. [Google Scholar] [CrossRef]
- Brown, S.R. Simple mathematical model of a rough fracture. J. Geophys. Res. Earth Surf. 1995, 100, 5941–5952.7. [Google Scholar] [CrossRef]
- Brown, S.R. A note on the description of surface roughness using fractal dimension. Geophys. Res. Lett. 1987, 14, 1095–1098. [Google Scholar] [CrossRef]
- Charkaluk, E.; Bigerelle, M.; Iost, A. Fractals and fracture. Eng. Fract. Mech. 1998, 61, 119–139. [Google Scholar] [CrossRef]
- Mandelbrot, B.B. The Fractal Geometry of Nature, 3rd ed.; W.H. Freeman and Company: New York, NY, USA, 1983; p. 468. [Google Scholar]
- Santos, S.F.D.; Rodrigues, J.D.A. Correlation between fracture toughness, work of fracture and fractal dimensions of Alumina-mullite-zirconia composites. Mater. Res. 2003, 6, 219–226. [Google Scholar] [CrossRef]
- Nagahama, H. A fractal criterion for ductile and brittle fracture. J. Appl. Phys. 1994, 75, 3220–3222. [Google Scholar] [CrossRef]
- Eker, E.; Akin, S. Lattice Boltzmann Simulation of Fluid Flow in Synthetic Fractures. Transp. Porous Media 2006, 65, 363–384. [Google Scholar] [CrossRef] [Green Version]
- Zambrano, M.; Pitts, A.D.; Salama, A.; Volatili, T.; Giorgioni, M.; Tondi, E. Analysis of Fracture Roughness Control on Permeability Using SfM and Fluid Flow Simulations: Implications for Carbonate Reservoir Characterization. Geofluids 2019, 2019, 4132386. [Google Scholar] [CrossRef] [Green Version]
- Ogilvie, S.R.; Isakov, E.; Glover, P.W. Fluid flow through rough fractures. II: A new matching model for rough rock fractures. Earth Planet. Sci. Lett. 2006, 241, 454–465. [Google Scholar] [CrossRef]
- Wang, Y.; Witten, I.H. Induction of Model Trees for Predicting Continuous Classes; (Working Paper 96/23); University of Waikato, Department of Computer Science: Hamilton, New Zealand, 1996. [Google Scholar]
- Goyal, M.K. Modeling of Sediment Yield Prediction Using M5 Model Tree Algorithm and Wavelet Regression. Water Resour. Manag. 2014, 28, 1991–2003. [Google Scholar] [CrossRef]
- Etemad-Shahidi, A.; Mahjoobi, J. Comparison between M5′ model tree and neural networks for prediction of significant wave height in Lake Superior. Ocean Eng. 2009, 36, 1175–1181. [Google Scholar] [CrossRef]
- Hall, M.; Frank, E.; Holmes, G.; Pfahringer, B.; Reutemann, P.; Witten, I.H. The WEKA data mining software: An update. ACM SIGKDD Explor. Newsl. 2009, 11, 10–18. [Google Scholar] [CrossRef]
- Mallat, S. A Wavelet Tour of Signal Processing; Elsevier: Amsterdam, The Netherlands, 1999. [Google Scholar]
- Zhang, J.; Li, Y.; Zhao, Y.; Hong, Y. Wavelet-cointegration prediction of irrigation water in the irrigation district. J. Hydrol. 2017, 544, 343–351. [Google Scholar] [CrossRef]
- McCuen, R.H.; Knight, Z.; Cutter, A.G. Evaluation of the Nash–Sutcliffe Efficiency Index. J. Hydrol. Eng. 2006, 11, 597–602. [Google Scholar] [CrossRef]
- Perlich, C.; Świrszcz, G. On cross-validation and stacking: Building seemingly predictive models on random data. ACM SIGKDD Explor. Newsl. 2011, 12, 11–15. [Google Scholar] [CrossRef]





| Fracture Name | Physical Size (mm2) | Fractal Dimension Df | Mismatch Length (mm) | Standard Deviation (mm) | Mean Aperture (mm) |
|---|---|---|---|---|---|
| Fracture-1 | 200 × 200 | 2.2 | 30 | 2 | 2.04 |
| Fracture-2 | 2.4 | 30 | 2 | 3.07 | |
| Fracture-3 | 2.3 | 10 | 2 | 0.94 | |
| Fracture-4 | 2.2 | 10 | 3 | 0.70 |
| Fracture | Flow and Intermediate Flow | α = 45° | α = 55° | α = 65° |
|---|---|---|---|---|
| 1 | flow path | 1 | 1 | 1 |
| 1 | Intermediate channel | 3 | 3 | 4 |
| 2 | flow path | 1 | 2 | 2 |
| 2 | Intermediate channel | 2 | 2 | 3 |
| 3 | flow path | 2 | 2 | 2 |
| 3 | Intermediate channel | 3 | 3 | 4 |
| 4 | flow path | 3 | 4 | 4 |
| 4 | Intermediate channel | 4 | 3 | 6 |
| t | F-1 α = 45° | F-1 α = 55° | F-1 α = 65° | F-2 α = 45° | F-2 α = 55° | F-2 α = 65° | F-3 α = 45° | F-3 α = 55° | F-3 α = 65° | F-4 α = 45° | F-4 α = 55° | F-4 α = 65° |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 10 | 3 | 3 | 4 | 2 | 2 | 3 | 3 | 3 | 4 | 4 | 4 | 5 |
| 20 | 3 | 4 | 4 | 3 | 4 | 4 | 4 | 5 | 5 | 4 | 5 | 5 |
| 30 | 3 | 4 | 5 | 4 | 5 | 5 | 5 | 5 | 6 | 5 | 5 | 5 |
| 40 | 4 | 5 | 6 | 5 | 6 | 6 | 5 | 6 | 6 | 6 | 6 | 6 |
| 50 | 6 | 6 | 7 | - | - | - | - | - | - | 5 | 6 | 6 |
| 60 | 6 | 6 | 6 | - | - | - | - | - | - | - | - | - |
| Parameters | Minimum Value | Maximum Value |
|---|---|---|
| 8.96 | 10.94 | |
| 10 | 30 | |
| 0.707 | 0.906 |
| Linear Model Number | Logical Condition | Linear Relation |
|---|---|---|
| 0 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ranjbar, A.; Cherubini, C.; Pastore, N. Experimental Investigation on Water Seepage through Transparent Synthetic Rough-Walled Fractures. Water 2022, 14, 3199. https://doi.org/10.3390/w14203199
Ranjbar A, Cherubini C, Pastore N. Experimental Investigation on Water Seepage through Transparent Synthetic Rough-Walled Fractures. Water. 2022; 14(20):3199. https://doi.org/10.3390/w14203199
Chicago/Turabian StyleRanjbar, Ali, Claudia Cherubini, and Nicola Pastore. 2022. "Experimental Investigation on Water Seepage through Transparent Synthetic Rough-Walled Fractures" Water 14, no. 20: 3199. https://doi.org/10.3390/w14203199
APA StyleRanjbar, A., Cherubini, C., & Pastore, N. (2022). Experimental Investigation on Water Seepage through Transparent Synthetic Rough-Walled Fractures. Water, 14(20), 3199. https://doi.org/10.3390/w14203199








