Investigation of Hyperparameter Setting of a Long Short-Term Memory Model Applied for Imputation of Missing Discharge Data of the Daihachiga River
Abstract
:1. Introduction
2. Materials and Methods
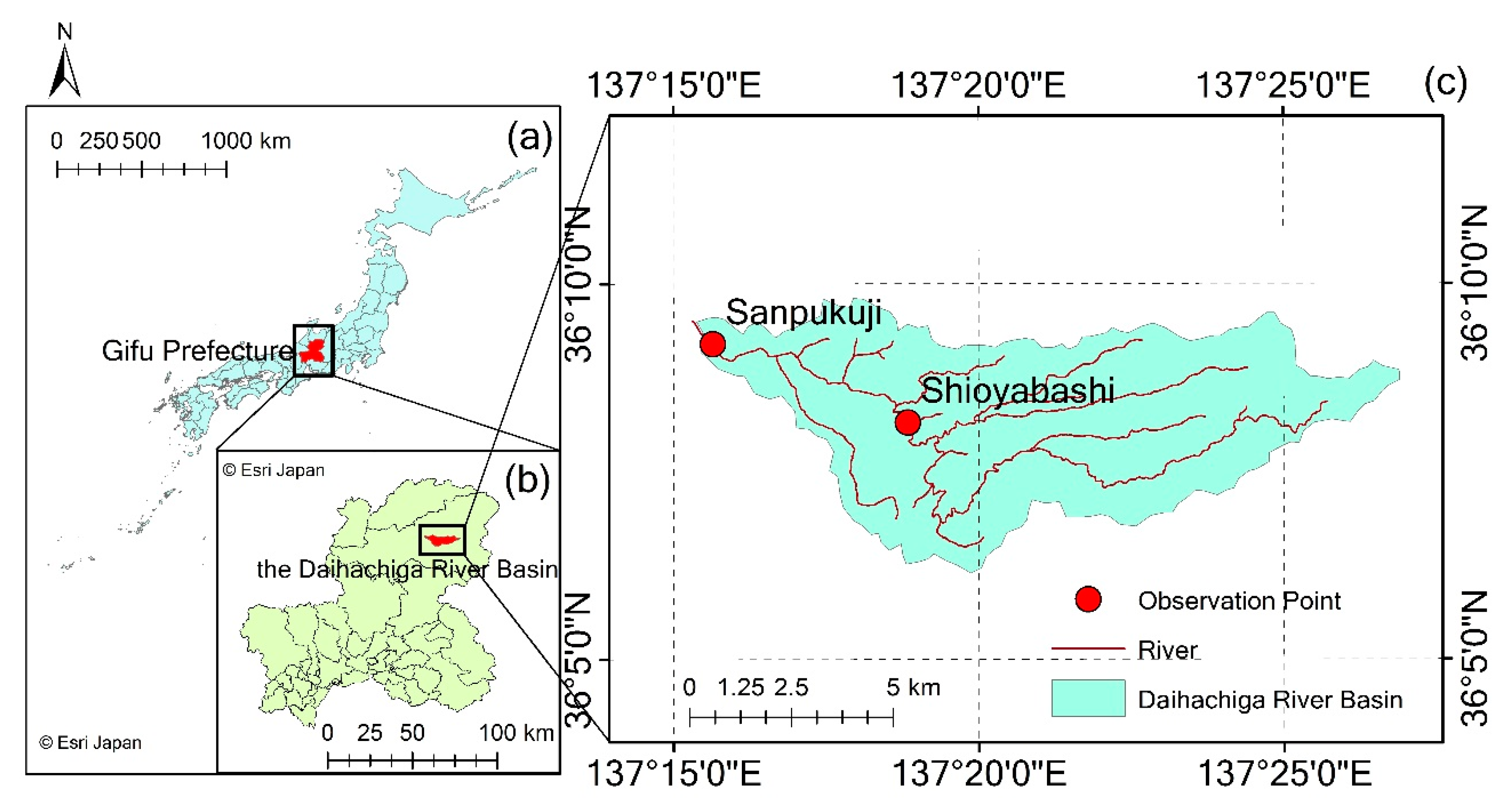
2.1. Study Area
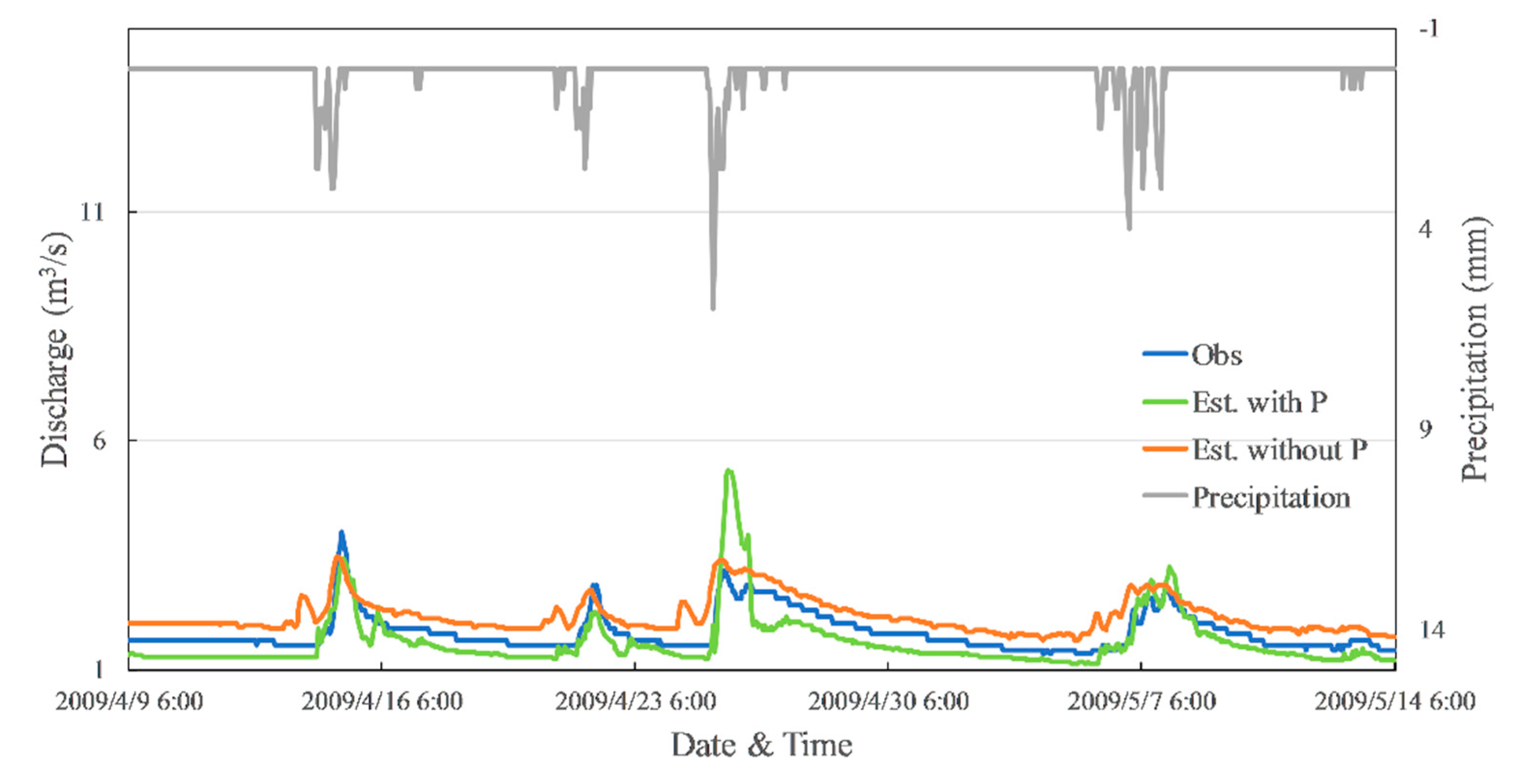
2.2. Data
2.3. Method
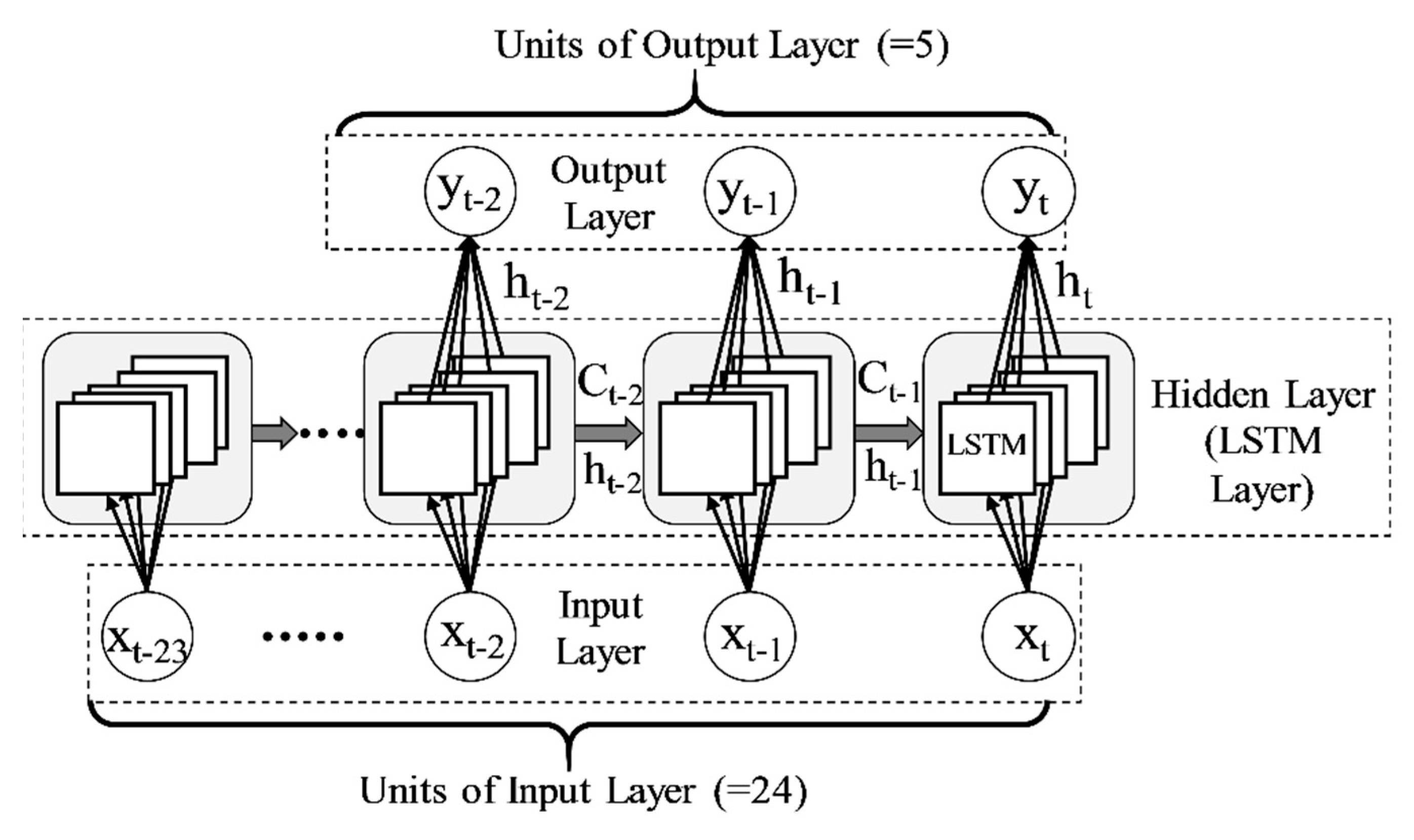
2.3.1. LSTM Model
- : number and type of input variables.
- : backtracked time steps of data used for the training.
- : number of units of hidden layer.
- : dropout.
- : recurrent dropout.
2.3.2. Hyperparameter Settings and Data Training
2.3.3. Traditional Method
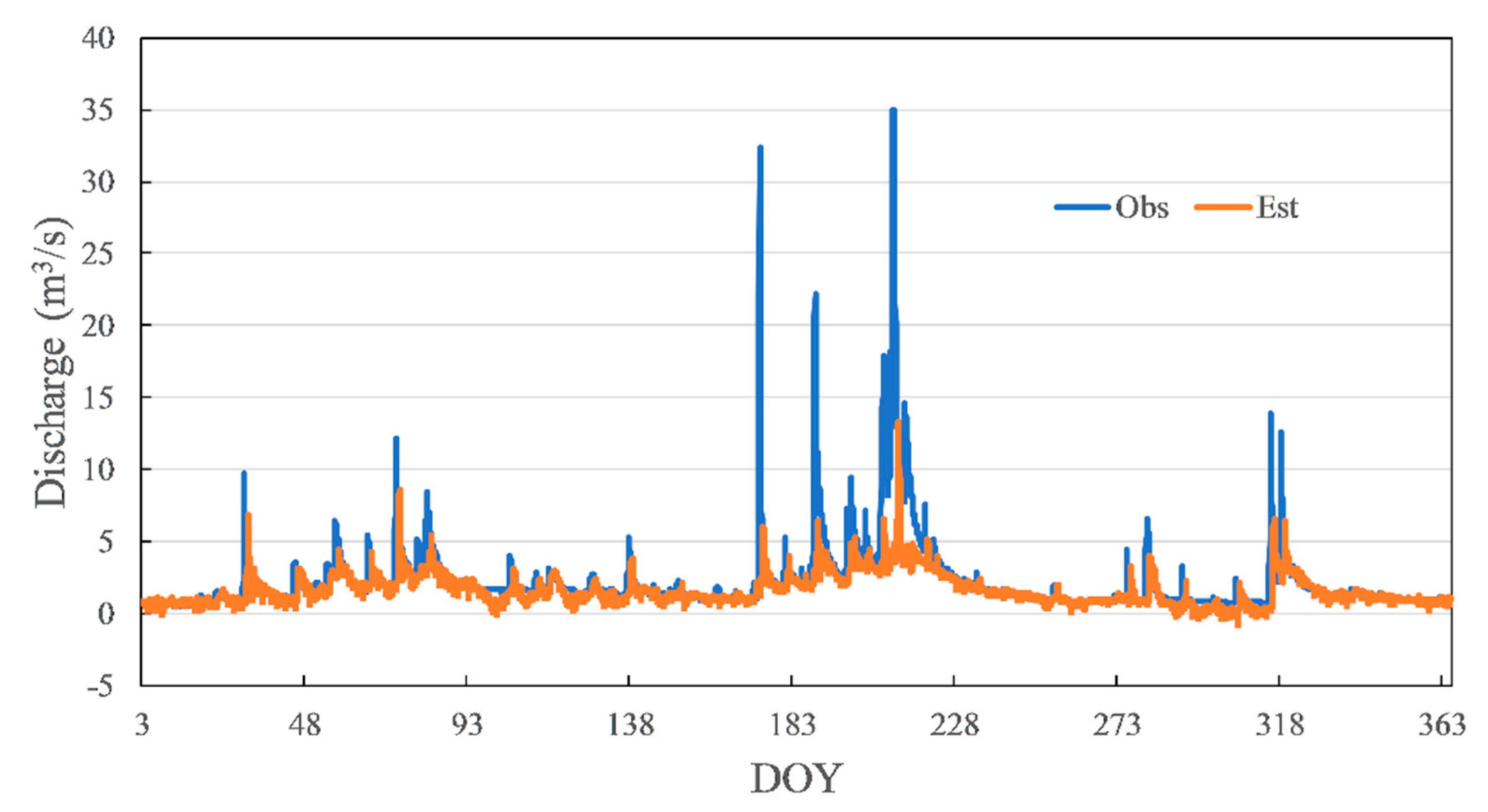
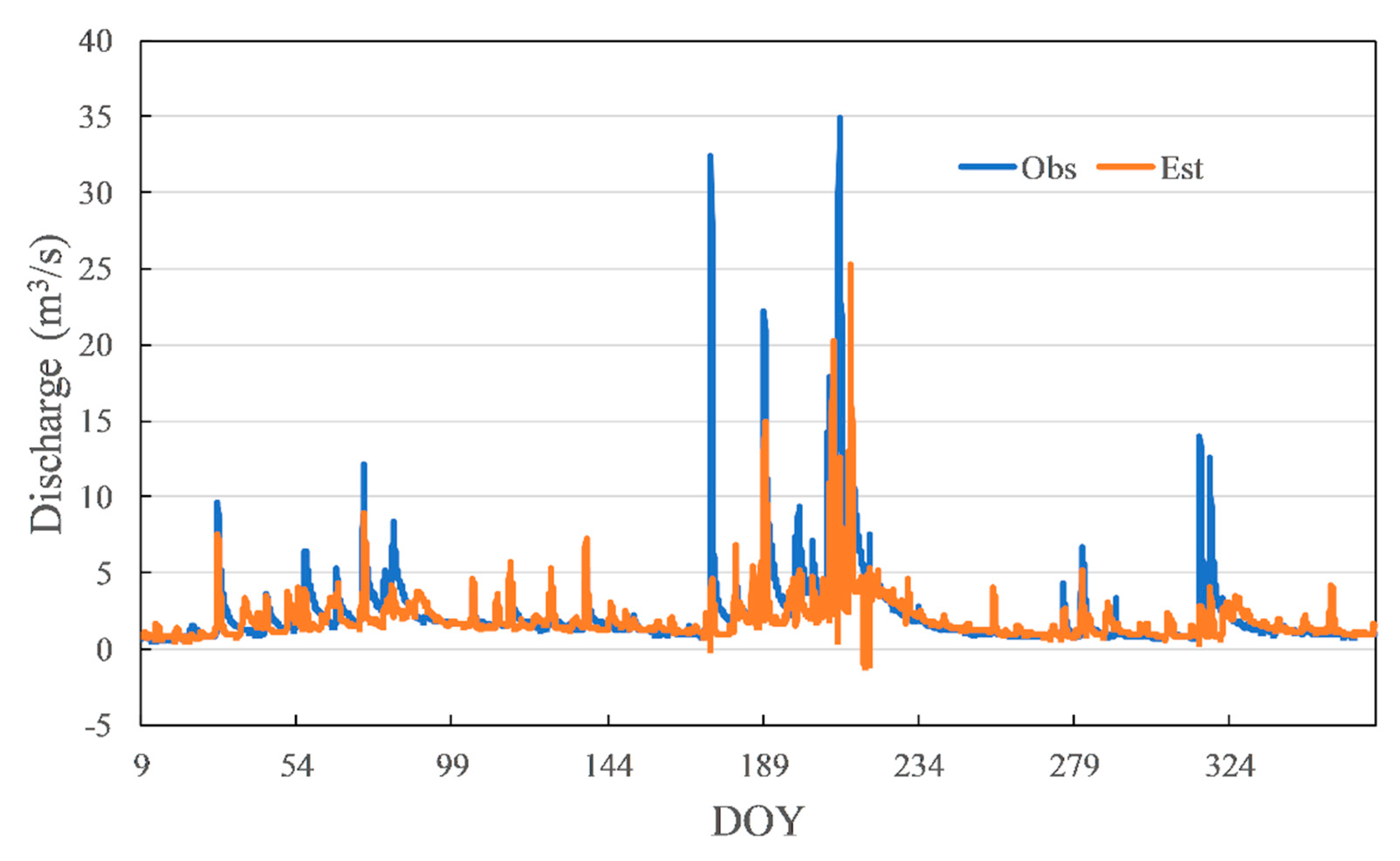
3. Results and Discussion
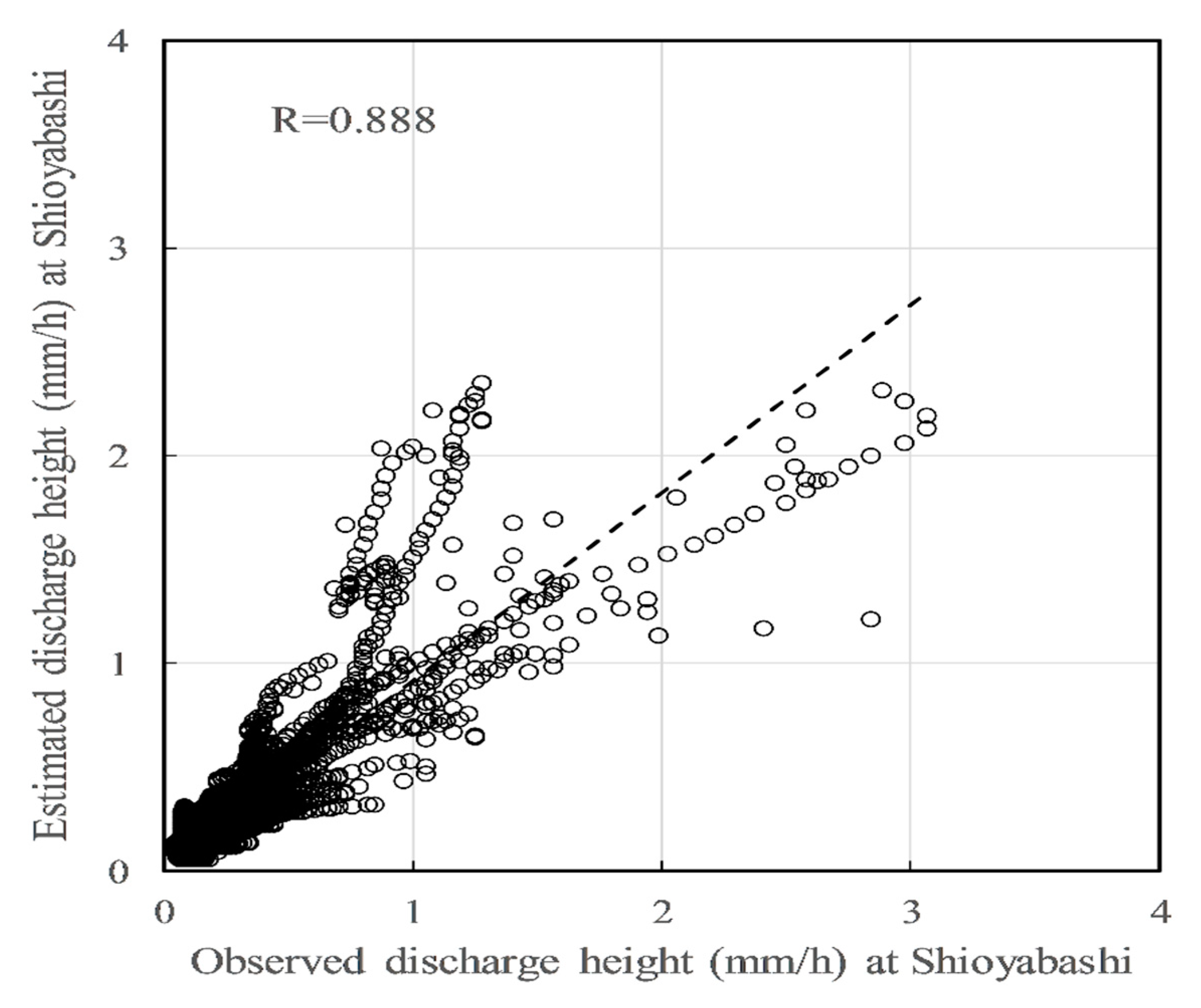
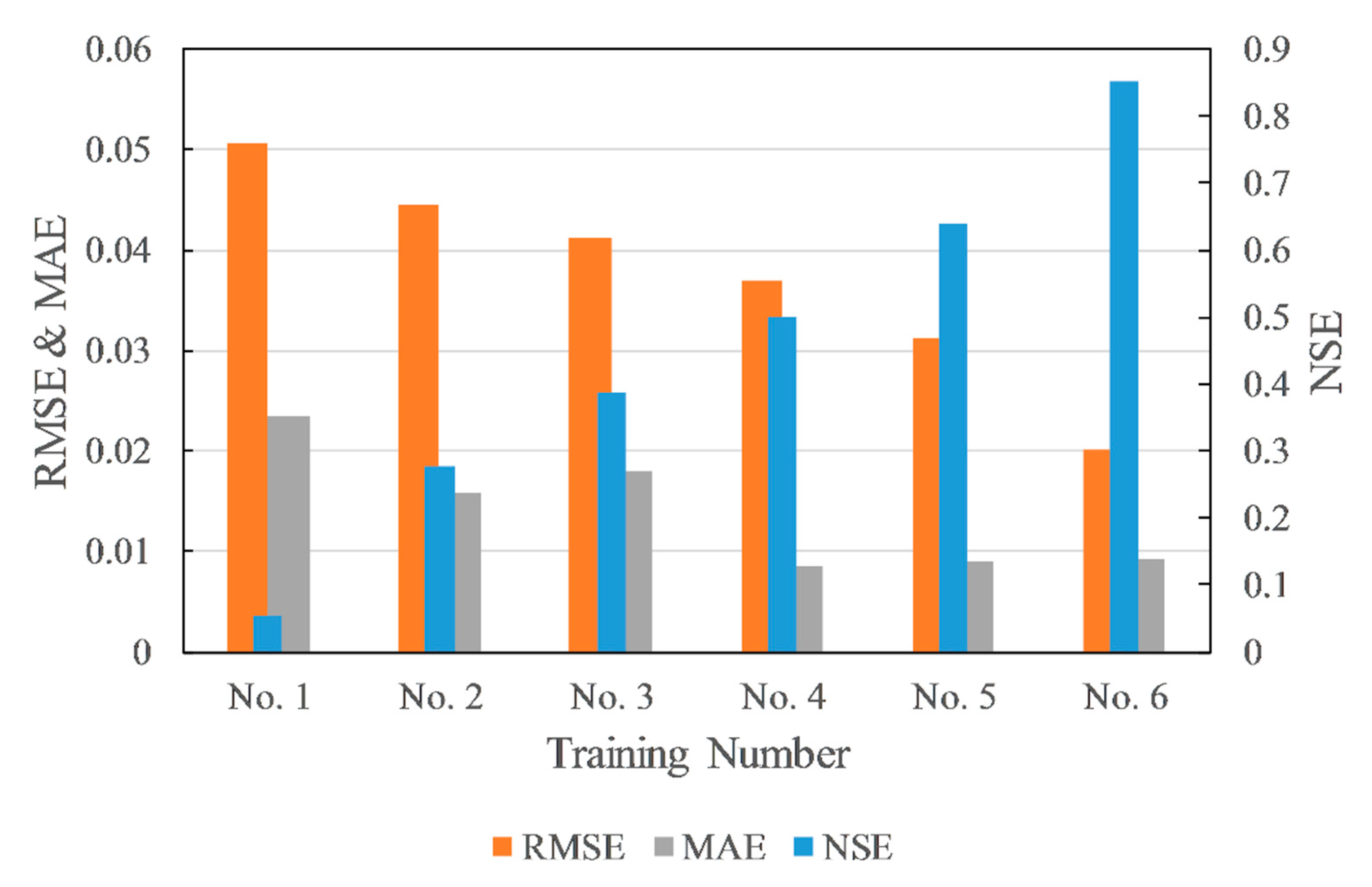
3.1. Evaluation Metrics
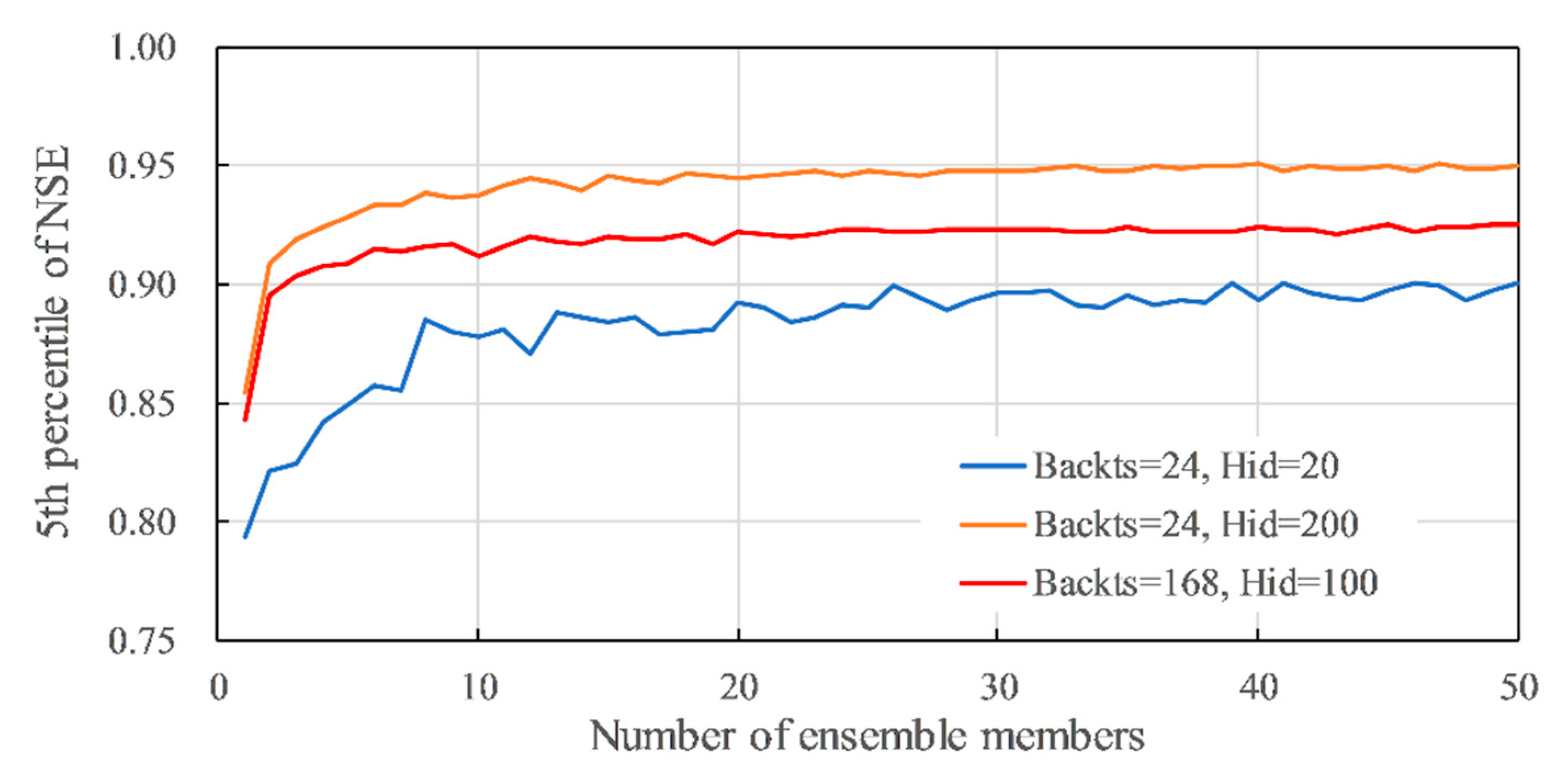
3.2. Number of Members for Ensemble Average
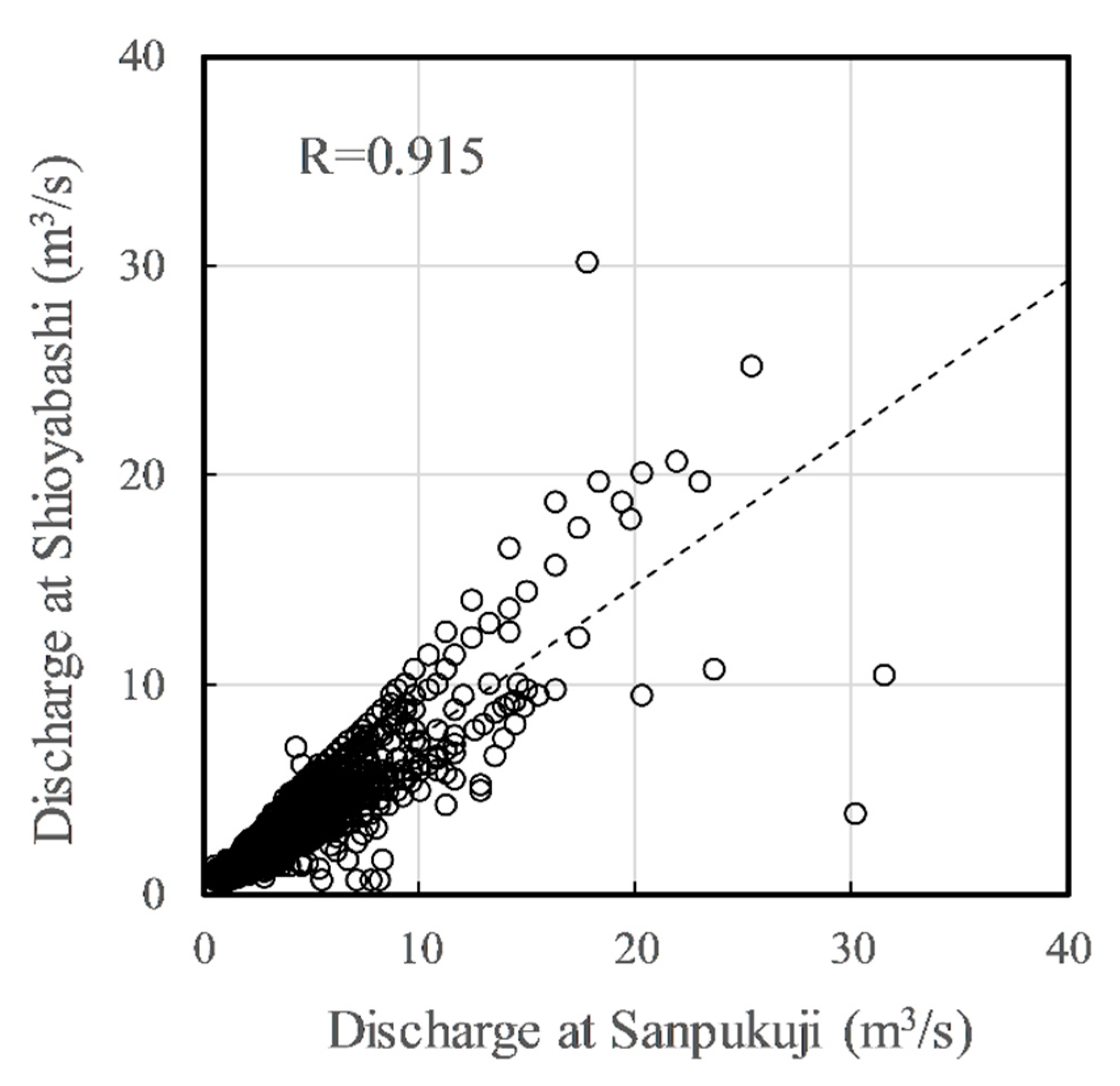
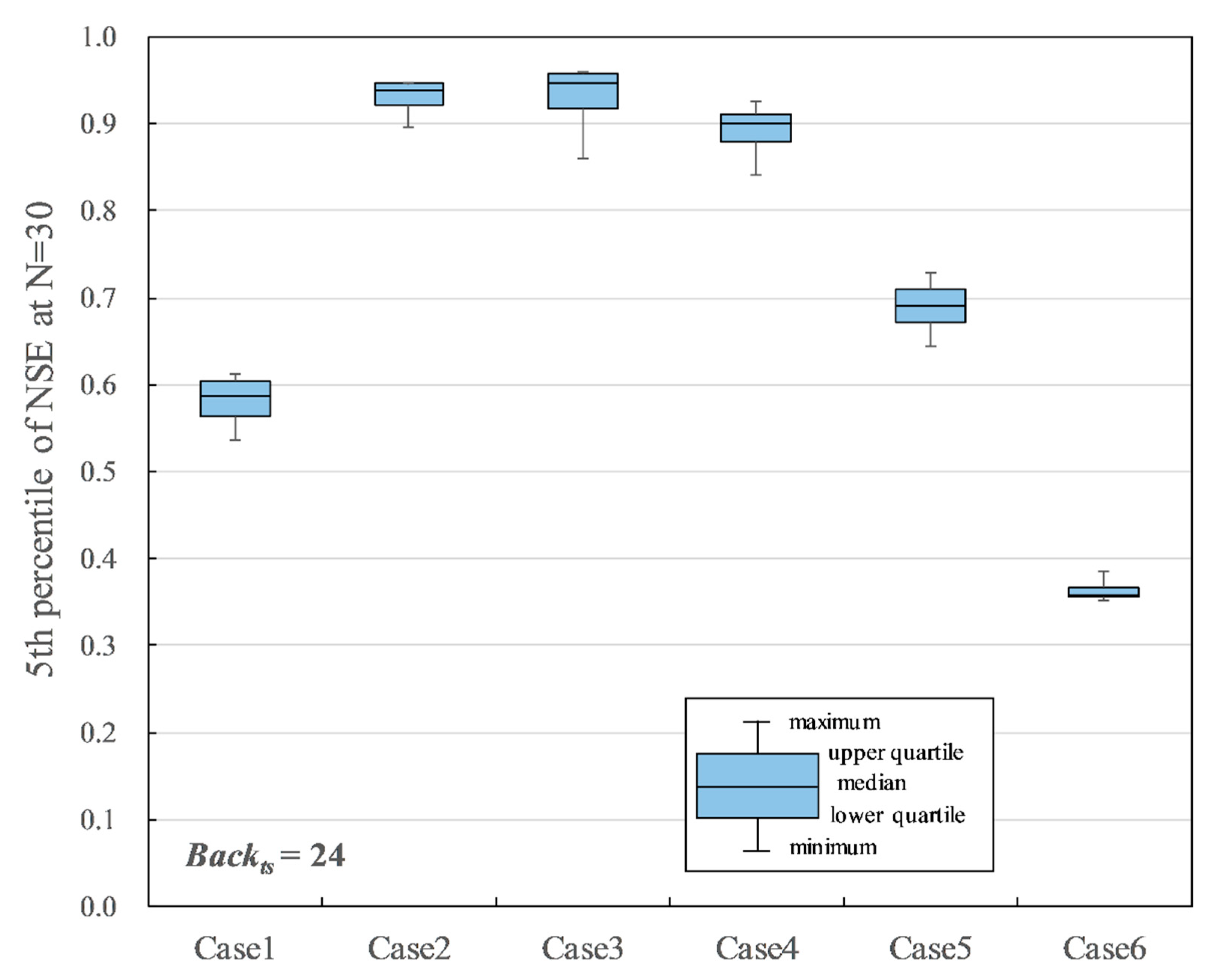
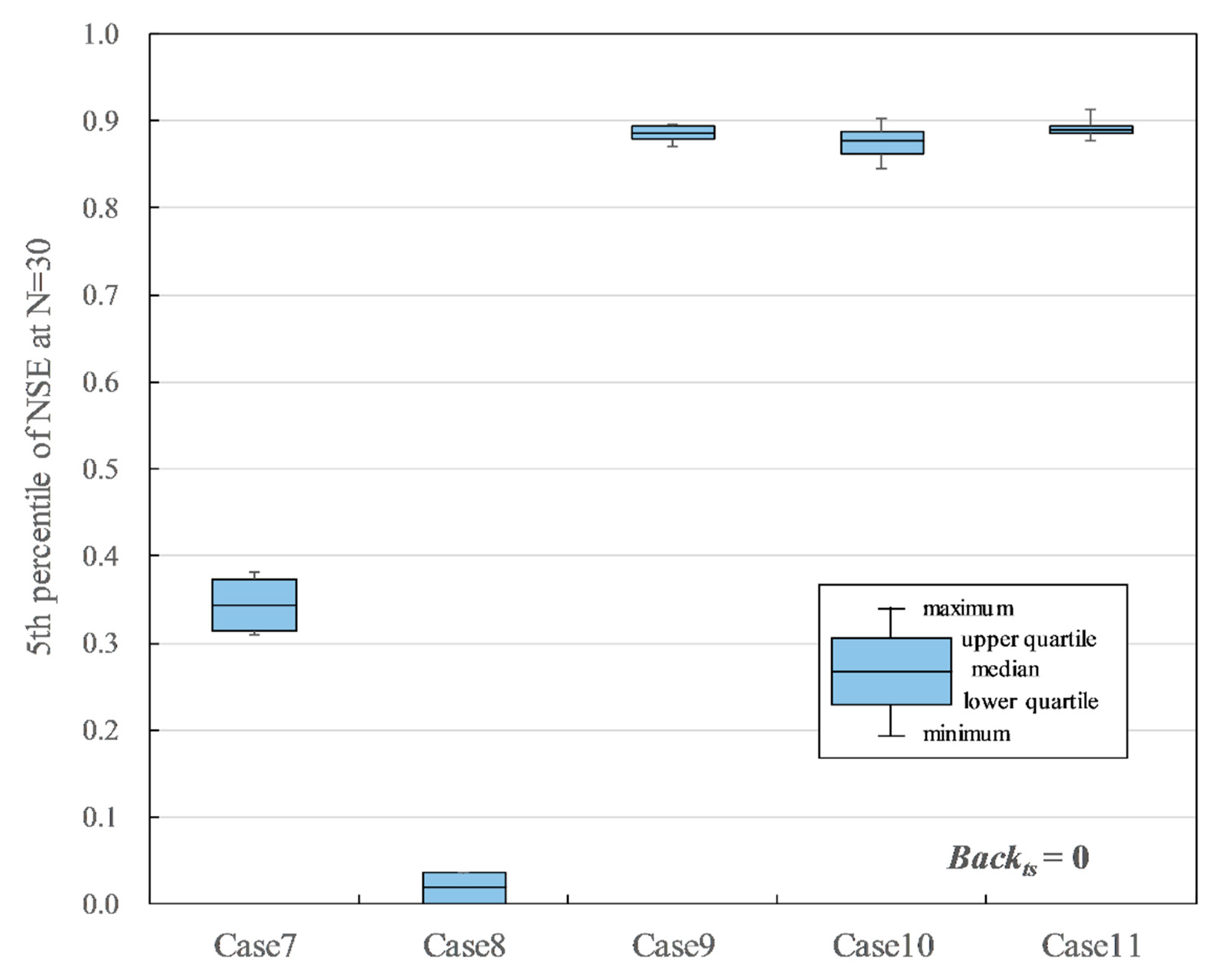
3.3. Type of Input Variables
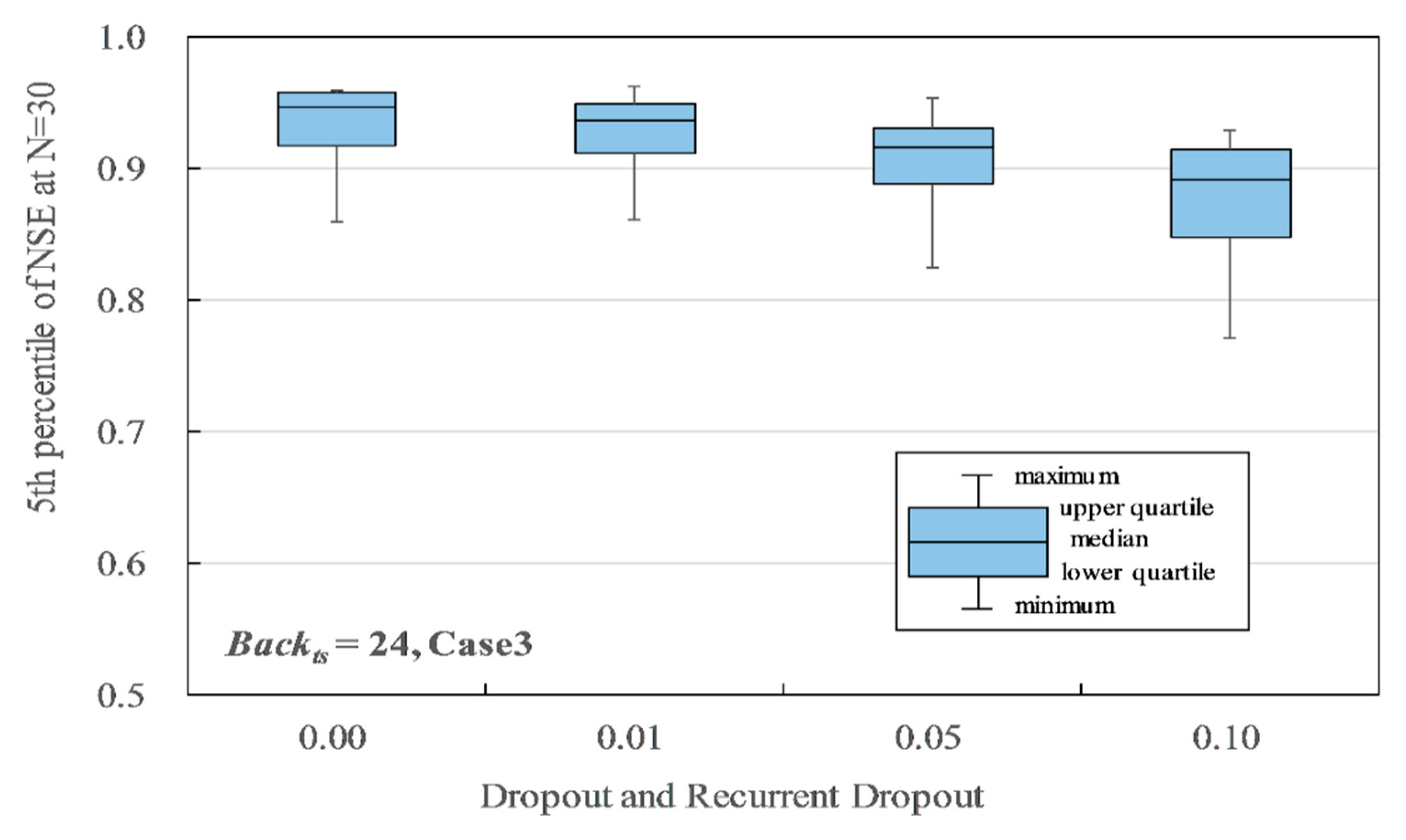
3.4. Dropout and Recurrent Dropout
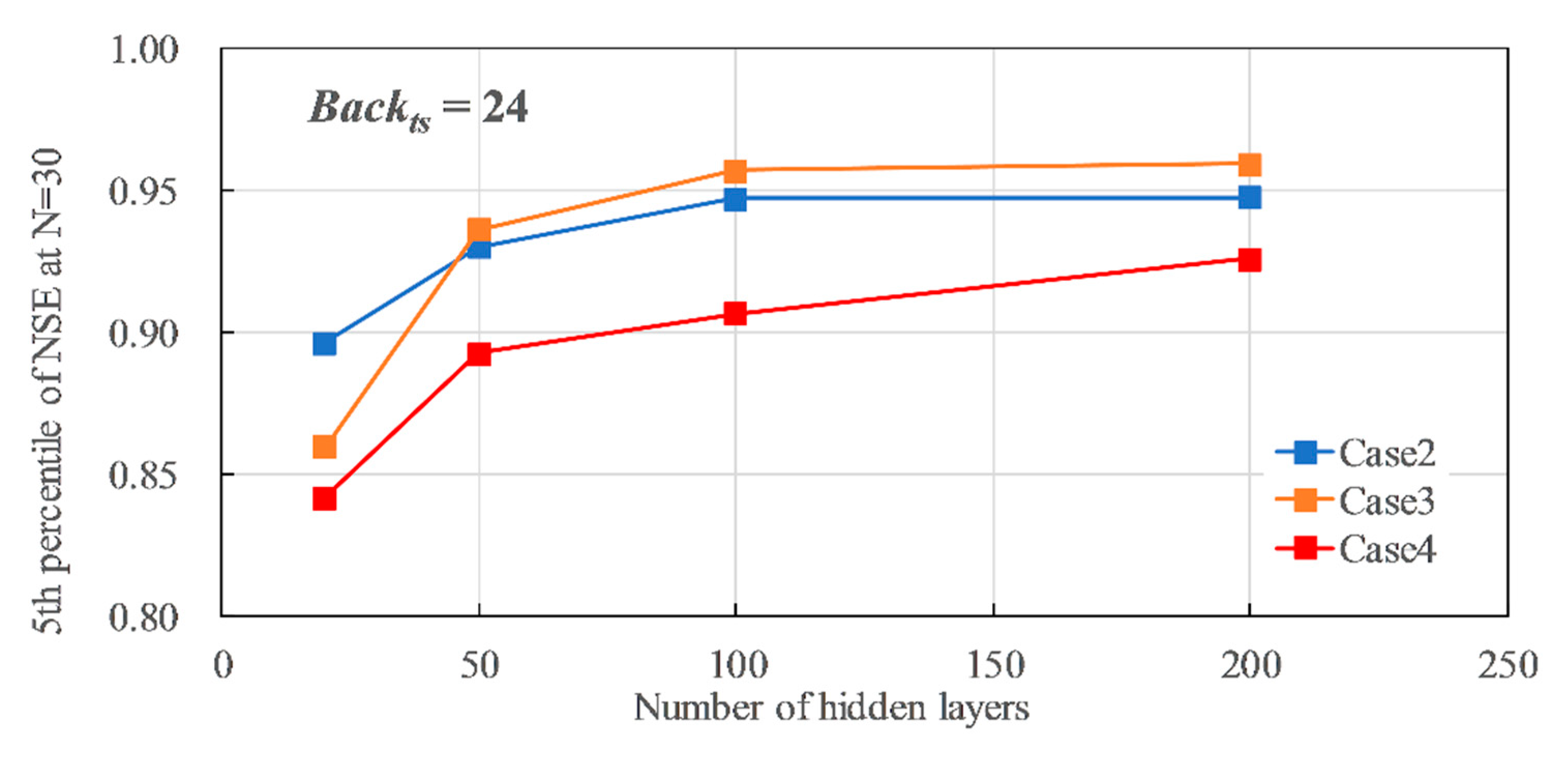
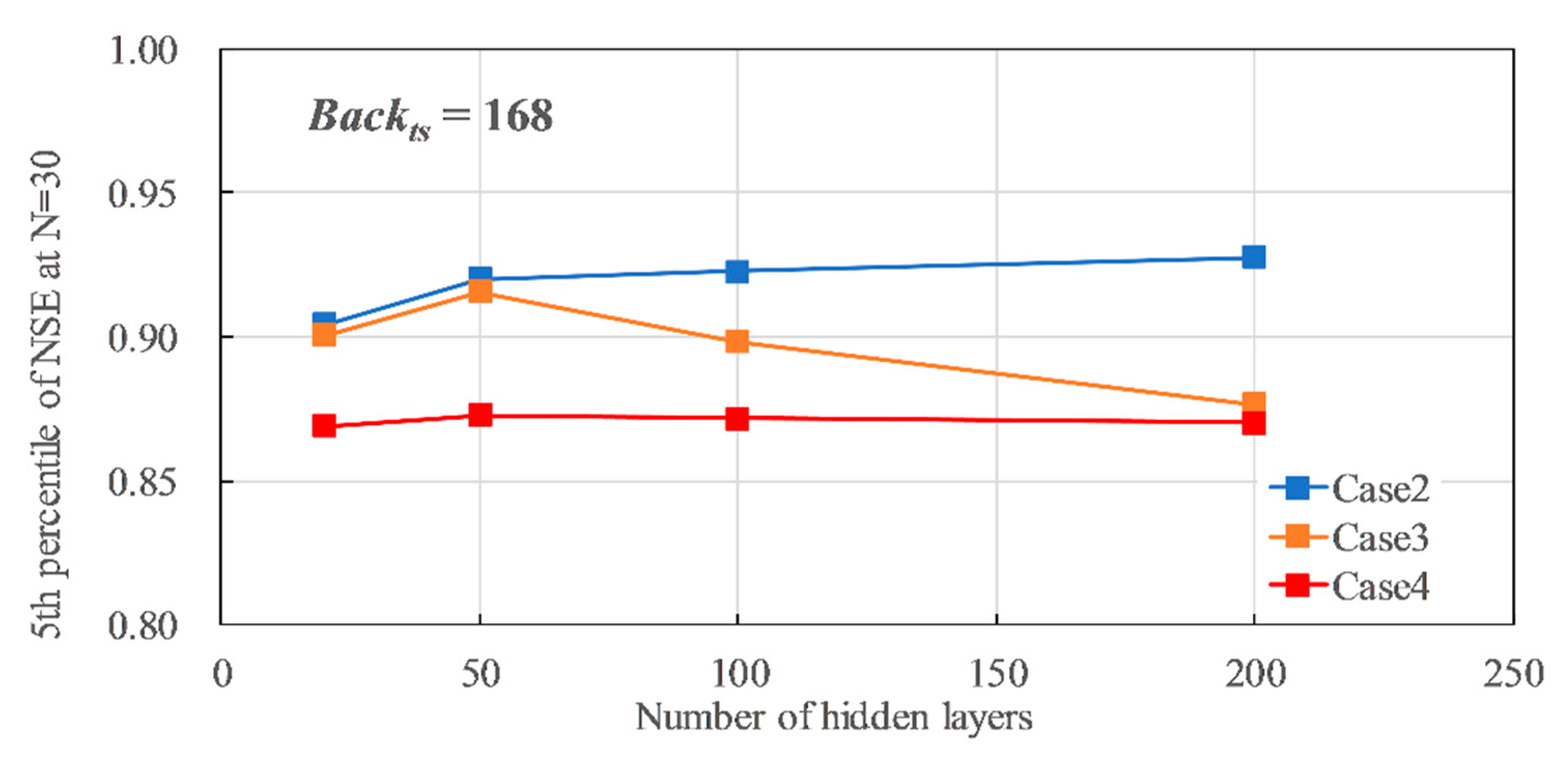
3.5. Number of Hidden Layers
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Gao, Y.; Merz, C.; Lischeid, G.; Schneider, M. A Review on Missing Hydrological Data Processing. Environ. Earth Sci. 2018, 77, 47. [Google Scholar] [CrossRef]
- Kojiri, T.; Panu, U.S.; Tomosugi, K. Complement Method of Observation Lack of Discharge with Pattern Classification and Fuzzy Inference. J. Jpn. Soc. Hydrol. Water Resour. 1994, 7, 536–543. [Google Scholar] [CrossRef]
- Tezuka, M.; Ohgushi, K. A Practical Method To Estimate Missing. In Proceedings of the 18th IAHR APD Congress, Jeju, Korean, 22–23 August 2012; pp. 547–548. [Google Scholar]
- Ding, Y.; Zhu, Y.; Feng, J.; Zhang, P.; Cheng, Z. Interpretable Spatio-Temporal Attention LSTM Model for Flood Forecasting. Neurocomputing 2020, 403, 348–359. [Google Scholar] [CrossRef]
- Li, W.; Kiaghadi, A.; Dawson, C. Exploring the Best Sequence LSTM Modeling Architecture for Flood Prediction. Neural Comput. Appl. 2020, 33, 5571–5580. [Google Scholar] [CrossRef]
- Le, X.H.; Ho, H.V.; Lee, G.; Jung, S. Application of Long Short-Term Memory (LSTM) Neural Network for Flood Forecasting. Water 2019, 11, 1387. [Google Scholar] [CrossRef] [Green Version]
- Taniguchi, J.; Kojima, T.; Sota, Y.; Hukumoto, S.; Satou, H.; Machida, Y.; Mikami, T.; Nagayama, M.; Nishikohri, T.; Watanabe, A. Application of Recurrent Neural Network for Dam Inflow Prediction. Adv. River Eng. 2019, 25, 321–326. [Google Scholar]
- Hu, C.; Wu, Q.; Li, H.; Jian, S.; Li, N.; Lou, Z. Deep Learning with a Long Short-Term Memory Networks Approach for Rainfall-Runoff Simulation. Water 2018, 10, 1543. [Google Scholar] [CrossRef] [Green Version]
- Xiang, Z.; Yan, J.; Demir, I. A Rainfall-Runoff Model With LSTM-Based Sequence-to-Sequence Learning. Water Resour. Res. 2020, 56, e2019WR025326. [Google Scholar] [CrossRef]
- Sahoo, B.B.; Jha, R.; Singh, A.; Kumar, D. Long Short-Term Memory (LSTM) Recurrent Neural Network for Low-Flow Hydrological Time Series Forecasting. Acta Geophys. 2019, 67, 1471–1481. [Google Scholar] [CrossRef]
- Sudriani, Y.; Ridwansyah, I.; Rustini, H.A. Long Short Term Memory (LSTM) Recurrent Neural Network (RNN) for Discharge Level Prediction and Forecast in Cimandiri River, Indonesia. In Proceedings of the IOP Conference Series: Earth and Environmental Science; Institute of Physics Publishing: Bristol, UK, 2019; Volume 299. [Google Scholar]
- Lee, G.; Lee, D.; Jung, Y.; Kim, T.-W. Comparison of Physics-Based and Data-Driven Models for Streamflow Simulation of the Mekong River. J. Korea Water Resour. Assoc. 2018, 51, 503–514. [Google Scholar] [CrossRef]
- Bai, P.; Liu, X.; Xie, J. Simulating Runoff under Changing Climatic Conditions: A Comparison of the Long Short-Term Memory Network with Two Conceptual Hydrologic Models. J. Hydrol. 2021, 592, 125779. [Google Scholar] [CrossRef]
- Fan, H.; Jiang, M.; Xu, L.; Zhu, H.; Cheng, J.; Jiang, J. Comparison of Long Short Term Memory Networks and the Hydrological Model in Runoff Simulation. Water 2020, 12, 175. [Google Scholar] [CrossRef] [Green Version]
- Granata, F.; di Nunno, F. Forecasting Evapotranspiration in Different Climates Using Ensembles of Recurrent Neural Networks. Agric. Water Manag. 2021, 255, 107040. [Google Scholar] [CrossRef]
- Chen, Z.; Zhu, Z.; Jiang, H.; Sun, S. Estimating Daily Reference Evapotranspiration Based on Limited Meteorological Data Using Deep Learning and Classical Machine Learning Methods. J. Hydrol. 2020, 591, 125286. [Google Scholar] [CrossRef]
- Ferreira, L.B.; da Cunha, F.F. Multi-Step Ahead Forecasting of Daily Reference Evapotranspiration Using Deep Learning. Comput. Electron. Agric. 2020, 178, 105728. [Google Scholar] [CrossRef]
- Reimers, N.; Gurevych, I. Optimal Hyperparameters for Deep LSTM-Networks for Sequence Labeling Tasks. arXiv 2017, arXiv:1707.06799. [Google Scholar]
- Hossain, M.D.; Ochiai, H.; Fall, D.; Kadobayashi, Y. LSTM-Based Network Attack Detection: Performance Comparison by Hyper-Parameter Values Tuning. In Proceedings of the 2020 7th IEEE International Conference on Cyber Security and Cloud Computing (CSCloud)/2020 6th IEEE International Conference on Edge Computing and Scalable Cloud (EdgeCom), New York, NY, USA, 1–3 August 2020; pp. 62–69. [Google Scholar]
- Yadav, A.; Jha, C.K.; Sharan, A. Optimizing LSTM for Time Series Prediction in Indian Stock Market. Procedia Comput. Sci. 2020, 167, 2091–2100. [Google Scholar] [CrossRef]
- Yi, H.; Bui, K.N. An Automated Hyperparameter Search-Based Deep Learning Model for Highway Traffic Prediction. IEEE Trans. Intell. Transp. Syst. 2020, 22, 5486–5495. [Google Scholar] [CrossRef]
- Kratzert, F.; Klotz, D.; Shalev, G.; Klambauer, G.; Hochreiter, S.; Nearing, G. Benchmarking a Catchment-Aware Long Short-Term Memory Network (LSTM) for Large-Scale Hydrological Modeling. Hydrol. Earth Syst. Sci. Discuss. 2019, 2019, 1–32. [Google Scholar] [CrossRef]
- Afzaal, H.; Farooque, A.A.; Abbas, F.; Acharya, B.; Esau, T. Groundwater Estimation from Major Physical Hydrology Components Using Artificial Neural Networks and Deep Learning. Water 2020, 12, 5. [Google Scholar] [CrossRef] [Green Version]
- Ayzel, G.; Heistermann, M. The Effect of Calibration Data Length on the Performance of a Conceptual Hydrological Model versus LSTM and GRU: A Case Study for Six Basins from the CAMELS Dataset. Comput. Geosci. 2021, 149, 104708. [Google Scholar] [CrossRef]
- Alizadeh, B.; Ghaderi Bafti, A.; Kamangir, H.; Zhang, Y.; Wright, D.B.; Franz, K.J. A Novel Attention-Based LSTM Cell Post-Processor Coupled with Bayesian Optimization for Streamflow Prediction. J. Hydrol. 2021, 601, 126526. [Google Scholar] [CrossRef]
- Kojima, T.; Weilisi; Ohashi, K. Investigation of Missing River Discharge Data Imputation Method Using Deep Learning. Adv. River Eng. 2020, 26, 137–142. [Google Scholar]
- River Division of Gifu Prefectural Office. Ojima Dam. Available online: https://www.pref.gifu.lg.jp/page/67841.html (accessed on 7 January 2022).
- Kojima, T.; Shinoda, S.; Mahboob, M.G.; Ohashi, K. Study on Improvement of Real-Time Flood Forecasting with Rainfall Interception Model. Adv. River Eng. 2012, 18, 435–440. [Google Scholar]
- Gers, F.A.; Schmidhuber, J.A.; Cummins, F.A. Learning to Forget: Continual Prediction with LSTM. Neural Comput. 2000, 12, 2451–2471. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Nash, J.E.; Sutcliffe, J.V. River Flow Forecasting through Conceptual Models Part I—A Discussion of Principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Semeniuta, S.; Severyn, A.; Barth, E. Recurrent Dropout without Memory Loss. In Proceedings of the COLING 2016, the 26th International Conference on Computational Linguistics: Technical Papers, Osaka, Japan, 11–16 December 2016; Matsumoto, Y., Prasad, R., Eds.; The COLING 2016 Organizing Committee: Osaka, Japan, 2016; pp. 1757–1766. [Google Scholar]
- Gal, Y.; Ghahramani, Z. A Theoretically Grounded Application of Dropout in Recurrent Neural Networks. In Proceedings of the 30th International Conference on Neural Information Processing Systems (NIPS’16), Barcelona, Spain, 5–10 December 2016; Curran Associates Inc.: Barcelona, Spain, 2016; pp. 1027–1035. [Google Scholar]

| Hyperparameter | Value1 | Value2 | Value3 | Value4 |
|---|---|---|---|---|
| Backts | 24 | 168 | 0 | |
| Hid | 20 | 50 | 100 | 200 |
| Drp | 0 | 0.01 | 0.05 | 0.1 |
| Drpr | 0 | 0.01 | 0.05 | 0.1 |
| Type of Input Variables | Number of Input Variables | |
|---|---|---|
| Case1 | Qshio + P | 2 |
| Case2 | Qshio + Qsan | 2 |
| Case3 | Qshio + Qsan + P | 3 |
| Case4 | Qshio + Qsan + P + T | 4 |
| Case5 | Qshio | 1 |
| Case6 | Qshio + T | 2 |
| Case7 | P | 1 |
| Case8 | T | 1 |
| Case9 | Qsan | 1 |
| Case10 | Qsan + P | 2 |
| Case11 | Qsan + T | 2 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Weilisi; Kojima, T. Investigation of Hyperparameter Setting of a Long Short-Term Memory Model Applied for Imputation of Missing Discharge Data of the Daihachiga River. Water 2022, 14, 213. https://doi.org/10.3390/w14020213
Weilisi, Kojima T. Investigation of Hyperparameter Setting of a Long Short-Term Memory Model Applied for Imputation of Missing Discharge Data of the Daihachiga River. Water. 2022; 14(2):213. https://doi.org/10.3390/w14020213
Chicago/Turabian StyleWeilisi, and Toshiharu Kojima. 2022. "Investigation of Hyperparameter Setting of a Long Short-Term Memory Model Applied for Imputation of Missing Discharge Data of the Daihachiga River" Water 14, no. 2: 213. https://doi.org/10.3390/w14020213






