1. Introduction
Under laminar condition of the flow, the most common hydraulic law used to model groundwater flow in saturated media are the Darcy and Poiseuille laws.
The so-called Darcy law comes from the French hydraulic engineer Henry Darcy, who investigated the flow of water through horizontal beds of sand to be used for water infiltration [
1]. The general form of the Darcy law expresses the velocity of the groundwater flow,
v, in relation to hydraulic head lost,
dh, in the length path
dl [
2]:
where
K is a hydraulic constant, with dimension of [
L × T
−1], function of the characteristics of the porous media and of the liquid. The minus sign is needed as the differential term
dh is negative; the dimensionless ratio
dh/
dl is known as hydraulic gradient,
i, which controls the flow velocity by a linear law.
Hubbert [
3] described as the Equation (1), found empirically, can be derived by the Navier-Stokes equations, providing its physical-based meaning.
The so-called Poiseuille law comes from the French physiologist-physicist Jean Leonard Marie Poiseuille, who investigated the velocity of distilled water flow in small conduits in the 1830s [
4]. Initially, he planned to maintain a constant temperature of 10 °C; later, he examined the influence of a wide range of water temperature and extended his studies to a great variety of other liquids [
5]. During the 1880s, the German hydraulic engineer Gotthilf Heinrich Ludwig Hagen reached similar results to those of Poiseuille on the flow of water in cylindrical tubes; for this reason, the Poiseuille law is also known as Poiseuille-Hagen law. In their review on the Poiseuille law, Sutera and Skalak [
6] stated that the results of Hagen were less extensive and less accurate than Poiseuille’s.
The general form of the Poiseuille law expresses the velocity of a liquid,
v, in a tube with constant diameter,
d, length
L, in relation to the difference of the liquid pressure between the ends of the tube, Δ
P:
where
μ is the dynamic viscosity of the liquid.
Also Equation (2), found empirically, can be derived from physical-based assumptions [
7,
8].
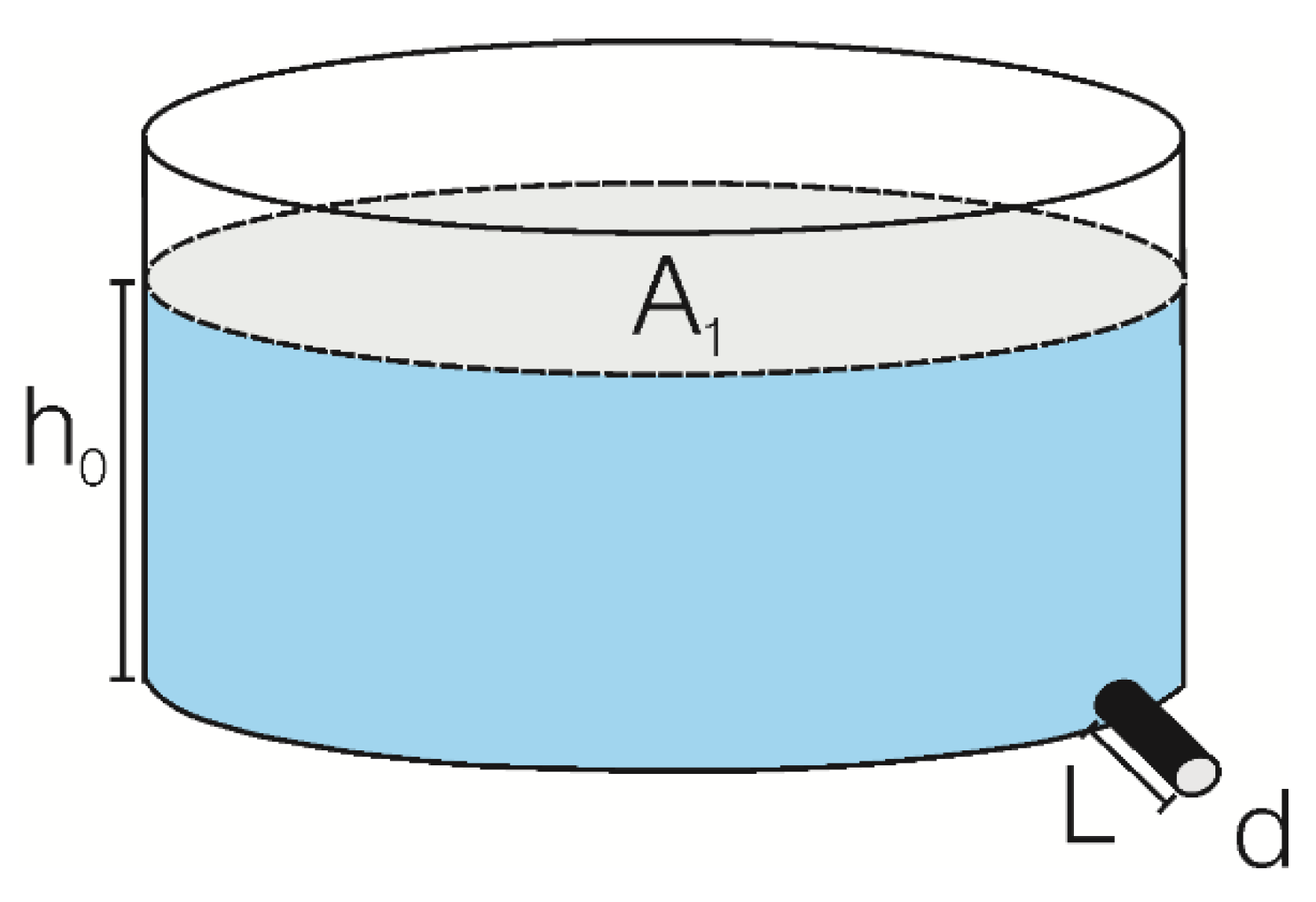
Both hydraulic laws describe the velocity of groundwater flow in saturated zones, but refer to different physical approaches (conduits and porous systems). To investigate their possible relationship, a simple tank-reservoir is drained by a hole and different physical laws are applied (
Figure 1).
The analytical relationship found between these hydraulic laws allows to convert the discharge of a Poiseuille system (conduit medium) in the same amount flowing inside a darcian system (porous medium), and vice versa; scaling processes of the hydraulic sections have been also considered. These changing of the flow conditions occur, for example, in karst aquifers, from the matrix to karst conduits during discharge phases, and from conduits to matrix during recharge phases.
2. Tank-Reservoir Models
In the tank-reservoir of
Figure 1, the drainage occurs by a tank-tube, with diameter
d and length
L, located at the bottom of the tank. The effect of the water viscosity decreases if the diameter of the tube increases; in particular, if the diameter is sufficiently wide, the water viscosity can be ignored and drainage occurs in terms of the Torricelli efflux velocity [
9].
If the diameter of the tube is small, the water viscosity effect cannot be ignored, and drainage can be analyzed by the Poiseuille law, which assumes that the flow is laminar. Filling the tank-tube with sand, the drainage can be modelled using the Darcy law, which also assumes a laminar flow condition.
The above different tank-drainage systems have been called Torricelli, Poiseuille and Darcy reservoir, respectively [
9].
The discharge-time plot for these different reservoirs has been analytically provided by Fiorillo [
9], starting from an initial water height in the reservoir,
h0, at time
t0 = 0, and applying the principle of mass and volume conservation. Thus, water has been considered as an incompressible liquid; a compressible case [
10] would require a different and complex approach.
The water pressure in the tube is directly controlled by the water height, h, in the reservoir; besides, it has been assumed null at the end of tube when the drainage starts at time t0.
For the Poiseuille reservoir, the following equations describe the discharge,
Q, from the tank-tube with diameter
dP [
9]:
where:
The parameter has a dimension of [T−1] and expresses the drainage characteristics of the Poiseuille reservoir; the gravity acceleration, g, and the water density, ρ, appear from the substitution of the term ΔP of Equation (2) by the ρ⋅g⋅h.
If the tank-tube, with section area
AD (and diameter
dD) and length
L, is filled by sand with hydraulic conductivity
K, the Darcy law can be used to simulate the drainage from the tank-reservoir. The following formula describes the discharge,
Q, from the tank [
9]:
where
The parameter has a dimension of [T−1] and expresses the drainage characteristics of the Darcy reservoir.
Equations (3) and (6) are that of Maillet [
11], and the constant
α is a recession coefficient, which controls the exponential decay of the discharge by the time. The recession coefficient depends on the geometric and hydraulic characteristics of the reservoir (Equations (4) and (8)); it is also the constant linking the discharge,
Q(t), to the water volume stored
V(t) in a linear reservoir:
3. Comparison between Darcy and Poiseuille Laws
The fixed geometric and hydraulic conditions of the tank-reservoir of
Figure 1 allow for the comparison of the Darcy and Poiseuille laws.
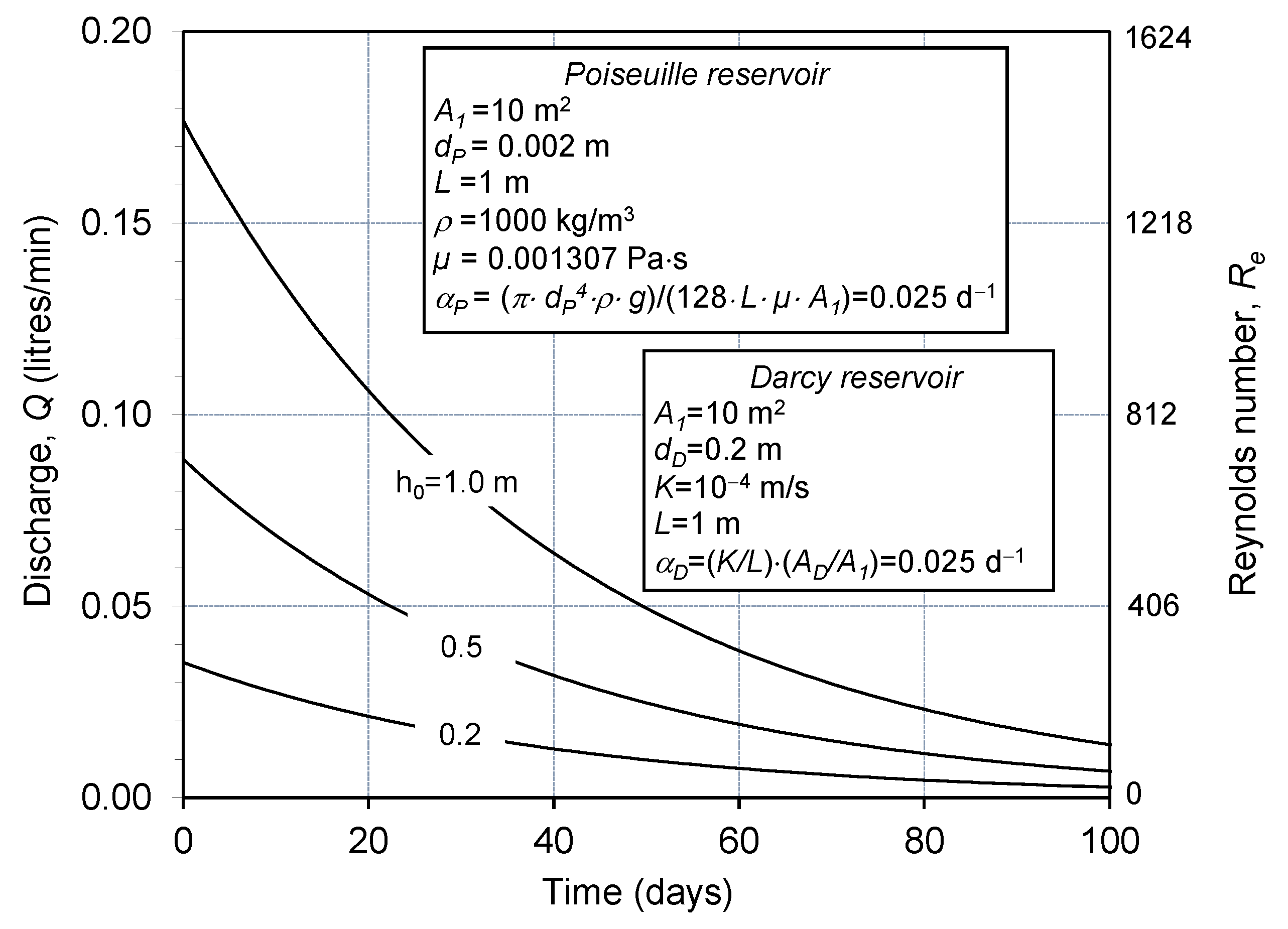
Figure 2 shows an example of the discharge-time plot using the Darcy and the Poiseuille laws with the same recession coefficient (
=
= 0.025 d
−1).
Three exponential decays are shown in
Figure 2, and correspond to different initial water level heights,
h0; the three different curves have the same recession coefficients (Equations (4) and (8)), and would provide straight lines in the semilogarithmic plot with the same slope, which is precisely the recession coefficient [
9].
On the right-hand axis of
Figure 2 is shown the Reynolds number,
Re, computed for the flow in the tube of the Poiseuille reservoir by:
For the flow in the tube filled by sand (Darcy reservoir), the Reynolds number has been computed by [
12]:
where
d50 is the median grain size of the porous medium as a proxy for the characteristic pore length, and
q is the specific discharge (
q = QD/
AD). In the example of
Figure 2, for a value of
d50 = 0.02 mm, compatible with the hydraulic conductivity
K = 1 × 10
−4 m/s of the sand, values of the Reynolds number (Equation (11)) are
Re << 1.
Imposing
=
of Equations (4) and (8), the relationship between diameter
dD and
dP can be obtained:
with
ki is the intrinsic permeability of the material,
ki = (
μ·K)/(
ρ·g) with dimension [
L2].
The Equation (12) provides the link between the Darcy and Poiseuille laws; it can be written also in terms of section areas:
Of course, the diameter of the Darcy tube,
dD, cannot be minor than diameter of Poiseuille tube,
dP, as the first is filled by sand which reduces the actual section of the tube. Imposing as the limit condition the same diameter for
dD and
dP (
dD ≡
dP), Equations (12) and (13) reduce in:
The Equation (15) would connect the size of the area of the Poiseuille conduit, AP, and the intrinsic permeability of a porous medium, ki.
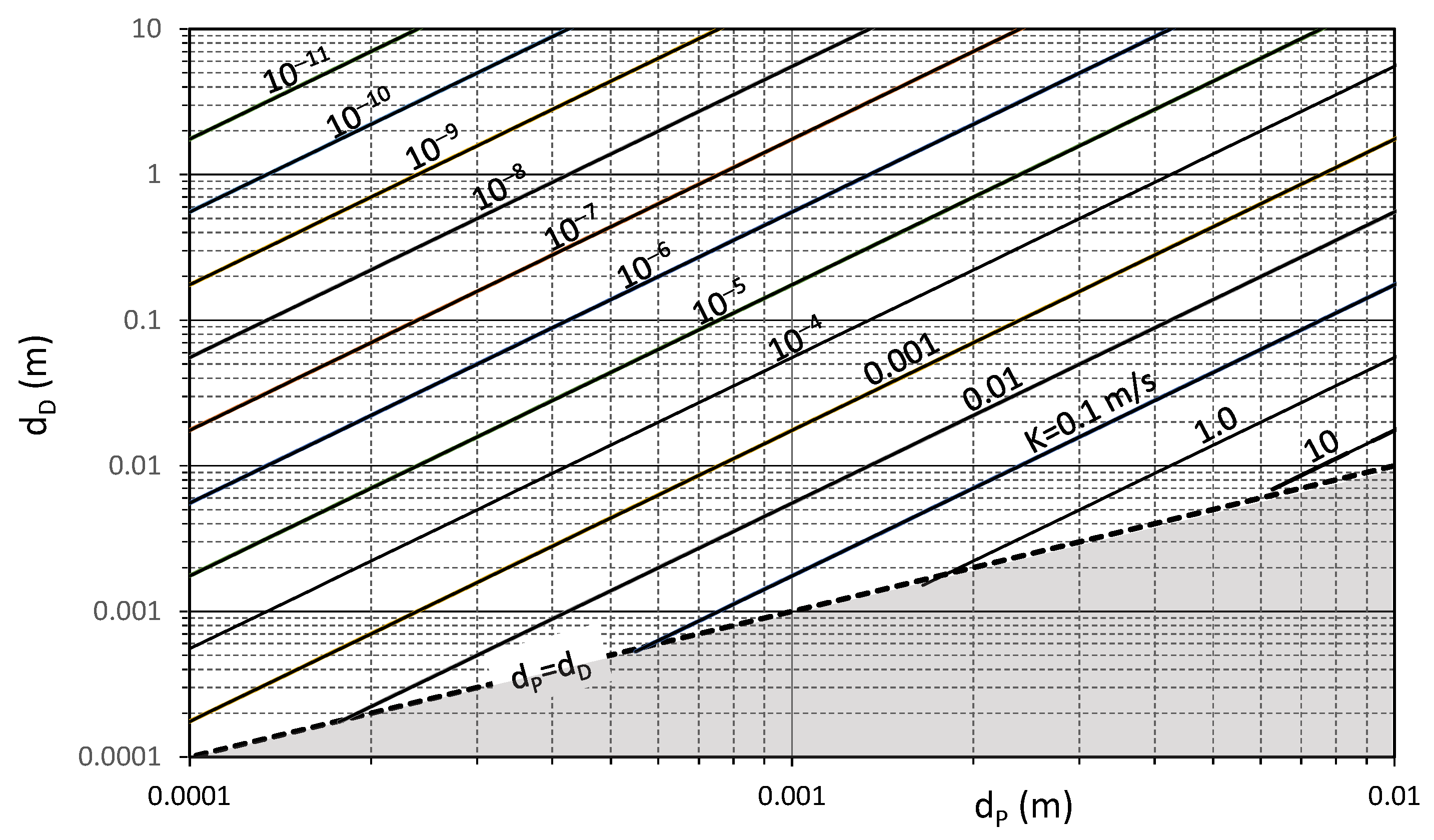
Figure 3 shows the relation between the
dP and
dD (Equation (12)) for different hydraulic conductivity,
K. The grey field characterizes the zones with
dP ≥
dD, and does not have physical meaning, and it has been delimited by Equation (14).
4. Discussion
In a smoothed tube, the Poiseuille law can be used for a Reynolds number below a threshold value,
Re < 2000 [
13]; above this value, the flow progressively changes in the turbulent type.
In the porous medium, the turbulent flow occurs progressively from the laminar condition when the velocity of the flow increases, and it is strictly connected to the structure of the medium. Thus, a threshold cannot be fixed, and values
Re < 1 could be required to guaranty the laminar condition of the flow [
12].
For the Poiseuille law, since the discharge is proportional to the fourth power of the diameter of the tube, large tubes are very much more conductive than smaller ones. In
Figure 2, the single tube with diameter of 2 mm could be replaced by 10,000 tubes with diameter of 0.2 mm to maintain the same drainage of the Poiseuille reservoir; this factor dominates the processes of the drainage and the cave patter construction in karst media [
14]. For the Darcy reservoir of
Figure 2, the single tube with diameter of 0.2 m could be replaced by 100 tubes with diameter of 0.02 m to maintain the same drainage of the reservoir.
In particular, in the Darcy reservoir there is a linear relationship between the discharge,
QD, and the area of the tube,
AD, for a fixed hydraulic conductivity,
K; that is:
In the Poiseuille reservoir the relationship between the discharge,
QP, and the area of the tube,
AP, is quadratic, that is:
In term of diameters the above relationship they are quadratic and to the fourth, respectively:
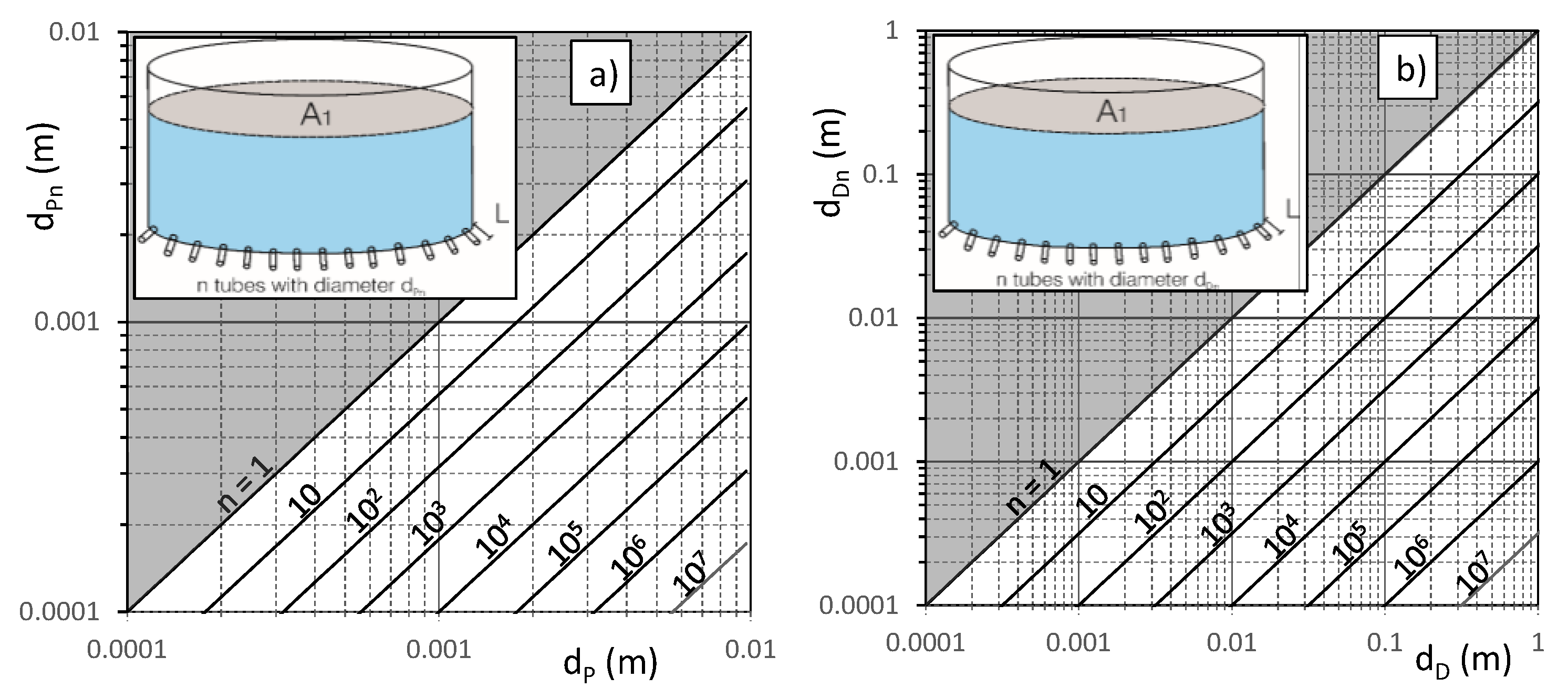
If several small tubes in number
n, with same diameter
dPn or
dDn replace the larger tube
dP or
dD, for the Poiseuille or Darcy reservoir, respectively, the following relationships are obtained:
For example, in the Poiseuille reservoir, n = 104 tubes with diameter dPn = 0.0001 m discharge as one tube with diameter dP = 0.001 m. In the Darcy reservoir, n = 102 tubes with diameter dDn = 0.0001 m discharge as one tube with diameter dP = 0.001 m.
The different behavior of the two reservoirs highlighted by the Equations (19) and (20), are only apparent. From Equation (13), considering the relationship:
it appears that there are two contributions areas for the Darcian flow: the section area,
AD, and the intrinsic permeability,
ki. Thus, the reason of why in the Darcy reservoir the discharge is proportional to the area of the tube,
AD (Equation (16)) lies in the fact that the intrinsic permeability,
ki, is considered constant. Instead, the Equation (15) would provide the intimate relationship between the size of
AP and
ki.
The above relationships (Equations (19) and (20)) are shown in
Figure 4.
Figure 4 shows how the number,
n, of smaller tubes (
dPn; dDn) rapidly increase as their diameter decreases. Of course, as a corollary, a single tube can drain the discharge of many smaller tubes. These aspects have an important role in the groundwater flow, both in porous and fractured/conduit systems, with particular emphasis in the karst systems, where a complex conduit network is “immersed” in a low permeability fractured limestone volume [
15]. Here the karstification processes lead to a hierarchical conduit network into the aquifer [
16], which cause the drainage to be converged to specific points: the karst springs. Therefore, the drainage of a karst spring appears “similar” with that of the venous system that leads the blood flow to the heart from the more peripheral areas. In these systems, a single conduit could require a huge number of smaller conduits to be supplyed.
Table 1 shows the relationship between the conduit diameter,
dP, and the conduit number,
n, following Equation (19); the total volume occupied by conduits,
V, rapidly increases when
dP decreases. That is, a large volume of water into the smallest conduits is needed to maintain the discharge of a few wide conduits. For the smallest values of
dP, the conduits system could be replaced by a porous medium, where the hydraulic conductivity,
K, has been estimated by the Equation (14).
The volume,
V, estimated in
Table 1, represents the complex of total voids volume in the system, both of conduits net and matrix porosity (which replaces conduit porosity for smallest conduits); its ratio to rock volume defines the porosity of the system.
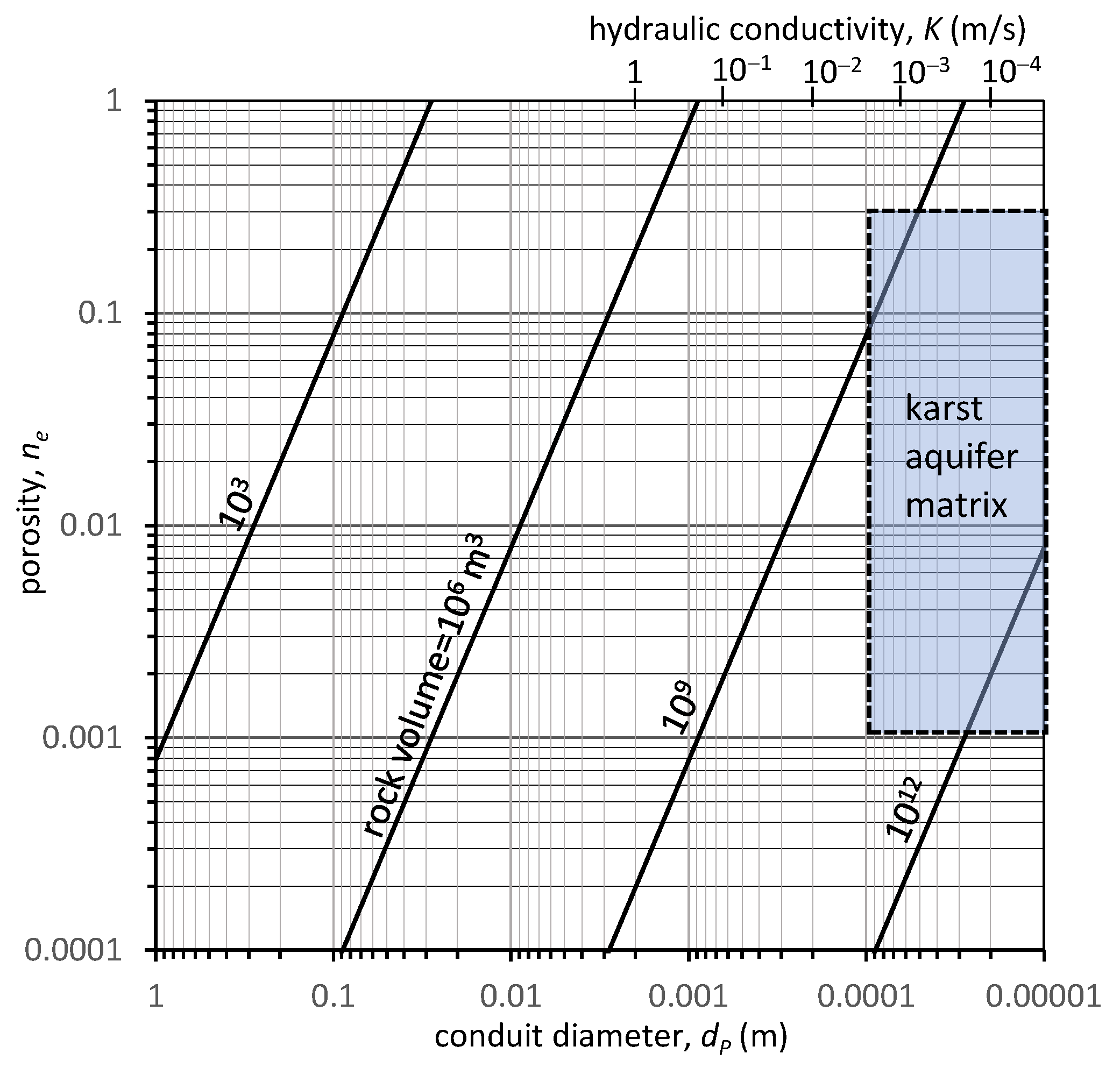
Figure 5 shows the variation of the porosity of the system,
ne, in relation to
dP, for different rock volumes. The porosity,
ne, increases as the conduits diameter decreases, and it decreases when the rock volume increases. To support the discharge of wide conduits by the smallest conduits or matrix, a large rock volume would be required; furthermore, in the smallest conduits or matrix, the water volume is huge compared to that flowing in the wider conduits. The matrix of karst aquifers occupies a zone characterized by the smallest conduits, approximately by
dP < 0.0001 mm (or
K < 2.3 × 10
−3 m/s) and range of porosity of 0.3 <
ne < 0.001.
5. Conclusions
The Darcy law has a wide use in groundwater hydrology not only in the porous medium, but also in fractured/conduit systems, where the hydraulic conductivity, K, is considered as a mean value of a wide portion of rock masses. The Poiseuille law describes specifically the flow velocity in the conduit systems, where the diameter of conduits controls the articulation of the flow inside the rock mass.
Based on the tank-reservoir drainage, the link between these two hydraulic laws has been discussed. The comparison of the Darcy law with the Poiseuille law highlights how the discharge in a porous medium depends on two areas: the section area interested by the flow (AD for the Darcy reservoir) and by intrinsic permeability, ki, of the medium. In the Poiseuille law, the flow depends directly on the square of the section area interested by the flow ( for the Poiseuille reservoir). Even if these characteristics were already known individually for each hydraulic law, their analytical relationship has been poorly described.
Theoretically, it is possible to switch from a hydraulic law to the other using the Equations (12) and (14), or Equations (13) and (15); the Equations (19) and (20) could help in scaling (or vice versa) the conduit diameter in a net system.
All relationships found are valid under laminar conditions of the flow, which almost always occur in porous aquifers; in the discontinuities of fractured aquifers and in the conduit systems of karst aquifers the Poiseuille law could have a limitation due to the presence of a turbulent flow. In any case, its fourth power law highlights well the natural hierarchization observed in many natural systems, as, for example, from the quasi-porous system of the matrix to the final conduit of karst springs.