Spatiotemporal Analysis on the Teleconnection of ENSO and IOD to the Stream Flow Regimes in Java, Indonesia
Abstract
:1. Introduction
2. Data and Methods
2.1. Streamflow Data
2.2. Climate Indices
2.3. Temporal Variation Sets
2.4. Multiple Polynomial Regression
2.5. Model Evaluation
3. Results
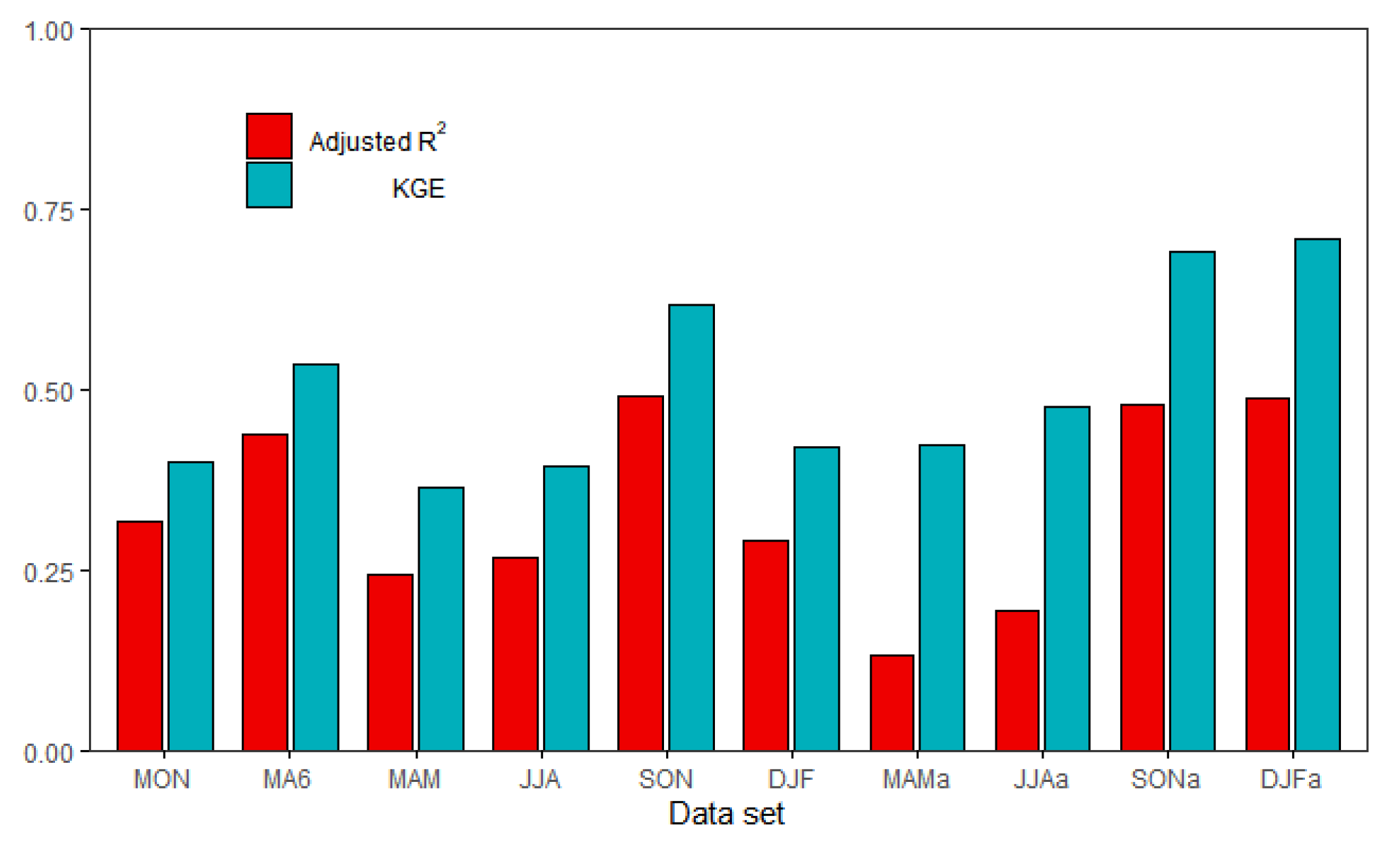
3.1. Temporal Variability
3.2. Spatial Variability
4. Discussion
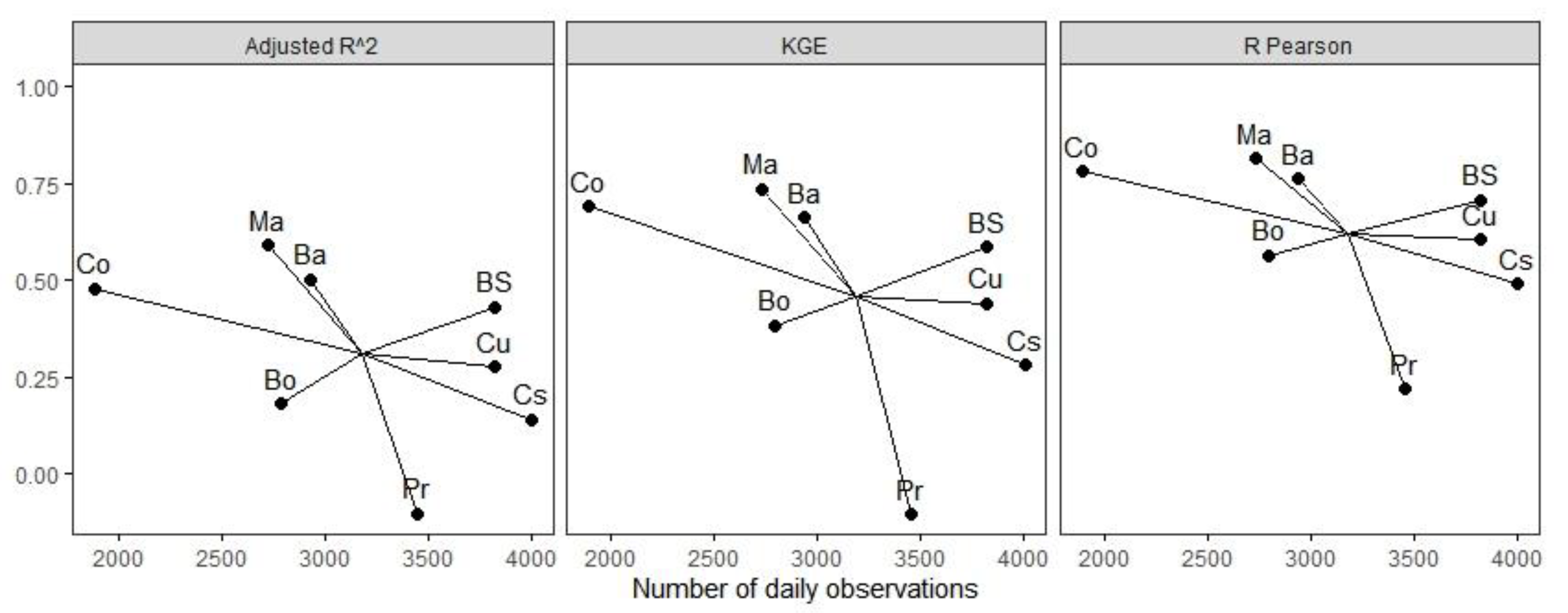
4.1. Predictability Tendency by the Number of Observations
4.2. Change of Predictability over Periods
4.3. Good Predictability in Code River
4.4. Streamflow Prediction by ENSO and IOD
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A

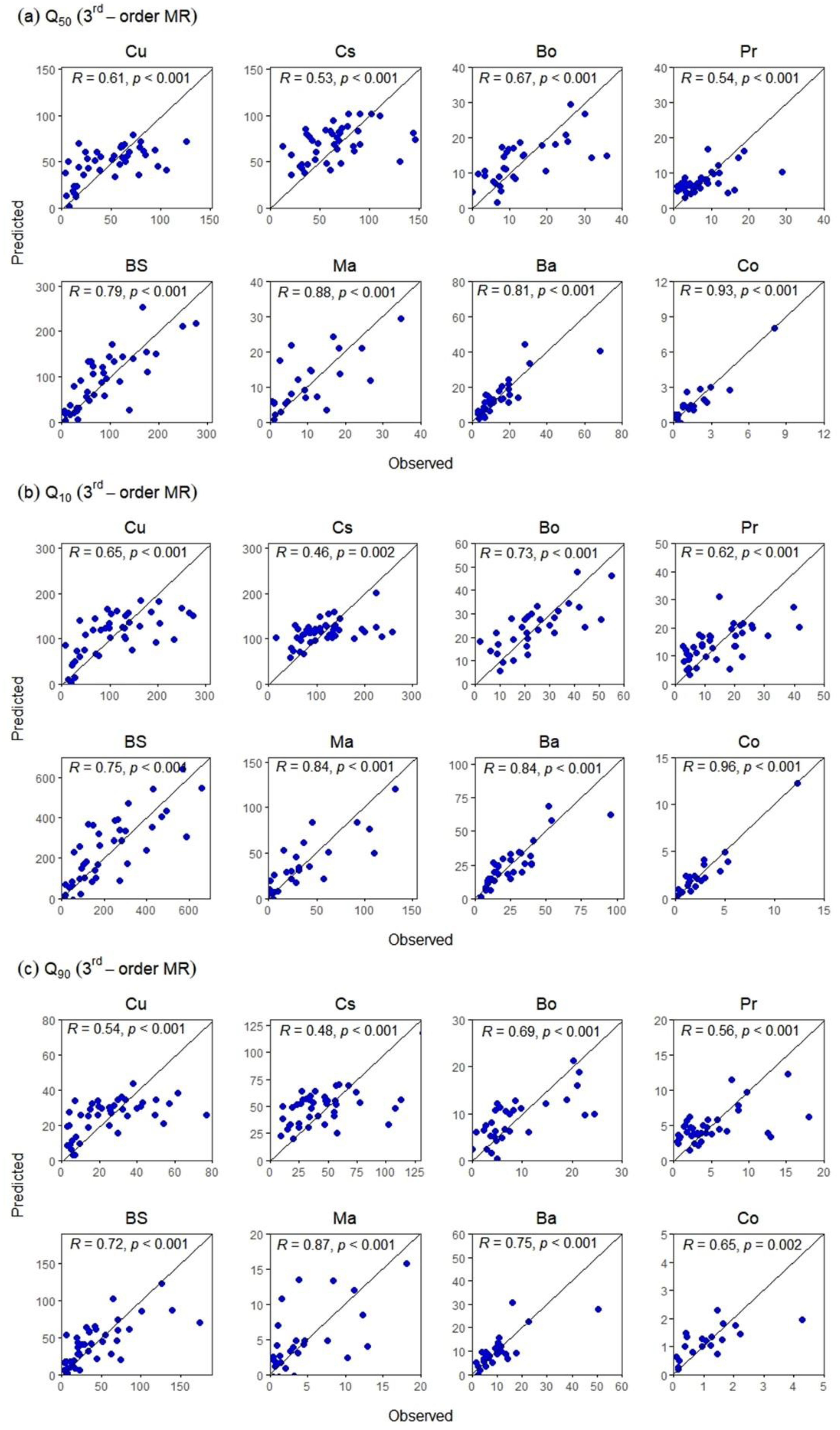
Appendix B
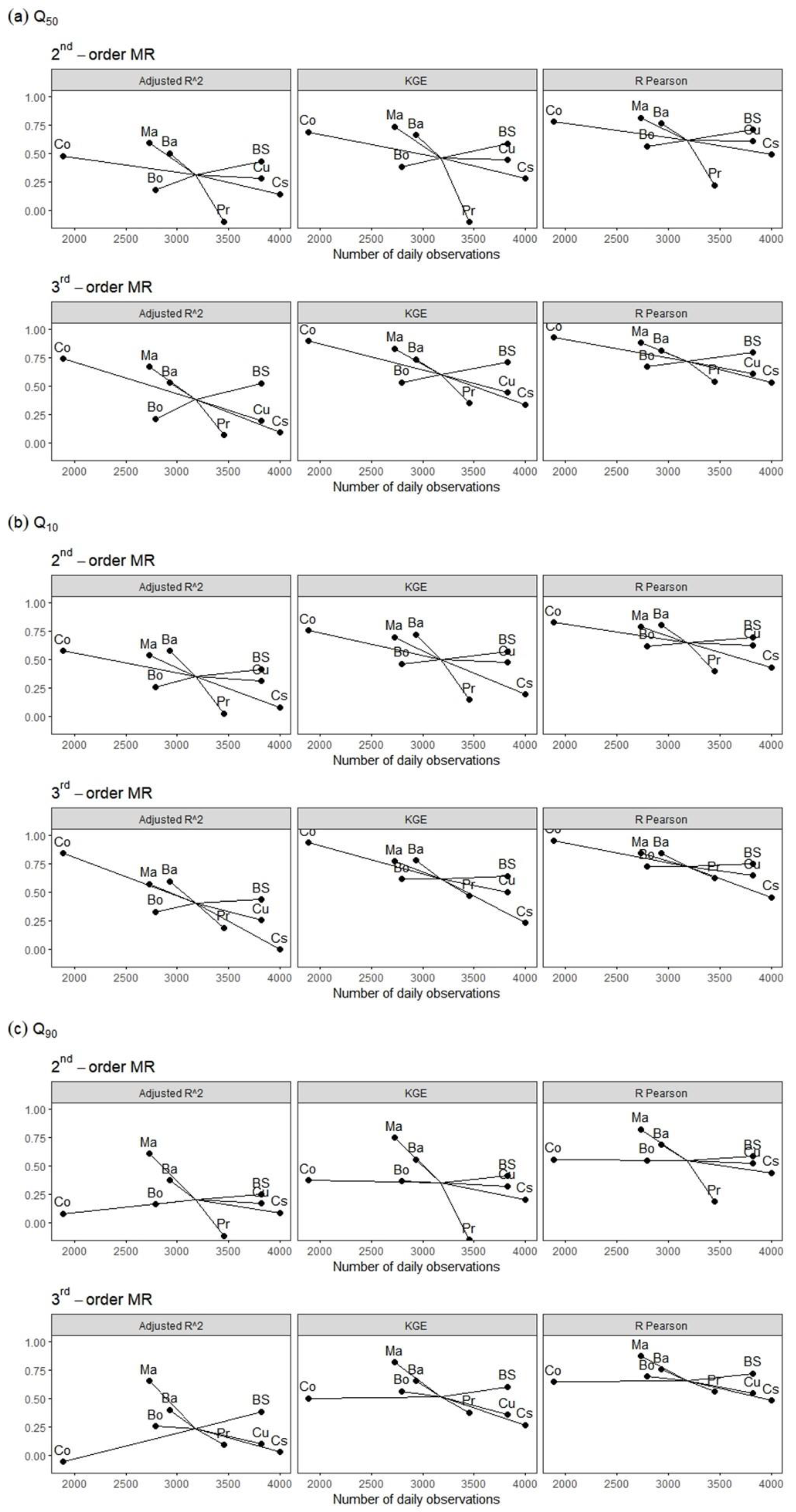
Appendix C
| River | 1970–2018 | 1970–1989 | 1990–2018 | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Q50 | Q10 | Q90 | Q50 | Q10 | Q90 | Q50 | Q10 | Q90 | |
| Cu | 0.277 | 0.309 | 0.170 | 0.618 | 0.478 | 0.568 | 0.090 | 0.100 | −0.001 |
| Cs | 0.142 | 0.078 | 0.085 | 0.615 | 0.027 | 0.579 | 0.029 | 0.055 | 0.011 |
| Bo | 0.181 | 0.260 | 0.162 | 0.533 | 0.411 | 0.626 | −0.037 | 0.022 | −0.009 |
| Pr | −0.101 | 0.025 | −0.117 | 0.231 | 0.329 | 0.189 | −0.149 | −0.184 | −0.122 |
| BS | 0.431 | 0.415 | 0.248 | 0.653 | 0.738 | 0.361 | 0.362 | 0.398 | 0.147 |
| Ma | 0.590 | 0.537 | 0.606 | 0.568 | 0.508 | 0.188 | 0.727 | 0.771 | 0.741 |
| Ba | 0.502 | 0.576 | 0.372 | 0.711 | 0.653 | 0.527 | 0.502 | 0.548 | 0.389 |
| Co | - | - | - | - | - | - | 0.479 | 0.575 | 0.078 |
| River | 1970–2018 | 1970–1989 | 1990–2018 | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Q50 | Q10 | Q90 | Q50 | Q10 | Q90 | Q50 | Q10 | Q90 | |
| Cu | 0.192 | 0.257 | 0.099 | 0.563 | 0.294 | 0.505 | 0.160 | 0.284 | −0.048 |
| Cs | 0.093 | −0.002 | 0.030 | 0.564 | −0.326 | 0.560 | −0.178 | −0.148 | −0.216 |
| Bo | 0.212 | 0.328 | 0.255 | 0.525 | 0.580 | 0.645 | −0.222 | −0.297 | −0.060 |
| Pr | 0.065 | 0.188 | 0.091 | 0.540 | 0.648 | 0.318 | −0.189 | −0.253 | 0.040 |
| BS | 0.526 | 0.433 | 0.383 | 0.887 | 0.876 | 0.655 | 0.361 | 0.353 | 0.086 |
| Ma | 0.670 | 0.571 | 0.652 | 0.643 | 0.419 | −0.254 | 0.863 | 0.893 | 0.839 |
| Ba | 0.530 | 0.596 | 0.401 | 0.625 | 0.514 | 0.300 | 0.708 | 0.674 | 0.653 |
| Co | - | - | - | - | - | - | 0.741 | 0.841 | −0.058 |
| River | 1970–2018 | 1970–1989 | 1990–2018 | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Q50 | Q10 | Q90 | Q50 | Q10 | Q90 | Q50 | Q10 | Q90 | |
| Cu | 0.441 | 0.323 | 0.473 | 0.800 | 0.771 | 0.718 | 0.334 | 0.230 | 0.345 |
| Cs | 0.281 | 0.205 | 0.194 | 0.792 | 0.771 | 0.377 | 0.254 | 0.232 | 0.284 |
| Bo | 0.383 | 0.362 | 0.462 | 0.769 | 0.818 | 0.701 | 0.371 | 0.395 | 0.420 |
| Pr | −0.105 | −0.152 | 0.146 | 0.573 | 0.544 | 0.637 | 0.085 | 0.125 | 0.028 |
| BS | 0.587 | 0.410 | 0.572 | 0.826 | 0.657 | 0.870 | 0.575 | 0.383 | 0.604 |
| Ma | 0.735 | 0.747 | 0.696 | 0.797 | 0.586 | 0.767 | 0.865 | 0.872 | 0.887 |
| Ba | 0.663 | 0.555 | 0.719 | 0.875 | 0.789 | 0.849 | 0.711 | 0.634 | 0.741 |
| Co | - | - | - | - | - | - | 0.689 | 0.371 | 0.753 |
| River | 1970–2018 | 1970–1989 | 1990–2018 | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Q50 | Q10 | Q90 | Q50 | Q10 | Q90 | Q50 | Q10 | Q90 | |
| Cu | 0.441 | 0.356 | 0.502 | 0.858 | 0.837 | 0.761 | 0.560 | 0.417 | 0.637 |
| Cs | 0.337 | 0.268 | 0.230 | 0.847 | 0.845 | 0.453 | 0.287 | 0.251 | 0.314 |
| Bo | 0.533 | 0.564 | 0.615 | 0.875 | 0.907 | 0.890 | 0.597 | 0.659 | 0.567 |
| Pr | 0.351 | 0.375 | 0.464 | 0.863 | 0.792 | 0.897 | 0.387 | 0.536 | 0.339 |
| BS | 0.708 | 0.604 | 0.642 | 0.968 | 0.899 | 0.964 | 0.673 | 0.497 | 0.668 |
| Ma | 0.829 | 0.819 | 0.773 | 0.920 | 0.694 | 0.867 | 0.961 | 0.954 | 0.969 |
| Ba | 0.737 | 0.653 | 0.777 | 0.932 | 0.870 | 0.911 | 0.887 | 0.865 | 0.873 |
| Co | - | - | - | - | - | - | 0.895 | 0.500 | 0.937 |
References
- Poff, N.L. Beyond the natural flow regime? Broadening the hydro-ecological foundation to meet environmental flows challenges in a non-stationary world. Freshw. Biol. 2018, 63, 1011–1021. [Google Scholar] [CrossRef]
- Ropelewski, C.F.; Halpert, M.S. Global and Regional Scale Precipitation Patterns Associated with the El Niño/Southern Oscillation. Mon. Weather Rev. 1987, 115, 1606–1626. [Google Scholar] [CrossRef] [Green Version]
- Hendon, H.H. Indonesian rainfall variability: Impacts of ENSO and local air-sea interaction. J. Clim. 2003, 16, 1775–1790. [Google Scholar] [CrossRef]
- Aldrian, E.; Susanto, R.D. Identification of three dominant rainfall regions within Indonesia and their relationship to sea surface temperature. Int. J. Climatol. 2003, 23, 1435–1452. [Google Scholar] [CrossRef]
- Lee, H.S. General Rainfall Patterns in Indonesia and the Potential Impacts of Local Seas on Rainfall Intensity. Water 2015, 7, 1751–1768. [Google Scholar] [CrossRef]
- Saji, N.; Goswami, B.; Vinayachandran, P.; Yamagata, T. A dipole mode in the Tropical Ocean. Nature 1999, 401, 360–363. [Google Scholar] [CrossRef]
- Cardoso, A.O.; Silva Dias, P.L. The relationship between ENSO and Paraná River flow. Adv. Geosci. 2006, 6, 189–193. [Google Scholar] [CrossRef] [Green Version]
- Cluis, D.; Laberge, C. Analysis of the El Niño Effect on the Discharge of Selected Rivers in the Asia-Pacific Region. Water Int. 2002, 27, 279–293. [Google Scholar] [CrossRef]
- Zhang, Q.; Xu, C.Y.; Jiang, T.; Wu, Y. Possible influence of ENSO on annual maximum streamflow of the Yangtze River, China. J. Hydrol. 2007, 333, 265–274. [Google Scholar] [CrossRef]
- Mohsenipour, M.; Shahid, S.; Nazemosadat, M.J. Effects of El Nino Southern Oscillation on the Discharge of Kor River in Iran. Adv. Meteorol. 2013, 2013, 1–7. [Google Scholar] [CrossRef]
- Sahu, N.; Behera, S.K.; Yamashiki, Y.; Takara, K.; Yamagata, T. IOD and ENSO impacts on the extreme stream-flows of Citarum River in Indonesia. Clim. Dyn. 2012, 39, 1673–1680. [Google Scholar] [CrossRef]
- Nugroho, A.R.; Tamagawa, I.; Harada, M. The Relationship between River Flow Regimes and Climate Indices of ENSO and IOD on Code River, Southern Indonesia. Water 2021, 13, 1375. [Google Scholar] [CrossRef]
- Searcy, J.K. Flow-Duration Curves; United States Government Printing Office: Washington, DC, USA, 1959. [Google Scholar] [CrossRef]
- Goetz, J.; Schwarz, C.J. Fasstr: Analyze, Summarize, and Visualize Daily Streamflow Data, R package version 0.3.3; CRAN, 2021; Available online: https://cran.r-project.org/package=fasstr (accessed on 29 November 2021).
- Ropelewski, C.F.; Halpert, M.S. Precipitation Patterns Associated with the High Index Phase of the Southern Oscillation. J. Clim. 1989, 2, 268–284. [Google Scholar] [CrossRef] [Green Version]
- Kurniadi, A.; Weller, E.; Min, S.K.; Seong, M.G. Independent ENSO and IOD impacts on rainfall extremes over Indonesia. Int. J. Climatol. 2021, 41, 3640–3656. [Google Scholar] [CrossRef]
- Bamston, A.G.; Chelliah, M.; Goldenberg, S.B. Documentation of a Highly ENSO-Related SST Region in the Equatorial Pacific: Research Note. Atmos.-Ocean 1997, 35, 367–383. [Google Scholar] [CrossRef]
- Hendrawan, I.G.; Asai, K.; Triwahyuni, A.; Lestari, D.V. The interanual rainfall variability in Indonesia corresponding to El Niño Southern Oscillation and Indian Ocean Dipole. Acta Oceanol. Sin. 2019, 38, 57–66. [Google Scholar] [CrossRef]
- Rao, J.; Ren, R. Parallel comparison of the 1982/83, 1997/98 and 2015/16 super El Niños and their effects on the extratropical stratosphere. Adv. Atmos. Sci. 2017, 34, 1121–1133. [Google Scholar] [CrossRef]
- Qian, H.; Xu, S.-B. Prediction of Autumn Precipitation over the Middle and Lower Reaches of the Yangtze River Basin Based on Climate Indices. Climate 2020, 8, 53. [Google Scholar] [CrossRef] [Green Version]
- Hidayat, R.; Kizu, S. Influence of the Madden-Julian Oscillation on Indonesian rainfall variability in austral summer. Int. J. Climatol. 2010, 30, 1816–1825. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing, R version 4.1.2; 2021; Available online: http://www.r-project.org/ (accessed on 29 November 2021).
- Wickham, H. Modelr: Modelling Functions that Work with the Pipe, R package version 0.1.8; CRAN, 2020; Available online: https://cran.r-project.org/package=modelr (accessed on 29 November 2021).
- Zambrano-Bigiarini, M. Hydrogof: Goodness-of-Fit Functions for Comparison of Simulated and Observed Hydrological Time Series, R package version 0.4-0; CRAN, 2020; Available online: https://cran.r-project.org/package=hydroGOF (accessed on 29 November 2021).
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models part I—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Gupta, H.V.; Kling, H.; Yilmaz, K.K.; Martinez, G.F. Decomposition of the mean squared error and NSE performance criteria: Implications for improving hydrological modelling. J. Hydrol. 2009, 377, 80–91. [Google Scholar] [CrossRef] [Green Version]
- Knoben, W.J.M.; Freer, J.E.; Woods, R.A. Technical note: Inherent benchmark or not? Comparing Nash-Sutcliffe and Kling-Gupta efficiency scores. Hydrol. Earth Syst. Sci. 2019, 23, 4323–4331. [Google Scholar] [CrossRef] [Green Version]
- Kling, H.; Fuchs, M.; Paulin, M. Runoff conditions in the upper Danube basin under an ensemble of climate change scenarios. J. Hydrol. 2012, 424–425, 264–277. [Google Scholar] [CrossRef]
- Hamada, J.I.; Yamanaka, M.D.; Matsumoto, J.; Fukao, S.; Winarso, P.A.; Sribimawati, T. Spatial and temporal variations of the rainy season over Indonesia and their link to ENSO. J. Meteorol. Soc. Japan 2002, 80, 285–310. [Google Scholar] [CrossRef] [Green Version]
- Jun-Ichi, H.; Mori, S.; Kubota, H.; Yamanaka, M.D.; Haryoko, U.; Lestari, S.; Sulistyowati, R.; Syamsudin, F. Interannual rainfall variability over northwestern Jawa and its relation to the Indian Ocean Dipole and El Niño-Southern Oscillation events. Sci. Online Lett. Atmos. 2012, 8, 69–72. [Google Scholar] [CrossRef] [Green Version]
- Hidayat, R.; Ando, K.; Masumoto, Y.; Luo, J.J. Interannual Variability of Rainfall over Indonesia: Impacts of ENSO and IOD and Their Predictability. IOP Conf. Ser. Earth Environ. Sci. 2016, 31, 012043. [Google Scholar] [CrossRef]
- Maryono, A. River Restoration, 4th ed.; Gadjah Mada University Press: Yogyakarta, Indonesia, 2020; ISBN 978-979-420-667-6. [Google Scholar]
- Kali Cisadane. Catalogue of Rivers for Southeast Asia and the Pacific-Volume V; Tachikawa, Y., James, R., Abdullah, K., Desa, M.N.b.M., Eds.; The UNESCO-IHP Regional Steering Committee for Southeast Asia and the Pacific, 2004; pp. 45–56. ISBN 4-902712-00-8. Available online: https://hywr.kuciv.kyoto-u.ac.jp/ihp/riverCatalogue/Vol_05/index.html (accessed on 29 November 2021).
- Bengawan Solo. In Catalogue of Rivers for Southeast Asia and the Pacific-Volume I; Takeuchi, K.; Jayawardena, A.W.; Takahasi, Y. (Eds.) The UNESCO-IHP Regional Steering Committee for Southeast Asia and the Pacific, 1995; pp. 91–102. ISBN 962-8014-07-2. Available online: https://hywr.kuciv.kyoto-u.ac.jp/ihp/riverCatalogue/Vol_01/index.html (accessed on 29 November 2021).
- Gornitz, V.; Rosenzweig, C.; Hillel, D. Effects of anthropogenic intervention in the land hydrologic cycle on global sea level rise. Glob. Planet. Change 1997, 14, 147–161. [Google Scholar] [CrossRef]
- Vorosmarty, C.J.; Sahagian, D. Anthropogenic disturbance of the terrestrial water cycle. Bioscience 2000, 50, 753–765. [Google Scholar] [CrossRef] [Green Version]
- Tang, Y.; Zhang, R.H.; Liu, T.; Duan, W.; Yang, D.; Zheng, F.; Ren, H.; Lian, T.; Gao, C.; Chen, D.; et al. Progress in ENSO prediction and predictability study. Natl. Sci. Rev. 2018, 5, 826–839. [Google Scholar] [CrossRef]
- Feba, F.; Ashok, K.; Collins, M.; Shetye, S.R. Emerging Skill in Multi-Year Prediction of the Indian Ocean Dipole. Front. Clim. 2021, 3, 1–8. [Google Scholar] [CrossRef]





| Code-Name | River Name | Flow Records Used (year) | Gauge’s Catchment Area (km2) | Region in Java | Gauge’s Location Coordinates |
|---|---|---|---|---|---|
| Cu | Ciujung | 42 | 1562.7 | West | −6.133, 106.300 |
| Cs | Cisadane | 44 | 850.2 | West | −6.514, 106.678 |
| Bo | Bodri | 31 | 522.3 | Central | −7.011, 110.137 |
| Pr | Progo | 38 | 423.4 | Central | −7.340, 110.209 |
| BS | Bengawan Solo | 42 | 11,125.0 | East | −7.150, 111.599 |
| Ma | Madiun | 30 | 2126.0 | East | −7.645, 111.513 |
| Ba | Baru | 33 | 454.0 | East | −8.413, 114.094 |
| Co | Code | 21 | 40.0 | Central | −7.849, 110.375 |
| Set Name | Code-Name | Time Scale | Calculation Method |
|---|---|---|---|
| Ordinary monthly | MON | monthly flow | Q50: median of daily flow distribution in a month. Q90: 10% percentile of daily flow distribution in a month. Q10: 90% percentile of daily flow distribution in a month. Thus, there are 12 data sets for each year. |
| Six-month moving average | MA6 | monthly flow with six-month information | Mean of each flow regime monthly series for six months. Thus, there are 12 data sets for each year. |
| Seasonal monthly (SM) | MAM/ JJA/ SON/ DJF | monthly flow | The same as with the ordinary monthly flow series, except the series is limited only to three months according to each season (e.g., Q50 of the MAM series includes the monthly Q50 of only March, April, and May, from 1970 to 2018). Thus, there are three data sets for each year. |
| Seasonal average (SMa) | MAMa/ JJAa/ SONa/ DJFa | three-month flow | Mean of the seasonal monthly series (e.g., the first datum in the MAMa series is the mean of three months: March, April, and May, in 1970). Thus, there is only one datum set for each year. |
| River | 2nd-Order MR | 3rd-Order MR | ||||
|---|---|---|---|---|---|---|
| Q50 | Q10 | Q90 | Q50 | Q10 | Q90 | |
| Cu | 0.28 | 0.17 | 0.31 | 0.19 | 0.10 | 0.26 |
| Cs | 0.14 | 0.09 | 0.08 | 0.09 | 0.03 | 0.00 |
| Bo | 0.18 | 0.16 | 0.26 | 0.21 | 0.26 | 0.33 |
| Pr | −0.10 | −0.12 | 0.02 | 0.07 | 0.09 | 0.19 |
| BS | 0.43 | 0.25 | 0.41 | 0.53 | 0.38 | 0.43 |
| Ma | 0.59 | 0.61 | 0.54 | 0.67 | 0.65 | 0.57 |
| Ba | 0.50 | 0.37 | 0.58 | 0.53 | 0.40 | 0.60 |
| Co | 0.48 | 0.08 | 0.57 | 0.74 | −0.06 | 0.84 |
| River | 2nd-Order MR | 3rd-Order MR | ||||
|---|---|---|---|---|---|---|
| Q50 | Q10 | Q90 | Q50 | Q10 | Q90 | |
| Cu | 0.24 | −0.04 | 0.30 | 0.24 | 0.05 | 0.35 |
| Cs | −0.15 | −0.40 | −0.44 | 0.00 | −0.19 | −0.31 |
| Bo | 0.11 | 0.06 | 0.28 | 0.41 | 0.46 | 0.54 |
| Pr | −2.65 | −3.48 | −0.64 | 0.04 | 0.09 | 0.28 |
| BS | 0.49 | 0.17 | 0.47 | 0.67 | 0.52 | 0.58 |
| Ma | 0.70 | 0.72 | 0.65 | 0.82 | 0.80 | 0.75 |
| Ba | 0.61 | 0.44 | 0.68 | 0.70 | 0.59 | 0.76 |
| Co | 0.64 | 0.08 | 0.73 | 0.89 | 0.35 | 0.94 |
| River | 2nd-Order MR | 3rd-Order MR | ||||
|---|---|---|---|---|---|---|
| Q50 | Q10 | Q90 | Q50 | Q10 | Q90 | |
| Cu | 0.60 | 0.63 | 0.52 | 0.61 | 0.65 | 0.54 |
| Cs | 0.49 | 0.43 | 0.44 | 0.53 | 0.46 | 0.48 |
| Bo | 0.56 | 0.62 | 0.55 | 0.67 | 0.73 | 0.69 |
| Pr | 0.22 | 0.40 | 0.19 | 0.54 | 0.62 | 0.56 |
| BS | 0.71 | 0.70 | 0.58 | 0.79 | 0.75 | 0.72 |
| Ma | 0.81 | 0.79 | 0.82 | 0.88 | 0.84 | 0.87 |
| Ba | 0.76 | 0.80 | 0.69 | 0.81 | 0.84 | 0.75 |
| Co | 0.78 | 0.83 | 0.56 | 0.93 | 0.96 | 0.65 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nugroho, A.R.; Tamagawa, I.; Harada, M. Spatiotemporal Analysis on the Teleconnection of ENSO and IOD to the Stream Flow Regimes in Java, Indonesia. Water 2022, 14, 168. https://doi.org/10.3390/w14020168
Nugroho AR, Tamagawa I, Harada M. Spatiotemporal Analysis on the Teleconnection of ENSO and IOD to the Stream Flow Regimes in Java, Indonesia. Water. 2022; 14(2):168. https://doi.org/10.3390/w14020168
Chicago/Turabian StyleNugroho, Adam Rus, Ichiro Tamagawa, and Morihiro Harada. 2022. "Spatiotemporal Analysis on the Teleconnection of ENSO and IOD to the Stream Flow Regimes in Java, Indonesia" Water 14, no. 2: 168. https://doi.org/10.3390/w14020168
APA StyleNugroho, A. R., Tamagawa, I., & Harada, M. (2022). Spatiotemporal Analysis on the Teleconnection of ENSO and IOD to the Stream Flow Regimes in Java, Indonesia. Water, 14(2), 168. https://doi.org/10.3390/w14020168






